The conventional experimental method for the data acquisition on the predominant orientations of the crystal planes is the measurement of pole figures (PFs), which describes the distribution of the normals to the crystal planes. The most exhaustive information on texture is given by the orientation distribution function (ODF) of crystallites. In this case, a possible approach to eliminate difficulties, which are related to nonuniqueness of the solution and its instability to experimental errors, is to investigate the solution in a particular class and optimize the parameters of the texture model using regularization [1, 2].

The aim of this work is to compare the texture of the materials under study possessing high and low symmetry of lattice and specimen [5–7] of the methods for ODF restoration from PFs, namely, the method of texture components using the radial normal distributions with various spreading [1–3] and the method of superposition of a large number of radial normal distributions with an identical small spreading [1, 2, 4].

The texture was studied on the specimens of the median section of the hot-pressed band from Mg–4.5% Nd magnesium alloy. (Because the material possesses low lattice and specimen symmetry, the use of other methods for modeling of the ODF (along with those mentioned above) for the existing set of experimental data is almost impossible.) Primary information was obtained in the form of incomplete lines of PFs {0004}, {10\(\overline{1}\)0}, {11\(\overline{2}\)0}, {10\(\overline{1}\)1}, {10\(\overline{1}\)2}, and {10\(\overline{1}\)3} recorded on a DRON-7 X-ray diffractometer in CoKα radiation (the scanning step by radial and azimuthal angles is 5° and the range is 0°–70° of radial angle). In order to increase the exactness of the initial experimental data, the background on the left and right was recorded by the 2θ angle with the subsequent averaging for each PF (the scanning step and the range are the same).

Before the ODF restoration, the mean background intensity was subtracted from the PF intensity at the corresponding measurement points. The drop of the intensity at the peripheral part of PF due to the defocusing effect was corrected using correction coefficients, which were calculated from the X-ray recording conditions of PF [8]. (PFs were not normalized and the values of unknown adjustment coefficients were obtained during optimization.)

Both of the considered methods are based on the representation of ODF in the form of a superposition of several standard functions (texture components and ideal orientations with spreading):

$$f(g) = \sum\limits_{K = 1}^K {{{I}_{k}}{{f}_{k}}(g,{{g}_{{0k}}},\varepsilon _{k}^{2})} ,$$
((1))

where K is the number of standard functions, Ik and g0k are the volume fraction and the position of the center of kth component, and εk is the spreading parameter.

The method of texture components suggests that the ODF can be represented by the superposition of peak (Kp) and axial (Ka) components.

Each peak component becomes maximal at point g0 of the orientation space, while spreading around the maximum is determined by the parameter ε:

$$\begin{gathered} {{f}^{p}}(g,{{g}_{0}},{{\varepsilon }^{2}}) \\ = \sum\limits_{l = 0}^\infty {(2l + 1)\exp [ - l(l + 1){{\varepsilon }^{2}}]\frac{{\sin [(2l + 1)\omega ({{g}_{0}},{{g)} \mathord{\left/ {\vphantom {{g)} 2}} \right. \kern-0em} 2}]}}{{\sin [\omega ({{g}_{0}},{{g)} \mathord{\left/ {\vphantom {{g)} 2}} \right. \kern-0em} 2}]}}} , \\ \end{gathered} $$
((2))

where

$${{\omega }_{k}}({{g}_{0}},g) = \arccos \{ 0.5[{\text{Tr}}(g_{0}^{{ - 1}}g) - 1]\} $$
((3))

is the orientational distance. In this case, full width at half maximum b [9] is related to the spreading parameter using the following relation: b ≈ \(4\varepsilon \sqrt {\ln 2} .\)

The axial component of the radial normal distribution represents the averaging of the peak component during rotation around the fixed axis and appears as follows:

$$\begin{gathered} {{f}^{a}}(g,{{g}_{0}},{{\varepsilon }^{2}},{\mathbf{n}}) \\ = \sum\limits_{l = 0}^\infty {(2l + 1)\exp [ - l(l + 1){{\varepsilon }^{2}}]{{P}_{l}}(g{\mathbf{n}}{{g}_{0}}{\mathbf{n}}).} \\ \end{gathered} $$
((4))

It achieves maximum at a particular circumference in the orientation space, which is determined by the axis of the component n and rotation g0 (one of the possible positions of the maximum of the distribution on the circumference), which is determined by the constant angular distance ρ from the axis of the component (apex angle).

The parameter ε, as in the case of the peak component, describes the spreading near the maximum. The model ODF is averaged over all equivalent rotations in accordance with the lattice symmetry of the specimen and appears as follows:

$$\begin{gathered} {{f}^{{{\text{model}}}}}(g) = {{I}_{0}} + \left[ {\sum\limits_{k = 1}^{{{K}_{p}}} {{{I}_{k}}f_{k}^{p}(g,{{g}_{{0k}}},\varepsilon _{k}^{2})} } \right] \\ + \,\,\left[ {\sum\limits_{k = {{K}_{p}} + 1}^{{{K}_{p}} + {{K}_{a}}} {{{I}_{k}}f_{k}^{a}(g,{{g}_{{0k}}},\varepsilon _{k}^{2},{{{\mathbf{n}}}_{k}})} } \right], \\ \end{gathered} $$
((5))

where I0 and Ik are the fractions of the background component (textureless component) and kth component (peak or axial) and \(\sum\nolimits_{k = 0}^{{{K}_{p}} + {{K}_{a}}} {{{I}_{k}}} = 1.\)

Let us assume that the reciprocal-lattice vector hλ specifies the direction in the crystallite, while y specifies the direction in the specimen. The model ODF (5) generates a PF of the following form:

$$\begin{gathered} P_{{{{h}_{\lambda }}}}^{{{\text{model}}}}({\mathbf{y}}) = {{I}_{0}} + \left[ {\sum\limits_{k = 1}^{{{K}_{p}}} {{{I}_{k}}{{P}^{{p,k}}}({{{\mathbf{h}}}_{\lambda }},{\mathbf{y}},{{g}_{{0k}}},\varepsilon _{k}^{2})} } \right] \\ + \,\,\left[ {\sum\limits_{k = {{K}_{p}} + 1}^{{{K}_{p}} + {{K}_{a}}} {{{I}_{k}}{{P}^{{a,k}}}({{{\mathbf{h}}}_{\lambda }},{\mathbf{y}},{{g}_{{0k}}},\varepsilon _{k}^{2},{{{\mathbf{n}}}_{k}})} } \right]. \\ \end{gathered} $$
((6))

In this case, the peak and axial components of the PF are represented by Legendre polynomials:

$$\begin{gathered} {{P}^{p}}({{{\mathbf{h}}}_{\lambda }},{\mathbf{y}},{{g}_{0}},{{\varepsilon }^{2}}) \\ = \sum\limits_{l = 0(2)}^\infty {(2l + 1)} \exp [ - l(l + 1){{\varepsilon }^{2}}]{{P}_{l}}(({{{\mathbf{h}}}_{\lambda }}{{g}_{0}}{\mathbf{y}})), \\ \end{gathered} $$
((7))
$$\begin{gathered} {{P}^{a}}({{{\mathbf{h}}}_{\lambda }},{\mathbf{y}},{{g}_{0}},{{\varepsilon }^{2}},{\mathbf{n}}) \\ = \sum\limits_{l = 0(2)}^\infty {(2l + 1)\exp [ - l(l + 1){{\varepsilon }^{2}}]{{P}_{l}}({\mathbf{yn}}){{P}_{l}}({{{\mathbf{h}}}_{\lambda }}{{g}_{0}}{\mathbf{n}}).} \\ \end{gathered} $$
((8))

The ODFs were simulated by the optimization of the parameters {I0, Ik, g0k, \(\varepsilon _{k}^{2},\)nk} (5); for this purpose, the minimization of the weighted residual between the sets of experimental {\({{P}_{{{{{\mathbf{h}}}_{\lambda }}}}}\exp ({\mathbf{y}}),\) λ = 1…Λ} and model PFs (6) was used:

$$\begin{gathered} {\text{re}}{{{\text{s}}}^{2}} = \sum\limits_{\lambda = 1}^\Lambda {\sum\limits_{{\mathbf{y}} \in {{S}^{2}}} {W({\mathbf{y}})} } \left[ {\left( {{{N}_{\lambda }}P_{{{{{\mathbf{h}}}_{\lambda }}}}^{{\exp }}({\mathbf{y}})} \right.} \right. \\ {{\left. {\left. { - \,\,P_{{{{{\mathbf{h}}}_{\lambda }}}}^{{{\text{model}}}}({\mathbf{y}},\{ {{I}_{0}},{{I}_{k}},{{g}_{{0k}}},\varepsilon _{k}^{2},{{{\mathbf{n}}}_{k}}\} )} \right)} \right]}^{2}} \to \min , \\ \end{gathered} $$
((9))

where {W(y)} is the specified set of weights determining the significance of the measurement point and {Nλ, λ = 1…Λ} are unknown adjusting coefficients of PF.

The minimization of residual (9), which is related to the problems of nonlinear optimization, is solved iteratively. The number of textural components; their type; and initial position of centers, axes, and spreading parameters are determined interactively in graphical form. This implies that the participation of the researcher is necessary in this approach at the initial stage, who evaluates the initial values of the parameters. At the following stage, linear characteristics (weights) and adjusting coefficients are optimized [10, 11]. The resulting normal systems of equations are usually ill-conditioned owing to the strong overlap of the components. Therefore, at this stage, regularization was used along with the pseudo-inverse algorithm of the array of the normal system. The threshold of remaining singular values was chosen in accordance with the degree of experimental errors. Then, nonlinear optimization of other parameters of the model was carried out using the Levenberg–Marquardt regularization method [11].

The validity of the model was evaluated using the parameters [12]

$$RP(\Delta ) = \frac{1}{{J(\Delta )}}\sum\limits_{j = 1}^{J(\Delta )} {\left| {\frac{{P_{{{{{\mathbf{h}}}_{\lambda }}}}^{{\exp }}({{{\mathbf{y}}}_{j}}) - P_{{{{{\mathbf{h}}}_{\lambda }}}}^{{{\text{model}}}}({{{\mathbf{y}}}_{j}})}}{{P_{{{{{\mathbf{h}}}_{\lambda }}}}^{{\exp }}({{y}_{j}})}}} \right|} \times 100\% ,$$
((10))

as well as through the calculation of the square of residual \({\text{res}}_{\lambda }^{2}\) individually for each PF and the standard deviation of residuals σλ [10]:

$$\begin{gathered} {\text{res}}_{\lambda }^{2} = \sum\limits_{{\mathbf{y}} \in {{S}^{2}}} {W({\mathbf{y}})} \left[ {{{N}_{\lambda }}P_{{{{{\mathbf{h}}}_{\lambda }}}}^{{\exp }}({\mathbf{y}})} \right. \\ {{\left. { - \,\,P_{{{{{\mathbf{h}}}_{\lambda }}}}^{{{\text{model}}}}({\mathbf{y}},{{I}_{0}},{{I}_{k}},{{g}_{{0k}}},\varepsilon _{k}^{2},{{{\mathbf{n}}}_{k}})} \right]}^{2}}, \\ {{\sigma }_{\lambda }} = \frac{{{\text{re}}{{{\text{s}}}_{\lambda }}}}{{\sqrt n }}, \\ \end{gathered} $$
((11))

where n is the volume of the data measured on PF.

The method of superposition of a large number of radial normal distributions is represented by the superposition (1) of standard distributions with equivalent small spreading ε in contrast with the method of texture components:

$$f(g) = \sum\limits_{k = 1}^K {{{I}_{k}}{{f}^{s}}(g,{{g}_{{0k}}},\varepsilon ).} $$
((12))

The centers of standard functions g0k are located on a three-dimensional network in orientational space. As f s(g, g0k, ε), the superposition of symmetrized peaks with the form (2) symmetrized according to the lattice and specimen symmetry was chosen. In calculations, we considered that function f s(g, g0k, ε2) in the case of narrow peaks (ε < 0.3) appears in the following analytical approximation [1]:

$$\begin{gathered} {{f}^{s}}(g,{{g}_{0}},\varepsilon ) \equiv f(\omega ,s) \\ = \left[ {\frac{{\sqrt \pi }}{{{{\varepsilon }^{3}}}}\exp \frac{{{{\varepsilon }^{2}}}}{4}{\text{erfc}}\frac{\varepsilon }{2} + \frac{1}{{{{\varepsilon }^{2}}}}} \right]\frac{{{\omega \mathord{\left/ {\vphantom {\omega 2}} \right. \kern-0em} 2}}}{{\sin ({\omega \mathord{\left/ {\vphantom {\omega 2}} \right. \kern-0em} 2})}}\exp \left( { - \frac{{{{\omega }^{2}}}}{{4{{\varepsilon }^{2}}}}} \right) \\ \end{gathered} $$
((13))

[ω is the orientational distance (3)].

The PFs corresponding to the distribution (13) appear as follows [1]:

$$\begin{gathered} {{P}^{s}}({\mathbf{h}},{\mathbf{y}},{{g}_{0}},\varepsilon ) \equiv P(\theta ,\varepsilon ) \\ = \frac{1}{{2{{\varepsilon }^{2}}}}\left[ {\exp \left( { - \frac{{{{\theta }^{2}}}}{{4{{\varepsilon }^{2}}}}} \right) + \exp \left( { - \frac{{{{{(\pi - \theta )}}^{2}}}}{{4{{\varepsilon }^{2}}}}} \right)} \right], \\ \end{gathered} $$
((14))

where h and y are the directions in crystallite and specimen, respectively, and θ = arccos(hg0y).

Eq. (14) approximates Eq. (7) well. Thus, we have the function as the model of PF

$$P({\mathbf{h}},{\mathbf{y}}) = \sum\limits_{k = 1}^K {{{I}_{k}}{{P}^{s}}({\mathbf{h}},{\mathbf{y}},{{g}_{k}},\varepsilon ).} $$
((15))

The spreading parameter ε is determined by the angular distance between the lattice points. Standard functions should overlap at least at half-height of the peaks. It is clear that the number of standard functions should be very large (their spreading should be significantly less than the distance of each component of real texture). In this case, they cannot be considered the components of texture function (each component of texture function is represented as the superposition of standard functions).

In order to determine unknown weights Ik, we have the system of linear equations whose matrix consists of the coefficients of the effect of standard function fs(g, g0k, ε) on the pole density. During its solution, an iterative projection method was used [13, 14]. At ill-conditioned matrix of the system, it provides regularization of the solution by one of the smoothness functionals \(\left( {\sum {I_{k}^{2} \to \min } } \right)\) and additionally considers the condition of positivity of peak amplitudes.

The initial parameters of the model of the specimen in the method of texture components (Table 1) was chosen interactively.

Table 1.   Initial approximations of the parameters of the model
Full size table

As a result of subsequent optimization, it was determined that the pole density of the specimen is fit by the superposition of seven axial components and a textureless component (Table 2). In Fig. 1, experimental PFs {0004} and {11\(\overline{2}\)0} and their models prepared by the method of components are given.

Table 2.   Parameters of the model in the method of texture components
Full size table
Fig. 1.
figure 1

(a, c) Direct experimental and (b, d) calculated PFs {0004} and {11\(\overline{2}\)0} using the method of components (RD is the rolling direction and TD is the transverse direction).

Full size image

Statistical parameters of the models are given in Table 3 (errors correspond to the measurement error of experimental PFs).

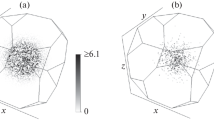
Table 3.   Statistical parameters of the models
Full size table

In Fig. 2, the sections of ODF obtained using the methods under study are given. It is evident that both methods give similar results; however, the capacity of the textureless component of ODF obtained by superposition is significantly less, while the maximum of ODF is less than the analogous maximum derived from the method of textural components.

Fig. 2.
figure 2

ODFs calculated from PFs using (a) the method of components (fmin = 0.15 and fmax = 9.20) and (b) a large number (3000) of orientations (fmin = 0.04 and fmax = 8.70).

Full size image

This is caused by the fact that each textural component in the superposition method, as previously mentioned, is the sum of a large number of standard distributions. This can be stated about the textureless component, which is also approximated by the sum of the distributions with almost equivalent weights. It is reasonable to further include the constant corresponding to the volume fraction of the textureless component in the model function in order to develop the superposition method (the parameter is linear and can be determined iteratively, as well as other weights). A great advantage of this method is that it is completely automated.

Using the method of texture components, the first stage of optimization, which consists of the choice of the number of textural components and the initial values of nonlinear parameters of the model, cannot be formalized and requires the participation of the researcher. Further iterations occur in automatic mode. However, the method provides the description of complex texture formations using a small number of parameters which are necessary for the further study of the properties of polycrystal materials.

During the generation of the ODF model of the specimen under study, the experimental data were specified. In this case, the parameters of the model remained stable and only the parameters which were used for the evaluation of validity were varied. The model generated using the superposition method varied more significantly, though with the retention of intrinsic features of texture. A greater stability of the model in the method of texture components is rationalized by the small number of model parameters.

Thus, ODFs calculated using both methods agree well with each other. The considered methods for the ODF restoration can be employed during the study of the texture of the materials possessing low symmetry of lattice and specimen. In this case, the main advantage of the method of components is that the quantitative description of texture is achieved by using a limited number of orientations in the form of radial normal distributions with different spreading and volume fraction, which facilitates the analysis of the evolution of texture formation of materials during plastic deformation and heat treatment. However, the choice of initial values of textural components is not formalized and requires the direct participation of the researcher. On the contrary, the method of superposition of a large number of radial normal distributions is completely automated.