Integrated preprocessing techniques with linear stochastic approaches in groundwater level forecasting

Abstract

Accurate modeling of groundwater level (GWL) is a critical and challenging issue in water resources management. The GWL fluctuations rely on many nonlinear hydrological variables and uncertain factors. Therefore, it is important to use an approach that can reduce the parameters involved in the modeling process and minimize the associated errors. This study presents a novel approach for time series structural analysis, multi-step preprocessing, and GWL modeling. In this study, we identified the time series deterministic and stochastic terms by employing a one-, two-, and three-step preprocessing techniques (a combination of trend analysis, standardization, spectral analysis, differencing, and normalization techniques). The application of this approach is tested on the GWL dataset of the Kermanshah plains located in the northwest region of Iran, using monthly observations of 60 piezometric stations from September 1991 to August 2017. By removing the dominant nonstationary factors of the GWL data, a linear model with one autoregressive and one seasonal moving average parameter, detrending, and consecutive non-seasonal and seasonal differencing were created. The quantitative assessment of this model indicates the high performance in GWL forecasting with the coefficient of determination (R²) 0.94, scatter index (SI) 0.0004, mean absolute percentage error (MAPE) 0.0003, root mean squared relative error (RMSRE) 0.0004, and corrected Akaike's information criterion (AICc) 151. Moreover, the uncertainty and accuracy of the proposed linear-based method are compared with two conventional nonlinear methods, including multilayer perceptron artificial neural network (MLP-ANN) and adaptive neuro-fuzzy inference systems (ANFIS). The uncertainty of the proposed method in this study was ± 0.105 compared to ± 0.114 and ± 0.126 for the best results of the ANN and the ANFIS models, respectively.

Introduction

In recent decades, challenging factors such as population growth, climate factors, as well as socio-economic developments have led to an increase in demand for water resources (Asnaashari et al. 2015; Betts et al. 2015; Salek et al. 2018; Salimi et al. 2020). The exploitation of groundwater resources is an emerging problem due to water scarcity in many parts of the world (Motiee et al. 2006; Perera et al. 2013; Harvey et al. 2015; Nalley et al. 2019). Thus, the need for integrated management of these resources is essential including groundwater level prediction.

Iran is in a semiarid region. The average annual rainfall is about one-third of the world's average rainfall. However, in the Kermanshah province of Iran, agricultural activities dominate other economic activities. Factors such as drought and inefficient water management policy have resulted in a irrigation water ban more than 30% of the plains in the province, meaning that groundwater extraction is forbidden in these plains (Taheri et al. 2016). Therefore, the long-term trends of groundwater level changes in this province are of particular importance. The groundwater models are the main traditional tools in forecasting groundwater level (GWL). The need for many input variables in these traditional models is the main drawback of using them. In practice, the available data are often limited, and often providing accurate forecasts is more important than understanding underlying theory. Hence, a new generation of data-driven machine learning models must be considered as suitable alternatives to the traditional physically based models.

Groundwater level changes due to the effect of various parameters such as hydrological variables, geology, and soil science are considered a highly nonlinear and complex problem (Coppola et al. 2003; Daliakopoulos et al. 2005). Recently, different artificial intelligence (AI) and machine learning-based techniques have been applied to forecast the groundwater level, including artificial neural network (ANN) (Bonakdari et al. 2020; Emamgholizadeh et al. 2014; Gong et al. 2015; Golami et al. 2019; Moosavi et al. 2013; Nourani and Mousavi 2016; Mukherjee and Ramachandran 2018), adaptive neuro-fuzzy inference systems (ANFIS) (Emamgholizadeh et al. 2014; Fallah-Mehdipour et al. 2013; Gong et al. 2015; Moosavi et al. 2013; Nourani and Mousavi 2016; Stajkowski et al. 2020a, b; Zare and Koch 2018).

Like the other techniques, AI-based techniques have many advantages, such as high-speed modeling and simplicity of usage, and disadvantages, such as low generalizability and overtraining. GWL variations prediction is considered a nonlinear problem. So, to solve this problem, nonlinear methods are required. In modeling a time series, the lack of understanding of the required problem may cause inappropriate input combinations to be chosen, and consequently, modeling with acceptable accuracy is not provided. Also, recent studies show that accurate knowledge of the problem can have a considerable impact on the modeling process (Moeeni et al. 2017a, 2017b). Recent studies suggest that even some nonlinear problems can be modeled linearly (Bonakdari et al. 2018; Ebtehaj et al. 2019; Zeynoddin et al. 2019; Zeynoddin and Bonakdari 2019).

Bonakdari et al. (2018) presented a stochastic model based on soil temperature forecasting at two stations and different depths (four different time series). They declared that the proposed methodology outperformed nonlinear ANN and ANFIS models so that it provides a precise model and has less complexity than nonlinear models (i.e., ANN and ANFIS). To predict soil temperature at different depths, Zeynoddin et al. (2019) employed a linear method based on recognizing deterministic elements in a studied time series. Results demonstrated that the proposed linear model has better performance than nonlinear models in terms of accuracy and simplicity. Zeynoddin et al. (2020) and Ebtehaj et al. (2019) also responded to a fundamental question about lake level forecasting. Is lake level forecasting solvable as a linear problem, or it needs to be modeled nonlinearly? They evaluated their suggested generalized linear stochastic model for different time intervals of case study lake levels. By comparing results with several AI methods, they claimed that accurate and desirable results can be attained by using a suitable approach.

Understanding and evaluating the time series structure is a crucial step before embarking on data modeling. This step becomes paramount when linear models. No preprocessing method alone can completely eliminate nonstationary factors. Hence it is required to assess the data structure in multiple levels and apply multi-preprocessing methods. This point is less addressed in previous studies. Therefore, in this study, a new methodology is presented based on which the groundwater time series is analyzed, preprocessed, and modeled. This methodology has not yet been applied to groundwater time series to the best knowledge of the authors.

To develop the proposed methodology, the new linear stochastic-based method and the integrated multi-step evaluation and preprocessing approaches are coded in the MATLAB environment. This novel set of techniques and approaches are applied to groundwater level (GWL) time series forecasting-based one-step-forward values. The introduced methodology includes two approaches: (I) a one- and two-step and (II) a two- and three-step preprocessing techniques. In the first approach, each method of differencing, spectral analysis, standardization, and detrending is employed on time series separately to stationarize it as a one-step preprocessing. Detrending, meanwhile, is applied before the other mentioned methods, as the two-step preprocessing in the first approach. In the second approach, following the steps of the first approach, a normalization transform is applied. Afterward, in case of meeting the conditions, stochastic modeling is performed. Model residual white noise is investigated by cumulative periodogram and Ljung-Box tests.

Besides, the results of the proposed stochastic-based methodology are compared with the two most popular AI-based techniques (i.e., ANFIS and ANN) using uncertainty analysis and different statistical indices. The reason for using these two methods is the acceptable performance of them in groundwater level forecasting: (1) Successful application of the ANN and ANFIS as two well-known machine learning techniques in modeling groundwater level forecasting in the recent studies (He et al. 2014; Jafari et al. 2021; Seifi et al. 2020; Shirmohammadi et al. 2013, Vetrivel and Elangovan 2017). (2) High performance of these models in solving nonlinear problems, especially in hydrology. (3) Existing a low number of adjustable parameters compared with other machine learning techniques so that developing a model with less adjustable parameters makes the model simpler and reduces the model complexity.

Regional description and hydrological data

With an area of 24,998 km², Kermanshah accounts for 1.5% of the area and 2.44% of the country's population. Despite historic attractions and mines in the latest industrial rankings in Iran, this city has been fallen within the undeveloped provinces. In terms of climate diversity, the province presents a great variety, with tropical weather in the west, cold and mountainous weather in the east, and moderate climate in central regions. Due to the climatic conditions, numerous crops are produced in this province, and most of the province's economic income is earned in the same way. Multiple droughts (Moradi et al. 2016); the pattern of inappropriate use of water consumption over the years; and the lack of legislation and inefficient management have led to the fact that agricultural activities and water extractions are prohibited in 8 plains from the 23 plains in the province during the year 2017–2018 (Taheri et al. 2016). Influenced by the province's severe dependency on the agricultural industry and the problems introduced, a prerequisite is the study of the plains groundwater conditions, forecasting, and management of consumption patterns (Soltani and Dadashi 2013).

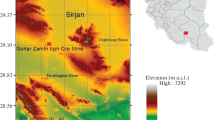
Groundwater data of Kermanshah plain were collected monthly from 60 piezometric stations from September 1991 to August 2017. Choosing the stations, long-term statistics (minimum 26 years), the lowest errors, and missing data are considered. The area, location, and coordinates of the stations are illustrated in Fig. 1. After reviewing and interpolating the data of stations that did not have statistics by a suitable interpolation method, the unit hydrograph of the Kermanshah plain's groundwater level was prepared, as shown in Fig. 2. The methods of interpolation and unit hydrograph extraction are explained in the methodology section. The 312-month’ unit hydrograph data are divided into two categories: train with 218 months, and test (94 months). The statistical characteristics of the hydrograph in these two data partitions are presented in Table 1.

Fig. 1

Map and location of piezometers of the studied area (Kermanshah plain, Kermanshah province, Iran)

Fig. 2

Unit hydrograph of Kermanshah plain, from Sep. 1991 to Aug. 2017 obtained from information of 60 stations gathering data in the Kermanshah plain

Table 1 Statistical Indices of GWL data, divided into Train and Test Parts

Methodology

Geostatistical concepts

Many problems and limitations have always accompanied information collection about the phenomena around us. One of the problems and limitations is the lack of access to the data collection sites, lack of good tools, devices, and operator errors. Hence, in many cases, the data provided are a sample of the entire data and always have defects and errors. Researchers have endeavored to find mathematical and statistical methods to eliminate these defects and transform hydrological phenomena into interpretable models using two general categories of deterministic and geostatistical techniques. Deterministic techniques are established on mathematical equations and measured points such as inverse distance weight (IDW), spline, local polynomial interpolation (Childs 2004; Ly et al. 2011). Geostatistical techniques are based on statistical relationships and concepts that include methods such as Kriging (simple, ordinary, universal) and empirical Bayesian kriging (Bhunia et al. 2016; Childs 2004; Goovaerts 2000). In the current study, the inverse distance weighted (IDW) method was employed to interpolate data of stations, which had missing records. The relationship of this method is presented below (Eq. 1):

$$Z_{i,j,\tau } = \frac{{\sum\limits_{i = 1}^{N} {\left( {{{X_{i,j,\tau } } \mathord{\left/ {\vphantom {{X_{i,j,\tau } } {D_{i}^{\alpha } }}} \right. \kern-\nulldelimiterspace} {D_{i}^{\alpha } }}} \right)} }}{{\sum\limits_{i = 1}^{N} {\left( {{1 \mathord{\left/ {\vphantom {1 {D_{i}^{\alpha } }}} \right. \kern-\nulldelimiterspace} {D_{i}^{\alpha } }}} \right)} }},$$

(1)

where Z_i,j,τ is the interpolated value, X_i,j,τ is the measured groundwater level in X_i station at month j and year τ, D_i is the distance between the station with missing data and the nearest reliable station, α is the weighting parameter, and N is the number of all sample. The α parameter is used to evaluate the data of stations with a different distance from the station. So, if the value of α > 1, the values of closer stations worth more than the farther stations. The α parameter for the IDW method is usually considered 2 in various studies (Goovaert 2000; Lloyd 2005; Ly et al. 2011). Therefore, α = 2 is considered in this study.

Another method of interpolation is the Thiessen polygon. In this method, an area is assigned to each set of points (in this study, piezometric stations), and the value of the un-sampled points is considered equal to the values of the sampled neighbor points. Thiessen polygon determines the regions of influence surrounding each piezometric station, and hence, sample points take the nearest point data (Tatalovich 2005). This method has many applications in hydrology, including calculating the precipitation amount, the distribution of spatiotemporal air temperature in a region, interpolation of missing data, and derivation of the unit hydrograph (Chuanyan et al. 2005; Fiedler 2003; Gorgij et al. 2017). After determining the influencing areas and obtaining the weight of each station data, the unit hydrograph using the following equation can be obtained (Eq. 2):

$$GWL(t) = Z_{i,j,\tau } \times \frac{{A_{i} }}{{\sum\limits_{i = 1}^{K} {A_{i} } }},$$

(2)

where Z_i,j,τ is the interpolated data, A_i is the area of each station, and K is the number of each station. GWL(t) is the unit hydrograph groundwater level at tth month.

Stochastic process concepts

A linear stochastic model as a subset of statistical models follows a set of rules and statistical relationships. The simplest stochastic model is autoregressive (AR(p)) model, which contains one non-seasonal autoregressive parameter (p). The seasonal autoregressive moving average (SARIMA(p,d,q)(P.D.Q)_ω) model is the general stochastic model with the seasonal and non-seasonal parameters. These models are established based on different situations and problems described in detail by Box et al. (2015). The related equations of the introduced stochastic model are presented in the Appendix section (equations A1–A3).

By using the historical series, the model can predict one-step forward values after calculating the model parameters with high accuracy. For modeling by sing stochastic methods, it is required to stationarize and normalize the studied time series distribution before modeling (the constancy of statistical characteristics, such as mean and standard deviation, means stationarity).

Since most hydrological phenomena such as GWL are non-stationery and lacking normal distribution, it is requisite to preprocess the time series with appropriate methods. Each time series dataset is made of 4 terms of the trend, jump, period, and stochastic terms [GWL (t) = Trend (t) + Jump (t) + Period (t) + Stochastic (t)]. Each one of the first three elements (deterministic terms) in a given time series dataset, alone or simultaneously together, can cause non-stationarity. Thus, to achieve accurate results by using the simplest methods, three stationarizing methods are used, including differencing (Diff), detrending (Dtr), standardization (Std), and spectral analysis (Sf) (Bonakdari et al. 2018). Non-seasonal differencing (Eq. A4) eliminates trend in mean and variance, jumps in mean, and eliminates periodic changes in variance. Trend analysis (Eq. A5), the other stationary time series method, can fit a linear equation to the dataset and eliminates the trend in the dataset by subtracting the value of the equation from the given time series (Jain and Kumar 2012). Standardization (Eq. A6), in addition to normalization of the data, eliminates jump and trend. Spectral analysis (Eqs. A7–A10) also transmits time series to the frequency domain and, by using Fourier series expansion, eliminates seasonal fluctuations (Zeynoddin et al. 2018). For equations A4–A10, please refer to Appendix.

Various methods have been offered to transform the distribution of time series, which do not follow the normal distribution. One of these methods is the normalization method presented by Manly (Stajkowski et al. 2020a, b), which is developed based on the Box-Cox transformation (Eq. A11, Appendix). This transformation can transform the time series with both positive and negative intervals and can convert data distribution to normal distribution, unlike the Box-Cox transformation, which works merely on the positive intervals.

There are several tests for assessing the time series's distribution, including the Jarque–Bera (JB) (Eq. A12) test. This test is a goodness-of-fit test, which compares the value of skewness and kurtosis of a given sample with the corresponding values in a normal distribution (Bai and Ng, 2005). The test’s equation is presented in Appendix (Eq. A12). If the JB value is less than its critical value (JB_CR = 5.99) or the corresponding probability (P_JB > 5%), then the normal time series distribution is normal.

Time series components investigation methods

To meet the two conditions of stochastic modeling, namely stationarity and the normal distribution of time series, it is essential to identify the time series components. Therefore, methods and tests are provided for this purpose. The first test that is applied to any time series is the KPSS (Eqs. A13–A15) test (Murat et al. 2018). This test examines the overall stationarity of time series. If the series is not stationary, it is necessary to examine the reasons for non-stationarity (finding deterministic terms) by other methods. In the KPSS test, the time series (GWL_t) is assumed to be a regression equation with three parts: deterministic term (r_t), trend term, the random term (β_t), and stationarity error (ε_t), as follows: GWL_t = r_t + β_t + ε_t. In this equation, r_t = r_t-1 + u_i, r_t is a random walk, u_i represents independent variables with the same distribution, β_t is the deterministic term of the trend, ε_t is stationary errors. The latter equations of the test are presented in Appendix.

The existence of seasonal or non-seasonal trends is one of the reasons for having a nonstationary time series. The Mann–Kendall (M_K) test (Eq. A16–A18) allows us to identify the trend in time series (Jain and Kumar 2012). The above relationship is employed to detect the ongoing changes in time series. If these changes have occurred seasonally and have created a seasonal trend, the seasonal Mann–Kendall (S_MK) test will be used (Eq. A19–A21). If the probability corresponding to these tests' statistic is greater than 0.05 (significant level), then the series has no trend. Some natural phenomena occur suddenly, which are named jumps, causing these changes to occur as a climb or sudden descent into the series. Usually, such changes can be detected intuitively in the time series. Still, there are tests to distinguish these variations, including the Mann–Whitney (MW_U) test, a non-parametric test, as presented in Appendix (Eq. A23) (Clarke et al. 2011). If the values of MW_U become higher than the confidence level α (α = 1%), the assumption of the equal distribution of series is confirmed, and the main time series is jump-free.

The proposed stochastic-based methodology for GWL modeling

As mentioned earlier, the main goal is to accurately forecast Kermanshah's groundwater level by using the simplest methods. Furthermore, the effect of normalization on the modeling results which, were scrutinized in previous work, is also measured in this study. In Fig. 3, the modeling process is presented thoroughly. The figure shows that preparation of the Kermanshah plain groundwater level time series is performed, before defining the two approaches of preprocessing and modeling. In the first approach, preprocessing is done by using stationarizing methods. In this approach, stationary is divided into two stages A and B. In step A, each one of the stationary methods is applied individually.

Fig. 3

Flowchart of GWL modeling using proposed integrated preprocessing techniques with linear stochastic approaches

In step B, the trend is omitted primarily, and with the help of the other two methods, then the series is stationarized. In the second approach, all stages of the first approach are investigated before the normalization transform being applied to the series. After performing these preprocesses and verifying stationarity tests' conditions, the time series generated by the preprocessing methods are modeled, and the results are evaluated using various indices. Eventually, the best approach and methodology for modeling groundwater level in the Kermanshah plain is selected.

Verification indices to evaluate each model

To examine the performance of obtained results in GWL prediction using the proposed method in this study, a set of various indices, including a coefficient of determination (R², Eq. 3), is used. Comparing different models, it is compulsory to consider the model's performance in different conditions by presenting different indices. In addition to R², the scatter index (SI, Eq. 4), mean absolute percentage error (MAPE, Eq. 5), and root mean squared relative error (RMSRE, Eq. 6) are also used. In addition, to examine the simplicity with goodness-of-fit of developed models, the corrected Akaike's information criterion (AICc, Eq. 7) (Burnham & Anderson 2002; Stajkowski et al. 2020a, b) is used as well.

$$R^{2} = \left( {\frac{{\left( {\sum\limits_{i = 1}^{n} {\left( {GWL_{obs,i} - \overline{GWL}_{obs,i} } \right)\left( {GWL_{P,i} - \overline{GWL}_{P,i} } \right)} } \right)}}{{\sqrt {\sum\limits_{i = 1}^{n} {\left( {GWL_{obs,i} - \overline{GWL}_{obs,i} } \right)^{2} } \sum\limits_{i = 1}^{n} {\left( {GWL_{P,i} - \overline{GWL}_{P,i} } \right)^{2} } } }}} \right)^{2}$$

(3)

$$SI = \,\frac{{\sqrt {\frac{1}{n}\sum\limits_{i = 1}^{n} {\left( {GWL_{obs,i} - GWL_{P,i} } \right)^{2} } } }}{{\overline{GWL} }}$$

(4)

$$MAPE = \frac{100}{n}\sum\limits_{i = 1}^{n} {\left( {\frac{{\left| {GWL_{Obs,i} - GWL_{P,i} } \right|}}{{GWL_{Obs,i} }}} \right)}$$

(5)

$$RMSRE = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^{n} {\left( {\frac{{GWL_{Obs,i} - GWL_{P,i} }}{{GWL_{Obs,i} }}} \right)^{2} } }$$

(6)

$$AICc = \frac{{2kn + \left( {n\ln (\sigma_{\varepsilon }^{2} )(n - k - 1)} \right)}}{n - k - 1},$$

(7)

where k and n are the number of parameters and the months, respectively, σ_ε is the residuals’ standard deviation, GWL_obs,i and GWL_P,_i are the ith value of observed and predicted groundwater level. The accuracy of the time series modeling is another index of the conditions that should be investigated after modeling the time series, which is done by analyzing the independence of the model's residual. The Ljung-Box test (Eq. 8) is employed to verify the independence of the residuals as follows (Dabral and Murry 2017):

$$Q_{Ljung - Box} = \left( {N^{2} + 2N} \right)\sum\limits_{h = 1}^{m} {\frac{{r_{h} }}{N - 1}}.$$

(8)

In this relationship, r_h is the residual coefficient of the autoregression (ε_t) in delay h, N is the number of samples, the value of m is also equal to ln(N). If the Ljung-Box test statistic value in the χ 2 distribution is greater than the α-level (in this case P_Q > α = 0.05), the residues series is white noise model is appropriate.

Results and discussion

Raw data preparing

After collecting and sorting the data of piezometric stations, stations with statistical defects were identified. There was a total of 326 months of statistical failure, accounting for less than 2% of the total data, comparing to the 18,720 months of recorded data by the 60 piezometric stations.

To use the IDW method to retrieve data from stations without statistics, 5 to 8 adjacent stations were chosen, which were assured of their data accuracy. These stations were located in all directions and at the nearest distances to stations with missing data. By measuring the distances and using the IDW method, the months that were not recorded for the groundwater level were rebuilt. Following, by determining the region of influence of each of the piezometric stations, using the Thiessen method, the weight of each station's data was determined, and the unit hydrograph of the groundwater level of Kermanshah plain was obtained (Fig. 2). ArcGIS software (ArcMap, V10.4.1) was used in all stages of the process.

Preprocessing procedure

Groundwater level unit hydrograph (UH) of Kermanshah plain was divided into two intervals train (first 218 months) and test (remaining 94 months). As shown in the UH graph (Fig. 2), the data have a downwards trend and seasonal fluctuations. In Fig. 4, the UH ACF and PACF charts were plotted. The existence of intense correlations between the primary 27 lags, trends, and fluctuations in the ACF graph can be seen. The PACF plot on the other hand has been negative after the first lag and then after 6 lags were completely damped. The spectral density can demonstrate the periodicity in time series and the lag of the periodic pattern in it. Therefore, the spectral density of the time series was drawn (Fig. 5) and it was observed that there is a peak in the spectral density graph at the frequency equivalent to the lag 12. This means the GWL data have a periodic pattern with a lag of 12.

Fig. 4

Autocorrelation and partial autocorrelation diagram of Unit Hydrograph (UH) of Kermanshah plain groundwater level

Fig. 5

Spectral density diagram of Unit Hydrograph (UH) of Kermanshah plain groundwater level

To ensure that the UH time series is nonstationary and deterministic terms exist in its structure, the numerical tests presented before were applied to the series, and then the mentioned preprocessing was applied on the time series. Table 2 provides information on the processes and test results. It should be noted that the time series of the Kermanshah plain groundwater unit hydrograph (KSH UH) has seasonal and non-seasonal trends (P_Mk and P_SMK < 0.05) and jumps (P_MWU < 0.01). Additionally, as mentioned before, periodicity with lag 12 exists. Subsequently, the series is nonstationary (P_KPSS < 0.05) with non-normal distribution (PJB < 0.05).

Table 2 Results of tests on the original GWL time series (KSH UH) and time series obtained from preprocessing techniques

In both approaches of part I of Table 2, only, the methods were able to reduce the impact of non-stationarity factors, in which trend analysis was initially applied. These methods even normalized the time series distribution (Dtr, Dtr-Std, Dtr -Sf, Dtr-Mn, Dtr-Std-Mn, Dtr-Sf-Mn). This indicates the effect of eliminating the trend as the dominant factor of non-stationarity at the beginning of the preprocessing and the time series stationarizing. However, the nonstationary factors were not completely eliminated (such as seasonal and periodic trends), which caused to low stationarity percentage in these methods (with an average of 10.35%). In the ACF and PACF graphs of these time series, the effect of the detrending was well observed, so that the lags’ correlations reduced up to a maximum of 5 non-seasonal lags and 3 seasonal lags. An example of the ACF chart is presented in Fig. 6 (due to the similarity of the results of the methods, presentation of others is avoided, and only Dtr-Sf-Mn is provided). In the first diagram (Dtr-Sf-Mn), the trend elimination effect is observed in the series. Other methods that could not stationarize the time series, their ACF and PACF charts were similar to the original UH series with high correlations and trends. With the preprocessing done in Part I for stationary methods, the SARIMA model (p, 0, q) (P, 0, Q)₁₂ was found to be suitable, and it is not possible to model other methods that are not stationary. The main feature of the SARIMA model is the seasonal and non-seasonal differencing within the model itself to stationary the time series when they are not. Therefore, all the time series generated by the proposed approaches were non-seasonal and then seasonal differenced of first order by lag 12. The results are provided in PART II and III of Table 2.

Fig. 6

Alternations of autocorrelation function (ACF) diagram of sample preprocessing technique (Dtr-Sf-Mn) before and after differencing

As shown in PART II of Table 2, all time series have been stationary after non-seasonal differencing, even the KSH UH time series, which is the original series with no preprocessing. Averaging the results of the tests, the probability corresponding to each statistic after the non-seasonal difference is significantly increased (average% P: M_K = 67.91, S_MK = 54.09, MW_U = 50.04, KPSS = 74.93, JB = 15.92). After the non-seasonal differencing, the ACF and PACF charts were calculated. The number of non-seasonal correlations considerably decreased (maximum 3 lags) and the number of seasonal correlations reached a maximum of 6 seasonal lags. This value for the preprocessed series that were stationary in PART I (Dtr-Std / Sf-Mn) means growth in seasonal correlations and, as a result, an increase in the order of seasonal parameters of the SARIMA model, which is not appropriate (Fig. 6). Since the modeling time increases and the number of model parameters and subsequently, the complexity of the model surges. Therefore, the preprocessed series also were seasonally differenced.

The results of applying both non-seasonal and seasonal differencings are provided in PART III of Table 2. It is observed that the percentage of probability corresponding to all test statistic has been reduced except for the stationarity test (KPSS). The increase in the probability associated with the KPSS test can be seen in reducing the effect of seasonal variations caused by non-seasonal differencing.

By drawing the ACF and PACF plots for all of the preprocessed time series, it was observed that the number of seasonal and non-seasonal correlations of the series has decreased so that the non-seasonal correlations are continued to a maximum of 3 and the seasonal correlations have reached 1 (Fig. 6). Figure 6 demonstrates the ACF plots preprocessing data with the Dtr-Sf-Mn method before and after the differencing. As seen in this graph b, the non-seasonal correlation decreased to 2 lags and the seasonal correlations on the other hand were increased to 6 lags. But after seasonal differencing (Fig. 6c), this problem also was solved, and all seasonal correlations were removed. Moreover, the magnitude of the non-seasonal correlation was reduced, so only 2 non-seasonal lags remained. After the non-seasonal and seasonal differences, although the probability of corresponding tests decreased, on the one hand, all series were stationary and, as against Part I, all percentages have increased averagely (average% P: M_K = 16.64 S_MK = 26.73 MW_U = 18.52 KPSS = 87.89). Methods Sf-Mn (%P: M_K = 71.77 S_MK = 76.63 MW_U = 20.32 KPSS = 95.19 JB = 0.01), Std-Mn (%P: M_K = 32.57 S_MK = 25.86 MW_U = 33.97 KPSS = 97.03 JB = 0.01) showed the best results.

Monthly groundwater modeling

By stationarizing time series after different preprocessings and determining the order of each of the parameters using the ACF and PACF graphs, the number of parameters and the differencing orders for one-step-ahead stochastic forecast was chosen as p and q = {0,1,2,3} and P and Q = {0,1}, d = 1 and D = 12. The modeling results are recapitulated in Table 3. In this table, the selected models and percentage of model accuracy indices are presented. The coefficient of determination and error indices for all models as well as modeling complexity indices (AICc) are very close and very good, which indicates the power of stochastic linear modeling methods in modeling time series of the groundwater level. However, the best and the worst R², SI, MAPE, and RMSE indices do not belong to specific models and the highest and lowest indices are scattered among different methods. Therefore, selecting a sole superior model based on these criteria is challenging. In this case, the evaluation is done based on the complexity of the models. In other words, since the models' accuracy is almost equal, the simplicity of the models can be considered an important parameter. Hence, the AICc index is used to select the superior model. The lower the value of this index, the better the model is obtained. The lowest value of AICc is related to the Dtr and Std method in the first approach (A).

Table 3 Superior stochastic models assessment results (indices%)

Using the cumulative periodogram of models residual series and locating all quantities within Kolmogorov–Smirnov 1% limits, it was ensured that by eliminating the periodicity in the models and the absence of leakage in the residual (Fig. 7; 4 samples of the methods). Moreover, Fig. 8 indicates the Ljung-Box test results that all values for the 60 primary lags are above the confidence level of 0.05, and the validity of the provided models is confirmed.

Fig. 7

Cumulative periodogram of sample superior models’ residuals

Fig. 8

Ljung-Box residuals test to check modeled series fitness of GWL

Comparison of the proposed linear-based methodology with MLP and ANFIS

To evaluate the proposed linear model's performance in comparison with nonlinear methods known in GWL prediction, stochastic models are examined and evaluated by ANN and ANFIS methods. To use these models, the input combinations should be defined first; in this study, the ACF presented in Fig. 4 is used. According to this diagram, four different models are presented that consider the effects of 1 to 4 previous lags in modeling (Table 5). After determining the models, the adjustable parameters for both ANN and ANFIS methods should be adjusted. It should be noted that the lack of precise selection of these parameters may significantly increase the complexity of the model or cause problems in achieving an optimal solution. Therefore, in this study, with the help of trail-and-error, the adjustable parameters were determined to present simple and accurate models (Table 4).

Table 4 The optimal values of adaptable parameters of ANN and ANFIS techniques

The results of nonlinear modeling for both methods and four proposed models, along with the best linear model, are provided in Table 5. In the table, the ANN (InV, HidN, OutV) model indicates the number of inputs as InV, the number of hidden neurons as HidN, and the output of the model is OutV. Additionally, the ANFIS (FCM, InV, MF) model indicates that the FCM method is used (Moradi et al. 2018). Considering simultaneously the accuracy and complexity of the model, the values of the models are adjusted. In the ANN method, the number of hidden layer neurons has a considerable effect on the accuracy of modeling and increasing of the complexity of the model as well, yet in the ANFIS method; the membership function (MF) has a considerable impact on the accuracy and simplicity of the model. It is noticeable that, for ANNs with 4 parameters, the simplest mode of a hidden layer neuron is considered simultaneously along with a model with good accuracy of 7 hidden layer neurons. Although the AICc value of the simpler model is better than the other one, the former is markedly lower in terms of accuracy. In ANFIS, MF = 2 and 3 are considered for all four simultaneously. By increasing the number of MFs, although the accuracy of the model has not increased considerably, its complexity grew significantly. Hence, the further increase of this parameter cannot be considered as an appropriate strategy for increasing the accuracy. The linear model presented has the highest R² value rather than all other models of nonlinear methods.

Table 5 Comparison of the proposed linear-based methodology with nonlinear techniques (indices%)

In addition to that, the linear method, also has the smallest amount of the AICc index, considering the complexity and accuracy simultaneously. Conspicuously, the least amounts of SI, MAPE, and RMSRE indices are for the linear method. Accordingly, the linear model presented more precisely than nonlinear models and is simpler than ANN and ANFIS.

Uncertainty analysis

The quantitative appraisal of the uncertainties in predicting the GWL is provided using the linear methodology for KSH UH versus ANN and ANFIS. The uncertainty analysis (UA) results are applied for test data. By calculating the individual forecasting error (IFE), the standard deviation of IFE (SDIFE), and the mean of IFE (MIFE) and using the Wilson score method without continuity correction, a confidence band across the predicted samples is defined (Azimi et al. 2018; Ebtehaj et al. 2018). The results of the UA for linear and nonlinear techniques are presented in Table 6. In addition to MIFE and SDIFE, the 95% forecasted error interval (FEI) and the width of the uncertainty band (WUB) are calculated and illustrated in this table, as well. It can be concluded that the proposed linear stochastic methodology has been implemented better than ANN and ANFIS methods with less calculated uncertainty. The positive MIFE for a linear method and three ANN-based models (ANN (1,18,1), ANN (3,13,1), ANN (4,7,1)), indicates overestimate the performance of these approaches in GWL predicting while the negative MIFE for the other models showed the underestimate performance of the desired models. The lowest SDIFE and WUB are 0.515 and ± 0.105, concerning the proposed stochastic linear methodology. Therefore, the UA shows the higher performance of the proposed method versus ANN and ANFIS as the two most popular nonlinear techniques in GWL forecasting.

Table 6 Uncertainty analysis for the linear methodology for ANN and ANFIS techniques

Advantages, limitations, and future improvements

The proposed linear stochastic-based methodology integrated with multi-step preprocessing techniques was developed in the current study for one-step-ahead groundwater level forecasting at Kermanshah plain. The main advantages of the proposed methodology are as: (1) Easy to implement. Application of the proposed multi-step preprocessing-stochastic method is straightforward so that anyone can apply them with basic knowledge of time series. (2) Less user-defined parameters. In the developed method, the user needs to adjust only the autoregressive and moving average parameters. (3) Less training time. The proposed method requires less training time than the AI methods. (4) Providing a simpler model with a smaller number of adjustable parameters through the training phase in comparison to AI methods. (5) The stochastic model parameters are predetermined, and the model offers an interpretable general equation that can be used for other data at different times. This feature provides a constant determined uncertainty which prioritizes it over machine learning methods that do not have a constant uncertainty.

Each method has its own disadvantages. The disadvantages of the proposed method are combining several different methods and steps to achieve the final results and the need for basic knowledge of time series. In the current study, knowing the structure of the time series is important. Therefore, the application of several tests and preprocessing techniques is required to provide a completely stationary series. In some cases, the data have a complex structure, similar to this study’s data, multiple evaluations, and consequently, multi-step preprocessing techniques are required. This can be considered a time-consuming process which some researchers may consider as a disadvantage. Also, preprocessing methods are not always capable of removing or reducing the impact of nonstationary factors properly. In this case, the results of the linear models will not be acceptable. To solve this problem some researchers, tend to AI models or their hybridization. Finally, it is recommended to investigate the impact of smoothing methods on preprocessing of GWL time series. Since the GWL data are periodic and trend, the smoothing methods Holt-Winters can be to the data. Moreover, since the deep learning models are developed to model and forecast the time series exclusively, the combination of the proposed methods with deep learning methods like the long-short-term-memory model is suggested.

Conclusions

We have presented a novel linear stochastic-based methodology for groundwater level forecasting and demonstrated its application for a case study in Kermanshah city, west of Iran. The proposed new methodology is an integration of preprocessing technique with linear stochastic approaches, including standardization, spectral analysis, normalization, and differencing techniques as one-, two-, and three-step preprocessing methodology.

The proposed methodology's performance was verified against the two most conventional nonlinear methods (i.e., ANN and ANFIS) in terms of simplicity and accuracy, simultaneously. After reviewing the preprocessing results, we noticed that in the case of no-differencing mode, the methods of Dtr-Std, Dtr-Sf, Dtr-Sf-Mn present the best results, respectively.

These methods stationarize the Kermanshah plain groundwater level and extended the distribution of the series to a normal distribution. Other methods were not able to stationarize or normalize the UH time series properly. By drawing the ACF and PACF graphs of preprocessed time series, high seasonal and non-seasonal correlations were noticed. As a result, the order of model parameters increases and so errors may occur.

Hence, non-seasonal and seasonal differencing was applied. After applying the non-seasonal and seasonal differencing, the non-seasonal correlation decreased to a maximum of 3 lags and less in different methods, e.g., the Dtr-Sf-Mn method only required 2 non-seasonal parameters to be modeled. The seasonal correlation also decreased for all methods to one seasonal lag. For example, the mentioned Dtr-Sf-Mn method only required one seasonal parameter for modeling after consecutive differencing. Therefore, choosing the order of parameters for linear modeling is important.

Since the optimized selection of the parameters reduces the modeling time and reduces the associated errors, estimation of each parameter is accompanied by errors. Therefore, adding any extra parameter results in adding errors to the model equation. After modeling and analyzing the related indices, the linear one-step-forward forecast modeling method can forecast the groundwater level of Kermanshah’s plain judiciously.

The proposed methods without differencing, which managed to stationarize and normalize the time series, also succeeded in producing accurate model results and achieved the best forecasts. On the other hand, the UH series modeling without preprocessing has also produced very good results. Finally, the proposed linear method outperformed the ANN and ANFIS nonlinear methods in terms of simplicity and accuracy simultaneously.

Appendix

If P represents{φ,θ} and Pω represent {Φ,Θ} and ω be the periodicity, then the expansion of the stochastic modeling [SARIMA(p,d,q)(P,D, Q)ω] is as follows (Eqs. A3 - A5) (Box et al. (2015):

$$j\left( B \right)\Phi (B^{\omega } ) \, \left( {1 - B} \right)^{d} (1 - B^{\omega } )^{D} GWL\left( t \right) = \theta \left( B \right)\Theta (B^{\omega } )e\left( t \right)$$

(A1)

$$P\left( B \right) \, = \, 1 \, {-} \, P_{1} B \, {-} \, P_{2} B^{2} {-} \, P_{3} B^{3} - \, \ldots \, - \, P_{n} B^{n} ,$$

(A2)

$$P_{\omega } \left( {B^{\omega } } \right) \, = \, 1 \, {-} \, P_{\omega 1} B^{\omega } {-}P_{\omega 2} B^{2\omega } {-}P_{\omega 3} B^{3\omega } - \, \ldots \, - \, P_{\omega n} B^{n\omega }.$$

(A3)

This model is defined using non-seasonal parameters of φ and θ (moving average and autoregressive parameters respectively) and seasonal parameters of Φ and Θ (moving average and autoregressive parameters respectively). The number of these parameters with p, q, P, Q respectively indicate the order of stochastic parameters (n). Both d and D parameters represent the differencing orders in this model that show the number of non-seasonal and seasonal differencing times. (B(GWL_t) = GWL (t-1)) is the differencing operator. The differencing operator in the SARIMA model makes the nonstationary series stationary and uses seasonal parameters to model seasonal variations in time series.

The equation of the introduced preprocessing techniques in Sect. 3.2 is as follows (Jain and Kumar 2012; Bonakdari et al. 2018; Zeynoddin et al. 2018).

$$Dif{f_{GWL}} = G\left( t \right) - GWL\left( {t - 1} \right)$$

(A4)

$$Dt{r_{GWL}} = GWL(t) - \left( {GW{L_{trend{\text{ }}line}} = Const. + {\beta _t}t} \right)$$

(A5)

$$St{{d_{GWL}}} = (GWL(t) - ({\overline{GWL}_t}\left( t \right))\;)/N$$

(A6)

$$Sf(t)\, = \,GWL(t)\, - \,\left[ {\overline{GWL} \, + \,\sum\nolimits_{{}}^{{}} {(\alpha_{u} {\text{Cos}} (\omega ) + \beta_{u} {\text{Sin}} (\omega )) + \varepsilon (t)} } \right.$$

(A7)

$$\alpha_{u} = \frac{2}{N}\left( {\sum\limits_{t = 1}^{N} {GWL\left( t \right)\cos \left( {2\pi f_{u} t} \right)} } \right)\,$$

(A8)

$$\beta_{u} = \frac{2}{N}\left( {\sum\limits_{t = 1}^{N} {GWL\left( t \right)\sin \left( {2\pi f_{u} t} \right)} } \right)$$

(A9)

$$fu = {\raise0.7ex\hbox{$u$} \!\mathord{\left/ {\vphantom {u N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}\,{\text{and}}\,\omega {\text{ = 2}}\pi {{\text{f}}_u}t;\,u\, = 1,2,3, \ldots ,k;\,t\, = 1,2,3, \ldots N.$$

(A10)

$\overline{GWL}_{t} (t)$ is the mean of GWL(t); βt is the average change from one period to the next; ε(t) is the Fourier series expansion residuals or residuals series.

The equation of the Manly normalization transform is as follows (Stajkowski et al. 2020a, b):

$$Manly_{GWL} = \left\{ \begin{gathered} (e^{\lambda GWL(t)} - 1)/\lambda ,\,\,\lambda \ne 0 \hfill \\ GWL(t),\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\lambda = 0 \hfill \\ \end{gathered} \right\},$$

(A11)

where λ is the Manly normalization parameter.

The Jarque–Bera test equation is as follows (Bai and Ng, 2005):

$$JB = n\left( {\frac{{S_{K}^{2} }}{6} + \frac{{\left( {K_{u} - 3} \right)^{2} }}{24}} \right),$$

(A12)

where K_u is skewness and S_k is kurtosis. For samples with values of more than 2000, the value of this test is compared with the χ² distribution with two degrees of freedom, and for samples with low values, since the chai distribution yields invalid results, the critical values of this test are based on Monte Carlo simulation calculations.

By considering n as the number of stages of the time series and ε_t = e_t for trend stationary which results $e_{t} \, = \, GWLt - \overline{GWL}_{t}$, to examine the time series stationarity and applying the KPSS test, the following relationships can be employed (Murat et al. 2018):

$$KPSS = \frac{1}{{n^{2} }}\sum\limits_{t = 1}^{n} {\frac{{S_{t}^{2} }}{{S^{2} \left( l \right)}}}$$

(A13)

$$S^{2} \left( l \right) = \frac{1}{n}\sum\limits_{t = 1}^{n} {e_{t}^{2} + } \frac{2}{n}\sum\limits_{j = 1}^{l} {w\left( {j,l} \right)} \frac{1}{n}\sum\limits_{t = j + 1}^{n} {e_{t} e_{t - s} }$$

(A14)

$$w\left( {j,l} \right) = 1 - j/\left( {l + 1} \right),$$

(A15)

where S_t = Σe_t, l is the truncation lag of stationary statistic at level or trend. As noted, in the case of non-stationarity, it is necessary to find its justification.

The non-seasonal Mann–Kendall test is as follows (Jain and Kumar 2012):

$$MK_{Std} = \left\{ \begin{gathered} \left( {M_{K} - 1} \right)\sigma^{2} \left( {M_{K} } \right)^{ - 0.5} ,\,\,\,\,\,\,M_{K} > 0 \hfill \\ \,\,\,\,\,0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,,\,\,\,\,\,\,M_{K} = 0 \hfill \\ \left( {M_{K} + 1} \right)\sigma^{2} \left( {M_{K} } \right)^{ - 0.5} ,\,\,\,\,\,\,M_{K} < 0, \hfill \\ \end{gathered} \right.$$

(A16)

where MK_Std is the standard of Mann–Kendall statistic, M_K is the Mann–Kendall statistic, and σ2(MK) is the variance of MK. The MK and σ²(MK) are defined as:

$$M_{K} = \sum\limits_{i = 1}^{N - 1} {\sum\limits_{j = i + 1}^{N} {{\text{sgn}} \left( {GWL_{j} - GWL_{i} } \right)} }$$

(A17)

$$\sigma^{2} \left( {M_{K} } \right) = \left( {\left( {2N^{3} - 7N^{2} - 5N} \right) - \sum\limits_{j}^{g} {N_{{Obs_{j} }} \left( {N_{{Obs_{j} }} - 1} \right)\left( {2N_{{Obs_{j} }} + 5} \right)} } \right)/18,$$

(A18)

where GWL is the groundwater llevel, g represents the number of matching groups, sgn is the sign function, N and N_Obs,j are the number of samples and observations respectively.

The seasonal Mann–Kendall test equations are as follows:

$$S_{k} = \sum\limits_{i = 1}^{{N_{k} 1}} {\sum\limits_{j = i + 1}^{{N_{k} - 1}} {{\text{sgn}} \left( {GWL_{ki} - GWL_{kj} } \right)} }$$

(A19)

$$S_{{M_{K} }} = \sum\limits_{k = 1}^{\omega } {\left( {S_{k} - {\text{sgn}} \left( {S_{k} } \right)} \right)}$$

(A20)

$$\sigma^{2} \left( {S_{{M_{K} }} } \right) = 2\sum\limits_{i = 1}^{\omega - 1} {\sum\limits_{j = i + 1}^{\omega } {Cov._{ij} } } + \sum\limits_{k}^{\omega } {\left( {2N^{3}_{k} - 7N^{2}_{k} - 5N_{k} } \right)/18}$$

(A21)

$$S_{{M_{K} }} (STD) = M_{K} \,\sigma^{2} \left( {S_{{M_{K} }} } \right)^{ - 0.5},$$

(A22)

where ω is the number of seasons in a year and Cov._ij represents the covariance of statistic test in season i and j.

The Mann–Whitney test is defined as follows (Clarke et al. 2011):

$$MW_{U} = \frac{{\sum\limits_{t = 1}^{{N_{1} }} {\left( {Dg\left( {GWL{}_{ordered}} \right) - \frac{{N_{m1} \left( {N_{m1} + N_{m2} + 1} \right)}}{2}} \right)} }}{{\sqrt {N_{m1} N_{m2} \left( {N_{m1} + N_{m2} + 1} \right)} /12}}.$$

(A23)

In this relationship: GWL_ordered sorted by GWL(t), Dg(GWL_ordered) GWL_ordered, N_m1, and N_m2 are the number of members of the original subseries, as N_m1 + N_m2 = N_total.