Keywords

1 Introduction

Over the past decade, groundwater depletion is one of the major issues worldwide, which is posing direct or indirect impacts on human livelihoods, flora and fauna, natural habitat, and ecosystems. Depletion of groundwater storage, land subsidence, reductions in stream flow and lake water levels, saltwater intrusion, loss of wetland and riparian ecosystems, and variations in groundwater quality are some of the vital factors influencing the sustainability of groundwater resources [1]. Sustainable groundwater resources development is the key issue to be addressed by policy makers or water managers by implementing various alternative management strategies. Groundwater restoration or recycle is not equally fast as that of surface water; it may take place after many years. Thus, constant monitoring of groundwater levels is extremely important for reliable assessment of temporal availability of groundwater at any required location [2]. The benefits of groundwater level forecasting include assessment of annual and long-term changes in groundwater storage, estimation of recharge rates, manage drinking water demand, and to ensure the sustainable use of groundwater resources [3].

Till date, several deterministic, stochastic and time-series based models have been developed for the forecasting of groundwater levels [4–7]. In the recent past, soft computing tools like Artificial Neural Network (ANN), ANFIS, Support Vector Regression (SVR), and so on have also been widely utilized for groundwater level prediction studies [8–14]. Quite a few hybrid artificial intelligence models developed by incorporating wavelet analysis efficiently forecast groundwater levels at different time scales [15–18]. Determining a model which is capable to efficiently capture the nonlinearities of the data without overfitting is the crucial job while modeling using time-series data. The ability to select the hyper parameters of the kernel automatically is one of the prominent benefits of Gaussian processes over conventional kernel interpretations of regression. The Bayesian learning algorithm-based Gaussian Process Regression is successfully applied for prediction of nonstationary time-series [19], monthly stream flow forecasting [20], and stream water temperature prediction [21], and so on. Compared to the conventional time-series forecasting methods, GPR model is said to possess strong nonlinear mapping ability, estimation of uncertainty, and is greatly fault-tolerant [22, 23]. Hence, in this paper, we demonstrate the state-of-the-art capability of Gaussian process regression for multistep lead time probabilistic forecast of groundwater level fluctuations. The ANFIS model is also employed for comparative study with GPR forecasts.

2 Study Area and Data Analysis

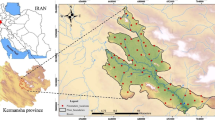
The study area (Fig. 1) is located near to southwest coast in the state of Karnataka, India. The observation wells selected for the current study are located inside the Kumaradhara river basin which covers a geographical area of 1776 sq km and is located in between 12º 29′ 04″ and 12º 58′ 33″ north latitude and from 75º 09′ 58″ to 75º 47′ 48″ east longitudes. The observation well located at Bellare lies at 12° 39′ 53″ north latitude and 75° 17′ 18″ east longitude, while the other well at Guttigaru lies at 12° 37′ 53″ north latitude and 75° 31′ 44″ east longitude as shown in Fig. 1.

Fig. 1
figure 1

Study area (location of observation wells)

Full size image

The study area has a tropical monsoon climate dominated by the southwest monsoon (June–October). The mean annual rainfall over the basin is around 3,500 mm. The geology of the area is predominantly characterized by Lateritic soil with highly porous and permeable nature. Due to this lateritic soil property, shallow groundwater levels in the selected unconfined aquifers follow a regular cyclic pattern of seasonal fluctuation, typically rising during the monsoon due to greater precipitation and recharge, then declining during the summer.

The groundwater level data of the observation wells located at Bellare and Guttigaru for the years 2000–2013 were retrieved from Department of Mines and Geology, Dakshina Kannada Dist., Govt. of Karnataka, India. The topographic elevation of these wells is about 100–130 m above mean sea level. This data comprises of 166 monthly observations, in which 10 years of data during Jan 2000–Dec 2009 is used for model training and remaining 4 years of data during Jan 2010–Oct 2013 is used as out-of-sample set or testing set to measure the predictability of the developed models.

The descriptive statistics of the observed groundwater levels in the two observation wells are presented in Table 1. The X max, X min, X mean, X mode, S d , and C v denotes the maximum, minimum, mean, mode, standard deviation and coefficient of variation respectively. Since the mean and coefficient of variation of the observed groundwater level dataset don’t vary ominously during training and testing periods, it could be inferred as a reasonable stationary time-series. In the present scenario, GPR and ANFIS models are explored to forecast 1, 3 and 6 months ahead groundwater level fluctuations. Monthly groundwater level time-series up to previous four time steps are taken as input variables. In order to test the hypothesis that GWL(t–2),...GWL(t–p) further help in forecasting GWL(t), beyond GWL(t–1), one can use an F-test. The lag order p = 4 was determined from the F-test statistic. F-test is the test statistic to examine the significance of the components in the model [24]. The expected output from the developed models is the groundwater level at time step t, t + 3, and t + 6. The input-output combinations are as presented below.

Table 1 Statistical parameters of groundwater level dataset
Full size table
  1. I.

    \( {\text{GWL}}_{{({{t}} - 4)}} + {\text{GWL}}_{{({{t}} - 3)}} + {\text{GWL}}_{{({{t}} - 2)}} + {\text{GWL}}_{{({{t}} - 1)}} = {\text{GWL}}_{{({{t}})}} \)

  2. II.

    \( {\text{GWL}}_{{({{t}} - 4)}} + {\text{GWL}}_{{({{t}} - 3)}} + {\text{GWL}}_{{({{t}} - 2)}} + {\text{GWL}}_{{({{t}} - 1)}} = {\text{GWL}}_{{({{t}} + 3)}} \)

  3. III.

    \( {\text{GWL}}_{{({{t}} - 4)}} + {\text{GWL}}_{{({{t}} - 3)}} + {\text{GWL}}_{{({{t}} - 2)}} + {\text{GWL}}_{{({{t}} - 1)}} = {\text{GWL}}_{{({{t}} + 6)}} \)

3 Methodology

In the present study, Gaussian Process Regression (GPR) and Adaptive Neuro Fuzzy Inference System (ANFIS) approaches are proposed for model development of groundwater level time-series forecasting. GPR and ANFIS is used for 1, 3, and 6 month lead groundwater level time-series forecasting using lagged input data up to 4 months in the past.

3.1 Gaussian Process Regression

Gaussian process regression is a standard method in probability theory wherein the interpolated values are modeled by a Gaussian process governed by prior covariance. Incorporating appropriate assumptions on the priors, GPR renders the best linear unbiased prediction of the values [25]. GPs constitute one of the most important Bayesian discriminative kernel learning approach due to its practical and theoretical simplicity and outstanding generalization ability. A sequence of random variables {X n } defining a stationary process can have any probability distribution. A stationary process {X n } is called a Gaussian process, if the joint distribution of (X n+1, X n+2,…, X n+k ) is a k-variate normal for every positive integer k.

Consider an observation space χ. A GP f(x), where x ∊ χ, is defined by a set of random variables, any finite number of which possess a joint Gaussian distribution function which is fully specified by its mean function m(x) and covariance k(x, x′) [26].

So let,

$$ \begin{aligned} m(x) & = {E}\left[ {f\left( x \right)} \right] \\ k\left( {x,x^{\prime}} \right) & = {E}\left[ {\left( {f\left( x \right) - m\left( x \right)} \right) \cdot \left( {f\left( {x^{\prime}} \right) - m\left( x \right)} \right)} \right] \\ \end{aligned} $$
(1)

Now we can write GP as

$$ f\left( x \right) \sim {\mathbb{N}}\left( {m\left( x \right),k\left( {x,x^{\prime}} \right)} \right) $$
(2)

Consider a training set \( {D} = \left\{ {\left. {\left( {{{x}}_{{i}} , {{y}}_{{i}} } \right)} \right|{{i}} = 1 , 2 ,\ldots , {{N}}} \right\} \), with m-dimensional input variables, x i being the observed data related to the phenomenon that is to be modeled and scalars y i being the associated target values given by \( y_{i} = f\left( {x_{i} } \right) + \epsilon_{i} \), where ϵ i is Gaussian noise with zero mean and variance σ 2 n .

The joint normality of the training target values y = [y i ] N i=1 and some unknown target value y *, are estimated by the value f * of the hypothesized GP assessed at the observation point x *, yields

$$ \left[ {\begin{array}{*{20}c} y \\ {f_{ * } } \\ \end{array} } \right] \sim {\mathbb{N}}\left( {0,\left[ {\begin{array}{*{20}c} {K\left( {X,X} \right) + \sigma_{N}^{2} I_{N} } & {k\left( {x_{ * } } \right)} \\ {k\left( {x_{ * } } \right)^{\rm T} } & {k\left( {x_{ * } ,x_{ * } } \right)} \\ \end{array} } \right]} \right) $$
(3)

where,

$$ k\left( {x_{ * } } \right) \triangleq \left[ {k\left( {x_{1} ,x_{ * } } \right), \ldots ,k\left( {x_{N} ,x_{ * } } \right)} \right]^{T} $$
(4)

X = [x i ] N i=1 , I N , is the N × N identity matrix, k(x *) is the vector of covariance between f * and the training latent function values, and K is the matrix of the covariance between the N training data points (design matrix)

$$ K\left[ {X,X} \right] \triangleq \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {k\left( {x_{1} ,x_{1} } \right)} & {k\left( {x_{1} ,x_{2} } \right)} & { \ldots \ldots } & {k\left( {x_{1} ,x_{N} } \right)} \\ \end{array} } \\ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {k\left( {x_{2} ,x_{1} } \right)} & {k\left( {x_{2} ,x_{2} } \right)} \\ \end{array} } & {\begin{array}{*{20}c} { \ldots \ldots } & {k\left( {x_{2} ,x_{N} } \right)} \\ \end{array} } \\ \end{array} } \\ {} \\ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} . \\ . \\ \end{array} } \\ {k\left( {x_{N} ,x_{1} } \right)} \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} . \\ . \\ \end{array} } \\ {k\left( {x_{N} ,x_{2} } \right)} \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} {} & {\begin{array}{*{20}c} . \\ . \\ \end{array} } \\ \end{array} } \\ {\begin{array}{*{20}c} { \ldots \ldots } & {k\left( {x_{N} ,x_{N} } \right)} \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right] $$
(5)

Then, from (Eq. 3) and conditioning on the available training samples, we can derive the expression for the model predictive distribution, yielding

$$ p\left( {\left. {f_{ * } } \right|x_{ * } ,D} \right) = {\mathbb{N}}\left( {\left. {f_{ * } } \right|\mu_{ * } ,\sigma_{ * }^{2} } \right) $$
(6)

, where

$$ \left\{ {\begin{array}{*{20}l} {\mu_{ * } = k\left( {x_{ * } } \right)^{\rm T} \left( {K\left( {X,X} \right) + \sigma_{N}^{2} I_{N} } \right)^{ - 1} \times y} \hfill \\ {\sigma_{ * }^{2} = \sigma_{N}^{2} - k\left( {x_{ * } } \right)^{\rm T} \left( {K\left( {X,X} \right) + \sigma_{N}^{2} I_{N} } \right)^{ - 1} k\left( {x_{ * } } \right) + k\left( {x_{ * } ,x_{ * } } \right)} \hfill \\ \end{array} } \right. $$
(7)

The covariance function is parameterized by optimal value of hyper parameters. The predictive variance of the GP model is as given in Eq. (7), and it does not depend on the training target values, but depends only on the training input values [27]. The optimal value of hyper parameters of a Gaussian process with any kernel θ, for any distinct data set can be derived by maximizing the log marginal likelihood by means of general optimization procedures. The log marginal likelihood function under the GPR model is presented in Eq. 8 given below.

$$ \left\{ \begin{aligned} \log \, p\left( {\left. y \right|X;\theta ,\sigma^{2} } \right) & = - \frac{N}{2}\log 2\pi - \frac{1}{2}{ \log }\left| {K\left( {X,X} \right) + \sigma_{N}^{2} I_{N} } \right| \\ & \quad - \frac{1}{2}y^{\rm T} \left( {K\left( {X,X} \right) + \sigma_{N}^{2} I_{N} } \right)^{ - 1} y \\ \end{aligned} \right\} $$
(8)

3.2 Adaptive Neuro Fuzzy Inference System (ANFIS)

ANFIS is the fuzzy-logic based paradigm integrated with the learning power of Artificial Neural Network (ANN) to improve the intelligent system’s performance utilizing knowledge acquired after learning. For a given input-−output data set, ANFIS constructs a hybrid learning algorithm that associates the backpropagation gradient descent and least squares methods to frame a fuzzy inference system whose membership function (MF) parameters are iteratively tuned or adjusted. Adaptive Neuro Fuzzy inference systems comprise of mainly five layers–rule base, database, fuzzification interface, defuzzification interface and decision-making unit. The generalized ANFIS architecture proposed by Jang [28] is summarized below (Fig. 2).

Fig. 2
figure 2

General ANFIS architecture with two membership functions on each of the two inputs

Full size image

ANFIS architecture comprises of five layers. Every single node in layer 1 is an adaptive node with a node function which may be anyone among the membership functions. Every node of layer 2 is a fixed node labeled ‘M’ which signposts the firing strength of each rule. All nodes of layer 3 are fixed nodes labeled as ‘N’ which demonstrates the normalized firing strength of each rule. The Layer 4 is as similar to layer 1 wherein every node is an adaptive node governed by a node function. The layer 5 being a single fixed node labeled ‘S’, representing the overall output (z), defined as the summation of all incoming signals [29].

In the present study, we examine three types of membership functions (MFs) namely trapezoidal, gaussian, and generalized bell. Among all the three types of the MFs, we impart two MFs on each of our four inputs, in which eight altogether. With this, the FIS structure consists of 16 fuzzy rules with 104 parameters. A hybrid algorithm integrating the least squares method and the backpropagation gradient descent method is applied to optimize and adjust the generalized bell membership function parameters and coefficients of the output linear equations. The number of epochs and error tolerance is set to 1000 and 0, respectively. From the result as presented in Table 3, it is determined that the ANFIS structure with Generalized bell MF to be better performing than Trapezoidal and Gaussian shaped MFs based on the performance evaluation using correlation coefficient statistic as mentioned below in Sect. 4. Hence, generalized bell MF-based ANFIS models are developed for all the 1, 3 and 6 month lead time forecasting scenarios.

4 Performance Evaluation

The following statistical indices are used to evaluate the performance of both the GPR and ANFIS models in forecasting groundwater level time-series.

$$ \text{CC} = \frac{{\sum\limits_{i = 1}^{N} {\left\{ {\left( {X_{i} - \overline{X} } \right) \cdot \left( {Y_{i} - \overline{Y} } \right)} \right\}} }}{{\sqrt {\sum\limits_{i - 1}^{N} {\left\{ {\left( {X_{i} - \overline{X} } \right)^{2} \cdot \left( {Y_{i} - \overline{Y} } \right)^{2} } \right\}} } }} $$
(9)
$$ \text{RMSE} = \sqrt {\frac{{\sum\limits_{i = 1}^{N} {\left( {X_{i} - Y_{i} } \right)} }}{N}} $$
(10)
$$ \text{NSE} = 1 - \frac{{\sum\limits_{i = 1}^{N} {\left( {X_{i} - Y_{i} } \right)^{2} } }}{{\sum\limits_{i = 1}^{N} {\left( {X_{i} - \overline{X}} \right)^{2}}}} $$
(11)

where,

CC:

Correlation Coefficient;

RMSE:

Root Mean Squared Error;

NSE:

Nash-Sutcliffe Efficiency;

X:

Observed/Actual values;

Y:

Modeled/Computed values;

\( \overline{X} \) :

Mean of Actual data.

5 Results and Discussion

An appealing characteristic of time-series modeling is that it is based on relatively few assumptions which usually lead to yield good fits. The GPR package in the WEKA 3.6 software [30] is employed to develop the GPR models. The GPR employing Pearson VII function-based universal kernel (PuK) is used for model development. The GPR model developed in the present study is propelled to provide better groundwater level forecasting results. Table 2 presents the developed GP regression model equations. The statistical adequacies of the GPR and ANFIS models for 1, 3 and 6 month ahead forecasts are summarized in Tables 4, 5, and 6, respectively. For both study sites (Bellare and Guttigaru), the GPR models are found to provide more accurate groundwater level forecasts than that of ANFIS models for 1, 3 and 6 month lead time forecasting. The GPR models for the Bellare and Guttigaru well sites have a testing RMSE of 0.632 and 1.05 m, respectively (Table 4), and are superior to the ANFIS model forecast, which has a testing RMSE of 0.742 m for the Bellare well site and 1.39 m for the Guttigaru well site during 1 month lead time forecasting (Table 3).

Table 2 Values of Gaussian process regression equations
Full size table
Table 3 Performance of ANFIS models at 1 month lead time forecasting
Full size table

It can be observed (from Tables 4, 5 and 6) that the correlation coefficients of both the GPR and ANFIS models are high during training (calibration). However, during the testing phase, the GPR model is better when compared to ANFIS model. It is noteworthy that the GPR model shows enhanced performance in contrast to ANFIS model, in case of both the wells. The RMSE statistic of multistep lead time forecasting is presented in Fig. 3 wherein it can be inferred that the GPR and ANFIS models are more capable in the shorter lead time forecast. It can be seen that the forecasting efficiency declines during longer lead time forecast. The ANFIS model performs marginally similar to GPR model for 1 month ahead groundwater level forecasting, but for the higher lead times, such as 3 and 6 month lead time, GPR performance is observed better than ANFIS model results as presented in Tables 4, 5 and 6.

Table 4 Performance of GPR and ANFIS models during 1 month lead time forecasting
Full size table
Table 5 Performance of GPR and ANFIS models during 3 month lead time forecasting
Full size table
Table 6 Performance of GPR and ANFIS models during 6 month lead time forecasting
Full size table
Fig. 3
figure 3

RMSE of GPR and ANFIS models at multistep lead time forecasting

Full size image

Figures 4 and 5 illustrate observed versus forecasted groundwater level time-series using GPR and ANFIS models. It can be seen from Figs. 4 and 5 that the GPR model can efficiently mimic observed groundwater level time-series better than ANFIS model during 1 month lead forecasting. Figures 6 and 7 are scatter plots comparing the observed and forecasted groundwater levels using the GPR and ANFIS models for 1 month lead time forecasting during the testing period at the Bellare and Guttigaru sites. It can be observed that the band of scatter plot is very narrow and close to the line of perfect fit in case of GPR forecast, On the other hand ANFIS shows marginally lesser performance as compared to the GPR model in test phase. On a whole, it can be concluded that the GPR model provided more accurate forecasting results at both the study sites than the best ANFIS model at all the 1, 3 and 6 month lead times considered.

Fig. 4
figure 4

Plot of observed versus forecasted groundwater level time-series with respect to the well location at Bellare of 1 month lead time forecasting models

Full size image
Fig. 5
figure 5

Plot of observed versus forecasted groundwater level time-series with respect to well location at Guttigaru of 1 month lead time forecasting models

Full size image
Fig. 6
figure 6

Scatter plot of observed versus forecasted groundwater level with respect to well the location at Bellare of 1 month lead time forecasting models during test phase

Full size image
Fig. 7
figure 7

Scatter plot of observed versus forecasted groundwater level with respect to well location at Guttigaru of 1 month lead time forecasting models during test phase

Full size image

6 Conclusions

The application of the Gaussian Process Regression to forecast monthly groundwater level fluctuations at multistep lead times is investigated in the present study. ANFIS modeling is also adopted for comparative performance evaluation of the developed models. It is observed that the performance of the GPR is quite satisfactory providing relatively close agreement predictions when compared to that of ANFIS model in terms of the performance measures utilized in this study. It is envisaged that GPR model could serve as a better alternate for forecasting groundwater level fluctuation at multistep lead time. The GPR model has advantages over other models in terms of model accuracy, feature scaling, and probabilistic variance. In future one can test the applicability of GPR model with multivariate input data to forecast groundwater levels by including rainfall, temperature, and evaporation data.