Introduction

The research for battery performance reflects in several aspects [1,2,3,4]. Among them, the SOC estimation is one of research hotspots due to its accurate prediction deciding the effective use of battery and playing a vital role in the battery management system.

The SOC estimation methods

The general classification for SOC estimation

Due to SOC being unable directly measured, it can only be computed by using the battery operating voltage and current [5,6,7,8], etc. At present, well-known methods for SOC estimation include the following:

  • The traditional SOC estimation methods contain the ampere-hour (AH) integration method [9] and the OCV method [10,11,12].

  • The data-driven model-based methods [13,14,15,16,17,18,19] mainly include the fuzzy logic method [13, 14], the neural network model-based method [15,16,17], the support vector machine [18], and the difference equation model [19], mostly do not have a physical significance.

  • The mechanism model-based SOC estimation methods [20, 21] contain the electrochemical model methods [22, 23] and the equivalent circuit model (ECM) methods [24,25,26], etc.

The comparison of SOC estimation methods

The traditional SOC estimation methods

The traditional methods are simple in theory and easy to implement. However, the AH integration method is difficult to precisely get the initial SOC, and easy to cause cumulative errors. The OCV method must be in the case of a broken circuit, after the battery is rest for a period of time; this requirement makes online measurement impossible.

The data-driven model-based methods

The neural network and fuzzy model are two main branches of artificial intelligence [13,14,15,16,17] that belong to the data-driven model-based methods. Their corresponding SOC estimation methods do not rely on accurate battery models, but infer the characteristics or mechanism of the battery by analyzing the sampled input-output data of the battery according to the black-box principle. The disadvantage is that they do not give a clear physical meaning.

The mechanism model-based methods

The mechanism model-based methods continuously catch attentions in the lithium battery modeling field due to the definite physical meaning of the battery model. The electro-chemical model is accurate, but the parameters in the model are fairly difficult to obtain.

Among them, the equivalent circuit model (ECM) method is more popular due to its simple and definite physical meaning, and easy to be expressed into a state space equation with SOC being a state [24,25,26]. In all the SOC estimation methods, the ECM method takes a compromise between model precision and complexity; thus it is the most appropriate SOC online estimation technique.

The ECM-based Kalman filter (KF) method

The Kalman filter is the mainstream mean to solve state estimation with SOC being one state in a state space equation formed from the ECM. The basic KF method is a popular linear state identification technique which recursively estimates the state of a linear state space equation by seeking the minimum of the mean square error between the practical state and the optimal estimated state [27, 28]. Because the process and measurement models of the lithium battery are nonlinear functions, the linear KF does not suitable; the extension of a linear KF algorithm becomes necessary.

The extended Kalman filter (EKF) algorithm

The EKF is a well-known nonlinear version of the linear KF algorithm [29]; it adopts the linearization method of the nonlinear function which takes the Taylor expansion to approximate the battery nonlinear function into a linear function [30,31,32], so as to use the KF algorithm to estimate the battery SOC [33]. The limitation is that the error caused by taking the first-order in the Taylor expansion would accumulate with the recursion increasing. The drawback of ignoring higher order terms in Taylor expansion leads to the search of a novel EKF technique. The adaptive EKF algorithm adaptively updates the covariance matrices in Kalman filter estimation method [34]. In addition, the robust EKF could effectively promote the SOC estimation precision caused by the error from incorrect initial SOC values [35].

The unscented Kalman filter (UKF) algorithm

Different from the EKF algorithm, the UKF adopts the unscented transformation (UT) for linearization, introduces sigma points to catch the state posterior mean and covariance without using Taylor expansion for the linearization of the nonlinear battery equation [36,37,38,39], and achieves the precision of second-order Taylor series expansion. Huang et al. evaluated the performance between the EKF and the UKF algorithms [29] to verify the high precision and fast convergence speed of the UKF algorithm. He et al. used the self-adjust UKF to compute the SOC with high precision [40]. But the EKF and UKF algorithms exist problems of dimensionality and divergence. To adapt the high-dimensional state estimation, Arasaratnam et al. presented the cubature Kalman filter technique in 2010 [41].

The cubature Kalman filter (CKF) algorithm

By adopting the radial-spherical cubature rule, the CKF algorithm in SOC estimation is more stable and accurate than the EKF and UKF algorithms [42,43,44]. In addition, the computation of the CKF is more efficient than that of the UKF, especially for high-dimensional system [45]. The comparison among the CKF, the EKF, and the UKF algorithms is carried out in Ref. [46], with the highest accuracy result of the CKF. To promote the CKF performance, Xia et al. explored an adaptive CKF (ACKF) algorithm to estimate SOC [47], compared it with the CKF and EKF algorithms, and verified that the ACKF is the most accurate and robust against measurement error. But the ACKF needs more computation time than that of the CKF and the EKF.

The dual extended Kalman filter (DEKF) algorithm

The thought of the DEKF is to simultaneously estimate the battery SOC and the equation parameters through two filters [48, 49]. By using a state filter and a parameter filter, the DEKF performs online estimation of the equation states and parameters, so as to overcome the influence of measurement and system noises and to provide superior SOC estimation results [50, 51].

The Kalman filtering method introduces the truncation error in the local linearization process for nonlinear battery systems which causes an increase in the error between the estimated value and the real value. In a strong nonlinear system, the filtering may even cause a divergence phenomenon, which seriously affects the SOC estimation accuracy. Most improved Kalman filter algorithms promote SOC estimation accuracy to some extent, but still need further improvements.

The estimation influence under noise corruption

The effect of noises on battery parameter identification is much more dominant due to noises often causing the biased battery parameter estimation in some cases. Wei et al. investigated a recursive total least squares (RTLS)-based observer to effectively attenuate the model identification bias caused by noise destruction, and studied an adaptive forgetting RTLS to compensate the influence of noise and reduce the identification deviation of model parameters [52, 53]. Li et al. explored a bias compensation RLS and EKF co-estimation algorithm for battery SOC estimation under noise corrupted measurements [54].

The Kalman filter type algorithms usually are unbiased. As described in [55], the smaller the value of noise variances, the smaller the estimation error will be. Zhang et al. adopted the cubature Kalman (CKF) filter algorithm to generate the proposal distribution of the particle filter algorithm order, and used the state and measurement residuals to adaptively adjust the weight of sigma points so as to reduce the influence of noise on the CKF algorithm [56]. He et al. adopted an adaptive extended Kalman filter algorithm to estimate battery SOC by continuously using the observation data to estimate and modify the filter under unknown system noise and the observation noise [57]. Dong et al. studied an adaptive anti-interference extended Kalman filter by using an innovation-based adaptive estimator [32].

The multi-innovation method

The multi-innovation theory is originated in 2007 [58], and is used in gradient identification of a linear regression model. The thought of the multi-innovation theory is to extend a scalar innovation at current instant to an innovation vector with current and previous innovations, so as to enhance the error information and promote the estimation accuracy. This paper investigates the multi-innovation EKF (MI-EKF) algorithm [58,59,60,61] to improve the SOC estimation accuracy of the EKF algorithm. The principle is, at each filtering step, to expand the single innovation at current instant to multi- innovations containing information from current and previous instants, to increase the amount of information, and to get the more accurate estimated SOC.

The motivation of this paper is to explore multi-innovation extended Kalman filter (MI-EKF) algorithm to estimate the battery SOC by expanding a single innovation at current instant to multi-innovations containing more information from current and previous instants. The purpose is to increase the amount of information, and to get the more accurate estimated SOC, so as to decrease the SOC estimation error caused by the Kalman filtering method.

The features of this research list are as follows:

  1. 1.

    For a lithium battery, an equivalent circuit model is adopted by analyzing the battery characteristic, and a state space equation with SOC being one state is constructed.

  2. 2.

    State estimates of the MI-EKF algorithm are corrected by multi-innovations containing current and previous innovations rather than the single innovation at only current instant, which improves the SOC estimation accuracy.

  3. 3.

    Simulation experiment results verify that the MI-EKF algorithm can effectively and accurately compute battery SOC by using data sampling from a lithium battery test device.

This research is arranged as follows. The next section describes the lithium battery circuit, constructs a state space equation for the lithium battery and identifies the battery parameters; Section 3 investigates the MI-EKF-based SOC estimation method; Section 4 sets up an experimental platform to collect data and carry out simulation experiment by using the classical EKF algorithm and the investigated MI-EKF algorithm and analyze the results; Finally, the conclusion is evaluated in Section 5.

The modeling of the battery

This section introduces a suitable battery equivalent circuit and constructs a nonlinear battery state space equation.

The circuit model of the battery

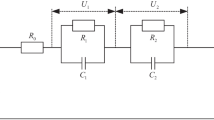
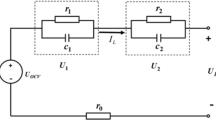
Common battery equivalent circuits have the Thevenin equivalent circuit, the PNGV circuit, the fourth-order dynamic circuit, and the second-order RC circuit [62,63,64]. This research chooses a second-order RC circuit, which is simple in structure, easy to implement, easy to calculate, and easy to combine with battery estimation algorithms. Refer to Fig. 1; the circuit contains UOC, the internal resistance R0, and the equivalent resistances R1C1 and R2C2. U is the battery terminal voltage, I is the terminal current, and the specified current direction is stipulated as discharge being positive and charge being negative.

Fig. 1
figure 1

The battery equivalent circuit

Full size image
Fig. 2
figure 2

The procedures of the MI-EKF algorithm

Full size image

According to the Kirchhoff law, the sum of voltage around the entire circuit equals to zero, and then at k instant, we have:

$$ {U}_{\mathrm{k}}={U}_{OC,\mathrm{k}}\left({SOC}_{\mathrm{k}}\right)-{I}_{\mathrm{k}}{R}_0-{U}_{\mathrm{k}}^{R_1{C}_1}-{U}_{\mathrm{k}}^{R_2{C}_2} $$
(1)

The zero-state voltage responses of the R1 and R2 are:

$$ \left\{\begin{array}{c}{U}_{k, zerostate}^{C_1{R}_1}={I}_{k-1}{R}_1\times \left(1-\exp \left(- Ts/{\tau}_1\right)\right)\\ {}{U}_{k, zerostate}^{C_2{R}_2}={I}_{k-1}{R}_2\times \left(1-\exp \left(- Ts/{\tau}_2\right)\right)\end{array}\right. $$
(2)

where the time constant are τ1 = R1C1 and τ2 = R2C2, respectively; Ts is the sampling period.

The zero-input voltage responses of the R1 and R2 are:

$$ \left\{\begin{array}{c}{U}_{k, zeroinput}^{C_1{R}_1}=\exp \left(- Ts/{\tau}_1\right)\times {U}_{k-1}^{C_1{R}_1}\\ {}{U}_{k, zeroinput}^{C_2{R}_2}=\exp \left(- Ts/{\tau}_2\right)\times {U}_{k-1}^{C_2{R}_2}\end{array}\right. $$
(3)

The full voltage responses of the R1 and R2 are:

$$ \left\{\begin{array}{c}\begin{array}{c}{U}_{\mathrm{k}}^{C_1{R}_1}={U}_{\mathrm{k},\mathrm{zerostate}}^{C_1{R}_1}+{U}_{\mathrm{k},\mathrm{zeroinput}}^{C_1{R}_1}\\ {}={I}_{\mathrm{k}-1}{R}_1\times \left(1-\exp \left(- Ts/{\tau}_1\right)\right)+\exp \left(- Ts/{\tau}_1\right)\times {U}_{\mathrm{k}-1}^{C_1{R}_1}\end{array}\\ {}\begin{array}{c}{U}_{\mathrm{k}}^{C_2{R}_2}={U}_{\mathrm{k},\mathrm{zerostate}}^{C_2{R}_2}+{U}_{\mathrm{k},\mathrm{zeroinput}}^{C_2{R}_2}\\ {}={I}_{\mathrm{k}-1}{R}_2\times \left(1-\exp \left(- Ts/{\tau}_2\right)\right)+\exp \left(- Ts/{\tau}_2\right)\times {U}_{\mathrm{k}-1}^{C_2{R}_2}\end{array}\end{array}\right. $$
(4)

Circuit parameter estimation

The stochastic gradient algorithm with forgetting factor (FFSG) is used to identify the battery parameters. The parameters to be identified include R0, R1, R2, C1, C2. The transfer function of the system can be obtained from Fig. 1:

$$ {\displaystyle \begin{array}{c}G(S)=\frac{U(S)}{I(S)}=\frac{U_{OC}(S)-{U}_L(S)}{I(S)}\\ {}={R}_0+\frac{R_1}{1+{R}_1{C}_1S}+\frac{R_2}{1+{R}_2{C}_2S}\end{array}} $$
(5)

Using bilinear transformation to discretize continuous functions, let:

$$ S=\frac{2\left(1-{Z}^{-1}\right)}{T\left(1+{Z}^{-1}\right)} $$
(6)

where T is the sampling period. The transfer function is discretized as:

$$ G(Z)=\frac{U(Z)}{I(Z)}=\frac{b_0+{b}_1{Z}^{-1}+{b}_2{Z}^{-2}}{1+{a}_1{Z}^{-1}+{a}_2{Z}^{-2}} $$
(7)

where:

$$ \left\{\begin{array}{c}{a}_1=\frac{2{T}^2-8{\tau}_1{\tau}_2}{\left(T+2{\tau}_1\right)\left(T+2{\tau}_2\right)}\\ {}{a}_2=\frac{\left(T-2{\tau}_1\right)\left(T-2{\tau}_2\right)}{\left(T+2{\tau}_1\right)\left(T+2{\tau}_2\right)}\\ {}{b}_0={R}_0+\frac{R_1T}{T+2{\tau}_1}+\frac{R_2T}{T+2{\tau}_2}\\ {}{b}_1=\frac{R_0\left(2{T}^2-8{\tau}_1{\tau}_2\right)+2\left({R}_1+{R}_2\right){T}^2}{\left(T+2{\tau}_1\right)\left(T+2{\tau}_2\right)}\\ {}{b}_2=\frac{R_0\left(T-2{\tau}_1\right)\left(T-2{\tau}_2\right)+{R}_1T\left(T-2{\tau}_2\right)+{R}_2T\left(T-2{\tau}_1\right)}{\left(T+2{\tau}_1\right)\left(T+2{\tau}_2\right)}\end{array}\right. $$

The corresponding difference equation derived from the discretized transfer function is:

$$ {\displaystyle \begin{array}{c}U(t)=-{a}_1U\left(t-1\right)-{a}_2U\left(t-2\right)+{b}_0I(t)+{b}_1I\left(t-1\right)+{b}_2I\left(t-2\right)+v(t)\\ {}={\varphi}^T(t)\theta +v(t)\end{array}} $$
(8)

where:

  1. 1.

    a1, a2, b0, b1, b2 are coefficients to be determined;

  2. 2.

    {U(t)} and {I(t)} are the output and input sequence of the model respectively;

  3. 3.

    {v(t)} is a random noise sequence with zero mean and no correlation.

Let:

$$ \varphi (t)={\left[-U\left(t-1\right),-U\left(t-2\right),I(t),I\left(t-1\right),I\left(t-2\right)\right]}^{\mathrm{T}} $$
(9)
$$ \theta ={\left[{a}_1,{a}_2,{b}_0,{b}_1,{b}_2\right]}^{\mathrm{T}} $$
(10)

where φ(t)is the information vector; θis the parameter vector.

Then we get the FFSG algorithm as follows [65,66,67,68]:

$$ \hat{\theta}(t)=\hat{\theta}\left(t-1\right)+\frac{\varphi (t)}{r(t)}\left[U(t)-{\varphi}^{\mathrm{T}}(t)\hat{\theta}\left(t-1\right)\right] $$
(11)
$$ r(t)=\lambda r(t)+{\left\Vert {\varphi}^{\mathrm{T}}(t)\right\Vert}^2,r(0)=1,0<\lambda <1 $$
(12)
$$ v(t)=U(t)-{\varphi}^{\mathrm{T}}(t)\hat{\theta}(t) $$
(13)

where \( \hat{\theta}(t) \)represents the estimated parameter vector. By using the FFSG algorithm and the equation (7), we can get the estimates of R0, R1, R2, C1 and C2, shown in Table 1.

Table 1 Parameter estimates of the FFSG algorithm.
Full size table

The nonlinear battery equation

The circuit model includes three energy storage elements, so the state variable of the lithium battery is set to:

$$ {x}_{\mathrm{k}}={\left[{SOC}_{\mathrm{k}}\kern0.5em {U}_{\mathrm{k}}^{R_1{C}_1}\kern0.5em {U}_{\mathrm{k}}^{R_2{C}_2}\right]}^{\mathrm{T}} $$
(14)

According to the definition of SOC, we have

$$ {SOC}_{\mathrm{k}}={SOC}_{\mathrm{k}\hbox{-} 1}\hbox{-} \frac{\eta Ts}{C_N}{i}_{\mathrm{k}\hbox{-} 1} $$
(15)

where

  1. 1.

    ηindicates the charge and discharge efficiency, acquired by charge and discharge test. Generally, when charging η = 1, when discharging η < 1

  2. 2.

    CN indicates the rated battery capacity.

From eqs. (4), (14), and (15), the state space equation for a Lithium battery with noises can be written as:

$$ {\displaystyle \begin{array}{c}{x}_{\mathrm{k}}=\left[\begin{array}{c} SO{C}_{\mathrm{k}}\\ {}{U}_{\mathrm{k}}^{R_1{C}_1}\\ {}{U}_{\mathrm{k}}^{R_2{C}_2}\end{array}\right]=\left[\begin{array}{ccc}1& 0& 0\\ {}0& {e}^{\raisebox{1ex}{$- Ts$}\!\left/ \!\raisebox{-1ex}{${\tau}_1$}\right.}& 0\\ {}0& 0& {e}^{\raisebox{1ex}{$- Ts$}\!\left/ \!\raisebox{-1ex}{${\tau}_2$}\right.}\end{array}\right]\times \left[\begin{array}{c} SO{C}_{\mathrm{k}-1}\\ {}{U}_{\mathrm{k}-1}^{R_1{C}_1}\\ {}{U}_{\mathrm{k}-1}^{R_2{C}_2}\end{array}\right]\\ {}+\left[\begin{array}{c}-\eta Ts/{C}_N\\ {}{R}_1\left(1-{e}^{\raisebox{1ex}{$- Ts$}\!\left/ \!\raisebox{-1ex}{${\tau}_1$}\right.}\right)\\ {}{R}_2\left(1-{e}^{\raisebox{1ex}{$- Ts$}\!\left/ \!\raisebox{-1ex}{${\tau}_2$}\right.}\right)\end{array}\right]\times {i}_{\mathrm{k}-1}+{w}_{\mathrm{k}-1}\end{array}} $$
(16)
$$ {U}_k={U}_{OC,k}\left({SOC}_k\right)-{i}_k{R}_0-{U}_k^{R_1{C}_1}-{U}_k^{R_2{C}_2}+{v}_k $$
(17)

where

  1. 1.

    wk ‐ 1indicates the system process noise with 0 mean and the covariance matrix Qk ‐ 1, i.e., wk ‐ 1~(0, Qk ‐ 1)

  2. 2.

    vkindicates the measurement noise with 0 mean and the covariance matrix Rk, i.e., vk~(0, Rk).

Let:

$$ f\left({x}_{\mathrm{k}\hbox{-} 1},{i}_{\mathrm{k}\hbox{-} 1},{w}_{\mathrm{k}\hbox{-} 1}\right)=\left[\begin{array}{ccc}1& 0& 0\\ {}0& {e}^{\raisebox{1ex}{$- Ts$}\!\left/ \!\raisebox{-1ex}{${\tau}_1$}\right.}& 0\\ {}0& 0& {e}^{\raisebox{1ex}{$- Ts$}\!\left/ \!\raisebox{-1ex}{${\tau}_2$}\right.}\end{array}\right]\times {x}_{\mathrm{k}\hbox{-} 1}+\left[\begin{array}{c}-\eta Ts/{C}_N\\ {}{R}_1\left(1-{e}^{\raisebox{1ex}{$- Ts$}\!\left/ \!\raisebox{-1ex}{${\tau}_1$}\right.}\right)\\ {}{R}_2\left(1-{e}^{\raisebox{1ex}{$- Ts$}\!\left/ \!\raisebox{-1ex}{${\tau}_2$}\right.}\right)\end{array}\right]\times {i}_{\mathrm{k}\hbox{-} 1}+{w}_{\mathrm{k}\hbox{-} 1} $$
(18)
$$ h\left({x}_k,{i}_k,{v}_k\right)={U}_{OC,k}\left({x}_k\left[1\right]\right)-{i}_k{R}_0-{x}_k\left[2\right]-{x}_k\left[3\right]+{v}_k $$
(19)

where \( {x}_{\mathrm{k}}\left[1\right]={SOC}_{\mathrm{k}},{x}_{\mathrm{k}}\left[2\right]={U}_{\mathrm{k}}^{R_1{C}_1},{x}_{\mathrm{k}}\left[3\right]={U}_{\mathrm{k}}^{R_2{C}_2} \).

Then eqs. (18) and (19) can be simply expressed as

$$ {x}_{\mathrm{k}}=f\left({x}_{\mathrm{k}\hbox{-} 1},{i}_{\mathrm{k}\hbox{-} 1},{w}_{\mathrm{k}\hbox{-} 1}\right) $$
(20)
$$ {U}_{\mathrm{k}}=h\left({x}_{\mathrm{k}},{i}_{\mathrm{k}},{v}_{\mathrm{k}}\right) $$
(21)

The MI-EKF method for SOC estimation

The classical EKF algorithm

The Taylor expansions of xk and Uk are, respectively,

(22)
(23)

According to the EKF principle, Jacobian matrices of f(•) and h(•) are given by:

$$ {\displaystyle \begin{array}{c}{A}_{\mathrm{k}}={\left.\frac{\partial f\left({x}_{\mathrm{k}-1},{i}_{\mathrm{k}-1},{w}_{\mathrm{k}-1}\right)}{\partial {x}_{\mathrm{k}}}\right|}_{x_{\mathrm{k}-1}={\hat{x}}_{\mathrm{k}-1}}=\left[\begin{array}{ccc}1& 0& 0\\ {}0& {e}^{\raisebox{1ex}{$- Ts$}\!\left/ \!\raisebox{-1ex}{${\tau}_1$}\right.}& 0\\ {}0& 0& {e}^{\raisebox{1ex}{$- Ts$}\!\left/ \!\raisebox{-1ex}{${\tau}_2$}\right.}\end{array}\right]\\ {}{L}_{\mathrm{k}}={\left.\frac{\partial f\left({x}_{\mathrm{k}-1},{i}_{\mathrm{k}-1},{w}_{\mathrm{k}-1}\right)}{\partial {w}_{\mathrm{k}-1}}\right|}_{w_{\mathrm{k}-1}={\hat{w}}_{\mathrm{k}-1}}=\left[\begin{array}{ccc}1& 0& 0\\ {}0& 1& 0\\ {}0& 0& 1\end{array}\right]\\ {}{H}_{\mathrm{k}}={\left.\frac{\partial h\left({x}_{\mathrm{k}},{i}_{\mathrm{k}},{v}_{\mathrm{k}}\right)}{\partial {x}_{\mathrm{k}}}\right|}_{x_{\mathrm{k}}={\hat{x}}_{\mathrm{k}-1}}=\left[{\left.\frac{d{U}_{OC}}{dSO{C}_{\mathrm{k}}}\right|}_{SOC= SO{C}_{\mathrm{k}-1}}\kern0.5em -1\kern0.5em -1\right]\\ {}{M}_{\mathrm{k}}={\left.\frac{\partial h\left({x}_{\mathrm{k}},{i}_{\mathrm{k}},{v}_{\mathrm{k}}\right)}{\partial {v}_{\mathrm{k}}}\right|}_{v_{\mathrm{k}}={\hat{v}}_{\mathrm{k}}}=1\end{array}} $$

Thus, the EKF algorithm can be expressed as:

$$ {\hat{x}}_{k,k-1}=\left[\begin{array}{ccc}1& 0& 0\\ {}0& {e}^{\raisebox{1ex}{$- Ts$}\!\left/ \!\raisebox{-1ex}{${\tau}_1$}\right.}& 0\\ {}0& 0& {e}^{\raisebox{1ex}{$- Ts$}\!\left/ \!\raisebox{-1ex}{${\tau}_2$}\right.}\end{array}\right]\times {\hat{x}}_{k-1}+\left[\begin{array}{c}-\eta Ts/{C}_N\\ {}{R}_1\left(1-{e}^{\raisebox{1ex}{$- Ts$}\!\left/ \!\raisebox{-1ex}{${\tau}_1$}\right.}\right)\\ {}{R}_2\left(1-{e}^{\raisebox{1ex}{$- Ts$}\!\left/ \!\raisebox{-1ex}{${\tau}_2$}\right.}\right)\end{array}\right]\times {i}_{k-1} $$
(24)
$$ {P}_{k,k-1}={A}_k{P}_{k-1}{A}_k^{\mathrm{T}}+{L}_k{Q}_{k-1}{L}_k^{\mathrm{T}} $$
(25)
$$ {K}_k=\frac{P_{k,k-1}{H}_k^{\mathrm{T}}}{H_k{P}_{k,k-1}{H}_k^{\mathrm{T}}+{M}_k{R}_k{M}_k^{\mathrm{T}}} $$
(26)
$$ {\hat{x}}_k={\hat{x}}_{k,k-1}+{K}_k\left\{{U}_k-{U}_{OC,k}\left({\hat{x}}_k\left[1\right]\right)+{i}_k{R}_0+{\hat{x}}_k\left[2\right]+{\hat{x}}_k\left[3\right]\right\} $$
(27)
$$ {P}_k=\left[I-{K}_k{H}_k\right]{P}_{k,k-1} $$
(28)

The investigated MI-EKF algorithm

For nonlinear battery systems, the standard EKF algorithm uses a single innovation to update the state estimates, while the MI-EKF algorithm uses multi-innovations to correct the state estimates, so as to promote the estimation precision [58,59,60,61].

The specific approach is to expand the single innovation:

$$ {e}_k={U}_k-{U}_{OC,k}\left({\hat{x}}_k\left[1\right]\right)+{i}_k{R}_0+{\hat{x}}_k\left[2\right]+{\hat{x}}_k\left[3\right] $$
(29)

to an innovation vector Eg, k (i.e., multi-innovations):

$$ {\displaystyle \begin{array}{c}{E}_{g,k}=\left[\begin{array}{c}{e}_k\\ {}{e}_{k-1}\\ {}\vdots \\ {}{e}_{k-g+1}\end{array}\right]\\ {}=\left[\begin{array}{c}{U}_k-{U}_{OC,k}\left({\hat{x}}_k\left[1\right]\right)+{i}_k{R}_0+{\hat{x}}_k\left[2\right]+{\hat{x}}_k\left[3\right]\\ {}{U}_{k-1}-{U}_{OC,k-1}\left({\hat{x}}_{k-1}\left[1\right]\right)+{i}_{k-1}{R}_0+{\hat{x}}_{k-1}\left[2\right]+{\hat{x}}_{k-1}\left[3\right]\\ {}\vdots \\ {}{U}_{k-g+1}-{U}_{OC,k-g+1}\left({\hat{x}}_{k-g+1}\left[1\right]\right)+{i}_{k-g+1}{R}_0+{\hat{x}}_{k-g+1}\left[2\right]+{\hat{x}}_{k-g+1}\left[3\right]\end{array}\right]\end{array}} $$
(30)

where g is the innovation length.

Correspondingly, expand the KF gain Kk to a gain matrix Kg, k.

$$ {K}_{g,k}=\left[{K}_k\kern0.5em {K}_{k-1}\kern0.5em \cdots \kern0.5em {K}_{k-g+1}\right] $$
(31)

Then replacing the single innovation ek and the gain Kk in the state estimation equation \( {\hat{x}}_k={\hat{x}}_{k,k-1}+{K}_k{e}_k \) with the innovation vector Eg, k and the gain matrix Kg, k gives the optimized state:

$$ {\displaystyle \begin{array}{c}{\hat{x}}_k={\hat{x}}_{k,k-1}+{K}_{g,k}{E}_{g,k}\\ {}={\hat{x}}_{k,k-1}+\sum \limits_{j=0}^{g-1}{K}_{k-j+1}e\left(k-j\right)\kern0.33em \left(j=1,2,\cdots, g-1\right)\end{array}} $$
(32)

In the equation \( {\hat{x}}_k={\hat{x}}_{k,k-1}+{K}_k{e}_k \), the state corrected term Kkek is obtained by Kk multiplying a single innovation ek. Through expanding ek to Eg, k and Kkto Kg, k, the optimized state \( {\hat{x}}_k={\hat{x}}_{k,k-1}+{K}_{g,k}{E}_{g,k} \) is achieved, and the term Kg, kEg, k is obtained by Kg, k multiplying an innovation vector Eg, k(i.e., multi-innovations). The innovation vector Eg, kcontains multiple innovations (more error corrected information); thus the multi-innovation EKF algorithm is more accurate than the EKF algorithm in SOC estimation.

Summarizing the above derivation yields the multi- innovation EKF (MI-EKF) algorithm as follows:

$$ {\hat{x}}_{k,k-1}=\left[\begin{array}{ccc}1& 0& 0\\ {}0& {e}^{\raisebox{1ex}{$- Ts$}\!\left/ \!\raisebox{-1ex}{${\tau}_1$}\right.}& 0\\ {}0& 0& {e}^{\raisebox{1ex}{$- Ts$}\!\left/ \!\raisebox{-1ex}{${\tau}_2$}\right.}\end{array}\right]\times {\hat{x}}_{k-1}+\left[\begin{array}{c}-\eta Ts/{C}_N\\ {}{R}_1\left(1-{e}^{\raisebox{1ex}{$- Ts$}\!\left/ \!\raisebox{-1ex}{${\tau}_1$}\right.}\right)\\ {}{R}_2\left(1-{e}^{\raisebox{1ex}{$- Ts$}\!\left/ \!\raisebox{-1ex}{${\tau}_2$}\right.}\right)\end{array}\right]\times {i}_{k-1} $$
(33)
$$ {P}_{k,k-1}={A}_k{P}_{k-1}{A}_k^{\mathrm{T}}+{L}_k{Q}_{k-1}{L}_k^{\mathrm{T}} $$
(34)
$$ {K}_k=\frac{P_{k,k-1}{H}_k^{\mathrm{T}}}{H_k{P}_{k,k-1}{H}_k^{\mathrm{T}}+{M}_k{R}_k{M}_k^{\mathrm{T}}} $$
(35)
$$ {e}_k={U}_k-{U}_{OC,k}\left({\hat{x}}_k\left[1\right]\right)+{i}_k{R}_0+{\hat{x}}_k\left[2\right]+{\hat{x}}_k\left[3\right] $$
(36)
$$ {\displaystyle \begin{array}{c}{E}_{g,k}=\left[\begin{array}{c}{e}_k\\ {}{e}_{k-1}\\ {}\vdots \\ {}{e}_{k-g+1}\end{array}\right]\\ {}=\left[\begin{array}{c}{U}_k-{U}_{OC,k}\left({\hat{x}}_k\left[1\right]\right)+{i}_k{R}_0+{\hat{x}}_k\left[2\right]+{\hat{x}}_k\left[3\right]\\ {}{U}_{k-1}-{U}_{OC,k-1}\left({\hat{x}}_{k-1}\left[1\right]\right)+{i}_{k-1}{R}_0+{\hat{x}}_{k-1}\left[2\right]+{\hat{x}}_{k-1}\left[3\right]\\ {}\vdots \\ {}{U}_{k-g+1}-{U}_{OC,k-g+1}\left({\hat{x}}_{k-g+1}\left[1\right]\right)+{i}_{k-g+1}{R}_0+{\hat{x}}_{k-g+1}\left[2\right]+{\hat{x}}_{k-g+1}\left[3\right]\end{array}\right]\end{array}} $$
(37)
$$ {K}_{g,k}=\left[{K}_k\kern0.5em {K}_{k-1}\kern0.5em \cdots \kern0.5em {K}_{k-g+1}\right] $$
(38)
$$ {\hat{x}}_k={\hat{x}}_{k,k-1}+{K}_{g,k}{E}_{g,k} $$
(39)
$$ {P}_k=\left[I-{K}_k{H}_k\right]{P}_{k,k-1} $$
(40)

The steps of the MI-EKF algorithm in eqs. (33)–(40) are listed as follows:

Experiment and simulation

The battery test platform

Referring to Fig. 3, take an actual battery charging and discharging system as an example. Its configuration diagram is displayed in Fig. 4. The battery experiment platform includes a battery tester (NEWARE BTS-4008-5V12A-TB), a median machine, a battery holder, 18,650 (2900 mAh) lithium batteries, and a host computer. The battery specifications are shown in Table 2.

Fig. 3
figure 3

The battery test platform

Full size image
Fig. 4
figure 4

The configuration diagram of the battery test system

Full size image
Table 2 General parameters of the battery.
Full size table

The OCV-SOC relation

The OCV-SOC curve is obtained through a battery static test. The battery static test refers to a method of measuring the OCV in a stable state after stopping charging and discharging for a period of time. The length of the static time determines the accuracy of the OCV measurement.

The principles of the static experiment are as follows:

  1. 1)

    The SOC measurement: the SOC of the battery is unable to get by direct measurement, so the principle of the AH integration method is used for computing SOC.

  2. 2)

    The OCV measurement: it can be seen from the eq. (1) (i.e., \( {U}_k={U}_{OC,k}\left({SOC}_k\right)-{I}_k{R}_0-{U}_k^{R_1{C}_1}-{U}_k^{R_2{C}_2} \)) that during the battery discharging, if the current is turned off and rests for a period of time, the voltages across R0, R1, and R2 become zero as the discharging ends, and the terminal voltage measured at this time can be used as the OCV value.

The steps of the static experiment are as follows:

  1. 1.

    Use different constant current to fully charge the battery for 2 h, and left it for 60 min.

  2. 2.

    The discharge experiment process is shown in Table 3, the sampled data is shown in Table 4.

Table 3 Cyclic intermittent discharge experiment with different discharge rates.
Full size table
Table 4 The OCV and SOC relation.
Full size table

By using the MATLAB curve fitting toolbox to fit the data of the OCV and SOC calculated by the AH integration method, the OCV-SOC curve is obtained, referring to Fig. 5. The static experiment shows that the OCV measurement accuracy can be improved under the smaller discharge current.

Fig. 5
figure 5

The OCV-SOC curve of the battery

Full size image

Considering the actual use of lithium batteries in electric vehicles, the lithium battery discharge experimental data is sampled under urban dynamometer driving schedule (UDDS) conditions. Apply the AH method, the EKF technique, and the explored MI-EKF technique to compute SOC based on MATLAB simulation. The simulation results are displayed in Figs. 6, 7, 8, and 9; for the convenience of observation, a partial enlargement map is drawn in the graph.

Fig. 6
figure 6

The estimated/measured SOC by the EKF and the AH methods

Full size image
Fig. 7
figure 7

The SOC/terminal voltage estimation by the MI-EFK (g = 2) and the AH methods

Full size image
Fig. 8
figure 8

The SOC/terminal voltage estimation by the MI-EFK (g = 3) and the AH methods

Full size image
Fig. 9
figure 9

Comparison of the SOC estimation by the MI-EFK algorithm under different g

Full size image

Figure 6 displays the estimated SOC of the EKF (i.e., the MI-EKF, g = 1) algorithm and the AH method.

Figure 7 displays the SOC and terminal voltage computed by the MI-EKF algorithm (g = 2) and the AH method.

Figure 8 displays the SOC and terminal voltage computed by the MI-EKF algorithm (g = 3) and the AH method.

Figure 9 displays the SOC computed by the MI-EKF algorithm under different g and the AH method, and displays the SOC error of the MI-EKF algorithm and the AH method.

From Fig. 6, 7, 8, and 9, we can get that the SOC estimation error by using the EKF algorithm (i.e., the MI-EKF g = 1) is much larger than the SOC estimation error by using the MI-EKF algorithm (g = 2 and g = 3). Generally, when taking the innovation length g = 3 in the MI-EKF algorithm, the estimated SOC is the most accurate and the SOC error is the smallest.

Noise influence on SOC estimates

The MI-EKF algorithm is unbiased estimation method under random noises corruption, especially under white noise corruption, but the SOC estimation accuracy varies under different variances.

Add an uncorrelated white noise sequence {v(t)} with zero mean and variance σ2 = 0.12, 0.32, 0.52, respectively. The SOC estimation errors under different σ2by using the MI-EFK algorithm are shown in Fig. 10. The following can be seen from the figure:

  1. 1)

    The parameter estimation errors given by the MI-EFK algorithm are generally smaller and approach zero which shows the effectiveness of the proposed algorithms.

  2. 2)

    The estimated SOC errors change small under different white noises. Generally, the estimated SOC errors by the MI-EFK algorithm are close to the true SOC as the noise variance becomes small.

Fig. 10
figure 10

SOC estimation error under different σ values

Full size image

Conclusion

According to the characteristics of lithium battery, an equivalent battery circuit is adopted and further a nonlinear state space equation is constructed. Through the linearization of the nonlinear battery equation, the EKF technique and the MI-EKF technique are carried out and are compared with the AH method. The experiment results prove that the MI-EKF algorithm can compute the SOC of the lithium battery more accurate and effective than that of the EKF algorithm, and as the innovation length increasing, the errors of the estimated SOC get smaller and smaller. Adding an uncorrelated white noise can slightly influence the SOC estimation error which will be small under small noise.

Due to the increase of the matrix dimension, the computation load of the MI-EKF algorithm is larger compared with that of the standard EKF algorithm, but the calculation precision of the MI-EKF algorithm is much improved compared with that of the EKF algorithm. The proposed method can be extended to study remaining useful life prediction for supercapacitors in Refs. [69, 70], and can apply to model block-oriented dynamic systems in Refs. [71,72,73].