Introduction

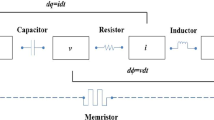
In 1971, Chua discovered the fourth element in circuit theory and named it as memristor (short for memory resistor). Chua mathematically revealed that memristor has the relationship between the magnetic flux and electric charge as in Chua (1971). Almost after 40 years, Stanley Williams and his group formulated the practical memristor in May 2008 in Strukov et al. (2008). The rapid variation of voltage at certain instants leads to irregular change of memristance which is similar to the switching behaviors in a dynamical system. The most fascinating trait of the memristor is that it can memorize the direction of flow of electric charge in the past. Thus, it performs as a forgetting and remembering (memory) process in human brains and hence the memristor is acknowledged well and its potential applications are in next generation computers and powerful brain-like computers. In order to replicate the artificial neural networks of human brain better, the conventional resistor of self feedback connection weights and connection weights of the primitive neural networks are replaced by the memristor.

Time delay is a common phenomenon that describes the fact that the future state of a system depends not only on the present state but also on the past state, and often encountered in many fields such as engineering, biological and economical systems. In reality, time delays often occur in many systems due to the finite switching speed of amplifiers in electronic neural networks or due to the finite signal propagation time in biological networks. In neural networks, the inner delay time that frequently occurs in the processing of information storage and telecommunication affects the dynamical behavior of the networks. Hence it is reasonable to consider time delay in modeling dynamical networks (Cao et al. 2016). In neural networks literature, research work on second-order states are very few compare to the first-order states. The second order states of the system is due to the inertial term or influence of inductance. There are some biological background for the inclusion of an inductance term in a neural system. For example, the membrane of a hair cell in the semicircular canals of some animals can be described by equivalent circuits that contain an inductance (Jagger and Ashmore 1999; Ospeck et al. 2001). The addition of inductance makes the membrane to have an electrical tuning, filtering behaviors and so on. The inertia can be treated as a helpful tool in the generation of chaos in neural systems. From the literature review of inertial neural networks, the bifurcation in a single inertial neuron model is discussed in He et al. (2012), Li et al. (2004), Liu et al. (2009) and the stability of an inertial two-neuron system in Wheeler and Schieve (1997). Furthermore, the stability analysis of Bidirectional Associative Memory (BAM) inertial neural networks has been discussed in Cao and Wan (2014), Yunkuan and Chunfang (2012), Zhang et al. (2015) and Ke and Miao (2013) deals with the inertial Cohen–Grossberg type neural networks in the literature.

The stability analysis of neural networks with time delay has received much more attention. Noticeable results on the stability analysis of neural networks with time delay has been projected by various authors. For instance, in Yunkuan and Chunfang (2012), the stability of an inertial BAM neural network with time delay is discussed by constructing suitable Lyapunov functional. Further, the stability of an inertial BAM neural network with time delay has been investigated by matrix measure theory in Cao and Wan (2014). The authors in Qi et al. (2014), Rakkiyappan et al. (2015), deals with the stability of a class of memristor-based recurrent neural networks with time delays using Lyapunov method and Banach contraction principle. In Chen et al. (2015), the global asymptotic stability of fractional memristor-based delayed neural networks has been discussed by employing the comparison theorem of fractional-order linear systems with time delay.

Synchronization of a complex network is a fascinating phenomena which is observed in fields such as physical, biological, chemical, technological, etc., and it has potential applications in biological systems, chemical reactions, secure communication, image processing and so on (Pan et al. 2015; Yang and Cao 2014, 2012). Synchronization of coupled inertial neural networks means that multiple neural networks can achieve a common trajectory, such as a common equilibrium, limit cycle or chaotic trajectory. The authors in Dai et al. (2016) have analyzed, the problem of neutral-type coupled neural networks with Markovian switching parameters by placing the adaptive controllers to part of nodes, and the sufficient conditions for exponential synchronization are drawn with the help of Lyapunov stability theory, stochastic analysis and matrix theory. Outer synchronization of partially coupled dynamical networks via pinning impulsive controller has been discussed in Lu et al. (2015). The global exponential synchronization of coupled neural networks with stochastic perturbations and mixed time-varying delays has been discussed in Wang et al. (2015) and synchronization criteria have been derived based on multiple Lyapunov theory. Two types of coupled neural networks with reaction–diffusion terms have been considered in Wang et al. (2016) and the general criterion for ensuring network synchronization has been derived by pinning a small fraction of nodes with adaptive feedback controllers. A sufficient condition for the exponential synchronization of fractional-order complex networks via pinning impulsive control has been derived using Lyapunov function and Mittag-Leffler function in Wang et al. (2015). In Yang et al. (2015), exponential synchronization of neural networks with discontinuous activations with mixed delays has been discussed by combining state feedback control and impulsive control techniques. Moreover, Pinning synchronization of coupled inertial delayed neural networks using matrix measure and Lyapunov–Krasovskii functional has been done in Hu et al. (2015). To the best of our knowledge, upto now no work in the literature have been carried out on the stability and synchronization problem for inertial Memristive neural networks (MNNs) with time-delay by using matrix measure and Halanay inequality.

Motivated by the above discussion, in this paper the stability of inertial memristive neural networks and pinning synchronization of coupled inertial memristive neural networks are presented. The main contribution of this paper are as follows: (1) The analysis on inertial MNNs is discussed. (2) The stability of inertial MNNs using matrix measure strategy is introduced. (3) In the literature, the stability of memristive-based first order system and fractional-order system are discussed but no work is done on inertial MNNs. Further, the synchronization of inertial MNNs is considered and pinning feedback control is used to synchronize the coupled inertial MNNs to the objective trajectory. In general, the matrix measure method utilizes the information of matrix elements, especially the diagonal elements of a matrix more sufficiently.

The rest of the paper is organized as follows. In “Problem formulation” section, model description and preliminaries are presented. Stability of the equilibrium point is investigated in “Stability analysis” section, and the pinning synchronization analysis of inertial MNNs are stated in “Synchronization analysis” section. In “Numerical simulation” section, some examples are given to show the validity of our results. Finally, in “Conclusion” section, conclusions are drawn.

Notations

Throughout this paper, \(\mathbb {R}^{n}\) and \(\mathbb {R}^{n\times n}\) denotes the n-dimensional Euclidean space and the set of all \(n \times n\) matrices, respectively. \(\overline{a}_{ij}=\max \{\hat{a}_{ij}, \check{a}_{ij}\}\), \(\underline{a}_{ij}=\min \{\hat{a}_{ij}, \check{a}_{ij}\}\), \(\overline{b}_{ij}=\max \{\hat{b}_{ij}, \check{b}_{ij}\}\), \(\underline{b}_{ij}=\min \{\hat{b}_{ij}, \check{b}_{ij}\}\) for \(i,j=1,2,\ldots ,n\). \(\overline{a}_{rs}=\max \{\hat{a}_{rs}, \check{a}_{rs}\}, \underline{a}_{rs}=\min \{\hat{a}_{rs}, \check{a}_{rs}\}, \overline{b}_{rs}=\max \{\hat{b}_{rs}, \check{b}_{rs}\}, \underline{b}_{rs}=\min \{\hat{b}_{rs}, \check{b}_{rs}\}\) for \(r,s=1,2,\ldots ,n\). \(\overline{A}=(\overline{a}_{rs})_{n\times n}\), \(\underline{A}=(\underline{a}_{rs})_{n\times n}\), \(\overline{B}=(\overline{b}_{rs})_{n\times n}\), \(\underline{B}=(\underline{b}_{rs})_{n\times n}\). co\(\{u,v\}\) denotes closure of the convex hull generated by real numbers u and v or real matrices u and v. \(AC^{1}([0,1],\mathbb {R}^{n})\) denote the space of differential functions \(x:[0,1]\rightarrow \mathbb {R}\), whose first derivative, \(x^{'}\), is absolutely continuous. \(I_{n}\) and \(diag\{\alpha _{1},\alpha _{2},\ldots ,\alpha _{n}\}\) denotes the identity matrix and the diagonal matrix of order \(n \times n\). \(I_{Nn}\) stands for the identity matrix with Nn dimension. Let A and B be the arbitrary matrices, then \(A \otimes B\) denotes the Kronecker product of the matrices A and B.

Problem formulation

In this paper, we consider the following inertial memristive delayed neural networks,

$$\frac{{\text{d}}^{2}s_{i}(t)}{{\text{d}}t^{2}}= -d_{i}\frac{{\text{d}}s_{i}(t)}{{\text{d}}t}-c_{i}s_{i}(t)+\sum \limits _{j=1}^na_{ij}(s_{i}(t))f_{j}(s_{j}(t))+\sum \limits _{j=1}^nb_{ij}(s_{i}(t))f_{j}(s_{j}(t-\tau (t))) +I_{i},$$
(1)

where \(s_{i}(t)\) is the state vector of the ith neuron, \(d_{i}>0\), \(c_{i}>0\) are constants, \(c_{i}\) denotes the rate with which the ith neuron will reset its potential to the resetting state in isolation when disconnected from the networks and external inputs. The second derivative of \(s_{i}(t)\) is known as inertial term of system (1). \(a_{ij}(s_{i}(t))\) and \(b_{ij}(s_{i}(t))\) represent the memristive connective weights which changes based on the feature of memristor and current–voltage characteristic. They are given as,

$$\begin{aligned} a_{ij}(s_{i}(t))=\left\{ \begin{array}{ll} \hat{a}_{ij}, &\quad |s_{i}(t)| \le T_{i}, \\ \check{a}_{ij}, &\quad |s_{i}(t)|> T_{i}, \end{array} \right. \quad b_{ij}(s_{i}(t))=\left\{ \begin{array}{ll} \hat{b}_{ij}, &\quad |s_{i}(t)| \le T_{i}, \\ \check{b}_{ij}, &\quad |s_{i}(t)| > T_{i}, \end{array} \right. \end{aligned}$$
(2)

for \(i,j=1,2,\ldots ,n\) in which switching jumps \(T_{i}>0\), \(\hat{a}_{ij}\), \(\check{a}_{ij}\), \(\hat{b}_{ij}\), \(\check{b}_{ij}\) are known constants with respect to memristance. \(f_{i}\) denotes the nonlinear activation function of the ith neuron at time t. \(I_{i}\) is the external input of the ith neuron. The time delay of the system (1) is defined as \(\tau (t)\ge 0\). The initial conditions of the system (1) is given as,

$$\begin{aligned} s_{i}(\chi )=\Phi _{i}(\chi ) \quad \text{and} \quad \displaystyle {\frac{\text{d}s_{i}(\chi )}{\text{d}\chi }}=\Psi _{i}(\chi );\quad -\tau \le \chi \le 0, \end{aligned}$$
(3)

where \(\Phi _{i}(\chi ),\Psi _{i}(\chi )\in \mathrm {C}^{(1)}([-\tau ,0],\mathbb {R}^n)\), \(\mathrm {C}^{(1)}([-\tau ,0],\mathbb {R}^n)\) denotes the set of all n-dimensional continuously differentiable functions defined on the interval \([-\tau ,0]\) with \(\tau =\text{ sup }_{t\ge 0}\{\tau (t)\}\).

To proceed, the following assumption, definitions and lemmas are given.

Assumption 1

The activation function \(f_{i}\) satisfies the Lipschitz condition, i.e., there exist constants \(l_{i}>0\) such that \(\forall\) x, y \(\in \mathbb {R}\), we have

$$\begin{aligned} |f_{i}(x)-f_{i}(y)| \le l_{i} |x-y|,\quad i=1,2,\ldots ,n. \end{aligned}$$

Definition 1

(Benchohra et al. 2010) A function \(s_{i} \in \mathrm {AC^{1}}((0,1),\mathbb {R}^{n})\) is said to be a solution of (1), (3) if \(s_{i}''(t)+d_{i}s_{i}'(t) \in F(t,s_{i}(t))\) almost everywhere on [0, 1], where \(d_{i}>0\) and the function \(s_{i}\) satisfies conditions (3). For each \(s_{i} \in \mathrm {C}([0,1],\mathbb {R}^{n})\), define the set of selections of F by,

$$\begin{aligned} S_{F,s_{i}}=\{v_{i} \in L^{1}([0,1],\mathbb {R}^{n}) : v_{i}(t) \in F(t,s_{i}(t)) \quad \text{a.e.}\quad t \in [0,1]\}. \end{aligned}$$

By applying the theories of set-valued maps and differential inclusion to system (1) as stated in Definition 1, where \(d_{i}>0\) and \(F(s_{i},t)=-c_{i}s_{i}(t)+\sum \nolimits _{j=1}^na_{ij}(s_{i}(t))f_{j}(s_{j}(t))+\sum \nolimits _{j=1}^nb_{ij}(s_{i}(t))f_{j}(s_{j}(t-\tau (t)))+I_{i}\).

The system (1) can be written as the following differential inclusion:

$$\frac{\mathrm {d}^{2}s_{i}(t)}{\mathrm {d}t^{2}}+d_{i}\frac{\mathrm {d}s_{i}(t)}{\mathrm {d}t} \in -c_{i}s_{i}(t)+\sum _{j=1}^nco[\underline{a}_{ij},\overline{a}_{ij}]f_{j}(s_{j}(t))+\sum _{j=1}^nco[\underline{b}_{ij},\overline{b}_{ij}]f_{j}(s_{j}(t-\tau (t))) + I_{i},$$
(4)

or equivalently, for \(i,j=1,2,\ldots ,n\) there exist measurable functions \(\tilde{a}_{ij}(s_{i}(t)) \in co[\underline{a}_{ij},\overline{a}_{ij}], \tilde{b}_{ij}(s_{i}(t)) \in co[\underline{b}_{ij},\overline{b}_{ij}]\), such that

$$\frac{\mathrm {d}^{2}s_{i}(t)}{\mathrm {d}t^{2}}+d_{i}\frac{\mathrm {d}s_{i}(t)}{\mathrm {d}t}= -c_{i}s_{i}(t)+\sum _{j=1}^n\tilde{a}_{ij}(s_{i}(t))f_{j}(s_{j}(t))+\sum _{j=1}^n\tilde{b}_{ij}(s_{i}(t))f_{j}(s_{j}(t-\tau (t))) +I_{i},$$
(5)

where \(i=1,2,\ldots ,n\).

Consider the following variable transformation to the system (5):

$$\begin{aligned} p_{1i}(t)&= s_{i}(t), \\ p_{2i}(t)&= \displaystyle {\frac{\mathrm {d}s_{i}(t)}{\mathrm {d}t}}+s_{i}(t). \end{aligned}$$

Then we have the system (5) as,

$$\begin{aligned} \left\{ \begin{array}{l} \dot{p}_{1i}(t)=-p_{1i}(t)+p_{2i}(t), \\ \dot{p}_{2i}(t)=-\mathbf {c}_{i}p_{1i}(t)-\mathbf {d}_{i}p_{2i}(t)+\sum _{j=1}^n\tilde{a}_{ij}(p_{1i}(t))f_{j}(p_{1j}(t))\\ \quad +\sum _{j=1}^n\tilde{b}_{ij}(p_{1i}(t))f_{j}(p_{1j}(t-\tau (t)))+I_{i}, \end{array}\right. \end{aligned}$$
(6)

where \(\mathbf {c}_{i}=c_{i}+1-d_{i}\) and \(\mathbf {d}_{i}=d_{i}-1\) with the initial values \(p_{1i}(\chi )=\Phi _{i}(\chi )\) and \(p_{2i}(\chi )=\Psi _{i}(\chi )+\Phi _{i}(\chi ), -\tau \le \chi \le 0\).

Definition 2

For the system \(p_{i}(t) \in f(p_{i})\). Since \(0 \in f(0)\) it follows that \(p_{i}=0\) is the equilibrium point. i.e.,

$$\begin{aligned} 0&= -p_{1i}^{*}(t)+p_{2i}^{*}(t), \\ 0&= -\mathbf {c}_{i}p_{1i}^{*}(t)-\mathbf {d}_{i}p_{2i}^{*}(t)+\sum _{j=1}^n\tilde{a}_{ij}(p_{1i}^{*}(t))f_{j}(p_{1j}^{*}(t))+\sum _{j=1}^n\tilde{b}_{ij}(p_{1i}^{*}(t))f_{j}(p_{1j}^{*}(t))+I_{i}. \end{aligned}$$

Definition 3

(He and Cao 2009) The matrix measure of a real square matrix \(W=(w_{ij})_{n\times n}\) is as follows:

$$\begin{aligned} \mu _{p}(W)=\lim \limits _{h\rightarrow 0^{+}}\frac{\Vert I_{n}+hW\Vert _{p}-1}{h}, \end{aligned}$$

where \(\Vert \cdot \Vert _{p}\) is an induced matrix norm on \(\mathbb {R}^{n\times n}\), \(I_{n}\) is an identity matrix and \(p=1,2,\infty ,\omega\). When the matrix norm,

$$\begin{aligned}&\Vert W\Vert _{1}=\max \limits _{j}\sum \limits _{i=1}^{n}|w_{ij}|, \quad \Vert W\Vert _{2}=\sqrt{\lambda _{max}(W^{T}W)}, \\&\Vert W\Vert _{\infty }=\max \limits _{i}\sum \limits _{j=1}^{n}|w_{ij}|, \quad \Vert W\Vert _{\omega }=\max \limits _{j}\sum \limits _{i=1}^{n}\frac{\omega _{i}}{\omega _{j}}|w_{ij}|. \end{aligned}$$

We can obtain matrix measures as,

$$\begin{aligned}&\mu _{1}(W)=\max \limits _{j}\left\{ w_{jj}+\sum \limits _{i=1,i\not =j}^{n}|w_{ij}|\right\} ,\quad \mu _{2}(W)=\lambda _{max}\displaystyle {\left( \frac{W^{T}+W}{2}\right) },\\&\mu _{\infty }(W)=\max \limits _{i}\left\{ w_{ii}+\sum \limits _{j=1,i\not =j}^{n}|w_{ij}|\right\} , \quad \mu _{\omega }(W)=\max \limits _{j}\left\{ w_{jj}+\sum \limits _{i=1,i\not =j}^{n}\frac{\omega _{i}}{\omega _{j}}|w_{ij}|\right\} , \end{aligned}$$

where \(\lambda _{max}(\cdot )\) represents the maximum eigenvalue of the matrix \((\cdot )\) and \(\omega _{i} > 0\) for \(i=1,2,\ldots ,n\) are any constant numbers.

Remark 1

\(\mu _{p}(W)\) is the one-sided directional derivative of the mapping \(\Vert \cdot \Vert _{p} : \mathbb {R}^{n \times n}\rightarrow \mathbb {R}_{+}\) at the point \(I_{n}\), in the direction of W. Matrix norm \(\Vert \cdot \Vert _{p}\) holds the non-negative property. But \(\mu _{p}(\cdot )\) is not restricted to be non-negative. It may take negative values since it emphasizes more information about the diagonal elements of the matrix.

Definition 4

(Ke and Miao 2013) The equilibrium point \(s^{*}\) of the system (1) is said to be globally exponentially stable, if there exist constants \(\eta > 0\) and \(M > 0\) such that

$$\begin{aligned} |s_{i}(t)-s_{i}^{*}|^{2} \le Me^{-\eta t}\Vert \Phi -s^{*}\Vert ^{2},\quad t>0, \end{aligned}$$

where \(i=1,\cdots ,n\), \(s(t)=(s_{1}(t),s_{2}(t),\ldots ,s_{n}(t))^{T}\) is a solution of system (1) with the initial value (3).

Lemma 1

(Chandrasekar et al. 2014) Under Assumption 1, if \(f_{j}(\pm T_{j})=0\) \((j=1,2,\ldots ,n)\) then

$$\begin{aligned} |K(a_{ij}(u_{j}))f_{j}(u_{j})-K(a_{ij}(v_{j}))f_{j}(v_{j})| \le \tilde{a}_{ij}^{u}\lambda _{j}|u_{j}-v_{j}|, \end{aligned}$$

for \(i,j=1,2,\ldots ,n\), i.e., for any \(\eta _{ij}(u_{j})\in K(a_{ij}(u_{j})), \eta _{ij}(v_{j})\in K(a_{ij}(v_{j})),\)

$$\begin{aligned} |\eta _{ij}(u_{j})f_{j}(u_{j})-\eta _{ij}(v_{j})f_{j}(v_{j})| \le \tilde{a}_{ij}^{u}\lambda _{j}|u_{j}-v_{j}|, \end{aligned}$$

for \(i,j=1,2,\ldots ,n\), where \(\tilde{a}_{ij}^{u}=\text{ max }\{|\hat{a}_{ij}|,|\check{a}_{ij}|\}\).

Lemma 2

If the activation function \(f_{i}\) is bounded, i.e., \(|f_{i}(x)|\le M_{i}\), for each \(i=1,2,\ldots ,n\) then for any given input \(I=diag\{I_{1},\ldots ,I_{n}\}\), there exists an equilibrium for (1).

Proof

It is clear that \(s^{*}\) is an equilibrium of (1) if and only if it is a solution of the following equation

$$\begin{aligned} -c_{i}s_{i}^{*}+\sum _{j=1}^na_{ij}(s_{i}(t))f_{j}(s_{j}^{*})+\sum _{j=1}^nb_{ij}(s_{i}(t))f_{j}(s_{j}^{*})+I_{i}=0. \end{aligned}$$

By applying the theories of set-valued maps and differential inclusion, we have

$$\begin{aligned} -c_{i}s_{i}^{*}+\sum _{j=1}^nco[\underline{a}_{ij},\overline{a}_{ij}]f_{j}(s_{j}^{*})+\sum _{j=1}^nco[\underline{b}_{ij},\overline{b}_{ij}]f_{j}(s_{j}^{*})+I_{i} \in 0, \end{aligned}$$

or equivalently, for \(i,j=1,2,\ldots ,n\), there exist measurable functions \(\tilde{a}_{ij}(s_{i}^{*}(t)) \in co[\underline{a}_{ij},\overline{a}_{ij}], \tilde{b}_{ij}(s_{i}^{*}(t)) \in co[\underline{b}_{ij},\overline{b}_{ij}]\), such that

$$\begin{aligned} -c_{i}s_{i}^{*}+\sum _{j=1}^n\tilde{a}_{ij}(s_{i}^{*}(t))f_{j}(s_{j}^{*})+\sum _{j=1}^n\tilde{b}_{ij}(s_{i}^{*}(t))f_{j}(s_{j}^{*})+I_{i} = 0. \end{aligned}$$

Noting that \(c_{i}>0\), \(|f_{i}(x)| \le M_{i}, \forall i,j=1,2,\ldots ,n\), one yields that,

$$\begin{aligned} |s_{i}^{*}|&\,\triangleq\, |h_{i}(s_{1}^{*},\ldots ,s_{n}^{*})|=\left| \frac{1}{c_{i}}\left[ \sum _{j=1}^{n}(\tilde{a}_{ij}+\tilde{b}_{ij})f_{j}(s_{j}^{*})+I_{i}\right] \right| , \\&\le \frac{1}{c_{i}}\sum _{j=1}^{n}(|\tilde{a}_{ij}|+|\tilde{b}_{ij}|)M_{j}+|I_{i}|, \\&\triangleq\, D_{i},\quad i=1,2,\ldots ,n. \end{aligned}$$

Thus the function \(h(s)=(h_{1},h_{2},\ldots ,h_{n})^{T}\) maps \(D=[-D_{1},D_{1}]\times \ldots \times [-D_{n},D_{n}]\) into itself. According to Brower’s fixed point theorem, the existence of an equilibrium is obtained. \(\square\)

Lemma 3

(Vidyasagar 1993) Let \(\Vert \cdot \Vert _{p}\) be an induced matrix norm on \(\mathbb {R}^{n\times n}\) and \(\mu _{p}(\cdot )\) be the corresponding matrix measure. Then \(\mu _{p}(\cdot )\) has the following properties:

  1. 1.

    For each \(W \in \mathbb {R}^{n \times n}\), the limit indicated in Definition 3 exists and is well-defined;

  2. 2.

    \(-\Vert W\Vert _{p} \le \mu _{p}(W) \le \Vert W\Vert _{p}\);

  3. 3.

    \(\mu _{p}(\alpha W)=\alpha \mu _{p}(W)\), \(\forall\) \(\alpha \ge 0\), \(\forall W \in \mathbb {R}^{n\times n}\) and in general, \(\mu _{p}(W) \not = \mu _{p}(-W)\);

  4. 4.

    \(\max \{\mu _{p}(A)-\mu _{p}(-B),\mu _{p}(B)-\mu _{p}(-A)\} \le \mu _{p}(A+B)\le \mu _{p}(A)+\mu _{p}(B)\), \(\forall\) \(A,B \in \mathbb {R}^{n \times n}\);

  5. 5.

    \(\mu _{p}(\cdot )\) is a convex function, i.e., \(\mu _{p}(\alpha A +(1-\alpha )B) \le \alpha \mu _{p}(A)+(1-\alpha )\mu _{p}(B)\), \(\forall \,\alpha \in [0,1]\), \(\forall \,A,B \in \mathbb {R}^{n \times n}\).

Lemma 4

(Halanay 1966) Let \(k_{1}\) and \(k_{2}\) be constants with \(k_{1}>k_{2}>0\) and y(t) is a non-negative continuous function defined on \([t_{0}-\tau ,+\infty ]\) which satisfies the following inequality for \(t\ge t_{0}\)

$$\begin{aligned} D^{+}y(t) \le -k_{1}y(t)+k_{2}\overline{y}(t), \end{aligned}$$

where \(\overline{y}(t) \triangleq \sup \nolimits _{t-\tau \le s \le t} y(s)\). Then, \(y(t) \le \overline{y}(t_{0}) e^{-r(t-t_{0})}\), where r is a bound on the exponential convergence rate and is the unique positive solution of \(r=k_{1}-k_{2}e^{r\tau }\), where the upper right Dini derivative \(D^{+} y(t)\) is defined as

$$\begin{aligned} D^{+} y(t)=\lim \limits _{h \rightarrow 0^{+}} \displaystyle {\frac{y(t+h)-y(t)}{h}}, \end{aligned}$$

where \(h\rightarrow 0^{+}\) means that h approaches zero from the right-hand side.

Lemma 5

(He and Cao 2009) Under Assumption 1, let \(\mu _{p}(\cdot )\) be the corresponding matrix measure associated with the induced matrix norm \(\Vert \cdot \Vert _{p}\) on \(\mathbb {R}^{n\times n}\). Then

$$\begin{aligned} \mu _{p}(AF(e(t))) \le \mu _{p}(A^{*}L), \end{aligned}$$

where \(F(e(t))=diag\left\{ \frac{f_{1}(e_{1}(t))}{e_{1}(t)},\ldots ,\frac{f_{n}(e_{n}(t))}{e_{n}(t)}\right\}\), \(L=diag\{l_{1},\ldots ,l_{n}\}\), \(p=1,\infty ,\omega\) and \(A^{*}=(a^{*}_{ij})_{n\times n}=\left\{ \begin{array}{ll} max\{0,a_{ii}\}, &\quad i=j, \\ a_{ij}, &\quad i\not =j. \end{array}\right.\)

Stability analysis

In this section, we will investigate the exponential stability of inertial memristive neural networks using matrix measure strategy. The main result is given in the following theorem.

Theorem 1

Under the Assumption 1, further

$$\begin{aligned} -(\mu _{p}(\mathbb {G})+l\Vert \tilde{A}\Vert _{p})> l\Vert \tilde{B}\Vert _{p}>0, \end{aligned}$$
(7)

where \(\mathbb {G}=\left( \begin{array}{cc} -I_{n} &\quad I_{n} \\ -\mathcal {C} &\quad -\mathcal {D} \end{array} \right)\), \(\mathcal {C}=C+I_{n}-D\), \(\mathcal {D}=D-I_{n}\) and \(l=\max \nolimits _{1\le i \le n} \{l_{i}\}\). Then the equilibrium \((p_{1}^{*}(t),p_{2}^{*}(t))^{T}\) of the system (6) is globally exponentially stable for \(p=1,2,\infty ,\omega\).

Proof

Let us define the error between the trajectory of the system (6) and the corresponding equilibrium \((p_{1}^{*}(t),p_{2}^{*}(t))^{T}\) as,

$$\begin{aligned} e(t)=\left( \begin{array}{c} e_{1}(t) \\ e_{2}(t)\end{array}\right) =\left( \begin{array}{c} p_{1}(t)-p_{1}^{*}(t) \\ p_{2}(t)-p_{2}^{*}(t)\end{array}\right) . \end{aligned}$$

According to the error system, the upper-right Dini derivative of \(\Vert e(t)\Vert _{p}\) with respect to ‘t’ is calculated as follows:

$$\begin{aligned} D^{+} \Vert e(t)\Vert _{p}= \lim \limits _{h\rightarrow 0^{+}}\frac{\Vert e(t+h)\Vert _{p}-\Vert e(t)\Vert _{p}}{h}=\lim \limits _{h\rightarrow 0^{+}}\frac{\Vert e(t)+h\dot{e}(t)+o(h)\Vert _{p}-\Vert e(t)\Vert _{p}}{h}. \end{aligned}$$

We have,

$$\begin{aligned} \left( \begin{array}{c} \dot{e}_{1i}(t) \\ \dot{e}_{2i}(t) \end{array}\right)= \left( \begin{array}{c} -e_{1i}(t)+e_{2i}(t) \\ -\mathbf {c}_{i}e_{1i}(t)-\mathbf {d}_{i}e_{2i}(t)+\sum \limits ^n_{j=1}[\tilde{a}_{ij}(p_{1i}(t))f_{j}(p_{1j}(t))-\tilde{a}_{ij}(p_{1i}^{*}(t))f_{j}(p_{1j}^{*}(t))]\\ +\sum \limits ^n_{j=1}[\tilde{b}_{ij}(p_{1i}(t))f_{j}(p_{1j}(t-\tau (t)))-\tilde{b}_{ij}(p_{1i}^{*}(t)) f_{j}(p_{1j}^{*}(t))]\end{array}\right) . \end{aligned}$$

According to Lemma 1, the above equation can be written as follows:

$$\begin{aligned} \left( \begin{array}{c} \dot{e}_{1i}(t) \\ \dot{e}_{2i}(t) \end{array}\right)= \left( \begin{array}{c} -e_{1i}(t)+e_{2i}(t)\\ -\mathbf {c}_{i}e_{1i}(t)-\mathbf {d}_{i}e_{2i}(t)+\sum \limits ^n_{j=1}\tilde{a}_{ij}^{u}(f_{j}(p_{1j}(t))-f_{j}(p_{1j}^{*}(t))) \\ +\sum \limits ^n_{j=1}\tilde{b}_{ij}^{u}(f_{j}(p_{1j}(t-\tau (t)))-f_{j}(p_{1j}^{*}(t))) \end{array} \right) , \end{aligned}$$

where \(\tilde{a}_{ij}^{u}=max\{|\hat{a}_{ij}|,|\check{a}_{ij}|\}\quad \text{ and }\quad \tilde{b}_{ij}^{u}=max\{|\hat{b}_{ij}|,|\check{b}_{ij}|\}\).

The vector form of the above equation is,

$$\begin{aligned} \dot{e}(t)=\left( \begin{array}{c} \dot{e}_{1}(t) \\ \dot{e}_{2}(t) \end{array}\right) = \left( \begin{array}{c} -e_{1}(t)+e_{2}(t) \\ -\mathcal {C}e_{1}(t)-\mathcal {D}e_{2}(t)+\tilde{A}(f(p_{1}(t))-f(p_{1}^{*}(t)))\\ +\tilde{B}(f(p_{1}(t-\tau (t)))-f(p_{1}^{*}(t))) \end{array}\right) , \end{aligned}$$
(8)

where \(\mathcal {C}=C+I_{n}-D\), \(\mathcal {D}=D-I_{n}\), \(\tilde{A}=(\tilde{a}_{ij}^{u})_{n\times n}\) and \(\tilde{B}=(\tilde{b}_{ij}^{u})_{n\times n}\).

We have the upper right Dini-derivative as,

$$\begin{aligned}&D^{+} \Vert e(t)\Vert _{p}\\&\quad =\lim \limits _{h\rightarrow 0^{+}}\frac{\left\| e(t)+h\left( \begin{array}{c} \dot{e_{1}}(t) \\ \dot{e_{2}}(t) \end{array}\right) +o(h)\right\| _{p} -\Vert e(t)\Vert _{p}}{h} \\&\quad =\lim \limits _{h\rightarrow 0^{+}}\frac{\left\| e(t)+h\left( \begin{array}{c} -e_{1}(t)+e_{2}(t) \\ \xi \end{array}\right) +o(h)\right\| _{p} -\Vert e(t)\Vert _{p}}{h} \\&\quad \le \lim \limits _{h\rightarrow 0^{+}}\frac{\left\| e(t)+h\left( \begin{array}{cc} -I_{n} &\quad I_{n} \\ -\mathcal {C} &\quad -\mathcal {D} \end{array}\right) e(t) \right\| _{p}-\Vert e(t)\Vert _{p}}{h} + \Vert \tilde{A}(f(p_{1}(t))-f(p_{1}^{*}(t)))\Vert _{p} \\&\quad \quad +\Vert \tilde{B}(f(p_{1}(t-\tau (t)))-f(p_{1}^{*}(t)))\Vert _{p} \\&\quad \le \lim \limits _{h\rightarrow 0^{+}}\frac{\left\| e(t)+h\left( \begin{array}{cc} -I_{n} &\quad I_{n} \\ -\mathcal {C} &\quad -\mathcal {D} \end{array}\right) e(t) \right\| _{p}-\Vert e(t)\Vert _{p}}{h} +l\Vert \tilde{A}\Vert _{p}\Vert p_{1}(t)-p_{1}^{*}(t)\Vert _{p}\\&\quad \quad +l\Vert \tilde{B}\Vert _{p}\Vert p_{1}(t-\tau (t))-p_{1}^{*}(t)\Vert _{p} \\&\quad \le \lim \limits _{h\rightarrow 0^{+}}\frac{\Vert I_{n}+h(\mathbb {G})\Vert _{p}-1}{h} \Vert e(t)\Vert _{p} +l\Vert \tilde{A}\Vert _{p}\Vert e_{1}(t)\Vert _{p}+l\Vert \tilde{B}\Vert _{p}\Vert e_{1}(t-\tau (t))\Vert _{p} \\&\quad =\mu _{p}(\mathbb {G})\Vert e(t)\Vert _{p}+l\Vert \tilde{A}\Vert _{p}\Vert e(t)\Vert _{p}+l\Vert \tilde{B}\Vert _{p}\Vert e(t-\tau (t))\Vert _{p} \\&\quad \le (\mu _{p}(\mathbb {G})+l\Vert \tilde{A}\Vert _{p})\Vert e(t)\Vert _{p}+l\Vert \tilde{B}\Vert _{p}\sup \limits _{t-\tau \le \chi \le t}\Vert e(\chi )\Vert _{p} \\&\quad =-(-\mu _{p}(\mathbb {G})-l\Vert \tilde{A}\Vert _{p})\Vert e(t)\Vert _{p}+l\Vert \tilde{B}\Vert _{p}\sup \limits _{t-\tau \le \chi \le t}\Vert e(\chi )\Vert _{p}, \end{aligned}$$

where \(\xi =-\mathcal {C}e_{1}(t)-\mathcal {D}e_{2}(t)+\tilde{A}(f(p_{1}(t))-f(p_{1}^{*}(t)))+\tilde{B}(f(p_{1}(t-\tau (t)))-f(p_{1}^{*}(t)))\). Using Lemma 4, by considering \(k_{1}=-(\mu _{p}(\mathbb {G})+l\Vert \tilde{A}\Vert _{p})\), \(k_{2}=l\Vert \tilde{B}\Vert _{p}\) and the assumption of Theorem 1, \(-(\mu _{p}(\mathbb {G})+l\Vert \tilde{A}\Vert _{p})>l\Vert \tilde{B}\Vert _{p}>0\). We have the result as,

$$\begin{aligned} \Vert e(t)\Vert _{p} \le \sup \limits _{t-\tau \le \chi \le t}\Vert e(\chi )\Vert _{p}e^{-r(t-t_{0})}, \end{aligned}$$

where r is a bound on the exponential convergence rate with

$$\begin{aligned} r=k_{1}-k_{2}e^{r\tau }=-(\mu _{p}(\mathbb {G})+l\Vert \tilde{A}\Vert _{p})-l\Vert \tilde{B}\Vert _{p}e^{r\tau }. \end{aligned}$$

Thus we conclude that, e(t) converges exponentially to zero with a convergence rate r. That is, every trajectory of the system (6) converges exponentially towards the equilibrium \((p_{1}^{*}(t),p_{2}^{*}(t))^T\) with a convergence rate r. This completes the proof. \(\square\)

Remark 2

The fundamental concept of the Lyapunov direct method is that if the total energy of a system is continuously dissipating, then the system will eventually reach an equilibrium point and remain at that point. Hence, the Lyapunov direct method consists of two steps. Firstly, a suitable scalar function is chosen and this function is referred as Lyapunov function Hahn (1967), Bacciotti and Rosier (2005). Secondly, we have to evaluate its first-order time derivative along the trajectory of the system. If the derivative of a Lyapunov function is decreasing along the system trajectory as time increases, then the system energy is dissipating and the system will finally settle down. However, it should be noted that much of the previous work in the stability analysis of neural networks is based on Lyapunov direct methods, where constructing a proper Lyapunov function is important for the stability analysis. Moreover, to construct a proper Lyapunov function for a given system is very difficult and there are no general rules to follow. Compared with Lyapunov direct method, matrix measure strategy is an efficient tool to address the stability problem of nonlinear systems. Generally, the established results by using matrix measure are more superior than common algebraic criterion due to the fact that matrix measure can not only be taken to be positive value but also it can be a negative value. Inspired by the above method, we introduce the so called matrix measure and Halanay inequality to study the stability of the system (1), and some simple but generic criteria have been derived.

Remark 3

Compared to the matrix norm \(\Vert \cdot \Vert _{p}\), the matrix measure, \(\mu _{p}(\cdot )\) are sign sensitive which ensure that the obtained results are more precise and less computational burden those obtained by using matrix norm.

Corollary 1

Under the Assumption 1 and if further there exists matrix \(\Lambda =diag\{\xi _{1},\xi _{2},\ldots ,\xi _{n}\}\) such that

$$\begin{aligned} -(\mu _{p}(\mathbb {G})+l\Vert \tilde{A}\Vert _{p})> l\Vert \tilde{B}\Vert _{p}>0, \end{aligned}$$
(9)

holds where \(\mathbb {G}=\left( \begin{array}{cc} -\Lambda &\quad I_{n} \\ -\mathcal {C} &\quad -\mathcal {D} \end{array} \right)\), \(\mathcal {C}=C+I_{n}-D\), \(\mathcal {D}=D-I_{n}\) and \(l=\max \nolimits _{1\le i \le n} \{l_{i}\}\). Then the equilibrium \((p_{1}^{*}(t),p_{2}^{*}(t))^{T}\) of the system (6) is globally exponentially stable for \(p=1,2,\infty ,\omega\).

Proof

To the system (5), we consider the following transformation:

$$\begin{aligned} p_{1i}(t)&= s_{i}(t), \\ p_{2i}(t)&= \displaystyle {\frac{\mathrm {d}s_{i}(t)}{\mathrm {d}t}}+\xi _{i}s_{i}(t). \end{aligned}$$

and proceed as stated before and the proof is similar to the Theorem 1. \(\square\)

Remark 4

The condition of Theorem 1 certainly does not holds for \(p=1,\infty\). On that case, it is better to introduce \(\xi _{i}>0\), \(i=1,2,\ldots ,n\) in the variable transformation as in Corollary 1. So that the condition holds for \(p=1,\infty\) and leads to the better performance.

Theorem 2

Under the Assumption 1, further

$$\begin{aligned} -(\mu _{p}(\mathbb {G})+\mu _{p}(\mathcal {A}L^{*}))>l\Vert \tilde{B}\Vert _{p}>0, \end{aligned}$$
(10)

holds where \(L^{*}=diag\{l_{1},l_{2},\ldots ,l_{n},1,1,\ldots ,1\}\) and \(\mathcal {A}=\left( \begin{array}{cc} 0 &\quad 0 \\ \tilde{A} &\quad 0 \end{array} \right)\). Then the equilibrium \((p_{1}^{*}(t),p_{2}^{*}(t))^{T}\) of the system (6) is globally exponentially stable for \(p=1,\infty ,\omega\).

Proof

Similar to the proof of Theorem 1, first let us calculate the upper-right Dini-derivative as,

$$\begin{aligned} D^{+} \Vert e(t)\Vert _{p}= \lim \limits _{h\rightarrow 0^{+}}\frac{\Vert e(t+h)\Vert _{p}-\Vert e(t)\Vert _{p}}{h}=\lim \limits _{h\rightarrow 0^{+}}\frac{\Vert e(t)+h\dot{e}(t)+o(h)\Vert _{p}-\Vert e(t)\Vert _{p}}{h}. \end{aligned}$$

The error system is defined as,

$$\begin{aligned} e(t)=\left( \begin{array}{c} e_{1}(t) \\ e_{2}(t) \end{array}\right)= \left( \begin{array}{c} p_{1}(t)-p_{1}^{*}(t) \\ p_{2}(t)-p_{2}^{*}(t) \end{array}\right) . \end{aligned}$$

Also note that, \(e_{1}(t)=(e_{11}(t),e_{12}(t),\ldots ,e_{1n}(t))\), \(f_{i}(p_{1i}(t))-f_{i}(p_{1i}^{*}(t))=f_{i}(p_{1i}^{*}(t){+}e_{1i}(t))-f_{i}(p_{1i}^{*}(t))\), \(f(p_{1}(t))-f(p_{1}^{*}(t))=(f_{11}(p_{11}(t))-f_{11}(p_{11}^{*}(t)),\ldots ,f_{1n}(p_{1n}(t))-f_{1n}(p_{1n}^{*}(t)))\).

Define the function as,

$$\begin{aligned} F_{1}(p_{1}(t))-F_{1}(p_{1}^{*}(t))&= diag\left\{ \frac{f_{11}(p_{11}(t))-f_{11}(p_{11}^{*}(t))}{p_{11}(t)-p_{11}^{*}(t)},\ldots ,\frac{f_{1n}(p_{1n}(t))-f_{1n}(p_{1n}^{*}(t))}{p_{1n}(t)-p_{1n}^{*}(t)}\right\} , \\ F_{2}(p_{2}(t))-F_{2}(p_{2}^{*}(t))&\equiv I_{n}. \end{aligned}$$

Then, \(f(p_{1}(t))-f(p_{1}^{*}(t))\) and \(f(p_{2}(t))-f(p_{2}^{*}(t))\) can be written as,

$$\begin{aligned} f(p_{1}(t))-f(p_{1}^{*}(t))&= (F_{1}(p_{1}(t))-F_{1}(p_{1}^{*}(t)))(p_{1}(t)-p_{1}^{*}(t)), \\ f(p_{2}(t))-f(p_{2}^{*}(t))&= p_{2}(t)-p_{2}^{*}(t)=(F_{2}(p_{2}(t))-F_{2}(p_{2}^{*}(t)))(p_{2}(t)-p_{2}^{*}(t)). \end{aligned}$$

It follows from (8) that,

$$\begin{aligned} \dot{e}(t)&= \left( \begin{array}{c} \dot{e}_{1}(t) \\ \dot{e}_{2}(t) \end{array}\right) = \left( \begin{array}{c} -e_{1}(t)+e_{2}(t)\\ -\mathcal {C}e_{1}(t)-\mathcal {D}e_{2}(t)+\tilde{A}(f(p_{1}(t))-f(p_{1}^{*}(t)))\\ \qquad +\tilde{B}(f(p_{1}(t-\tau (t)))-f(p_{1}^{*}(t))) \end{array} \right) \\&= \left( \begin{array}{cc} -I_{n} &\quad I_{n} \\ -\mathcal {C} &\quad -\mathcal {D} \end{array}\right) \left( \begin{array}{c} e_{1}(t) \\ e_{2}(t) \end{array} \right) + \left( \begin{array}{c} 0 \\ \tilde{A}(f(p_{1}(t))-f(p_{1}^{*}(t))) \end{array} \right) \\&\quad+ \left( \begin{array}{c} 0 \\ \tilde{B}(f(p_{1}(t-\tau (t)))-f(p_{1}^{*}(t))) \end{array} \right) \\&= \left( \begin{array}{cc} -I_{n} &\quad I_{n} \\ -\mathcal {C} &\quad -\mathcal {D} \end{array}\right) \left( \begin{array}{c} e_{1}(t) \\ e_{2}(t) \end{array} \right) +\left( \begin{array}{cc} 0 &\quad 0 \\ \tilde{A} &\quad 0 \end{array}\right) \left( \begin{array}{c} f(p_{1}(t))-f(p_{1}^{*}(t)) \\ f(p_{2}(t))-f(p_{2}^{*}(t)) \end{array}\right) \\&\quad+ \quad \left( \begin{array}{c} 0 \\ \tilde{B}(f(p_{1}(t-\tau (t)))-f(p_{1}^{*}(t))) \end{array} \right) \\&= \left( \begin{array}{cc} -I_{n} &\quad I_{n} \\ -\mathcal {C} &\quad -\mathcal {D} \end{array}\right) \left( \begin{array}{c} e_{1}(t) \\ e_{2}(t) \end{array} \right) + \mathcal {A}\left( \begin{array}{c} F_{1}(p_{1}(t))-F_{1}(p_{1}^{*}(t))(p_{1}(t)-p_{1}^{*}(t)) \\ F_{2}(p_{2}(t))-F_{2}(p_{2}^{*}(t))(p_{2}(t)-p_{2}^{*}(t)) \end{array}\right) \\&\quad+\left( \begin{array}{c} 0 \\ \tilde{B}(f(p_{1}(t-\tau (t)))-f(p_{1}^{*}(t)))\end{array} \right) . \end{aligned}$$

Now by letting,

$$\begin{aligned} F(p(t))-F(p^{*}(t))&= diag\left\{ \frac{f_{11}(p_{11}(t))-f_{11}(p_{11}^{*}(t))}{p_{11}(t)-p_{11}^{*}(t)},\ldots ,\frac{f_{11}(p_{11}(t))-f_{11}(p_{11}^{*}(t))}{p_{11}(t)-p_{11}^{*}(t)} \right\} , \\&=\left( \begin{array}{cc} F_{1}(p_{1}(t))-F_{1}(p_{1}^{*}(t)) &\quad 0 \\ 0 &\quad F_{2}(p_{2}(t))-F_{2}(p_{2}^{*}(t)) \end{array}\right) . \end{aligned}$$

We have the error system as,

$$\begin{aligned} \dot{e}(t)&= \left( \begin{array}{cc} -I_{n} &\quad I_{n} \\ -\mathcal {C} &\quad -\mathcal {D} \end{array}\right) e(t) +\mathcal {A}(F(p(t))-F(p^{*}(t)))(p(t)-p^{*}(t))\\&\quad +\left( \begin{array}{c} 0 \\ \tilde{B}(f(p_{1}(t-\tau (t)))-f(p_{1}^{*}(t)))\end{array} \right) . \end{aligned}$$

Then, we have the upper-right Dini derivative as,

$$\begin{aligned}&D^{+} \Vert e(t)\Vert _{p}\\&\quad\le \lim \limits _{h\rightarrow 0^{+}}\displaystyle {\frac{\left\| e(t)+h\left( \left( \begin{array}{cc} -I_{n} &\quad I_{n} \\ -\mathcal {C} &\quad -\mathcal {D} \end{array}\right) e(t)+\mathcal {A}(F(p(t))-F(p^{*}(t)))(p(t)-p^{*}(t))\right) \right\| _{p}-\Vert e(t)\Vert _{p}}{h}}\\&\quad\quad+ \Vert \tilde{B}(f(p_{1}(t-\tau (t)))-f(p_{1}^{*}(t)))\Vert _{p} \\&\quad\le \lim \limits _{h\rightarrow 0^{+}}\displaystyle {\frac{\Vert e(t)+h(\mathbb {G}+\mathcal {A}(F(p(t))-F(p^{*}(t)))e(t)\Vert _{p}-\Vert e(t)\Vert _{p}}{h}}\\&\quad\quad+\Vert \tilde{B}(f(p_{1}(t-\tau (t)))-f(p_{1}^{*}(t)))\Vert _{p}\\&\quad=\mu _{p}(\mathbb {G}+\mathcal {A}(F(p(t))-F(p^{*}(t))))\Vert e(t)\Vert _{p}+l\Vert \tilde{B}\Vert _{p}\Vert e(t-\tau (t))\Vert _{p}. \end{aligned}$$

It follows from Lemmas 3 and 5 that,

$$\begin{aligned} \mu _{p}(\mathbb {G}+\mathcal {A}(F(p(t))-F(p^{*}(t))))&\le \mu _{p}(\mathbb {G}) + \mu _{p}(\mathcal {A}(F(p(t))-F(p^{*}(t)))), \\&\le \mu _{p}(\mathbb {G}) + \mu _{p}(\mathcal {A}L^{*}), \end{aligned}$$

where \(L^{*}=diag\{l_{1},l_{2},\ldots ,l_{n},1,1,\ldots ,1\}\). Hence, we have

$$\begin{aligned} D^{+} \Vert e(t)\Vert _{p}&\le (\mu _{p}(\mathbb {G}) + \mu _{p}(\mathcal {A}L^{*}))\Vert e(t)\Vert _{p} +l\Vert \tilde{B}\Vert _{p} \sup \limits _{t-\tau \le \chi \le t} \Vert e(\chi )\Vert _{p}, \\ D^{+} \Vert e(t)\Vert _{p}&\le -(-\mu _{p}(\mathbb {G}) - \mu _{p}(\mathcal {A}L^{*}))\Vert e(t)\Vert _{p} +l\Vert \tilde{B}\Vert _{p} \sup \limits _{t-\tau \le \chi \le t} \Vert e(\chi )\Vert _{p}. \end{aligned}$$

Using Lemma 4, by considering \(k_{1}=-(\mu _{p}(\mathbb {G})+\mu _{p}(\mathcal {A}L^{*}))\), \(k_{2}=l\Vert \tilde{B}\Vert _{p}\) and the assumption of our Theorem 2, \(-(\mu _{p}(\mathbb {G})+\mu _{p}(\mathcal {A}L^{*}))> l\Vert \tilde{B}\Vert _{p} > 0\). We have the result as,

$$\begin{aligned} \Vert e(t)\Vert _{p} \le \sup \limits _{t-\tau \le \chi \le t}\Vert e(\chi )\Vert _{p}e^{-r(t-t_{0})}, \end{aligned}$$

where r is a bound on the exponential convergence rate with

$$\begin{aligned} r=k_{1}-k_{2}e^{r\tau }=-(\mu _{p}(\mathbb {G})+\mu _{p}(\mathcal {A}L^{*}))-l\Vert \tilde{B}\Vert _{p} e^{r\tau }. \end{aligned}$$

Thus we conclude that, e(t) converges exponentially to zero with a convergence rate r. That is, every trajectory of the system (6) converges exponentially towards the equilibrium \((p_{1}^{*}(t),p_{2}^{*}(t))^{T}\) with a convergence rate r. This completes the proof. \(\square\)

Remark 5

The stability condition of Theorem 1 utilize only the maximum Lipschitz constant and not the information of each \(l_{i}\). But the stability condition of Theorem 2 utilizes the information of each Lipschitz constant \(l_{i}\). Thus, by letting some terms, we make the term \(\Vert \tilde{A}\Vert _{p}\) as \(\mu _{p}(\mathcal {A}L^{*})\) in Theorem 2 and hence the result is more precise than Theorem 1. But the condition of Theorem 2 holds only for \(p=1,\infty ,\omega\).

Synchronization analysis

Consider the following memristive delayed neural networks,

$$\frac{\mathrm {d}^{2}\overline{y}_{r}(t)}{\mathrm {d}t^{2}}= -d_{r}\frac{\mathrm {d}\overline{y}_{r}(t)}{\mathrm {d}t}-c_{r}\overline{y}_{r}(t)+\sum _{s=1}^{n}a_{rs}(\overline{y}(t))f_{s}(\overline{y}_{s}(t))+\sum _{s=1}^{n}b_{rs}(\overline{y}(t))f_{s}(\overline{y}_{s}(t-\tau (t)))+I_{r}, \quad r=1,\ldots ,n,$$
(11)

where \(\overline{y}(t)=(\overline{y}_{1}(t),\ldots ,\overline{y}_{n}(t))^{T} \in \mathbb {R}^{n}\). \(d_{r}>0\), \(c_{r}>0\) are constants, \(c_{r}\) denotes the rate with which the rth neuron will reset its potential to the resetting state in isolation when disconnected from the networks and external inputs. \(I_{r}=(I_{1},\ldots ,I_{n})^{T}\) and \(f(\overline{y}(t))=(f_{1}(\overline{y}_{1}(t)),\ldots ,f_{n}(\overline{y}_{n}(t)))^{T}\) denotes the external input and the non-linear activation function respectively. \(A(\overline{y}(t))=(a_{rs}(\overline{y}(t)))_{n\times n}\) and \(B(\overline{y}(t))=(b_{rs}(\overline{y}(t)))_{n\times n}\) are memristive connection weights which changes based on the feature of memristor and current–voltage characteristics are defined as,

$$\begin{aligned} a_{rs}(\overline{y}(t))=\left\{ \begin{array}{ll} \hat{a}_{rs}, &\quad|\overline{y}(t)| \le T_{r}, \\ \check{a}_{rs}, &\quad |\overline{y}(t)|> T_{r}, \end{array} \right. \quad b_{rs}(\overline{y}(t))=\left\{ \begin{array}{ll} \hat{b}_{rs}, &\quad{} |\overline{y}(t)| \le T_{r}, \\ \check{b}_{rs}, &\quad|\overline{y}(t)| > T_{r}, \end{array} \right. \end{aligned}$$
(12)

for \(r,s=1,2,\ldots ,n\) in which switching jumps \(T_{r}>0\), \(\hat{a}_{rs}\), \(\check{a}_{rs}\), \(\hat{b}_{rs}\), \(\check{b}_{rs}\) are known constants with respect to memristance. When N inertial MNNs are coupled by a network, we can obtain the following array of linearly coupled inertial MNNs with the dynamics of the kth node as,

$$\frac{\mathrm {d}^{2}x_{k}(t)}{\mathrm {d}t^{2}}= -D\frac{\mathrm {d}x_{k}(t)}{\mathrm {d}t}-Cx_{k}(t)+A(x_{k}(t))f(x_{k}(t))+B(x_{k}(t))f(x_{k}(t-\tau (t)))+I +\alpha \sum _{l=1}^{N}W_{kl}\Gamma \left( \frac{\mathrm {d}x_{l}(t)}{\mathrm {d}t}+x_{l}(t)\right) ,$$
(13)

where \(k=1,\ldots ,N\). \(x_{k}(t)=(x_{k1}(t),\ldots ,x_{kn}(t))^{T} \in \mathbb {R}^{n}\) is the state of the kth neural network. \(D=diag\{d_{1},d_{2},\ldots ,d_{n}\}\) and \(C=diag\{c_{1},c_{2},\ldots ,c_{n}\}\) denote the positive definite matrices. \(A(x_{k}(t))\) and \(B(x_{k}(t))\) are memristive connection weights defined in (12). \(\alpha\) is the positive constant which represents network coupling strength. \(\Gamma\) is the inner coupling matrix. The matrix \(W=(W_{kl})_{N \times N}\) is the constant coupling configuration matrix which is considered to be diffusive. i.e., \(W_{kl} \ge 0\) \((k\not = l)\) and \(W_{kk}=-\sum \nolimits _{l=1,l\not =k}^{N}W_{kl}\). Also, W is not required to be symmetric or irreducible.

The initial condition of the system (13) is given as,

$$\begin{aligned} x_{k}(\chi )=\Phi _{k}(\chi )\quad \text{and}\quad \displaystyle {\frac{\mathrm {d}x_{k}(\chi )}{\mathrm {d}\chi }}=\Psi _{k}(\chi ); \quad -\tau \le \chi \le 0, \end{aligned}$$
(14)

where \(\Phi _{k}(\chi )\), \(\Psi _{k}(\chi ) \in \mathrm {C}^{(1)}([-\tau ,0],\mathbb {R}^n)\). The isolated node of network (13) is given as,

$$\frac{\mathrm {d}^{2}s(t)}{\mathrm {d}t^{2}}= -D\frac{\mathrm {d}s(t)}{\mathrm {d}t}-Cs(t)+A(s(t))f(s(t))+B(s(t))f(s(t-\tau (t)))+I.$$
(15)

The connection weight matrices of A(s(t)) and B(s(t)) are defined as in (12). The initial condition of the system (15) is given as,

$$\begin{aligned} s(\chi )=\Phi (\chi )\quad \text{and}\quad \displaystyle {\frac{\mathrm {d}s(\chi )}{\mathrm {d}\chi }}=\Psi (\chi ); \quad -\tau \le \chi \le 0, \end{aligned}$$
(16)

where \(\Phi (\chi )\), \(\Psi (\chi ) \in \mathrm {C}^{(1)}([-\tau ,0],\mathbb {R}^n)\). By applying the theories of set-valued maps and differential inclusion to (15) as stated in Definition 1 we have,

$$\begin{aligned} \frac{\mathrm {d}^{2}s(t)}{\mathrm {d}t^{2}}+D\frac{\mathrm {d}s(t)}{\mathrm {d}t} \in -Cs(t)+co[\underline{A},\overline{A}]f(s(t))+co[\underline{B},\overline{B}]f(s(t-\tau (t)))+I, \end{aligned}$$
(17)

or equivalently, there exist measurable functions \(\widetilde{A}(s(t)) \in co[\underline{A},\overline{A}], \widetilde{B}(s(t)) \in co[\underline{B},\overline{B}]\), such that

$$\begin{aligned} \frac{\mathrm {d}^{2}s(t)}{\mathrm {d}t^{2}}+D\frac{\mathrm {d}s(t)}{\mathrm {d}t}=-Cs(t)+\widetilde{A}(s(t))f(s(t))+\widetilde{B}(s(t))f(s(t-\tau (t)))+I. \end{aligned}$$
(18)

Consider the following transformation to the system (18),

$$\begin{aligned} p(t)&= s(t), \\ q(t)&= \displaystyle {\frac{\mathrm {d}s(t)}{\mathrm {d}t}}+s(t). \end{aligned}$$

Then we have the system (18) as,

$$\begin{aligned} \left( \begin{array}{c} \dot{p}(t) \\ \dot{q}(t)\end{array}\right) = \left( \begin{array}{c} -p(t)+q(t) \\ -\mathcal {C}p(t)-\mathcal {D}q(t)+\widetilde{A}(p(t))f(p(t))\\ +\widetilde{B}(p(t))f(p(t-\tau (t)))+I \end{array}\right) , \end{aligned}$$
(19)

where \(\mathcal {C}=C+I_{n}-D\) and \(\mathcal {D}=D-I_{n}\). The pinning controlled networks of the system (13) is given as,

$$\begin{aligned} \frac{\mathrm {d}^{2}x_{k}(t)}{\mathrm {d}t^{2}}&= -D\frac{\mathrm {d}x_{k}(t)}{\mathrm {d}t}-Cx_{k}(t)+A(x_{k}(t))f(x_{k}(t))+B(x_{k}(t))f(x_{k}(t-\tau (t)))+I \nonumber \\&\quad+\alpha \sum _{l=1}^{N}W_{kl}\Gamma \left( \frac{\mathrm {d}x_{l}(t)}{\mathrm {d}t}+x_{l}(t)\right) \nonumber \\&\quad-\alpha \sigma _{k}\Gamma \left( \frac{\mathrm {d}(x_{k}(t)-s(t))}{\mathrm {d}t}+(x_{k}(t)-s(t))\right) , \end{aligned}$$
(20)

where \(k=1,2,\ldots ,N\) and \(\sigma _{k}=1\) if the node is pinned, otherwise \(\sigma _{k}=0\). \(A(x_{k}(t))\), \(B(x_{k}(t))\) and the initial condition of the system are given in (12) and (14) respectively.

By applying the theories of set-valued maps and differential inclusion to the form as stated in Definition 1 to the system (20) we have,

$$\begin{aligned}&\frac{\mathrm {d}^{2}x_{k}(t)}{\mathrm {d}t^{2}}+D\frac{\mathrm {d}x_{k}(t)}{\mathrm {d}t} \in -Cx_{k}(t)+co[\underline{A},\overline{A}]f(x_{k}(t))+co[\underline{B},\overline{B}]f(x_{k}(t-\tau (t)))+I\\&\quad +\alpha \sum _{l=1}^{N}W_{kl}\Gamma \left( \frac{\mathrm {d}x_{l}(t)}{\mathrm {d}t}+x_{l}(t)\right) \\&\quad -\alpha \sigma _{k}\Gamma \left( \frac{\mathrm {d}(x_{k}(t)-s(t))}{\mathrm {d}t}+(x_{k}(t)-s(t))\right) , \end{aligned}$$

or equivalently, there exist measurable functions \(\widetilde{A}(x_{k}(t)) \in co[\underline{A},\overline{A}], \widetilde{B}(x_{k}(t)) \in co[\underline{B},\overline{B}]\), such that

$$\begin{aligned} \frac{\mathrm {d}^{2}x_{k}(t)}{\mathrm {d}t^{2}}+D\frac{\mathrm {d}x_{k}(t)}{\mathrm {d}t}&= -Cx_{k}(t)+\widetilde{A}(x_{k}(t))f(x_{k}(t))+\widetilde{B}(x_{k}(t))f(x_{k}(t-\tau (t)))+I \\&\quad+\alpha \sum _{k=1}^{N}W_{kl}\Gamma \left( \frac{\mathrm {d}x_{l}(t)}{\mathrm {d}t}+x_{l}(t)\right) \\&\quad-\alpha \sigma _{k}\Gamma \left( \frac{\mathrm {d}(x_{k}(t)-s(t))}{\mathrm {d}t}+(x_{k}(t)-s(t))\right) . \end{aligned}$$

Consider the following transformation to the above system,

$$\begin{aligned} y_{k}(t)&= x_{k}(t),\\ z_{k}(t)&= \displaystyle {\frac{\mathrm {d}x_{k}(t)}{\mathrm {d}t}}+x_{k}(t). \end{aligned}$$

Then we have,

$$\begin{aligned} \left( \begin{array}{c} \dot{y}_{k}(t) \\ \dot{z}_{k}(t) \end{array}\right) = \left( \begin{array}{c} -y_{k}(t)+z_{k}(t) \\ -\mathcal {C}y_{k}(t)-\mathcal {D}z_{k}(t)+\widetilde{A}(y_{k}(t))f(y_{k}(t))+\widetilde{B}(y_{k}(t)) f(y_{k}(t-\tau (t))) \\ +I+\alpha \sum \limits _{l=1}^{N}W_{kl}\Gamma (z_{l}(t))-\alpha \sigma _{k}\Gamma (z_{k}(t)-q(t))\end{array}\right) , \end{aligned}$$

where \(\mathcal {C}=C+I_{n}-D\) and \(\mathcal {D}=D-I_{n}\). Now, let us introduce a Laplacian matrix \(L=(l_{kl})_{N \times N}\) of the coupling network and define \(L=-W\). Then we have,

$$\begin{aligned} \left( \begin{array}{c} \dot{y}_{k}(t) \\ \dot{z}_{k}(t) \end{array}\right) =\left( \begin{array}{c}-y_{k}(t)+z_{k}(t) \\ -\mathcal {C}y_{k}(t)-\mathcal {D}z_{k}(t)+\widetilde{A}(y_{k}(t))f(y_{k}(t))+\widetilde{B}(y_{k}(t)) \\ \times\, f(y_{k}(t-\tau (t)))+I -\alpha \sum \limits _{l=1}^{N}l_{kl}\Gamma (z_{l}(t))-\alpha \sigma _{k}\\ \times \,\Gamma (z_{k}(t)-q(t))\end{array}\right) . \end{aligned}$$
(21)

Let us define the error dynamical network as,

$$\begin{aligned} e_{k}(t)=\left( \begin{array}{c} e_{1k}(t) \\ e_{2k}(t)\end{array}\right) =\left( \begin{array}{c} y_{k}(t)-p(t) \\ z_{k}(t)-q(t)\end{array}\right) . \end{aligned}$$

Subtracting (19) from (21), we obtain the following,

$$\begin{aligned} \dot{e}_{k}(t)=\left( \begin{array}{c} \dot{e}_{1k}(t) \\ \dot{e}_{2k}(t)\end{array}\right) =\left( \begin{array}{c} -y_{k}(t)+z_{k}(t)+p(t)-q(t) \\ -\mathcal {C}y_{k}(t)-\mathcal {D}z_{k}(t)+\widetilde{A}(y_{k}(t))f(y_{k}(t))+\widetilde{B}(y_{k}(t)) f(y_{k}(t-\tau (t))) \\ -\alpha \sum \limits _{l=1}^{N}l_{kl}\Gamma (z_{l}(t))-\alpha \sigma _{k}\Gamma (z_{k}(t)-q(t))+\mathcal {C}p(t)+\mathcal {D}q(t)\\ -\widetilde{A}(p(t)) f(p(t))-\widetilde{B}(p(t))f(p(t-\tau (t))) \end{array}\right) , \end{aligned}$$

According to Lemma 1, the above system can be written as follows:

$$\begin{aligned} \left( \begin{array}{c} \dot{e}_{1k}(t) \\ \dot{e}_{2k}(t)\end{array}\right) =\left( \begin{array}{c} -e_{1k}(t)+e_{2k}(t) \\ -\mathcal {C}e_{1k}(t)-\mathcal {D}e_{2k}(t)+\tilde{\tilde{A}}(f(y_{k}(t))-f(p(t))) \\ +\tilde{\tilde{B}}(f(y_{k}(t-\tau (t)))-f(p(t-\tau (t)))) \\ -\alpha \sum \limits _{l=1}^{N}l_{kl}\Gamma (e_{2l}(t))-\alpha \sigma _{k}\Gamma (e_{2k}(t))\end{array}\right) , \end{aligned}$$

where \(\tilde{\tilde{A}}=\text{ max }\{|\overline{a}_{rs}|,|\underline{a}_{rs}|\}\quad \text{ and }\quad \tilde{\tilde{B}}=\text{ max }\{|\overline{b}_{rs}|,|\underline{b}_{rs}|\}.\)

Using the Kronecker product, the above system can be written in the following compact form,

$$\begin{aligned} \left( \begin{array}{c}\dot{e}_{1}(t) \\ \dot{e}_{2}(t)\end{array}\right) =\left( \begin{array}{c} -e_{1}(t)+e_{2}(t) \\ -(I_{N}\otimes \mathcal {C})e_{1}(t)-(I_{N}\otimes \mathcal {D})e_{2}(t)+(I_{N}\otimes \tilde{\tilde{A}})(f(y_{k}(t))-f(p(t)))\\ +(I_{N}\otimes \tilde{\tilde{B}})(f(y_{k}(t-\tau (t)))-f(p(t-\tau (t))))\\ -\alpha ((L+\Sigma )\otimes \Gamma )e_{2}(t) \end{array}\right) . \end{aligned}$$
(22)

Lemma 6

(Cao et al. 2006) For matrices A, B, C and D with appropriate dimensions, one has

1.:

\((\alpha A)\otimes B=A \otimes (\alpha B)\).

2.:

\((A+B)\otimes C= A\otimes C+B\otimes C\).

3.:

\((A\otimes B)(C\otimes D)=(AC)\otimes (BD)\).

Definition 5

The linearly coupled inertial MNNs (13) is said to be exponentially synchronized if the error system (22) is exponentially stable, i.e., there exist two constants \(\overline{\alpha }>1\) and \(\overline{\beta }>0\) such that

$$\begin{aligned} \Vert e(t)\Vert _{p} \le \overline{\alpha }\sup _{t_{0}-\tau \le \theta \le t_{0}}\Vert e(\theta )\Vert _{p}e^{-\overline{\beta } (t-t_{0})},\quad t\ge t_{0}. \end{aligned}$$

Now, we present the synchronization result in the following theorem based on the above transformations.

Theorem 3

Under the Assumption 1, further

$$\begin{aligned} -(\mu _{p}(\mathcal {K})+l\Vert I_{N}\otimes \tilde{\tilde{A}}\Vert _{p})>l\Vert I_{N}\otimes \tilde{\tilde{B}}\Vert _{p}>0, \end{aligned}$$
(23)

where \(\mathcal {K}=\left( \begin{array}{cc} -I_{Nn} &\quad I_{Nn} \\ -(I_{N}\otimes \mathcal {C}) &\quad -(I_{N}\otimes \mathcal {D})-\alpha (L+\Sigma )\otimes \Gamma \end{array}\right)\) and \(l=\max \nolimits _{1 \le i \le n}\{l_{i}\}\). Then the pinning controlled inertial MNNs (22) is globally exponentially synchronized for \(p=1,2,\infty ,\omega\).

Proof

The upper-right Dini derivative of the synchronization error, \(\Vert e(t)\Vert _{p}\) with respect to t is calculated as follows,

$$\begin{aligned} D^{+} \Vert e(t)\Vert _{p}&= \lim \limits _{h\rightarrow 0^{+}}\frac{\Vert e(t+h)\Vert _{p}-\Vert e(t)\Vert _{p}}{h}=\lim \limits _{h\rightarrow 0^{+}}\frac{\Vert e(t)+h\dot{e}(t)+o(h)\Vert _{p}-\Vert e(t)\Vert _{p}}{h} \\&= \lim \limits _{h\rightarrow 0^{+}}\frac{\left\| e(t)+h\left( \begin{array}{c} \dot{e_{1}}(t) \\ \dot{e_{2}}(t) \end{array}\right) +o(h)\right\| _{p} -\Vert e(t)\Vert _{p}}{h} \\&= \lim \limits _{h\rightarrow 0^{+}}\frac{\left\| e(t)+h\left( \begin{array}{c} -e_{1}(t)+e_{2}(t) \\ \lambda \end{array}\right) +o(h)\right\| _{p} -\Vert e(t)\Vert _{p}}{h} \\&\le \lim \limits _{h\rightarrow 0^{+}}\frac{\left\| e(t)+h\left( \begin{array}{cc} -I_{Nn} &\quad I_{Nn} \\ -(I_{N}\otimes \mathcal {C}) &\quad -(I_{N}\otimes \mathcal {D})-\alpha (L+\Sigma )\otimes \Gamma \end{array}\right) e(t) \right\| _{p}-\Vert e(t)\Vert _{p}}{h} \\&\quad+ \Vert (I_{N}\otimes \tilde{\tilde{A}})(f(y_{k}(t))-f(p(t)))\Vert _{p}\\&\quad+\Vert (I_{N}\otimes \tilde{\tilde{B}})(f(y_{k}(t-\tau (t)))-f(p(t-\tau (t))))\Vert _{p} \\&\le \lim \limits _{h\rightarrow 0^{+}}\frac{\left\| e(t)+h\left( \begin{array}{cc} -I_{Nn} &\quad I_{Nn} \\ -(I_{N}\otimes \mathcal {C}) &\quad -(I_{N}\otimes \mathcal {D})-\alpha (L+\Sigma )\otimes \Gamma \end{array}\right) e(t) \right\| _{p}-\Vert e(t)\Vert _{p}}{h} \\&\quad+l\Vert I_{N}\otimes \tilde{\tilde{A}}\Vert _{p}\Vert y_{k}(t)-p(t)\Vert _{p}+l\Vert I_{N}\otimes \tilde{\tilde{B}}\Vert _{p}\Vert y_{k}(t-\tau (t))-p(t-\tau (t))\Vert _{p} \\&\le \lim \limits _{h\rightarrow 0^{+}}\frac{\Vert I_{n}+h(\mathcal {K})\Vert _{p}-1}{h} \Vert e(t)\Vert _{p} +l\Vert I_{N}\otimes \tilde{\tilde{A}}\Vert _{p}\Vert e_{1}(t)\Vert _{p}\\&\quad+l\Vert I_{N}\otimes \tilde{\tilde{B}}\Vert _{p}\Vert e_{1}(t-\tau (t))\Vert _{p} \\&= \mu _{p}(\mathcal {K})\Vert e(t)\Vert _{p}+l\Vert I_{N}\otimes \tilde{\tilde{A}}\Vert _{p}\Vert e(t)\Vert _{p}+l\Vert I_{N}\otimes \tilde{\tilde{B}}\Vert _{p}\Vert e(t-\tau (t))\Vert _{p} \\&\le (\mu _{p}(\mathcal {K})+l\Vert I_{N}\otimes \tilde{\tilde{A}}\Vert _{p})\Vert e(t)\Vert _{p}+l\Vert I_{N}\otimes \tilde{\tilde{B}}\Vert _{p}\sup \limits _{t-\tau \le \chi \le t}\Vert e(\chi )\Vert _{p} \\&= -(-\mu _{p}(\mathcal {K})-l\Vert I_{N}\otimes \tilde{\tilde{A}}\Vert _{p})\Vert e(t)\Vert _{p}+l\Vert I_{N}\otimes \tilde{\tilde{B}}\Vert _{p}\sup \limits _{t-\tau \le \chi \le t}\Vert e(\chi )\Vert _{p}, \end{aligned}$$

where \(\lambda =-(I_{N}\otimes \mathcal {C})e_{1}(t)-(I_{N}\otimes \mathcal {D})e_{2}(t)+(I_{N}\otimes \tilde{\tilde{A}})(f(y_{k}(t))-f(p(t)))+(I_{N}\otimes \tilde{\tilde{B}})(f(y_{k}(t-\tau (t)))-f(p(t-\tau (t))))-\alpha ((L+\Sigma )\otimes \Gamma )e_{2}(t)\). Using Lemma 4 by considering \(k_{1}=-(\mu _{p}(\mathcal {K})+l\Vert I_{N}\otimes \tilde{\tilde{A}}\Vert _{p})\), \(k_{2}=l\Vert I_{N}\otimes \tilde{\tilde{B}}\Vert _{p}\) and the assumption of Theorem 3, \(-(\mu _{p}(\mathcal {K})+l\Vert I_{N}\otimes \tilde{\tilde{A}}\Vert _{p})> l\Vert I_{N}\otimes \tilde{\tilde{B}}\Vert _{p}>0\). We have the result as,

$$\begin{aligned} \Vert e(t)\Vert _{p} \le \sup \limits _{t_{0}-\tau \le \chi \le t_{0}}\Vert e(\chi )\Vert _{p}e^{-r(t-t_{0})}, \end{aligned}$$

where r is a bound on the exponential convergence rate with

$$\begin{aligned} r=k_{1}-k_{2}e^{r\tau }=-(\mu _{p}(\mathcal {K})+l\Vert I_{N}\otimes \tilde{\tilde{A}}\Vert _{p})-l\Vert I_{N}\otimes \tilde{\tilde{B}}\Vert _{p}e^{r\tau }. \end{aligned}$$

Thus, we conclude that e(t) converges exponentially to zero with a convergence rate r. It implies that the global synchronization of the system (22) is achieved. This completes the proof. \(\square\)

Theorem 4

Under Assumption 1, if there exists a matrix measure \(\mu _{p}(\cdot )(p=1,\infty ,\omega )\) such that

$$\begin{aligned} -(\mu _{p}(\mathcal {K})+\mu _{p}(\mathcal {A}L^{*})> l\Vert I_{N} \otimes \tilde{\tilde{B}}\Vert _{p} > 0, \end{aligned}$$
(24)

where \(\mathcal {A}=\left( \begin{array}{cc} 0 &\quad 0 \\ I_{N}\otimes \tilde{\tilde{A}} &\quad 0 \end{array}\right)\), \(L^{*}=diag\{{l_{1},l_{2},\ldots ,l_{n},1,1,\ldots ,1\}}\). Then the pinning controlled coupled inertial MNNs (22) is globally exponentially synchronized.

Proof

Similar to the proof of Theorem 2. \(\square\)

Remark 6

Compared with the results on pinning synchronization of the coupled inertial delayed neural networks of Hu et al. (2015), our results on pinning synchronization are with discontinuous right-hand side. So the results in this paper are more superior than in Hu et al. (2015).

Remark 7

Recently, many of the researchers have developed synchronization results by constructing suitable Lyapunov–Krasovskii functional and by using linear matrix inequality techniques. Several effective methods such as delay decomposition approach, convex combination, free weighting matrix approach and inequalities technique have been explored and developed in the literature, see for examples Balasubramaniam et al. (2011), Balasubramaniam and Vembarasan (2012). Moreover, in Wang and Shen (2015), authors have concerned the synchronization of memristor-based neural networks with time-varying delays is investigated by employing the Newton–Leibniz formulation and inequality technique. In Bao and Cao (2015), authors deal with the problem of projective synchronization of fractional-order memristor-based neural networks in the sense of Caputo’s fractional derivative. However, to the best of our knowledge, upto now the memristor based neural networks have been investigated by the Lyapunov–Krasovskii method but the result discussed in this paper is more superior than the results that are obtained by constructing a Lyapunov–Krasovskii functional. Another important feature of the derived results is because of the usage of matrix measure and Halanay inequality.

Remark 8

In the real world, resistors are used to model connection weight to emulate the synapses in analog implementation of neural networks. By making use of the memristor which has memory and behaviour more like biological synapses we can able to develop memristor based neural network models. The memristive neural networks have characteristics of complex brain networks such as node degree, distribution and assortativity both at the whole-brain scale of human neuroimaging. With the development of application as well as many integrated technologies, memristive neural networks have proven as a promising architecture in neuromorphic systems for the high-density, non-volatility, and unique memristive characteristic. Due to the promising applications in wide areas, various memristive materials, such as ferroelectric materials, chalcogenide materials, metal oxides have attracted great attention. Further, several physical mechanisms have been proposed to illustrate the memristive behaviors, such as electronic barrier modulation from migration of oxygen vacancies, voltage-controlled domain configuration, formation and annihilation of conducting filaments via diffusion of oxygen vacancies, trapping of charge carriers and metal ions from electrodes. Motivated by the aforementioned applications, in this paper we investigate the problem of stability and synchronization analysis of inertial memristive neural networks with time delays.

Numerical simulation

In this section, numerical examples are presented to illustrate the effectiveness and usefulness of the theoretical result.

Example 1

Consider the following inertial MNNs:

$$\begin{aligned} \frac{\mathrm {d}^{2}s_{i}(t)}{\mathrm {d}t^{2}} &= -d_{i}\frac{\mathrm {d}s_{i}(t)}{\mathrm {d}t}-c_{i}s_{i}(t)+\sum _{i=1}^n a_{ij}(s_{i}(t))f_{j}(s_{j}(t)) \nonumber \\&\quad+\sum _{i=1}^n b_{ij}(s_{i}(t))f_{j}(s_{j}(t-\tau (t)))+I_{i}, \end{aligned}$$
(25)

where the activation function is given as, \(f_{j}(x)=\sin (|x|-1)\) for \(j=1,2\), \(d_{1}=c_{1}=6\), \(d_{2}=c_{2}=8\), \(I_{1}=I_{2}=6\), and \(\tau (t)=\frac{e^{t}}{1+e^{t}}\). Also the memristive weights of the system (25) is given as,

$$\begin{aligned} \begin{array}{ll} a_{11}(s_{1}(t))=\left\{ \begin{array}{ll}\frac{-0.01\pi \sqrt{2}}{8}, &{}\quad |s_{1}(t)| \le 1, \\ \frac{-0.07\pi \sqrt{2}}{8}, &{}\quad |s_{1}(t)|> 1, \end{array} \right. &{}\quad b_{11}(s_{1}(t))= \left\{ \begin{array}{ll} 0.01, &{}\quad |s_{1}(t)| \le 1, \\ 0.05, &{}\quad |s_{1}(t)|> 1, \end{array} \right. \\ a_{12}(s_{1}(t))=\left\{ \begin{array}{ll} 0.06, &{}\quad |s_{1}(t)| \le 1, \\ 0.04, &{}\quad |s_{1}(t)|> 1, \end{array} \right. &{}\quad b_{12}(s_{1}(t))= \left\{ \begin{array}{ll} 0.04+\frac{\pi }{16}, &{}\quad |s_{1}(t)| \le 1, \\ 0.01+\frac{\pi }{16}, &{}\quad |s_{1}(t)|> 1, \end{array} \right. \\ a_{21}(s_{2}(t))=\left\{ \begin{array}{ll} \frac{-0.01\pi \sqrt{2}}{8}, &{}\quad |s_{2}(t)| \le 1, \\ \frac{-0.07\pi \sqrt{2}}{8}, &{}\quad |s_{2}(t)|> 1,\end{array} \right. &{}\quad b_{21}(s_{2}(t))=\left\{ \begin{array}{ll} 0.02, &{}\quad |s_{2}(t)| \le 1, \\ 0.06, &{}\quad |s_{2}(t)|> 1, \end{array} \right. \\ a_{22}(s_{2}(t))=\left\{ \begin{array}{ll} 0.06, &{}\quad |s_{2}(t)| \le 1, \\ 0.04, &{}\quad |s_{2}(t)|> 1, \end{array} \right. &{}\quad b_{22}(s_{2}(t))=\left\{ \begin{array}{ll} 0.09+\frac{\pi }{16}, &{}\quad |s_{2}(t)| \le 1, \\ 1.01+\frac{\pi }{16}, &{}\quad |s_{2}(t)| > 1. \end{array} \right. \end{array} \end{aligned}$$

In order to show that the system is globally exponentially stable, we have to prove \(-(\mu _{p}(\mathbb {G})+l\Vert \tilde{A}\Vert _{p})>l\Vert \tilde{B}\Vert _{p} > 0\), where \(\mathbb {G}=\left( \begin{array}{cc} -I_{n} &\quad I_{n} \\ -\mathcal {C} &\quad -\mathcal {D}\end{array}\right)\).

From the given example we calculate the following,

$$\begin{aligned} \mathcal {C}&= C+I_{n}-D=\left( \begin{array}{cc} 1 &\quad 0 \\ 0 &\quad 1 \end{array}\right) ,\quad \mathcal {D}=D-I_{n}=\left( \begin{array}{cc} 5 &\quad 0 \\ 0 &\quad 7 \end{array}\right) , \\ \tilde{A}&= \left( \begin{array}{cc} \frac{-0.04\pi \sqrt{2}}{8} &\quad 0.05 \\ \frac{-0.04\pi \sqrt{2}}{8} &\quad 0.05 \end{array}\right) , \quad \tilde{B}=\left( \begin{array}{cc} 0.03 &\quad 0.025+\frac{\pi }{16} \\ 0.04 &\quad 0.55+\frac{\pi }{16} \end{array}\right) \end{aligned}$$

and \(l_{i}=1\) for \(i=1,2\).

Fig. 1
figure 1

a, b The state trajectories of inertial memristive neural networks of Example 1 with different initial values

Full size image

When \(p=2\), we have \(\mu _{2}(G)=-1, \Vert \tilde{A}\Vert _{2}=0.0774, \Vert \tilde{B}\Vert _{2}=0.7799\). Hence we have \(0.9226>0.7763>0\). By choosing \(\xi _{1}=\xi _{2}=2.1\) and \(p=\infty\) we have, \(\mu _{\infty }(\mathbb {G})=-1.1\), \(\Vert \tilde{A}\Vert _{\infty }=0.0722\), \(\Vert \tilde{B}\Vert _{\infty }=0.7863\). Hence we obtain \(1.0278>0.7863>0\). Figure 1a, b, depicts the trajectories of system (25) for different initial values. It is clear that the equilibrium is globally exponentially stable. Hence, the Theorem 1 is verified.

Example 2

Consider the following pinned inertial MNNs with 10 nodes:

$$\begin{aligned} \frac{\mathrm {d}^{2}x_{k}(t)}{\mathrm {d}t^{2}}&= -D\frac{\mathrm {d}x_{k}(t)}{\mathrm {d}t}-Cx_{k}(t)+A(x_{k}(t))f(x_{k}(t))+B(x_{k}(t))f(x_{k}(t-\tau (t))) \nonumber \\&\quad+ I +\alpha \sum _{l=1}^{N}W_{kl}\Gamma \left( \frac{\mathrm {d}x_{l}(t)}{\mathrm {d}t}+x_{l}(t)\right) , \end{aligned}$$
(26)

where \(k=1,2,\ldots ,10\). \(x_{k}(t)=(x_{k1}(t),x_{k2}(t))^{T} \in \mathbb {R}^{2}\) is the state variable of kth node. The isolated node of MNNs (26) is given as,

$$\begin{aligned} \frac{\mathrm {d}^{2}s(t)}{\mathrm {d}t^{2}}=-D\frac{\mathrm {d}s(t)}{\mathrm {d}t}-Cs(t)+A(s(t))f(s(t))+B(s(t))f(s(t-\tau (t)))+I, \end{aligned}$$
(27)

where \(s(t)=(s_{1}(t),s_{2}(t))^{T} \in \mathbb {R}^{2}\). Let \(N=10\), \(f(x_{k}(t))=(\tanh (|x_{k1}(t)|-1),\tanh (|x_{k2}(t)|-1))^{T}\), \(I=(0.2, 0.6)^{T}\) and \(\tau (t)=\frac{0.15e^{t}}{1+e^{t}}\). So, it is easy to get \(l_{k}=1\) and \(\rho =0.0375\). The coefficient matrices are given as, \(C=\left( \begin{array}{cc} 0.2 &\quad 0 \\ 0 &\quad 0.1 \end{array}\right)\), \(D=\left( \begin{array}{cc} 0.9 &\quad 0 \\ 0 &\quad 0.8 \end{array}\right)\), and

$$\begin{aligned} \begin{array}{ll} a_{11}(x_{k}(t))=\left\{ \begin{array}{ll} -0.08, &\quad |x_{k}(t)| \le 1, \\ -0.95, &\quad |x_{k}(t)|> 1, \end{array} \right. &\quad b_{11}(x_{k}(t))=\left\{ \begin{array}{ll} 0.03, &\quad |x_{k}(t)| \le 1, \\ 0.05, &\quad |x_{k}(t)|> 1, \end{array} \right. \\ a_{12}(x_{k}(t))=\left\{ \begin{array}{ll} 0.05, &\quad |x_{k}(t)| \le 1, \\ 0.28, &\quad |x_{k}(t)|> 1, \end{array} \right. &\quad b_{12}(x_{k}(t))=\left\{ \begin{array}{ll} -0.005, &\quad |x_{k}(t)| \le 1, \\ -0.015, &\quad |x_{k}(t)|> 1, \end{array} \right. \\ a_{21}(x_{k}(t))=\left\{ \begin{array}{ll} 0.95, &\quad |x_{k}(t)| \le 1, \\ 0.05, &\quad |x_{k}(t)|> 1, \end{array} \right. &\quad b_{21}(x_{k}(t))=\left\{ \begin{array}{ll} -0.075, &\quad |x_{k}(t)| \le 1, \\ -0.095, &\quad |x_{k}(t)|> 1, \end{array} \right. \\ a_{22}(x_{k}(t))=\left\{ \begin{array}{ll} -0.06, &\quad |x_{k}(t)| \le 1, \\ -0.28, &\quad |x_{k}(t)|> 1, \end{array} \right. &\quad b_{22}(x_{k}(t))=\left\{ \begin{array}{ll} 0.02, &\quad |x_{k}(t)| \le 1, \\ 0.08, &\quad |x_{k}(t)| > 1. \end{array} \right. \end{array} \end{aligned}$$

From the given example we calculate the following,

$$\begin{aligned}&\mathbf {C}=C+I_{n}-D=\left( \begin{array}{cc} 0.3 &\quad 0 \\ 0 &\quad 0.3 \end{array}\right) , \quad \mathbf {D}=D-I_{n}=\left( \begin{array}{cc} -0.1 &\quad 0 \\ 0 &\quad -0.2 \end{array}\right) ,\\&\tilde{\tilde{A}}=\left( \begin{array}{cc} -0.5 &\quad 0.2 \\ 0.5 &\quad -0.1 \end{array}\right) \quad \hbox {and}\quad \tilde{\tilde{B}}=\left( \begin{array}{cc} 0.04 &\quad -0.01 \\ -0.08 &\quad 0.05 \end{array}\right) . \end{aligned}$$

The coupling matrix W is determined by the directed topology given in Fig. 2. From Fig. 2, it is clear that the pinning node is 1 and 9. The inner coupling matrix \(\Gamma\) is given as, \(\Gamma =diag\{6,4\}\) and the coupling strength is chosen as \(\alpha =20\). In order to show that the system is synchronizable, \(-(\mu _{p}(\mathcal {K})+l\Vert \tilde{\tilde{A}}\Vert _{p})>l\Vert \tilde{\tilde{B}}\Vert _{p}>0\). Choosing \(p=2\) we have, \(\mu _{2}(\mathcal {K})=-0.9805, \Vert \tilde{\tilde{A}}\Vert _{p}=0.7616\) and \(\Vert \tilde{\tilde{B}}\Vert _{p}=0.1023\). Hence we have, \(0.2189>0.1023>0\). Based on the conclusion of Theorem 3 the coupled inertial memristive neural networks can be exponentially synchronized. The synchronization state trajectories \(x_{k}(t), k=1,2,\ldots ,10\) and objective state trajectory s(t) are given in Fig. 3a, b respectively. The synchronization of error system \(e_{k}(t), k=1,2,\ldots ,10\) is given in Fig. 4. Hence, the Theorem 3 is verified.

Remark 9

Note that coupled complex dynamical networks can be represented by a large number of interconnected nodes, in which each node consists of a dynamical system. Owing to their applications in real life, many researchers have studied coupled complex dynamical networks recently. In addition, it can be seen from previous researches that most of the authors have attempted to find a proper controller such that the considered coupled complex network can achieve synchronization, i.e., the synchronization error dynamical network is asymptotically stable. However, controlling all nodes in a network may result in a high cost, and is hard to implement. To tackle these issues, the pinning control scheme has been adopted to study synchronization of coupled complex networks, in which only some selected nodes need to be controlled.

Remark 10

The condition of Theorem 3 is difficult to verify for the case \(p=1,\infty ,\omega\) in our example. In Example 1, by introducing the coefficient matrix \(\xi _{i}\) in variable transformation we verified the stability condition for \(p=\infty\). But this transformation is not applicable in our synchronization case.

Fig. 2
figure 2

Digraph with 10 nodes

Full size image
Fig. 3
figure 3

a State trajectories \(x_k(t)\) of system (26) and b objective state trajectory s(t) of system (27)

Full size image
Fig. 4
figure 4

Synchronization error for Example 2

Full size image

Conclusion

In this paper, we have discussed the global exponential stability of inertial memristive neural networks and global exponential pinning synchronization of coupled inertial memristive neural networks by using matrix measure strategy and Halanay inequality. Firstly, matrix measure strategies are utilized to analyze the closed-loop error system, under which two sufficient criteria have been established such that the exponential synchronization can be achieved. The model based on the memristor widens the application scope for the design of neural networks. Finally, numerical simulations have been given to demonstrate the effectiveness of our theoretical results. Our future works may involve the stability and synchronization analysis of inertial memristive neural networks under different control schemes.