Patchy Invasion of Stage-Structured Alien Species with Short-Distance and Long-Distance Dispersal

Abstract

Understanding of spatiotemporal patterns arising in invasive species spread is necessary for successful management and control of harmful species, and mathematical modeling is widely recognized as a powerful research tool to achieve this goal. The conventional view of the typical invasion pattern as a continuous population traveling front has been recently challenged by both empirical and theoretical results revealing more complicated, alternative scenarios. In particular, the so-called patchy invasion has been a focus of considerable interest; however, its theoretical study was restricted to the case where the invasive species spreads by predominantly short-distance dispersal. Meanwhile, there is considerable evidence that the long-distance dispersal is not an exotic phenomenon but a strategy that is used by many species. In this paper, we consider how the patchy invasion can be modified by the effect of the long-distance dispersal and the effect of the fat tails of the dispersal kernels.

1 Introduction

Biological invasion of alien (exotic) species is regarded as one of the major threats to ecosystems all around the world (Vitousek et al. 1996; Williamson 1996) and often has a significant negative effect on agriculture, forestry, fishery, etc., with direct and indirect economic losses being on the order of hundreds of billions of dollars (U.S. Congress OTA 1993; Pimentel 2002). For this reason, biological invasion has been a focus of intense research for several decades. Indeed, an effective management of invasive species can hardly be possible unless the underlying mechanisms are well understood, controlling factors are revealed, and typical scenarios are identified. Common research approaches include data collection, statistical analysis of the data and mathematical modeling. In particular, mathematical modeling has been very helpful as it creates a ‘virtual laboratory’ where various hypotheses about invasive species dynamics can be tested and refined (Hengeveld 1989; Shigesada and Kawasaki 1997).

Biological invasion has a few clearly distinguishable stages (Shigesada and Kawasaki 1997; Sakai et al. 2001). Once the introduced species has been established locally, it usually starts spreading; this stage is referred to as geographical spread. Patterns of spread have been attracting considerable attention recently (Sherratt et al. 1995; Hastings 1996; Parker 2004; Johnson et al. 2006). The conventional idea about the pattern of spread is based on seminal theoretical results by Fisher (1937) and Kolmogorov et al. (1937) and is supported by many field observations, e.g., Skellam (1951), Andow et al. (1990), Dwyer (1992); see Shigesada and Kawasaki (1997) for more references. It predicts the existence of a self-organized steep gradient in the population density, a so-called traveling population front, which separates invaded and non-invaded areas. The front propagates into the open space (i.e., away from the place of the original species introduction) so that the invaded area grows with time, although the growth of the corresponding population size may not necessarily be monotonous (cf. Wilder et al. 1995; Morozov et al. 2006).

This baseline scenario of species spread has, however, been at odd with some field studies. It has been observed that a continuous front does not always exist. Instead, the spread of invasive species can take place by means of creating separate ‘patches’ or isolated colonies. Several cases of such a ‘patchy invasion’ have been studied, both empirically and theoretically; examples are given by the invasion of house finch (Mundinger and Hope 1982; Shigesada et al. 1995), cordgrass Spartina alterniflora (Davis et al. 2004; Taylor et al. 2004) and gypsy moth (Liebhold et al. 1992; Liebhold and Tobin 2006; Petrovskii and McKay 2010; Jankovic and Petrovskii 2013).

The underlying mechanisms of the patchy invasion are not always clear, and different cases can be attributed to the effect of different factors. Apparently, it may occur as a result of external forcing when patches of land favorable for the given invasive species are surrounded by a less suitable environment (e.g., With 2002). It can occur due to a specific density-dependent behavior resulting in a small-group migration, the phenomenon known as the ‘stratified diffusion’ (Hengeveld 1989; Shigesada et al. 1995). An extension to this mechanism is given by the stratified diffusion due to either wind- or water-borne long-distance dispersal (e.g., Davis et al. 2004) or vector-borne dispersal (Tobin and Blackburn 2008; also Petrovskii and Li 2006, section 8.3). Patchy invasion can also occur due to the impact by either predators (Petrovskii et al. 2002; Mistro et al. 2012) or pathogens (Petrovskii et al. 2005; Petrovskii and McKay 2010; Jankovic and Petrovskii 2013), or due to more complex multi-species interactions (Davis et al. 1998; Morozov et al. 2008). Patchy invasion can also be a generic pattern of stochastic invasion hence reflecting the inherent stochasticity of the population dispersal (Lewis 2000; Lewis and Pacala 2000), especially long-distance dispersal (Clark et al. 2001; Taylor et al. 2004).

In this paper, we focus on the patchy invasion arising as a result of inter-species interactions. While other possible mechanisms of the patchy invasion have been studied relatively well, see the references above, the prerequisites of the patchy spread due to inter-species interactions yet remain obscure. It has been shown theoretically that, in simple systems like predator–prey or host–pathogen, patchy invasion becomes possible in a certain parameter range if the growth rate of prey or host is affected by the strong Allee effect¹; see Petrovskii et al. (2002, 2005), respectively. It has also been shown that the scenario of patchy invasion is robust with respect to the model. In particular, it can be observed in space-time discrete models (Mistro et al. 2012) as well as in continuous ones, which proves that it is not an artifact of a specific modeling framework. However, it remains unclear how sensitive is the invasion pattern, e.g., patchy or not, to the dispersal properties of the interacting species.

It is well known that the properties of the spatiotemporal dynamics of interacting species may depend significantly on their relative dispersal abilities. The classical example is given by the Turing instability (cf. Segel and Jackson 1972), but non-Turing mechanisms resulting in spatiotemporal pattern formation have been discovered as well (Hastings et al. 1997; Petrovskii and Malchow 2001; Morozov and Petrovskii 2009). The effect of differential diffusivity on the spread of invasive species has also been observed (Shigesada and Kawasaki 1997). Most of the studies, however, were done using diffusion–reaction models where dispersal is reduced to diffusion². Diffusion is a local phenomenon in the sense that its rate is fully determined by the density gradients at a given location; therefore, it takes into account only a short-range population dispersal. Meanwhile, importance of a long-range (non-local) dispersal has been increasingly recognized, for both animals and plants; in particular, it has been shown that it can increase the invasion rate by an order of magnitude or even more (Hengeveld 1989; Liebhold et al. 1992; Kot et al. 1996).

Diffusion–reaction models have been very useful in ecology (Skellam 1951; Okubo 1980; Holmes et al. 1994; Okubo and Levin 2001), but they have also been criticized for giving an oversimplified caricature of population dynamics, in particular, by assuming that individuals disperse and reproduce at the same time. In reality, many animal species are stage-structured so that these processes are clearly separated in time, e.g., there are the dispersal stage and the reproductive stage of the life cycle. Eventually, an alternative modeling framework was developed based on kernel-based integro-difference equations (Kot and Schaffer 1986; Andersen 1991; Neubert et al. 1995). This modeling approach is free from the limitations of the diffusion–reaction equations and is hence thought to provide a more adequate description of the spatiotemporal dynamics of a stage-structured population (cf. Hastings et al. 2005).

It is well known that the properties of the dispersal kernel can significantly affect the invasion rates (cf. Andersen 1991; Kot et al. 1996), but the question remains open as to how much it can affect the invasion pattern. The goal of this paper is to reveal typical invasion patterns during the spread of stage-structured alien species. The problem is considered theoretically and by numerical simulations using a kernel-based model consisting of two coupled integro-difference equations. In particular, we want to demonstrate that the patchy invasion can be observed subject to relative mobility of the interacting species. Our other goal is to reveal the effect of the long-distance dispersal (described by fat-tailed dispersal kernels) on the pattern and rate of species spread.

2 Model

Consider a system of two interacting species N and P that, at each generation t, are described by their densities $N_t(\mathbf {r})$ and $P_t(\mathbf {r})$ over a continuous space $\mathbf {r}=(x,y)$. We consider the case that the species are stage-structured so that generation t disperses after reaching maturity but before giving birth (e.g., laying eggs or producing seeds) to the next generation $(t+1)$. We assume that both species have a similar life cycle so that they interact during their maturation stage:

$$\begin{aligned} \tilde{N}_t(\mathbf {r})=f\left( N_t\left( \mathbf {r}\right) ,P_t\left( \mathbf {r} \right) \right) , \quad \tilde{P}_t(\mathbf {r})=g\left( N_t\left( \mathbf {r} \right) ,P_t\left( \mathbf {r}\right) \right) , \end{aligned}$$

(1)

where $\tilde{N}_t(\mathbf {r})$ and $\tilde{P}_t(\mathbf {r})$ are thus the population densities prior to the dispersal stage.

The dispersal of the populations is described by the dispersal kernels $k_N\left( \mathbf {r},\mathbf {r}^{\prime }\right)$ and $k_P\left( \mathbf {r}, \mathbf {r}^{\prime }\right)$ so that

$$\begin{aligned} N_{t+1}(\mathbf {r})=\int _\Omega k_N \left( \mathbf {r},\mathbf {r}^{\prime }\right) \tilde{N}_t(\mathbf {r}^{\prime }) d\mathbf {r}^{\prime }, \quad P_{t+1}(\mathbf {r})=\int _\Omega k_P \left( \mathbf {r},\mathbf {r}^{\prime }\right) \tilde{P}_t(\mathbf {r}^{\prime }) d\mathbf {r}^{\prime }, \end{aligned}$$

(2)

where $\Omega$ is the dispersal domain. The dispersal kernel $k_i\left( \mathbf {r},\mathbf {r}^{\prime }\right)$ (where $i=N,P$) gives the probability density of the event that an individual of species i located before dispersal at position $\mathbf {r}^{\prime }=(x^{\prime },y^{\prime })$ moves after dispersal to the position $\mathbf {r}$; e.g., see Lewis et al. (2006). Obviously, if dispersal takes place in an infinite space, or the dispersal domain is closed (so that there is no loss of individuals because of their moving out of the domain), then $\int _\Omega k_i \left( \mathbf {r},\mathbf {r}^{\prime }\right) \mathrm{d}\mathbf {r}^{\prime }=\int _\Omega k_i \left( \mathbf {r},\mathbf {r}^{\prime }\right) \mathrm{d}\mathbf {r}=1$. We assume that dispersal is homogeneous and isotropic so that the probability of travel from $\mathbf {r}$ to $\mathbf {r}^{\prime }$ depends only on the distance between the two positions, $k_i \left( \mathbf {r},\mathbf {r}^{\prime }\right) =k_i \left( |\mathbf {r}-\mathbf {r}^{\prime }|\right) =k_i \left( |\mathbf {r}^{\prime }-\mathbf {r}|\right)$.

Having combined (1) with (2), one can conveniently write the model in an equivalent form as a system of integro-difference equations:

$$\begin{aligned} N_{t+1}(\mathbf {r})= & {} \int _\Omega k_N\left( |\mathbf {r}-\mathbf {r}^{\prime }|\right) f\left( N_t\left( \mathbf {r}^{\prime }\right) ,P_t\left( \mathbf {r}^{\prime }\right) \right) \mathrm{d}\mathbf {r}^{\prime }, \end{aligned}$$

(3)

$$\begin{aligned} P_{t+1}(\mathbf {r})= & {} \int _\Omega k_P\left( |\mathbf {r}-\mathbf {r}^{\prime }|\right) g\left( N_t\left( \mathbf {r}^{\prime }\right) ,P_t\left( \mathbf {r}^{\prime } \right) \right) \mathrm{d}\mathbf {r}^{\prime }. \end{aligned}$$

(4)

For the interspecific interactions, we consider species N to be prey and species P to be predator. More specifically, we consider the case where the growth rate of prey is affected by the strong Allee effect and that P is a specialist predator, and choose functions f and g as follows:

$$\begin{aligned} f\left( N_t,P_t\right)= & {} \frac{A\left( N_{t}\right) ^{2}}{1+B^2\left( N_{t}\right) ^{2}} \cdot \exp \left( -\kappa P_{t}\right) , \end{aligned}$$

(5)

$$\begin{aligned} g\left( N_t,P_t\right)= & {} \delta N_{t}P_{t}, \end{aligned}$$

(6)

where A is the prey intrinsic growth rate, 1 / B is the prey density for which its per capita growth rate reaches its maximum, $\kappa$ is the predator efficiency, and $\delta$ is the predator growth rate. The biological rationale behind this parameterization is discussed in much detail in Rodrigues et al. (2012). Due to their biological meaning, all parameters are positive.

For convenience, we re-scale the population sizes as

$$\begin{aligned} N^{\prime }_{t}=\delta N_{t} \quad \text{ and }\quad P^{\prime }_{t}=\kappa P_{t}, \end{aligned}$$

(7)

so that Eqs. (5–6) turn into

$$\begin{aligned} f\left( N_t,P_t\right)= & {} \frac{a\left( N_{t}\right) ^{2}}{1+b\left( N_{t}\right) ^{2}} \cdot \exp \left( -P_{t}\right) , \end{aligned}$$

(8)

$$\begin{aligned} g\left( N_t,P_t\right)= & {} N_{t}P_{t}, \end{aligned}$$

(9)

where we have omitted the primes for the sake of notation simplicity. Here $a=A/\delta$ and $b=(B/\delta )^2$ are new parameters. Since Eqs. (8–9) correspond to the ‘reaction’ stage of the system dynamics, we will call a and b the reaction parameters.

It is readily seen (for details, see Rodrigues et al. 2012) that the system $f(N,P)=N$, $g(N,P)=P$ has at most four steady states, i.e., the extinction state (0, 0), two prey-only states $(N_1^*,0)$ and $(N_2^*,0)$ and the coexistence state $(N^*,P^*)$ where

$$\begin{aligned}&N_{1}^{*} = \frac{a-\sqrt{a^{2}-4b}}{2b}, \quad N_{2}^{*} = \frac{a+\sqrt{a^{2}-4b}}{2b}, \end{aligned}$$

(10)

$$\begin{aligned}&\left( N^{*},P^{*}\right) = \left( 1,\ln \left[ \frac{a}{b+1}\right] \right) . \end{aligned}$$

(11)

While (0, 0) always exists, the boundary states $(N_1^*,0)$ and $(N_2^*,0)$ are only feasible for $a>2\sqrt{b}$. They merge for $a=2\sqrt{b}$ and disappear for $a<2\sqrt{b}$. The coexistence state $(N^*,P^*)$ is feasible for

$$\begin{aligned} b+1<a. \end{aligned}$$

(12)

Applying the linear stability analysis, it is readily seen that (0, 0) is always stable. $(N_1^*,0)$ is always unstable, while $(N_2^*,0)$ is stable for $2<a<b+1$. Correspondingly, $(N_2^*,0)$ can only be stable for $b>1$. The coexistence state is stable for

$$\begin{aligned} a<a_{cr}=(b+1)\exp \left( \frac{b-1}{b+1}\right) . \end{aligned}$$

(13)

Fig. 1

The structure of the parameters space for the system (8–9); see details in the text. From Rodrigues et al. (2012), with permissions

The structure of the parameter plane (b, a) is shown in Fig. 1. The coexistence equilibrium is feasible and stable for parameters from Domain 1. The solid curve in Fig. 1 corresponds to $a=a_{cr}$, see (13), where $(N^*,P^*)$ loses its stability through the Hopf bifurcation; on this line, the determinant of the Jacobian matrix at the coexistence equilibrium is equal to one (cf. Allen 2007). Inside Domain 2, the local dynamics is oscillatory according to the (multi-point) limit cycle. When crossing the long-dashed curve (obtained numerically), the limit cycle disappears so that, for parameters from Domain 3, the only attractor is the extinction state. The straight dotted line corresponds to $a=b+1$, cf. (12); therefore, for Domains 4, 5 and 6, the coexistence state is not feasible. In particular, in Domain 5, the only steady state is (0, 0), and in Domains 4 and 6 (above the short-dashed curve which corresponds to $a=2\sqrt{b}$) also the two ‘prey-only’ states exist. The prey-only equilibrium $(N^*_1,0)$ is never stable, while $(N^*_2,0)$ is stable for parameter values inside Domain 6.

2.1 Parameterization of Dispersal

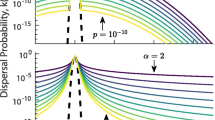
The choice of the dispersal kernels is a controversial issue. While earlier studies usually considered it to be either the normal distribution or a distribution with exponential decay (Kot and Schaffer 1986; Andersen 1991) and there is some experimental evidence of this (Kareiva 1983; Turchin 1998), later papers tended to assume a lower rate of decay at large distances (Kot et al. 1996; Clark et al. 2001). Lower rate of decay means higher frequency of long-distance travel; therefore, a dispersal kernel with a lower rate of decay (often referred to as a fat-tailed kernel) takes into account the so-called long-distance dispersal. One mechanism that is thought to result in the long-distance dispersal is the pattern of individual movement known as the Levy flight (Klafter and Sokolov 2005; Viswanathan et al. 2011) when the probability distribution of the travel over distance r has a power-law tail, that is

$$\begin{aligned} k(r)\sim r^{-\mu }, \quad 1<\mu <3, \end{aligned}$$

(14)

for large r in the one-dimensional (1D) space, and

$$\begin{aligned} k(\mathbf {r})\sim |\mathbf {r}|^{-(\mu +1)}, \end{aligned}$$

(15)

for large $|\mathbf {r}|=\sqrt{x^2+y^2}$ in the two-dimensional (2D) space.

Correspondingly, for the purposes of this paper, we consider a few dispersal kernels with different properties. Firstly, we consider the 2D kernel described by the normal distribution:

$$\begin{aligned} k_{i}\left( |\mathbf {r}-\mathbf {r}^{\prime } | \right) =\frac{1}{2\pi \alpha _{i}^{2}}\exp \left( -\frac{|\mathbf {r}-\mathbf {r}^{\prime }|^{2}}{2\alpha _{i}^{2}}\right) , \end{aligned}$$

(16)

where $\alpha _{i}$ is a parameter quantifying the spatial scale of dispersal, $i=N,P$. Normal distribution corresponds to the standard Fickian diffusion, e.g., see Neubert et al. (1995), also Petrovskii and Li (2006), section 2.2. Kernel (16) therefore makes the properties of the system (3–4) comparable to those of diffusion–reaction systems.

Secondly, in order to account for the long-distance dispersal, we consider a dispersal kernel with the power-law rate of decay, cf. Eqs. (14–15). Since there is certain theoretical evidence that the case $\mu =2$ can optimize the search efficiency (Viswanathan et al. 1999) and hence may appear as a result of natural selection and evolution (cf. De Jager et al. 2011), we consider the case $\mu =2$. In the 1D space, the corresponding dispersal kernel is described by the Cauchy distribution:

$$\begin{aligned} k(r) = \frac{\beta }{\pi (\beta ^2+r^2)}. \end{aligned}$$

(17)

Generalization of (17) onto the 2D case is not straightforward as there is some ambiguity about it. In particular, Heinsalu et al. (2010) proposed the following expression:

$$\begin{aligned} k_{i}(\mathbf {r},\mathbf {r}^{\prime })=\frac{\beta _{i}}{\pi (\beta _{i}+|\mathbf {r}-\mathbf {r}^{\prime }|)^{3}}, \end{aligned}$$

(18)

where $\beta _{i}>0$ (note that we define the distribution parameter differently compared to the original paper) and $i=N,P$. Obviously, expression (18) has the required power-law tail as prescribed by (15).

However, it is readily seen that the following function

$$\begin{aligned} k_{i}(\mathbf {r},\mathbf {r}^{\prime })=\frac{\gamma _{i}}{2\pi (\gamma _{i}^{2}+|\mathbf {r}-\mathbf {r}^{\prime }|^{2})^{3/2}} \end{aligned}$$

(19)

(where $\gamma _{i}>0$ and $i=N,P$) has the same asymptotics as (18), i.e., the same power-law tail as in (15). Hence, one of our objectives is to find out whether the dispersal pattern—more specifically, patchy invasion—is robust to the choice of the kernel parameterization. We will call (18) as the 2D Cauchy kernel Type I and (19) as the 2D Cauchy kernel Type II.

In order to compare the results for different kernels, we consider the radius $\epsilon$ within which the probability of finding an individual after the dispersal is 1 / 2:

$$\begin{aligned} P_{\epsilon }=\int _0^{2\pi }\int _0^{\epsilon } k_i(r,\theta ) r\mathrm{d}r \mathrm{d}\theta =\frac{1}{2}. \end{aligned}$$

(20)

For the Gaussian kernel, we obtain that the required radius is

$$\begin{aligned} \epsilon =\alpha \sqrt{2\ln 2}. \end{aligned}$$

(21)

Having applied conditions (20–21) to each of the kernels (18) and (19), we find the corresponding parameter value as

$$\begin{aligned} \beta =\epsilon (\sqrt{2}-1)=\alpha (2-\sqrt{2})\sqrt{\ln 2}\approx 0.4877\alpha , \end{aligned}$$

(22)

for the Cauchy kernel Type I, and

$$\begin{aligned} \gamma =\frac{\epsilon }{\sqrt{3}}=\alpha \sqrt{\frac{2}{3}\ln 2} \approx 0.6798\alpha , \end{aligned}$$

(23)

for the Cauchy kernel Type II. We regard (22) and (23) as the conditions of equivalence between the normally distributed kernel (16) and the fat-tailed kernels (18) and (19), respectively.

3 Numerical Simulations and Preliminary Discussion

Equations (3–4) are solved in a square spatial domain $\Omega =\{(x,y): -L\le x\le L,-L\le y\le L\}$, parameter L thus quantifying the domain size. We consider the prey to be an invading alien species and use the initial conditions accordingly, i.e., at $t=0$ prey is only present inside a certain (small) area of the domain and absent everywhere else. As for the predator, we regard it as the biological control agent, so that it is initially present only inside a smaller subdomain of the area inhabited by prey (cf. Petrovskii et al. 2005).

3.1 Initial Conditions

Specifically, we use the following initial species distributions:

• 1. Symmetrical initial conditions. The prey population is distributed in the central part of the computational domain, and the predator is present in a smaller region also centered around the origin:

  $$\begin{aligned}&N_0(x,y)=N_2^* \quad \text{ for }~~-1\le x\le 1 \quad \text{ and }\quad -1\le y\le 1,\nonumber \\&\quad \text{ and }~~N_0(x,y)=0 \quad \text{ otherwise }, \end{aligned}$$

  (24)
  $$\begin{aligned}&P_0(x,y)=P^*\quad \text{ for }~~-0.1\le x\le 0.1\quad \text{ and } \quad -1\le y\le 1, \nonumber \\&\quad \text{ and }~~P_0(x,y)=0 \quad \text{ otherwise }, \end{aligned}$$

  (25)

  where $N_2^*$ is the prey equilibrium density in the absence of the predator and $P^*$ is the predator equilibrium density in the predator–prey system; see Eqs. (10–11).

The initial conditions (24–25) are obviously invariant with regard to the reflection $x\rightarrow -x$ and $y\rightarrow -y$, and hence, the mathematical problem as a whole, i.e., Eqs. (3–4) with (24–25), attains this reflectional symmetry as well. The emerging distributions of prey and predator are hence expected to be symmetrical, too. This can be regarded as a special case and is not entirely realistic. Correspondingly, in order to make the simulation results somewhat more general, along with (24–25) we consider the initial population distribution without any apparent symmetry:

• 2. Asymmetrical initial conditions. The prey population is distributed in the same central part of the domain as above, but the predator population is now initially distributed in an acentric region:

  $$\begin{aligned}&N_0(x,y)=N_2^*\quad \text{ for }~~-1\le x\le 1\quad \text{ and }\quad -1\le y\le 1, \nonumber \\&\quad \text{ and }~~N_0(x,y)=0\quad \text{ otherwise }, \end{aligned}$$

  (26)
  $$\begin{aligned}&P_0(x,y)=P^*~~\text{ for }\quad -1\le x\le 0.2\quad \text{ and }\quad -0.9\le y\le 0.4, \nonumber \\&\quad \text{ and }~~P_0(x,y)=0\quad \text{ otherwise }. \end{aligned}$$

  (27)

3.2 Boundary Conditions

Unlike partial differential equations where boundary conditions are required in order to ensure the uniqueness of the solution, the integro-difference Eqs. (3–4) do not necessarily require boundary conditions. The mathematical problem is well defined when system (3–4) is complemented just by the initial conditions. However, the absence of boundary conditions as such, i.e., the absence of additional constraints imposed at the domain boundary, in fact corresponds to a specific biological situation where at every time step a certain fraction of the population leaves the computational domain $\Omega$ because of the dispersal. Since the space outside of domain $\Omega$ is not taken into account by our model in any way, it means that this fraction never comes back and hence is lost forever. In the discussion below, we will refer to this situation as the ‘free outflow’ boundary conditions. The exact amount that is lost at every time step depends on the population density distribution across domain $\Omega$ and on the properties of the dispersal kernel. Although this situation is ecologically meaningful (e.g., if the environment outside of the domain is very harsh), it gives only one possible option out of the great multiplicity of possible ecological situations.

Different boundary conditions can have a different effect on the solution of the system (3–4) inside the computational domain $\Omega$, hence resulting in the population dynamics with different properties. In the literature, this situation is known as the boundary forcing. For instance, the free outflow boundary condition is likely to hamper the population growth inside the domain, or even bring it down to extinction altogether. Therefore, especially if the purpose of the study is the inherent dynamics of the system rather than the dynamics imposed by the boundary conditions, alternatively to the free outflow, one might need to consider some less intrusive boundary conditions in order to minimize the population flux through the boundary; see Appendix 1 for a detailed discussion of this issue. Also, different numerical methods may require different boundary conditions, e.g., periodical; see the discussion of the FFT method below.

However, the actual magnitude of the boundary forcing depends not only on the type of the boundary condition but also on the population distribution over domain $\Omega$ at the given time. For instance, if the population density is only significantly larger than zero in the central part of the domain but is approximately zero closer to the boundary, then, because the dispersal kernel is a fast decaying function, it may be expected that the outflowing fraction of the population is going to be very small. In this case, the effect of the boundary forcing is going to be very small too. Correspondingly, one can expect that the choice of the boundary condition (e.g., free outflowing, zero flux or periodical) will not have any significant effect on the population dynamics inside the domain.

Let us recall that, in this paper, we are mainly interested in the biological invasion scenario, i.e., in the population dynamics initiated by initial conditions (24–25) and (26–27). Therefore, based on the above argument, we hypothesize that the population dynamics will not be sensitive to the choice of the boundary condition over the time when the spreading populations remain sufficiently far from the domain boundary, i.e., if the domain is sufficiently large. In order to prove this hypothesis, we compared the simulations performed under two different boundary conditions (the periodic boundary conditions as is required by the FFT method, see below, and the free outflow boundary conditions) and obtained that the results did not show any significant difference over the simulation time. In order to find out what domain can be regarded as ‘sufficiently large,’ we performed simulations in domains of different size. We obtained that, for the simulations ran up to $t=200$, the domain size $L=20$ is sufficient to exclude any visible effect of the boundary forcing in the case of the Gaussian kernel (16) for the values of $\alpha _N$ and $\alpha _P$ being on the order 0.1 or less. However, the simulations with either of the Cauchy kernels (18) or (19) require a larger domain with $L=80$, which is in a good agreement with the semi-analytical analysis performed in Appendix 1. Finally, we applied a strong numerical test where, at each time step, the population densities at the two rows of the numerical grid adjacent to the boundary were replaced by zeros, and we did not observe any significant change in the simulation results for the time and domain size mentioned above.

3.3 Simulations and Results

Having chosen the initial and boundary conditions, Eqs. (3–4) cannot be solved analytically (except for a few trivial cases that we do not discuss here); therefore, we have to use numerical simulations. For this purpose, we discretize the domain $\Omega$ by changing the continuous space to a discrete one, i.e., by introducing a numerical grid with K nodes in each dimension, that is

$$\begin{aligned} \{-L\le x\le L\}\rightarrow \{x_{k+1}=x_k+\Delta ,k=1,\ldots ,K-1,x_1=-L,x_K=L\}, \end{aligned}$$

(28)

and

$$\begin{aligned} \{-L\le y\le L\}\rightarrow \{y_{k+1}=y_k+\Delta ,k=1,\ldots ,K-1,y_1=-L,y_K=L\}, \end{aligned}$$

(29)

so that the step size of the grid is $\Delta =2L/(K-1)$. The number of nodes K (and, correspondingly, the step size $\Delta$) is an important technical parameter as it is responsible for the accuracy of the numerical approximation, e.g., see Burden and Faires (2005). Hence, it is important to choose K sufficiently large (or $\Delta$ sufficiently small) in order to avoid numerical artifacts.

The most straightforward method of solving Eqs. (3–4) is the numerical integration, e.g., by using the trapezium method. Numerical integration does not require any additional information about the population density at the domain boundary except for that already given by the model (3–4) itself. According to the discussion in Section 3.2, it corresponds to the free outflow boundary conditions. By varying the number of nodes and the domain size L, we can obtain the baseline information about the numerical error and the minimum required number of nodes; see Appendix 1 for details.

Numerical integration is easy to implement, and it is a robust and reliable method to solve the system (3–4); however, it is computationally expensive as it requires $O(K^4)$ operations at each time step. Thus, for a sufficiently fine numerical grid, i.e., for a sufficiently large number of nodes K, it may require a very long computer time. A convenient alternative is the fast Fourier transform (FFT) method which appears to be much faster; see Appendix 2. Correspondingly, the simulation results shown below were obtained by the FFT method. Equations (3–4) were solved with the periodical boundary conditions (as required by the FFT) on the 2D grid consisting of $2^{10}\times 2^{10}$ nodes altogether (i.e., $K=2^{10}$ nodes in each direction x and y) in the domain of size $L=20$ in the case of the Gaussian kernel, and on the 2D grid of $2^{12}\times 2^{12}$ nodes in the domain of size $L=80$ in the case of the Cauchy kernels.

The next issue is the choice of the population dynamics parameters, i.e., a and b in Eqs. (8–9). Recall that in this paper, we are mostly interested in revealing the patchy invasion. Basing on the inferences made for other relevant models (e.g., Petrovskii et al. 2005; Mistro et al. 2012), the patchy invasion is likely to occur for parameters from Domain 3 where the only attractor in the non-spatial system is the extinction state. Correspondingly, for numerical simulations, we choose $a=4.5$, $b=0.68$. However, we want to emphasize that the results shown below are not specific for this parameter value but in fact are typical for the whole Domain 3 in the (b, a) parameter plane.

Fig. 2

Snapshots of the prey density spatial distribution at different moments t, a 20, b 80, c 120, d 180, e 200 and f 250, as obtained for reaction parameters $a=4.5$ and $b=0.68$, the Gaussian dispersal kernel with parameters $\alpha _N=0.1$ and $\alpha _P=0.125$, and the symmetrical initial conditions (24–25). Simulations are performed in a larger domain ($L=20$) of which only a central part is shown. Black color and white color show a high population density and the zero density, respectively, and shades of gray correspond to intermediate densities

We begin with the dispersal kernel described by the Gaussian distribution (16). Figure 2 shows snapshots of the spatial prey distribution³ obtained at different moments in the case that the dispersal parameters are set to some hypothetical values, $\alpha _N=0.1$ and $\alpha _P=0.125$. It is readily seen that the evolution of the initial conditions eventually results in an irregular patchy structure. The population density is high inside the patches and close to zero between the patches. Remarkably, at any time, there is no continuous boundary separating the invaded and non-invaded areas. The alien population (prey) invades the space by means of the movement of separate population patches that eventually moves away from the place of the initial species introduction described by the initial conditions (24–25). This is the pattern of spread known as the patchy invasion (Petrovskii et al. 2002, 2005; Morozov et al. 2006; Mistro et al. 2012). The spatial population distributions arising at a later time are completely irregular; below we will show that it corresponds to chaotic dynamics. We also mention here that, for the parameters of Fig. 2, the Turing instability is not possible (see Rodrigues et al. 2012 for details); therefore, the emerging patterns should be attributed to another, non-Turing mechanism.

Interestingly, although the kernel-based description of the population dynamics with kernel (16) is known to be to some extent equivalent to the diffusion–reaction systems (because the Gaussian kernel corresponds to the usual Brownian diffusion), the pattern of spread described by Eqs. (3–4) shows greater sensitivity to the choice of dispersal parameters $\alpha _N$ and $\alpha _P$ than the dependence on the diffusion coefficients in the PDE-based models reported in the literature. The patchy spread shown in Fig. 2 is obtained for the case where $\alpha _P$ is somewhat larger than $\alpha _N$. This appears to be important. Our simulations made for other values of the dispersal parameters (not shown here) demonstrate that the case of $\alpha _P=\alpha _N$ corresponds to the propagation of continuous front with the formation of a patchy pattern in the wake, thus following a scenario different from the patchy invasion. Interestingly, in the diffusion–reaction systems, the patchy invasion can be observed when the ratio of the diffusion coefficients for the prey and predator is anywhere between approximately 0.7 and 1.5 (Morozov et al. 2006), hence including the case of equal diffusivity.

Considering the simulated population distributions in the context of the real ecological dynamics, the reflectional symmetry observed in Fig. 2 is hardly realistic. However, this is obviously a consequence of the symmetrical initial conditions and would not be observed otherwise. Figure 3 shows the snapshots of the prey spatial distribution obtained for the same value of parameters $a,b,\alpha _N$ and $\alpha _P$ as in Fig. 2 but for the asymmetrical initial conditions (26–27). It is readily seen that the species spread takes place following the same scenario of patchy invasion; however, the emerging population distribution does not show any sign of symmetry.

Fig. 3

Snapshots of the prey spatial distribution at different moments t, a 20, b 80, c 140 and d 200, as obtained for the Gaussian dispersal kernel and the asymmetrical initial conditions (24–25). Other parameters are the same as in Fig. 2

Fig. 4

Snapshots of the prey spatial distribution at different moments t, a 40, b 100 and c 180, as obtained for the Cauchy kernel Type I and the asymmetrical initial conditions (24–25). Parameters are $\beta _N=0.0488$ and $\beta _P=0.061$

Fig. 5

Snapshots of the prey spatial distribution at different moments t, a 20, b 100, c 140 and d 190, as obtained for the Cauchy kernel Type I and the asymmetrical initial conditions (24–25). Parameters are $\beta _N=0.0488$ and $\beta _P=0.098$

Fig. 6

Snapshots of the prey spatial distribution at different moments t, a 40, b 80 and c 180, as obtained for the Cauchy kernel Type II and the asymmetrical initial conditions (24–25). Parameters are $\gamma _N=0.068$ and $\gamma _P=0.1$

Fig. 7

Snapshots of the prey spatial distribution at different moments t, a 40, b 80, c 140 and d 200, as obtained for the Cauchy kernel Type II and the asymmetrical initial conditions (24–25). Parameters are $\gamma _N=0.068$ and $\gamma _P=0.1205$

Now, we are going to consider how the pattern of spread may change when the long-distance dispersal is taken into account, i.e., when the dispersal kernel has a fatter tail than the normal distribution. Correspondingly, we now solve Eqs. (3–4) numerically (using the FFT method) in the case where the dispersal is described by the kernel with a power-law tail. Figure 4 shows the snapshots of the prey spatial distribution obtained for the Cauchy kernel Type I, see Eq. (18). In order to make the results comparable with the case of the short-distance dispersal (described by the Gaussian kernel), we use the equivalence condition (22) so that the values $\alpha _N=0.1$ and $\alpha _P=0.125$ used in Figs. 2 and 3 turn into $\beta _N=0.0488$ and $\beta _P=0.061$, respectively. Interestingly, patchy invasion does not occur and the species spread follows an alternative scenario, i.e., the propagation of the continuous front followed by the formation of irregular spatial pattern in the wake. Patchy invasion however is observed for a larger value of parameter $\beta _P$; Fig. 5 shows the snapshots obtained for $\beta _P=0.098$ (other parameters are the same as in Fig. 4). We therefore conclude that the effect of the long-distance dispersal makes the parameter constraints more restrictive for the patchy invasion to occur.

A situation appears to be similar in the case of Cauchy kernel Type II. Figure 6 shows the snapshots of the prey spatial distribution obtained for the dispersal kernel described by Eq. (19) with parameters $\gamma _N=0.0680$ and $\gamma _P=0.1$, which correspond to the dispersal parameters of Figs. 2 and 3 by the equivalence condition (23). Hence, we see it again that, while the short-distance dispersal results in the patchy invasion (see Fig. 2), the corresponding long-distance dispersal results in the propagation of the continuous front followed by the formation of irregular pattern in the wake. As well as in the previous case, patchy invasion can be observed for a higher predator dispersal; see Fig. 7 obtained for $\gamma _P=0.1205$.

3.4 Sensitivity to the Initial Conditions

So far we have shown that, in a certain parameter range, the evolution of initial conditions (24–25) or (26–27) (which describes the invasion of an alien species N biologically controlled by a predatory species P) results in the patchy invasion where the spread of the alien species occurs not by the propagation of the continuous population front but by the dynamics of separate population patches. This is observed for all three dispersal kernels (16), (18) and (19), i.e., both with the short-distance and long-distance dispersal.

The question remains as to whether the irregular spatial distributions shown in Figs. 3, 5 and 7 actually correspond to chaotic dynamics, in particular, whether the irregularity of the emerging spatial pattern is combined with an irregularity of the temporal dynamics. This is a non-trivial question as there are examples of population models where a regular spatial distribution corresponds to chaotic temporal oscillations (cf. Morozov et al. 2004) and examples where irregular spatial pattern shows periodical temporal oscillations (e.g., Kopell and Howard 1981).

A fingerprint of chaos is known to be the sensitivity of the dynamics to a perturbation of the initial conditions when the trajectories of the perturbed and unperturbed systems stay close to each other until a certain time (quantified by the dominant Lyapunov exponent $\lambda$, e.g., see Nayfeh and Balachandran 1995; Strogatz 2000) but then promptly become different. In order to investigate this issue, we run simulations with the same parameter values as in Figs. 3, 5 and 7 but with the initial prey density perturbed by 0.1 %, i.e., by changing $N_2^*$ to $1.001N_2^*$ in Eqs. (26–27). Since the comparison between the spatial distributions is technically challenging, instead we consider the prey density at the central point of the domain, i.e., N(0, 0, t), and the total population size in the computational domain $\Omega$:

$$\begin{aligned} N_\mathrm{tot}(t)= \int \int _{\Omega } N(x,y,t)\, \mathrm{d}x\mathrm{d}y, \end{aligned}$$

(30)

where the integral is calculated numerically on the computational grid (28–29).

Figure 8 shows these quantities vs time obtained for the perturbed and unperturbed initial conditions. It is readily seen that N(0, 0, t) and $N_\mathrm{tot}(t)$ exhibit qualitatively similar behavior. In all three cases, the perturbed and unperturbed trajectories are indistinguishable from each other during the early stage of the population dynamics but become completely different (i.e., the timing of the peaks and/or troughs does not coincide in the perturbed and unperturbed trajectories) at a later time. This sensitivity points out at the chaotic dynamics of the system for all three kernels. Note that the observed chaotic dynamics is essentially a spatiotemporal phenomenon as the corresponding system without space does not exhibit chaos in the given range of parameters a and b, cf. Eqs. (8–9) and Fig. 1.

Fig. 8

Sensitivity to the initial conditions. Left-hand side column the prey density N(0, 0, t) at the center of the domain for a Gaussian kernel, c Cauchy kernel Type I and e Cauchy kernel Type II. Right-hand side column the total population size $N_\mathrm{tot}(t)$ as obtained for b Gaussian kernel, d Cauchy kernel Type I and f Cauchy kernel Type II. In all panels, the solid curve is obtained for the asymmetrical initial condition (24–25), and the dashed curve is obtained for the slightly perturbed initial condition (see details in the text). Parameters correspond to those used in the figures above, i.e., (a, b) as in Fig. 3, (c, d) as in Fig. 5, (e, f) as in Fig. 7

Interestingly, the moment when the difference becomes noticeable is different for each of the kernels. The system with the Cauchy kernel Type II appears to be the most sensitive to the perturbation; the trajectories become visually different from about $t=45$ (see Fig. 8f) and completely different from $t=75$ (cf. Fig. 8e). In the system with the Gaussian kernel, these moments are, respectively, 100 and 130. The least sensitive appears to be the system with the Cauchy kernel Type I where the trajectories become visually different only from $t=120$ and become completely different from the time $t=175$. Altogether, it suggests that the corresponding Lyapunov exponents are ordered as

$$\begin{aligned} \lambda _\mathrm{Cauchy\,II}>\lambda _\mathrm{Gauss}>\lambda _\mathrm{Cauchy\,I}>0, \end{aligned}$$

(31)

although we cannot provide their exact numerical value.

3.5 Rate of Spread

The rate of spread, i.e., the rate at which the alien species or gene advances into the new space, is a quantity of high theoretical and practical importance, and it has been a focus of numerous studies (Fisher 1937; Andow et al. 1990; Hastings 1996; Kot et al. 1996; Lewis 2000; Clark et al. 2001). The rate of spread is known to depend strongly on the dispersal mode, so that the short-distance dispersal normally results in the advance with a constant speed, but the long-distance dispersal (described by a fat-tailed kernel with a power-law decay) may lead to a spread with accelerating speed (Kot et al. 1996). However, the analysis of this issue was restricted to the standard invasion pattern via the propagation of a population front and it is not immediately clear whether it applies to the patchy invasion too.

In order to make an insight into this issue, we calculated the rate of spread for the cases of patchy invasion shown in Figs. 3, 5 and 7. For this purpose, at every moment t, we first calculate the extent of the invaded area. Note that, since the dispersal kernels that we use are formally positive over the whole space, it means that the population density is positive everywhere in space at any $t>0$. However, very small densities are not biologically feasible. We therefore introduce a certain threshold density $\omega$ and assume that the position (x, y) in space is invaded at time t only if $N(x,y,t)\ge \omega$. The collection of all such positions gives the required extent. We then calculate the distance $r_{\omega }$ from the center of the domain (i.e., from the location of the species introduction) to the farthermost invaded position:

$$\begin{aligned} r_{\omega }(t)= \max _{(x,y)|N(x,y,t)\ge \omega } \sqrt{x^2+y^2}, \end{aligned}$$

(32)

and regard $r_{\omega }$ as the radius of the invaded area.

Figure 9 shows $r_{\omega }(t)$ (solid curve) calculated for all three kernels with $\omega =0.01$. In order to estimate the possible effect of chaotic dynamics on the results, the dashed curves show $r_{\omega }(t)$ calculated for the slightly perturbed initial conditions (see Sect. 3.4 for details). It is readily seen that the radius of invaded area oscillates with time, these oscillations being more prominent for the Cauchy kernels than for the Gaussian kernel. Interestingly, the oscillations occur around a certain average value which grows with time linearly. This constant growth rate appears to be about two times larger for the Cauchy kernels than for the Gaussian kernel, which we attribute to the effect of the long-distance dispersal. Perturbation of the initial conditions affects the exact value of $r_{\omega }(t)$ but does not affect the value of the average. We also observe that chaos does not seem to have much effect on the linear growth rate of the average (as the dashed curves in Fig. 9 follow qualitatively the same pattern as the solid curves), although the exact timing of the oscillations in the value of the radius $r_{\omega }(t)$ becomes different after a certain time, which is consistent with the results of Sect. 3.4.

Fig. 9

Rate of the population spread. Radius $r_{\omega }$ of the invaded area vs time obtained for a Gaussian kernel, b Cauchy kernel Type I and c Cauchy kernel Type II. Parameters correspond to those used in the figures above, i.e., (a) as in Fig. 3, (b) as in Fig. 5, (c) as in Fig. 7. Solid and dashed curves correspond to unperturbed and perturbed initial conditions, respectively, see details in the text

We therefore conclude that, in case of patchy invasion, the species spread takes place with a constant speed. There is no accelerating spread even for the kernels with a very fat tail such as (18) and (19). This apparently contradicts to some previous results (Kot et al. 1996; Medlock and Kot 2003; Garnier 2011). However, a closer look reveals that those previous results were obtained for a linearized system (i.e., for the system where the nonlinear function describing the population growth is replaced by the linear term of the Taylor series) at the leading edge of the invaded area where the population density is very small. This approach does not apply to the case where the population growth is affected by the strong Allee effect, cf. ‘pulled’ and ‘pushed’ population waves (Lewis and Kareiva 1993). The strong Allee effect changes the rate of spread dramatically and preclude accelerating invasion. Constant rate of species spread resulting from the interplay between the long-distance dispersal and the strong Allee effect was earlier observed for single-species models (Kot et al. 1996; Chen 1997; Wang et al. 2002). Here we show that this holds also in the case of patchy invasion in the two-species predator–prey system.

4 Discussion and Concluding Remarks

In this paper, we have considered biological invasion of an alien species that is affected by its predator, the latter presumably being introduced as a biological control agent. Both species have a structured life cycle with distinctly different stages of growth/reproduction and dispersal. The corresponding mathematical model is given by a system of two coupled integro-difference equations where the kernel can be either thin-tailed (Gaussian) or fat-tailed (Cauchy), hence taking into account short- and long-distance dispersal, respectively. We have shown that, in a certain parameter range, the invasion takes place by a somewhat unusual scenario where there is no population front and the species are spreading into space through the dynamics of separate patches of high population density. We call this scenario the patchy invasion.

Patterns of species spread during biological invasion have been a focus of attention for at least two decades (Sherratt et al. 1995; Shigesada et al. 1995; Davis et al. 1998; Lewis and Pacala 2000; Petrovskii et al. 2002; Parker 2004; Johnson et al. 2006; Morozov et al. 2006; Mistro et al. 2012) for both theoretical and practical reasons. It is important to distinguish between the cases where the population density behind the front is relatively uniform and where it exhibits large-amplitude oscillations (Sherratt et al. 1997), in particular because the latter may pose a much greater challenge for the monitoring and control of the invading species (Petrovskii et al. 2014). Even a greater challenge can be posed by the scenario of species spread where the continuous invasion front as such is missing altogether. In this case, the invasion takes place via the formation and dynamics of separate population colonies or patches of high population density separated by wide stretches of space where the population is virtually missing and hence is undetectable. Several cases of this patchy invasion have been observed including the notoriously famous case of the gypsy moth invasion (Liebhold et al. 1992; Liebhold and Tobin 2006). One possible mechanism resulting in the patchy invasion is the interaction of the spreading species with a predator (Petrovskii et al. 2002; Morozov et al. 2006) or a pathogen (Petrovskii et al. 2005; Jankovic and Petrovskii 2013) coupled with dispersal.

In the previous work, the patchy invasion was studied theoretically in much detail using diffusion-reaction models, which is a natural framework to describe a population with overlapping generations (i.e., stage-unstructured) spreading predominantly by means of the short-distance dispersal. In this paper, we extended those results far beyond the diffusion–reaction framework and showed that the patchy invasion can be observed as well in the invasion of a stage-structured species spreading by predominantly long-distance dispersal. We have observed that, in agreement with the properties of patchy invasion studied previously in terms of different models (e.g., Petrovskii et al. 2005; Mistro et al. 2012), in the discrete-time space-continuous kernel-based model (3–4), patchy invasion occurs in the parameter range close to the species extinction. (In particular, the corresponding non-spatial system exhibits only trivial dynamics always resulting in the extinction of both species.) Note that this applies not only to the parameters of the equations but also to the choice of the initial conditions; for the initial conditions similar to (26–27) but with a somewhat different distribution of predator, the system’s dynamics can result in species extinction.

We emphasize that the extension of the results obtained for the short-range dispersal onto the case of the long-distance dispersal, e.g., as described by the Cauchy-type kernels, is non-trivial and is hardly possible to predict intuitively. In particular, the characteristic spatial scale of the chaotic patchy pattern is known to be controlled by the spatial correlations so that, for instance, the characteristic size of the patch coincides (up to a numerical coefficient on the order of unity) with the correlation length of the system (Petrovskii et al. 2003; Malchow et al. 2008). The much fatter tail of the Cauchy distribution means the existence of long-range spatial correlation; in fact, it is sometimes thought about as an infinite-range correlation because the Cauchy distribution has infinite variance. Thus, the onset of the spatiotemporal chaos as a result of the patchy spread is a highly counter-intuitive result.

Fig. 10

Symmetry breaking because of the chaotic amplification of numerical noise. Snapshots of the prey density at different moments t, a 20, b 80, c 100, d 120, e 130 and f 200, as obtained for the Gaussian kernel with the symmetrical initial conditions (24–25). Parameters are $a=4.5$, $b=0.68$, $\alpha _N=0.1$ and $\alpha _P=0.125$

We mention here that numerical simulations of chaotic dynamics are challenging and have to be done with great care. In particular, chaotic dynamics of the system (3–4) can result in a curious effect that can be called an artificial loss of symmetry. The matter is that, when the problem is solved numerically by a computer, there is usually a very small random noise present in the computer memory. This noise can be cleared out in various ways, e.g., by introducing a technical threshold, say $\eta$, so that once the content of the memory cell is less than $\eta$ than it becomes exactly zero. In case of the regular dynamics, this small noise normally would not have any effect on the results. However, the situation can be different in case of chaos because of its inherent sensitivity to perturbations. Consider Eqs. (3–4) with initial conditions (24–25). As was discussed in Sect. 3.1, this mathematical problem is symmetrical with regard to reflection $x\rightarrow -x$ and $y\rightarrow -y$. Therefore, the solution N(x, y, t) should possess this symmetry at any time t, and this is indeed what is seen in the snapshots shown in Fig. 2. The results shown in Fig. 2 are obtained with the noise clearing at the threshold $\eta =10^{-8}$. However, the situation becomes different if the noise is not cleared. Figure 10 shows the simulation results obtained for the same parameters and initial conditions as Fig. 2 but without noise clearing. It is readily seen that the snapshots obtained at the earlier stage of the dynamics (Figs. 10a–c) demonstrate clear reflectional symmetry. However, the symmetry starts breaking at about $t=100$ and the patterns obtained for a later time promptly become irregular, see Figs. 10d–f. Note that the moment when the symmetry starts breaking due to the chaotic amplification of the random noise is in a good agreement with the results of Sect. 3.4. We also mention that this loss of symmetry due to the effect of computer noise is not a unique property of the kernel-based model and it has previously been reported for diffusion–reaction systems (Petrovskii et al. 2005).

In this paper, we were mostly interested in demonstrating that the ecologically highly relevant scenario of patchy invasion can occur for an alien species that spreads across space by means of long-distance dispersal. Having achieved that, our study leaves a number of open questions. In particular, considering our mathematical model in the context of real-world biological invasions, a question arises as to whether the properties of the emerging patchy spatial pattern are actually close to the properties of the spatial population distribution of invading species observed in nature. In order to address this problem, one can quantify the patterns in various ways, e.g., by calculating the powers spectra (Ranta et al. 2005), by applying the wavelet analysis (Dale and Mah 1998), by calculating the fragmentation index (Garnier et al. 2012) or by applying more specific methods of pattern recognition (Duda et al. 2001). Comparison between the results of such analysis for the real-world patterns and for simulation results obtained from different relevant models may help to identify ‘the best model’ and hence to shed the light onto the mechanisms behind the patchy invasion. In its turn, a better understanding of the invasion mechanisms and scenarios is likely to lead to more efficient control strategies. Although this challenging and ambitious task clearly lies behind the scope of this paper, it should become the focus of the future research.

Appendices

Appendix 1: Details of numerical integration

1.1 Boundary Conditions, Stationary Case

For the purposes of this paper, we need a boundary condition as non-intrusive as possible in order to minimize the boundary effect on the population dynamics in the interior of the domain. Since the kernel-based model is non-local, the relevant boundary condition is expected to be non-local as well.

Consider the normally distributed symmetrical kernel in the 1D domain $\Omega$:

$$\begin{aligned} \displaystyle {k(x,y)=\frac{1}{\sqrt{2\pi \alpha ^2}}\exp \left( -\frac{(x-y)^2}{2\alpha ^2}\right) }. \end{aligned}$$

(33)

where $(x,y) \in \Omega$. In the context of individual organism’s movement, the dispersal kernel k(x, y) gives the probability density of the event that an individual located at the position y before the dispersal will be found at the position x after the dispersal, and parameter $\alpha$ quantifies the spatial scale of the dispersal. We therefore require that the total probability is

$$\begin{aligned} P(x)=\int \limits _{\Omega }k(x,y)\mathrm{d}x = \int \limits _{\Omega }k(x,y)\mathrm{d}y \equiv 1. \end{aligned}$$

(34)

The boundary can be regarded as non-intrusive when the requirement (34) holds at any point in the computational domain $\Omega$. However, it is obviously not so when x is sufficiently close to the domain’s boundary regardless the size of the domain, see Fig. 11.

Fig. 11

Validation of the condition (34) in the domain $\Omega$. The kernel (33) has the variance $\alpha =3$. The domain size is $\Omega =[-L,L]$, where a $L=10$ and b $L=50$

In order to understand how the problem should be modified in order to make sure that condition (34) holds everywhere in the computational domain, we now consider the 1D domain $\Omega =[-L,L]$. From (33) and (34), we obtain:

$$\begin{aligned} P(x) = \int \limits _{\Omega }k(x,y)\mathrm{d}y = \int \limits _{-L}^L k(x,y)\mathrm{d}y = \frac{1}{2}\left[ \text{ erf }\left( \frac{L-x}{\sqrt{2}\alpha }\right) +\text{ erf }\left( \frac{L+x}{\sqrt{2}\alpha }\right) \right] , \end{aligned}$$

where $\text{ erf }(\xi )$ is the error function. Clearly, in order to satisfy (34), we need to ensure that $\text{ erf }\left( (L-x)/(\sqrt{2}\alpha )\right) \approx 1$ and $\text{ erf }\left( (L+x)/(\sqrt{2}\alpha )\right) \approx 1$ with sufficient precision.

We recall that $\text{ erf }(-\xi )=-\text{ erf }(\xi )$, and $\text{ erf }(\xi )$ is a monotone function of its argument $\xi$, $\text{ erf }(\xi ) \rightarrow 1$ as $\xi \rightarrow \infty$. It is well known that $\text{ erf }(\xi )$ is very close to 1 for $\xi \ge 3$, as we have $\text{ erf }(3)=0.99998$. Hence, we require that

$$\begin{aligned} \frac{L-x}{\sqrt{2}\alpha } \ge 3 \quad \text{ and } \quad \frac{L+x}{\sqrt{2}\alpha } \ge 3 \end{aligned}$$

(35)

in order to make $P \approx 1$ with sufficient precision. That can be achieved by performing the integration on a smaller domain, i.e., $x \in [-L+3\sqrt{2}\alpha , L-3\sqrt{2}\alpha ]$. Alternatively, however, if our domain of interest is $[-L,L]$, we can consider an extended domain $\Omega _\mathrm{ext}$ where the integration is performed. From the conditions (35), it is obvious that the extended domain preserving the condition (34) with sufficient accuracy can be defined as follows:

$$\begin{aligned} \Omega _\mathrm{ext}=[-L-3\sqrt{2}\alpha , L+3\sqrt{2}\alpha ]. \end{aligned}$$

(36)

Note that, apart from the size of the extended domain, parameter $\alpha$ also gives us a rough estimate of the grid step size in the problem, as we require that the interval of the length $\alpha$ should contain at least one grid point. For instance, if $L=10$ and $\alpha =0.1$, then the minimum size of the domain $\Omega _\mathrm{ext}$ is $\Omega _\mathrm{ext}=[-10.425, 10.425]$ and the minimum sensible number of grid points should be $n_{\min }=210$. For $n<n_{\min }$, the poor approximation will result in P being considerably less than 1 or may lead to $P>1$ which is senseless.

The analysis similar to that performed above for the normal distribution can be carried out for a different type of the kernel. Consider now the Cauchy-distributed kernel,

$$\begin{aligned} \displaystyle {k(x,y)=\frac{\beta }{\pi ((x-y)^2+\beta ^2)}}, \end{aligned}$$

(37)

where $\beta$ is a parameter. Again, we require that the condition (34) holds. Let us fix the value of x in (37) and consider it as the Cauchy distribution of the variable y. Integration over the domain $\Omega =[-L,L]$ gives

$$\begin{aligned} P(x)=\int \limits _{-L}^Lk(y)\mathrm{d}y=\frac{1}{\pi }\left[ \arctan \left( \frac{L-x}{\beta }\right) +\arctan \left( \frac{L+x}{\beta }\right) \right] . \end{aligned}$$

(38)

In order to meet the requirement $P=1$, we need to ensure that $\arctan \left( (L-x)/\beta \right) =\pi /2$ and $\arctan \left( (L+x)/\beta \right) =\pi /2$.

Let $v^*$ be a parameter that provides the required accuracy of the integration, such that $\arctan (v^*) \approx \pi /2$ with the desired precision. We then require

$$\begin{aligned} \frac{L-x}{\beta } \ge v^* \quad \text{ and }\quad \frac{L+x}{\beta } \ge v^*, \end{aligned}$$

(39)

in order to approximate $P \approx 1$ in the expression (38). That will give us the necessary range of x as

$$\begin{aligned} x \in [-L+\beta v^*, L-\beta v^*]. \end{aligned}$$

Therefore, the extended domain $\Omega _\mathrm{ext}$ can be defined as

$$\begin{aligned} \Omega _\mathrm{ext}=[-L-\beta v^*, L+\beta v^*]. \end{aligned}$$

(40)

Clearly, for any chosen accuracy $v^*$, the size of the domain is fully controlled by the value of the parameter $\beta$.

We notice here that the asymptotic convergence of the function $\arctan (v)$ is much slower than the convergence of the function $\text{ erf }(v)$. Correspondingly, in simulations with the Cauchy kernel, the domain extension has to be considerably larger than in simulations with the normally distributed kernel. By the way of example, several relevant values of $\arctan (v)$ are given in Table 1. Considering, for instance, the minimum accuracy of 0.2 % (i.e., at most 0.002 of the total population is lost because of its dispersal through the domain boundary), we observe that factor $v^*\approx 200$. For a hypothetical value $\beta =0.1$, it leads to the requirement that the margin separating the spreading population from the domain boundary should be about 20 or larger.

Table 1 Convergence of $\arctan (v)$ to its limiting value $\pi /2$ for large argument v

The above approach readily applies to the 2D problem as well, with the obvious modification that it should be used in both directions x and y.

1.2 Accumulation of Integration Error with Time

We now investigate how fast the numerical error is accumulated with time when the kernel is defined in either the original domain $\Omega$ or the extended domain $\Omega _\mathrm{ext}$. For this purpose, we consider

$$\begin{aligned} N_t(x)=\int \limits _{\Omega }k(x,y) N_{t-1}(y)\mathrm{d}y, \end{aligned}$$

(41)

where, at each generation t, we take into account only dispersal but not reproduction. Consider the case where the dispersal kernel is normally distributed; see (33). Assuming for the sake of simplicity that the initial condition is given by the normal distribution as well, i.e.,

$$\begin{aligned} N_0(y)=\frac{1}{\sqrt{2\pi \alpha _0^2}}\exp \left( -\frac{(y-\mu )^2}{2\alpha _0^2}\right) , \end{aligned}$$

(42)

the population density after t generations is given by the following normal distribution:

$$\begin{aligned} N_t(x)=\frac{1}{\sqrt{2\pi \alpha _t^2}}\exp {-\frac{(x-\mu )^2}{2\alpha _t^2}}, \end{aligned}$$

(43)

where the variance is

$$\begin{aligned} \alpha _t^2=\alpha _0^2+t\alpha ^2, \end{aligned}$$

(44)

$t=1,2,3\ldots$.

Let us now compute the function $\tilde{N}_t(x)$ by numerical integration in the domain $\Omega$ and compare it with the exact solution $N_t(x)$ given by (43). For any fixed t, the error $e_i=|N_t(x_i)-\tilde{N}_t(x_i)|$ is computed at every point $i=1,2,\ldots ,K$ of a uniform computational grid where K is the total number of grid nodes. The error norm is then defined as

$$\begin{aligned} ||e|| = \max \limits _{i=1,\ldots ,K}e_i. \end{aligned}$$

(45)

The graph of the error norm (45) as a function of t is shown in Fig. 12 by the dashed curve. The parameters of this test case are $\alpha =3.0$, $\alpha _0=1.0$, $\mu =0$, $t=10$ and $\Omega =[-20,20]$. The number of grid nodes on a uniform computational grid is $K=2049$. Here and below, the error is shown on the logarithmic scale. It is readily seen that the error increases rapidly as the time progresses. Further refinement of the grid does not result in any significant improvement in accuracy. Hence, we conclude that poor accuracy of numerical integration for $t>10$ is related to inaccurate kernel computation at the domain boundaries as discussed in the previous section.

Fig. 12

Computation of the convolution by numerical integration. The test case parameters are $\alpha =3.0$, $\alpha _0=1.0$, $\mu =0$, $t=10$ and $\Omega =[-20,20]$. The graph of the error norm (45) as a function of t. The computation is made in the domain $\Omega _\mathrm{ext}$ (solid line, open square) and the domain $\Omega$ (dashed line, closed circle)

We now make use of the findings in the previous section and compute the solution of Eq. (41), which we denote as $\tilde{N}_t(x)$, by numerical integration in the extended domain $\Omega _\mathrm{ext}$. The numerical solution $\tilde{N}_t(x)$ is then compared with the exact solution $N_t(x)$ in the domain $\Omega$. We emphasize that the domain $\Omega _\mathrm{ext}$ should be thought of as an auxiliary domain only used for accurate computation of the kernel. The resulting function $\tilde{N}_t(x)$ is still considered in the domain $\Omega$ where we assume the species population exists in the framework of our model.

The error norm for the function $\tilde{N}(t,x)$ when the computation is performed in the domain $\Omega _\mathrm{ext}$ is shown in Fig. 12 by the solid curve. The problem parameters remain the same as in the previous test case. According to the analysis done in the previous section, see (36), the size of the extended domain is $\Omega _\mathrm{ext}=[-32.7279, 32.7279]$. It is therefore clear that computation in the extended domain $\Omega _\mathrm{ext}$ provides very good accuracy for the solution evaluation in the original domain $\Omega$.

Note that the error only becomes large when the integrand function $\tilde{N}_{t-1}(x)$ has relatively large values close to the endpoints of the domain. Let us fix the time t and vary the parameter $\alpha$ in the formula (33). The corresponding graphs of the function $N_t(x)$ are shown in Fig. 13a. For each value of $\alpha$, we compute the error norm shown in Fig. 13b, where the results of computation are presented in the domain $\Omega$ and the domain $\Omega _\mathrm{ext}$.

Fig. 13

Computation of the convolution by numerical integration when the kernel parameter $\alpha$ is varied. The other parameters are $\alpha _0=1.0$, $\mu =0$, $\Omega =[-20,20]$ and $t=25$. a The graph of the function N(t, x) given by (43) for $\alpha =0.05$, $\alpha =0.5$ and $\alpha =2.0$. b The graph of the error norm (45) as a function of $\alpha$. The computation is made in the domain $\Omega$ (dashed line, closed circle) and the domain $\Omega _\mathrm{ext}$ (solid line, open square)

We therefore conclude that the accuracy of computation will deteriorate with time, provided that the support of the integrand $N_{t-1}(x)$ gets bigger as the time progresses. The ‘critical’ time $t_c$ when the error becomes unacceptably large can be roughly estimated from the condition $3\alpha _t=L$, where $\alpha _t$ is given by the Eq. (44). For $L=20$, $\alpha _0=1.0$ and $\alpha =3.0$, we have $t_c \approx 4$ and this estimate appears to be in a good agreement with the results of Fig. 13a.

1.3 Grid Convergence Test

Now we consider a nonlinear integro-difference equation that takes into account both dispersal and reproduction:

$$\begin{aligned} N_t(x)=\int \limits _{\Omega }k(x,y)f(N_{t-1}(y))\mathrm{d}y. \end{aligned}$$

(46)

In order to test the quality of our numerical approach, we need a function f that could provide a non-trivial spatiotemporal dynamics such as pattern formation. Correspondingly, we consider

$$\begin{aligned} \displaystyle {f(N)=rN\exp {(-N)}}. \end{aligned}$$

(47)

As for the dispersal, we consider the normally distributed kernel given by (33).

Fig. 14

Comparison of the solution on a fine grid of 8193 nodes (a bold line) with the solution on a coarse grid of 129 nodes at the fixed time $t=20$. The domain size is $[-L,L]$, where $L=15.0$. The other parameters are $\alpha =0.1$ and $r=7.0$

Equation (46) is solved numerically in the domain $[-L,L]$ to obtain the solution $N_t(x)$ at generation t from the solution $N_{t-1}(x)$ at the previous generation $t-1$. We use a regular grid, so that the location of each grid node in the domain is given by $x_{i+1}=x_i+\Delta$, where the grid step size $\Delta =2L/K$ and K is the number of grid nodes. For any fixed time t, the accuracy of the solution depends on the total number of nodes in the spatial grid used for numerical integration. The example of numerical solution on a coarse grid of $K=129$ nodes and a fine grid of $K=8193$ nodes at the fixed time $t=20$ is shown in Fig. 14. It is readily seen that the solution accuracy is lost on the coarse grid where the grid step size is not sufficiently small to resolve the solution oscillations.

Fig. 15

The error norm as a function of the number K of grid nodes

The above observations can be summarized by computing the solution error on a sequence of spatial grids when the time t is fixed. Namely, we first compute a numerical solution on a very fine grid of $K_f=8193$ nodes. We consider this numerical solution as this ‘exact’ solution and denote it $N^\mathrm{exact}(x)$. We then generate a sequence of uniformly refined grids where the ‘exact’ solution obtained on the fine grid should be available on each grid in the sequence. Hence, we consider a projection of fine grid onto a uniform coarse grid of K nodes. The number K is defined as $K=sK_0+1$, where $K_0=32$ is the number of grid subintervals on the initial coarse grid and the scaling coefficient is $s=2^{p}, p=0,1,2,\ldots ,7$. The nodal coordinates $x_i^{c}$, $i=1,\ldots ,K$ and $x_i^{f}$, $k=1,\ldots ,K_f$, considered on the coarse and fine grid, respectively, are related as $x_i^{c}=x_k^{f}$, where $k=si$. Once the grid projection has been made, the ‘exact’ solution is readily available at nodes $x_i$ of a coarse grid and the solution error

$$\begin{aligned} e_i=|N(t,x_i)-N^\mathrm{exact}(t,x_i)| \end{aligned}$$

(48)

is computed at each node. The error norm is defined accordingly as $||e||=\max _i e_i$.

The graph of the error norm as a function of the number K of grid nodes is shown in Fig. 15. It is seen from the figure that very good accuracy of computation is approached when the number of grid nodes is $K \ge 513$, i.e., the grid step size is $\Delta <0.0586$. Meanwhile, the solution is very poorly resolved on coarse grids with $K \le 65$ where the maximum error is $||e|| \sim 1$.

Appendix 2: Details of the FFT Numerical Technique

Let the function f(x) be defined in the domain $x \in (-\infty , +\infty )$. The Fourier transform $\widehat{f}(s)$ of the function f(x) is given by

$$\begin{aligned} \widehat{f}(s)=\int \limits _{-\infty }^{+\infty }f(x)e^{-2\pi isx}\mathrm{d}x, \end{aligned}$$

(49)

and the inverse Fourier transform is

$$\begin{aligned} f(x)=\int \limits _{-\infty }^{+\infty }\widehat{f}(s)e^{2\pi isx}\mathrm{d}s. \end{aligned}$$

Consider now two functions f(x) and g(x) defined for $x \in (-\infty , +\infty )$. Their convolution denoted ${f *g}$ is defined as

$$\begin{aligned} {f *g}=\int \limits _{-\infty }^{+\infty }f(y)g(x-y)\mathrm{d}y. \end{aligned}$$

(50)

Obviously, the convolution ${f *g}$ is a function of x, ${f *g}\equiv {f *g}(x)$ and we can apply (49) to ${f *g}(x)$ to obtain the Fourier transform $\widehat{f *g}(s)$ of the convolution.

Let $\widehat{f}(s)$ be the Fourier transform of a function f(x) and $\widehat{g}(s)$ be the Fourier transform of a function g(x). The convolution theorem states that

$$\begin{aligned} \widehat{f *g}(s)=\frac{1}{2\pi }\widehat{f}(s) \widehat{g}(s), \end{aligned}$$

(51)

i.e., the Fourier transform of the convolution of two functions is equal to the product of their Fourier transforms (e.g., see Champeney 1973). Thus, the convolution ${f *g}(x)$ of two functions can be found by calculating and inverting the Fourier transform $\widehat{f *g}(s)$ rather than by performing straightforward integration in (50).

It is important to note that the convolution theorem (51) can be applied in the multi-dimensional case where $f(\mathbf {x})$ and $g(\mathbf {x})$ are functions of the vector argument $\mathbf {x}$. The following discussion refers to the one-dimensional case as all basic results can be readily extended to a two-dimensional problem.

The functions f and g in the theorem (51) are generally supposed to be complex functions. Clearly, real functions in the generic population dynamics model (2) present a particular case of complex functions and the theorem (51) can therefore be employed in our problem to compute

$$\begin{aligned} {f *k}=\int _{-L}^{L}f(y)k(x-y)\mathrm{d}y, \end{aligned}$$

(52)

where ${f *k}$ is required to obtain population distributions and the definition of the kernel k(x) is given in the text. The interval L has to be chosen large enough so that in the time considered in the simulation, there is no boundary effects on the solution and we can assume that $y \in [-L,L]$ is a good approximation of the infinite interval (see also the discussion in Appendix 1).

The convolution theorem gives us the theoretical background for finding the values of a continuous function ${f *k}$ in the formula (52). However, when the problem (2) is solved numerically, see Sect. 3.3, both the population density and the kernel are only defined at nodes of a computational grid. Thus, the continuous Fourier transform has to be replaced with the discrete Fourier transform (DFT).

Let a continuous function f(x) be discretized over the interval $x \in [0,1]$ so that only the values $f_k \equiv f(x_k)$ are considered, where $x_k=k\Delta x$, $k=0,\ldots K-1$, $\Delta x=1/(K-1)$ is the grid step size and K is the number of grid nodes chosen in the problem. We denote $[f_k]$ the discrete function given by the set of numbers $f_0,f_1,\ldots ,f_{K-1}$. The DFT of the function $[f_k]$ denoted $F_s$ is defined as

$$\begin{aligned} F_s=\displaystyle {\frac{1}{K}\sum _{k=0}^{K-1} f_{k}e^{2\pi iks/K}}. \end{aligned}$$

(53)

The corresponding inverse transform is

$$\begin{aligned} f_k=\displaystyle {\sum _{s=0}^{K-1} F_{s}e^{-2\pi iks/K}}. \end{aligned}$$

(54)

The discrete Fourier transform can be loosely thought of as approximation of the integral (49) by the finite sum (53).

One important consequence of the definition (53) is that the convolution theorem is still valid in the discrete case stating that the product of the two individual DFTs will give the DFT of the discrete convolution (e.g., see Nussbaumer 1982). Thus, the task of computing the convolution (52) can be decomposed as computing $\widehat{k}$ and $\widehat{f}$ to produce $\widehat{k *f}=\widehat{k} \widehat{f}$ and then computing the inverse DFT of the product.

Computing and inverting the DFT can be done efficiently with help of the fast Fourier transform (FFT) numerical algorithms. The key idea behind any FFT computational routine is to reduce the number of operations required to compute the DFT and its inverse transform.

While the number of operations in a straightforward DFT computation using the formula (53) is $O(K^2)$, an FFT algorithm reduces that number to $O(K\log _2(K))$. It is worth noting here that the FFT is also superior to methods of numerical integration. For instance, numerical integration of (52) by a composite trapezoidal rule can be done in $O(K^2)$ operations.

The significant reduction in the number of operations requires a sophisticated algorithm incorporating a number of computational tricks, e.g., choosing the number K to be $K=2^m$ for some integer m and interchanging the first and second parts of the output vector in a computer program. The detailed explanation of the FFT algorithm can be found elsewhere (e.g., Press et al. 2007). In our problem, there also are some small modifications to the standard FFT routine dictated by the problem statement: We have to multiply the result by 2L (as the standard FFT algorithm assumes that the functions are defined on the interval [0, 1]) and remove the imaginary vector components created during the calculations as we deal with real functions only.

In the two-dimensional case, the FFT can be split into a series of one-dimensional FFTs resulting in the total number of operations $O(K^2\log _2(K))$. We use internal Mathematica routines to calculate the two-dimensional Fourier transform by FFT and, hence, obtain the population distributions over the lattice.

The results of the FFT computation performed for several test cases have been verified by direct numerical integration of (52), and very good agreement between the results of the two methods (i.e., the FFT and the trapezoidal rule of integration) was demonstrated in all test cases.