1 Introduction

Malaria is caused by parasites (species plasmodium) transmitted to people through the bites of infected female mosquitoes. Plasmodium falciparum and Plasmodium vivax are the two most common species, and plasmodium falciparum is the most deadly (World Health Organization 2010). In the tropical and subtropical areas of the globe, plasmodium falciparum malaria is a major cause of mortality and morbidity. According to the 2009 Malaria World Report (World Health Organization 2009), half of the world’s population is at risk of malaria, with an estimated 243 million cases that led to about 863, 000 deaths in 2008, a slight drop from the 2006 statistics. This decrease can be attributed to a number of improved policies, including increases in international funding, research, the use of insectide-treated bednets and artemisinin-based combination therapy, and a revival of support for indoor residential insectide spraying (World Health Organization 2009). Despite this slight drop, there are still challenges that may lead to significant increase in the malaria burden. These include the global financial slow down and the changing climatic conditions, both of which affect the endemic malaria regions (Lindsay and Martens 1998; Zhou et al. 2004). The number and severity of malaria cases are also being exacerbated by high levels of HIV infection that weaken the immune system rendering people with HIV more susceptible to contracting the disease (Bush et al. 2001) and also enhancing mortality in advanced HIV patients by a factor of about 25 % in non-stable malaria areas (Grimwade et al. 2004).

Drug resistance malaria is caused by drug misused or non-compliance to drug regimens, and this development is feared will thwart the malaria control efforts and will significantly increase the disease burden. This concern is fueled by the emergence of resistance to artemisinin-based combination therapy in western Cambodia and western Thailand (Cheeseman et al. 2012; Phyo et al. 2012). Artemisinin resistance is marked by reduced parasite clearance upon treatment (Cheeseman et al. 2012; Phyo et al. 2012). In 2002, an indication pointing to artemisinin resistance arose in Cambodia when failure rates of the artesunate (a class of artemisinins) and mefloquine combination therapy began (Denis et al. 2006). A study conducted in 2009, to investigate the efficacy of artemisinin-based combination therapy and artesunate monotherapy in western Cambodia compared to northwestern Thailand (Dondorp et al. 2009), found that in western Cambodian P. falciparum parasites had significantly reduced susceptibility to artesunate, an indication that the parasites were surviving longer against the effects of the drug. A more recent study Phyo et al. (2012), examining over 3,000 patients in Thailand–Myanmar border, which is on the western border of Cambodia, found that it took significantly longer for malaria parasites to be killed in the course of treatment with artemisinin therapies than it had in 2001. These new instances of drug resistance were found 800 km away from the 2009 cases of anti-malarial resistance, indicating that movement of people plays a role in the spread of drug resistance malaria.

Chloroquine resistance in P. falciparum was first observed among Thai gem workers returning from nearby Cambodia in 1957 (Carrara et al. 2006). Following a 13 year study in which artemisinin combination treatments (ACT) of mefloquine and artesunate regimen were deployed continuously as first-line treatment in camps for displaced persons and in clinics for migrant population along the Thai–Myanmar border, a modest increase in resistance was observed Carrara et al. (2009). Thus, imported malaria to areas with low malaria transmission or movement into areas aiming for elimination serves as another challenge against the public health bid at reducing the local malaria transmission. The movement of people between areas with different malaria transmission rates will impact the effectiveness of control interventions. For instance, frequent movement of infected individuals into an area that had eliminated malaria through extensive interventions could increase the time over which the intervention will have to be held in place in order to prevent resurgence of the disease.

A number of studies have been carried out following the pioneering work of Ross (1911), in order to understand the transmission and spread of malaria (Ross 1911; Chitnis et al. 2006; Dietz 1988; Feng et al. 2004; Smith et al. 2006). Using simple probabilistic models, Hastings (1997) and Mackinnon (2005) studied the factors influencing the appearance of mutations that confer resistance to malaria drugs. Aneke (2002) and Koella and Antia (2003) captured the epidemiological effects of drug treatment and resistance development via population dynamics models; the models used inoculation rate to model the vector dynamics at steady-state vector population with respect to changes in the human population. Bacaer and Sokna (2005) used a reaction diffusion system to model the spatial spread of resistance; modeling resistance development in terms of primary infection with the resistant strain. Esteva and Gumel (2009) used a deterministic model to monitor the epidemiological impact of the anti-malarial drug and how this impact is influenced by the evolution of resistance as well as the fitness of the resistant strain in a given population. Pongtavornpinyo et al. (2008) constructed a model which incorporated the epidemiological and biological factors of human, mosquito, parasite, and treatment in order to evaluate different anti-malarial policy options focusing on ACT deployment.

Various studies incorporating human movement between spatially heterogeneous regions have been carried out with the aim of quantifying the potential burden of malaria infection in humans. Rodrguez and Torres-Sorando (2001) considered models with hosts distributed in subpopulations as a consequence of spatial partitioning using two types of models with direct and indirect transmission. Considering two types of visit: one in which the visit time is independent of the distance traveled, and the other in which visit time decreases with distance. Ariey et al. (2003) used a patch occupancy discrete-time metapopulation model to study the spread of resistance to chloroquine in the pathogen. Menach and Ellis Mckenzie (2005) gave a detailed description of mosquito oviposition behavior in metapopulation setting. Smith and Dushoff (2005) used metapopulations to model malaria transmission assuming only migration of mosquitoes. Auger et al. (2008) generalize the Ross–Macdonald malaria model to \(n\) patches and incorporated the fact that some patches can be vector free. They assume that the hosts can migrate between patches, but not the vectors. Adams and Kapan (2009) numerically investigated the effect of short-term human movement. Cosner et al. (2009) developed spatial models of vector-borne disease dynamics on a network of patches to examine how the movement of humans in heterogeneous environments affects transmission. They constructed two classes of models using different approaches: one that mimic human commuting behavior using Lagrangian models and the other that mimic human migration using Eulerian models. A metapopulation malaria model was proposed by Arino et al. (2012) using SI and SIRS models for the vectors and hosts. The model was then applied to study the spread of malaria to non-endemic areas, and the interaction between rural and urban areas are given. Using type reproduction numbers, the reservoirs of infection was identified, and the effect of control measures evaluated. To address the role of human movement and spatial heterogeneity in malaria transmission and malaria control, (Prosper et al. 2012) considered a two patch metapopulation model connected by human movement and with different degrees of malaria transmission in each patch. Sensitivity analysis of the reproduction number and the endemic equilibrium to various parameters in the two patch was performed in order to determine which patch will be the better target for control measures and what type of control measure should be implemented within the patch.

Understanding the dynamics of the spread of both drug-sensitive and drug-resistance malaria with mobility of individuals between regions is crucial to the efforts of controlling or eradicating the disease burden. The existing studies of transmission dynamics of malaria with mobility in spatially homogeneous regions (Adams and Kapan 2009; Ariey et al. 2003; Arino et al. 2012; Auger et al. 2008; Cosner et al. 2009; Menach and Ellis Mckenzie 2005; Rodrguez and Torres-Sorando 2001; Smith and Dushoff 2005) focused only on the transmission dynamics of drug sensitive malaria between the spatial locations. This current work (to the best of my knowledge) is the first to attempt to consider the dynamics of drug-sensitive and drug-resistance malaria with mobility of individuals between regions. Hence, this current study presents a deterministic model for the transmission dynamics of drug resistance malaria with mobility of individuals between different spatial locations. The aim of this study is to determine the impact of human movement on the prevalence of drug resistance malaria in the population and the role of human movement on the persistence or extinction of the malaria drug sensitive and drug resistance strains. The study extend the aforementioned studies particularly those in Auger et al. (2008), Prosper et al. (2012), Smith and Dushoff (2005), and the model in Cosner et al. (2009) with Lagrangian movement, by incorporating the development of drug resistance malaria transmission. Furthermore, the study will present a rigorous analysis of the resulting model.

2 Formulation of the Basic Malaria Model

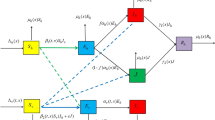
The model is formulated with human and mosquito groups (see Fig. 1). The model sub-divides the total human population in patch \(i~\) at time \(t\), denoted by \(N_{hi}(t)\), into the following sub-populations of susceptible individuals \((S_i(t))\), infected individuals with drug sensitive malaria \((I_i(t))\), and infected individuals with drug resistance malaria \((J_i(t))\), where \(i=1\ldots n\). So that

$$\begin{aligned} N_{hi}(t) = S_i(t) + I_i(t) + J_i(t). \end{aligned}$$

The rates at which the proportion of susceptible humans (\(S_{i}\)) changes over time in patch \(i\) is given by

$$\begin{aligned} \displaystyle \frac{d S_i}{dt} = \displaystyle \Pi _i + \gamma _i I_i + \tau _i J_i - \frac{\alpha _{hi}\beta _{hi}I_{vi}}{N_{hi}} S_i - \frac{\alpha _{hi}\theta _{hi}J_{vi}}{N_{hi}} S_i - \mu _h S_i. \end{aligned}$$
(1)

The parameter \(\Pi _{i}\) is the recruitment rate into the susceptible human class. The parameter \(\alpha _{hi}\) is the rate at which susceptible humans in patch \(i\) receive mosquitoes bite. The parameter \(\beta _{hi}\) is the probability that a susceptible human becomes infected with drug sensitive malaria having been bitten by an infectious mosquito with the drug sensitive strain. The parameter \(\theta _{hi}\) correspond to the probability that a susceptible human becomes infected with drug resistance malaria having been bitten by an infectious mosquito with the drug resistance strain, it is assumed that \(\theta _{hi}<\beta _{hi}\). The natural death rate is denoted by \(\mu _h\).

Fig. 1
figure 1

Systematic flow diagram of the Malaria Model (7) without movement

Full size image

The rate at which the proportion of infected humans (\(I_{i}\)) with drug sensitive malaria changes over time in patch \(i\) is given by

$$\begin{aligned} \displaystyle \frac{d I_i}{dt} = \displaystyle \frac{\alpha _{hi}\beta _{hi}I_{vi}}{N_{hi}} S_i - (\gamma _i +\xi _i+ \mu _h + \delta _{I_i})I_i . \end{aligned}$$
(2)

The parameter \(\gamma _i\) denotes the drug sensitive malaria recovery rate, while \(\xi _{i}\) is the rate at which humans develop resistance to malaria treatment drugs as a result of non-compliant to treatment regiment. The disease-induced death rate due to drug sensitive malaria in patch \(i\) is denoted by \(\delta _{I_i}\).

Similarly, the rate at which the proportion of infected humans (\(J_{i}\)) with drug resistance malaria changes over time in patch \(i\) is given by

$$\begin{aligned} \displaystyle \frac{d J_i}{dt} = \displaystyle \frac{\alpha _{hi}\theta _{hi}J_{vi}}{N_{hi}} S_i + \xi _i I_i - (\tau _i + \mu _h + \delta _{J_i}) J_i . \end{aligned}$$
(3)

The parameter \(\tau _i\) is the parameter indicating recovery rate with drug resistance malaria. It is assumed that once a human recovers from malaria infection, they do not gain immunity, but instead are susceptible to re-infection, this is a simplifying assumption since humans develop immunity against malaria with repeated exposure (Niger and Gumel 2008). The disease-induced death rate due to drug resistance malaria in patch \(i\) is denoted by \(\delta _{J_i}\).

The mosquito population in patch \(i\) at time \(t\) has three classes representing susceptible mosquitoes, \(S_{vi}(t)\), infected mosquitoes with drug sensitive malaria, \(I_{vi}(t)\), and infected mosquitoes with drug resistance malaria, \(J_{vi}(t)\). Thus, the total mosquito population is

$$\begin{aligned} N_{vi}(t) = S_{vi}(t) + I_{vi}(t) + J_{vi}(t). \end{aligned}$$

The rates at which the proportion of susceptible mosquitoes (\(S_{vi}\)) changes over time in patch \(i\) is given by

$$\begin{aligned} \frac{d S_{vi}}{dt} = \Pi _{vi} - \frac{\alpha _{vi}\beta _{vi}I_i}{N_{hi}} S_{vi} - \frac{\alpha _{vi}\theta _{vi}J_i}{N_{hi}} S_{vi} - \mu _v S_{vi}. \end{aligned}$$
(4)

The parameter \(\Pi _{vi}\) is the recruitment rate into the susceptible mosquito class. The parameter \(\alpha _{vi}\) is the rate at which mosquitoes bite humans in patch \(i\). The parameter \(\beta _{vi}\) is the probability that a susceptible mosquito becomes infected with drug sensitive malaria having bitten an infectious human with the drug sensitive strain. The parameter \(\theta _{vi}\) corresponds to the probability that a susceptible mosquito becomes infected with drug resistance malaria having bitten an infectious human with the drug resistance strain. The mosquito natural death rate is denoted by \(\mu _v\).

The rate at which the proportion of infected mosquitoes (\(I_{vi}\)) with drug sensitive malaria changes over time in patch \(i\) is given by

$$\begin{aligned} \frac{d I_{vi}}{dt} = \frac{\alpha _{vi}\beta _{vi}I_i}{N_{hi}}S_{vi} - \mu _v I_{vi} . \end{aligned}$$
(5)

Similarly, the rate at which the proportion of infected mosquitoes (\(J_{vi}\)) with drug resistance malaria changes over time in patch \(i\) is given by

$$\begin{aligned} \frac{d J_{vi}}{dt} = \frac{\alpha _{vi}\theta _{vi}J_i}{N_{hi}} S_{vi} - \mu _v J_{vi} , \end{aligned}$$
(6)

We assume here that only humans move between the patches and so, we include migration in Eqs. (1)–(3) above and also assuming that disease transmission occurs only between individuals that are in the same patch at the same time. Now adding the equations for the mosquitoes, we have the following system of ordinary differential equations

$$\begin{aligned} \displaystyle \frac{d S_i}{dt}&= \displaystyle \Pi _i +\gamma _i I_i + \tau _i J_i - \frac{\alpha _{hi}\beta _{hi}I_{vi}}{N_{hi}}S_i - \frac{\alpha _{hi}\theta _{hi}J_{vi}}{N_{hi}} S_i- \mu _h S_i - \sum ^n_{i=1,i\ne j}\psi _{_{ji}}S_i\nonumber \\&+ \sum ^n_{j=1,j\ne i}\psi _{_{ij}}S_j \nonumber \\ \displaystyle \frac{d I_i}{dt}&= \displaystyle \frac{\alpha _{hi}\beta _{hi}I_{vi}}{N_{hi}} S_i - (\gamma _i +\xi _i+ \mu _h + \delta _{I_i})I_i - \sum ^n_{i=1,i\ne j}\psi _{_{ji}}I_i + \sum ^n_{j=1,j\ne i}\psi _{_{ij}}I_j \nonumber \\ \displaystyle \frac{d J_i}{dt}&= \displaystyle \frac{\alpha _{hi}\theta _{hi}J_{vi}}{N_{hi}} S_i + \xi _i I_i - (\tau _i + \mu _h + \delta _{J_i}) J_i - \sum ^n_{i=1,i\ne j}\psi _{_{ji}}J_i + \sum ^n_{j=1,j\ne i} \psi _{_{ij}}J_j\nonumber \\ \displaystyle \frac{d S_{vi}}{dt}&= \displaystyle \Pi _{vi} - \frac{\alpha _{vi}\beta _{vi}I_i}{N_{hi}} S_{vi} - \frac{\alpha _{vi}\theta _{vi}J_i}{N_{hi}} S_{vi} - \mu _v S_{vi}\nonumber \\ \displaystyle \frac{d I_{vi}}{dt}&= \displaystyle \frac{\alpha _{vi}\beta _{vi}I_i}{N_{hi}}S_{vi} - \mu _v I_{vi} \nonumber \\ \displaystyle \frac{d J_{vi}}{dt}&= \displaystyle \frac{\alpha _{vi}\theta _{vi}J_i}{N_{hi}} S_{vi} - \mu _v J_{vi} \end{aligned}$$
(7)

The model (7) extends the model in Auger et al. (2008), Cosner et al. (2009), Prosper et al. (2012), Smith and Dushoff (2005) by incorporating the development and transmission of drug resistance malaria and the inclusion of human migration. The models in Auger et al. (2008), Cosner et al. (2009), Prosper et al. (2012), Smith and Dushoff (2005) only considered the transmission dynamics of drug sensitive malaria.

Since the model (7) represents human and mosquito populations, all parameters in the model are non-negative and one can show that the solutions of the system are non-negative, given non-negative initial values. The model (7) will be analyzed in a biologically feasible region as follows. The system (7) is split into two parts, namely the human population and the mosquitoes population. Consider the feasible region

$$\begin{aligned} \Gamma = \Gamma _i \subset \mathbb {R}^{6n}_+ \end{aligned}$$

with,

$$\begin{aligned} \Gamma _i&= \Bigg \{(S_i(t),I_i(t),J_i(t),S_{vi}(t),I_{vi}(t),J_{vi}(t))\in \mathbb {R}^{6n}_+ :0\le N_{hi}(t)\le K_h~~\mathrm{and }~~ 0\\&\quad \le N_{vi}(t)\le K_v\Bigg \}, \end{aligned}$$

The following steps are followed to establish the positive invariance of \(\Gamma \) (i.e., solutions in \(\Gamma \) remain in \(\Gamma \) for all \(t>0\)). The rate of change of the total human populations is obtained by adding the \(3n\) equations for humans in the model (7) to give

$$\begin{aligned} \displaystyle \frac{dN_{hi}(t)}{dt}= \displaystyle \Pi _i - \mu _h N_i - \delta _{I_i}I_i - \delta _{J_i} J_i - \sum ^n_{i=1,i\ne j}\psi _{_{ji}}N_{hi}(t) ~+ \sum ^n_{j=1,j\ne i}\psi _{_{ij}}N_{hj}(t), \nonumber \\ \end{aligned}$$
(8)

Now, summing (8) from \(i=1 \ldots n\) gives

$$\begin{aligned} \displaystyle \sum ^n_{i=1}\frac{dN_{hi}(t)}{dt}&= \displaystyle \sum ^n_{i=1}(\Pi _i - \mu _h N_i - \delta _{I_i}I_i - \delta _{J_i} J_i) \nonumber \\&+ \sum ^n_{i=1}\bigg ( - \sum ^n_{i=1,i\ne j}\psi _{_{ji}}N_{hi}(t) ~+ \sum ^n_{j=1,j\ne i}\psi _{_{ij}}N_{hj}(t)\bigg ). \end{aligned}$$
(9)

The double sum in (9) sums up to zero, i.e.

$$\begin{aligned} \displaystyle \sum ^n_{i=1}\bigg ( - \sum ^n_{i=1,i\ne j}\psi _{_{ji}}N_{hi}(t) ~+ \sum ^n_{j=1,j\ne i}\psi _{_{ij}}N_{hj}(t)\bigg ) = 0 \end{aligned}$$

Hence,

$$\begin{aligned} \begin{aligned} \displaystyle \sum ^n_{i=1}\frac{dN_{hi}(t)}{dt}&= \displaystyle \sum ^n_{i=1}(\Pi _i - \mu _h N_i - \delta _{I_i}I_i - \delta _{J_i} J_i)\\&\le \displaystyle \sum ^n_{i=1}(\Pi _i - \mu _h N_i).\\ \end{aligned} \end{aligned}$$
(10)

Similarly for the mosquito population

$$\begin{aligned} \begin{array}{l} \displaystyle \sum ^n_{i=1}\frac{dN_{vi}(t)}{dt}= \sum ^n_{i=1}\Pi _{vi}- \sum ^n_{i=1}\mu _vN_{vi}(t) . \\ \\ \end{array} \end{aligned}$$
(11)

A standard comparison theorem (Lakshmikantham et al. 1989) can then be used to show that

$$\begin{aligned} N_{hi}(t)&\le N_{hi}(0)e^{-\sum ^n_{i=1}\mu _ht}+\frac{\sum ^n_{j=1}\Pi _i}{\sum ^n_{i=1}\mu _h}(1-e^{-\sum ^n_{i=1}\mu _ht}),\\ \mathrm{and}\\ N_{vi}(t)&= N_{vi}(0)e^{-\sum ^n_{i=1}\mu _v t}+\frac{\sum ^n_{i=1}\Pi _{vi}}{\sum ^n_{i=1} \mu _v} (1-e^{-\sum ^n_{i=1}\mu _v t}). \end{aligned}$$

In particular, \(N_{hi}(t)\le \frac{\sum ^n_{j=1}\Pi _i}{\sum ^n_{i=1}\mu _h}\) and \(N_{vi}(t)=\frac{\sum ^n_{i=1}\Pi _{vi}}{\sum ^n_{i=1} \mu _v}\), if \(N_{hi}(0)\le \frac{\sum ^n_{j=1}\Pi _i}{\sum ^n_{i=1}\mu _h}\) and \(N_{vi}(0)=\frac{\sum ^n_{i=1}\Pi _{vi}}{\sum ^n_{i=1} \mu _v}\). Thus, the region \(\Gamma \) is positively invariant. Hence, it is sufficient to consider the dynamics of the flow generated by (7) in \(\Gamma \). In this region, the model is epidemiologically and mathematically well-posed (Hethcote 2000). Thus, every solution of the basic model (7) with initial conditions in \(\Gamma \) remains in \(\Gamma \) for all \(t > 0\). Therefore, the \(\omega \)-limit sets of the system (7) are contained in \(\Gamma \). This result is summarized below.

Lemma 1

The region \(\Gamma = \Gamma _i\subset \mathbb {R}^{6n}_+\) is positively invariant for the basic malaria model (7) with non-negative initial conditions in \(\mathbb {R}^{6n}_+\)

2.1 Stability of the Disease-Free Equilibrium (DFE)

The malaria model (7) has a disease free equilibrium (DFE), obtained by setting the right hand sides of the equations in the model to zero, given by

$$\begin{aligned} {\mathcal E}_{0}&= (S^*_i,I_i^*,J^*_i,S^*_{vi},I_{vi}^*,J^*_{vi}) \\&\quad =\left[ \frac{\sum ^n_{i=1}\Pi _{hi}}{\bigg (\sum ^n_{i=1} \mu _h +\sum ^n_{i=1,i\ne j}\psi _{_{ji}}-\sum ^n_{j=1,j\ne i}\psi _{_{ij}}\bigg )},0,0,\frac{\sum ^n_{i=1}\Pi _{vi}}{\sum ^n_{i=1} \mu _v},0,0\right] . \end{aligned}$$

The linear stability of \(\mathcal{E}_{0}\) can be established using the next generation operator method on the system (7). We take, \(I_i,J_i,I_{vi},J_{vi},~~i=1,\ldots ,n\), as our infected compartments, then using the notation in Driessche and Watmough (2002), the Jacobian matrices \(F\) and \(V\) for the new infection terms and the remaining transfer terms are, respectively, given by,

$$\begin{aligned} F=\begin{pmatrix} 0 &{}\quad \! F_{11} \\ \\ F_{22} &{}\quad \! 0 \end{pmatrix} \end{aligned}$$

where

$$\begin{aligned} \displaystyle F_{11}= \mathrm{diag}\bigg ({\alpha _{h1}\beta _{h1}},~{\alpha _{h2}\beta _{h2}} , \ldots , {\alpha _{hn}\theta _{hn}},~{\alpha _{h1}\theta _{h1}},~{\alpha _{h2}\theta _{h2}} , \ldots , {\alpha _{hn}\theta _{hn}}\bigg ) \end{aligned}$$

and

$$\begin{aligned} \displaystyle F_{22}&= \mathrm{diag}\left( \frac{\alpha _{v1}\beta _{v1}N^*_{v1}}{N^*_{h1}},~\frac{\alpha _{v2}\beta _{h2}N^*_{v2}}{N^*_{h2}} ,\ldots ,\frac{\alpha _{vn}\beta _{vn}N^*_{vn}}{N^*_{h1}}, \right. \nonumber \\&\left. \frac{\alpha _{v1}\theta _{v1}N^*_{v1}}{N^*_{h1}},~\frac{\alpha _{v2}\theta _{h2}N^*_{v2}}{N^*_{h2}} ,\ldots ,\frac{\alpha _{vn}\theta _{vn}N^*_{vn}}{N^*_{h1}}\right) . \end{aligned}$$

And

$$\begin{aligned} V=\begin{pmatrix} V_{11} &{}\quad \! 0\\ \\ 0 &{}\quad \! V_{22} \end{pmatrix} \end{aligned}$$

where

$$\begin{aligned} V_{11}=\begin{pmatrix} V_1 &{}\quad \! 0\\ \\ V_3 &{}\quad \! V_{4} \end{pmatrix} \end{aligned}$$

with

$$\begin{aligned} V_{1} = \begin{pmatrix} k_1+\sum ^n_{i=1,i\ne j}\psi _{j1}&{} -\psi _{12}&{} \cdots &{} -\psi _{1n}\\ -\psi _{21}&{} k_3+\sum ^n_{i=1,i\ne j}\psi _{j2} &{} \cdots &{}\vdots \\ \vdots &{}\vdots &{} \vdots &{} \vdots &{} \\ 0&{} 0 \\ \\ -\psi _{21} -\psi _{n1}&{} \cdots &{} &{} k_{n-1}+\sum ^n_{i=1,i\ne j}\psi _{jn} \\ \end{pmatrix}, \end{aligned}$$

and \(k_1 =\gamma _1+\xi _1+\mu _h+\delta _{I_1}, ~k_2=\tau _1+\mu _h+\delta _{J_1}, ~k_3=\gamma _2+\xi _2+\mu _h+\delta _{I_2},~\cdots ,~ ~k_{n-1}=\gamma _n+\xi _n+\mu _h+\delta _{I_n}, ~k_n=\tau _n+\mu _h+\delta _{J_n}\).

\(\displaystyle V_{3}= -\mathrm{diag}[\xi _1,\xi _2 ,\ldots ,\xi _n].\)

$$\begin{aligned} V_{4} = \begin{pmatrix} k_2+\sum ^n_{i=1,i\ne j}\psi _{j1}&{} -\psi _{12}&{} \cdots &{} -\psi _{1n}\\ -\psi _{21}&{} k_4+\sum ^n_{i=1,i\ne j}\psi _{j2} &{} \cdots &{} \vdots \\ \vdots &{} \vdots &{} \cdots &{} \vdots \\ -\psi _{n1}&{} \cdots &{} &{} k_n+\sum ^n_{i=1,i\ne j} \psi _{jn}\\ \end{pmatrix}. \end{aligned}$$

It follows that the basic reproduction number of the system (7), denoted by \(\mathcal {R}_{0_{_{DSR}}}\), is given by

$$\begin{aligned} \mathcal {R}_{0_{_{DSR}}} \!&= \! \rho (FV^{-1}) \nonumber \\ \!&= \! \rho \bigg \{\displaystyle \mathrm{diag}\bigg ({\alpha _{h1}\beta _{h1}},~{\alpha _{h2}\beta _{h2}} , \ldots , {\alpha _{hn}\theta _{hn}},~{\alpha _{h1}\theta _{h1}},~{\alpha _{h2}\theta _{h2}} , \ldots , {\alpha _{hn}\theta _{hn}}\bigg )V^{-1}_{11}, \nonumber \\&\quad \mathrm{diag}\bigg (\frac{\alpha _{v1}\beta _{v1}N^*_{v1}}{N^*_{h1}},~\frac{\alpha _{v2}\beta _{h2}N^*_{v2}}{N^*_{h2}},\ldots ,~\frac{\alpha _{vn}\beta _{vn}N^*_{vn}}{N^*_{h1}},\nonumber \\&\quad \frac{\alpha _{v1}\theta _{v1}N^*_{v1}}{N^*_{h1}},~\frac{\alpha _{v2}\theta _{h2}N^*_{v2}}{N^*_{h2}} ,\ldots ,\frac{\alpha _{vn}\theta _{vn}N^*_{vn}}{N^*_{h1}}\bigg )V^{-1}_{22}\bigg \}, \end{aligned}$$
(12)

where \(\rho \) is the spectral radius.

Further, using Theorem 2 in Driessche and Watmough (2002), the following result is established.

Lemma 2

The DFE of the malaria model (7), given by \(\mathcal{E}_{0}\), is locally asymptotically stable (LAS) if \(\mathcal {R}_{0_{_{DSR}}} < 1\), and unstable if \(\mathcal {R}_{0_{_{DSR}}} > 1\).

The basic reproduction number (\(\mathcal{R}_{0_{_{DSR}}}\)) measures the average number of new infections generated by a single infected individual in a completely susceptible population (Anderson and May 1991; Diekmann et al. 1990; Hethcote 2000; Driessche and Watmough 2002). Thus, Lemma 2 implies that malaria can be eliminated from human population (when \(\mathcal {R}_{0_{_{DSR}}} < 1)\) if the initial sizes of the sub-populations are in the basin of attraction of the DFE, \(\mathcal{E}_{0}\). To ensure the elimination of disease regardless of initial population sizes, a global stability proof for the disease-free equilibrium is needed. This is done below, using a comparison theorem.

Theorem 1

The DFE of the basic malaria model (7), given by \(\mathcal{E}_{0}\), is globally asymptotically stable (GAS) in \(\Gamma \) whenever \(\mathcal {R}_{0_{_{DSR}}} < 1\).

Proof

The equations for the infected components of the model (7) with the order \(I_i,J_i,I_{vi},J_{vi},~~i=1,\ldots ,n\) can be re-written as:

$$\begin{aligned} \begin{pmatrix} \displaystyle \frac{d I_i}{dt}\\ \displaystyle \frac{d J_i}{dt}\\ \displaystyle \frac{d I_{vi}}{dt} \\ \displaystyle \frac{d J_{vi}}{dt} \end{pmatrix} = (F-V)\begin{pmatrix} \displaystyle I_i\\ \displaystyle J_i\\ \displaystyle I_{vi} \\ \displaystyle J_{vi} \end{pmatrix} - M_1Q_1\begin{pmatrix} \displaystyle I_i\\ \displaystyle J_i\\ \displaystyle I_{vi} \\ \displaystyle J_{vi} \end{pmatrix} - M_2Q_2\begin{pmatrix} \displaystyle I_i\\ \displaystyle J_i\\ \displaystyle I_{vi} \\ \displaystyle J_{vi} \end{pmatrix} \end{aligned}$$

where the matrices \(F\) and \(V\) are as defined above, \(M_1 = 1-S_i/N_{hi}\), \(M_2 = 1-S_{vi}/N_{hi}\), and \(Q_1, ~Q_2\) are non-negative matrix, where

$$\begin{aligned} \displaystyle Q_{1}= \mathrm{diag}\bigg ({\alpha _{h1}\beta _{h1}},~{\alpha _{h2}\beta _{h2}} , \cdots , {\alpha _{hn}\theta _{hn}},~{\alpha _{h1}\theta _{h1}},~{\alpha _{h2}\theta _{h2}} , \cdots , {\alpha _{hn}\theta _{hn}}\bigg ) \end{aligned}$$

and

$$\begin{aligned} \displaystyle Q_{2}&= \mathrm{diag}\bigg (\frac{\alpha _{v1}\beta _{v1}N^*_{v1}}{N^*_{h1}},~\frac{\alpha _{v2}\beta _{h2}N^*_{v2}}{N^*_{h2}} ,\cdots ,\frac{\alpha _{vn}\beta _{vn}N^*_{vn}}{N^*_{h1}},~\frac{\alpha _{v1}\theta _{v1}N^*_{v1}}{N^*_{h1}},\\&\qquad \quad \frac{\alpha _{v2}\theta _{h2}N^*_{v2}}{N^*_{h2}} ,\cdots ,\frac{\alpha _{vn}\theta _{vn}N^*_{vn}}{N^*_{h1}}\bigg ). \end{aligned}$$

Thus,

$$\begin{aligned} \begin{pmatrix} \displaystyle \frac{d I_i}{dt}\\ \\ \displaystyle \frac{d J_i}{dt}\\ \\ \displaystyle \frac{d I_{vi}}{dt} \\ \\ \displaystyle \frac{d J_{vi}}{dt} \end{pmatrix} \le (F-V)\begin{pmatrix} \displaystyle I_i\\ \\ \displaystyle J_i\\ \\ \displaystyle I_{vi} \\ \\ \displaystyle J_{vi} \end{pmatrix} \end{aligned}$$
(13)

Using the fact that the eigenvalues of the matrix \(F - V\) all have negative real parts by the local stability result given in Lemma 2, where \(\rho (FV^{-1}) < 1\) if \(\mathcal {R}_{0_{_{DSR}}} < 1\), which is equivalent to \(F - V\) having eigenvalues with negative real parts when \(\mathcal {R}_{0_{_{DSR}}} < 1\) (Driessche and Watmough 2002). It follows that the linearized differential inequality system (13) is stable whenever \(\mathcal {R}_{0_{_{DSR}}} < 1\). Consequently, \((I_i(t),J_i(t),I_{vi},J_{vi}(t)) \rightarrow (0, \cdots , 0, \cdots , 0, \cdots , 0),~~i=1,\cdots ,n\) as \(t\rightarrow \infty \) for the linear ODE. Thus, by comparison theorem (Lakshmikantham et al. 1989; Smith and Waltman 1995), \((I_i(t),J_i(t),I_{vi},J_{vi}(t)) \rightarrow (0, \cdots , 0,\cdots ,0, \cdots , 0)\) as \(t\rightarrow \infty \) as well for the nonlinear system (7) for \(\mathcal {R}_{0_{_{DSR}}} < 1\). Hence, the DFE \({\mathcal E}_{0}\) is GAS in \(\Gamma \) if \(\mathcal {R}_{0_{_{DSR}}} < 1\). \(\square \)

In the next section, we consider a two patch malaria transmission model with drug resistance.

2.2 Two Patch Malaria Drug Resistance Model

The two patch malaria transmission model with drug resistance model is stated below; and in this model, we have drug resistance malaria developing and circulating in both patches.

$$\begin{aligned} \displaystyle \frac{d S_1}{dt}&= \displaystyle \Pi _1 \!+\! \gamma _1 I_1 \!+\! \tau _1 J_1 - \frac{\alpha _{h1}\beta _{h1}I_{v1}}{N_{h1}} S_1 \!-\! \frac{\alpha _{h1}\theta _{h1}J_{v1}}{N_{h1}} S_1 \!-\! \mu _h S_1 \!-\! \psi _{_{21}}S_1 \!+\! \psi _{_{12}}S_2\nonumber \\ \displaystyle \frac{d I_1}{dt}&= \displaystyle \frac{\alpha _{h1}\beta _{h1}I_{v1}}{N_{h1}} S_1 - (\gamma _1 +\xi _1+ \mu _h + \delta _{I_1})I_1 - \psi _{_{21}}I_1 + \psi _{_{12}}I_2\nonumber \\ \displaystyle \frac{d J_1}{dt}&= \displaystyle \frac{\alpha _{h1}\theta _{h1}J_{v1}}{N_{h1}} S_1 + \xi _1 I_1 - (\tau _1 + \mu _h + \delta _{J_1}) J_1 - \psi _{_{21}}J_1 + \psi _{_{12}}J_2\nonumber \\ \displaystyle \frac{d S_{v1}}{dt}&= \displaystyle \Pi _{v1} - \frac{\alpha _{v1}\beta _{v1}I_1}{N_{h1}} S_{v1} - \frac{\alpha _{v1}\theta _{v1}J_1}{N_{h1}} S_{v1} - \mu _v S_{v1}\nonumber \\ \displaystyle \frac{d I_{v1}}{dt}&= \displaystyle \frac{\alpha _{v1}\beta _{v1}I_1}{N_{h1}}S_{v1} - \mu _v I_{v1}\nonumber \\ \displaystyle \frac{d J_{v1}}{dt}&= \displaystyle \frac{\alpha _{v1}\theta _{v1}J_1}{N_{h1}} S_{v1} - \mu _v J_{v1}\\ \displaystyle \frac{d S_2}{dt}&= \displaystyle \Pi _2 \!+\! \gamma _2 I_2 \!+\! \tau _2 J_2 - \frac{\alpha _{h2}\beta _{h2}I_{v2}}{N_{h2}} S_2 - \frac{\alpha _{h2}\theta _{h2}J_{v2}}{N_{h2}} S_2 - \mu _h S_2 - \psi _{_{12}}S_2 \!+\! \psi _{_{21}}S_1\nonumber \\ \displaystyle \frac{d I_2}{dt}&= \displaystyle \frac{\alpha _{h2}\beta _{h2}I_{v2}}{N_{h2}} S_2 - (\gamma _2 +\xi _2+ \mu _h + \delta _{I_2})I_2 - \psi _{_{12}}I_2 + \psi _{_{21}}I_1\nonumber \\ \displaystyle \frac{d J_2}{dt}&= \displaystyle \frac{\alpha _{h2}\theta _{h2}J_{v2}}{N_{h2}} S_2 + \xi _2 I_2- (\tau _2 + \mu _h + \delta _{J_2}) J_2 - \psi _{_{12}}J_2 + \psi _{_{21}} J_1\nonumber \\ \displaystyle \frac{d S_{v2}}{dt}&= \displaystyle \Pi _{v2} - \frac{\alpha _{v2}\beta _{v2}I_2}{N_{h2}} S_{v2} - \frac{\alpha _{v2}\theta _{v2}J_2}{N_{h2}} S_{v2} - \mu _v S_{v2}\nonumber \\ \displaystyle \frac{d I_{v2}}{dt}&= \displaystyle \frac{\alpha _{v2}\beta _{v2}I_2}{N_{h2}}S_{v2} - \mu _v I_{v2}\nonumber \\ \displaystyle \frac{d J_{v2}}{dt}&= \displaystyle \frac{\alpha _{v2}\theta _{v2}J_2}{N_{h2}} S_{v2} - \mu _v J_{v2}.\nonumber \end{aligned}$$
(14)

It follows that the basic reproduction number of the model (14) with movement between the patches, denoted by \(\mathcal {R}^2_{0_{_{DSR}}}(\psi _{_{21}},\psi _{_{12}})\), is given by

$$\begin{aligned} \mathcal {R}^2_{0_{_{DSR}}}(\psi _{_{21}},\psi _{_{12}}) = \rho (FV^{-1}) = \max \{\mathcal {R}^2_{0_{_{DS}}}(\psi _{_{21}},\psi _{_{12}}),\mathcal {R}^2_{0_{_{DR}}}(\psi _{_{21}},\psi _{_{12}})\}, \end{aligned}$$

where

$$\begin{aligned} \mathcal {R}^2_{0_{_{DS}}}(\psi _{_{21}},\psi _{_{12}})&= \frac{1}{2\sigma _1}\bigg [u_1v_2 + u_2v_1 + \sqrt{(u_1v_2 - u_2v_1)^2 + 4u_1u_2\psi _{_{12}}\psi _{_{21}}} \bigg ] \nonumber \\ \mathcal {R}^2_{0_{_{DR}}}(\psi _{_{21}},\psi _{_{12}})&= \frac{1}{2\sigma _2}\bigg [p_1q_2 + p_2q_1 + \sqrt{(p_1q_2 - p_2q_1)^2 + 4p_1p_2\psi _{_{12}}\psi _{_{21}}} \bigg ]. \qquad \quad \end{aligned}$$
(15)

\(\mathcal {R}^2_{0_{_{DR}}}(\psi _{_{21}},\psi _{_{12}}) \) is the drug sensitive reproduction number while \(\mathcal {R}^2_{0_{_{DR}}}(\psi _{_{21}},\psi _{_{12}})\) is the drug resistance reproduction number and

$$\begin{aligned} u_1&= \frac{\beta _{h1}\alpha _{h1}\beta _{v1}\alpha _{v1}N^*_{v1} }{\mu _vN^*_{h1} } ~~=~~k_1\mathcal {R}^2_{0_{_{DS_1}}}(0,0), \nonumber \\ u_2&= \frac{\beta _{h2}\alpha _{h2}\beta _{v2}\alpha _{v2}N^*_{v2} }{\mu _vN^*_{h2} }~~=~~k_2\mathcal {R}^2_{0_{_{DS_1}}}(0,0), \nonumber \\ p_1&= \frac{\theta _{h1}\alpha _{h1}\theta _{v1}\alpha _{v1}N^*_{v1} }{\mu _vN^*_{h1} }~~=~~k_3\mathcal {R}^2_{0_{_{DR_1}}}(0,0), \nonumber \\ p_2&= \frac{\theta _{h2}\alpha _{h2}\theta _{v2}\alpha _{v2}N^*_{v2} }{\mu _vN^*_{h2} }~~=~~ k_4\mathcal {R}^2_{0_{_{DR_2}}}(0,0), \nonumber \\ v_1&= k_1 + \psi _{_{21}},~~~~v_2 ~=~ k_3 + \psi _{_{12}},~~~~ q_1~=~ k_2+\psi _{_{21}},~~~~ q_2~=~ k_4+\psi _{_{12}}\nonumber \\ \sigma _1&= k_1 k_3+k_1\psi _{_{12}}+k_3\psi _{_{21}}, ~~~~\sigma _2 ~=~k_2 k_4+k_2\psi _{_{12}}+k_4\psi _{_{21}}. \end{aligned}$$
(16)

where \(k_1 =\gamma _1+\xi _1+\mu _h+\delta _{I_1}, ~k_2=\tau _1+\mu _h+\delta _{J_1}, ~k_3=\gamma _2+\xi _2+\mu _h+\delta _{I_2}, ~k_4=\tau _2+\mu _h+\delta _{J_2}\).

In the absence of movement between the patches, the drug sensitive and resistance reproduction numbers are given as

$$\begin{aligned} \mathcal {R}^2_{0_{_{DS_1}}}(0,0) = {\frac{\alpha _{v1}\beta _{v1}\alpha _{h1}\beta _{h1}N^{*}_{v{1}}}{k_1\mu _vN^{*}_{h1}}},&\displaystyle \mathcal {R}^2_{0_{_{DR_1}}}(0,0) = {\frac{\theta _{v1}\alpha _{v1}\theta _{h1}\alpha _{h1}N^{*}_{v1}}{k_2\mu _v N^{*}_{h1}}},\\ \mathcal {R}^2_{0_{_{DS_2}}}(0,0) = {\frac{\alpha _{v2}\beta _{v2}\alpha _{h2}\beta _{h2}N^{*}_{v2}}{k_3\mu _vN^{*}_{h2}}},&\displaystyle \mathcal {R}^2_{0_{_{DR_2}}}(0,0) = {\frac{\alpha _{v2}\theta _{v2}\alpha _{h2}\theta _{h2}N^{*}_{v2}}{k_4\mu _v N^{*}_{h2}}}. \end{aligned}$$

Theorem 2

The drug resistance basic reproduction number, \(\mathcal {R}^2_{0_{_{DR}}} (\psi _{_{12}},\psi _{_{21}})\), for the two patch malaria-drug resistance model (14) satisfies the following inequality,

$$\begin{aligned} \min \{\mathcal {R}^2_{0_{_{DR_1}}}(0,0),\mathcal {R}^2_{0_{_{DR_2}}}(0,0) \} \!\le \! \mathcal {R}^2_{0_{_{DR}}} (\psi _{_{12}},\psi _{_{21}}) \!\le \! \max \{\mathcal {R}^2_{0_{_{DR_1}}}(0,0) ,\mathcal {R}^2_{0_{_{DR_2}}}(0,0) \} \end{aligned}$$

Theorem 2 can be proved using the approaches in Arino and Driessche (2003), Arino and Driessche (2003), Hsieh et al. (2007), Salmani and Driessche (2006).

Similar result was obtained for the drug sensitive malaria.

Theorem 3

The drug sensitive basic reproduction number, \(\mathcal {R}^2_{0_{_{DS}}} (\psi _{_{12}},\psi _{_{21}})\), for the two patch malaria-drug resistance model (14) satisfies the following inequality,

$$\begin{aligned} \min \{\mathcal {R}^2_{0_{_{DS_1}}}(0,0),\mathcal {R}^2_{0_{_{DS_2}}}(0,0) \} \le \mathcal {R}^2_{0_{_{DS}}} (\psi _{_{12}},\psi _{_{21}}) \le \max \{\mathcal {R}^2_{0_{_{DS_1}}}(0,0) ,\mathcal {R}^2_{0_{_{DS_2}}}(0,0) \}. \end{aligned}$$

Theorem 3 can be proved using the approaches in Arino and Driessche (2003), Arino and Driessche (2003), Hsieh et al. (2007), and Salmani and Driessche (2006).

Theorem 2 indicates that in the absence of movement between the patches, the global drug resistance reproduction number, \(\mathcal {R}^2_{0_{_{DR}}} (\psi _{_{12}},\psi _{_{21}})\), is the larger of the two isolated patch reproductive numbers (\(\mathcal {R}^2_{0_{_{DR_1}}} ,\mathcal {R}^2_{0_{_{DR_2}}} \)); similar indication holds for Theorem 3 in the case of the global drug sensitive reproduction number, \(\mathcal {R}^2_{0_{_{DS}}} (\psi _{_{12}},\psi _{_{21}})\).

Theorem 4

If \(\mathcal {R}^2_{0_{_{DR_1}}} > \mathcal {R}^2_{0_{_{DR_2}}}\), then for the migration rates \((\psi _{_{12}},\psi _{_{21}}) \in [0,\infty ) \times [0,\infty )\), \(\max \bigg \{ \frac{\mathcal {R}^2_{0_{_{DR_1}}}}{ 1+ \frac{\psi _{_{21}}}{k_2}},\mathcal {R}^2_{0_{_{DR_2}}}\bigg \} \le \mathcal {R}^2_{0_{_{DR}}} \le \mathcal {R}^2_{0_{_{DR_1}}}.\)

The proof is given in Appendix 1. Similar result was obtained for the drug sensitive malaria.

Theorem 5

If \(\mathcal {R}^2_{0_{_{DS_1}}} > \mathcal {R}^2_{0_{_{DS_2}}}\), then for the migration rates \((\psi _{_{12}},\psi _{_{21}}) \in [0,\infty ) \times [0,\infty )\), \(\max \bigg \{ \frac{\mathcal {R}^2_{0_{_{DS_1}}}}{ 1+ \frac{\psi _{_{21}}}{k_1}},\mathcal {R}^2_{0_{_{DS_2}}}\bigg \} \le \mathcal {R}^2_{0_{_{DS}}} \le \mathcal {R}_{0_{_{DS_1}}}.\)

This result show that in the presence of migration between the two patches, the global drug resistance reproduction number, \(\mathcal {R}^2_{0_{_{DR}}}\), is always between the two isolated-patch reproductive numbers (\(\mathcal {R}^2_{0_{_{DR_1}}}\) and \(\mathcal {R}^2_{0_{_{DR_2}}}\)), and similarly for the global drug sensitive reproduction number, \(\mathcal {R}^2_{0_{_{DS}}}\) as observed in Arino and Driessche (2003), Arino and Driessche (2003), Hsieh et al. (2007), Prosper et al. (2012), and Salmani and Driessche (2006). This is contrary to the result observed by Cosner et al. (2009) (in their model with Lagrangian movement) in which the reproduction number is less than unity in each isolated patch, yet the global reproduction number is larger than one. This indicates that it may be possible to have a system where without migration, the disease goes extinct in both patches, but once with certain level of migration, the disease becomes endemic. However, Theorem 4 (similarly Theorem 5) indicate that the global drug resistance reproduction number, \(\mathcal {R}^2_{0_{_{DR}}}\) will always be bounded by the isolated patch reproduction numbers.

Theorem 6

Suppose \(\mathcal {R}_{0_{_{DR_1}}}(0,0)>\mathcal {R}_{0_{_{DR_2}}}(0,0)\). If \(\mathcal {R}_{0_{_{DR}}}(\psi _{_{12}},\psi _{_{21}})\) is a function of the migration rates \(\psi _{{12}}\) and \(\psi _{{21}}\), where \(\psi _{{12}}, \psi _{{21}} \in [0,\infty )\). Then for a fixed \(\psi \) in the interval \([0,\infty ), ~\mathcal {R}_{0_{_{DR}}}(\psi _{_{12}},\psi )\) is an increasing function of \(\psi _{_{12}}\) and \(\mathcal {R}_{0_{_{DR}}}(\psi ,\psi _{_{21}})\) is a decreasing function of \(\psi _{_{21}}\).

The proof is given in Appendix 2. Similarly for drug sensitive malaria.

Theorem 7

Suppose \(\mathcal {R}_{0_{_{DS_1}}}(0,0)>\mathcal {R}_{0_{_{DS_2}}}(0,0)\). If \(\mathcal {R}_{0_{_{DS}}}(\psi _{_{12}},\psi _{_{21}})\) is a function of the migration rates \(\psi _{{12}}\) and \(\psi _{{21}}\), where \(\psi _{{12}}, \psi _{{21}} \in [0,\infty )\). Then, for a fixed \(\psi \) in the interval \([0,\infty ), ~\mathcal {R}_{0_{_{DS}}}(\psi _{_{12}},\psi )\) is an increasing function of \(\psi _{_{12}}\), and \(\mathcal {R}_{0_{_{DS}}}(\psi ,\psi _{_{21}})\) is a decreasing function of \(\psi _{_{21}}\).

Remark 1

The proof of Theorem 4, indicates that the minimum value of \(\mathcal {R}^2_{0_{_{DR}}}(\psi _{{12}},\psi {_{21}})\) on the domain \([0,\infty ) \times [0, \psi )\) is \(\max \bigg \{\frac{\mathcal {R}^2_{0_{_{DR_1}}}(0,0)}{1 + \frac{\psi _{_{21}}}{k_2}},\mathcal {R}^2_{0_{_{DR_2}}}(0,0)\bigg \}\), and the maximum value is \(\mathcal {R}^2_{0_{_{DR_1}}}(0,0)\), for some migration rate \(\psi > 0\). Hence, if \(\mathcal {R}^2_{0_{_{DR_2}}}(0,0) < 1\) and \(\frac{\mathcal {R}^2_{0_{_{DR_1}}}(0,0)}{1 + \frac{\psi _{{21}}}{k_2}}> 1\) for some \(\psi > 0\) (thus, \(\mathcal {R}^2_{0_{_{DR_1}}}(0,0) > 1\)), then \(\mathcal {R}^2_{0_{_{DR}}}(\psi _{_{12}},\psi _{_{21}}) > 1\) for all migration pairs \((\psi _{_{12}}, \psi _{_{21}}) \mathrm{~in~} [0,\infty ) \times [0, \psi )\). This shows that it is possible to have a case in which the strain dies out in one patch but not the other without migration, yet the strain persists with migration in both patches for all \(\psi _{_{12}} \ge 0\) and for \(0 \le \psi _{_{21}}\le \psi \). If \(\mathcal {R}^2_{0_{_{DR_2}}}(0,0),\frac{\mathcal {R}^2_{0_{_{DR_1}}}(0,0)}{1 + \frac{\psi _{{21}}}{k_2}}<1\) (but \(\mathcal {R}^2_{0_{_{DR_1}}}(0,0)>1\)), then for some migration pairs \((\psi _{_{12}}, \psi _{_{21}})\), \(\mathcal {R}^2_{0_{_{DR}}}(\psi _{_{12}},\psi _{_{21}}) > 1\) and for other pairs, \(\mathcal {R}^2_{0_{_{DR}}}(\psi _{_{12}},\psi _{_{21}}) < 1\). Furthermore,there exists a value \(\psi ^*<\psi \) such that \(\mathcal {R}^2_{0_{_{DR}}}(\psi _{_{12}},\psi _{_{21}}) > 1\) for all \((\psi _{_{12}}, \psi _{_{21}}) \mathrm{~in~} [0,\infty ) \times [0, \psi ^*)\). Finally, if \(\mathcal {R}^2_{0_{_{DR_2}}}(0,0,)\) and \(\mathcal {R}^2_{0_{_{DR_1}}}(0,0)\) are both less than one, then \(\mathcal {R}^2_{0_{_{DR}}}(\psi _{_{12}},\psi _{_{21}})\) will always be less than one, regardless of the migration rates between patches.

3 Existence and Stability of Endemic Equilibrium

In this Section, the conditions for the existence and stability of endemic equilibrium of the two patch model (14) will be explored for the special case where the disease-induced mortality is negligible (so that, \(\delta _{I_1} = \delta _{J_1} =\delta _{I_2}= \delta _{J_2} = 0\)). Although this assumption may not be biologically realistic, it allows for the ensuing mathematical analyses to be tractable (considering the non-linearity of the differential equation system (14)). In the absence of disease-induced death (\(\delta _{I_1} = \delta _{J_1} = \delta _{I_2} = \delta _{J_2} = 0\)), the total human population (\(N_{h1}(t)\) and \(N_{h2}(t)\)) in both patches are asymptotically constant. That is, \(N^{**}_{h1} = \Pi _2/\mu _h\) and \(N^{**}_{h2} = \Pi _2/\mu _h\). Using these definitions in the model (14), noting that \(S_1(t) = N^{**}_{h1}(t) - I_1(t) - J_1(t),~~S_2(t) = N^{**}_{h2}(t) - I_2(t) - J_2(t),~~S_{v_1}(t) = N^{**}_{v_1}(t) - I_{v1}(t) - J_{v1}\), and \(S_{v2} = N^{**}_{v2}(t) - I_{2}(t) - J_{v2}(t)\), gives the following reduced model for the dynamics of the drug resistance malaria system:

$$\begin{aligned} \begin{array}{lll} \displaystyle \frac{d I_1}{dt} &{}=&{} \displaystyle \frac{\alpha _{h1}\beta _{h1}I_{v1}}{N_{h1}} (N^{**}_{h1} - I_1 - J_1) - (\gamma _1 +\xi _1+ \mu _h)I_1 - \psi _{_{21}}I_1 + \psi _{_{12}}I_2\\ \displaystyle \frac{d J_1}{dt} &{}=&{} \displaystyle \frac{\alpha _{h1}\theta _{h1}J_{v1}}{N_{h1}} (N^{**}_{h1} - I_1 - J_1) + \xi _1 I_1 - (\tau _1 + \mu _h) J_1 - \psi _{_{21}}J_1 + \psi _{_{12}}J_2\\ \displaystyle \frac{d I_{v1}}{dt} &{}=&{} \displaystyle \frac{\alpha _{v1}\beta _{v1}I_1}{N_{h1}}(N^{**}_{v1} - I_{v1} - J_{v1}) - \mu _v I_{v1}\\ \displaystyle \frac{d J_{v1}}{dt} &{}=&{} \displaystyle \frac{\alpha _{v1}\theta _{v1}J_1}{N_{h1}} (N^{**}_{v1} - I_{v1} - J_{v1}) - \mu _v J_{v1}\\ \end{array} \end{aligned}$$
(17)
$$\begin{aligned} \begin{array}{lll} \displaystyle \frac{d I_2}{dt} &{}=&{} \displaystyle \frac{\alpha _{h2}\beta _{h2}I_{v2}}{N_{h2}} (N^{**}_{h2} - I_2 - J_2) - (\gamma _2 +\xi _2)I_2 - \psi _{_{12}}I_2 + \psi _{_{21}}I_1\\ \\ \displaystyle \frac{d J_2}{dt} &{}=&{} \displaystyle \frac{\alpha _{h2}\theta _{h2}J_{v2}}{N_{h2}} (N^{**}_{h2} - I_2 - J_2) + \xi _2 I_2- (\tau _2 + \mu _h) J_2 - \psi _{_{12}}J_2 + \psi _{_{21}} J_1\nonumber \\ \displaystyle \frac{d I_{v2}}{dt} &{}=&{} \displaystyle \frac{\alpha _{v2}\beta _{v2}I_2}{N_{h2}}(N^{**}_{hv2} - I_{v2} - J_{v2}) - \mu _v I_{v2}\\ \displaystyle \frac{d J_{v2}}{dt} &{}=&{} \displaystyle \frac{\alpha _{v2}\theta _{v2}J_2}{N_{h2}} (N^{**}_{v2} - I_{v2} - J_{v2}) - \mu _v J_{v2} . \end{array} \end{aligned}$$

Let

$$\begin{aligned} {\mathcal E}_{1} = (I^{**}_1,J^{**}_1,I^{**}_{v1},J^{**}_{v1},I^{**}_2,J^{**}_2,I^{**}_{v2},J^{**}_{v2}) \end{aligned}$$

be an arbitrary endemic equilibrium of model (17). The existence and stability of endemic equilibrium involving only one of the disease strain (boundary equilibria) are now investigated by considering the special case of the model where the two patches are in isolation (i.e., \(\psi _{_{12}}= \psi _{_{21}}=0\)). Since the patches are in isolation, the boundary equilibria is studied for only patch one, similar results can be obtained for patch two.

3.1 Drug Sensitive-Only Boundary Equilibrium

This is the equilibrium where only the drug sensitive strain is present. It should be noted that with the development and transmission of the drug resistant strain is due to the use of anti-malaria treatment, hence, there will always be inflow from the population of infected individuals with drug sensitive strain into the class of individuals infected with the drug resistant strain. To investigate the existence of a drug sensitive strain-only equilibrium, we consider the special case of the model where there is no development of drug resistance (i.e., \(\xi _1 = 0\)) due to treatment failure or non-compliant to treatment regime.

Let \(\displaystyle \mathcal {R}^2_{0_{_{DR_1}}}<1\) and \(\displaystyle \mathcal {R}^2_{0_{_{DS_1}}} >1\) (i.e., the drug resistance-only strain are eliminated). Thus,

$$\begin{aligned} (J_1(t),J_{v1}(t))\rightarrow (0,0) ~\mathrm{as }~ t\rightarrow \infty . \end{aligned}$$
(18)

Substituting (18) into the model (17) gives the following reduced system

$$\begin{aligned} \begin{array}{lll} \displaystyle \frac{d I_1}{dt} &{}=&{} \displaystyle \frac{\alpha _1\beta _1 I_1}{N_{h1}} (N_{h1}-I_1-J_1) - k_1 I_1 \\ \displaystyle \frac{d I_{v1}}{dt} &{}=&{} \displaystyle \frac{\alpha _{v1}\beta _{v1}I_1(N_{v1}-I_{v1}-J_{v1})}{N_{h1}}-\mu _v I_{v1}. \end{array} \end{aligned}$$
(19)

The drug sensitive-only equilibrium of system (19) is given by the following after some algebraic manipulations

$$\begin{aligned} {\mathcal E}_{1S} = (I^{**}_1,0,I^{**}_{v1},0), \end{aligned}$$

where

$$\begin{aligned} I^{**}_1&= \displaystyle \frac{\mu _vk_1(N^{**}_{h1})^2(\mathcal {R}^2_{0_{_{DS_1}}}-1)}{\alpha _{v1}\beta _{v1} (N^{**}_{v1}\beta _{h1}\alpha _{h1}+k_1 N^{**}_{h1})}\\ I^{**}_{v1}&= \displaystyle \frac{\mu _vk_1N^{**}_{h1}(\mathcal {R}^2_{0_{_{DS_1}}}-1)}{\beta _{h1}\alpha _{h1}(\alpha _{v1}\beta _{v1}+\mu _v)} \end{aligned}$$

The drug sensitive-only boundary equilibrium, \({\mathcal E}_{1S}\), is biologically feasible if and only if \(\mathcal {R}^2_{0_{_{DS_1}}} > 1\). This result is summarized below.

Lemma 3

The model (19) has a drug sensitive-only boundary equilibrium, given by \({\mathcal E}_{1S}\), whenever \(\mathcal {R}^2_{0_{_{DS_1}}} > 1\).

Theorem 8

If \(\mathcal {R}^2_{0_{_{DS_1}}}>1\), the drug sensitive-only boundary equilibrium of model (19) is LAS whenever \(\mathcal {R}^2_{0_{_{DS_1}}} > \mathcal {R}^2_{0_{_{DR_1}}}\).

The proof is given in Appendix 3.

3.2 Drug Resistance-Only Boundary Equilibrium

The drug resistance-only reduced system is given by

$$\begin{aligned} \begin{array}{lll} \displaystyle \frac{d J_1}{dt} &{}=&{} \displaystyle \frac{\alpha _{h1}\theta _{h1}J_{v1}}{N_{h1}} (N^{**}_{h1} - I_1 - J_1) - k_2 J_1\\ \displaystyle \frac{d J_{v1}}{dt} &{}=&{} \displaystyle \frac{\alpha _{v1}\theta _{v1}J_1}{N_{h1}} (N^{**}_{v1} - I_{v1} - J_{v1}) - \mu _v J_{v1}. \end{array} \end{aligned}$$
(20)

The equilibrium of system (20) is given by the following after some algebraic manipulations

$$\begin{aligned} {\mathcal E}_{1R} = (0,J^{**}_1,0,J^{**}_{v1}), \end{aligned}$$

where

$$\begin{aligned} J^{**}_1&= \displaystyle \frac{k_2\mu _v(N^{**}_{h1})^2(\mathcal {R}^2_{0_{_{DR_1}}}-1)}{N^{**}_{v1}\theta _{h1}\alpha _{h1}+k_2 N^{**}_{h1}\alpha _{v1}\theta _{v1}},\\ J^{**}_{v1}&= \displaystyle \frac{k_2\mu _vN^{**}_{h1} (\mathcal {R}^2_{0_{_{DR_1}}}-1)}{\theta _{h1}\alpha _{h1}(\theta _{v1}\alpha _{v1}+\mu _v)}. \end{aligned}$$

The drug resistance-only boundary equilibrium, \({\mathcal E}_{1R}\), is biologically feasible if and only if \(\mathcal {R}^2_{0_{_{DR_1}}} > 1\). This result is summarized below.

Lemma 4

The model (20) has a drug resistance-only boundary equilibrium, given by \({\mathcal E}_{1R}\), whenever \(\mathcal {R}^2_{0_{_{DR_1}}} > 1\).

Theorem 9

If \(\mathcal {R}^2_{0_{_{DR_1}}}>1\), the drug resistance-only boundary equilibrium of model (20) is LAS whenever \(\mathcal {R}^2_{0_{_{DR_1}}} > \mathcal {R}^2_{0_{_{DS_1}}}\!.\)

The proof is given in Appendix 4. The theoretical results given in Theorems 8 and 9 are illustrated numerically in Fig. 2a, b using parameter values in Table 1, in the isolated case when \(\psi _{_{12}}= \psi _{_{21}}=0\) with no development of resistance \(\xi _1 =0\) and when \(\mathcal {R}_{0_{_{DS_1}}} > \mathcal {R}_{0_{_{DR_1}}}\!.\)

Fig. 2
figure 2

Simulations of the model (14) as a function of time for the total number of infected human population. (a) \(\mathcal {R}_{0_{_{DR_1}}} < \mathcal {R}_{0_{_{DS_1}}}\) (\( \mathcal {R}_{0_{_{DS_1}}} = 5.4964,~\mathcal {R}_{0_{_{DR_1}}} = 5.1995\) with \(\theta _h = 0.011, \mu _h =0.047, \gamma = 0.6, \eta = 0.65, v = 0.67,k_h =1/20, \kappa = 0.65, \sigma _v = 1/9, b_h = 0.5, b_v = 0.5, \beta _h = 0.75, \beta _v = 0.5258 \), other parameter values used are as given in Table 1). (b) \(\mathcal {R}_{0_{_{DS_1}}} < \mathcal {R}_{0_{_{DR_1}}}\) (\( \mathcal {R}_{0_{_{DR_1}}}= 18.0713, ~\mathcal {R}_{0_{_{DS_1}}}= 13.7385,\) with \(\theta _h = 0.011, \mu _h =0.047, \gamma = 0.6, \eta = 0.65, v = 0.67,k_h =1/20, \kappa = 0.65, \sigma _v = 1/9, b_h = 0.5, b_v = 0.5, \beta _h = 0.75, \beta _v = 0.5258\), other parameter values used are as given in Table 1)

Full size image
Table 1 Description of the Variables and Parameters of the Malaria Model (7)
Full size table

3.3 Co-existence Equilibrium

Let

$$\begin{aligned} \tilde{{\mathcal E}}_{1} = (I^{**}_1,J^{**}_1,I^{**}_{v1},J^{**}_{v1}) \end{aligned}$$

be an arbitrary co-existence equilibrium of the system (17) for the case \(\psi _{_{12}}= \psi _{_{21}}=0\). Thus, \(\tilde{\mathcal E}_{1}\) is given by the solution of the right hand side of system (17) set to zero. Solving for \(I_{v1},~J_{v1} \) in the equations of \(I_1,J_1\) in the right hand system (17) set to zero gives

$$\begin{aligned} I^{**}_{v1}&= \frac{\alpha _{v}1 \beta _{v1} I_1}{\mu _v \mathcal {R}^2_{0_{_{DS_1}}} (N_{h1}-I_1-J_1)},\\ J^{**}_{v1}&= \frac{\theta _{v1}\alpha _{v1}(J_1-\xi _1 I_1)}{\mu _v \mathcal {R}_{0_{_{DR_1}}} (N_{h1}-I_1-J_1)}, \end{aligned}$$

Substituting these expressions into the equations of \(I_{v1},~J_{v1}\) in the right hand side of system (17) set to zero, shows that, after some manipulations, \(I^{**}_1,J^{**}_1\) are the solutions of the following system of equations:

$$\begin{aligned}&\frac{\alpha _{v1}\beta _{v1}I_1}{N_{h1}}\bigg [N_{v1}-\frac{\alpha _{v1}\beta _{v1}I_1}{\mu _v\mathcal {R}^2_{0_{_{DS_1}}}(N_{h1}-I_1-J_1)}-\frac{\theta _{v1}\alpha _{v1}(J_1-\xi _1I_1)}{\mu _v\mathcal {R}_{0_{_{DR_1}}}(N_{h1}-I_1-J_1)}\bigg ]\nonumber \\&\qquad -\frac{\alpha _{v1}\beta _{v1}I_1}{\mathcal {R}^2_{0_{_{DS_1}}}(N_{h1}-I_1-J_1)}=0, \nonumber \\&\frac{\theta _{v1}\alpha _{v1}J_1}{N_{h1}}\bigg [N_{v1}-\frac{\alpha _{v1}\beta _{v1}I_1}{ \mu _v\mathcal {R}^2_{0_{_{DS_1}}}(N_{h1}-I_1-J_1)}-\frac{\theta _{v1}\alpha _{v1}(J_1-\xi _1I_1)}{ \mu _v\mathcal {R}_{0_{_{DR_1}}}(N_{h1}-I_1-J_1)}\bigg ]\nonumber \\&\qquad -\frac{\theta _{v1}\alpha _{v1}(J_1-\xi _1I_1)}{\mathcal {R}_{0_{_{DR_1}}}(N_{h1}-I_1-J_1)}=0. \end{aligned}$$
(21)

Substituting the first equation of (21) into the second equation of (17) with \(\psi _{_{12}}= \psi _{_{21}}=0\) and solving for \(J^{**}_1,J^{**}_2\) gives

$$\begin{aligned} J^{**}_1&= \frac{ \xi _1 I_1\mathcal {R}^2_{0_{_{DS_1}}}}{\alpha _{v1}\beta _{v1}(\mathcal {R}^2_{0_{_{DS_1}}}-\mathcal {R}^2_{0_{_{DR_1}}})}. \end{aligned}$$
(22)

Finally, substituting (22) into the first equation of (17) gives

$$\begin{aligned} I^{**}_1&= {\alpha _{v1}\beta _{v1}\mu _v\mathcal {R}^2_{0_{_{DR_1}}}N_{h1}(\mathcal {R}^2_{0_{_{DS_1}}}-\mathcal {R}_{0_{_{DR_1}}})(\mathcal {R}^2_{0_{_{DS_1}}}-1)}\nonumber \\&\backslash \{(\mathcal {R}^2_{0_{_{DS_1}}}\!-\!\mathcal {R}^2_{0_{_{DR_1}}})\alpha _{v1}\beta _{v1}[\mathcal {R}^2_{0_{_{DR_1}}}(\alpha _{v1}\beta _{v1}\!+\!N_{v1}\mu _v\mathcal {R}^2_{0_{_{DS_1}}}) \!-\!\mathcal {R}^2_{0_{_{DR_1}}}\theta _{v1}\alpha _{v1}\xi _1]\nonumber \\&+\xi _1(\mathcal {R}^2_{0_{_{DS_1}}})^2(\theta _{v1}\alpha _{v1}+N_{v1}\mu _v\mathcal {R}_{0_{_{DR_1}}})\},\nonumber \\ J^{**}_1&= {\xi _1\mu _v\mathcal {R}^2_{0_{_{DR_1}}}N_{h1}(\mathcal {R}^2_{0_{_{DS_1}}}-1)\mathcal {R}^2_{0_{_{DS_1}}}} \nonumber \\&\backslash \{(\mathcal {R}^2_{0_{_{DS_1}}}\!-\!\mathcal {R}^2_{0_{_{DR_1}}})\alpha _{v1}\beta _{v1}[\mathcal {R}_{0_{_{DR_1}}}(\alpha _{v1}\beta _{v1}\!+\!N_{v1}\mu _v\mathcal {R}^2_{0_{_{DS_1}}})\!-\!\mathcal {R}^2_{0_{_{DR_1}}}\theta _{v1}\alpha _{v1}\xi _1]\nonumber \\&+\xi _1(\mathcal {R}^2_{0_{_{DS_1}}})^2(\theta _{v1}\alpha _{v1}+N_{v1}\mu _v\mathcal {R}^2_{0_{_{DR_1}}})\}.\nonumber \end{aligned}$$

Thus, the co-existence equilibrium, \({\mathcal E}_{1}\), is biologically feasible if and only if \(\mathcal {R}^2_{0_{_{DS_1}}} > 1\), and \(\mathcal {R}^2_{0_{_{DS_1}}} > \mathcal {R}^2_{0_{_{DR_1}}}>1\). This result is summarized below.

Lemma 5

The model (17) has a co-existence equilibrium, given by \({\mathcal E}_{1}\), whenever \(\mathcal {R}^2_{0_{_{DS_1}}} > 1\), and \(\mathcal {R}^2_{0_{_{DS_1}}}>\mathcal {R}^2_{0_{_{DR_1}}}>1\).

The asymptotic stability of the co-existence equilibrium is established by the following theorem,

Theorem 10

The co-existence equilibrium of model (17) is locally asymptotically stable (LAS) whenever \(\mathcal {R}^2_{0_{_{DS_1}}} > 1\), \(\mathcal {R}^2_{0_{_{DR_1}}}>1\) and \(\mathcal {R}^2_{0_{_{DS_1}}} > \mathcal {R}^2_{0_{_{DR_1}}}\).

The proof is given in Appendix 5.

It is worth mentioning that extensive numerical simulations of the model (14), using the parameter values given in Table 1 for the case with movement between the two patches (\(\psi _{_{12}}\ne 0, ~\psi _{_{21}} \ne 0\)) and \(\mathcal {R}_{0_{_{DS_i}}} > \mathcal {R}_{0_{_{DR_i}}}>1\), \(i=1,2\), show that the two strains co-exist, with the drug sensitive strain dominating (but does not drive out the drug resistance strain) in both patches as can be seen from Fig. 3a, b. Furthermore, if \(\mathcal {R}_{0_{_{DR_i}}} > \mathcal {R}_{0_{_{DS_i}}}\) and with movement between the two patches, the model exhibits competitive exclusion (where the drug resistance strain drives to extinction the drug sensitive strain), as depicted in Fig. 4a, b. These simulations suggest the following conjectures.

Fig. 3
figure 3

Simulation of the model (14) as a function of time for the total number of infected human population with \(\mathcal {R}_{0_{_{DS_i}}} > \mathcal {R}_{0_{_{DR_i}}}, ~i=1,2, ~ (\mathcal {R}_{0_{_{DS_i}}} = 11.9196,~\mathcal {R}_{0_{_{DR_i}}} = 9.5471\)), using \(\theta _{h1} = \theta _{h2} = 0.53, ~\theta _{v1} = \theta _{v2} = 2.50, ~\xi _1 =~\xi _2 = 0.000126, ~\psi _{21} = 0.08, ~\psi _{12} = 0.04\), other parameter values used are as given in Table 1

Full size image
Fig. 4
figure 4

Simulation of the model (14) as a function of time using \(\xi _1 = 0.00126, ~\xi _2 = 0.000126, ~\psi _{21} = ~\psi _{12} = 0.04\), other parameter values used are as given in Table 1. (a) Total number of infected human population with \(\mathcal {R}_{0_{_{DR_1}}} > \mathcal {R}_{0_{_{DS_1}}}\) (\( \mathcal {R}_{0_{_{DR_1}}} = 9.5471, ~\mathcal {R}_{0_{_{DS_1}}} = 5.4389\)). (b) Total number of infected human population with \(\mathcal {R}_{0_{_{DR_2}}} > \mathcal {R}_{0_{_{DS_2}}}\) (\(\mathcal {R}_{0_{_{DS_2}}} = 13.7385,~\mathcal {R}_{0_{_{DR_2}}} = 9.5471\))

Full size image

Conjecture 1

Consider the model (14). The drug sensitive strain dominates the drug resistance strain (but does not drive it to extinction) whenever \(\psi _{_{12}}\ne 0, ~\psi _{_{21}} \ne 0\) and \( \mathcal {R}_{0_{_{DS_i}}} > \mathcal {R}_{0_{_{DR_i}}}>1\), \(i=1,2\).

Conjecture 2

Consider the model (14). The drug resistance strain drives out the drug sensitive strain to extinction if \(\psi _{_{12}}\ne 0, ~\psi _{_{21}} \ne 0\), and \(\mathcal {R}_{0_{_{DR_i}}} > \mathcal {R}_{0_{_{DS_i}}}>1\), \(i=1,2\).

3.4 Two Patch Malaria Drug Resistance Model: Special Case

In this scenario, it is assumed that drug resistance malaria develops and circulates among individuals in patch 1 only. And in patch 2, drug resistance malaria is as the result of movement of infected individuals from patch 1. The model stated below depicts this scenario

$$\begin{aligned} \frac{d S_1}{dt}&= \Pi _1 \!+\! \gamma _1 I_1 \!+\! \tau _1 J_1 - \frac{\alpha _{h1}\beta _{h1}I_{v1}}{N_{h1}} S_1 - \frac{\alpha _{h1}\theta _{h1}J_{v1}}{N_{h2}} S_1 - \mu _h S_1 - \psi _{_{21}}S_1 \!+\! \psi _{_{12}}S_2\nonumber \\ \frac{d I_1}{dt}&= \frac{\alpha _{h1}\beta _{h1}I_{v1}}{N_{h1}} S_1 - (\gamma _1 + \xi _1+\mu _h + \delta _{I_1})I_1 - \psi _{_{21}}I_1 + \psi _{_{12}}I_2\nonumber \\ \frac{d J_1}{dt}&= \frac{\alpha _{h1}\theta _{h1}J_{v1}}{N_{h1}} S_1 + \xi _1 I_1- (\tau _1 + \mu _h + \delta _{J_1}) J_1 - \psi _{_{21}}J_1 + \psi _{_{12}}J_2\nonumber \\ \frac{d S_{v1}}{dt}&= \Pi _{v1} - \frac{\alpha _{v1}\beta _{v1}I_1}{N_{h1}} S_{v1} - \frac{\alpha _{v1}\theta _{v1}J_1}{N_{h1}} S_{v1} - \mu _v S_{v1}\nonumber \\ \frac{d I_{v1}}{dt}&= \frac{\alpha _{v1}\beta _{v1}I_1}{N_{h1}}S_{v1} - \mu _v I_{v1}\nonumber \\\nonumber \\ \frac{d J_{v1}}{dt}&= \frac{\alpha _{v1}\theta _{v1}J_1}{N_{h1}} S_{v1} - \mu _v J_{v1}\nonumber \\ \frac{d S_2}{dt}&= \Pi _2 + \gamma _2 I_2 + \tau _2 J_2 -\frac{\alpha _{h2}\beta _{h2}I_{v2}}{N_{h2}} S_2 - \mu _h S_2 - \psi _{_{12}}S_2 + \psi _{_{21}}S_1\nonumber \\ \frac{d I_2}{dt}&= \frac{\alpha _{h2}\beta _{h2}I_{v2}}{N_{h2}} S_2 - (\gamma _2 + \mu _h + \delta _{I_2})I_2 - \psi _{_{12}}I_2 + \psi _{_{21}}I_1\nonumber \\ \frac{d J_2}{dt}&= - (\tau _2 + \mu _h + \delta _{J_2}) J_2 - \psi _{_{12}}J_2 + \psi _{_{21}} J_1\nonumber \\ \frac{d S_{v2}}{dt}&= \Pi _{v2} - \frac{\alpha _{v2}\beta _{v2}I_2}{N_{h2}} S_{v2} S_{v2} - \mu _v S_{v2}\nonumber \\ \frac{d I_{v2}}{dt}&= \frac{\alpha _{v2}\beta _{v2}I_2}{N_{h2}}S_{v2} - \mu _v I_{v2}. \end{aligned}$$
(23)

It follows that the basic reproduction number of the model (23) with movement between the patches, denoted by \(\mathcal {R}^2_{0_{_{DSR}}}(\psi _{_{21}},\psi _{_{12}})\), is given by

$$\begin{aligned} \mathcal {R}^2_{0_{_{DSR}}}(\psi _{_{21}},\psi _{_{12}}) = \max \{\mathcal {R}^2_{0_{_{DS}}}(\psi _{_{21}},\psi _{_{12}}),\mathcal {R}^2_{0_{_{DR}}}(\psi _{_{21}},\psi _{_{12}})\}, \end{aligned}$$

where the drug sensitive and resistance reproduction numbers are given as

$$\begin{aligned} \mathcal {R}^2_{0_{_{DS}}}(\psi _{_{12}},\psi _{_{21}})&= \frac{1}{2\sigma _1}\bigg [u_1v_2 + u_2v_1 + \sqrt{(u_1v_2 - u_2v_1)^2 + 4u_1u_2\psi _{_{12}}\psi _{_{21}}} \bigg ], \qquad \quad \end{aligned}$$
(24)
$$\begin{aligned} \mathcal {R}^2_{0_{_{DR}}}(\psi _{_{12}},\psi _{_{21}})&= \frac{p_1q_2}{\sigma _2}. \end{aligned}$$
(25)

Without movement between the patches, the drug sensitive and resistance reproduction number is given as

$$\begin{aligned}&\mathcal {R}^2_{0_{_{DS_1}}}(0,0) = { \frac{\beta _{h1}\alpha _{h1}\beta _{v1}\alpha _{v1}N^*_{v1} }{k_1\mu _vN^*_{h1} }}, ~~~~\mathcal {R}^2_{0_{_{DR_1}}}(0,0) = {\frac{\theta _{h1}\alpha _{h1}\theta _{v1}\alpha _{v1}N^*_{v1} }{k_2\mu _vN^*_{h1} }},~~~~ \\&\mathcal {R}^2_{0_{_{DS_2}}}(0,0) = {\frac{\beta _{h2}\alpha _{h2}\beta _{v2}\alpha _{v2}N^*_{v2} }{k_3\mu _vN^*_{h2} }}. \end{aligned}$$

Theorem 11

The drug resistance basic reproduction number for the two patch malaria-drug resistance model (23) satisfies the following,

$$\begin{aligned} \mathcal {R}^2_{0_{_{DR_1}}}(0,0) = \mathcal {R}^2_{0_{_{DR}}} (\psi _{_{12}},\psi _{_{21}}). \end{aligned}$$

Similarly,

Theorem 12

The drug sensitive basic reproduction number, \(\mathcal {R}^2_{0_{_{DS}}} (\psi _{_{12}},\psi _{_{21}})\), for the two patch malaria-drug resistance model (23) satisfies the following inequality,

$$\begin{aligned} \min \{\mathcal {R}^2_{0_{_{DS_1}}}(0,0),\mathcal {R}^2_{0_{_{DS_2}}}(0,0) \} \!\le \! \mathcal {R}^2_{0_{_{DS}}} (\psi _{_{12}},\psi _{_{21}}) \!\le \! \max \{\mathcal {R}^2_{0_{_{DS_1}}}(0,0) ,\mathcal {R}^2_{0_{_{DS_2}}}(0,0) \}. \end{aligned}$$

Theorem 12 can be proved using the approaches in Sect. 2.2.

Simulation of model (23), using the parameter values given in Table 1 for the case with slow movement rates between the two patches (\(\psi _{_{12}}=\psi _{_{21}} = 0.00033\)) and slow treatment failure rates (\(\xi _1 = 0.000126,~\xi _2 = 0\)) with \(\mathcal {R}_{0_{_{DS_1}}} > \mathcal {R}_{0_{_{DR_1}}}>1\) and \(\mathcal {R}_{0_{_{DS_2}}} > 1\), shows that the two strains co-exist, with the drug sensitive strain dominating (but does not drive out the drug resistance strain) in both patches as can be seen in Figures 5a and 5b. With \(\mathcal {R}_{0_{_{DR_1}}} > \mathcal {R}_{0_{_{DS_1}}}>1\) and a slightly higher treatment failure rate in patch 1 (\(\xi _1 = 0.00126\)), the two strains co-exist in both patches; however, the drug resistance strain dominates in patch 1, while the drug sensitive strain dominates in patch 2, as depicted in Figures 6a and 6b. Furthermore, with a faster movement between the patches (\(\psi _{_{12}}= 0.04, ~\psi _{_{21}} = 0.04\)) and a higher treatment failure rate in patch 1 (\(\xi _1 = 0.0126\)) the drug resistance strain dominates in both patches, as depicted in Figures 7a and 7b.

Fig. 5
figure 5

Simulation of the model (23) as a function of time. (a) Total number of infected human population with \(\mathcal {R}_{0_{_{DR_1}}} < \mathcal {R}_{0_{_{DS_1}}}\) (\(\mathcal {R}_{0_{_{DS_1}}} = 11.9196, ~\mathcal {R}_{0_{_{DR_1}}} = 9.5471\)), using \(\xi _1 = 0.0001260, ~\xi _2 = 0.0\), other parameter values used are as given in Table 1. (b) Total number of infected human population with \(\mathcal {R}_{0_{_{DS_2}}} > \mathcal {R}_{0_{_{DR_2}}}\) (\(\mathcal {R}_{0_{_{DS_2}}} = 13.7385,~\mathcal {R}_{0_{_{DR_2}}} = 0\)), using \(\xi _1 = 0.000126, ~\xi _2 = 0, ~\psi _{21} = 0.00033, ~\psi _{12} = 0.00033\), other parameter values used are as given in Table 1

Full size image
Fig. 6
figure 6

Simulation of the model (23) as a function of time. (a) Total infected human population with \(\mathcal {R}_{0_{_{DR_1}}} > \mathcal {R}_{0_{_{DS_1}}}\) (\( \mathcal {R}_{0_{_{DR_1}}} = 9.5471, ~\mathcal {R}_{0_{_{DS_1}}} = 5.4389\)), using \(\xi _1 = 0.001260, ~\xi _2 = 0.0\), \(\psi _{_{12}}= 0.00033, ~\psi _{_{21}} = 0.00033\), other parameter values used are as given in Table 1. (b) Total infected human population with \(\mathcal {R}_{0_{_{DS_2}}} > \mathcal {R}_{0_{_{DR_2}}}\) (\(~\mathcal {R}_{0_{_{DS_2}}} = 13.7385,~\mathcal {R}_{0_{_{DR_2}}} = 0\)), using \(\xi _1 = 0.00126, ~\xi _2 = 0, ~\psi _{21} = 0.00033, ~\psi _{12} = 0.00033\), other parameter values used are as given in Table 1

Full size image
Fig. 7
figure 7

Simulation o the model (23) as a function of time. (a) Total number of infected human population with \(\mathcal {R}_{0_{_{DR_1}}} > \mathcal {R}_{0_{_{DS_1}}}\) (\( \mathcal {R}_{0_{_{DR_1}}} = 9.5471, ~\mathcal {R}_{0_{_{DS_1}}} = 5.4389\)), using \(\xi _1 = 0.001260, ~\xi _2 = 0.0\), other parameter values used are as given in Table 1. (b) Total number of infected human population with \(\mathcal {R}_{0_{_{DS_2}}} > \mathcal {R}_{0_{_{DR_2}}}\) (\(~\mathcal {R}_{0_{_{DS_2}}} = 13.7385,~\mathcal {R}_{0_{_{DR_2}}} = 0\)), using \(\xi _1 = 0.00126, ~\xi _2 = 0, ~\psi _{21} = 0.04, ~\psi _{12} = 0.04\), other parameter values used are as given in Table 1

Full size image

4 Conclusions

A deterministic model for the transmission dynamics of drug sensitive and drug resistance malaria incorporating human migration was designed and rigorously analyzed. Some of the main theoretical and epidemiological findings of this study are summarized below:

  1. (i)

    The DFE of the model is globally asymptotically stable whenever the associated reproduction number is less than unity;

  2. (ii)

    For the two patch model (14) when the patches are isolated (i.e., there is no movement between the patches)

    1. (a)

      The drug sensitive-only and drug resistance-only boundary equilibria of the model are shown to be locally asymptotically stable when they exist;

    2. (b)

      The co-existence equilibrium is locally asymptotically stable whenever the reproduction number for the drug sensitive malaria is greater than the reproduction number for the resistance malaria;

  3. (iii)

    For the two patch model (14) when the patches are connected (i.e., there is movement between the patches), the disease persist in the two patches;

  4. (iv)

    Numerical simulations of the model (14) show that:

    1. (a)

      When \( \mathcal {R}_{0_{_{DS_i}}} > \mathcal {R}_{0_{_{DR_i}}}>1\), \(i=1,2\) the drug sensitive strain dominates the drug resistance strain;

    2. (b)

      When \( \mathcal {R}_{0_{_{DR_i}}} > \mathcal {R}_{0_{_{DS_i}}}>1\) the drug resistance strain drives out the drug sensitive strain to extinction.

  5. (v)

    Numerical simulations of the model (23) show that the strains co-exist:

    1. (a)

      with the drug sensitive strain dominating the drug resistance strain with a slow movement (or low migration) between the patches;

    2. (b)

      with the drug resistance strain dominating the drug sensitive strain with a fast movement (or high migration) between the patches.

In the present study, we have theoretically gained insight into the asymptotic behavior of the transmission dynamics of malaria drug resistance with human mobility and spatial heterogeneity. However, there are still more work to be done. As further work along these lines, it will be interesting to address the issue of control of possible expansion of resistance parasites by applying optimal control; an interesting question therefore will be: given \(n\) connected patches how do we optimally control malaria prevalence; could we by controlling malaria in one patch reduce its prevalence in the other patches? What should we do to prevent expansion of the resistant strain?