A Non-phenomenological Model of Competition and Cooperation to Explain Population Growth Behaviors

Abstract

This paper is an extension of a previous work which proposes a non-phenomenological model of population growth that is based on the interactions among the individuals of a population. In addition to what had already been studied—that the individuals interact competitively—in the present work it is also considered that the individuals interact cooperatively. As a consequence of this new consideration, a richer dynamics is observed. For instance, besides getting the population models already reached from the original version of the model (as the Malthus, Verhulst, Gompertz, Richards, Bertalanffy and power-law growth models), the new formulation also reaches the von Foerster growth model and also a regime of divergence of the population at a finite time. An agent-based model is also presented in order to give support to the analytical results. Moreover, this new approach of the model explains the Allee effect as an emergent behavior of the cooperative and competitive interactions among the individuals. The Allee effect is the characteristic of some populations of increasing the population growth rate in a small-sized population. Whereas the models presented in the literature explain the Allee effect with phenomenological ideas, the model presented here explains this effect by the interactions between the individuals. The model is tested with empirical data to justify its formulation. Another interesting macroscopic emergent behavior from the model proposed is the observation of a regime of population divergence at a finite time. It is interesting that this characteristic is observed in humanity’s global population growth. It is shown that in a regime of cooperation, the model fits very well to the human population growth data from 1000 AD to nowadays.

1 Introduction

The study of population growth is applicable to many areas of knowledge, such as biology, economics and sociology (Murray 2002; Solomon 1999; Strzalka 2009; Kohler and Gumerman 2000). In recent years, this wide spectrum of applicability has motivated a quest for universal growth patterns that could account for different types of systems by means of the same idea (Chester 2011; Guiot et al. 2003; West et al. 2001; Bettencourt et al. 2007). To model a more embracing context, generalized growth models have been proposed to address different systems without specifying functional forms (Kuehn et al. 2011). These generalized models have helped guide the search for such universal growth patterns (Cabella et al. 2011, 2012; Ribeiro et al. 2014; Barberis and Condat 2011).

The first population growth models were proposed to describe a very simple context or a specific empirical situation. For instance, the Malthus model (Malthus 1798; Murray 2002) was proposed to explain populations whose growth is strictly dependent on the number of individuals in the population, i.e., populations that have a constant growth rate. The model yields an exponential growth of the population, and although it fits very well to some empirical data when the population is sufficiently small, it fails after a long period of time (Edelstein-Keshet 2005; Murray 2002). To describe a more realistic population, Verhulst introduced (Verhulst 1845, 1847; Murray 2002) a negative quadratic term in the Malthus equation to represent an environment with limited resources. The Verhulst model yields the logistic growth curve, which fits many empirical data very well; examples include bacterial growth and human population growth (Edelstein-Keshet 2005; Murray 2002). Another important model is the Gompertz model, which was introduced by Gompertz (1825) to describe the human life span but has many others applications (Haybittle 1998). The model is a modification of Malthus’s original model by the substitution of a constant growth rate with an exponentially decaying growth rate (Ausloos 2012). The model yields an asymmetric sigmoid growth curve.

In the last few decades, a search for theoretical models that describe as many situations as possible has been conducted; the idea is that the larger the applicability of the model is, the better the theory is Chester (2011). For instance, the Richards model, which was introduced to describe plants’ growth dynamics (Richards 1959; Gregorczyk 1998), has the Verhulst and Gompertz growth models as particular cases. Another model important in this context is the Bertalanffy model (von Bertalanffy 1957, 1960; Savageau 1980), which summarizes many classes of animal growth using the same approach. An additional model, which was introduced by Strzalka et al. (2008), presents a generalization of the Malthus and Verhust models based on the generalized logarithm and exponential function. The generalized forms of the logarithm and exponential function are discussed in the “Appendix 1.” Other types of models that deserve attention are the ones that use an expansion of the Verhulst term in a power series and apply it to multiple-species systems (Kuehn et al. 2011; Solomon 1999). Furthermore, there are models that use second-order differential equations to describe growth, and these models have been strongly corroborated by empirical data (Chester 2011; Ginzburg 1972).

All of the models cited above can be seen as phenomenological models, because the only assumption that such models take into account in their formulation is the population’s—macroscopic level—information. This information includes, for example, the population’s size, density, and average quantities. The particularities of the individuals—the microscopic level—are removed from the formulation of these models. It is the approach of most of the models presented in the literature. This approach is very appropriate, as it is difficult to know in detail the particularities of all of the components of the population. Indeed, taking these details into account complicates the calculus and computations that are necessary to predict the population behavior from the model. However, finding universal patterns of growth is extremely helpful in observing how the components of the system behave. There would most likely be some types of individual behaviors that are common even in different systems. If that is the case, then one can justify the same pattern of growth being observed in completely different type of systems as a consequence of similarities at the microscopic level.

It is observed in many fields of science that simple interaction rules of the components of a system can result in complex macroscopic behavior. Moreover, some properties of such systems are universal, such as the same critical exponents in magnetic and fluid systems; these properties are universal even in systems that are completely different (Yeomans 1992; Kadanoff 2000). In the language of complex system theory, it is said that the collective behavior (macroscopic level) emerges from the interactions of the components of the system (microscopic level). Thus, the collective effects are called emergent behavior (Boccara 2003; Mitchell 2011). The idea of Mombach et al. (2002), which will hereafter be referred to as the MLBI model, was to apply the idea of emergent behavior to population growth. Hence, in opposition to the common models that present modeling from a phenomenological point of view, this model is based on microscopic assumptions. As a result, the (non-phenomenological) MLBI model, which was formulated in the context of inhibition patterns in cell populations, recapitulates many well-known phenomenological growth models (such as the Malthus, Verhulst, Gompertz, and Richards models) as an emergent behavior from individuals’ interactions. Recently, this model was analyzed by d’Onofrio (2009), Ribeiro et al. (2014), and Cabella et al. (2011, 2012).

The model that is proposed here continues the main idea of the MLBI model. However, the proposal of the present work is to increase the scope of this model. It will be considered that the individuals that constitute the population interact with each other not only through competition, as was proposed in the original MLBI model, but also through cooperation. This new formulation permits other models which were not permitted in the previous formulation to be embraced. For instance, the new formulation permits the Von Foerster growth model and the divergence of the population at a finite time to be obtained. Another interesting property of this extended version presented here is to get the Allee effect as an emergent behavior from cooperation and competition at a microscopic interaction level. The Allee effect is the property of some biological populations to increase their growth rate with increases in the population size for small population. This behavior cannot be deduced from the original MLBI model. Another interesting macroscopic emergent behavior from the model proposed here includes the observation of a regime of population divergence after a finite amount of time. It is interesting that this characteristic is observed in humanity’s global population growth, as will be shown in the following sections of the paper.

The paper is organized as follows: In the Sect. 2, a model based on the interactions—cooperation or competition—between the individuals of the population is presented. In the Sect. 3, it will be shown that the model can explain the Allee effect in a non-phenomenological way; that is, the Allee effect can be explained by the interactions between the individuals of the population. The model is tested with empirical data to justify its formulation. In the Sect. 4, it will be shown that some very important models in the literature can be obtained by changing some variables of the present model, such as the strength of the interaction, the geometry in which the population is embedded, and the spatial distribution of the population. In the Sect. 5, an agent-based model simulation is presented in order to give support to the analytical results.

2 The Model

The work presented here is an extension of the MLBI model, which was introduced by Mombach et al. (2002) and reworked by d’Onofrio (2009). The MLBI model was proposed to explain the population growth of cells considering the inhibitory interactions between them. As a result, these researchers discovered that some well-known phenomenological models present in the literature (such as Verhulst, Gompertz, and Richard’s models) can be obtained as a consequence of the microscopic interactions between individuals.

The present work follows the idea of the MLBI model and expands its applicability to other ecological systems. In particular, cooperative interactions between individuals are introduced. Then, one shows that the model can deal not only with populations of cells (the context that inspired the original version of the model), but also with the population growth of some mammals and even human populations. Moreover, the expanded version of the model can explain the Allee effect, which is not possible by regarding only its original version. These additional properties of the extended version will be presented in the next section.

First, consider that the replication rate $R$ of a single individual in a population is given by

$$\begin{aligned} R&= {\text {{[Self-stimulated replication]}}} - {\text {{[competition from field]}}}+\nonumber \\&+\, {\text {{[cooperation from field].}}} \end{aligned}$$

(1)

This idea is identical to the one proposed by Mombach et al. (2002) [in the first line of (1)], except for the cooperative stimulus term (the second line). Following the MLBI model, suppose that the interaction field $I_{ij}^{(l)}$ between two individuals $i$ and $j$ decays accordingly to the distance $r_{ij}$ between them in the form

$$\begin{aligned} I_{ij}^{(l)} = \left\{ \begin{array}{ll} \frac{1}{r_{ij}^{\gamma _l}} ,&{}{\text { if }\,r_{ij}>r_0 } \\ 1 ,&{} {\text { otherwise}} \end{array} \right. \; ; \end{aligned}$$

(2)

where $l=1$ is in respect of competitive interaction and $l=2$ in respect of cooperative interaction. This way it is assumed that the cooperative and competitive interaction fields behave in the same qualitative way; $\gamma _l$ is the exponent decay of the competitive interaction ($l=1$), or the cooperative interaction ($l=2$); $r_0$ can be, for instance, the size of the individual or the minimal distance between two individuals¹ (see Fig. 1). As in MLBI, $r_0=1$ is considered . Thus, the replication rate of the $i$th individual of the population has the form

$$\begin{aligned} R_i = k_i - J_1 \sum _{j \ne i} I_{ij}^{(1)} + J_2 \sum _{j \ne i} I_{ij}^{(2)}. \end{aligned}$$

(3)

This equation mathematically represents the idea introduced in Eq. (1), where $k_i$ is the self-stimulated replication of the $i$th individual and $J_l >0$ represents the strength of the competitive ($l=1$) or cooperative($l=2$) interaction.

Fig. 1

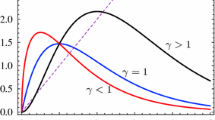
A graph that represents the intensity of the interactions between two individuals ($i$ and $j$)—see Eq. (2)—as a function of the distance $r_{ij}$, according to some values of $\gamma _l$. As $\gamma _l$ (the exponent decay) increases, the intensity of the interaction field decreases more rapidly with the distance. When $\gamma _l=0$, the interaction range is infinite; that is, the intensity of the interaction does not depend on the distance

The update of the population must obey the rule $N(t+~\Delta t) = N(t)+~\Delta t\sum _{i=1}^N R_i$. In the limit $\Delta t \rightarrow 0$, one has the differential equation $\hbox {d}N/\hbox {d}t = \sum _{i=1}^N R_i$. By the Eq. (3), one has

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}t}N = \sum _{i=1}^N \left( k_i - J_1 I_i^{(1)} +J_2 I_i^{(2)} \right) . \end{aligned}$$

(4)

where

$$\begin{aligned} I_i^{(l)} \equiv \sum _{j\ne i} I_{ij} \end{aligned}$$

(5)

is the (cooperative or competitive) interaction field that individual $i$ feels from its neighbors.

In “Appendix 2” an extended version of the calculus of the sum in Eq. (5) done by Mombach et al. (2002) is presented. One can prove (see the “Appendix”) that the interaction field $I_i^{(l)}$ is mathematically identical for all individuals if considered that the density $\rho$ of individuals depends only on the distance $r$ by $\rho (r) \propto r^{D_{f} - D}$. Here, $D(=1,2,3)$ is the Euclidian dimension of the space in which the population is embedded and $D_{f}$ the dimension of the spatial structure formed by the population. If $D_{f}=D$, then the interaction field will be equal to all individuals of the population if and only if the system presents a homogeneous distribution of the population. This way the interaction field of any individual, that is $I^{(l)} = I_i^{(l)}$ (regardless of $i$), will have the form

$$\begin{aligned} I^{(l)} = \frac{\omega _{D}}{D_{f}(1- \frac{\gamma _l}{D_{f}})}\left[ \left( \frac{D_{f}}{\omega _{D}}N \right) ^{1- \frac{\gamma _l}{D_{f}}} -1 \right] + \frac{\omega _{D}}{D_{f}} . \end{aligned}$$

(6)

Here, $\omega _{D}$ is a constant that depends exclusively on the euclidean dimension $D$. To maintain the physical property that $I^{(l)}$ is positive (note that the sum in Eq. (5) is over absolute terms), the model must be restricted to the case where $\omega _{D}/D_{f} < N$. In fact, it is demonstrated in the analysis around Eq. (47) (“Appendix 2”) that $\omega _{D}/D_{f} \sim 1$ (which is much smaller than the population size).

As presented by Cabella et al. (2011), one can write the term on the right-hand side of expression (6) by means of the generalized logarithm (see “Appendix 1”):

$$\begin{aligned} I^{(l)} = \frac{\omega _{D}}{D_{f}} \ln _{\tilde{q}_l} \left( \frac{D_{f}}{\omega _{D}} N \right) + \frac{\omega _{D}}{D_{f}}, \end{aligned}$$

(7)

where

$$\begin{aligned} \tilde{q}_l\equiv 1- \gamma _l/D_{f}. \end{aligned}$$

(8)

The parameter $\tilde{q}_l$ gives information about the relation between the decay exponent and the fractal dimension of the population.

By introducing the average of the intrinsic growth rate $\langle k \rangle \equiv (1/N) \sum _{i=1}^N k_i$, employing the definitions

$$\begin{aligned} J_l'\equiv J_l \frac{\omega _{D}}{D_{f}} \end{aligned}$$

(9)

and

$$\begin{aligned} k' \equiv \langle k \rangle + (J_2- J_1) \frac{\omega _{D}}{D_{f}}, \end{aligned}$$

(10)

and using the result (7), the Richard-like model

$$\begin{aligned} G(N) = \frac{1}{N} \frac{\hbox {d}}{\hbox {d}t}N = k' - J_1'\ln _{\tilde{q_1}} \left( \frac{D_{f}}{\omega _{D}} N \right) + J_2' \ln _{\tilde{q_2}} \left( \frac{D_{f}}{\omega _{D}} N \right) \end{aligned}$$

(11)

is obtained from (4).

The per-capita growth rate $G(N)$ gives information about the type of interaction that predominates in the population. For instance, $\hbox {d}G(N)/\hbox {d}N > 0$ means that cooperation predominates: The larger the population is, the larger the per-capita growth rate is. However, $\hbox {d}G(N)/\hbox {d}N < 0$ means that competition predominates: the larger the population is, the smaller the per-capita growth rate is.

2.1 Comments

The result (11) depends only on the macroscopic parameters of the system, although it was deduced from microscopic (or individual level) premises; that is a remarkable result, and it was first obtained by Mombach et al. (2002) in the context of inhibitory interactions and is now expanded to cooperative interactions. This result represents a significant advance in the knowledge of patterns in population growth. It is because the model is not a phenomenological one; that is, it is not a model that is constructed to fit macroscopic data. The MLBI model, which was extended here, is deduced from individual interactions. Then, the macroscopic behavior emerges as a consequence of the interactions between the individuals.

Moreover, the model presented in this work is more robust than its original version. The original model is fully obtained by assuming that $J'_2=0$ in (11). In this case, the per- capita growth rate $G(N)$ is a monotonically decreasing function of the size of the population (because if $J'_2=0$, then $\hbox {d}G/\hbox {d}N <0$ for any population size). Consequently, the simpler form of expression (11), which does not present the cooperative effects, cannot explain the Allee effect. However, if the cooperative term is considered [$J'_2 \ne 0$ in (11)], the Allee effect can be predicted by the model. This effect will be discussed in more detail in the next section.

3 The Allee Effect

The Allee effect is the property of some populations to increase their per-capita growth rates with increasing population size when the population is small (Courchamp et al. 1999; Sibly et al. 2005). There are many situations that can cause such effect, for instance, collective foraging, collective anti-predator behavior, reduction in inbreeding, among others. However, all the biological systems which present such features have two processes in common which have an opposing relationship to the population size. There is a process which tends to increase the population, and it is evident when the population is sufficiently small; there is another process which tends to decrease the population size, and it is evident when the population is sufficiently large. For instance, in Fig. 3, the experimental data of the per-capita growth rate of the muskox and marmot population are presented as a function of the population size. For a small population, the experimental data show an increasing trend of $G(N)$ with respect to the population size increasing. Then, when the population is sufficiently large, $G(N)$ decreases.

The Allee effect can be seen in two forms: the weak and strong Allee effect (dos Santos et al. 2014). In the weak Allee effect, $G(N)$ is always positive (for small $N$) with respect to the population size. In the strong Allee effect, $G(N)$ increases when the population size is small, but it is negative for $N$ smaller than a specific value: the so-called Allee threshold. In this sense, when the population is smaller than the Allee threshold, the population becomes extinct. When the population is larger than the Allee threshold, the population converges to the carrying capacity.

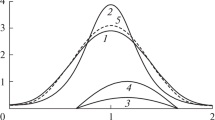
The Allee effect has been studied in recent theoretical models (Sibly et al. 2005; Courchamp et al. 1999; dos Santos et al. 2014). However, these models are restricted to the macroscopic approach and do not consider the microscopic level of the system. In the model proposed here, the Allee effect can not only be obtained, but also be interpreted as a macroscopic behavior that is observed as a consequence of the interactions of the individuals of the population. To show that model (11) can present the Allee effect, Fig. 2 is included. In this figure, a case of strong Allee effect is presented. The lower graph of this figure presents the form of $G(N)$ when $J_2'>J_1'$ and $\tilde{q}_1>\tilde{q}_2$. In this specific case, the per-capita growth rate reaches its maximum at $N=N^*$. This result can be explained by analyzing the two terms that composed $G(N)$ in Eq. (11). The upper graph of this figure presents the curves $k' + J_2' \ln _{\tilde{q_2}} \left( \frac{D_{f}}{\omega _{D}} N \right)$ (a constant related to the intrinsic reproductive rate and the cooperative term) and $J_1'\ln _{\tilde{q_1}} \left( \frac{D_{f}}{\omega _{D}} N \right)$ (the competitive term) as a function of $N$. The two curves are monotonically increasing functions of $N$, but they have different forms. The per-capita growth rate $G(N)$ is the difference between these two functions. For small $N, G(N)$ is an increasing function of the population size, that is, the Allee effect. Moreover, it is possible to see by the figure that the signal of $k'$ dictates the kind of Allee effect (whether strong or weak). In this specific case presented in the figure, $k'$ is negative, what implies a strong Allee effect (note that $G(N)$ is negative for $N < N_c$ and that $G(N \rightarrow 0) \approx k'$).

Fig. 2

Upper graph presents separately the functions that compos $G(N)$ as a function of $N$, which conform to Eq. (11): $k' + J_2' \ln _{\tilde{q_2}} \left( \frac{D_{f}}{\omega _{D}} N \right)$ (the constant related to the intrinsic replication rate and the cooperative term); $J_1'\ln _{\tilde{q_1}} \left( \frac{D_{f}}{\omega _{D}} N \right)$ (the competitive term). In this particular case, it was assumed $J_2'>J_1', q_1>q_2$, and $k' < 0$ in order to get a strong Allee effect. The lower graph presents $G(N)$ (which is obtained by the difference between the above two functions) as a function of $N$. The vertical dotted lines represent the value of $N$ in which $G(N)$ is maximum or null

One can find the population size $N^*$ at which $G$ is at its maximum by taking $\hbox {d}G(N)/\hbox {d}N =~0$ in (11), which gives

$$\begin{aligned} N^* = \frac{\omega _{D}}{D_{f}} \left( \frac{J_2}{J_1} \right) ^{\frac{1}{\tilde{q}_1 -\tilde{q}_2 }}. \end{aligned}$$

(12)

Note that if $J_2=0$, which is the MLBI model, then $N^*$ is null or indeterminate; that is, the MLBI model cannot explain Allee effect.

One can also find when $G(N)$ becomes null, which happens at the threshold value $N=N_c$; that is, $G(N_c) = 0$. This threshold population value can be determined by solving the transcendental equation

$$\begin{aligned} N_c = \frac{\omega _{D}}{D_{f}} e_{q_1}\left[ \frac{k'}{J_1'} \ln _{q_2} \left( \frac{D_{f}}{\omega _{D}} N_c\right) \right] , \end{aligned}$$

(13)

where $\hbox {e}_q(x)$ is the generalized exponential function (see “Appendix 1”). The equation above presents a single solution (>0) when $k' > 0$ (weak Allee effect); in this case $N_c= K$, that is, the solution is the carrying capacity of the system. On the other hand, when $k'<0$ (strong Allee effect), the equation above presents two distinct solutions: $N_{c1}$ and $N_{c2}$, with $N_{c1}<N_{c2}$. While $N_{c2}$ is the carrying capacity of the system, $N_{c1}$ is the Allee threshold. Note that the maximum value of $G$ happens when the difference between the two functions plotted in the upper graph of Fig. 2 is maximal, and the threshold value $N_c$ happens when these two functions are equal.

Model (11) fits very well to the muskox and marmot population data, which are presented in Fig. 3. According to the model and result (12), the transition from cooperation to competition for the muskox and marmot data is $~N^*\approx 246$ and $N^*\approx 255$, respectively. Moreover, the muskox population presents a weak Allee effect, once $k'$ is positive, and the marmot population presents a strong Allee effect, once $k'$ is negative. The Allee threshold for the marmot population is $N_{c1} \approx 185$. The fit curve obtained for muskox data is quite similar to the one obtained by a phenomenological model presented by Santos et al. (2014).

Fig. 3

Experimental data (points) of the per-capita growth rate $G(N)$ for populations of muskox (upper) and marmot (down). The data were obtained directly from Gregory et al. (2009). Note that the muskox population presents a weak Allee effect and the marmot population presents a strong Allee effect. The lines are the fit from model (11) with the following parameters. For the muskox data: $J_1' \approx 1.0305$; $J_2'\approx 1.0327$; $q_1 \approx 0.9859$; $q_2 \approx 0.9855$; and $k' \approx 0.0683$. For the marmot data: $J_1' \approx 1.33538$; $J_2'\approx 1.33539$; $q_1 \approx 2.485136$; $q_2 \approx 2.485135$; and $k' \approx -2.1$. The term $D_{f}/\omega _{D} \equiv 1$ was kept fixed. For muskox, $k' > 0$ (weak Allee effect); for marmot, $k'<0$ (strong Allee effect). The statistical analysis using the Levenberg–Marquardt algorithm shows $R^2= 0.10694$ (for muskox) and $R^2= 0.580802$ (for marmot)

3.1 Comments

One can interpret the Allee effect as cooperative and competitive interactions between the individuals of the population. When the population is too small, cooperation predominates, which favors the increase of the per-capita growth rate as $N$ increases. However, when the population is sufficiently large, competition predominates, which implies a decrease in the population growth rate as the population increases.

With respect to the spatial structure of the population and its representation by the model presented here, a good example is pollination in plants. The smaller the inter-individual distance is, the greater the efficiency of the pollination is Courchamp et al. (1999), Ghazoul et al. (1998), Roll et al. (1997), Groom (1998). As result, there is a cooperative effect (or facilitation, as argued by Allee 1949) that is strongly dependent on the distance between the individuals. However, when the inter-individual distance is small, competitive effects begin to appear in form of sunlight disputes, elimination of inhibitory toxins, or competition for soil or other resources. In this way, there is a trade-off between the individuals to stay close or more distant. The Allee effect is an example of an emergent phenomenon that can emerge as a consequence of these types of individual–individual mechanisms.

4 Analysis of a Special Case: $\gamma \equiv \gamma _1 = \gamma _2$

This section will be restricted to the special case in which the two decay exponents (for competition and cooperation) have equal values; that is, $\gamma \equiv \gamma _1 = \gamma _2$, which is equivalent to saying that $\tilde{q} \equiv \tilde{q}_1 = \tilde{q}_2$. It shall also consider, by convenience only, that $k' > 0$. In this particular case, model (11) becomes

$$\begin{aligned} \frac{1}{N} \frac{\hbox {d}N}{\hbox {d}t} = k' + J'\ln _{\tilde{q}} \left( \frac{D_{f}}{\omega _{D}} N \right) , \end{aligned}$$

(14)

where it is assumed

$$\begin{aligned} J'\equiv J_2' - J_1'. \end{aligned}$$

(15)

The parameter $J'$, which can assume both positive and negative values, determines what type of interaction has more strength: cooperation ($J'>0$) or competition ($J'<0$). When $\tilde{q}=0$, i.e., when $\gamma = D_{f}$, the generalized logarithm function becomes the usual logarithm, and then, Eq. (14) is the Gompertz growth model.

Using the properties of the generalized logarithm, one can show that Eq. (14) can be rewritten as

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}t} N = aN^{1+\tilde{q}} - bN. \end{aligned}$$

(16)

with solution

$$\begin{aligned} N(t) = \left[ \frac{a}{b} + \left( N_0^{-\tilde{q}} - \frac{a}{b} \right) \hbox {e}^{b\tilde{q}t} \right] ^{-\frac{1}{\tilde{q}}}. \end{aligned}$$

(17)

In the last two equations, the parameters $a$ and $b$ are given by

$$\begin{aligned} a \equiv \frac{J'}{\tilde{q}}\left( \frac{D_{f}}{\omega _{D}} \right) ^{\tilde{q}}, \end{aligned}$$

(18)

and

$$\begin{aligned} b \equiv \frac{J'}{\tilde{q}} - k', \end{aligned}$$

(19)

respectively. Model (16) is the Richards model (Richards 1959), which is utilized by von Bertalanffy (1960), Savageau (1980), and West et al. (2001) to describe animal growth. Recently, this model was studied by Bettencourt et al. (2007) in the context of the growth of cities. Thus, the Richards model is the same model that was deduced here from the individuals’ interactions. In the Sect. 5, an agent-based model simulation in the particular case $D=D_{f}=2$ is presented. As will be seen, the solution (17) describes quite well the results of the simulations.

The sign of the argument of the exponential in (17) is important, as it determines the convergence (or divergence) of the population. When $b\tilde{q}<0$, the exponential term goes to zero at $t\rightarrow \infty$, and then, the population has a saturation. However, when $b\tilde{q}>0$ the exponential diverges. Thus, there is a change in the population growth behavior when $b\tilde{q}=0$, which happens when $\gamma = \gamma ^*$, where

$$\begin{aligned} \gamma ^* \equiv D_{f} \left( 1- \frac{J'}{k'}\right) \end{aligned}$$

(20)

[according to the definitions (19) and (8)].

The term $\gamma ^*$ plays an important role in the analysis of the population growth behavior, and it will be discussed in more detail in the next section. The sign of the exponent (that is, $-1/\tilde{q}$) in (17) is also important in the analysis of the dynamics. Transition behavior happens when $1/\tilde{q} =0$, that is, when $\gamma = D_{f}$ [according to (8)].

Let us analyze the particular case in which the system described by model (14) presents cooperation predominance, that is, when $J'>0$. In this case, given $k'$ positive, the population always grows, without saturation. However, the way the population grows depends on the value of the exponent decay.

For instance, when $\gamma > D_{f}$, then $b<0, - 1/\tilde{q}>0$ and $b\tilde{q}>0$. The solution for this case [see (17)] can be written as

$$\begin{aligned} N(t \gg 1) \sim \left[ \hbox {e}^{b\tilde{q}t} \right] ^{-\frac{1}{\tilde{q}}} = \hbox {e}^{ \left( k' - \frac{J'}{\tilde{q}} \right) t}. \end{aligned}$$

(21)

That is, $\gamma > D_{f}$ implies exponential growth of the population, which is the Malthus model with growth rate $-b = k' - \frac{J'}{\tilde{q}}$ [see Eq. (19)]. When $\gamma = D_{f}$ (the Gompertz model), the population diverges asymptotically as $N(t \gg 1) \sim \hbox {e}^{\hbox {e}^{J'\frac{\omega _{D}}{D_{f}}t}}$. When $\gamma <D_{f}$, the population diverges at a finite time $t_c$ given by

$$\begin{aligned} t_c \equiv \frac{-1}{b\tilde{q}} \ln \left( 1- \frac{b}{a} N_0^{-\tilde{q}} \right) . \end{aligned}$$

(22)

In the same way that the Malthus model fails to describe biological systems after a long period of time, when $\gamma < D_{f}$ the present model only makes some biological sense for ${t \ll t_c }$ (Bettencourt et al. 2007). These results are summarized in Fig. 4.

Fig. 4

A schema of the population growth according to the exponent decay $\gamma$ when cooperation predominates ($J'>0$). The upper graph is the phase diagram corresponding to $\gamma$-x-$D_{f}$; the lower graph presents the population growth behavior as a function of $\gamma$, where $D_{f}$ is fixed. The exponent decay represents the following models: $\gamma =0$ implies that one has the Verhulst model; $\gamma =\gamma ^*$ implies one has Von Foerster model; $\gamma = D_{f}$ implies one has the Gompertz model. When $\gamma < D_{f}$, one has the Richards model, and hence, the population diverges at a finite time $t_c$ given by (22). When $\gamma = D_{f}$ (the Gompertz model), the population diverges as $t\rightarrow \infty$. Lastly, when $\gamma > D_{f}$, the population grows exponentially (the Malthus model), as in Eq. (21)

When competition predominates, that is, when $J'<0$, the model described here is exactly the MLBI model. Thus, the analysis of the convergence or divergence of the population is identical to the analysis discussed and presented by d’Onofrio (2009). When $\gamma < \gamma ^*$, which implies $-1/q>0$ and $bq<0$, solution (17) implies that the population converges to a finite size—which is the carrying capacity—and is given by $K= (a/b)^{-1/q}$. When $\gamma >\gamma ^*$ (which implies $\tilde{q}<0$), at $t\gg 1$ solution (17) becomes $N(t) \sim \hbox {e}^{\left( k' - \frac{J'}{\tilde{q}} \right) t} = \hbox {e}^{\left( k' - |\frac{J'}{\tilde{q}}|\right) t}$, i.e., one has exponential growth (the Malthus model). Figure 5 summarizes the conclusion for $J'<0$. In the Sect. 5, these analytical results are verified using an agent-based simulation.

Fig. 5

A schema of the population growth according to the exponent decay $\gamma$, when competition predominates ($J'<0$). The graph presents the population growth behavior as a function of $\gamma$, where $D_{f}$ is fixed. The exponent decay represents the following models: $\gamma =0$ implies one has the Verhulst model; $\gamma =\gamma ^*$ implies power-law growth; $\gamma = D_{f}$ implies one has the Gompertz model. When $\gamma < \gamma ^*$, the population converges to a finite size (the carrying capacity $K$). When $\gamma >\gamma ^*$, the population presents exponential growth

4.1 Comments about $\gamma \rightarrow \gamma *$ and the Human Population Growth

The particular case that $\gamma \rightarrow \gamma ^* \equiv D_{f}(1-J'/k')$ must receive more attention. In this case, the parameter $b$ goes to zero [according to Eq. (20) and (19)], and then, the model (17) becomes

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}t}N = aN^{1+\tilde{q}}. \end{aligned}$$

(23)

This is the von Foerster growth model, which was studied by von Foerster et al. (1960) and more recently by Strzalka (2009) to describe human population growth. The solution of model (23) is

$$\begin{aligned} N(t) = N_0 \hbox {e}_{\tilde{q}}\left( \frac{a}{N_0^{\tilde{q}}} t\right) , \end{aligned}$$

(24)

which was presented by Cabella et al. (2012, 2011), where $\hbox {e}_q(x)$ is the generalized exponential function (see “Appendix 1”). The result (24) is exactly the model proposed by Strzalka et al. (2008). In this reference, the model was introduced by a modification of the exponential term of the Malthus model solution without any justification. However, with the formulation of the microscopic model proposed here, all of the involved quantities have a physical interpretation, and the growth behavior described by (24) is a consequence of the of interactions of the individuals.

Given that $\omega _{D}, D_{f}$, and $k'$ are positive parameters, the manner in which the population grows for large $t$ is totally dependent on $J'$. For instance, when $J'=0$, the population grows exponentially because the competitive and cooperative strength completely cancel each other out, and then, the population grows without individual interactions.

When $J'<0$, solution (24) behaves asymptomatically as a power law:

$$\begin{aligned} N(t \gg 1) \sim t^{- \frac{k'}{J'}}. \end{aligned}$$

(25)

In this way, if $J'<0$, then the population diverges only when $t \rightarrow \infty$. The concavity of $N(t)$ is also determined by $J'$: if $J'> - k'$, then $N(t)$ is a convex function, and it is concave otherwise. Whereas $J'<0$ the population diverges only when $t \rightarrow \infty$, for $J'>0$ the population diverges at a finite time $t_c$, which is given by

$$\begin{aligned} t_c = \frac{1}{J'} \left( \frac{N_0 D_{f}}{\omega _{D}}\right) ^{- \frac{J'}{k'}}. \end{aligned}$$

(26)

This equation is the particular case of the Eq. (22) when $b\rightarrow 0$ (because $\gamma \rightarrow \gamma ^*$). Figure 6 summarizes these conclusions. In the next section, the divergent behavior at finite time and the power-law growth behavior are presented using an agent-based model simulation.

Fig. 6

Time evolution of the population according to the strength of the interaction $J'$ for $\gamma \rightarrow \gamma ^*$. When $J'>0$, that is, when one has cooperation, the population diverges at a finite time $t_c$ (von Foerster model). When $J'=0$, the population has exponential growth. In this case, the interaction effect is fully nullified and the growth rate is given only by the intrinsic growth rate $k'$. When $J'<0$, that is, when one has competition, the population diverges only as $t\rightarrow \infty$. The special cases are: $J'= -k'$, linear growth; $J'< -k'$, logarithmic growth. $N(t)$ is a convex function when $J'> - k'$, and it is a concave function otherwise

When $J'>0$, it is interesting to write solution (23) in terms of the critical time $t_c$ in which the population diverges. Thus, solution (24) behaves as

$$\begin{aligned} N(t) \sim (t_c-t)^{- \frac{k'}{J'}} \end{aligned}$$

(27)

when cooperation predominates. An interesting application of this result is in human population growth, as represented in Fig. 7. Note that Eq. (27) applies very well to human population growth, as the data from 1000 AD until 2014 according to what was presented by Strzalka (2009), von Foerster et al. (1960). However, with the presentation of the microscopic point of view of the interactions between the individuals, one can argue that the “divergent behavior” of the human population can be seen as a result of cooperative effects, as the parameter $J'$ must be positive (i.e., cooperation predominates) to fit the data.

Fig. 7

Human population as a function of time since the Middle Ages. The data were obtained from Strzalka (2009) and from the US Census Bureau http://www.census.gov/population/international/index.html. The curve is a plot of the equation $N(t) = 65,6(2026 -t)^{-0,78}$ [from Eq. (27)], whose parameters values were obtained via a data fit

5 A Two-Dimensional ($D=D_{f}=2$) Agent-Based Model Simulation

In this section, a two-dimensional agent-based model (ABM) simulation of the model proposed will be presented. It will be shown that the ABM simulations give plausibility to the analytical results presented in previous sections.

The simulations that will be presented here were performed considering that both the medium and the structure formed by the population are two-dimensional, that is $D=D_{f}=2$. In this case, following the consideration (40), the population must grow maintaining a constant superficial density $\rho _0$ of individuals. Let us consider that in each time step—a generation—the individuals are randomly positioned in a square of area $L \times L$. The distance $L$ is not fixed, but it increases or decreases in order to maintain the superficial density $\rho _0$ constant. In fact, $L = L(N) = \sqrt{N/\rho _0}$. Figure 8 illustrates the dynamics of the ABM. The strength of the interaction between every two individuals, which depends only on the distance between them, is given by the rule (2). A periodic boundary condition is also considered; that is, the individuals in the extreme right region are neighbors of the individuals of the extreme left region. The same is applied for individuals in the upper and lower regions.

Fig. 8

Dynamics of the agent-based model in three consecutive times (generations). The points represent the individuals of the population in a specific time step, randomly positioned in the square of size $L$. Every two individuals interact with each other with interaction strength given by the rule (2). The lattice, of size $L$ and area $L^2$, increases or decreases in order to maintain the individual surface density $\rho _0$ constant over the time steps

This ABM is a particular case of the general model proposed in the Sect. 4, where $\gamma \equiv \gamma _1=\gamma _2$, which has the solution (17)— with parameters [from Eq. (8), (9), (10), (15), (18), and (19)]:

$$\begin{aligned} \tilde{q}&= 1- \frac{\gamma }{2}, \end{aligned}$$

(28)

$$\begin{aligned} a&= \frac{ \pi ^{\frac{\gamma }{2}}J\rho _0^{\frac{\gamma }{2}}}{ 1- \frac{\gamma }{2}}, \end{aligned}$$

(29)

and

$$\begin{aligned} b = \frac{J\pi \rho _0 \gamma }{2-\gamma } -\langle k \rangle , \end{aligned}$$

(30)

where

$$\begin{aligned} J \equiv J_2 - J_1. \end{aligned}$$

(31)

Figure 9 presents the result of the ABM simulation for a competitive kind of interaction ($J<0$). The ABM simulation and the analytical solution agree quite well, showing three different population growth behaviors: exponential growth, power-law growth, and convergence to carrying capacity (as showed by the diagram of Fig. 5. The value of the exponent decay $\gamma$ which conducts to the power law growth is

$$\begin{aligned} \gamma ^* = \frac{2 \langle k \rangle }{ J\pi \rho _0 + \langle k \rangle } \end{aligned}$$

(32)

a particular case of the Eq. (20). The graph was built in a log–log scale in order to highlight the power-law behavior of the population growth when $\gamma = \gamma ^*$. This specific value of $\gamma$ also represents a change of the dynamic behavior, from a convergence growth dynamics ($\gamma < \gamma ^*$) to a divergent growth dynamics ($\gamma >\gamma ^*$) (see diagram of Fig. 5).

Fig. 9

Log–log graph of the population size dynamics in a competitive kind of interaction ($J<0$) for different values of $\gamma$. The points represent the agent-based model simulations and the lines the analytical solution. The simulations attest the results presented in the diagram of Fig. 5; that is, convergence to carrying capacity when $\gamma <\gamma ^*$, and exponential growth when $\gamma >\gamma ^*$. The inner graphic presents the analytical solution plot for $N$ large in order to show the asymptoptic power-law growth behavior for $\gamma = \gamma ^*$. The dashed straight line of the inner graphic is a power law with exponent $6.63942$ computed from the expression (25). The parameters used were: $N_0=100, \langle k \rangle =1.2, \rho _0=1$, and $J=-0.05$

The assimptopic power-law growth behavior exhibited by the model when $\gamma = \gamma ^*$ is quite similar to the behavior of the tumor spheroids growth, according to the empirical data presented by Drasdo and Hohme (2003) and Freyer and Sutherland (1985). This fact suggests that the microscopic model presented here can give some insight about the way that the cancer cells interact in order to promote the emergence of macroscopic patterns of growth.

Figure 10 presents the result of the ABM simulation for a cooperative kind of interaction ($J>0$). As in the competitive case, the results of the simulations agree with the theoretical prediction present in previous sections. As presented in the diagram of Fig. 4, when $\gamma < D=2$ the population diverges at finite time $t_c$ [given by (22)]. When $\gamma >D=2$, the population presents an exponential growth, characterized by the straight line in the log–normal plot.

Fig. 10

Log–normal graph of the population size dynamics in a cooperative kind of interaction ($J>0$) for different values of $\gamma$. The points represent the agent-based model simulations and the line the analytical solution. In some cases, the points overlap the lines. The simulations attest the results presented in the diagram of Fig. 4; that is, when $\gamma <D_{f}=2$, then the population diverges at finite time; when $\gamma >D_{f}=2$, then the population grows exponentially (straight line in a log–normal graph). The dashed lines represent the critical time [by Eq. (22)], as a function of $\gamma$, in which the population diverges. The parameters used were: $N_0=1,000, \langle k \rangle =1.2, \rho _0=1$, and $J=+0.01$

6 Conclusion

In the present work, an extension of the MLBI model was proposed. This previous work reaches some well-known phenomenological models present in the literature as a consequence of the interaction of the individuals that constitute the population. While this original version considers only a competitive interaction among the individuals, the present paper considers both competitive and cooperative interactions among the individuals. As a consequence of this new consideration, a richer dynamics of the model was observed by analytical and simulation approaches, for instance, presenting divergence of the population at finite time and reaching the von Foerster population growth model, in addition to reaching the other models already verified from the original version (as Malthus, Verhulst, Gompertz, Richards, Bertalanffy, and power-law growth models). Moreover, it was verified that the introduction of cooperation between the individuals allows us to explain the Allee effect as an emergent behavior from the individual–individual interactions. This approach differs from the common phenomenological explanation presented in the literature. It is important to stress that the MLBI model, which considers only competitive interactions, cannot explain this effect.

It was observed that the relation between the decay exponent ($\gamma$), the fractal dimension ($D_{f}$) of the population, and the interaction strength ($J$) determines the behavior of the population growth. For instance, one has presented a phase diagram in which one related diverse types of growth as consequences of the distance dependent interactions (by the exponent decay $\gamma$) and the fractal dimension of the population. Moreover, one has shown how the strength of the interaction gives both the concavity of the growth (as a function of time) and the saturation or divergence of the population.

In conclusion, the model proposed here incorporates many types of macroscopic ecological patterns by focusing on the balance of cooperative and competitive interactions at the individual level. In this way, the model presents a new direction in the search for universal patterns, which could shed more light on population growth behavior.

Appendices

Appendix 1: The Generalized Logarithm and Exponential Function

In this appendix, one presents the generalizations of the logarithmic and exponential functions and some of their properties. The introduction of the functions is shown to be very useful for dealing with the mathematical representation of the population growth model that is presented in this work.

The $\tilde{q}$-logarithm function is defined as

$$\begin{aligned} \ln _{\tilde{q}}(x) = \lim _{\tilde{q}' \rightarrow \tilde{q}}\frac{x^{\tilde{q}'} -1 }{\tilde{q}'} = \int _1^x \frac{dt}{t^{1-\tilde{q}}} \; , \end{aligned}$$

(33)

which is the area of the crooked hyperbole and is controlled by $\tilde{q}$. This equation is a generalization of the natural logarithm function, which is reproduced when $\tilde{q} = 0$. This function was introduced in the context of nonextensive statistical mechanics Tsallis (1988; 1994) and was studied recently by Arruda et al. (2008), Martinez et al. (2008) and Martinez et al. (2009). Some of the properties of this function are as follows: for $\tilde{q} < 0, \ln _{\tilde{q}}(\infty )=-1/\tilde{q}$; for $\tilde{q} > 0, \ln _{\tilde{q}}(0)=-1/\tilde{q}$; for all $\tilde{q}, \ln _{\tilde{q}}(1)=0$; $\ln _{\tilde{q}}(x^{-1}) = - \ln _{-\tilde{q}}(x)$; $\hbox {d} \ln _{\tilde{q}}(x)/\hbox {d}x = x^{\tilde{q}-1}$. Moreover, the $\tilde{q}$-logarithm is a function: convex for $\tilde{q}>1$, linear for $\tilde{q}=1$, and concave for $\tilde{q}<1$.

The inverse of the $\tilde{q}$-logarithm function is the $\tilde{q}$-exponential function, which is by

$$\begin{aligned} \hbox {e}_{\tilde{q}}(x) = \left\{ \begin{array}{ll} \lim _{\tilde{q}^{'} \rightarrow \tilde{q}} (1+ \tilde{q}^{'} x)^{ \frac{1}{ \tilde{q}^{'}} } &{},\quad {\text { if }}\,\tilde{q}x > -1 \\ 0,&{}\quad {\text {otherwise}} \end{array} \right. . \end{aligned}$$

(34)

Some properties of this function are as follows: $\hbox {e}_{\tilde{q}}(0)=1$, for all $\tilde{q}$; $\left[ \hbox {e}_{\tilde{q}}(x) \right] ^a = \hbox {e}_{\tilde{q}/a}(ax)$, where $a$ is a constant; for $a=-1$, one has $1/\hbox {e}_{\tilde{q}}(x) = \hbox {e}_{-\tilde{q}}(-x)$. Moreover, the $\tilde{q}$-exponential is a function: convex for $\tilde{q}<1$; linear for $\tilde{q}=1$; concave for $\tilde{q}>1$.

Appendix 2: A Detailed Calculus of $I_i^{(l)}$

In this appendix, one presents a detailed calculus for the intensity of the interaction felt by a single individual $i$ from the other individuals of the population, which is represented by $I_i^{(l)}$ (see Sect. 2). One follows Mombach et al. (2002) to show that this intensity is independent of the individual; that is, it is the same for all individuals of the population and depends only on the size of the population. More specifically, one shows that $I_i^{(l)} = I^{(l)}(N)$ regardless of $i$.

First, from the Sect. 2 one has

$$\begin{aligned} I_i^{(l)} = \sum _{j \in r_{ij} \ge r_0} \frac{\left( 1-\delta _{ij}\right) }{|\mathbf {r}_i-\mathbf {r}_j |^{\gamma _l}} + \sum _{j \in r_{ij} < r_0} \left( 1-\delta _{ij}\right) , \end{aligned}$$

(35)

where $\delta _{ij}$, which is the Kronecker’s delta, was introduced to avoid the restriction in the sum. Moreover, $\mathbf {r}_i$ and $\mathbf {r}_j$ represent the position vectors of the individuals $i$ and $j$, respectively, and consequently $r_{ij} = |\mathbf {r}_i - \mathbf {r}_j |$ is the distance between them. Introducing the property

$$\begin{aligned} f(\mathbf {r}_0) = \int _{V_{D}} \hbox {d}^D\mathbf {r} \delta (\mathbf {r} - \mathbf {r}_0) f(\mathbf {r}), \end{aligned}$$

(36)

where $\delta (\cdots )$ is the Dirac’s delta, the expression (35) becomes

$$\begin{aligned} I_i^{(l)}&= \sum _{j=1}^N (1-\delta _{ij}) \Big [ \int _{V_{D} \in r \ge r_0} \hbox {d}^D\mathbf {r} \delta \Big ( \mathbf {r} - (\mathbf {r}_j - \mathbf {r}_i)\Big ) |\mathbf {r}|^{- \gamma _l} \nonumber \\&+ \int _{V_{D} \in r<r_0} \hbox {d}^D\mathbf {r} \delta \Big ( \mathbf {r} - (\mathbf {r}_j - \mathbf {r}_i)\Big ) \Big ] . \end{aligned}$$

(37)

In the last two expressions, was introduced: $D (=1,2, 3)$, which is the Euclidean dimension in which the population is embedded, and $V_{D}$, which is the total (hyper) volume (in $D$ dimensions) that contains the population. The form represented in (37) was obtained by the variable substitution $\mathbf {r}_j - \mathbf {r}_i$ by $\mathbf {r}$, using Dirac’s delta.

Some algebraic manipulation and the introduction of $r\equiv |\mathbf {r}|$ allows to write

$$\begin{aligned} I_i^{(l)}&= \int _{V_{D} \in r \ge r_0}\frac{\hbox {d}^D \mathbf {r} }{\mathbf {r}^{\gamma _l}} \sum _{j \ne i} \delta \Big ( \mathbf {r} - (\mathbf {r}_j - \mathbf {r}_i)\Big ) + \nonumber \\&\int _{V_{D} \in r< r_0} \hbox {d}^D \mathbf {r} \sum _{j \ne i} \delta \Big ( \mathbf {r} - (\mathbf {r}_j - \mathbf {r}_i)\Big ) . \end{aligned}$$

(38)

Note that $dN(\mathbf {r})\equiv \hbox {d}^D \mathbf {r} \sum _{j \ne i} \delta \Big ( \mathbf {r} - (\mathbf {r}_j - \mathbf {r}_i)\Big )$ is the number of individuals which is at the element of (hipper)volume $d^D\mathbf {r}$ at the distance $\mathbf {r}$ from the individual $i$, localized at $\mathbf {r}_i$. In this way, the density of individuals at $\mathbf {r}_i + \mathbf {r}$ (neighbors of $i$), that is $\rho (\mathbf {r}_i~+~\mathbf {r}) =\hbox {d}N(\mathbf {r})/\hbox {d}^D \mathbf {r}$, can be written as

$$\begin{aligned} \rho (\mathbf {r}_i + \mathbf {r}) = \sum _{j \ne i} \delta \Big ( \mathbf {r} - (\mathbf {r}_j -\mathbf {r}_i)\Big ). \end{aligned}$$

(39)

The density of individuals can also be thought of in terms of the scale of the system (in conformity with Falconer 1990). The volume of the system grows in the form $V_{D} \sim L^D$, where $L$ is the typical size of the system. However, the number of individuals grows as the form $N \sim L^{D_{f}}$, where $D_{f}$ is the fractal dimension formed by the spatial structure of the population. By considering $r$, which is the absolute distance from $i$, as a typical distance of the system, one can say that the density of individuals ($V_{D}/N$) has the form

$$\begin{aligned} \rho (\mathbf {r}_i + \mathbf {r}) \equiv \rho (r) = \rho _0 \frac{r^{D_{f}}}{r^D}, \end{aligned}$$

(40)

where $\rho _0$ is a constant which is related to the density of individuals. In fact, if $D=D_{f}$ and the population is homogeneously distributed, then $\rho _0$ is the usual density of individuals.

Using results (40) and (39) in (38), one obtains

$$\begin{aligned} I_i^{(l)} = \rho _0 \int _{V_{D} \in r \ge r_0}d^D \mathbf {r} r^{D_{f} -D -\gamma _l} + \rho _0 \int _{V_{D} \in r < r_0}d^D \mathbf {r} r^{D_{f} -D } . \end{aligned}$$

(41)

Note that the integration argument does not depend on the angular coordinates. Thus, one can write $\hbox {d}^D \mathbf {r}=~r^{D-1}\hbox {d}r \hbox {d}\Omega _{D}$, where $\hbox {d}\Omega _{D}$ is the solid angle, which implies

$$\begin{aligned} I_i^{(l)} = \rho _0\frac{\Omega _{D}}{D_{f}} \int _{0}^{r_0=1} \hbox {d}r r^{D_{f} -1} +\rho _0 \Omega _{D} \int _{r_0=1}^{R_{\hbox {max}}} \hbox {d}r r^{D_{f} -1-\gamma _l}, \end{aligned}$$

(42)

where $\Omega _{D} = \int \hbox {d}\Omega _{D}$. Note that the only term that depends on the Euclidean dimension is the solid angle, and $\Omega _{D}$ assumes the following values according to these tree possibilities: $\Omega _1 = 2$; $\Omega _2 = 2\pi$; $\Omega _3 = 4\pi$. By introducing the constant $\omega _{D} = \rho _0 \Omega _{D}$, which depends only on $D$, one obtains

$$\begin{aligned} I^{(l)} \equiv I_i^{(l)} = \omega _{D} \left( \frac{R_{\hbox {max}}^{D_{f} - \gamma _l} -1 }{D_{f} - \gamma _l}\right) + \frac{\omega _{D}}{D_{f}} \end{aligned}$$

(43)

Thus, $I_i^{(l)}$ does not depend on the label $i$ anymore. As a result, one can say that $I_i^{(l)} = I^{(l)}$ regardless of $i$.

Furthermore, one can introduce the total number of individuals in the relation above by the following thinking. The total number of individuals in the population can be determined by the integral

$$\begin{aligned} N = \int \hbox {d}N(r) =\int _{V_{D}}\hbox {d}^D\mathbf {r} \rho (r). \end{aligned}$$

(44)

Using Eq. (40) and integrating the solid angle, one obtains

$$\begin{aligned} N&= \omega _{D} \int _{0}^{R_{\hbox {max}}} r^{D_{f}-1}\hbox {d}r \end{aligned}$$

(45)

$$\begin{aligned}&= \omega _{D} \int _{0}^{r_0} r^{D_{f}-1} + \omega _{D} \int _{r_0}^{R_{\hbox {max}}} r^{D_{f}-1} \end{aligned}$$

(46)

$$\begin{aligned}&= \omega _{D} \frac{r_0^{D_{f}}}{D_{f}} + \omega _{D} \frac{R_{\hbox {max}}^{D_{f}}}{D_{f}} - \omega _{D} \frac{r_0^{D_{f}}}{D_{f}} . \end{aligned}$$

(47)

Note that the first term on the right in (46) and (47) can be zero (indicating the absence of individuals) or 1 (indicating the presence of a single individual). These values are possible because the ratio of the individual is $r_0$, and hence, there can be at most one individual inside the region that consists of the length between $0$ and $r_0$. Thus, for $r_0=1, \omega _d/D_{f} \sim 1$. $R_{\hbox {max}}$ can be obtained from (47), which is a function of $N$ according to

$$\begin{aligned} R_{\hbox {max}} = \left( \frac{D_{f}}{\omega _{D}} N \right) ^{\frac{1}{D_{f}}}. \end{aligned}$$

(48)

Returning to relation (43), one finds

$$\begin{aligned} I^{(l)} = I^{(l)}(N) = \frac{\omega _{D}}{D_{f}(1- \frac{\gamma _l}{D_{f}})}\left[ \left( \frac{D_{f}}{\omega _{D}}N \right) ^{1- \frac{\gamma _l}{D_{f}}} -1 \right] + \frac{\omega _{D}}{D_{f}}. \end{aligned}$$

(49)

By introducing $\tilde{q}_l=1- \gamma _l/D_{f}$ and the properties of the generalized logarithm (Appendix 1), one obtains

$$\begin{aligned} I^{(l)} = I^{(l)}(N| D, \tilde{q}_l) = \frac{\omega _{D}}{D_{f}} \ln _{\tilde{q}_l} \left( \frac{D_{f}}{\omega _{D}}N \right) + \frac{\omega _{D}}{D_{f}}. \end{aligned}$$

(50)