Modeling the Dynamics of Populations in a Heterogeneous Environment: Invasion and Multistability

Abstract—We model the interaction of two populations based on evolutionary equations that consider diffusion, taxis, and logistic growth. Scenarios of biological invasion are under study, considering the heterogeneity of the environment. We develop the approach based on the cosymmetry of the model. Here, multistability arises - a family of stable stationary distributions of species. Population scenarios with violations of cosymmetry were studied using a computational experiment. For the diffusion and growth parameters that satisfy the cosymmetry conditions, the structure of the plane of taxis parameters divides into six zones corresponding to different scenarios (survival of individual species and their coexistence). When one of the growth parameters changes, the structure of the partitions is kept, but the boundaries of the zones deform. With a significant deviation of the growth parameter, additional zones of species coexistence may arise.

INTRODUCTION

The problem of invasion of biological species is of great socio-economic importance. Invading species can significantly affect the ecological balance by competing with native species and displacing them [1–4]. To study the threats of unwanted invasions and control the processes of invasion, it is necessary to develop tools for predicting the dynamics of ecosystems [5, 6]. Field experiments in this case are difficult and sometimes dangerous, which makes the development and study of models of population dynamics relevant. At the same time, both studies focused on the description of specific ecosystems and the construction and analysis of models that take the key processes of population dynamics are important into account.

It is topical to study problems in which the effects of diffusion, taxis (directed migration), and competition for resources are significant [7–9]. The systems of equations used in this case are, as a rule, nonlinear and contain many parameters. At the same time, natural questions arise about determining the areas of parameters for which various population scenarios can be implemented, and a qualitative analysis of the processes leading to the coexistence and extinction of species.

In this paper, a system of nonlinear equations that describes the dynamics of two populations competing for a heterogeneously distributed resource is considered. One population is an aboriginal or resident population that occupies an ecological niche and the other is an invader. The model takes the diffusion distribution of species, directed migration due to the heterogeneity of the resource (environment capacity), and local growth of the logistic type into account. Particular attention is paid to the study of multistability, that is, the possibility of implementing various scenarios of population dynamics, including the form of a family of stable stationary distributions of coexisting species [10–12].

MATHEMATICAL AND COMPUTATIONAL MODELS

The space–time interaction of two species on a one-dimensional area of length a: Ω = [0, a] is considered. The population density balance equations u(x, t) and v(x, t) are written similarly to [11, 12], using migration flows q_i and local interaction:

$$\begin{gathered} \frac{{\partial u}}{{\partial t}} = - \frac{{\partial {{q}_{1}}}}{{\partial x}} + {{\eta }_{1}}u{{f}_{0}}, \\ {{q}_{1}} = - {{k}_{1}}\frac{{\partial u}}{{\partial x}} + {{\alpha }_{1}}u\frac{{\partial p}}{{\partial x}},\,\,\,\,{{f}_{0}} = 1 - \frac{{u + {v}}}{p}, \\ \end{gathered} $$

(1)

$$\frac{{\partial {v}}}{{\partial t}} = - \frac{{\partial {{q}_{2}}}}{{\partial x}} + {{\eta }_{2}}{v}{{f}_{0}},\,\,\,\,{{q}_{2}} = - {{k}_{2}}\frac{{\partial {v}}}{{\partial x}} + {{\alpha }_{2}}{v}\frac{{\partial p}}{{\partial x}}.$$

(2)

Migration flows q₁ and q₂ consider diffusion propagation and directed migration, that is, taxis, which is determined by the uneven distribution of the carrying capacity p(x).

Relative densities and carrying capacity are also called resource in modern literature [2].

In formulas (1) and (2), k₁ and k₂ are diffusion coefficients, and α₁ and α₂ are directional migration coefficients. The change in population density is determined by the logistic law with growth parameters η₁ and η₂. Further, u(x, t) is aboriginal population and v(x, t) is an invader population.

At the boundary of the range Ω = [0, a], the conditions for the absence of flows are set:

$${{q}_{1}}(0,t) = {{q}_{1}}(a,t) = {{q}_{2}}(0,t) = {{q}_{2}}(a,t) = 0.$$

(3)

The system of equations (1)–(3) is supplemented with the initial distributions of population densities:

$$u(x,0) = {{u}^{0}}(x),\,\,\,\,{v}(x,0) = {{{v}}^{0}}(x).$$

(4)

For the numerical solution of problem (1)–(4), the method of lines with discretization based on shifted grids is used similarly to that described in [12]. A uniform grid is introduced for the variable x: +1, h = a/n. The distribution densities of populations at the node x_r are further denoted by u_r and v_r. To calculate flows q_i, a shifted grid is used: x_r + 1/2 = –h/2 + rh, r = 1, 2, …, n.

In terms of spatial variables, a first-order difference operator on a two-point template and an average calculation operator are introduced:

$${{(d\omega )}_{{r + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} = \frac{{{{\omega }_{{r + 1}}} - {{\omega }_{r}}}}{h},\,\,\,\,{{(\delta \omega )}_{{r + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} = \frac{{{{\omega }_{{r + 1}}} + {{\omega }_{r}}}}{2}.$$

As a result of the approximation of equations (1), (2) based on the integro-interpolation method [13], the following system of ordinary differential equations is obtained:

$$\frac{{\partial {{u}_{r}}}}{{\partial t}} = {{\left[ { - d{{q}_{1}} + {{\eta }_{1}}{{u}_{r}}{{f}_{0}}} \right]}_{r}},$$

(5)

$$\frac{{\partial {{{v}}_{r}}}}{{\partial t}} = {{\left[ { - d{{q}_{2}} + {{\eta }_{2}}{{{v}}_{r}}{{f}_{0}}} \right]}_{r}},\,\,\,\,r = 0,...,n,$$

(6)

$${{f}_{{0,r}}} = 1 - \frac{{{{u}_{r}} + {{{v}}_{r}}}}{{{{P}_{r}}}},\,\,\,\,{{P}_{r}} = {{\left[ {\frac{1}{h}\int\limits_{{{x}_{{r - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}^{{{x}_{{r + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} {\frac{{dxdy}}{{p(x)}}} } \right]}^{{ - 1}}}.$$

(7)

Flows q_i, r–1/2 (r = 1, …, n) are calculated from the following formulas:

$$\begin{gathered} {{({{q}_{1}})}_{{r - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} = {{\left[ { - {{k}_{1}}du + {{\alpha }_{1}}dp\delta u} \right]}_{{r - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}, \\ {{({{q}_{2}})}_{{r - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} = {{\left[ { - {{k}_{2}}du + {{\alpha }_{2}}dp\delta u} \right]}_{{r - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}. \\ \end{gathered} $$

(8)

Discrete analogues of the boundary conditions are made with the use of contour nodes:

$${{q}_{{i, - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} = {{q}_{{i,{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}};\,\,\,\,{{q}_{{i,n + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} = {{q}_{{i,n - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},\,\,\,\,i = 1,2.$$

(9)

Equation (4) yields the initial conditions for expressions (5)–(9):

$${{u}_{r}} = {{u}^{0}}({{x}_{r}}),\,\,\,\,{{{v}}_{r}} = {{{v}}^{0}}({{x}_{r}}).$$

(10)

COSYMMETRY AND MULTISTABILITY

The Gause principle [14] states that stable coexistence of two populations is impossible if growth is limited to one vital resource. However, it was shown in [11] that, under certain relations for the parameters of system (1)–(4), there is a strong nonuniqueness of solutions of coexisting species.

In this case, the model itself belongs to the class of cosymmetric dynamical systems [15], for which continuous families of stationary states may arise. For an equation $\dot {Y} = F(Y)$, cosymmetry L is a nontrivial operator that is orthogonal to F at every point in the phase space [16]. It was proved in [11] that a vector function

$$L = M{{(\gamma {v}, - u)}^{T}},\,\,\,\,M = \exp ({{ - {{a}_{2}}p} \mathord{\left/ {\vphantom {{ - {{a}_{2}}p} {{{k}_{2}}}}} \right. \kern-0em} {{{k}_{2}}}})$$

will be a cosymmetry of system (1)–(4) if the following relations on the parameters are satisfied:

$$\frac{{{{k}_{2}}}}{{{{k}_{1}}}} = \frac{{{{\alpha }_{2}}}}{{{{\alpha }_{1}}}} = \frac{{{{\eta }_{2}}}}{{{{\eta }_{1}}}} = \gamma .$$

(11)

In this case, the problem has a continuum family of stable stationary solutions, which can be parametrized as follows:

$$u = (1 - \theta )w,\,\,\,\,{v} = \theta w,\,\,\,\,\theta \in [0,1],$$

(12)

where w is the solution of the boundary value problem

$$\begin{gathered} 0 = [{{k}_{2}}w'\,\, - {{\alpha }_{2}}wp']' + {{\eta }_{2}}w\left( {1 - \frac{w}{p}} \right), \\ {{k}_{2}}w'\,\, - {{\left. {{{\alpha }_{2}}wp'} \right|}_{{x = 0,a}}} = 0. \\ \end{gathered} $$

(13)

This fact is established by substituting expressions (12) into the original system of equations (1)–(3) taking into account relations (11) and (13). At the same time, each member of the cosymmetric family, characterized by an individual ratio of species densities in the range, has its own area of initial data, from which this solution is implemented.

The fulfillment of all conditions (11) is a rather rare occurrence in modeling real processes. This means an ideal situation of coexistence of species in any of their combinations. An analysis of the conditions under which family breakup occurs allows a better understanding of the dynamics of the system. For this, an approach based on the theory of a cosymmetric defect and the concept of a selective function is used [15]. For a differential equation Y = F(Y) + Q(Y, ε) in a Hilbert space H, the cosymmetric defect is defined by the formula S(Y) = –(Q(Y, ε)), L(Y)), where L is the cosymmetry of the vector field F, and Q(Y, ε) is a perturbation of the system, and Q(Y, ε) = 0. The selective equation on the family Y(θ) ∈ [0, 1] is given by the equality S(Y(θ)) = 0 and automatically holds for ε = 0.

Hypothesis. For system (1)–(4), there are sets of parameters that do not satisfy the cosymmetry conditions (11), at which multistability is observed.

To analyze this assumption, a computational experiment and an approach based on [15] are used. Two perturbation parameters are used: population growth and migration coefficients v, violating conditions (11):

$$\eta _{2}^{*} = \gamma {{\eta }_{1}} + \varepsilon ,\,\,\,\,\alpha _{2}^{*} = \gamma {{\alpha }_{1}} + \delta .$$

(14)

The asterisks denote the parameters considering perturbations. The cosymmetric defect is then given by the formula

$$\begin{gathered} D = \int\limits_\Omega {\left( {\left( { - \frac{{\partial {{q}_{1}}}}{{\partial x}} + {{\eta }_{1}}u{{f}_{0}}} \right)M\gamma {v} - \left( { - \frac{{\partial q_{2}^{*}}}{{\partial x}} + \eta _{2}^{*}uf} \right)Mu} \right)dx} , \\ q_{2}^{*} = {{k}_{2}}\frac{{\partial {v}}}{{\partial x}} + \alpha _{2}^{*}{v}\frac{{\partial p}}{{\partial x}}. \\ \end{gathered} $$

As a result of integration by parts and taking the boundary conditions into account, the defect D is written as:

$$D = \int\limits_\Omega {\left[ {({{k}_{1}}u'\,\, - {{\alpha }_{1}}up')\gamma (M{\kern 1pt} '{v}\,\, + M{v}{\kern 1pt} ') + {{\eta }_{1}}uM{v}\gamma {{f}_{0}} + ({{k}_{2}}{v}{\kern 1pt} '\,\, - \alpha _{2}^{*}{v}p{\kern 1pt} ')(M{\kern 1pt} '{\kern 1pt} u + Mu{\kern 1pt} ') - \eta _{2}^{*}Mu{v}{{f}_{0}}} \right]} dx.$$

(15)

Taking into account the conditions on the coefficients (11),

$$D = \int\limits_\Omega {\left[ {\delta {v}p'\left( {\frac{{{{\alpha }_{2}}p{\kern 1pt} '{\kern 1pt} u}}{{{{k}_{2}}}} - u{\kern 1pt} '} \right) - \varepsilon u{v}{{f}_{0}}} \right]} Mdx.$$

(16)

After substituting the parametrized family of solutions (12), we obtain a selective function depending on the parameters ε and δ:

$$\begin{gathered} S\left( \theta \right) = \theta (1 - \theta ) \\ \times \,\,\int\limits_\Omega {M\left[ {\delta wp{\kern 1pt} '\left( {\frac{{{{\alpha }_{2}}p{\kern 1pt} 'w}}{{{{k}_{2}}}} - w{\kern 1pt} '} \right) - \varepsilon {{w}^{2}}\left( {1 - \frac{w}{p}} \right)} \right]} dx. \\ \end{gathered} $$

(17)

The zeros of the selective function are θ = 0 and θ = 1, corresponding to the survival of one of the populations. If the parameters ε and δ are related by the relation δ = με, then a selective function with one parameter ε is obtained. Then, for ε = 0, we also obtain S(θ) = 0. Formally, the vanishing of function (17) corresponds to the transformation into a new family of solutions, at least for

$$\begin{gathered} {{\left. {\frac{{d\varepsilon }}{{d\delta }}} \right|}_{{\delta = 0}}} = I = \frac{{{{I}_{1}}}}{{{{I}_{2}}}}, \\ {{I}_{1}} = \int\limits_\Omega {M\left( {\frac{{{{\alpha }_{2}}}}{{{{k}_{2}}}}{{w}^{2}}{{p}^{{'2}}} - ww{\kern 1pt} '{\kern 1pt} p{\kern 1pt} '} \right)} dx, \\ {{I}_{2}} = \int\limits_\Omega {M{{w}^{2}}\left( {1 - \frac{w}{p}} \right)} dx. \\ \end{gathered} $$

(18)

In computational experiments, it was found that there are sets of values of ε and δ $\left( {\alpha _{2}^{*},\eta _{2}^{*}} \right)$ for which distributions of coexisting populations are realized.

THE RESULTS OF THE COMPUTATIONAL EXPERIMENT

Below are the results of calculations of population dynamics in the range Ω = [0, 2], (a = 2).

Calculations were carried out for different values of migration parameters α₁ and α₂, growth coefficient η₂, and for the following fixed parameters: diffusion coefficients k₁ = 0.03, k₂ = 0.04, and growth coefficients η₁ = 3. Thus, in relation (11) γ = k₁/k₂ = 3/4, and the resource function is given by the formula corresponding to the case of an area with one favorable zone:

$$p(x) = 3{{\left[ {\sin \frac{{\pi x}}{a}} \right]}^{3}} + 0.1.$$

The initial distribution of the population u (resident) corresponds to the complete filling of the ecological niche in the absence of directed migration (α₁ = 0) and in its presence (α₁ = 0.06), see Fig. 1. It was shown in [17] that migration caused by the unevenness of the resource affects the occupancy of the area, and it was established that there is an optimal value of the migration parameter, at which the highest density is observed in the area. The initial distributions of population v (invader) were localized and differed in the invasion concentration:

$$\begin{gathered} {v}_{1}^{0}(x) = \left\{ \begin{gathered} 0.6\sin \frac{{2\pi }}{a}x,\,\,\,\,x \in {{\Omega }_{0}}, \hfill \\ 0,\,\,\,\,x \in \Omega {\kern 1pt} \backslash {\kern 1pt} {{\Omega }_{0}},\,\,\,\,{{\Omega }_{0}} = [0.66;1.66]; \hfill \\ \end{gathered} \right. \\ {v}_{2}^{0}(x) = \left\{ \begin{gathered} \sin \frac{{2\pi }}{a}x,\,\,\,\,x \in {{\Omega }_{0}}, \hfill \\ 0,\,\,\,\,x \in \Omega {\kern 1pt} \backslash {\kern 1pt} {{\Omega }_{0}}. \hfill \\ \end{gathered} \right. \\ \end{gathered} $$

(19)

Fig. 1.

The initial distributions of u at α₁ = 0 (curve 1) and α₁ = 0.06 (curve 2); initial distributions v (curves 3 and 4); resource function (curve 5).

It is worth noting that for any combination of initial distributions u and v, the inequality is satisfied $\int_\Omega {pdx} \leqslant \int_\Omega {{{u}^{0}}dx} + \int_\Omega {{{{v}}^{0}}dx}$. This leads to competition between species at the initial stage of the dynamic process.

Figure 2 shows maps of parameters α₁ and α₂ with zones corresponding to the coexistence of species (III) and the survival of one of the populations (I and II). The dotted line in Fig. 2a shows the boundaries of the zones according to the results of calculations at η₂ = 4, and straight line 1 (α₂ = γα₁) corresponds to the existence of a cosymmetric family of equilibria (12), whose members are stationary distributions of each type and their various combinations.

Fig. 2.

A map of migration parameters α₁ and α₂ with areas corresponding to the coexistence of species (III) and the survival of the population u (I) or v (II) at η₂ = 4.0 and 4.5 (a); at η₂ = 1.0 (b).

In the case of cosymmetry, the coexistence of species is observed, and the stability spectrum for the final stationary distributions has almost zero eigenvalues.

The remaining eigenvalues are in the left half-plane, which means stability in the transversal direction to the family.

Figure 2a also shows the results of calculations for the growth factor η₂ = 4.5, which does not satisfy relations (11). In this case, there is a shift in the line corresponding to the existence of a family of stationary distributions (straight line 2). The stability spectrum of these solutions contains practically zero eigenvalues (σ ≈ 10^–6). This fact demonstrates the validity of the hypothesis formulated in the Cosymmetry and multistability section.

Formula (18) gives a good estimate for determining the perturbation parameters ε and δ (see formula (14)). For example, for given k₁ = 0.03, η₁ = 3, γ = 3/4, and α₁ = 0.06, a numerical solution of problem (13) was found, integrals (18) were calculated using quadrature formulas, and ${{I}_{*}}$ ≈ 90.7 was obtained.

In computational experiments with system (1)–(4) at α₁ = 0.06, multistability was obtained for $\eta _{2}^{*}$ = 4.5 and $\alpha _{2}^{*}$ = 0.08536.

Thus, the perturbation parameters turned out to be ε = 0.5 and δ = 0.00536, and their ratio was δ/ε ≈ 93.5, which is close to ${{I}_{*}}$

Calculations have shown that an increase in η₂ compared to the value that satisfies relations (11) gives an expansion of regions II at the expense of regions I. This means that the provider has more opportunities to compete with the resident. It should be noted that lines 1 and 2 in Fig. 2a intersect at the point (${{\hat {\alpha }}_{1}},{{\hat {\alpha }}_{2}}$) where the areas corresponding to different population distribution scenarios touch.

Figure 2b shows a map of migration parameters corresponding to the case η₂ = 1. It can be seen that a sufficiently large deviation of η₂ from the value η₂ = 4 corresponding to condition (11) leads to a deformation of the structure of areas for different modes of population survival. In this case, an area of coexistence of species appears between zones I and II (zone III).

Various invasion scenarios are shown in Fig. 3. The calculations were carried out for the sets of parameters corresponding to points A and B in Figs. 2a, the resident had no resource-directed migration (α₁ = 0). The dynamics of displacement of the aborigine population is given in Fig. 3a, while Fig. 3b illustrates the species coexistence scenario. At a low value of the invader migration coefficient (α₂ = 0.02), the resident is displaced, and when it increases (α₂ = 0.08), the range is divided: the invader concentrates in a favorable zone, displacing the resident to the borders of the range.

Fig. 3.

The establishment of stationary distributions α₂ = 0.02 (a) and α₂ = 0.08 (b); α₁ = 0, η₂ = 4.0.

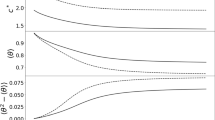
Figure 4 shows the trajectories of establishment to stable stationary states (points A, B, C₁, C₂, D₁, D₂) from various initial distributions marked in Fig. 1. The curves are given on the plane of standard deviations of distributions σu and σv:

$$\begin{gathered} \bar {u} = \frac{1}{{(n + 2)}}\sum\limits_{r = 0}^{n + 1} {\{ {{u}_{r}},{{{v}}_{r}}\} } , \\ \sigma u = \sqrt {\frac{1}{{(n + 2)}}\sum\limits_{r = 0}^{n + 1} {{{{({{u}_{r}} - \bar {u})}}^{2}}} } . \\ \end{gathered} $$

Fig. 4.

The establishment of equilibria (A, B, C_j, D_j) from initial distributions (S_j, Q_j) for different α₁ and α₂ (see Table 1 and Fig. 1); lines 1 and 2 correspond, respectively, to families of equilibria at α₁ = α₂ = 0 and α₁ = 0.06, α₂ = 0.08; η₂ = 4.0.

Figure 4 shows the possible strategies of the invader depending on the value of the migration parameter of the resident α₁. For α₁ = 0 and α₂ = 0, η₂ = 4, the cosymmetric relation for the parameters of system (11) is satisfied. In this case, stationary solutions corresponding to the coexistence of populations (points C₁, C₂) are realized from various initial distributions (points S₁, S₂). These solutions are included in the continuous family of stationary states (line 1 in Fig. 4). The calculations show that in the absence of directed migration in an resident, the invader can use a strategy based on choosing an appropriate taxis coefficient α₂. In this case, both the displacement of the resident (point A in Fig. 4) and the solution corresponding to the coexistence of species (point B in Fig. 4) are possible. We note that the initial distribution affects the trajectory of the establishment to the final state.

A cosymmetric family of stationary distributions of coexisting populations also arises for α₁, α₂ ≠ 0. Line 2  in Fig. 4 corresponds to a family of stationary states under conditions (11) for the following parameter values: α₁ = 0.06, α₂ = 0.08, η₂ = 4. In this case, due to a nonzero taxis (α₁ = 0.06), the density of the resident is redistributed (see Fig. 1), which leads to a shift in the initial data (points Q₁, Q₂). As a result of the establishment of equilibria, distributions of coexisting populations of resident and invader are obtained.

Both in the absence of taxis and when it is taken into account, the density of the invader distribution depends on the density at the initial moment of time.

Figure 5 shows the dynamics of populations from different initial data (see Table 1 and Fig. 1) for two sets of parameters: α₁ = 0, α₂ = 0.0029, η₂ = 3.5 and α₁ = 0.06, α₂ = 0.0746, η₂ = 3.5. These parameter values were obtained in the course of a computational experiment and are close to the values corresponding to relations (18), but violate conditions (11). For both sets of parameters, from different initial states, stable population distributions are obtained, similar to those displayed in Fig. 4. The presence of almost zero eigenvalues (σ ≈ 10^–6) in the stability spectrum of these solutions indicates multistability—the coexistence of species and the success of invasion. Table 2 shows the elements of the stability spectrum of these final states closest to the imaginary axis.

Fig. 5.

Equilibrium establishment C_j (D_j) from initial distributions S_j (Q_j) at α₁ = 0, α₂ = 0.0029 and α₁ = 0.06, α₂ = 0.0746; lines 1 and 2 correspond to families of equilibria (see Fig. 4); η₂ = 3.5.

Table 1. Migration parameters and evolution from initial distributions (points S_j, Q_j in Fig. 4) to final ones (points A, B, C_j, D_j)

Table 2. The main elements of the spectrum of stability of stationary distributions

Figure 6 shows the time evolution of population distribution profiles corresponding to the Q₂D₂ trajectory in Fig. 5. It can be seen that at the beginning of the establishment of equilibrium there is a sharp decline in the density of the aboriginal population due to the appearance of an invader; a smooth transition to a stationary solution then occurs.

Fig. 6.

The spatio-temporal evolution of population densities corresponding to the Q₂D₂ trajectory in Fig. 5.

CONCLUSIONS

The interaction of two populations was considered on the basis of a system of nonlinear parabolic equations that take diffusion, taxis (directed migration) and logistic growth into account. Maps of migration parameters have been constructed that describe various scenarios of competition under conditions of biological invasion. Using the apparatus of the theory of cosymmetry and numerical-analytical studies, it was shown that, in comparison with [11, 12], the formation of a continuous family of coexisting populations (multistability) is possible for a larger set of parametric dependencies. The method described in this paper allows one to specify combinations of parameters for successful invasion. This approach can be used to study the phenomenon of multistability in nonlinear multiparameter problems of mathematical biology [18]. These results will improve the methods of analysis of invasion and its consequences.