1 Introduction

Traumatic brain injury (TBI) is a common pathology and a major health problem worldwide. Each year, an average of 1.4 million cases of TBI are reported in the USA [1]. TBI may happen due to the sudden movement of the head, impact, shock waves due to a blast, and generally any mechanical load applied to the head. State of the art research suggests that the primary reason for TBI is the deformation and mechanical strain happening in the brain [2]. Common symptoms associated with TBI include dizziness, headaches, and loss of memory which studies have shown that diffuse axonal injury (DAI) is its primary cause [3]. DAI which is characterized by the formation of contusions and lesions in the brain white matter happens due to the shear deformation of axons in brain white matter. Corpus callosum and corona radiata are parts of the brain white matter which are known to be commonly affected by the DAI [4]. Understanding the extent of DAI severity and its mechanism can be helpful in preventing such a pathology.

Due to the infeasibility and risks associated with experimental tests, computational techniques are suitable procedures for the simulation of the incidents leading to TBI. In this respect, different scenarios such as coup and contrecoup injuries in impact-induced TBIs [5, 6], ballistic impacts [7,8,9], and blast-induced injury [10,11,12] have been simulated through numerical modeling to find the stress and strain distribution of the brain at the moment of the incident. Different factors and parameters lend help to make those simulations more accurate among which, geometrical model exactness, inclusion of different organs of the head and brain in the model, and choice of material properties can be mentioned. As such, extensive efforts have been made to characterize the brain tissue properties and biomedical materials in general [13,14,15,16,17,18]. Brain tissue is an ultra-soft, strain rate sensitive material which shows a nonlinear behavior under loading. Hyperelastic models have been used in numerous studies to model such a behavior. Mihai et al. [19] introduced several hyperelastic models for brain tissue modeling. They focused on development of an appropriate strain energy function that can predict behavior of human brain tissue in mixed loadings of shear, compression, and tension. They found that Ogden model provides a better solution compared to other hyperelastic models such as Mooney-Rivlin, Neo-Hookean, Gent, and Fung in the case of multiaxial loading. Budday et al. [20] tested the human brain tissue in tension, compression, and shear and the mechanical response of the tissue was fitted with several hyperelastic constitutive models. They found that the material property parameters for a specific loading mode cannot be used for other loading modes. In order to obtain one set of material property parameters to be used for general loading cases, they calibrated the material properties for being used in all the three mentioned loading modes. They also found that the Ogden model outperforms other hyperelastic models in describing the mechanical behavior of brain in all three loading modes by one set of parameters. Another category of commonly used technique for brain tissue characterization is the indentation test. Feng et al. and Qiu et al. [21, 22] used this test for characterization of injured brain tissue using elastic and viscoelastic constitutive models respectively. Budday et al. [23] performed long-range and short-range flat punch indentation tests on different parts of the bovine brain tissue. They found out that the white matter was approximately 40% stiffer compared to gray matter. Feng et al. [24] used inverse finite element modeling in conjunction with experimental asymmetrical indentation tests to find the hyperelastic transversely isotropic parameters of the porcine brain white matter under large strain deformation. Moreover, by performing the indentation tests parallel and perpendicular to the brain axonal fiber direction, the orientational dependency of the material parameters were investigated as well.

The study of TBI is usually associated with evaluating the dynamic response of the brain. Brain as a soft material shows a time-dependent behavior where hyperelastic models are not able to capture it. The time-varying stiffness of the solids and specifically soft materials are referred to as viscosity and should be addressed in studying the dynamic behavior of the brain. Hosseini-Farid et al. [25] investigated the dynamic response of brain tissue by measuring the instantaneous and equilibrium response of the brain tissue in different strain rates. The instantaneous response was calculated using quasi-linear viscoelasticity theory and the equilibrium response was measured through equilibrium stress evaluation. Rashid et al. [26] performed relaxation compression tests on brain in different strain rates with the strain values of 0.3 and characterized its response by using hyper-viscoelastic model. The Ogden-based hyper-viscoelastic model which its relaxation time-dependent part is based on Prony series expansion was used for this purpose. The strain energy function was derived in the form of convolution integral. Hyper-viscoelastic models have also been proposed for describing the behavior of other soft biological tissues such as ligaments [27].

Micromechanical analysis has been used to find the mechanical response of the brain white matter and its constituents. The studies in this area were inspired by the micromechanical study of composite materials [28, 29]. Abolfathi et al. [30] found the linear anisotropic properties of brain white matter through micromechanical analysis. A viscoelastic constitutive model which is appropriate for small deformation was used with Prony series expansion to account for time-dependent properties of both axons and extracellular matrix (ECM) as the constituents of the brain white matter. To obtain all the anisotropic coefficients of the linear viscoelastic model, six different simulations including three uniaxial tensile loading in three different direction and three simple shear tests were performed by the means of finite element simulations. In their study, the material properties of axons and ECM were obtained from another published paper [31]. Moreover, the effects of axons undulation and volume fraction on the overall properties of brainstem were studied as well. Nonlinear modeling of brain white matter was the target of a study in the paper of Karami et al. [32]. Using the mechanical properties of axons and ECM from [33], the mechanical response of brain white matter was found for large deformation cases by the assumption of isotropic behavior of brain white matter.

The aforementioned studies in the area of the micromechanical analysis were aimed at finding the mechanical response of the homogenous brain white matter by knowing the mechanical properties of heterogeneous representative volume element (RVE) consisted of the constituents. However, the availability of the experimental data to calculate the properties of micro-level constituents is a point of challenge since experimental techniques such as nano-indentation [34] and atomic force microscopy (AFM) [35] can be quite complex and laborious in terms of design of experiments and sample preparation for soft biological tissues. On the contrary, the macro-level tests such as uniaxial loading tests can be done with much lower cost and with higher availability and accessibility. Therefore, several studies were aimed at finding the mechanical properties of brain white matter micro-level constituents (including axons and ECM) by using the experimental data from macro-level tests performed on brain white matter. Javid et al. [36] tried to find the mechanical properties of axons and ECM of the porcine brainstem through relaxation tensile tests for up to 5% of deformation. The viscoelastic constitutive model was used for both axons and ECM in micromechanical simulations. Applying the averaging technique for homogenization, they minimized the difference between micromechanical simulations and experimental results through conducting iterative finite element simulations. Moreover, the effect of different types of RVE including hexagonal, square, and randomly distributed were studied as well. The obtained results showed good agreements between micromechanical simulation and experimental data. While the viscoelastic model can only be used in the cases associated with small deformation, it still captures the time-dependent response of the brain. Yousefsani et al. [37] used an embedded element technique to perform transverse-plane hyperelastic micromechanical simulation of brain white matter. The RVE used in their study was formed by probabilistic distribution of axons embedded in ECM. Directional dependency was observed in transverse plane loading mode.

2 Materials and methods

2.1 Material constitutive modeling

The Ogden hyperelastic model has been extensively used for describing the behavior of rubber-like materials and soft tissues including brain. The Ogden strain energy function can be written as the following:

$$ {W}_{\mathrm{Ogden}}=\sum \limits_{i=1}^N\frac{2{\mu}_{0i}}{\alpha_i^2}\left({\lambda}_1^{\alpha_i}+{\lambda}_2^{\alpha_i}+{\lambda}_3^{\alpha_i}-3\right) $$
(1)

where λ1, λ2, and λ3 denote the principal stretch values, μ0i and αi are the Ogden model parameters with the μ0 known as the initial shear modulus, and N is the number of terms used in the Ogden model. As expected, increasing the number of terms N in the Ogden model will consequently increase the accuracy of curve fitting to the experimental data. However, as demonstrated in various studies, using one term will be sufficient most of the time, which is the case in our study as well.

Relaxation test is one of the most common types of tests used for characterizing the time-dependent behavior of soft materials [38,39,40]. Soft materials such as brain exhibit time-varying stiffness when being held under specific deformation for a period of time. As brain is subjected to constant deformation, the induced stress value drops over time. As a result, a time-dependent model is required to express such a behavior. Miller et al. [41] proposed the following strain energy function for soft biological tissues. While this strain energy function was originally used to describe the behavior of brain tissue in tension, there is no inherent loading mode specific constraint involved and it has been utilized successfully for the compression mode as well [26, 42].

$$ W=\frac{2}{\alpha^2}\underset{0}{\overset{t}{\int }}\left[\mu \left(t-\tau \right)\frac{d}{d\tau}\left({\lambda}_1^{\alpha }+{\lambda}_2^{\alpha }+{\lambda}_3^{\alpha }-3\right)\ \right] d\tau $$
(2)

As stated in Eq. (2), convolution integral is employed for formulation of the strain energy function. The term μ which represents the relaxed shear modulus, is calculated based on the following equation:

$$ \mu ={\mu}_0\left[1-\sum \limits_{i=1}^n{g}_i\Big(1-\exp \left(-\frac{t}{\tau_i}\right)\right] $$
(3)

where μ0 is the instantaneous shear modulus, gi is the relaxation coefficient, t denotes the time, and τi is the characteristic time coefficient. n is the number of terms utilized in the Prony series expansion and usually two terms (n = 2) can provide a good approximation.

2.2 Micromechanical modeling

Micromechanical modeling studies the materials at the scale of their constituents by using a heterogeneous RVE, hence, providing an insight into stress and strain distribution at the micro-level. The key idea behind micromechanical modeling is to find the heterogeneous RVE that can represent the whole structure of macro-level homogenous material. The concept of the micromechanical modeling has been tested in the analysis of composite materials [43,44,45,46,47]. Brain white matter has a fibrous structure with the axons highly oriented and dispersed in the ECM material. The axons stem surrounded by myelin, also known as nerve fibers, are highly oriented. Therefore, attempts have been made to model the brain white matter as a fibrous composite structure. From one point of view, the research in this area can be divided into two separate categories. One contains the studies that are aimed at finding the material properties of brain white matter when the properties of its constituents are known [30, 32]. Second category includes those studies conducted to find properties of brain white matter constituents from known response and mechanical properties of the brain white matter [36, 48] through macro tests.

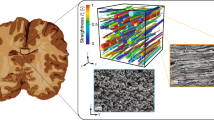
The first step toward micromechanical analysis is to identify the appropriate RVE. This is usually done through microscopic images of materials, which shows the micro-level structure, the volume fraction of each constituent, and geometrical shape of them. The scanning electron microscopy (SEM) images of porcine brainstem [36] and histology slide of guinea pig optic nerve [33] can be seen in Fig. 1 a and b. These figures can be used for estimating the volume fraction of axons and verifying their orientation in the matrix. As it can be seen in Fig. 1a, the axons vary in diameter size, and show random distribution. While it seems that the most realistic representation of RVE can be created by considering this randomness, different independent studies [36, 48] confirmed that simplified representation of RVE with uniform diameter of axons and organized dispersion structure can lead to results just as accurate as the more complicated randomly dispersed RVE. Moreover, using random RVE has its own challenges, since the meshing in RVE must be completely symmetrical with respect to all coordinate axis, which would be almost impossible for random RVEs. In this study, we use the square RVE as shown in Fig. 1c. To make representation of a whole brain white matter possible, certain equations need to be applied on the meshed RVE. These equations that ensure the repetition of RVE in all directions are known as the periodic boundary conditions (PBC) and must be applied as constraints to the meshed RVE in the finite element simulations, for which the readers are referred to [14, 28].

Fig. 1
figure 1

The overview of tissues with nerve fibers structure. a Porcine brain stem scanning electron microscopy (SEM) showing dispersion of axons in ECM [36]. b Immunohistochemistry of the guinea pig optic nerve [33]. c The square RVE for representing the patterned structure of brain white matter and other tissues with oriented dispersion of axons and nerve fibers

Full size image

As mentioned, applying PBC makes RVE to repeat and extend itself in all directions, thus the RVE represents a small point in macro-sized material and this is the key idea behind the micromechanical analysis. The RVE can then be used in different finite element simulations of interest including relaxation test which is used in this study. For homogenization purposes, the macro-level stress and strain will be found by volume averaging of the micro-level stress and strain fields over the RVE, based on the following equations:

$$ \overline{\sigma}=\frac{1}{V}\sum \limits_{i=1}^m{\sigma}_i{v}_i\kern4em \overline{\varepsilon}=\frac{1}{V}\sum \limits_{i=1}^m{\varepsilon}_i{v}_i $$
(4)

where σi, εi, and vi denote the stress, strain, and volume of the ith element of the meshed RVE respectively, and V the is total volume of the RVE.

2.3 A framework for the simulation-based optimization

Time-dependent characterization of human brain white matter has been performed for different parts of the brain [49]. However, there is no similar experimental data for dynamic behavior of micro-level constituents of brain white matter. By the use of derivative-free optimization methods in the context of micromechanical finite element modeling, we aim to find the visco-hyperelastic properties of axons and ECM. The key idea is the fact that if right material properties are chosen for those constituents, the overall response of brain white matter obtained from micromechanical finite element modeling will be close to that of the experimental relaxation tests. To this end, an iterative optimization framework must be defined which changes the material properties of constituents until the desired results will be obtained. The schematic representation of the optimization framework is shown in Fig. 2.

Fig. 2
figure 2

The flowchart of the optimization framework for finding the parameters of brain white matter constituents

Full size image

In Fig. 2, J(p) is the objective (cost) function which is dependent to the parameters of the visco-hyperelastic model including μ, gi, and τi introduced in Eq. (3). These parameters must be separately assigned to both constituents of the brain white matter. Therefore, the number of parameters in the constitutive model doubles up in the objective function to account for the material properties of both axon and ECM. Consequently, the following cost function is defined to perform the optimization procedure in the context of iterative finite element simulation.

$$ J(p)=\underset{t_1=0}{\overset{t_2=500}{\int }}{\left[{\sigma}_{FE}\left(p,t\right)-{\sigma}_{exp}(t)\right]}^2 dt $$
(5)

in which J denotes the cost function, σFE represents the averaged stress values obtained from the numerical micromechanical finite element simulation, t is the time, p represents the independent variables on which the cost function (and hence, numerical simulated stress) is dependent on (listed in Table 1), and σexp denotes the experimental stress corresponding to the data presented in Figs. 3 and 4 in the subsequent section of this paper.

Table 1 List of the arguments p in the cost function defined in Eq. (5) which correspond to the constitutive model described in Eqs. (1) to (3)
Full size table
Fig. 3
figure 3

The ramp part of the relaxation test at different strain rates of 0.0001, 0.01, and 1 s−1 obtained from [42]. As can be seen, the stiffness of the tissue increases with the increase in the strain rate value

Full size image
Fig. 4
figure 4

The compression relaxation test data of Forte et al. [42] at the stretch value of λ = 0.7. The relaxation test is done by holding the sample for 500 s. The points in the original paper are digitized through image processing techniques

Full size image

As listed in Table 1, total number of 12 variables control the finite element obtained stress values which consequently, the cost function will be dependent on. Moreover, the following constraints must be held between the variables for both axons and ECM.

$$ {g}_1+{g}_2<1 $$
(6)
$$ {\tau}_1-{\tau}_2<0 $$
(7)

Different derivative-free optimization algorithms can be used for the proposed optimization framework in Fig. 2 [50,51,52]. In this study, we will use the particle swarm optimization (PSO) algorithm. The PSO algorithm is widely used for black box optimization problems where the function of interest is not explicitly stated in terms of its independent variable or when the function is time-consuming to be evaluated. PSO algorithm was originally introduced by Kennedy and Eberehart [53]. In PSO, several particles are randomly placed in the search domain of the objective function. The search domain is n-dimensional space where n denotes the number of variables associated with the objective function. For the initial iteration, each particle will be randomly located in the search space and objective function will be evaluated at those points. In the next iterations, the particles will displace themselves in the search domain by using the information from the history of their own and the communicative information acquired from other particles in the swarm. This process continues until the whole swarm is converged, i.e., gets very close to a specific point in the search domain. This point is the optimum solution to the objective function. The swarm particles update their trajectory based on the following equations:

$$ {\overrightarrow{v}}_i^{k+1}={\overrightarrow{v}}_i^k+{c}_1{r}_1\left({\overrightarrow{x}}_{\ast i}^k-{\overrightarrow{x}}_i^k\right)+{c}_2{r}_2\left({\overrightarrow{x}}_g^k-{\overrightarrow{x}}_i^k\right) $$
(8)
$$ {\overrightarrow{x}}_i^{k+1}={\overrightarrow{x}}_i^k+{v}_i^{k+1} $$
(9)

In the above equations, k denotes the iteration number, \( {\overrightarrow{v}}_i^k \) represents the velocity of the ith particle, \( {\overrightarrow{x}}_g^k \)is the global best location experienced by the whole swarm in the kth iteration, \( {\overrightarrow{x}}_{\ast i}^k \) denotes the best location experienced by the ith particle up to the kth iteration, r1 and r2 are uniform random numbers, and finally c1 and c2 are constant coefficients which can be adjusted from problem to problem. Commonly, c1 = c2 = 2.05 is employed in this implementation of PSO. The second and third terms on the right-hand side of Eq. (8) qualifies the cognitive and social behavior of particles in their search process and therefore, the choice of c1 and c2 affects the weights of these terms in evolution of particles and balances the self-learning and swarm-learning effects. Usually, boundaries can be set up for the search space domain, and therefore, the velocity quantity must be bounded as well. Restricting the velocity of particles, however, can slow down the process of convergence, but it helps to avoid the divergence of particles. It should be noted that while mostly in the literature and particle swarm optimization terminology, the term \( {\overrightarrow{v}}_i \) is referred to as the velocity of the particles, in fact, it corresponds to the displacement of a particle in the two consecutive iterations.

As can be speculated from Eq. (8), all the particles are learning from the swarm by moving toward the global best experienced location. Therefore, there is a probability that all or a majority of particles will be attracted to the global best point and get stuck in the local optimum of the objective function. Linearly decreasing weighted PSO balances the local and global search properties of the swarm by applying a decreasing weight on the velocity of the particles from previous iteration as stated in the following equations [54]:

$$ {\overrightarrow{v}}_i^{k+1}=\omega\ {\overrightarrow{v}}_i^k+{c}_1{r}_1\left({\overrightarrow{x}}_{\ast i}^k-{\overrightarrow{x}}_i^k\right)+{c}_2{r}_2\left({\overrightarrow{x}}_g^k-{\overrightarrow{x}}_i^k\right) $$
(10)
$$ \omega ={\omega}_{\mathrm{max}}-\left({\omega}_{\mathrm{max}}-{\omega}_{\mathrm{min}}\right)\frac{k}{k_{\mathrm{max}}} $$
(11)

where k denotes the current iteration number, kmax is the maximum number of iterations, and ωmax and ωmin are the upper and lower boundaries imposed on the ω which is the PSO velocity relaxation coefficients. In this study, the values of ωmax and ωmin was set to be 1.1 and 0.1, respectively. This way, the search procedure will be more inclined to global exploration in the initial iterations and more to the exploitation as the number of iterations increases.

It is worthy to mention that other derivative-free algorithms such as genetic algorithm or pattern search algorithm can be used for optimization process as well. However, the gradient-based optimization algorithms such as gradient descent may fail to provide a reasonable approximation since they can get stuck in the local minimum of the optimization problem [55]. The derivative-free optimization algorithms get around this problem and are more likely to find the global minimum. In this study, we stick to the PSO algorithm and will employ it in our optimization problem by imposing the constraints stated in Eqs. (6) and (7). For more details on how to configure PSO for imposing the constraints of the optimization problem, and on its modification for faster convergence, readers are referred to [55, 56].

3 Results

3.1 Micromechanical optimization of the constituent’s properties

The relaxation compression tests at different strain rates conducted in [42] were used as the input data for the optimization procedure. Based on [42], stress relaxation test on the brain white matter was performed by holding the sample at the compressive stretch value of λ = 0.7 (corresponding to the compressive strain value of 0.3) for the duration of 500 s. The finite element simulation of compression relaxation test was created in ABAQUS (ABAQUS Inc., Providence, RI) with the same deformation speed and relative sample size as that of the [42] by use of the meshed RVE introduced in previous sections. Figures 3 and 4 show the ramp and relaxation part of the relaxation tests performed by Forte et al. [42].

Using curve fitting techniques by the constrained particle swarm optimization (C-PSO) algorithm [55], the visco-hyperelastic material parameters of the brain white matter are found to be as presented in Table 2.

Table 2 Visco-hyperelastic material properties of brain white matter using the experimental data presented in Figs. 3 and 4
Full size table

Tables 3 and 4 list the obtained optimal material properties for axons and ECM after conducting the optimization framework using PSO method. These results are obtained by setting the volume fraction of axons in RVE, equal to 0.527 and the ratio of initial shear modulus of axon to the initial shear modulus of ECM equal to 3.0 (μ0axon/μ0ECM = 3.0). It should be noted that it is vital to impose the ratio of the initial shear modulus as a constraint into the optimization framework. Otherwise, the material properties of axon and ECM will be the same as the material properties of the brain white matter itself and the defined cost function stated in Eq. (5) will be exactly zero corresponding to its global minimum.

Table 3 The optimal material properties for axons with respect to the compression relaxation test
Full size table
Table 4 The optimal material properties for ECM with respect to the compression relaxation test
Full size table

Figure 5 demonstrates the averaged mechanical response of RVE in micromechanical finite element simulation using the acquired optimal material properties of axons, compared with the experimental data from the compressive relaxation test for three different deformation strain rates. As it can be seen, good agreement is observed which implies on the success of our proposed optimization framework. The cost function J has the value of 0.0248, 0.0359, and 0.0199 for three strain rates of 0.0001, 0.01, and 1 s−1, with the acquired optimal parameters and the coefficient of determination comparing the numerical micromechanical results with experimental result stand at high values of R2 = 99.59%, R2 = 99.14%, and R2 = 99.45% which again confirms the high accuracy of the resultant optimization process and micro-level constituents characterization of human brain white matter.

Fig. 5
figure 5

Comparison of the experimental results of relaxation test of corona radiata [49] and the obtained numerical results of micromechanical finite element simulation by using the acquired optimal parameters of axons and ECM presented in Table 3

Full size image

Figure 6 shows the relaxed stress of axons and ECM with respect to time. Since the obtained Prony series parameters of axon and ECM are close to each other, the overall pattern of Ogden shear modulus reduction for both materials seem to be nearly identical. Both axon and ECM experience more than 50% reduction in the shear modulus compared to the initial shear modulus expressed by Ogden constitutive model.

Fig. 6
figure 6

Relaxation stress of axon and ECM using the Ogden visco-hyperelastic constitutive model for different strain rates

Full size image

3.2 Strain rate dependency of the axons material properties

In this section, we are aimed at correlating the obtained material properties of axons with respect to the deformation strain rate. In Fig. 7, the obtained initial shear modulus of axons is depicted with respect to the strain rates of the compression tests. As represented in Fig. 7, if logarithmic scale is used for demonstration of strain rates values (), a linear relationship is observable between the strain rate and the axons initial shear modulus. In an attempt to predict the initial shear modulus of axons with respect to the strain rate, a linear regression is performed, and the predicted initial shear modulus of axons is also represented in Fig. 7 by a solid line. The prediction line can be stated by the following equation:

Fig. 7
figure 7

The obtained initial shear modulus of axons in different strain rates and the predicted initial shear modulus with respect to strain rate

Full size image
$$ {\mu}_0\left(\mathrm{kPa}\right)=0.1432\ln \left(\dot{\varepsilon}\right)+1.6432 $$
(12)

Moreover, finding the reduced shear modulus of axons can be of interest as well. Figure 8 shows the reduced shear modulus of axons at t = 5 s. The linear pattern seen for the initial shear modulus is not observable here anymore. The maximum reduced shear modulus after 5 s is seen for the strain rate of 0.01 s−1.

Fig. 8
figure 8

The obtained reduced shear modulus of axons at t = 5 s for different strain rate values and the corresponding first and second order regression for predicting the reduced shear modulus at intermediate strain rate values

Full size image

Equations (13) and (14) state the first- and second-order regression for predicting the reduced shear modulus of axons for the intermediate strain rate values respectively.

$$ {\mu}_5\left(\mathrm{kPa}\right)=0.0112\ln \left(\dot{\varepsilon}\right)+0.5381 $$
(13)
$$ {\mu}_5=-0.0053{\left(\ln \left(\dot{\varepsilon}\right)\right)}^2-0.0374\ln \left(\dot{\varepsilon}\right)+0.5008 $$
(14)

where μ5 stands for the reduced shear modulus (kPa) of axon at t = 5 s.

Figure 9 demonstrates several micromechanical finite element simulations with the obtained optimal parameters for the strain rate of 1 s−1, shown at different times of 1 s, 10 s, and 25 s. These simulations can provide us with a detailed understanding of the stress distribution at the micro-level. In this case, where the uniaxial compression relaxation test is performed, the stress is uniformly distributed in the axon and ECM, with the stress of axons being approximately 3 times greater than that of the ECM. This is true for the three shown instances, since the Prony series expansion parameters for both of the constituents are close to each other.

Fig. 9
figure 9

The micromechanical stress distribution in the RVE used for simulating human brain white matter in unconfined compression relaxation test at a t = 1 s, b t = 10s, and c t = 25 s

Full size image

4 Discussion

In order to bridge between the micromechanical simulations and the macro-level tests, and to plausibly find the micro-level constituents, the micromechanical simulation, and macro-level tests must be in high degree of resemblance to each other. One point that may raise concerns upon the validity of the micromechanical simulation is the orientational dependency of the brain white matter stiffness. Forte et al.’s paper [42], from which we obtained our experimental data, does not concern itself with the orientation of the axonal fibers in the brain white matter samples for the uniaxial tests and this seems to be a reasonable approximation and approach; since Budday et al. [20] performed uniaxial tests in different axonal fiber orientations and they posited that there is no statistically significant dependency between the shear modulus of axons and the axonal fiber orientation. Hence, in our study, we have performed the micromechanical simulation and uniaxial loading along the direction of the axonal nerves while using the macro-level compression test data from Forte et al. [42], on the premise of the conclusion asserted by Budday et al. [20], as explained. Moreover, the no-friction boundary condition of the uniaxial testing was considered in our micromechanical simulations as well.

There is a wide range of reported properties for axons in different biological tissues as can be found in the literature. The reported initial shear modulus of axons in guinea pig optic nerves, using the Ogden hyperelastic model by Meaney [33], was in the range of 0.28 to 0.29 kPa. The initial shear modulus of axons in porcine brain-stem under tensile test with the strain rate of 5.5 s−1 was found to be approximately 12.9 kPa, as reported by Javid et al. [36]. In this study, this value was found to be in the range of 0.4 to 1.7 kPa for axons of human brain white matter under compression. This variation may be originated from difference in tissues used for experimental tests, regional variation, load dependency, strain rate dependency, and the employed constitutive models. The degree of dependency of the axons shear modulus to the strain rate of deformation was found to be notable, showing 4.5 times increase as the strain rate rise from 0.0001 to 1.0 s−1.

The quality of the first- and second-order regression for approximating the initial and reduced shear modulus of axons is another point which deems to be worthy of discussion. Looking into Fig. 8, it can be elicited that the first-order regression with the independent variable of \( \ln \left(\dot{\varepsilon}\right) \), as reflected in Eq. (13), could not give a good approximation of reduced shear modulus of axons (at t = 5 s) for the intermediate range of strain rates. Alternatively, the second-order regression as stated in Eq. (14) can be used for approximating purposes; however, it should be noted that we should be cautious when using this equation for finding the reduced shear modulus in the strain rates outside the range of 0.0001 s−1to 1 s−1. In other words, extrapolation may lead to far inaccurate and irrational approximations. Moreover, since the regression is built upon 3 points, the second-order regression will be identical as the second-order interpolation and the associated error of prediction will be zero, which could result in overfitting and inaccurate results if used for the ranges of the strain rate beyond what was discussed here. Therefore, a great care should be taken upon the decision of whether using the first- or second-order regression for approximating the reduced shear modulus of axons in the intermediate strain rate values.

The resultant material properties for axons and ECM are dependent to some of the assumptions made in the optimization framework including the axons volume fraction and the ratio of the initial shear modulus of axons to ECM. As mentioned earlier, there must be a fixed initial shear modulus ratio, to carry on the optimization procedure since if the material properties of both axons and ECM are set to equal parameters, the RVE represents a homogenous material with the property equivalent to that of the assigned ones. The axons volume fraction is another factor that affects the constituent’s properties. In this paper, those parameters were assigned based on the previous published studies [32, 36]. However, those values are not specifically derived for human brain white matter tissue, and hence, experimental micro-level tests on human brain white matter could be beneficial for better approximation of that kind.

The utilization of biphasic constitutive models could open a new line of research in the field of micromechanical characterization of the brain [39, 57]. The biphasic model breaks down the brain structure into two independent phases of solid and fluid, as water constitutes 80% of the volume fraction of brain. A recent study involved with macro-characterization analysis, suggests a calibrated shear modulus of 1.8 kPa for bovine brain tissue in three deformation speed of 10, 100, and 1000 mm/s [39]. However, to the authors’ best knowledge, there is no reported biphasic properties for micromechanical constituents of brain tissue as there are some limitations and hindrances. Due to the lack of specific direct micro-level experimental tests, there are some parameters with unknown values such as hydraulic conductivity, permeability, and water fraction for both axons and ECM. Therefore, besides the added computational complexity to the optimization framework due to the increased number of parameters, more assumptions will be required to correlate between the properties of those microlevel constituents.

5 Conclusion

In this paper, we applied PSO as a derivative free optimization method in conjunction with finite element micromechanical simulation to find the visco-hyperelastic material properties of axons and ECM as micro-level constituents of human brain white matter. As brain white matter is a heterogeneous material at the micro-level, consisting of axons embedded in ECM, a sample RVE representing a smallest recognizable unit of brain white matter was developed with the axons volume fraction of 52.7% [36]. The experimental compressive relaxation experiment performed in [42] was used as the input experimental data in this study. The cost function was defined as the sum of the square of error between the finite element and experimental results. Thereafter, a particle swarm optimization algorithm was used to find the optimal material properties of axon and ECM. The Ogden hyperelastic model with Prony time series expansion was used to account for the viscous behavior of the brain in a relaxation test. Comparing the results of the micromechanical simulation carried on with the obtained optimal parameters and experimental data showed a high-quality agreement. A high coefficient of determination and low-cost function value proves the validity of the conducted optimization framework. The Prony series expansion parameters of axons and ECM were found to be close to that of the human brain white matter. In addition, the strain rate dependency of the initial shear modulus and reduced shear modulus of axons were studied through first- and second-order regression. It was shown that linear approximation may not be beneficial for approximating the reduced shear modulus of axons at the intermediate strain rate values. The results of this study can be used for the studies focused on the diffuse axonal injuries, drug delivery, or any other research which requires the knowledge of the micro-level constituent properties of human brain white matter.