1 Introduction

Tunnel squeezing refers to the occurrence of large amount of deformation in surrounding rock mass rock, which is normally more than the designed deformation. This phenomenon, which takes a long time to form, causes many difficulties during and after construction of tunnels [6, 11, 69]. The squeezing behavior of surrounding rock can be described as the time-dependent large deformation during tunnel excavation, which is essentially related to creep created by exceeding the ultimate shear stress [8, 19, 25, 59, 69]. Different studies showed that the compressive surrounding rock has the deformation features of large deformation amount, long deformation duration, high deformation speed, large destruction range of surrounding rock and various forms of supporting structure failures [19]. There are objective and subjective factors for the occurrence of tunnel squeezing, where the objective conditions involve rock properties, tectonic stress, tunnel dimensions, rock type, high in situ stress and large radius or span [8]. On the other hand, the typical subjective factors are associated with support installation, in which the deformation can be restrained if the support is installed on time [27, 42, 62]. Tunnel squeezing may cause several unwanted issues, e.g., budget increase, construction period extension and construction safety [8, 22]. In order to overcome these issues, many attempts have been done by various scholars, and they suggested several approaches for predicting tunnel squeezing, including empirical, semiempirical and theoretical methods [4, 24, 32, 33, 61, 68]. With the development of the computer science and various available technologies, numerical simulation and classical statistics methods have been widely used in tunnel squeezing prediction [13, 23, 37,38,39, 65].

In recent years, the successful applications of machine learning (ML) methods in solving regression, classification and time-series problems in science and engineering have been reported by many researchers all around the world [2, 3, 30, 31, 40, 41, 52, 77,78,79, 81, 82, 85,86,87,88,89, 92, 93, 95, 97,98,99,100,101,102]. These methods have been used by researchers in the areas of geotechnical [15, 55, 66, 99] and tunnel engineering [76, 82, 84] and also to solve problem related to tunnel squeezing [50, 65]. To estimate tunnel squeezing, ML techniques like artificial neural network (ANN), decision tree (DT), naive Bayes (NB) and support vector machine (SVM) have been used in the literature. As an example, Shafiei et al. [65] used and introduced a SVM classifier model, which was trained and tested based on 198 samples, in particular having two predictor variables (buried depth, H, and rock tunneling quality index, Q). The accuracy of their proposed model is 84.1%. In another interesting investigation, Sun et al. [71] constructed a multi-class SVM prediction model based on 117 samples. There were four predictor variables (H, Q, diameter, D, and support stiffness, K,) in the multi-class SVM model, and it was able to receive an accuracy of 88.1%. Zhang et al. [87, 88] established a classifier ensemble based on 166 cases, which includes five different ML classifiers: ANN, SVM, DT, k-nearest neighbor (KNN), and NB. The five variables, i.e., H, D, Q, K and strength stress ratio (SSR), were selected as input parameters for the classifier ensemble, and the final accuracy was obtained as 96%. Huang et al. [35] proposed a hybrid model of SVM mixed by back-propagation (BP) for identifying squeezing and non-squeezing problem based on a total of 180 data samples. In the SVM-BP model, the four indicators including H, K, D and Q were considered as model inputs. The accuracy of the SVM-BP model was obtained as 92.11%. In addition, other methods and accuracy comparison results are shown in Table1. In light of above discussion, the performance of the combined classifiers/models is higher than the single classifier. However, in most of the cases, the combined classifier models are complex with the lowest level of practicality, when the number of classifiers increases. To solve this problem, this article only uses a single classifier SVM. SVM has high generalization performance and can solve problems like small samples and high dimensionality [63]. According to the existing research, we can also found that support vector machines have become popular in engineering. Many researchers have applied support vector machines to tunnel extrusion prediction. It can be roughly divided into two applications. On the one hand, it uses SVM regression to predict the deformation of the tunnel [39, 72, 91]. On the other hand, it uses SVM classification to determine whether the tunnel will be squeezed. So far, most of the existing forecasting methods can be used to distinguish between squeezing and non-squeezing. However this article refers to the multi-class SVM proposed by Sun et al. [71] and introduces a SVM-based prediction model to predict the severity of tunnel squeezing. However, the difference is that we consider the effects of the percentage strain (ɛ). There are several commonly considered predictor variables in this field, which are H, K, D, K and SSR. It seems that there is a need to consider effects of other important parameters on tunnel squeezing like the percentage strain (ɛ). The mentioned parameters were rarely used as input parameter in the proposed ML classifier models. Table 2 is the list of commonly used predictors.

Table 1 Classification comparison of existing prediction models
Full size table
Table 2 List of commonly used predictors [9, 13, 21]
Full size table

Additionally, with the deepening of research, optimization algorithms are gradually introduced into machine learning methods to optimize hyper-parameters, such as whale optimization algorithm (WOA), gray wolf optimization (GWO), Harris Hawks optimizer (HHO) and moth-flame optimization (MFO). Therefore, various hybrid models have gradually formed such as GWO-SVM [80, 83], WOA-SVM [95], MFO-SVM, GS-SVM [46], HHO-SVM [92], WOA-XGBoost, GWO-XGBoost, BO-XGBoost [64, 101, 102] and SCA-RF [92]. The above research shows that the hybrid model has better performance than a single machine learning method. Therefore, the whale optimization algorithm is introduced to improve the prediction performance of multi-class SVM. Whale optimization algorithm (WOA) has simple structure, few parameters, strong search ability and easy to implement [7].

Finally, an optimized classifier model (WOA-SVM) is proposed to predict the severity of tunnel squeezing based on five parameters, that is, buried depth (H), support stiffness (K), rock tunneling quality index (Q), diameter (D), and the percentage strain (ɛ). Firstly, we establish a database containing above five surrounding rock indicators based on the existing literature and then preprocessing these data. Then, the WOA-SVM model was trained and tested of tunnel squeezing. This study copes with not only the development of the WOA-SVM model used for the anticipating of squeezing problems, but also the sensitivity analysis of predictor variables. Finally, in order to verify the advantage of the model proposed, an evaluation and comparison on the performance of different classifier models (WOA-SVM, ANN, SVM, and genetic programming, GP) based on the same database were implemented. The performance and accuracy of the mentioned models will be assessed and discussed to select the best model in predicting tunnel squeezing.

2 Predictor selection and database description

According to the published literatures, the research group collected 114 historical cases of tunnel squeezing from various locations like Greece, Bhutan, India, Austria, China, Nepal and Venezuela [1, 6, 18, 20, 32, 51, 62, 67, 71]. There are six parameters in each case where five of them (K, H, Q, D and ɛ) were set as input variables to predict tunnel squeezing. Among these six parameters, H, Q and D are often appeared in empirical formulas, such as \(H = 350Q^{0.33}\) and \(H = 275N^{0.33} B^{ - 0.1}\), which are proposed by Goel and Singh [27, 68]. The three parameters reflect the influence of in situ stress, surrounding rock properties and tunnel size on squeezing. The support stiffness is selected as the input parameter. The reason is that the support stiffness plays an important role in controlling the excessive deformation caused by the interaction between the support pressure and the rock mass deformation response [13]. SSR and ɛ are usually used as grading indicators such as in the research conducted by Jethwa et al. (1984), Barla [8] and Aydan et al. [4, 5].

In this study, we adopt the classification standard proposed by Hoek and Marinos [33]. Therefore, non-squeezing (NS) (with ε < 1%), minor squeezing (MS) (with 1% ≤ ε < 2.5%) and severe-to-extreme squeezing (SES) (with ε ≥ 2.5%) were represented by class 0, class 1 and class 2, respectively. A correlation scatter matrix was performed to know more about the used parameters, as shown in Fig. 1. The diagonal of the matrix presents probability distributions for each squeezing class, the lower panels show pairwise scatter plots of three classes of squeezing data along the axis and the upper triangle presents the Pearson's correlation coefficients. It can be clearly seen that all indicators have no relatively meaningful correlation with each other, and there is no clear separation among NS, MS and SES. The mentioned input and output parameters will be used in the next stage for classification modeling of tunnel squeezing.

Fig. 1
figure 1

Correlation scatter matrix of cumulative distributions and statistical evaluations for the squeezing database

Full size image

3 Concepts of predictive models

3.1 Support vector machine (SVM)

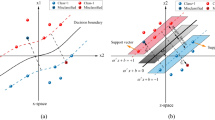
The SVM has high generalization performance and does not require prior knowledge of specific models; therefore, it is widely used to solve problems in different fields, for example, finance [47], energy [34], hydrological research [58], mechanical engineering [16, 48], civil engineering [63, 85] and other fields. Of course, SVM is also widely used for tunnel extrusion prediction [38, 65]. The initial concept of SVM is to input the training data set and output the separating classification decision function with the largest geometric interval [12, 16, 34, 47,48,49, 74]. The SVM has been widely used to solve multivariate classification and regression problems [45, 54, 58], although it is a binary classification model on nature. The advantage of the SVM model lies in the ability to transform nonlinear problems into linear problems in high-dimensional feature spaces with the help of kernel functions [54].

In practical problems, it is difficult to find a hyperplane that can separate different categories of samples when the training sets are nonlinearly separable in the sample space. To solve this problem, there is a need to allow SVM for making mistakes on some datasets. Therefore, the sense of "soft margin" was introduced into the SVM model. In this way, the optimization objective functions of SVM can be expressed in the following [45, 46, 73, 92, 95]:

$$\min_{w,b} \frac{1}{2}\left\| w \right\|^{2} + C\sum\limits_{i = 1}^{m} {l_{{{0 \mathord{\left/ {\vphantom {0 1}} \right. \kern-\nulldelimiterspace} 1}}} (y_{i} (w^{T} x_{i} + b) - 1)}$$
(1)

where \(l_{0/1}\) is 0/1 loss function, which can measure the deviation degree and can be defined as follows:

$$l_{{{0 \mathord{\left/ {\vphantom {0 1}} \right. \kern-\nulldelimiterspace} 1}}} (Z) = \left\{ \begin{gathered} 1,if^{{}} Z < 0 \hfill \\ 0,{\text{otherwise}} \hfill \\ \end{gathered} \right.$$
(2)

With the introduction of slack variables \(\xi_{i}\) and penalty factors \(C\) (the regularization constant), the original optimization problem can be rewritten as follows:

$$\begin{aligned} & \min_{w,b} \frac{1}{2}\left\| w \right\|^{2} + C\sum\limits_{i = 1}^{m} {\xi_{i} } \\ & s.t.y_{i} (w^{T} x_{i} ) \ge 1 - \xi_{i} \\ & \xi_{i} \ge 0,i = 1,2, \ldots ,m \\ \end{aligned}$$
(3)

By introducing the Lagrangian multipliers (\(\alpha_{i} \ge 0,^{{}} u_{i} \ge 0\)), the Lagrangian function is constructed to solve problems with constraints:

$$L(w,b,\alpha ,\xi ,u) = \frac{1}{2}\left\| w \right\|^{2} + C\sum\limits_{i = 1}^{m} {\xi_{i} } + \sum\limits_{i = 1}^{m} {\alpha_{i} } (1 - \xi_{i} - y_{i} (w^{T} x + b)) - \sum\limits_{i = 1}^{m} {u_{i} \xi_{i} }$$
(4)

When the partial derivative of the above formula to W, b, \(\xi_{i}\) is zero, the Lagrange dual problem can be described as follows:

$$\begin{aligned} & \max_{\alpha } \sum\limits_{i = 1}^{m} {\alpha_{i} } - \frac{1}{2}\sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{m} {\alpha_{i} } } \alpha_{j} y_{i} y_{j} x_{i}^{T} x_{j} \\ & s.t.\sum\limits_{i = 1}^{m} {\alpha_{i} } y_{i} = 0 \\ & 0 \le \alpha_{i} \le C,^{{}} i = 1,2, \ldots ,m \\ \end{aligned}$$
(5)

Optimization problems with inequality constraints need to meet the following conditions.

$$\begin{aligned} & \alpha_{i} \ge 0,^{{}} u_{i} \ge 0 \\ & y_{i} (w^{T} x + b) - 1 + \xi_{0} \ge 0 \\ & \alpha_{i} (y_{i} (w^{T} x + b) - 1 + \xi_{i} ) = 0 \\ & \xi_{i} \ge 0,u_{i} \xi_{i} = 0 \\ \end{aligned}$$
(6)

To overcome nonlinear classification and clustering issues, it is essential to choose the appropriate kernel function \(\Phi_{K} (x,z)\) as a substitute for inner product to construct and solve the convex quadratic programming issue [16, 34, 47]. That means Eq. (5) becomes Eq. (7). In this way, the input data can be mapped into a high-dimensional feature spaces [47], as shown in Fig. 2.

$$\begin{aligned} & \min_{\alpha } \frac{1}{2}\sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{m} {\alpha_{i} } } \alpha_{j} y_{i} y_{j} \Phi_{K} (x{}_{i},x_{j} ) - \sum\limits_{i = 1}^{m} {\alpha_{i} } \\ & s.t.\sum\limits_{i = 1}^{m} {\alpha_{i} } y_{i} = 0 \\ & 0 \le \alpha_{i} \le C,^{{}} i = 1,2, \ldots ,m \\ \end{aligned}$$
(7)
Fig. 2
figure 2

Mapping data from two dimensional to three dimensional

Full size image

Then, we will obtain \(w\) and b after calculation of the optimal solution \(\alpha^{*}\) \(\left( {\alpha^{*} { = }\left( {\alpha_{1}^{*} ,\alpha_{2}^{*} ,...,\alpha_{m}^{*} } \right)^{T} } \right)\) by the SMO (sequential minimal optimization) algorithm [73]. Finally, the classification decision function can be described as:

$$f(x) = \sum\limits_{i = 1}^{m} {\alpha_{i}^{*} y_{i} \Phi_{K} (x,x_{i} ) + b^{*} }$$
(8)
$$b^{*} = y_{i} - \sum\limits_{i = 1}^{m} {\alpha_{i}^{*} y_{i} \Phi_{K} (x_{i} ,x_{i} )}$$
(9)

3.2 Whale optimization algorithm (WOA)

Inspired by the bubble-net attacking technique which is humpback whale’s unique predation method, Mirjalili [53] suggested the WOA algorithm for solving and optimizing problems. Therefore, the WOA is widely used in energy, image processing and machine vision, structural optimization, management and other fields [53]. Humpback whales like to hunt a group of krill or small fish near the water surface. They are gradually evolved a special hunting method called foam feeding, that’s because they move slowly. Whale can construct a spiral path with a decreasing radius by creating bubbles for enforcing fish schools to approach the surface and then catching them [43, 57]. WOA concept can be described as (1) encircling prey, (2) bubble-net attacking method and (3) search for prey, which are discussed in detail as follows (in order to distinguish, the bold letters in the following formula represent vectors):

  • Encircling prey

The exact position of prey cannot be easily identified; therefore, the system considers the solution of the current candidate for the target prey [57]. In the next step, after recognizing the best search agent \((X^{*} ,Y^{*} )\), there is a need for the other search agents \((X,Y)\) to upgrade their locations using Eqs. 10 and 11. The nearby solutions around the best or optimized solution can be according to Eqs. 12 and 13 (Fig. 3).

$${\mathbf{R}} = \left| {{\varvec{C}} \cdot {\varvec{X}}_{\left( t \right)}^{*} - {\varvec{X}}_{\left( t \right)} } \right|$$
(10)
$${\varvec{X}}_{{\left( {t + 1} \right)}} = {\varvec{X}}_{\left( t \right)}^{*} - {\varvec{A}} \cdot {\mathbf{R}}$$
(11)
$${\mathbf{A}} = 2{\mathbf{a}} \cdot {\mathbf{r}}_{1} - {\mathbf{a}}$$
(12)
$${\mathbf{C}} = 2{\mathbf{r}}_{2}$$
(13)

where \({\mathbf{A}}\) and \({\mathbf{C}}\) represent the coefficient vectors, and the value of \({\mathbf{A}}\) is restricted to [1]. Parameter of \({\mathbf{a}}\) can be decreased from 2 to 0 in the search process, and it can be calculated by \({\mathbf{a}}{ = }2{ - }{{2t} \mathord{\left/ {\vphantom {{2t} {T_{\max } }}} \right. \kern-\nulldelimiterspace} {T_{\max } }}\) (\(t\) and \(T_{\max }\) represent the current number and the maximum number of iterations, respectively). Factors \({\mathbf{r}}_{1}\) and \({\mathbf{r}}_{2}\) are random vectors in the range of [1]; \({\varvec{X}}_{\left( t \right)}\) and \({\varvec{X}}_{\left( t \right)}^{*}\) denote the current whale position vector and the best whale solution vector (the possible location of the prey) in the tth iteration, respectively.

Fig. 3
figure 3

Different vector positions highlighting the best solutions

Full size image

  • Bubble-net attacking method

The humpback whales and their bubble-net attacking behavior can be mathematically simulated by designing two procedures, which are shrinking encircling and spiral updating. The spiral equation is described in the following equation:

$${\mathbf{X}}_{(t + 1)} = {\mathbf{R^{\prime}}} \cdot e^{bl} \cdot \cos (2\pi l){\mathbf{X}}_{(t)}^{*}$$
(14)

where the shape of the logarithmic spiral depends on \(b\) which is a constant, \(l\) is a random vector which distributed uniformly within [-1,1]. The distances between the ith search agent and the target prey are presented by \({\mathbf{R^{\prime}}}{ = |}{\mathbf{X}}_{(t)}^{*} - {\mathbf{X}}_{(t)} |\).

The shrinking encompassing mechanism and the spiral updating location have an equivalent probability to be selected by the humpback whale in the process of position updating. The process of simulation can be demonstrated as follows:

$${\mathbf{X}}_{(t + 1)} = \left\{ \begin{gathered} {\mathbf{X}}_{(t + 1)} = {\mathbf{X}}_{(t)}^{*} - {\mathbf{A}} \cdot {\mathbf{R}},\begin{array}{*{20}c} {if} & {p < 0.5} \\ \end{array} \hfill \\ {\mathbf{R^{\prime}}} \cdot e^{bl} \cdot \cos (2\pi l){\mathbf{X}}_{(t)}^{*} ,\begin{array}{*{20}c} {if} & {p \ge 0.5} \\ \end{array} \hfill \\ \end{gathered} \right.$$
(15)

where \(p\) is an arbitrary number in the range of [1].

  • (3) Search for prey

In order to update the whale places during the exploration phase, the equation of the model is presented as follows:

$$\begin{gathered} {\mathbf{R}} = |{\mathbf{C}} \cdot {\mathbf{X}}_{rand} - {\mathbf{X}}_{(t)} | \hfill \\ {\mathbf{X}}_{(t + 1)} = {\mathbf{X}}_{rand} - {\mathbf{A}} \cdot {\mathbf{R}} \hfill \\ \end{gathered}$$
(16)

where \({\mathbf{X}}_{rand}\) denotes the whale location vector which is selected randomly.

3.3 Multilayer perceptron (MLP)

In this paper, ANN refers to multilayer perceptron (MLP). Multilayer perceptron (MLP) is promoted from a single-layer perceptron. The main feature is that it has multiple neuron layers. Generally, the first layer of MLP is called the input layer, the middle layer is the hidden layer and the last layer is the output layer. MLP does not specify the number of hidden layers, so the appropriate number of hidden layers can be selected according to actual processing requirements. These hidden layers have different numbers of hidden neurons. The neurons in each hidden layer have the same activation function, and there is no limit to the number of neurons in each layer in the hidden layer and the output layer.

3.4 The Gaussian process (GP)

GP means Gaussian process classification. The Gaussian process is a general supervised learning method for solving regression and probability classification problems. The advantages are: (1) predictions can explain observations. (2) The prediction is probabilistic, so that the empirical confidence interval can be calculated. (3) Versatility.

4 Modeling results and discussion

4.1 Evaluation criteria

The ROC (receiver operating characteristic) curve is very popular in the performance evaluation phase of ML classifiers [87, 94, 96]. The ROC curve can be presented in a form of Cartesian coordinate system, in which FPR (false-positive rate) and TPR (true-positive rate) represent as the horizontal axis and the vertical axis, respectively. The key indicator of performance evaluation in the ROC curve is the AUC value that is defined as the area under the ROC curve. The larger AUC values, the higher the classification accuracy of the model or the better performance. On the other hand, accuracy and Cohen’s kappa can be also considered as performance indicators. The Kappa coefficient measures the effect of classification by evaluating the consistency between the prediction results of the model and the actual classification results. A normal range for results of kappa is in the range of 0–1. If this range is divided into five different classes, there are: 1) slight consistency (0 ~ 0.20), 2) fair consistency (0.21 ~ 0.40), 3) moderate consistency (0.41 ~ 0.60), 4) substantial consistency (0.61 ~ 0.80) and 5) almost perfect consistency (0.81 ~ 1.00). In addition to accuracy and Kappa, precision, recall and F1 can also be considered as performance indicators [87, 93]. The mentioned performance indicators (accuracy, Kappa, precision, recall and F1-score) can be computed based on the confusion matrix, as shown in Fig. 4. Based on the confusion matrix, MCC also was introduced as performance indicators. Matthews correlation coefficient is an index used in machine learning to measure the classification performance. This indicator considers true positives, true negatives, false positives and false negatives. It is generally considered to be a relatively balanced indicator, and it can be applied even when the sample content of the two categories differs greatly. MCC is essentially a correlation coefficient that describes the actual classification and the predicted classification. Its value range is [-1,1], 1 indicates a perfect prediction of the subject, and a value of 0 indicates that the predicted result is not as good as a random prediction, -1 means that the predicted classification is completely inconsistent with the actual classification. The calculation formula is as follows:

$$MCC = \frac{TP \times TN - FP \times FN}{{\sqrt {(TP + FP)(TP + FN)(TN + FP)(TN + FN)} }}$$
(17)
Fig. 4
figure 4

Confusion matrix and performance indicators

Full size image

4.2 WOA-SVM model development and validation

Main steps for constructing WOA-SVM model in predicting tunnel squeezing are as follows:

  • Step 1: Data preparation: The database collected from the existing literature has a total number of 114 cases. The source of the cited cases and the necessary information are listed in appendix. A. According to the most commonly used division ratio of 80%/20%, based on the Pareto principle [64, 75, 100], we randomly divide dataset into 80% training set and 20% testing set for model development and model validation, respectively [71].

  • Step 2: Initializing parameters of the SVM model. There are several main parameters in the SVM model, including the penalty parameter of the objective function (“C”), the kernel function and the coefficient of the kernel function (“g”). The hyper-parameters “C” and “g” need to be optimized by WOA algorithm. In this research, the kernel function is determined with the help of the model decision boundary diagram. The SVM model transforms the linearly inseparable problem into linearly separable with the help of the kernel functions like linear, polynomial, radial basis function (RBF), and sigmoid. According to the model decision boundary diagram in Fig. 5, it is easy and feasible to detect that the database in this article is close to linearly separable. Therefore, the linear kernel was applied to input parameter mapping for the SVM model.

  • Step 3: The relevant parameters of the WOA and their ranges are the constant \(b\), two random number \(l \in [ - 1,1]\) and \(r \in [0,1]\)\([0,1]\). It is necessary to determine and design the optimal hyper-parameters (C and g) of SVM using the WOA. Therefore, a WOA-SVM hybrid model can optimize the ability of the SVM classifier in predicting tunnel squeezing through WOA algorithm. The specific optimization process of the proposed WOA-SVM is shown in Fig. 6.

  • Step 4: Fitness evaluation of WOA-SVM model and determination of the optimal population size. It is necessary for developing a reliable WOA-SVM model with the best performance to fix the optimal population number. This is because swarm size has a significant impact on the performance of the WOA model. To search the optimal population number, five different swarm sizes (i.e., 50, 80, 100, 150 and 200) were selected and used in the process of model development. The fitness curve presented in Fig. 7 shows that the adaptation value changes with the number of iterations. When the number of iterations is greater than or equal to 80, the fitness values of the five fitness curves generated by the WOA-SVM model will tend to be stable. Table 3 presents the results of performance evaluation (accuracy and Kappa) for the optimization WOA-SVM model based on the training and testing sets. Based on this table and considering all performance indexes, the optimal population or swarm size was selected as 150 with accuracy = 0.9565 and Kappa = 0.9288.

Fig. 5
figure 5

Model decision boundary before and after optimization: (a) SVM; (b) WOA-SVM

Full size image
Fig. 6
figure 6

The whole analysis process of WOA-SVM classifier model

Full size image
Fig. 7
figure 7

Optimization of WOA-SVM with different population values

Full size image
Table 3 The performance of the SVM model optimized with WOA
Full size table

4.3 Analysis and comparison of classification performance

The optimized classifier model based on the training set needs to be validated based on testing datasets. The test datasets were randomly selected from the database prepared, i.e., 20% of the total cases (23 test samples). It is important to mention that they have not participated in the training process of the model. We will analyze and compare classification performance from different perspectives such as confusion matrix, performance evaluation indicators, violin graphs and so on. From the confusion matrix, we can get the accuracy, Kappa, MCC and other performance evaluation indicators and use then analyzing and comparing the classification performance of different models on the basis of these evaluation indicators. To examine the accuracy of the WOA-SVM model, the methods of GP, ANN and SVM were built for classification purpose of the same samples. The results of the verification are shown in Fig. 8, which represents the confusion matrix of four classification models (WOA-SVM, SVM, ANN and GP) for testing datasets. It is not difficult to observe that the WOA-SVM classifier demonstrates better performance than the other built models. Compared with the other un-optimized classifier models, the WOA-SVM classification model has the highest accuracy (approximately 0.9565). In addition, the Kappa values obtained for different classifiers from high to low are: 0.929 (WOA-SVM), 0.913 (ANN), 0.696 (SVM) and 0.565 (GP). In addition to accuracy and Kappa mentioned above, the number of cases classified correctly can be obtained from the main diagonal of the confusion matrix.

Fig. 8
figure 8

Confusion matrix different prediction methods: a WOA-SVM; b ANN; c SVM; and d GP

Full size image

The above analysis has shown that the WOA-SVM model has certain advantages. In order to present the difference between measured tunnel squeezing results and the predicted ones obtained from different classifiers, the resultant classification results are demonstrated in Fig. 9. We can see the 23 samples of the test dataset on the horizontal axis and the class of the sample on the vertical axis (class0: non-squeezing; class1: minor squeezing; class2: severe-to-extreme squeezing). There is a sample with the actual class: class 1 in Fig. 9a, which was misclassified as class 0, and this sample was defined as case No. 20. However, there are more than one sample in Fig. 9 (b, c and d), which was misclassified. The WOA-SVM model is more accurate and safer in predicting the level of tunnel squeezing.

Fig. 9
figure 9

Actual and predicted classification results on test datasets

Full size image

The above analysis aims to evaluate the classification performance of the model as a whole. However, imbalanced dataset may have a great impact on the prediction results of the model, but it is not enough to detect this influence based on the accuracy rate alone. Therefore, precision, recall, F1 and ROC curves were also applied and calculated to assess the prediction performance of WOA-SVM, SVM, ANN and GP models. Table 4 tabulates precision, recall and F1-score of different classification models based on non-squeezing (NS), minor squeezing (MS) and severe-to-extreme squeezing(SES). According to this table, the WOA-SVM model was able to receive a better performance and higher level of accuracy. Based on the above analysis, for the optimized ML classifier, the classification performance of the optimized SVM model was significantly improved compared to the base model which is SVM.

Table 4 Performance of different classifiers for the non-squeezing problems, minor squeezing problems and high squeezing problem
Full size table

ROC curves and AUC values of different individual classifiers for different classes are shown in Fig. 10. According to Fig. 10a, the AUC values based on the class 0 were calculated as 1, 0.99, 0.78, 0.93 and 0.94 for WOA-SVM, ANN, GP and SVM approaches, respectively. Figure 10b and c demonstrates AUC values of different classifiers based on class 1 and class 2, respectively. The specific values can be obtained from the figure. In Fig. 10, the AUC values obtained from the WOA-SVM model based on class 0, class 1 and class 2 are 1, 0.93 and 1, respectively. Obviously, the WOA-SVM model is the preferred ML classifier for squeezing degree prediction.

Fig. 10
figure 10

ROC curves and AUC values for different individual classifiers: a non-squeezing problems; b minor squeezing problems; c severe-to-extreme squeezing problems

Full size image

In order to understand the capability of our proposed model better, we have drawn Taylor graph for train and test sets separately, as shown in Fig. 11. Taylor chart is often used to evaluate the accuracy of a model. Commonly used accuracy indicators are MCC, standard deviation and root-mean-square error (RMSE). Generally speaking, the scattered points in the Taylor diagram represent the model, the radial line represents the MCC, the horizontal and vertical axis represents the standard deviation and the dashed line represents the root-mean-square error. The Taylor chart is a change from the previous scatter chart, which can only show two indicators to express the accuracy of the model. Similarly, we still can see that the WOA-SVM model is the preferred ML classifier for squeezing degree prediction.

Fig. 11
figure 11

Taylor graph a test sets, b train sets

Full size image

The above analysis is based on the test set. Below we will analyze and compare the performance of the model based on all the sample data in this article. The violin chart includes a combined specifications of the box plot and the kernel density plot. The main application of this chart is to present the probability density and distribution of datasets. Figure 12 shows the distribution and probability density of prediction accuracy for different classifier models considering all 114 samples. The prediction accuracy of WOA-SVM model is higher than the other classification models, and the distribution of accuracy is more concentrated, which sufficiently illustrates that the hybrid model (WOA-SVM) has visible advantages in squeezing prediction.

Fig. 12
figure 12

The violin chart presented for different classifier models

Full size image

4.4 Sensitivity analysis of predictor variables

The key to predicting tunnel squeezing is the selection of appropriate input parameters. The research of Huang et al. [35] showed that the coupling effect of different parameters has different effects on tunnel squeezing prediction. Therefore, it is particularly important to evaluate the contribution of input parameters to the developed model. The Shapley Additive Explanations was used to obtain the importance of predictive variables to WOA-SVM classification model. The calculation formula is shown as [100]:

$$\Phi_{i} = \sum\limits_{S \subseteq N/(i)} {\frac{\left| S \right|!(\left| N \right| - \left| S \right| - 1)!}{{\left| N \right|!}}} \left[ {q_{s \cup i} (x_{s \cup i} ) - q_{s} (x_{s} )} \right]$$
(18)

where N represents the set of all features in the data set, \(S\) is the set after index \(i\) is removed, the importance of feature \(i\) to the model output is represented by \(\Phi_{i}\), \(x_{s}\) represents the vector of input features in set \(S\), and the contribution of features is calculated with the corresponding function \(q\).

In practical applications, the prediction results based on the predictor variables with high contribution rates to model are more reliable and accurate. There are five features in this work, and the importance of predictor variables to the WOA-SVM classification model was calculated (Fig. 13). It can be intuitively seen that the percentage strain (ɛ) is the most important parameter in predicting tunnel squeezing, followed by K and H parameters. Due to the imbalance dataset of this article, the contribution of the parameters to model based on different types of data (class0, class1 and class2) was assessed (Fig. 13b) According to Fig. 13, ɛ is still the most influential parameter on the model for all classes. However, for class 1 and class 2, the parameter K ranks second only to ɛ in the contribution rate rankings, followed by H. For class 0, the parameter H ranks second only to ɛ, followed by K. In summary, the parameters that have important contribution to the WOA-SVM model are: ɛ, K, H and D.

Fig. 13
figure 13

Variable contribution analysis: a overall analysis; b analysis of variables for non-squeezing problems, minor squeezing problems, and high squeezing problem

Full size image

In order to verify the above conclusions, we randomly selected a sample from three different classes, and the probabilistic interpretation of the sample is given in Figs. 14–16. That means that Figs. 14, 15 and 16 demonstrate that the five parameters (ɛ, K, D, Q and H) have different contributions to the prediction of class0, class1 and class2. Figure 14 presents the process of the sample selected was considered class0 by WOA-SVM model according to input parameters. According to the information in Fig. 14, it can be easily observed that the probabilities of the sample to class0, class1 and class2 are 0.69, 0.24 and 0.07, respectively. Therefore, the final prediction result is class0 (light squeezing problem), and parameters ε, H and K are decisive predictor variables, where ε plays a decisive role in the prediction results.

Fig. 14
figure 14

Probabilistic interpretation of the non-squeezing category

Full size image

Similarly, Fig. 15 displays the process of the sample selected was judged to be class1. The sample will be judged to be class0, class1 and class2 with corresponding probability of 0.09, 0.52 and 0.39, respectively. Finally, this sample is considered as class1 (moderate squeezing problem). The decisive predictor variables are different from that presented in Fig. 14, and they are ε, H and D. Nevertheless, parameters ε still has the deepest effect on the proposed model. Figure 16 demonstrates that the sample will be regarded as class0, class1 and class2 with corresponding probability of 0.05, 0.28 and 0.67, respectively. Obviously, this sample is ultimately considered as class2 (high squeezing problem), and the percentage strain (ɛ) is the most important parameter for predicting tunnel squeezing, followed by the parameters K and H. In other words, Figs. 14, 15 and 16 illustrate that the parameters ɛ, K, H and D have a considerable impact on the WOA-SVM model, while ɛ is the most important input parameter among them.

Fig. 15
figure 15

Probabilistic interpretation of the minor squeezing category

Full size image
Fig. 16
figure 16

Probabilistic interpretation of the high squeezing category

Full size image

5 Conclusion

We proposed an optimized classifier model (WOA-SVM) to estimate the potential of tunnel squeezing according to 114 cases. There were five input parameters (H, K, D, Q and ɛ) considered in the modeling of all ML models in this study (WOA-SVM, ANN, SVM and GP). In order to assess the performance of different classifier models based on the same database, accuracy, kappa, precision, recall, F1-score and the AUC were calculated. The aim of the sensitivity analysis of predictor variables is to evaluate the contribution of input parameters to the model. The main results of this study are summarized as follows.

  1. (1)

    The WOA algorithm can effectively optimize the hyper-parameters of the SVM classifier and improve its classification performance. The WOA-SVM classification model has the highest accuracy (approximately 0.9565) than other un-optimized individual classifiers (SVM, ANN and GP). However, the model has a good classification effect, even if the data are unbalanced.

  2. (2)

    The results of the sensitivity analysis indicate that ɛ, H and K are the best combination of parameters for WOA-SVM model, where the percentage strain (ɛ) is the most influential factor on the WOA-SVM model, the parameter K ranks second only to ɛ in the contribution rate rankings, followed by H.

So far, most of the existing forecasting methods can distinguish between squeezing and non-squeezing. This article refers to the multi-class SVM proposed by Sun et al. [71] and introduces the whale optimization algorithm to optimize the prediction performance of the multi-class SVM. Therefore, the WOA-SVM model has higher prediction accuracy than empirical methods, ordinary binary SVM and multi-class SVM and can predict the severity of tunnel squeezing. However, compared with numerical simulation, the influencing factors considered by this paper are obviously limited. In addition, in the actual construction process, it is difficult to obtain more accurate input parameter values. According to the research of Zhang et al. [73,74], the prediction performance of the classifier ensemble model is higher than that of the individual classifier. In future, other advanced single classifiers can be introduced to construct a classifier ensemble. On this basis, the introduction of suitable optimization algorithms can greatly improve the prediction accuracy of the model. In addition, expanding the existing database can improve the generalization ability of the integrated model.