1 Introduction

The accurate determination of the elastic mechanical properties of rock is essential in the design, analysis, construction and implementation processes pertinent, but not limited to, the civil, construction, mining, tunneling, geophysics, geotechnical, waste storage and petroleum industries. Laboratory assessments of mechanical rock properties are commonly performed using static (e.g., biaxial/triaxial compression/extension), dynamic, acoustic measurement (e.g., ultrasonic pulse velocity (UPV) or seismic) and combinations of static–dynamic experiments on core samples. Recovering core samples is challenging due to the cost and risk of the acquisition process, depth limitations, discrete data resolution and the inherent chemical/physical instability of most rock formations [22, 37, 65]. Meanwhile, the determination of the mechanical properties of in situ rock using an acoustic method is dependent on the tool resolution and accuracy of the inversion/calibration methods. Laboratory measurements using acoustic methods (e.g., UPV) could provide quick, non-invasive measurements, but require a minimum sample size of 1–2 cm [18, 39, 80]. Critically, in several studies, discrepancies between the obtained static and dynamic moduli of rock have been associated with the presence of microcracks, testing stress state and testing strain amplitude [13, 29, 38, 55, 57, 60, 73, 77, 86].

Retrieved drill cuttings and rock fragments often represent valuable resources that can be cost-effectively used to characterize the mechanical properties of rock formations. For example, a substantial quantity of drill/rock cuttings smaller than 7 mm [8, 26, 45, 46, 51, 52, 62, 64, 76, 89] is produced during the well-drilling process. These rock cuttings are typically reinjected, discarded, buried in situ or placed in landfills at the end of drilling [69]. With the proper treatment, a mechanical characterization of these small rock fragments could be performed using small-scale mechanical testing methods such as instrumented indentation testing (IIT).

The results obtained from IIT are presented in terms of the experimental indentation modulus and hardness [34, 56]. The measured experimental indentation modulus is then related to the elastic mechanical properties of the rock (i.e., Young’s modulus, Poisson’s ratio and stiffness matrix). Previous research into the determination of the mechanical properties of rock using IIT methods has identified rocks as either isotropic [5, 15, 24, 47, 90, 91] or transversely isotropic (TI) [1, 2, 14, 19, 20, 50, 53, 58, 91, 92]. For isotropic rock, the correlation between the experimental indentation modulus, M, and Young’s modulus, E, is linear and can be represented by M = E/(1 − v2), where v is the Poisson’s ratio of the material. However, the majority of rocks are classified as TI materials [27, 30, 43, 81], indicating that they are anisotropic with rotational symmetry normal to the plane of isotropy (i.e., the bedding plane). This observed anisotropy is attributed to an anisotropic stress history in which greater vertical stress was applied than horizontal stress, the tendency of shale structures to align along the bedding direction, and the presence of plate-like clay particles with intrinsic TI mechanical properties. When considering TI mechanical properties, the elastic mechanical properties of rocks are defined by five elastic constants and related to the experimental indentation modulus using the anisotropic contact mechanics solution [71, 72, 82,83,84, 87].

The application of IIT has been extensive in the mechanical testing of rocks and is attracting increasing attention from researchers. At the nanoscale level, the grid nanoindentation technique, which consists of the application of a large array of nanoindentation tests, each with a probed microvolume sufficiently smaller than the characteristic size of the rock microstructure, has been applied to infer the mechanical properties of individual material phases (e.g., porous clay phase, porous calcite phase, etc.) [1, 2, 14, 19, 20, 50, 53, 58, 91, 92]. At the microscale level, microindentation testing, in which the scale of the indentation point is greater than the characteristic size of the microstructure of the rock, is used to assess the mechanical properties of bulk rock [3, 5, 9, 15, 24, 28, 31, 48, 49, 90]. The majority of studies at this scale considers the isotropic case to interpret the indentation measurements [5, 15, 24, 47, 90]; an assumption which makes the analysis incompetent in capturing true mechanical properties of rocks. Studies considering rock to be a TI material have often reported indentation measurements performed parallel and perpendicular to the bedding plane orientation [1, 2, 17, 19, 47, 50, 53, 78]. However, doing so requires that the bedding plane orientation be identified, though it is not distinguishable to the unaided eye for small samples such as cuttings. To the best of our knowledge, no study has been performed to identify the TI elastic properties of randomly oriented rock cuttings using microindentation.

In this study, therefore, a methodology was developed to approximate the TI elastic properties of randomly oriented rock cuttings based on experimental microindentation results. With no prior information on the bedding plane orientations of the cuttings, contact mechanics solutions for anisotropic materials were employed to obtain the elastic properties and corresponding bedding orientations from the microindentation results. Thus, microindentation testing was conducted to collect experimental data that were used to obtain the elastic mechanical properties of cuttings. As the objective of this study was to obtain the elastic properties, indentation data affected by fracture formation during the test were omitted from this analysis. The identification of both the stiffnesses and bedding orientations of the cuttings was conducted using a constrained inverse algorithm. The developed inverse algorithm was applied to minimize the difference between the experimentally obtained indentation modulus and the indentation modulus predicted using the proposed contact mechanics solutions. The predicted stiffness was then validated using UPV tests on 2.5 cm block samples.

The remainder of this paper is organized as follows. Section 2 provides details of the rock materials studied, sample preparation procedure, microindentation testing methodology and relevant theoretical background for the contact mechanics solutions and validation. The microindentation experiment results and elastic constant approximations based on the constrained inverse algorithm are presented in Sect. 3. The predicted elastic constants are validated against the results of UPV tests in Sect. 4, and conclusions are presented in Sect. 5.

2 Materials, testing methodology and theoretical background

2.1 Material description and specimen preparation

Ten samples of shale rock cuttings were prepared from retrieved rock fragments obtained from the Permian Wolfcamp B (PW-B) [48, 49] and Marcellus formations. Both X-ray diffraction and Rock–Eval pyrolysis analyses were then performed to acquire the composition and organic content of the samples, as shown in Fig. 1. Quartz, illite (clay) and feldspar were found to be the main constituents for the PW-B sample, whereas the Marcellus sample was primarily composed of quartz, calcite and muscovite (clay). The total organic carbon contents were found to be 5.15% and 4.15% for the PW-B and Marcellus samples, respectively. The results of Rock–Eval pyrolysis indicate that the PW-B shale and Marcellus shale samples, respectively, fall within the oil-prone and gas-prone maturity windows.

Fig. 1
figure 1

Rock sample compositions

Full size image

Shale rock cutting specimens were cut from rock fragments and core samples collected from the wells by dividing them into smaller pieces with thicknesses in the range of 2–5 mm. The specimens were cut at various orientations to ensure random bedding plane orientations. Each of these specimens was then mounted to a 20-gauge magnetic atomic force microscopy (AFM) disk made of stainless steel (Fig. 2a). Note that the levelness and smoothness of the specimen surface are crucial to ensure reliable measurements of the indentation modulus using IIT. Donnelly et al. [25] noted that the ratio of indentation depth to surface roughness should be maintained above 3:1 to minimize the effect of surface roughness on the measured mechanical properties. Furthermore, Hay and Pharr [34] also stressed the influence of the surface roughness on the mechanical properties derived from the contact depth and area function under the assumption that the specimen surface is flat. Accordingly, dry coarse polishing using a 400-grit sanding disk was performed to flatten the surfaces of the specimens and to ensure that both the top and bottom surfaces were parallel to each other. Next, polishing was performed using a perforated non-woven cloth (Buehler TexMet® PFootnote 1) and an oil-based diamond suspension fluid to accommodate the susceptibility of shale to water-based fluids. Removal of debris from the specimen surfaces was then accomplished using ultrasonic cleaning. Afterward, fine polishing was successively conducted using 12-, 9-, 3-, 1- and 0.3-µm abrasive aluminum oxide pads until a mirror-like finish was obtained [1, 48, 49]. Finally, the specimens were stored until they were ready to be tested.

Fig. 2
figure 2

a Polished shale cutting specimens mounted to 20-mm diameter AFM disks. b Comparison of nanoindentation results for specimens mounted on AFM disks and epoxy

Full size image

Note that in early trials, the mounting substrate was observed to have some effect on the indentation results: a lower indentation modulus was observed for specimens mounted on an epoxy substrate (Fig. 2b) than for specimens mounted on an AFM disk substrate (Fig. 2b). This difference was due to the more compliant support provided by the epoxy substrate. Furthermore, an epoxy substrate is non-magnetic and thus could shift as the specimen platform moves between the optical and indenter transducers. These limitations were addressed by opting for the magnetic AFM disk substrate, which can be securely held by the magnetic specimen platform.

2.2 Indentation test

2.2.1 Test equipment and procedure

Microindentation testing was performed on the prepared randomly oriented shale rock cutting specimens using a Hysitron TI-950 Triboindenter®Footnote 2 equipped with a 3D Omniprobe Berkovich tip capable of applying a load of up to 10 N. A trapezoidal loading function was applied in this study as shown in Fig. 3a. The associated load, P, and indentation depth, h, were recorded continuously throughout the testing and are shown in Fig. 3b. As the indenter was pushed into the specimen, the specimen exhibited both plastic and elastic deformation. Before unloading (at a depth of hmax, defined in Fig. 4), a 10-s holding period was specified to dissipate any viscous effects that could potentially influence the information obtained during the unloading process [34, 67, 79]. During the initial unloading process, the specimen recovers elastically, and the effect of plasticity is segregated [10,11,12, 23, 56, 66]. Note that for purely elastic specimens with no observed plastic deformation, the loading–unloading curve is reversible, and full specimen surface recovery is observed at the end of testing, unlike that shown in Fig. 4.

Fig. 3
figure 3

a Trapezoidal indentation test load function. b Indentation load–displacement plot

Full size image
Fig. 4
figure 4

Indentation surface profile before and after the test, where hmax and hf correspond to the maximum indentation depth and residual indentation depth, respectively

Full size image

Several specimens were tested at the beginning of this study to identify the best loading conditions. As the mechanical properties were to be derived based on the presumed elastic theory, crack/fracture formations during the test were minimized [28, 48, 49]. In this study, an optimum load of 0.3 N applied with a loading rate of 6.67 mN/s was determined to represent the most suitable loading for all considered specimens [48, 49]. Note that the effect of loading rate on the mechanical response was found to be minimal based on the results observed during this pilot study. Additionally, an indentation spacing of 15–20 times the observed maximum indentation depth was applied to avoid interactions between the indented regions [34].

2.2.2 Indentation modulus and hardness

In conventional mechanical testing, the stiffness is approximated from either the initial loading or unloading slope of the load–displacement curve. However, for the IIT technique, the stiffness, S, is acquired only from the initial unloading slope of the load–indentation depth curve, as shown in Fig. 3b and defined by Eq. 1 [10,11,12, 23, 56, 70, 74]. Two of the main properties used in IIT analysis are the indentation modulus, M, and hardness, H. The measured reduced indentation modulus measured, Mr, is a function of both the sample and indenter compliance, as shown in Eq. 2, in which the subscript i represents the properties of the indenter material and subscript s denotes the properties of the indented specimen. Thus, the indenter compliance must be deducted from the total compliance to obtain the true specimen modulus, Ms. For an anisotropic material such as rock, the correlation between the true specimen modulus and its elastic properties is complex due to the presence of numerous elastic parameters defining its stiffness [71, 72, 82,83,84, 87]. Another parameter that can be obtained from the indentation test is the hardness, calculated using Eq. 3, which is defined as the load-bearing capacity of the contact area obtained at the maximum applied load and can be simply determined by dividing the load, P, by the associated contact area, A. Further discussion of the contact area is provided in Sect. 2.3.1.

$$ S = \frac{{{\text{d}}P}}{{{\text{d}}h}} = \frac{2}{\sqrt \pi }M_{\text{r}} \sqrt A $$
(1)
$$ \frac{1}{{M_{\text{r}} }} = \left( {\frac{{1 - v^{2} }}{E}} \right)_{i} + \frac{1}{{M_{\text{s}} }} $$
(2)
$$ H = \frac{P}{A}$$
(3)

2.3 Theoretical background of indentation testing: contact mechanics

The study of the surface displacement due to a point load applied to an elastic half-space is known as contact mechanics. Solutions of the elastic contact mechanics for isotropic bodies were initially studied by Hertz and Boussinesq [9, 35]. Hertz [35] derived the elastic contact pressure distribution of two spherical solids with different radii based on the electrostatic potential theory; this is known as the Hertzian contact solution. A few years later, Boussinesq [9] provided a more specific approximation of the stress and displacement of an elastic half-space loaded by a rigid axisymmetric indenter (i.e., cylindrical and conical indenters) based on electrostatic potential theory. Sneddon [68] extended Boussinesq’s solution using the Hankel transformation to derive a general relationship between the load, displacement and contact area that is used as the basis of most IIT techniques today [5, 15, 24, 47, 90, 91].

An elastic solution for the contact mechanics of an anisotropic material was first proposed by Willis [87] in which paraboloid revolution was conducted through the implementation of the double Fourier transform of the Hertzian contact solution. The solution provided by Willis [87] has been found difficult to execute as it involves simultaneously solving six nonlinear integrations. To simplify Willis’ solution, Vlassak and Nix [82, 83] employed the surface Green’s function (Barnett and Lothe [7]) to determine the surface displacement for a circular contact area. Further refinement of the anisotropic contact solution was provided by Swadener and Pharr [71, 72] for conical and parabolic indenters, and by Vlassak et al. [84] for conical and spherical indenters.

Vlassak et al. [84] noted that the anisotropic contact mechanics solution provided by Swadener and Pharr [71, 72] was only applicable to a particular form of Green’s function, resulting in a less accurate approximation of mechanical properties. To address this limitation, Vlassak et al. extended the Barber’s theorem [6] to relate the contact area, load, displacement and stiffness of an anisotropic material. Their solution is used in this study to approximate the elastic mechanical properties and bedding orientations of the rock cutting specimens. This approach is validated in this study against previously published results by Jager et al. [40, 41] based on nanoindentation testing of TI wood materials.

2.3.1 Anisotropic contact mechanics solution

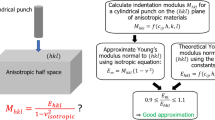
The anisotropic contact mechanics solution was adapted in this work to determine the mechanical properties of randomly oriented rock cuttings using the results obtained by microindentation tests. The TI elastic mechanical properties of rock can be described by the components of the stiffness matrix within a given material coordinate system. This material coordinate system is described by the orthogonal unit vector triad (x1, x2, x3), as shown in Fig. 5a. For TI rocks, the stiffness matrix, CTIijkl , is symmetrical and consists of five elastic constants. In this study, we considered x3 to be the axis of rotational symmetry perpendicular to the plane of symmetry (x1–x2) or the bedding orientation. The loading orientation with respect to the material axis was defined by the direction cosines k, with the expanded form of \( \left( {\beta_{1} ,\beta_{2} ,\beta_{3} } \right) \); or, i.e., \( \left( {{ \cos }\left( {90 - \delta } \right),0,{ \cos }\left( \delta \right)} \right) \), where δ is the angle between k and the axis of symmetry x3. When indented parallel and perpendicular to the bedding plane orientation, a direct correlation is available between the TI stiffness matrix and the indentation modulus, as will be shown in Sect. 2.3.2. When indented in any other direction, an anisotropic contact mechanics approach must be considered to obtain the elastic constants of the material.

Fig. 5
figure 5

a Measurement of surface displacement. b Barnett–Lothe configuration

Full size image

The stiffness matrix is related to the indentation modulus by means of the Green’s function [87]. A refined form of the surface Green’s function was defined by Vlassak and Nix [84] who implemented the Stroh’s formalism introduced by Barnett and Lothe [7]. The surface Green’s function, \( h(\theta ) \), defines the surface displacement, w(y), due to a point load, P, applied on the boundary of anisotropic half-space as

$$ w\left( {\mathbf{y}} \right) = \frac{1}{{8\pi^{2} \left| {\mathbf{y}} \right|}}\left[ {\beta_{k} B_{kn}^{ - 1} \left( {\frac{{\mathbf{y}}}{{\left| {\mathbf{y}} \right|}}} \right)\beta_{n} } \right] = \frac{h\left( \theta \right)}{r} $$
(4)

where the vector y is the position vector of observation point Q with respect to the point load P within a polar coordinate system (r, θ) (Fig. 5b); and Bkn is the symmetric and positive definite Barnett–Lothe matrix, which relates the TI stiffness matrix defined in the material coordinate system to the loading orientation, and can be obtained by

$$ B_{kn} \left( {\mathbf{t}} \right) = \frac{1}{{8\pi^{2} }}\mathop \int \nolimits_{0}^{2\pi } \left\{ {\left( {{\mathbf{mm}}} \right)_{kn} - \left( {{\mathbf{mn}}} \right)_{kl} \left( {{\mathbf{nn}}} \right)_{lm}^{ - 1} \left( {{\mathbf{nm}}} \right)_{mn} } \right\}{\text{d}}\phi $$
(5)

in which (ab)jk = aiCTIijkl bl; and (m, n, t) is the orthogonal unit vector triad, were t is the unit vector of y, located along the surface of the material, and m and n are the orthogonal unit vectors in the plane perpendicular to t. The orientation of (m, n, t) with respect to the material coordinate system is defined by angles ϕ and , where ϕ is the angle between vector m and the selected datum (i.e., k), and is the angle between the unit vector t and x2-axis on the surface of the half-space.

The extraction of the stiffness properties from the load–indentation depth data relies on the resulting contact area. The projected contact area for isotropic half-space created by a conical indenter is considered to be circular in shape [6], and the relationship between the contact area and the load-indentation depth for an isotropic half-space was described by Barber [6] using a Raleigh–Ritz approximation. By doing so, the demonstrated contact area maximized the applied load for a given penetration depth. A revision to Barber’s theorem to accommodate material anisotropy was defined by Vlassak et al. [84] by assuming an elliptical contact area with a major axis, a, minor axis, b and ellipse orientation, \( \varphi \) (Fig. 6a, b). The resulting contact pressure distribution under the indenter is given by [84]

$$ p_{1} \left( {x,y} \right) = \frac{{p_{0} }}{{\sqrt {1 - \left( {x^{2} /a^{2} } \right) - \left( {y^{2} /b^{2} } \right)} }} $$
(6)

where x and y are relative positions along a and b, as shown in Fig. 6b. The anisotropic pressure constant, p0, required for a unit indentation displacement is defined as

Fig. 6
figure 6

a Generalized saddle-shaped profile during/after indentation of an anisotropic material. b Anisotropic contact area

Full size image
$$ p_{0} = \frac{1}{{\pi b\alpha \left( {e,\varphi } \right)}}\quad {\text{where}},\quad \alpha \left( {e,\varphi } \right) = \mathop \int \nolimits_{0}^{\pi } \frac{{h\left( {\theta + \varphi } \right)}}{{\sqrt {1 - e^{2} \cos^{2} \theta } }}{\text{d}}\theta $$
(7)

As shown in Eq. 7, the pressure constant is a function of the surface Green’s function, \( h\left( {\theta + \varphi } \right) \), and the ellipse eccentricity, \( e = \sqrt {1 - \left( {{\raise0.7ex\hbox{${b^{2} }$} \!\mathord{\left/ {\vphantom {{b^{2} } {a^{2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${a^{2} }$}}} \right)} \). The observed eccentricity and contact area rotations (Fig. 6b) are due to the inclined loading, which will be discussed further in Sect. 3. When the contact ellipse orientation is aligned with the material coordinates or a chosen reference direction for the surface Green’s function \( h\left( {\theta + \varphi } \right) \), the angle \( \varphi \) in Eq. 7 is eliminated, and the surface Green’s function is reduced to \( h\left( \theta \right), \) as previously defined in Eq. 4. The elliptical axes ratio, b/a, is deduced by applying the Fourier transform to the surface Green’s function as follows [84]:

$$ \frac{b}{a} = \sqrt {\frac{{h_{0} + h_{c1} }}{{h_{0} - h_{c1} }}} $$
(8)

where \( h_{0} \) and \( h_{c1} \) are Fourier coefficients previously described by Argatov and Mishuris [4].

The following condition must be met for elastic materials to achieve the maximum displacement within the contact ellipse area [84]:

$$ h''\left( \theta \right) + h\left( \theta \right) \ge 0\quad {\text{for all}}\;\theta $$
(9)

where \( h''\left( \theta \right) \) is the second derivative of the surface Green’s function. Using Eqs. 6 and 9, the load, P(A), required to produce an elliptical area is given by

$$ P\left( A \right) = \mathop {\iint }\nolimits_{A}^{{}} \frac{{p_{0} u\left( {x,y} \right){\text{d}}x{\text{d}}y}}{{\sqrt {1 - \left( {x^{2} /a^{2} } \right) - \left( {y^{2} /b^{2} } \right)} }} $$
(10)

The solution to Eq. 10 can be obtained for a conical indenter by selecting the appropriate e and \( \varphi \). The resulting contact stiffness for a conical indenter is given by

$$ S = \frac{{{\text{d}}P}}{{{\text{d}}h}} = \frac{2}{\sqrt \pi }\sqrt A \frac{1}{{\alpha \left( {e,\varphi } \right)\left( {1 - e^{2} } \right)^{1/4} }} $$
(11)

The indentation modulus is then determined by comparing Eq. 1 with Eq. 11 and is given by

$$ M_{\text{eqv}} = \frac{1}{{\alpha \left( {e,\varphi } \right)\left( {1 - e^{2} } \right)^{1/4} }} $$
(12)

where \( \alpha \left( {e,\varphi } \right) \) is defined as described in Eq. 7. Thus, the analytical anisotropic indentation modulus described in this section was used in this study to predict the bedding orientation and the TI elastic constants of the specimens based on the microindentation results.

2.3.2 The transverse isotropic (TI) material case

An exact solution to the contact mechanics for a TI material was made available by Delafargue and Ulm [20]. In their approach, the loading orientation is initially considered to be aligned with the axis of symmetry of the TI rock or the x3-axis (where the direction cosines k are set to (0, 0, 1)), so the produced contact area is symmetrical and assumed to be circular (Fig. 7a). Therefore, the contact mechanics problem is derived similarly to the isotropic solution, and the indentation modulus can be determined based on:

$$ M_{3} = 2\sqrt {\frac{{C_{31}^{2} - C_{13}^{2} }}{{C_{11} }}\left( {\frac{1}{{C_{44} }} + \frac{2}{{C_{31} + C_{13} }}} \right)^{ - 1} } $$
(13)

where \( C_{31} = \sqrt {C_{33} C_{11} } > C_{13} \). An approximation of the TI contact problem for load applications parallel to the bedding orientation can be derived based on the anisotropic solution provided in Sect. 2.3.1, in which the produced contact area is assumed to be elliptical with the major and minor elliptical axes, respectively, parallel to the material axes x2 and x3 (Fig. 7b). Faithfully following the anisotropic solution developed by Vlassak et al. [84], Delafargue and Ulm [20] approximated the indentation modulus parallel to the plane of isotropy (the bedding orientation in rock) as given by:

$$ M_{1} \approx {\sqrt {{\sqrt{\frac{{C_{11}}}{{C_{33}}}}} {\frac{{C_{11}^{2} - C_{12}^{2} }}{{C_{11}} }}M_{3}}}$$
(14)
Fig. 7
figure 7

Contact areas: a perpendicular to the bedding contact area, and b parallel to the bedding contact area

Full size image

The solutions provided by Delafargue and Ulm [20] were therefore used in this study to validate the indentation moduli obtained parallel and perpendicular to the bedding orientation.

2.3.3 Validation of contact mechanics solutions

The contact mechanics solutions described in Sects. 2.3.1 and 2.3.2 are validated in this section. These validations were performed by comparing the forward contact mechanics solution developed in this study to results previously published by Jager et al. [40, 41] based on nanoindentation testing of TI wood materials. Jager et al. performed nanoindentation modulus measurements in the radial and the tangential orientations. Similar to the objective of the present study, they developed an inverse algorithm to identify the elastic constants (stiffness matrix) based on the experimental indentation modulus and the indentation loading direction with respect to the axis of symmetry.

The indentation moduli predicted based on the obtained elastic constants are provided in Fig. 8a (radial) and b (tangential), in which the lines labeled Jager-Min, Jager-Mean and Jager-Max represent the predictions, respectively, based on the minimum, average and maximum experimental indentation modulus data used as the input to the inverse algorithm. The experimental indentation modulus data are labeled Jager-exp in the figure, along with the associated experimental error bars. As the objective of this validation was to verify the forward contact mechanics algorithm developed in this study, the wood elastic constants obtained from the inverse algorithm were used to verify the configuration of the direction cosines used in this study. Using the same approximated elastic constants and measured loading orientations as Jager et al. as input to the forward algorithm in this study, the predicted indentation moduli were obtained based on the Fourier transform approximations of Vlassak et al. [84], with the results labeled as “2.3.1 Validation” in Fig. 8a, b. Validation was also performed using Delafargue and Ulm’s [20] TI solutions with the results shown as “2.3.2 Validation” in Fig. 8a, b. The forward algorithm approximations obtained in this study fall within the prediction bounds of the Jager et al. model. However, they do not match the experimental results precisely due to uncertainties in the experimental and optimization results (related to the optimization bounds). Note that errors of less than 2% were observed when comparing the approximations obtained in this study to the experimental results (labeled as “Jager-exp”).

Fig. 8
figure 8

Forward validation results: a Jager et al. [41] indentation moduli in the radial direction, and b Jager et al. [41] indentation moduli in the tangential direction

Full size image

3 Results and discussion

3.1 Microindentation test results

Microindentation testing was performed on several shale rock cutting specimens taken from the PW-B [48, 49] and Marcellus samples. Up to ten indentations were performed on each cutting specimen. The test results are presented in Fig. 9, in which each data point represents the average indentation modulus and hardness obtained for each specimen with an unknown orientation. The error bars in this figure represent the standard deviation range for each cutting specimen. The average indentation depth was 3651 ± 660 nm and 3352 ± 412 nm for the PW-B and the Marcellus samples, respectively. It should be noted that the obtained ratio of the indentation depth to the surface roughness is greater than the ratio recommended by Donnelly et al. [25]. These collected indentation moduli were used as input into the inverse algorithm to obtain the elastic constants of the material, as described in the next section.

Fig. 9
figure 9

Microindentation results for PW-B and Marcellus shale rock cutting specimens

Full size image

3.2 Approximation of elastic constants

The approximation of the indentation modulus for a given loading/cutting orientation and stiffness matrix is described in Sect. 2.3. In this study, however, a set of indentation moduli was experimentally obtained to infer the elastic constants and loading/cutting orientations. To do so, a constrained inverse algorithm was developed to identify the TI stiffness matrix (Eq. 15) of all rock cuttings belonging to the same formation from the microindentation results. Recall that a direct correlation exists between the indentation modulus and TI stiffness matrix when loading is performed perpendicular and parallel to the bedding plane orientation. This is due to the alignment of the loading orientation, k, with the material coordinate system (x1, x2, x3) (Fig. 10a). When indented in any other orientation, the direction cosines, k, no longer align with the material coordinate system. As a result, the produced contact area is rotated by an angle (Fig. 10b), eventually affecting the Green’s function and the obtained indentation modulus (Eqs. 4–5). The developed inverse algorithm was therefore used to determine the TI stiffness matrix and corresponding cutting orientations based on the indentation moduli obtained from the randomly oriented shale cutting specimens (Fig. 8). Note that unlike the inverse algorithm developed by Jager et al. [40, 41], which only approximates the elastic constants for known loading orientations, the inverse algorithm developed in this study predicts both the unknown loading orientations and the elastic constants (stiffness matrix). This was performed to replicate the challenge of determining the bedding plane orientation of small samples such as drill cuttings in a size range reported to be smaller than 7 mm [8, 26, 45, 46, 51, 52, 62, 64, 76, 89].

$$ {\mathbb{C}}^{\text{TI}} = \left[ {\begin{array}{*{20}c} {C_{11} } & {C_{12} } & {C_{13} } & 0 & 0 & 0 \\ {C_{12} } & {C_{11} } & {C_{13} } & 0 & 0 & 0 \\ {C_{13} } & {C_{13} } & {C_{33} } & 0 & 0 & 0 \\ 0 & 0 & 0 & {C_{44} } & 0 & 0 \\ 0 & 0 & 0 & 0 & {C_{44} } & 0 \\ 0 & 0 & 0 & 0 & 0 & {\frac{{\left( {C_{11} - C_{12} } \right)}}{2}} \\ \end{array} } \right] $$
(15)
Fig. 10
figure 10

Configuration of load–material axes: a perpendicular (aligned), and b inclined loadings

Full size image

The inverse algorithm was implemented as an error minimization problem using the MATLAB® Global optimization toolbox [75]. The algorithm minimizes the error or difference between the predicted indentation modulus, Mpred and the experimental indentation modulus, Mexp, as expressed by [40, 41]:

$$ E\left( {C_{ijkl}^{\text{TI}} ,\delta_{k} } \right) = \arg \hbox{min} \mathop \sum \limits_{k = 1}^{n} \left\| {M_{k}^{ \exp } - M^{\text{pred}} \left( {{\mathbb{C}}^{\text{TI}} ,\delta_{k} } \right)} \right\|^{2} $$
(16)

Recall that the predicted indentation modulus obtained by the analytical approach described in Sect. 2.3.1 is a function of both the TI elastic constants, CTIijkl , and the direction cosines, (1, 2, 3), which relate the loading orientation to the bedding orientation. Several inequality constraints are prescribed as listed in Eq. 17 to ensure a positive definite stiffness matrix [50]. Two additional inequality constraints were included to improve the approximation of the C13 and C44 constants. The approximated Poisson’s ratio was bound within 0.1 to 0.4 to improve the C13 approximation, as provided in Eq. 18. A constraint to the Thompsen’s δ-parameter was set to be less than 1 to bound C44, as presented in Eq. 19.

$$ \begin{aligned} & C_{11} + C_{12} + C_{33} + \tilde{C} > 0 \\ & C_{11} + C_{12} + C_{33} - \tilde{C} > 0 \\ & C_{11} - C_{12} > 0 \\ & C_{44} > 0 \\ & \tilde{C}^{2} = {C_{11}^{2} + C_{12}^{2} + 8C_{13}^{2} + C_{33}^{2} + 2C_{11} C_{12} - 2C_{11} C_{13} - 2C_{12} C_{33} } \\ \end{aligned} $$
(17)
$$ \upsilon = \frac{{C_{12} - C_{13}^{2} /C_{33} }}{{C_{11} - C_{13}^{2} /C_{33} }},\quad 0.1 \, < \upsilon < \, 0.35 $$
(18)
$$ \delta = \frac{1}{2}\frac{{\left( {C_{13} + C_{44} } \right)^{2} - \left( {C_{13} - C_{44} } \right)^{2} }}{{C_{33} \left( {C_{13} - C_{44} } \right)}},\quad \delta < 1 $$
(19)

The preliminary results of the inverse algorithm with no constraints showed some instabilities (i.e., widely spread solutions) in the predicted stiffness matrix and loading orientations. The observed instabilities were due to the ill-posed nature of the nonlinear inverse algorithm, the high-dimensionality of the predicted unknowns, and the input variability associated with the experimental data [16, 21, 32, 33, 44]. In this study, there were five unknowns affiliated with the stiffness matrix, \( {\mathbb{C}}^{\text{TI}} \), and a set of N unknowns affiliated with the loading/cutting orientations, δk (i.e., 5 + N). The total number of unknowns is related to the number of experimental data points being considered as input in the analysis (i.e., N). Several of the constraints described previously (Eqs. 17–19) were therefore introduced into the global optimization algorithm to accommodate its nonlinearity while at the same time improving its predictive capabilities and reducing the computational cost of solving the inverse algorithm [16, 21, 32]. The predicted results were observed to be more consistent following the inclusion of the constraints.

The observed variations in the experimental data produced uncertainty in the predicted parameters (\( {\mathbb{C}}^{\text{TI}} ) \) and constants (δk). In order to forecast the effects of these uncertainties on the corresponding predictions, the constrained problem was modeled using a Monte Carlo simulation, a statistical sampling methodology, to generate the input of the inverse algorithm [36, 54, 59, 63]. To do so, the experimental datasets were modeled as sets of random numbers generated by a Gaussian distribution random number generator available in the MATLAB® syntax based on the mean and standard deviation of the experimental measurements. One hundred sets of random numbers were generated and input into the inverse algorithm accordingly.

The resulting elastic constants and cutting orientation approximations are presented in Table 1 and Fig. 11. The predicted bedding orientations are plotted against the experimental moduli shown by the square dots in Fig. 11. The yellow line represents the indentation modulus distribution based on the predicted elastic constants for the loading orientations 0° <  < 90°. The experimental results parallel ( = 90°) and perpendicular ( = 0°) to the bedding orientations are, respectively, labeled M1,exp and M3,exp. To validate the elastic constants obtained from the inverse algorithm, a UPV test was conducted on larger cube specimens obtained from the same formations, with the results provided in the next section.

Table 1 Predicted elastic constants (GPa) from the proposed constrained inverse algorithm
Full size table
Fig. 11
figure 11

Experimental indentation modulus versus predicted bedding orientation obtained for a PW-B and b Marcellus rock cuttings. Sample Gaussian distributions for one data point in each graph are shown in the red box insets (colour figure online)

Full size image

4 Results validation: UPV Test

The UPV test was used in this study to validate the elastic constants obtained by the proposed methodology. The UPV test is a non-invasive dynamic test that measures the mechanical properties and quality of a material. It is typically applied to concrete, wood and rock materials that are assumed to be isotropic. Though the test is quick to run, equipment limitations require a minimum sample size of 1–2 cm on each side [18, 39, 80]. Thus, the UPV test is not suitable for drill cuttings. The interpretation of the mechanical properties (E and v) is performed based on the measured elastic wave velocities. For an isotropic material, the measured wave velocities are similar in any direction. This observation, however, does not hold for most rocks as they are TI materials, for which E and v vary with the measurement direction. For this reason, the UPV TI test configuration was applied to evaluate the mechanical properties of the shale rocks in this study.

The original UPV test configuration for measuring TI elastic properties was proposed by Podio et al. [61], who measured the elastic waves in multiple core plugs with various bedding plane orientations. However, measurements using multiple core plugs are time-consuming and subject to material variability from specimen to specimen. Jacobsen and Johansen [42] and Wang et al. [85] introduced an improved approach applying UPV to a single-core plug to measure the TI properties of shale rocks. In their approach, transducers were attached at various locations along the sample to measure the variations in the elastic wave velocities due to the anisotropy observed in the rock. Following this approach, a modified single-core plug UPV test was used in this study to validate the results obtained by microindentation.

The UPV test measurements were performed on small block samples with a minimum side length of 2.5 cm under ambient temperature and humidity. Endcap assemblies were attached on two opposite, parallel sides of the cubes using a suitable couplant (Fig. 12). Vibrational waves were then sent from the transmitter endcap and received by the receiver endcap to capture the wave travel time. The measured travel time and travel distance were used to compute the corresponding wave velocity, which is simply defined as the distance travelled over the elapsed time. The computed velocities were then used to evaluate the elastic constants of the samples according to Eq. 20 [42, 85, 88]. Two of the most common elastic wave velocities measured are compressional (P−) and shear (S−) wave velocities, identified as Vp and Vs, respectively, according to the density of the material.

$$ \begin{aligned} & C_{11} = \rho V_{{{\text{p}}0}}^{2} \quad C_{33} = \rho V_{{{\text{p}}90}}^{2} \quad C_{44} = \rho V_{{{\text{s}}1,90}}^{2} \quad C_{66} = \rho V_{{{\text{s}}2,90}}^{2} \\ & C_{12} = C_{11} - 2C_{66} \quad \sqrt {C_{33} C_{12} + C_{66}^{2} } - C_{66} < C_{13} < \sqrt {C_{33} C_{12} } \\ \end{aligned} $$
(20)
Fig. 12
figure 12

Ultrasonic pulse velocity (UPV) test setup

Full size image

The measured elastic wave velocities (Vp, Vs), bulk modulus (K), shear modulus (µ), Young’s modulus, Poisson’s ratio and constrained modulus (\( \varrho \)) are presented in Table 2. The equations used to obtain K, µ, E, v and \( \varrho \) are presented in Eq. 21. The associated elastic constants measured by UPV are presented in Table 3. A comparison of the results obtained by UPV and the proposed microindentation–inverse algorithm method is shown in Fig. 13, in which MDU1 and MDU3 refer to the indentation modulus for loading parallel (x1) and perpendicular (x3) to the bedding direction, respectively, and were determined based on the obtained elastic constants CTIijkl and the TI contact mechanics approximation (Eqs. 13–14). A satisfactory agreement between the two methods can be observed in Fig. 13.

$$ K = \rho \left( {V_{\text{P}}^{2} - \frac{4}{3}V_{\text{S}}^{2} } \right);\quad \mu = \rho V_{\text{S}}^{2} ;\quad E = \frac{9K\mu }{3K + \mu };\quad \nu = \frac{3K - 2\mu }{{2\left( {3K + \mu } \right)}}; \quad M = \rho V_{\text{P}}^{2} $$
(21)
Table 2 UPV measurement results and interpretation
Full size table
Table 3 Elastic constants (GPa) obtained from the UPV test
Full size table
Fig. 13
figure 13

Comparison of elastic mechanical properties determined by UPV and microindentation tests for a PW-B and b Marcellus samples

Full size image

5 Conclusion

The stiffness and bedding plane orientations of shale rock cuttings were determined in this study by means of microindentation measurements performed to obtain their indentation moduli. A constrained inverse algorithm was developed using anisotropic contact mechanics solutions to identify the elastic mechanical properties of the rock cuttings, while accommodating shale anisotropy. The experimental indentation moduli were then used as the input to the proposed inverse algorithm in order to determine the optimized TI stiffness and cutting orientation combinations that predict the best match to the experimentally obtained indentation moduli. This objective was achieved using an error minimization procedure. Good agreement was observed between the stiffness results obtained for the cuttings using the microindentation test with the proposed inverse algorithm and the UPV test performed on larger samples. The successful implementation of the developed methodology will lead to a more cost- and time-efficient approach for measuring the elastic mechanical properties of rocks using cuttings, especially when compared to the cost and time associated with conventional core testing methods.