1 Introduction

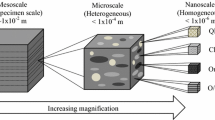
Shales are probably one of the most complicated and intriguing natural materials present on earth. The multiphase composition is permanently evolving over various scales of length and time, creating in the course of this process the most heterogeneous class of materials in existence. The heterogeneities manifest themselves from the nanoscale to the macroscopic scale (see multiscale structure in Fig. 1), which all contribute to a pronounced anisotropy and large variety of shale macroscopic behavior. Knowing and predicting the anisotropy plays a critical role in many fields of exploitation, ranging from seismic exploration (log-data interpretation), to well drilling (well bore stability) and production [28]. But so far all attempts have failed to identify the sources of anisotropy, and link mechanical (seismic) properties to composition and structure. The key question that must be addressed is whether there is a link between mineralogy of the clay particles (primarily composed of sandwiched Al–Si sheets) and their in-situ mechanical properties in highly compacted natural materials systems like shales?

Fig. 1
figure 1

Multiscale structure of shales (adapted from [30]): From top-down The macro-scale is the scale of visible deposition layers and detrital grains. The micro-scale (SEM picture) is the scale of a textured clay composite intermixed with silt size quartz grains. At the nano-scale (SEM picture, bar in right corner = 100 nm), individual clay particles are visible to form a nano-granular material. At a scale still below, one can distinguish different clay minerals from their mineral structure: kaolinite, smectite (displayed), illite, etc

Full size image

In this paper we attempt to provide a first answer to this question. To achieve our goal, we use relatively new advances in nanotechnology to investigate the sources of anisotropy of shale materials. In particular, we will apply a recently developed statistical grid-nanoindentation technique [4] to shale materials of different mineralogy and macroscopic properties. The paper is structured as follows: we first present the technique, and illustrate how the meanwhile classical nanoindentation technique can be adapted for highly heterogeneous and anisotropic materials, like shales, in order to extract meaningful material properties. This technique is then applied to shales of different mineralogy and macroscopic properties. In particular, we will focus on what these different shales have in common, and compare the indentation results with macroscopic small strain elasticity properties.

2 Materials and methods

2.1 Nanoindentation on natural composites

It is now well established that the response of a material upon the reversal of contact loading provides access to the elastic properties of the intended material (for recent review see [21] and [3]). The indentation technique consists of establishing contact between an indenter of known geometry and mechanical properties (typically diamond) and the indented material for which the mechanical properties are of interest, and subsequently acquiring the continuous change in penetration depth h as a function of increasing indentation load P (P–h curve, see Fig. 2). Typically, the extraction of mechanical properties is achieved by applying a continuum scale mechanical model to derive two quantities, indentation hardness H and indentation modulus M:

$$ H {\mathop = \limits^{\rm def}} \frac{P}{A_{\rm c}} $$
(1)
$$ M {\mathop = \limits^{\rm def}} \frac{\sqrt{\pi}}{2} \frac{S}{\sqrt{A_{\rm c}}}. $$
(2)

All quantities required to determine H and M are directly obtained from the P–h curves, with the exception of the projected area of contact A c. Chief among these are the maximum applied force P max and corresponding maximum depth h max, the unloading indentation stiffness \(S = ({\rm d}P/{\rm d}h)_{h=h_{\max}},\) and residual indentation depth h f upon full unloading of the material surface (Fig. 2). The contact area A c can also be extrapolated from the maximum depth h max. Furthermore, M can be linked to the elastic constants C ijkl of the indented material by applying a linear elastic model to the data [10, 26, 33, 36]. For instance, in the isotropic case, M reduces to the plane–stress elastic modulus,

$$ M = \frac{E}{1 - \nu^{2}} = \frac{C_{11}^{2} - C_{12}^{2}}{C_{11}},$$
(3)

where E is the Young’s modulus, ν the Poisson’s ratio; C 11=C 1111 and C 12=C 1122 are the forth order stiffness tensor coefficients of the indented isotropic material. In contrast to the isotropic case, for which the indentation modulus is the same for all directions of indentations, the indentation modulus of anisotropic materials depends on the direction of indentation. For instance, in the case of a transverse isotropic material, the indentation modulus obtained by indentation in the axis x3 of symmetry relates to the five independent C ijkl coefficients of the material in the following way [9, 12]:

$$ M_{3} = 2\,\sqrt{\frac{C_{31}^{2} - C_{13}^{2}}{C_{11}}\,\left( \frac{1}{C_{44}} + \frac{2}{C_{31} + C_{13}} \right)^{-1}}. $$
(4)

In turn, for indentation normal to the axis of material symmetry (direction x1 or x2) the indentation modulus reads [6]:

$$ M_{1} = \sqrt{ \frac{C_{11}^{2} - C_{12}^{2}}{C_{11}} \sqrt{ \frac{C_{11}}{C_{33}}} M_{3}}, $$
(5)

where we employ the reduced notations C 33=C 3333, C 13=C 1133=C 3311, \(C_{31} = \sqrt{C_{11}\;C_{33}} > C_{13}\) and C 44=C 2323=C 1313.

Fig. 2
figure 2

Typical indentation force–indentation depth curve, P–h, performed on a homogeneous material

Full size image

The classical indentation methods are restricted to monolithic systems as the underlying indentation model assumes indentation into a homogeneous material half-space. Very recently, Constantinides and Ulm [4] extended the domain of application of this powerful technique to heterogenous multi-scale and multi-phase composite materials, a category composing the majority of solids, including shales. The focus of the next sections is to show how this powerful technique can be employed for highly heterogeneous materials, like shales.

2.1.1 Gedanken experiment

Proposition 1 Consider a material to be composed of two phases of different mechanical properties and characterized by a length scale D . If the indentation depth is much smaller than the characteristic size of the phases, h ≪ D, then a single indentation test gives access to the material properties of either phase 1 or phase 2. If, in addition, a large number of tests (N ≫ 1) is carried out on a grid defined by a grid spacing ℓ that is larger than the characteristic size of the indentation impression, so to avoid interference in between individual indentation tests, and much larger than the characteristic size of the two phases, \(\ell \sqrt{N}\gg D,\) so that the locus of indentation has no statistical bias with respect to the spatial distribution of the two phases, the probability of encountering one or the other phase is equal to the surface fraction occupied by the two phases on the indentation surface. Consider next an indentation test performed to a maximum indentation depth that is much larger than the characteristic size of the individual phases, h≫ D. In this case, the indentation response is the average response of the composite material, and the properties extracted from such an indentation experiment are representative in a statistical sense of the average properties of the composite material.

This simple gedanken experiment has all the ingredients of the statistical grid-indentation technique that needs to be performed when it comes to natural composite materials. The key results of such analysis are distributions and their derivatives (e.g., histograms or frequency diagrams) of mechanical properties determined by a large number of indentation experiments at a specific scale of material observation defined by the indentation depth. Generally speaking, small indentation depths, roughly h/D < 1/10 [2] provide access to mechanical phase properties, while greater indentation depths (h/D > 6) provide access to homogenized material properties of the composite. In what follows, we will refer to the first as nanoindentation tests and to the second as microindentation tests.

2.1.2 Deconvolution technique

The above gedanken experiment is based on the premise that the two phases have two properties of sufficient contrast so that these can be separated in small scale indentation tests. Natural composite materials are generally more complex, requiring the use of some elementary statistics relations to analyze the indentation data. Let us assume that the distribution of the mechanical property x=M of each phase J is best approximated by the normal or Gaussian distribution:

$$ p_{J} (x) = \frac{1}{\sqrt{2 \pi s_{J}^{2}}} \exp \left( - \frac{\left( x - \mu_{J}\right)^{2}}{2s_{J}^{2}}\right), $$
(6)

where μ J is the arithmetic mean of all N J values of each phase, while the standard deviation s J is a measure of the dispersion of those values:

$$ \mu_{J} = \frac{1}{N_{J}} \sum\limits_{k=1}^{N_{J}} x_{k};\quad s_{J}^{2} = \frac{1}{N_{J}-1} \sum\limits_{k=1}^{N_{J}} \left( x_{k} - \mu_{J} \right)^{2}. $$
(7)

The case of a single phase, n=1, corresponds to the case of a homogenous material, for which mean value and standard deviation describe the properties of the material in a statistical sense. In the case of several phases (J=1, n), that all follow a normal distribution, and which do not (mechanically) interact with each other, the overall frequency distribution of the mechanical property x=M obeys to the following theoretical probability density function:

$$ P (x) = \sum\limits_{J=1}^{n} f_{J} p_{J} (x), $$
(8)

where f J =N J /N is the surface fraction occupied by phase J on the indented surface, which is subjected to the constraint:

$$ \sum\limits_{J=1}^{n} f_{J} = 1. $$
(9)

The problem so defined involves 3n − 1 unknowns; that is three unknown per phase, μ J , s J , f J , reduced by the compatibility condition (9). If empirical frequency densities or response distributions are obtained by nanoindentation in form of discrete values P i one can determine the unknowns by minimizing the standard error:

$$\begin{array}{*{20}c} \hbox{Find}\;\left( \mu_{J}, s_{J}, f_{J}\right)\;\hbox{from} \min \sum\limits_{i=1}^{m} \frac{\left( P_{i} - P \left(x_{i}\right) \right)^{2}}{m}\\ \hbox{subjected to}: \\ \sum\limits_{J=1}^{n} f_{J} = 1, \end{array}$$
(10)

where P i is the observed value of the experimental frequency density; \(P \left(x_{i}\right) = \sum_{J=1}^{n} f_{J} p_{J} \left( x_{i}\right)\) is the value of the theoretical probability density function shown in Eq. (8) at point x i , and m is the number of intervals (bins) chosen to construct the histogram. The number of observed values P i should exceed the number of unknowns, i.e. 3n − 1 ≤ m, and must necessarily be smaller than the total number of tests N > m carried out on the surface.

2.2 Materials

2.2.1 Sample preparation

Cylindrical shale specimens were cored in three perpendicular directions of shale cuttings, and stored in desiccators at their natural relative humidity until testing. For the indentation testing, the cylinder specimens were cut into slices of approximate thickness 5–10 mm. The surfaces were ground and polished with silicon carbide papers and diamond particle suspension to obtain flat and smooth surface finish. The roughness of the surface was checked for some specimen analyzing AFM images and was found to be on the order of 90 nm. The mineral composition was determined from X-ray diffraction measurements and translated into volume fractions using known mineral densities. The total porosity ϕ of the shale cuttings was obtained from Mercury Porosimetry, and was translated into the clay packing density by:

$$ \eta = 1 - \frac{\phi}{1 - f_{\rm I}}, $$
(11)

where f I is the silt (non-clay) inclusion fraction known from mineralogy. The mineralogy of the three shale materials is given in Table 1.

Table 1 Mineralogy (volume percent) and poromercury intrusion data for three shale materials
Full size table

2.2.2 Grid indentation testing

Force driven nanoindentation tests and microindentation tests were performed on the three shale materials with a diamond Berkovich indenter using a Triboindenter of Hysitron Inc. By nanoindentation we refer to indentation tests operated to average indentation depths of h = 200–300 nm. This indentation depth was chosen to restrict effects of the surface roughness, which is an experimental restriction to small scale testing of such materials. If we take the characteristic size of clay particles on the order of 500–1,000 nm, the chosen nanoindentation depth only satisfies approximately the scale separability condition for phase testing, h/D < 10. The repeatability of the test procedure (incl. surface preparation) was checked by several series of 100 indentation tests carried out on different specimen surfaces of the shale sample, and the data (indentation modulus, hardness) were analyzed statistically, using the deconvolution technique described above. The difference between test series performed on different specimen surfaces was found to be smaller than 10%.

Each indentation test series consisted of 100 tests on a surface carried out on a 10 × 10 grid of constant grid-size of 50,000 nm, which is sufficiently large that interactions between adjacent indents (of size ∼6 h) are avoided. In each test, the indentation force P and the indentation depth h was recorded for a loading, holding and unloading phase. The hardness H and the indentation modulus M were determined from the measured maximum force P max and the initial unloading slope \(S = ({\rm d}P/{\rm d}h)_{h = h_{\max}}\) according to relations (1) and (2). The contact area A c was estimated using the Oliver and Pharr method [20].

3 Indentation results

3.1 Indentation modulus–hardness relations

Figure 3 displays the ensemble of nanoindentation results in a log–log plot of indentation modulus versus indentation hardness. On-average, the M–H scaling relations for the different series is very similar, \(M \propto \sqrt{H}.\) This is not surprising, but rather a confirmation of the relevance of the employed continuous indentation analysis. Indeed, as M scales with A −1/2c (Eq. 2) and H with A −1c (Eq. 1), one would expect that \(M \propto \sqrt{H},\) provided that each individual indentation test satisfies the separation of scale condition so that a continuum analysis can be carried out with some confidence. The M–H scaling, therefore, is a good indication that the data sampled are of random nature, which is a necessary condition to employ the statistical analysis method presented next.

Fig. 3
figure 3

Nanoindentation results: indentation modulus–indentation hardness (M–H) scaling relations for the three shale materials tested in bedding (x3) and normal to the bedding direction (x1)

Full size image

3.2 Indentation modulus frequency densities

Figures 4, 5 and 6 display the experimental frequency distributions of the (nano)indentation modulus for the three shale materials, together with fitted frequency distribution functions using the deconvolution technique. In the application of the deconvolution technique, we sought for the minimum number of phases n required to represent the experimental frequency densities accurately. It turned out that n=3 is largely sufficient to model the data. Some of the experimental frequency densities display one dominating phase, while other show a bimodal or tri-modal frequency distributions. An important observation is that indentation moduli smaller than ∼5 GPa are mostly representative for indentation into a highly heterogeneous material dominated by large pores or surface roughness, which is observed in force-driven indentation depths by either excessive indentation depths (h > 500 nm) or by discontinuous P–h curves (break of self-similarity). Such indentation responses violate the separation of scale condition for continuum indentation analysis, and need to be excluded from further analysis of intrinsic properties. On this basis, we identify for each shale material a characteristic nanoindentation modulus. This nanoindentation modulus for indentation in the x1 and x3 directions, M 1=M (x1) and M 3=M(x3), correspond to the nanoindentation response that dominates the shale behavior, and that satisfies simultaneously the separation of scale condition h/D < 10. The values are summarized in Table 2 (labeled ‘Nano’), together with the applied maximum indentation force P max and the characteristic indentation depth h max upon unloading.

Fig. 4
figure 4

Nanoindentation modulus deconvolution for Shale #1. Bin-size for histogram construction is ΔM=2.5 GPa. x3 stands for indentation in the bedding direction, and x1 for indentation into the bedding plane

Full size image
Fig. 5
figure 5

Nanoindentation modulus deconvolution for Shale #2. Bin-size for histogram construction is ΔM=2.5 GPa. x3 stands for indentation in the bedding direction, and x1 for indentation into the bedding plane

Full size image
Fig. 6
figure 6

Nanoindentation modulus deconvolution for Shale #3. Bin-size for histogram construction is ΔM=2.5 GPa. x3 stands for indentation in the bedding direction, and x1 for indentation into the bedding plane

Full size image
Table 2 Characteristic values of nano- and microindentation results on three shale materials: P max is the applied maximum indentation force, h max is the indentation depth at unloading and M(xi) is the governing indentation modulus
Full size table

We also carried out microindentation tests on the three shale materials to maximum indentation depths of 1,500–2,500 nm. We then employed the deconvolution technique to extract the relevant indentation moduli. Figure 7 shows a typical deconvolution result we obtain in micro-indentation tests. In contrast to the nanoindentation tests, there is a clear trend towards a homogeneous composite response with one phase dominating the overall response. The corresponding indentation moduli are also summarized in Table 2 (labeled ‘Micro’), together with the applied maximum indentation force P max and the characteristic indentation depth h max upon unloading. A remarkable result is that the microindentation stiffness values extracted from the unloading portion at maximum indentation depths of 1,500–2,500 nm almost coincide with the nanoindentation stiffness values obtained from indentation tests operated to 200–300 nm. It therefore appears that the found elasticity values are characteristic, for each particular shale material, of the clay fabric response, which manifests itself at a scale of hundreds of nanometers and above.

Fig. 7
figure 7

Microindentation modulus deconvolution for Shale #2 for indentation in the bedding direction x3. In contrast to the nanoindentation response (compare with Fig. 5 top), there is a clear trend towards a homogeneous composite response with one phase dominating. Bin-size for histogram construction is ΔM=2.5 GPa

Full size image

4 Discussion

It is not surprising that the indentation stiffness increases with the clay packing density, as a matching of the characteristic packing densities and the indentation moduli in Tables 1 and 2 shows. However, as Fig. 8 shows, the nano- and the microindentation stiffness values scale with the clay packing density almost linearly. Most remarkable is the fact that a fitted straight line to those values yields a zero stiffness for a clay packing density of the clay fabric of roughly 50%. This particular behavior is a hallmark of granular materials, for which the random loose-packed limit (RLP) is known to be 52% [16], below which no continuous force path can be established through the granular assembly. In return, highly compacted shales have typical packing densities far above the RLP (see Table 1). A second interesting observation is that the stiffness–packing density scaling in Fig. 8 is (almost) not affected by the different mineralogy of the three tested shale materials; but only by the packing density and the mineral orientation (or deposition direction). The latter dependence is readily understood from the indentation stiffness relations (4) and (5) for transversely isotropic materials. An extrapolation of the experimental M(xi) − η scaling relations in Fig. 8 to η=1 provides a means to evaluate the asymptotic contact stiffness in the bedding direction (x3) and in the bedding plane (x1):

$$ \hbox{Nano}: M_{1}(\eta = 1) = 34.0\,\hbox{GPa};\quad M_{3} (\eta = 1) = 21.4\,\hbox{GPa}; \quad \frac{M_{1}}{M_{3}} = 1.6 $$
(12a)
$$ \hbox{Micro}: M_{1}(\eta = 1) = 29.0\,\hbox{GPa};\quad M_{3}(\eta = 1) = 18.1\,\hbox{GPa};\quad \frac{M_{1}}{M_{3}} = 1.6. $$
(12b)
Fig. 8
figure 8

Indentation modulus–clay packing density scaling (M − η) from nanoindentation (top) and microindentation (bottom). x3 stands for indentation in the bedding direction, and x1 for indentation into the bedding plane. To check the repeatability of the testing procedure, two series of indentation tests on two different surfaces of the shale samples were carried out in some cases, in which case two values are reported for the same clay packing density

Full size image

4.1 Comparison with reported clay mineral data

Unlike many other minerals, clay stiffness values are extremely rare in handbooks [19]. To our knowledge, the only direct measurements of the anisotropic elasticity of clay minerals were reported for large muscovite crystals [19], possessing transversely isotropy: C 11=178 GPa, C 33=55 GPa, C 44=12 GPa, C 12=42 GPa, C 13=15 GPa, or equivalently expressed in terms of indentation stiffness (Eq. 4) and (Eq. 5),

$$ M_{1, \exp}^{0} = 118\,\hbox{GPa};\quad M_{3, \exp}^{0} = 46\,\hbox{GPa};\quad \frac{M_{1, \exp}^{0}}{M_{3, \exp}^{0}} = 2.6. $$
(13)

The values are found to be much higher than the values (Eq. 4) we determined by nano- and microindentation, both in absolute terms and in terms of the anisotropy ratio M 1/M 3. The main difficulty of measuring the mineral elasticity stems from the fact that clay particles are too small to be tested in pure solid form. Several attempts to overcome this difficulty have been reported (Table 3):

  • The stiffness of compacted clay samples has been measured and extrapolated to a zero porosity assuming that this extrapolation technique yields a ‘pure clay’ stiffness value [15, 18, 32]. The reported stiffness values vary from 10–30 GPa, which comes closer to our values (Eq. 4). However, the main difficulty of these techniques is the assumed isotropy of the extrapolated clay stiffness values, which is not what we find by nano- and microindentation. Very recently, Prasad et al. [22] have made some dynamic measurement of clays using atomic force acoustic microscopy (AFAM). They reported a very low Young’s modulus for dicktite of 6.2 GPa, which is much lower than what we find for the porous clay composite, and which is as low as the first peak values we observe in the deconvolution attributable to imperfect surface conditions (see Figs. 4, 5, 6).

  • Ultrasonic velocities of composite mixture of individual clay particles (powder) diluted, at various concentrations, in an epoxy matrix have been measured [35]. Using a backward homogenization derivation, the Young’s modulus for randomly distributed clay particles was found to be on the order of 50–60 GPa for kaolinite, 65–80 GPa for illite, 40–50 GPa for montmorillonite, and greater than 100 GPa for Chlorite. These results were found to be consistent with theoretical estimates of single crystal elastic properties by Katahara (1996) for kaolinite, illite and chlorite, based on data of Alexandrov and Ryzhova (1961; cited from [35]). Translated into indentation moduli, the values are somewhat higher than the ones we obtain by nanoindentation.

Table 3 Reported elastic stiffness values of clay minerals. For purpose of comparison, values are expressed, if possible, as indentation stiffness
Full size table

The scarcity of experimental values for solid clay stiffness and the large range of reported values highlight the difficulty to assess the intrinsic elasticity of single clay crystals. We performed some nanoindentation tests on a kaolin powder composed of 97% kaolinite (EPK Kaolin Footnote 1, Feldspar Corporation, Atlanta Georgia) having an average particle size of 1.36 × 10−6 m, a specific surface area of 24.25 m2/g, and a loose (dense) mass density of 519–740 kg/m3. Using indentation depths of 70–90 nm, that is an order of length magnitude smaller than the grain size, we obtain indentation stiffness values of

$$ \hbox{EPK Kaolin}: M_{\exp}^{0} = 40.3 \pm 8.8\,\hbox{GPa}. $$
(14)

Figure 9 displays an atomic force microscopy image of a kaolin powder grain on which we indented, together with five force–indentation depth curves, from which we determine, from the unloading branch, the indentation stiffness. The order of magnitude of the indentation stiffness of kaolin powder is found to be situated in between the values reported in [18] and [35], respectively; and on the order of the weak axis indentation stiffness of Muscovite (see Table 3). However, these values are still higher than the in situ stiffness values (Eq. 4) we determine from extrapolation of nano- and microindentation results.

Fig. 9
figure 9

Nanoindentation on kaolin powder: top AFM image; bottom indentation load–indentation depth curves

Full size image

In summary, a comparison with reported values in the open literature and new data from indentation on Kaolin reveals that the in situ stiffness behavior exhibited by highly compacted sedimentary rocks is somewhat disconnected from the stiffness behavior of clay minerals.

4.2 Comparison with UPV measurements

A second comparison of the stiffness values can be made with dynamic ultra-pulse-velocity (UPV) measurements of the overall composite stiffness of shale materials. The material at this scale is composed of a textured clay matrix (see Fig. 1) with an in-general abundant population of poorly sorted detrital grains (quartz inclusions), that are either concentrated into laminations located between thinner, clay-rich (or quartz starved), lens shaped lams, or homogeneously distributed throughout. This scale has been extensively researched, in the shale acoustics and exploration geophysics community, by means of compressional and shear-wave velocity measurements [1, 14, 17, 23, 24, 27, 29, 34]; and it is now generally agreed that shales behave elastically as transverse isotropic media. The typical wave length employed in such studies operated at frequencies in the megahertz range, is in the millimeter range, which captures well the composite stiffness of the macroscopic clay–quartz inclusion composite. To compare our indentation data with these UPV measurements, we need to subtract from the measured values the effect of the silt inclusions. This is not an easy task. In a very first approximation, we subtract the inclusion by means of the Reuss bound:

$$ \left( C_{ijmn}^{\rm UPV}\right)^{-1} = S_{ijkl}^{\rm UPV} = \left( 1 - f_{\rm I}\right) S_{ijkl} - f_{\rm I}S_{ijkl}^{I}, $$
(15)

where C UPV ijmn is the measured dynamic (undrained) stiffness, C I ijkl =(S I ijkl )−1 is the stiffness of the inclusions that occupy a volume fraction f I and which is assumed to be isotropic (bulk modulus k I=37.9 GPa, shear modulus g I=44.3 GPa); and C ijkl =(S ijkl )−1 is the sought stiffness of the porous clay composite. This simple Reuss bound neglects any hydraulic stiffening effect of the composite response under undrained conditions of the porous material (see e.g. [5, 25]) or specific micromechanical features that affect the porous composite response (see e.g. [8, 31]). While no-doubt a rough estimate, our aim here is to compare this estimate of the composite stiffness response with the indentation results. We achieve this by substituting the porous clay composite stiffness C ijkl determined from Eq. 15 into the indentation moduli relations for transverse isotropic materials, Eqs. 4 and 5. The results are reported for the three tested shales in Table 2 (labeled ‘UPV’) and are displayed in Fig. 10 in an M(xi) − η scaling plot. It is remarkable that the found M 1 and M 3 values determined here from the UPV measurements almost coincide with the indentation stiffness values obtained by nano- and microindentation. This actually confirms and validates the novel grid-indentation technique for shales, showing that it provides access to the small strain elastic response of the porous clay composite of shales, much in the same way as sophisticated large-scale UPV measurements. As a consequence, we find a very similar scaling behavior of this elastic response with the clay packing density; that is, an almost linear scaling from a percolation threshold of η∼0.5, where the material looses its stiffness to asymptotic values where the material exhibits a pronounced anisotropy:

$$ \hbox{UPV}: M_{1}(\eta = 1) = 30.4\,\hbox{GPa};\quad M_{3} (\eta = 1) = 18.7\,\hbox{GPa};\quad \frac{M_{1}}{M_{3}} = 1.6. $$
(16)

Those asymptotic values almost coincide with the values reported in Eq. 4, and they are clearly much smaller than the stiffness values reported for muscovite crystals.

Fig. 10
figure 10

‘Equivalent’ indentation modulus–clay packing density scaling (M − η) determined from UPV measurements of the clay composite. x3 stands for the bedding direction, and x1 for the bedding plane

Full size image

5 Closure

What contributes to shales pronounced macroscopic anisotropy? We need to answer this question in the light of our experimental observations obtained from deconvoluting indentation results and UPV measurements:

  1. 1.

    The stiffness values of clay minerals are almost one order of magnitude greater than the in situ elasticity content of the clayfabric from the scale of hundreds of nanometer to the millimeter scale.

  2. 2.

    Above an observation scale of some hundred nanometers, we identify characteristic stiffness-packing density scaling relations that are insensitive to the different mineralogy of the tested shales.

  3. 3.

    The in situ elasticity of the clay composite exhibits a percolation threshold at a clay packing density of η∼0.5.

  4. 4.

    The higher the clay packing density, the more pronounced the anisotropy.

The overall picture that thus emerges is that shales behaves mechanically like a nanogranular material, whose behavior is driven by contact forces at particle-to-particle contact points, rather than by the mineral elasticity in the crystalline structure of the clay minerals. As a consequence, the intrinsic clay mineral elasticity properties are of secondary importance for the in situ stiffness properties of shale materials above a scale of roughly 100 nm. This conclusion is restricted to the elastic response, and mineralogy of course plays a decisive role when it comes to other phenomena such as swelling of clays. Furthermore, the mineralogy may affect the packing density a particular shale achieves in a highly compacted state; but not (or not decisive) the intrinsic particle-to-particle contact stiffness that governs shale elasticity.

The fact that the anisotropy is scaled by the packing density supports the simple idea that the actual source of the in situ anisotropy of shale elasticity results rather from the deposition structure of the clay particles than from the intrinsic mineral anisotropy: there is always more contact area between particles in contact normal to the bedding plane [contact area A(x 3)] than in the bedding plane [contact area A(x1)]. Indeed, if the asymptotic anisotropic ratio M 1/M 3 were a characteristic of an elementary shale building block, contact mechanics [analogously to Eq. (2)] allows one to estimate the asymptotic contact area ratio to be A(x 3)/A(x 1)=(M 1/M 3)α = 1.6−2.6 (where α=1 corresponds to a flat contact and α=2 to a conical contact). It is worthwhile to note that this contact area ratio is far lower than the typical clay particle aspect ratio of 10–20; and things, therefore, may be well more complicated than a pure deposition structural argument suggests. On the other hand, as the packing density decreases, both contact areas appear to decrease in similar proportions down to the percolation threshold of η∼0.5, where the granular assembly looses contact.

What are the implications of these findings for geophysics, clay mineralogy and engineering applications of earth materials? The most important finding is that there exists a fundamental unit of material invariant properties, characterized by universal stiffness–clay packing density scaling relations. Because of the colloidal nature (specific surface of 15–800 m2/g) of earth materials in general, and of clay bearing sedimentary rocks in particular, the role of the minerals in the overall elasticity is reduced to that of a highly compacted granular media in the nano-meter to micrometer range. The packing density is a function of size and aspect ratio of the particles and of course of the deposition direction. And while the granular mix may vary from shale to shale as a function of the clay mineralogy, it is not unlikely that the packing density achieved by each granular mix is close to its maximum, which is why one observes a consistent scaling of the stiffness values with the clay packing density. Indeed, the clay packing density of shales (Table 1) is typically on the order or greater than random packing density limits of mono-sized spheres (ρ=64%) and ellipsoids (ρ=73%), and can reach in some cases values as high as the conjectured maximal density of spherocylinders (ρ=91%). The behavior of such highly packed systems has been recently recognized to be governed by the number of particle contacts required to mechanically stabilize the packing [7]. The nature of these contact forces does not change from one material to another, which translates into material invariant properties. But what changes in such granular mixes are the number of contact points, surfaces and constraints which are closely related to the packing mode. We suggest that these two features of the nanofabric form the nano-mechanical blueprint of the elasticity of earth materials which can explain much of the diverse mechanical behavior at larger scales. This not only holds for clay-bearing rocks, but should hold for any colloidal material system in which mineral particles generate large specific surfaces. This is the case of most natural porous composites: bones [13], cement-based materials [4, 11], sandstones, carbonates, etc. Restricted here to elasticity properties, the micro-mechanical blueprint of the strength properties of these cohesive-frictional earth materials needs still to be found.