Seismic stability analysis of a hunchbacked retaining wall under passive state using method of stress characteristics

Abstract

The potential use of a hunchbacked retaining wall over a conventional retaining wall under the seismic passive state is emphasised in this study employing the method of stress characteristics coupled with the modified pseudo-dynamic approach. Unlike the available studies established with the limit equilibrium or the limit analysis method where a predefined failure mechanism is assumed prior to the analysis, the failure surface is continuously traced in due course of the present analysis. The seismic stability of a hunchbacked retaining wall under the passive condition is found to be affected greatly while considering the effect of damping of the soil-wall and the phase difference of the seismic waves. A detailed parametric study is conducted considering the influence of different soil and wall parameters such as soil-wall inertia, soil friction angle, wall inclination and roughness. The present results are obtained from a rigorous computational effort without assuming a failure mechanism and found to be in good agreement with the previous studies available in the literature.

1 Introduction

Gravity retaining walls are widely adopted structural solutions to retain the backfill soil. Using the self-weight and the base friction, such structures offer greater resistance to the lateral earth pressure exerted by the backfill soil. The stability of such an important structural element has always been a prime concern, especially under the influence of earthquakes. The prediction of earth pressure and stability of retaining walls under both static and seismic conditions was demonstrated by several researchers leading to various simplified theories [4, 5, 7, 26, 28, 30, 35, 45, 48, 49]. Mononobe–Okabe method [26, 30] is a notable theory developed in the framework of the limit equilibrium method to predict the earth pressure under the seismic condition using the pseudo-static approach. However, the assumed linear failure surface in the Mononobe–Okabe method performs better in the case of active condition, whereas in the case of passive condition the failure surface generally comes out to be nonlinear even under the static condition [27]. Hence, based on the pseudo-static approach, various theories were germinated to capture such nonlinear failure surface [20, 27, 42] behind a retaining wall, where a predefined failure mechanism was much demanded. However, Sokolovski [41] proposed the method of stress characteristics to capture the natural development of a failure surface and later, it was further explored by several researchers for different geotechnical problems [15, 21, 24, 39]. Employing the method of stress characteristics and the pseudo-static approach, Kumar and Chitikela [21] determined the seismic passive earth pressure without assuming a priori failure mechanism. However, it is commonly understood that in the pseudo-static approach, the seismic forces are assumed to pronounce a uniform acceleration throughout the disturbed soil domain. Hence, unlike the pseudo-static approach, the nonlinearity in the seismic effect was revisited by Steedman and Zeng [43] by including the time dependency and the phase effect of seismic waves in the analysis. This theory was supported by a series of centrifuge tests [50] and popularised as the original pseudo-dynamic (OPD) approach. Later, the OPD approach was utilised by several researchers to determine the seismic passive earth pressure and the bearing capacity of foundation under the seismic condition [6, 11,12,13,14, 39]. However, due to some mathematical limitations such as nonzero stress condition at the ground surface, the OPD approach was later modified as the modified pseudo-dynamic (MPD) approach by Bellezza [2] and Pain et al. [31] utilising a visco-elastic soil model along with the stress-free boundary conditions. In addition to the zero stress condition at the ground surface, the effect of frequency ratio, ground amplification and soil damping can also be admitted in the MPD approach. Recent advancements in the determination of seismic passive pressure distinctly demonstrate that either the limit equilibrium or the limit analysis is the favourable choice among the researchers for such a class of problem though it is an established fact that the assumption of a preconceived failure mechanism may not reflect the true behaviour of the backfill soil. Hence, there is a need to revisit the assumption of a predefined failure mechanism behind a retaining wall, especially under the seismic condition.

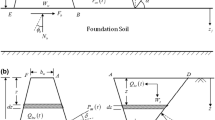
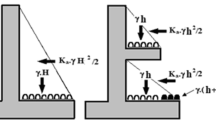
Further, the effect of soil inertia was considered to be the dominant parameter in the generation of seismic passive thrust in most of the available studies on the seismic analysis of retaining walls [6, 11, 14, 18, 20, 21, 25, 42, 49]. Though the argument is found to be quite reasonable for a cantilever retaining wall system, the effect of wall inertia cannot be neglected in the seismic design of gravity retaining walls [1, 29, 34]. However, due to bulky structure, the design of gravity retaining wall needs to be optimised well as it incurs huge construction cost. Sadrekarimi [37] explored the feasibility of using a hunchbacked retaining wall (Fig. 1a) as an effective alternative for a conventional gravity wall system (Fig. 1b) under the active condition by conducting several model tests followed by an analytical solution procedure based on the limit equilibrium method and the pseudo-static approach [38]. A hunchbacked retaining wall configuration not only alters the location of the dynamic thrust but also slashes the construction cost considerably. Among the few available studies on a hunchbacked gravity wall [32, 37, 38], none reported the performance of a retaining wall under the passive condition considering the cumulative effect of backface geometry of the wall, adaptive failure surface, soil and wall inertia force, and dynamic material properties. Hence, by employing the method of stress characteristics in association with the MPD approach, the seismic stability analysis of a hunchbacked retaining wall is performed in the present study considering all possible inertial effects and damping ratio.

Fig. 1

Schematic representation of different retaining wall configurations; a conventional wall, b hunchbacked wall

2 Problem definition

A hunchbacked gravity retaining wall of height H and top width B is considered to retain a dry, cohesionless, horizontal backfill subjected to a uniform surcharge q as shown in Fig. 2. The hunchback geometry of the wall is maintained on the backfill side by considering bilinear slopes (OO' and O'C), which make an angle α₁ and α₂ with the horizontal at the upper and the lower segments of the wall, respectively. δ₁ and δ₂ represent the wall roughness along the upper and the lower parts, respectively. The magnitude of wall height ratio (H₁/H₂), top wall inclination (α₁) and bottom wall inclination (α₂) are so chosen that the top width (OA) and the bottom width (CE) of the wall remain same to ensure the geometric closure. The effect of the earthquake is considered by employing the MPD approach. The seismic event was simulated by employing a harmonic base shaking with horizontal (a_h) and vertical (a_v) earthquake accelerations without causing the shear fluidisation [36]. The main objective of this study is to explore the passive resistance of a hunchbacked gravity wall under the seismic condition without assuming a predefined failure mechanism.

Fig. 2

Schematic representation of a hunchbacked retaining wall and associated forces

3 Methodology

The problem defined in this study was solved using the method of stress characteristics coupled with the MPD approach. As the solution of characteristic equations was developed in the framework of the theory of plasticity [41], the present analysis adhered to the following assumptions

• i. The backfill soil is homogeneous, isotropic and obeys the Mohr–Coulomb failure criterion within the plastic shear zone.

• ii. The problem is analysed under the two-dimensional plain strain condition.

• iii. The principle of superposition stays legitimate so that the effect of the surcharge component can be decoupled from the passive thrust to obtain the contribution of the unit weight of the soil alone.

3.1 Method of stress characteristics

The point O located at the top of the retaining wall is kept as the origin of the co-ordinate axes x–y, and their respective positive directions are illustrated in Fig. 2. The anticlockwise rotation measured from the positive x-axis is considered as positive in the whole analysis (Fig. 3a). The equations of equilibrium for a plane strain problem can be expressed as

$$\frac{{\partial \sigma_{x} }}{\partial x} + \frac{{\partial \tau_{xy} }}{\partial y} = X$$

(1)

$$\frac{{\partial \tau_{xy} }}{\partial x} + \frac{{\partial \sigma_{y} }}{\partial y} = Y$$

(2)

Fig. 3

Definition of stress parameters; a physical plane, b stress plane

where σ_x, σ_y and τ_xy are the normal and shear stress components acting on a typical soil element as shown in Fig. 3a; X and Y are the body forces acting along the x and y directions, respectively. From the typical Mohr–Coulomb failure criterion (Fig. 3b), the stress components can be determined and expressed as

$$\sigma_{x} = \sigma \left( {1 + \sin \phi \cos 2\theta } \right)$$

(3)

$$\sigma_{y} = \sigma \left( {1 - \sin \phi \cos 2\theta } \right)$$

(4)

$$\tau_{xy} = \sigma \sin \phi \sin 2\theta$$

(5)

By substituting Eqs. (3), (4) and (5) in Eqs. (1) and (2), the following expressions applicable along the two different families of characteristics can be derived,

Along (θ−μ) characteristic,

$$\frac{dy}{{dx}} = \tan \left( {\theta - \mu } \right); \frac{d\eta }{{dx}} = \frac{{X \sin \left( {\theta + \mu } \right) - Y \cos \left( {\theta + \mu } \right)}}{{2\sigma \sin \phi \cos \left( {\theta - \mu } \right)}}$$

(6)

Along (θ+μ) characteristic,

$$\frac{dy}{{dx}} = \tan \left( {\theta + \mu } \right); \frac{d\xi }{{dx}} = - \frac{{X \sin \left( {\theta - \mu } \right) - Y \cos \left( {\theta - \mu } \right)}}{{2\sigma \sin \phi \cos \left( {\theta + \mu } \right)}}$$

(7)

where μ = (π/4 – ϕ/2) and $\left. {\begin{array}{*{20}c} \eta \\ \xi \\ \end{array} } \right\} = 0.5\cot \phi ln\frac{\sigma }{q} \mp \theta$.

The detailed derivation of the characteristic equations can be obtained from various investigations [21, 24, 40] and hence, for the sake of brevity, the same is excluded from this paper. By generating a network of two different families of characteristics ((θ+μ)) and ((θ−μ)), a solution can be established from a known stress boundary to an unknown stress boundary, and the actual failure surface can be traced in due course of the analysis.

3.2 Seismic accelerations

Soil is generally considered as a visco-elastic material in the MPD approach, which mostly removes the limitation of the OPD approach. In this study, Kelvin–Voigt model was employed to capture the elastic and the damping component of the soil with the help of purely elastic spring and dashpot system, respectively [8]. The plane wave equations of motion propagating along the x-axis at any time t can be expressed as

$$\frac{\gamma }{g}\frac{{\partial^{2} u_{h} }}{{\partial t^{2} }} = G\frac{{\partial^{2} u_{h} }}{{\partial x^{2} }} + \nu_{h} \frac{{\partial^{3} u_{h} }}{{\partial x^{2} \partial t}}$$

(8)

$$\frac{\gamma }{g}\frac{{\partial^{2} u_{v} }}{{\partial t^{2} }} = \left( {\lambda + 2G} \right)\frac{{\partial^{2} u_{v} }}{{\partial x^{2} }} + \nu_{v} \frac{{\partial^{3} u_{h} }}{{\partial x^{2} \partial t}}$$

(9)

where u_v and u_h are the displacements along x and y direction, respectively; G and λ are the Lame’s constants; ν_h and ν_v are the soil viscosities along the respective plane of motion.

By imposing the stress-free boundary condition at the ground surface, the horizontal (a_hS) and the vertical (a_vS) seismic accelerations in the soil at any depth, x and any instant, t can be obtained from Eqs. (10) and (11) [2]. The detailed derivations of Eqs. (10) and (11) are also available in several recent works [3, 31, 33, 34].

$$a_{hS} \left( {x,t} \right) = \frac{{k_{h} g}}{{C_{sS}^{2} + S_{sS}^{2} }}\left[ {\left( {C_{sS} C_{sSx} + S_{sS} S_{sSx} } \right)\cos \left( {\omega t} \right) + \left( {S_{sS} C_{sSx} - C_{sS} S_{sSx} } \right)\sin \left( {\omega t} \right)} \right]$$

(10)

$$a_{vS} \left( {x,t} \right) = \frac{{k_{v} g}}{{C_{pS}^{2} + S_{pS}^{2} }}\left[ {\left( {C_{pS} C_{pSx} + S_{pS} S_{pSx} } \right)\cos \left( {\omega t} \right) + \left( {S_{pS} C_{pSx} - C_{pS} S_{pSx} } \right)\sin \left( {\omega t} \right)} \right]$$

(11)

where

$$C_{sSx} = \cos \left( {\frac{{y_{sS1} x}}{H}} \right)\cosh \left( {\frac{{y_{sS2} x}}{H}} \right); S_{sSx} = - \sin \left( {\frac{{y_{sS1} x}}{H}} \right)\sinh \left( {\frac{{y_{sS2} x}}{H}} \right)$$

(12)

$$C_{pSx} = \cos \left( {\frac{{y_{pS1} x}}{H}} \right)\cosh \left( {\frac{{y_{pS2} x}}{H}} \right); S_{sSx} = - \sin \left( {\frac{{y_{pS1} x}}{H}} \right)\sinh \left( {\frac{{y_{pS2} x}}{H}} \right)$$

(13)

and,

$$y_{sS1} = \frac{\omega H}{{V_{sS} }}\left[ {\frac{{\left( {1 + 4D_{S}^{2} } \right)^{0.5} + 1}}{{2\left( {1 + 4D_{S}^{2} } \right)}}} \right]^{0.5} ;y_{sS2} = \frac{\omega H}{{V_{sS} }}\left[ {\frac{{\left( {1 + 4D_{S}^{2} } \right)^{0.5} - 1}}{{2\left( {1 + 4D_{S}^{2} } \right)}}} \right]^{0.5}$$

(14)

$$y_{pS1} = \frac{\omega H}{{V_{pS} }}\left[ {\frac{{\left( {1 + 4D_{S}^{2} } \right)^{0.5} + 1}}{{2\left( {1 + 4D_{S}^{2} } \right)}}} \right]^{0.5} ;y_{pS2} = \frac{\omega H}{{V_{pS} }}\left[ {\frac{{\left( {1 + 4D_{S}^{2} } \right)^{0.5} - 1}}{{2\left( {1 + 4D_{S}^{2} } \right)}}} \right]^{0.5}$$

(15)

In Eqs. (10) – (15), the first subscripts ‘p’ and ‘s’ refer to the nature of the propagating waves (primary and shear waves), whereas the second subscript ‘_S’ refers to the soil only. At x = H, the coefficients depicted in Eqs. (12) and (13) simply reduce to the constants (C_sS, S_sS, C_pS and S_pS) used in Eqs. (10) and (11). Similarly, the acceleration equations for the wall (a_hW and a_vW) can be obtained by simply replacing the second subscript ‘_S’ with ‘_W’ and D_S with D_W. Though the pseudo-dynamic analysis was essentially evolved from the theory of elastic wave propagation, the OPD approach was endorsed with a series of centrifuge experiments performed by Zeng and Steedman [50]. Thereafter, the OPD and the MPD approaches were widely adopted in various earth pressure-related problems [1,2,3, 11, 18, 31, 33, 34]. Hence, it is worth concluding at this stage that the expressions of seismic accelerations discussed in Eqs. (10–15) can be applicable to this class of problem without much deviation though they are generally derived based on the theory of elastic wave propagation. Therefore, while establishing the solution of the method of characteristics as discussed in the previous section, the effect of the earthquake can be effectively incorporated in the present analysis by admitting Eqs. (10) and (11).

3.3 Boundary conditions

Figure 2 illustrates the existence of two singular points (O and O') due to the hunchback geometry of the wall backface [21, 23, 39, 40]. From the concept of rotation of stresses at these singular points, the magnitude of θ along the ground surface (θ_g), and the upper and the lower segments of the wall (θ_W1 and θ_W2) can be expressed as

$$\theta_{g} = 0.5\left[ {\pi + \kappa + \sin^{ - 1} \left( {\frac{\sin \kappa }{{\sin \phi }}} \right)} \right]$$

(16)

where $\kappa = \tan^{ - 1} \left( {\frac{{a_{hS} }}{{g - a_{vS} }}} \right)$

$$\theta_{W1} = 0.5\left( {2\alpha_{1} - \delta_{1} - \sin^{ - 1} \left( {\frac{{\sin \delta_{1} }}{\sin \phi }} \right)} \right)$$

(17)

$$\theta_{W2} = 0.5\left( {2\pi - 2\alpha_{2} - \delta_{2} - \sin^{ - 1} \left( {\frac{{\sin \delta_{2} }}{\sin \phi }} \right)} \right)$$

(18)

where a_hS and a_vS are horizontal and vertical seismic accelerations in the soil, respectively, as obtained from Eqs. (10) and (11).

Based on the magnitudes of θ_g, θ_W1 and θ_W2, different types of stress fields are encountered in the solution procedure. On account of the equal magnitudes of θ at the singular point, the solution becomes unique, and hence, a closed-form solution can be obtained by neglecting the unit weight of the soil [21, 40]. However, when the magnitudes of θ at the respective singular points are not equal, the effect of unit weight cannot be simply neglected due to the existence of a characteristic solution, which can only be solved using a rigorous solution procedure [21, 23, 39, 41].

3.4 Seismic lateral earth pressure

While employing the method of stress characteristics in a cohesionless soil, a nominal amount of surcharge is generally considered to maintain the numerical stability in the analysis [21]. However, the effect of applied surcharge in the analysis may be decoupled from the final solution with the help of the principle of superposition [39]. Hence, the analysis was initially performed by considering a surcharge without accounting for the unit weight component, i.e. q ≠ 0 and γ = 0 and the passive lateral thrusts acting on the upper (P_pq1) and the lower (P_pq2) segments of the wall were determined. Later, the analysis was carried out further by including the unit weight (q ≠ 0 and γ ≠ 0) to determine the lateral thrusts on the upper (P_pe1) and the lower (P_pe2) parts of the wall. The idealised earth pressure distribution for the latter case is shown in Fig. 4. Thus, the coefficient of seismic passive earth pressure for the upper segment of the wall due to surcharge (K_pq1) and unit weight (K_pγ1) can be expressed as

$$K_{pq1} = \frac{{P_{pq1} }}{{qH_{1} }}; K_{p\gamma 1} = \frac{{2\left( {P_{pe1} - P_{pq1} } \right)}}{{\gamma H_{1}^{2} }}$$

(19)

Fig. 4

Idealised earth pressure distribution behind a hunchbacked wall considering q = 0 and γ ≠ 0

Similarly, the coefficient of passive earth pressure for the lower segment of the wall (K_pq2 and K_pγ2) can be obtained as

$$K_{pq2} = \frac{{P_{pq2} }}{{qH_{2} }}; K_{p\gamma 2} = \frac{{2\left( {P_{pe2} - P_{pq2} - K_{pq2} \gamma H_{1} H_{2} } \right)}}{{\gamma H_{2}^{2} }}$$

(20)

From Fig. 4, it can be understood that the surcharge contribution (K_pq2γH₁) in Eq. (20) can be actually derived from the unit weight of the backfill soil engaged in the upper portion of the wall (H₁).

3.5 Stability analysis

A hunchbacked retaining wall needs to be displaced adequately for mobilising the passive resistance in the soil, and hence, the investigation on the seismic passive resistance numerically (finite element analysis) or experimentally is found to be practically difficult especially under a low level of seismic acceleration [47]. In this study, the stability of a hunchbacked retaining wall against the sliding mode of failure was examined using the allowable driving force (F_D), which was assumed to mobilise the full passive resistance in the system. With the known values of F_D, a hunchbacked gravity retaining wall can be effectively designed to ensure the stability of retaining structures under the seismic passive condition. Having adopted a suitable factor of safety (FS) under the seismic condition, the magnitude of F_D developed in the system can be calculated as

$$F_{N} = W_{W} - Q_{VW} - P_{pe1} \cos \left( {\delta_{1} - \alpha_{1} } \right) + P_{pe2} \cos \left( {\delta_{2} - \alpha_{2} } \right)$$

(21)

$$F_{T} = \mu_{b} F_{N} - P_{pe1} \sin \left( {\delta_{1} - \alpha_{1} } \right) - P_{pe2} \sin \left( {\delta_{2} - \alpha_{2} } \right)$$

(22)

$$F_{D} = \frac{{F_{T} }}{{FS_{S} }} - Q_{HW}$$

(23)

where F_N and F_T are the normal and the tangential forces acting at the base of the wall; W_W, Q_HW and Q_VW are the wall inertial forces due to self-weight, horizontal and vertical seismic accelerations, respectively, which can be obtained from the following expressions,

$$W_{W} = \gamma_{c} \left( {Area of AOO{\prime }CE} \right)$$

(24)

$$Q_{HW} \left( t \right) = \mathop \int \limits_{0}^{{H_{1} }} \frac{{\gamma_{c} }}{g}\left( {B - x\cot \alpha_{1} } \right)a_{hW} dx + \mathop \int \limits_{{H_{1} }}^{{H_{2} }} \frac{{\gamma_{c} }}{g}\left( {B - \left( {H - x} \right)\cot \alpha_{2} } \right)a_{hW} dx$$

(25)

$$Q_{VW} \left( t \right) = \mathop \int \limits_{0}^{{H_{1} }} \frac{{\gamma_{c} }}{g}\left( {B - x\cot \alpha_{1} } \right)a_{vW} dx + \mathop \int \limits_{{H_{1} }}^{{H_{2} }} \frac{{\gamma_{c} }}{g}\left( {B - \left( {H - x} \right)\cot \alpha_{2} } \right)a_{vW} dx$$

(26)

where a_hW and a_vW are the accelerations caused by the seismic waves propagating through the wall material, which can be determined by performing operations similar to Eqs. (10) – (15) with appropriate wall parameters [34].

4 Results and discussion

The defined problem was solved with the aid of an in-house computer code developed in MATLAB. As mentioned earlier, a nominal value of surcharge was needed to maintain the numerical stability during the analysis. However, the contribution of surcharge component was decoupled from the final results to obtain the contribution of the unit weight alone. Table 1 depicts the various input parameters used in the analysis. It is worth mentioning that the negative value of k_v shown in Table 1 denotes the propagation of primary waves along the negative x direction.

Table 1 Various input parameters used in the analysis

4.1 Passive thrust

The proposed hunchbacked gravity retaining wall counteracts the external driving force mainly using the self-weight of the wall and the seismic passive resistance offered by the backfill soil on the wall. While the inertial forces acting on the wall can be calculated from Eqs. (24), (25) and (26), the seismic passive resistance of the backfill soil can be determined from the seismic earth pressure coefficients described in Eqs. (19) and (20). The variation of seismic passive earth pressure coefficients (K_pq1 and K_pγ1) for the upper portion of the wall with the upper wall inclination (α₁) is shown in Fig. 5a. It can be observed that the passive resistance of the backfill soil decreases with an increase in the magnitude of α₁. Similarly, the variation of passive earth pressure coefficients (K_pq2 and K_pγ2 for the lower part of the wall with the lower wall inclination (α₂) is depicted in Fig. 5b. Considerable enhancement in the passive resistance of the soil can be seen with an increase in α₂. However, in any case, the magnitude of passive earth pressure coefficients is found to decrease with an increase in the seismic acceleration irrespective of the wall configuration. Hence, by adopting a retaining wall with such bilinear backface, the backfill soil can be effectively utilised to resist the driving forces under the seismic passive condition. It can also be conceived from Fig. 5 that the consideration of surcharge alone (γ = 0) generally under-predicts the passive resistance of the backfill soil, which convincingly recommends the inclusion of the self-weight of the backfill in the analysis unlike the available simplified closed form solutions [28, 40].

Fig. 5

Variation of a K_pq1, K_pγ1, b K_pq2, K_pγ2, with α₁ and α₂ for H₁/H₂ = 1, ϕ = 35°, δ₁ = δ₂ = 2ϕ/3, k_v = -0.5k_h and D_S = 10%

4.2 Driving force

In Fig. 6, the variation of the normalised allowable driving force (F_D/γH²) with different values of α₂ is presented, which actually demonstrates the stability of a hunchbacked wall against the sliding mode of failure. As mentioned earlier, a suitable factor of safety against sliding was assumed in the analysis following various standard recommendations [9, 16, 46]. Figure 6 also compares the performance of a hunchbacked (Fig. 1b) and a conventional (Fig. 1a) retaining wall against the sliding mode of failure under the seismic condition simulated by the pseudo-static as well as the modified pseudo-dynamic approaches. It can be observed that under the static as well as the seismic conditions, the magnitude of F_D (with FS_S = 1.2) for the hunchbacked wall is marginally higher up to a certain wall inclination (α₂) compared to the conventional wall. Figure 7 shows the variation of F_D/γH² with k_h for different values of wall geometry utilising the modified pseudo-dynamic accelerations. It is worth mentioning that the extreme boundaries (H₂ = H and H₁ = H) in Fig. 7 correspond to a conventional wall with single linear slope, whereas a hunchbacked wall is denoted by the wall height ratio (H₁/H₂). It is evident from Figs. 6 and 7 that a hunchbacked wall can perform even better by optimising the wall inclination and H₁/H₂ ratio accordingly. However, beyond a certain magnitude of H₁/H₂ ratio and α_2, the improvement in the sliding stability is found to be marginal. In Fig. 8, the variation of F_D/γH² with different values of FS_S is presented. The magnitude of F_D is found to decrease with the increase in k_h and FS_S. Hence, by adopting suitable wall geometry, a hunchbacked wall can be a better alternative to a conventional wall in terms of performance and economy.

Fig. 6

Variation of F_D/γH² with different values of α₂ for ϕ = 35°, δ₁ = δ₂ = 2ϕ/3, α₁ = α₂, k_v = -0.5k_h, D_S = 10%, D_W = 5% and FS_S = 1.2; a pseudo-static approach, b modified pseudo-dynamic approach

Fig. 7

Variation of F_D/γH² with k_h for different wall configurations with ϕ = 35°, δ₁ = δ₂ = 2ϕ/3, α₂ = 100°, k_v = -0.5k_h, D_S = 10%, D_W = 5% and FS_S = 1.2

Fig. 8

Variation of F_D/γH² with different values of FS_S for ϕ = 35°, δ₁ = δ₂ = 2ϕ/3, α₁ = α₂ = 100°, H₁/H₂ = 1, k_h = 0.2, k_v = -0.5k_h, D_S = 10% and D_W = 5%

4.3 Soil and wall properties

From Eqs. (3) – (7), it can be understood that σ and θ are the two important parameters corresponding to the stresses and their direction, respectively. Hence, in this section, the effect of various soil and wall parameters on the seismic passive earth pressure distribution behind a hunchbacked wall is briefly discussed in terms of σ.

4.3.1 Soil friction

The comprehensive effect of ϕ on the normalised stress (σ/γH) distribution behind a hunchbacked wall is shown in Fig. 9. The roughness of the upper and the lower parts of the wall is reasonably considered as two-third of the soil friction angle, that is, δ₁=δ₂=2ϕ3. From Fig. 9, it can be observed that the normalised stress increases significantly with the increase in ϕ throughout the height of the wall, similar to the observations made by earlier researchers on a conventional wall [17, 31]. However, the stress distribution is found to be significant at the lower portion of the wall.

Fig. 9

Normalised stress distribution for different values of ϕ with δ₁ = δ₂ = 2ϕ/3, α₁ = α₂ = 100°, H₁/H₂ = 1, k_h = 0.2, k_v = -0.5k_h and D_S = 10%

4.3.2 Wall roughness

Figure 10 shows the effect of wall roughness on the normalised stress distribution behind the wall. It can be conceived that an increase in the wall roughness results in an increase in the magnitude of σ/γH. Similar to the effect of soil friction, the stress distribution is greatly pronounced at the lower part of the wall for higher wall roughness. The wall roughness was kept constant throughout the height of the wall in this analysis. However, based on the observation from Fig. 10, it can be understood that the lower part of the wall majorly contributes to the mobilisation of the passive resistance offered by the soil. Hence, by improving the roughness of the lower part of the wall, greater stability of the system can be expected. Thus, the present observations from Figs. 9 and 10 conclude that the lower part of a hunchbacked wall contributes more towards the stability aspect of the wall.

Fig. 10

Normalised stress distribution for different values of δ₁ and δ₂ with ϕ = 35°, α₁ = α₂ = 100°, H₁/H₂ = 1, k_h = 0.2, k_v = -0.5k_h and D_S = 10%

4.3.3 Seismic waves

The seismic environment in the analysis was created with the help of MPD approach, where the direction of horizontal and vertical accelerations was chosen to capture the critical condition under the passive state. It was reported in the literature that the detrimental effect of the earthquake on a retaining structure was majorly due to the propagation of shear waves [50]. Hence, the effect of k_h on the normalised stress distribution along the height of the wall is presented in Fig. 11. The stress on the wall is found to decrease with the increase in k_h, which is in line with the observation made by previous researchers [1, 6, 11, 14, 21, 27, 31, 39, 42]. It is worth noting that the direction of k_h was always kept along the positive y direction to explore the critical condition under the passive state. Though the effect of shear waves is more pronounced in the seismic analysis, the influence of primary waves needs to be considered as well [6]. To capture the critical condition, the direction of k_v was generally considered upward, that is, along the negative x direction. However, the effect of other possible direction of k_v (along the positive x direction) on the stress distribution was also explored as it might be crucial at higher acceleration and different frequency ranges [2]. Hence, the effect of the direction of k_v on the variation of normalised stress is presented in Fig. 12, where it can be observed that at k_h = 0.2, ωH/V_sS = 0.95 and ωH/V_pS = 0.50, (σ/γH) decreases as k_v changes its direction from negative (upward) to positive (downward).

Fig. 11

Normalised stress distribution for different values of k_h with ϕ = 35°, δ₁ = δ₂ = 2ϕ/3, α₁ = α₂ = 100°, H₁/H₂ = 1, k_v = -0.5k_h and D_S = 10%

Fig. 12

Normalised stress distribution for different values of k_v with ϕ = 35°, δ₁ = δ₂ = 2ϕ/3, α₁ = α₂ = 100°, H₁/H₂ = 1, k_h = 0.2 and D_S = 10%

4.4 Failure surface

As mentioned earlier, the present methodology needs not to assume any predetermined failure mechanism, and the actual failure surface in the backfill soil evolves automatically from the solution of the method of stress characteristics. Figure 13 depicts typical failure patterns for a hunchbacked as well as a conventional retaining wall with different wall configurations under the static and the seismic conditions. It can be observed from Fig. 13 that for a particular wall configuration, the size of the failure domain increases with an increase in the seismic acceleration. It is worth noting that the size of the failure domain becomes maximum for the conventional wall with H₂ = H (Fig. 13c) and thus provides the highest passive resistance. However, a significant reduction in the consumption of wall material gets ensured in the case of a hunchbacked wall compared to other conventional wall configurations under both static and seismic conditions.

Fig. 13

Failure pattern for different wall configurations under static and seismic conditions with ϕ = 35°, δ₁ = δ₂ = ϕ, α₁ = α₂ = 100°, k_v = -0.5k_h and D_S = 10%; a H₁ = H, b H₁/H₂ = 1, c H₂ = H

4.5 Stress contours

Since the state of stress is completely known within the influence domain, the mobilisation of stresses within the soil domain can be captured in the form of stress contours. Figure 14 shows the normalised stress contours for a broken-back wall under both static and seismic conditions. It can be observed from Fig. 14 that the magnitude of σ/γH generally decreases with an increase in the seismic acceleration. It is worth noting that the rate of reduction is seen to be gradual near the lower part of the wall and hence, the lower segment of the broken-back wall enhances the stability of the wall by providing sufficient passive resistance.

Fig. 14

Normalised stress contours for different values of k_h under static and seismic conditions with ϕ = 35°, δ₁ = δ₂ = ϕ, α₁ = α₂ = 100°, k_v = -0.5k_h and D_S = 10%; a k_h = 0, b k_h = 0.1, c k_h = 0.2

5 Comparison

Under the static and the seismic conditions, a number of studies on the analysis of a conventional linear retaining wall (Fig. 1a) are available in the literature, whereas the same for a hunchbacked retaining wall with bilinear backface (Fig. 1b) are still scarce. Most of the previous studies on a hunchbacked wall were performed using the limit equilibrium method, where a priori rupture surface was assumed. However, the present analysis was carried out considering an adaptive rupture surface along with more appealing MPD approach, which imparted more insight and flexibility to the proposed problem. As virtually no studies related to the passive resistance of a hunchbacked wall are available in the literature, the present analysis was extended to obtain the passive earth pressure coefficients for a conventional vertical retaining wall (H₁ = H) using different seismic approaches such as pseudo-static, OPD and MPD. In Table 2, the present values of the passive earth pressure coefficient obtained from the pseudo-static approach for a vertical cantilever retaining wall (no wall inertia) are compared with the available studies reported in the literature [10, 19,20,21,22, 26,27,28, 30, 42, 44]. The magnitudes of the seismic passive pressure coefficient reported by Mylonakis et al. [28], Lancellotta [22] and Krabbenhoft [19] are found to be lower than the present values. This may be attributed to the closed form solution proposed by Mylonakis et al. [28] by considering the unit weight component of the soil partially and the lower bound limit analysis solution adopted by Lancellotta [22] and Krabbenhoft [19]. Generally, the results obtained from the method of stress characteristics are reported to lie between the lower and the upper bounds [5]. This observation is quite evident from Table 2, where the present values of the passive earth pressure coefficient fall between the lower [19, 22] and the upper [10, 42] bound results. However, the present results are seen to be in good agreement with that of Kumar and Chitikela [21], where the method of stress characteristics was employed in the analysis. When the current characteristic analysis is coupled with the OPD approach [43], the present results for a vertical retaining wall are generally found to be lower than the available limit equilibrium results [1, 6, 11, 14] based on a predefined failure mechanism (Table 3). The present results are found to be lower than that of Ghosh and Kolathayar [14] though Ghosh and Kolathayar [14] adopted a composite nonlinear failure surface in the analysis. Basha and Babu [1] also considered a composite nonlinear failure surface and reported lower values of earth pressure coefficient, but their analysis suffered from several limitations as discussed by Ghosh and Kolathayar [14]. However, the closed-form results of Santhoshkumar and Ghosh [40] are found to be the lowest, where the contribution of the unit weight of the soil was completely neglected. Hence, from Table 3, it can be conceived that the present analysis generally reports lower and thus better results among the available studies reported in the literature. In Table 4, the present results for a vertical wall obtained from the MPD approach are compared with that proposed by Pain et al. [31], Rajesh and Choudhury [33], Santhoshkumar and Ghosh [40] and Khatri [17]. It can be observed that the present values of the passive pressure coefficient are lower and thus better than that of Pain et al. [31] and Rajesh and Choudhury [33] though a predefined curved failure surface was considered in their analysis. However, the present results are found to be slightly higher than the lower bound solution of Khatri [17] for the obvious reason.

Table 2 Comparison of K_pγ1 for vertical wall under pseudo-static condition with ϕ = 30°, δ₁ = δ₂ =ϕ, α₁ = α₂ = 90°, H₁ = H and k_v = 0

Table 3 Comparison of K_pγ1 for vertical wall under OPD condition with ϕ = 30°, δ₁ = δ₂ =ϕ, α₁ = α₂ = 90°, H₁ = H, k_v = 0, D_s = 10% and ωH/V_ss = 1.87

Table 4 Comparison of K_pγ1 for vertical wall under MPD condition with ϕ = 30°, δ₁ = δ₂ =ϕ, α₁ = α₂ = 90°, H₁ = H, k_v = 0, D_s = 10% and ωH/V_ss = 0.95

6 Conclusions

The seismic stability of a hunchbacked retaining wall under the passive state was analysed using the method of stress characteristics in association with the modified pseudo-dynamic approach. While the solution of stress characteristics was able to generate the failure surface automatically along with the complete state of stress in the backfill soil, the MPD approach incorporated the necessary boundary conditions along with the effect of damping and frequency in the analysis. The effect of soil and wall inertia was effectively included in the analysis, which made the study more close to reality. A detailed parametric study was conducted to understand the influence of various parameters such as soil friction, wall roughness, wall backface geometry, seismic accelerations due to shear and primary waves on the seismic pressure distribution behind a hunchbacked wall. The allowable driving force for a hunchbacked wall is found to be 2–7% higher than that of a conventional wall. However, through the application of a hunchbacked wall, there exists a considerable reduction in the construction material along with a marginal improvement in the stability, which strongly advocates for the installation of a hunchbacked retaining wall in place of a conventional wall.