Keywords

1 Introduction

Seismic damage of highway system caused in seismic world wide indicated that modern highway system is still vulnerable, it may be damaged extensively and shut down the local traffic, which always makes big troubles for rescue in a past earthquake situation. The earthquake damage of highway system shows that the failure of retaining structures is one of the main causes of road damage. So it is key important to assess the reliability of retaining structure under seismic condition.

The seismic response of retaining structures is a complex soil-structure interaction problem. Wall movements and dynamic earth pressures depend on the response of the soil underlying the wall, the response of the backfill, the inertial and movement of the wall itself, and the nature of the input motions. Many efforts have been made in the field of seismic response of retaining wall, but it is not still sufficient. Most of the methods employed for the design of a retaining wall subjected to seismic loading are limit equilibrium. The pioneering work on earthquake induced lateral earth pressure under active and passive conditions acting on a retaining wall were published by Okabe (1926) and Mononobe and Matsuo (1929). The pseudo-static approach which is known as Mononobe–Okabe method, is widely used to calculate the dynamic earth pressure (either active or passive) on the back of retaining wall. The limit equilibrium method considers the response of the retaining wall as isolated from that of the soil. In other words, neither the interaction between the backfill and the retaining wall nor the displacement of retaining wall are considered in traditional limit equilibrium method. In order to take the soil-structure interaction into account, elastic analysis of the seismic response of retaining structures is used by Scott (1973). Ortigosa and Musante (1991) proposed a simplified kinematic method to calculate the seismic earth pressure against retaining wall with restrained displacement. Futhermore, Richards (Richards et al. 1999) established an alternate analysis model, in which the soil supported by the retaining wall is modeled by springs in parallel. The fundamental solution to the free-field seismic response considering nonlinear, plastic behavior of soil is included in the retaining analysis. In previous approach, the dynamic loading induced by earthquake is considered as time-independent, which ultimately assumes that the magnitude and phase acceleration is uniform throughout the backfill. To overcome this constraint, Steedman and Zeng (1990) developed the pseudo-dynamic method to predict the seismic active earth pressure behind retaining wall. Later Munwar Basha and Sivakumar Babu (2010) extended pseudo-dynamic method to compute the rotational displacements of gravity retaining walls under passive condition when subjected to seismic loads. Similar alternatives have been made by Syed Mohd Ahmad and Deepankar Choudhury (2010) and Choudhury and Nimbalkar (2008). For pseudo-dynamic method, equilibrium equations of force or moment are still needed, and the soil structure interaction is ignored.

In light of the previous methods, it appears that the development of a new method for assessing seismically-induced earth pressure and rotational displacement would be desirable. The purpose of this paper is trying to combining the pseudo-dynamic method and free field solution, and then calculating the earth pressure and the rotational displacement of retaining wall under seismic loads. In this paper, not only the soil-structure interaction is taken into account, but also the time and phase difference due to finite shear wave velocity is considered. One of the main features of this paper is the adoption of a new iterative program to evaluate the time-dependent seismic earth pressure and rotational displacement of retaining wall. The analysis of present is limit to cohesionless soil in elastic state.

2 Method of Analysis

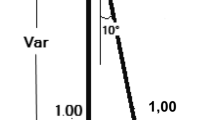
The basic system studied is a semi-infinite layer of cohesionless soil of unit weight \( \gamma \) that is free at its upper surface, is bonded to a rigid base at bottom, and is retained on its vertical boundary by a rigid retaining wall. The soil is approximately considered as elastic body, the backfill is supposed to be never yield or fail under seismic load. In general it is not appropriate to simulate the seismic response of a retaining structure using elastic models because such models neither capture the static or cyclic elasto-plastic behavior of the soil, nor any failure state that may be reached. However, elastic models provide a first approximation to wall and soil response and, in some cases, they may be even acceptable. As shown in Fig. 91.1, the height of the wall and the stratum is considered to be the same and is denoted by H.

Fig. 91.1
figure 1

Sketch of soil structure interaction model

Full size image

The free-field stress and deformation solutions are applied in the analysis of seismic response of retaining structures. The dynamic response of the soil-wall system can be analyzed using superposition for the particular case of rotation about the base, soil in the free field has the horizontal displacement u f and the wall has the horizontal displacement u w. The response of this soil-wall system is the sum of two cases: (1) the wall has the same deformation as the free field under the inertia body force and (2) the wall is pushed back with some horizontal displacement \( \Updelta u \) equal to the difference between the horizontal displacement of the free field u f and horizontal displacement of wall. This superposition approach is applicable no matter how the wall moves (Huang et al. 1999; Huang 1996).

The pseudo-dynamic analysis, which considers shear and primary wave velocity, can be developed by assuming that the shear modulus G is constant with depth through the backfill and the phase not the magnitude of acceleration varies. It is assumed that the base of the retaining wall is subjected to harmonic horizontal and vertical earthquake accelerations with amplitude k hg and k vg, the acceleration at any depth z below the ground surface and time t can be expressed as

$$ a_{h} \left( {z,t} \right){ = }k_{hd} \left( {z,t} \right)g,\,k_{hd} \left( {z,t} \right) = k_{h} \sin \left[ {\omega \left( {t - \frac{H - z}{{V_{s} }}} \right)} \right] $$
(91.1)
$$ a_{v} \left( {z,t} \right){ = }k_{vd} \left( {z,t} \right)g,\,k_{vd} \left( {z,t} \right) = k_{v} \sin \left[ {\omega \left( {t - \frac{H - z}{{V_{p} }}} \right)} \right] $$
(91.2)

where, \( \omega \) is the angular frequency, V s is the shear wave velocity, V p is the primary wave velocity. k h and k v are horizontal and vertical seismic amplitude coefficients respectively.

The total horizontal stress \( \sigma_{xw} \) acting on the wall is the sum of horizontal stress \( \sigma_{xf} \) in the free field and the stress increment \( \Updelta \sigma_{x} \) due to the relative displacement between the wall and soil in the free field

$$ \sigma_{xw} = \sigma_{xf} + \Updelta \sigma_{x} $$
(91.3)

The horizontal normal stress increment, \( \Updelta \sigma_{x} , \) can be expressed as

$$ \Updelta \sigma_{x} = K_{s} \left[ {u_{s} \left( t \right) - u_{w} \left( t \right)} \right] $$
(91.4)

where, K s is subgrade modulus of the backfill soil.

Since the springs in Fig. 91.1 can be thought of as bars with length proportional to the height of the wall (Scott 1973), their stiffness, defined as the subgrade modulus in Eq. (91.4) can be written as

$$ K_{s} = C_{2} G/H $$
(91.5)

In most cases, a value of C 2 = 1.35 seems appropriate based on finite-element analysis (Huang 1996).

3 Free Field Deformation and Stress Solutions of Backfill Without Retaining Structures

The two dimensional differential equations of equilibrium can be written as

$$ \frac{{\partial \sigma_{x} }}{\partial x} + \frac{{\partial \tau_{xz} }}{\partial z} = k_{hd} \gamma $$
(91.6)
$$ \frac{{\partial \tau_{xz} }}{\partial x} + \frac{{\partial \sigma_{z} }}{\partial z} = k_{vd} \gamma $$
(91.7)

Since we are dealing with the half-space, all stress, strain and displacement components of backfill soil are independent on the x coordinate. Thus, this free-field problem is actually a one-dimensional problem, Eqs. (91.6) and (91.7) becomes

$$ \frac{{\partial \tau_{xz} }}{\partial z} = k_{hd} \gamma $$
(91.8)
$$ \frac{{\partial \sigma_{z} }}{\partial z} = k_{vd} \gamma $$
(91.9)

Stress components can be solved from Eq. (91.8), with the condition of when z = 0 and t = 0, \( \tau_{xz} = 0,\sigma_{z} = 0. \)

$$ \tau_{xz} = \frac{{2k_{h} v_{s} \gamma }}{\omega }\{ \sin [\frac{{\omega (2tv_{s} + z - 2H)}}{{2v_{s} }}]\sin \frac{z\omega }{{2v_{s} }}\} $$
(91.10)
$$ \sigma_{z} = \frac{{2k_{v} v_{p} \gamma }}{\omega }\{ \sin [\frac{{\omega (2tv_{s} + z - 2H)}}{{2v_{p} }}]\sin \frac{z\omega }{{2v_{p} }}\} $$
(91.11)

The horizontal stress is usually written as a lateral earth pressure coefficient K times the vertical stress \( \sigma_{z} \). That is

$$ \sigma_{xf} = K\sigma_{z} $$
(91.12)

where, \( K = K_{0} {\text{ = 1 - sin}}\phi \) is the coefficient of lateral earth pressure in the elastic state.

For soil in the elastic state, the shear strain can be expressed as follow

$$ \gamma_{xz} = \frac{{\tau_{xz} }}{G} $$
(91.13)

According to elastic deformation theory, the horizontal displacement of soil in the free field is

$$ \begin{aligned} u_{s} =& - \int {\gamma_{xz} } dz \hfill \\ =& \frac{{k_{h} v_{s} \gamma }}{{G\omega^{2} }}{ v_{s} \sin \left[\frac{{\omega (tv_{s} + z - H)}}{{v_{s} }} - z\omega \cos \left[\omega \left(t - \frac{H}{{v_{s} }}\right)\right]\right]} \hfill \\ \end{aligned} $$
(91.14)

It is simply assumed that the rotational component of displacement can be ignored. The horizontal stress acting on the retaining wall can be expressed as

$$ \sigma_{xw} = \sigma_{xf} + K_{s} \left[ {u_{s} \left( t \right) - u_{w} \left( t \right)} \right] $$
(91.15)
$$ u_{w} \left( {z,t} \right) = \eta \left( {H - z} \right) $$
(91.16)

where, \( u_{w} \left( t \right) \) represents the displacement of retaining wall, \( \eta \) represents the rotating angle.

The total horizontal thrust acting on the retaining wall can be calculated by integrating the horizontal stress along the height of the retaining wall

$$ \begin{aligned} N_{e} =& \int\limits_{0}^{H} {\sigma_{xw} } dz \hfill \\ =& \frac{1}{{2G\omega^{3} }}\{ - GH^{2} K_{s} \eta \omega^{3} { - }2k_{h} K_{s} v_{s}^{3} \gamma \cos (\omega t) + k_{h} K_{s} v_{s} \gamma (2v_{s}^{2} - H^{2} \omega^{2} ) \hfill \\ &\times \cos m_{1} + 2GKk_{v} v_{p} \gamma \omega [H\omega \cos m_{2} + v_{p} (\sin m_{2} - \sin \omega t)]\} \hfill \\ \end{aligned} $$
(91.17)

where, \( m_{1} = \omega t - \frac{H\omega }{{v_{s} }};m_{2} = \omega t - \frac{H\omega }{{v_{p} }}. \)

The vertical force acting on the retaining wall is determined with knowledge of the wall frictional angle

$$ T_{e} = N_{e} \tan \delta $$
(91.18)

The total force acting on the retaining wall is expressed as

$$ P_{e} = \sqrt {T_{e}^{2} + N_{e}^{2} } $$
(91.19)

The moment of the acting earth pressure about the toe of the retaining wall is

$$ \begin{aligned} M_{e} = &\int\limits_{0}^{H} {\left( {H - z} \right)\sigma_{xw} dz} \hfill \\ =& \frac{1}{{6G\omega^{4} }}\{ - 2GH^{3} K_{s} \eta \omega^{4} + 6\gamma GKk_{v} v_{p}^{3} \omega \cos \omega t + 3\gamma GKk_{v} v_{p} \omega \hfill \\ &\times (H^{2} \omega^{2} - 2v_{p}^{2} )\cos m_{3} - 6\gamma GHKk_{v} v_{p}^{2} \omega^{2} \sin m_{3} + \gamma k_{h} K_{s} v_{s} [H\omega \hfill \\ &\times (6v_{s}^{2} - H^{2} \omega^{2} )\cos m_{1} + 6v_{s}^{3} (\sin m_{1} - \sin \omega t)]\} \hfill \\ \end{aligned} $$
(91.20)

where, \( m_{3} = \frac{{H\omega - \omega tv_{p} }}{{v_{p} }} \).

So the height of the resultant forces P ae from the base of the wall is

$$ h = \frac{{M_{e} }}{{N_{e} }} $$
(91.21)

4 Rotational Displacement of Retaining Wall

The following equations of motion are presented to estimate the rotational displacements of gravity retaining wall, similar to equations reported in Zeng (Zeng and Steedman 2000) and Choudhury (Choudhury and Nimbalkar 2007).

The moment of the acting earth pressure about the toe of the retaining wall is

$$ \sum {M_{0} } = M_{e} + W_{w} x_{c} $$
(91.22)

where, \( W_{w} \) is the weight of the gravity wall, x c is the horizontal distance from the center to toe of retaining wall.

Again, the motion equation of the retaining wall about its toe can be written as (Choudhury and Nimbalkar 2008)

$$ \sum {M_{0} } = - y_{c} \left( {{{W_{w} } \mathord{\left/ {\vphantom {{W_{w} } g}} \right. \kern-\nulldelimiterspace} g}} \right)\left( {a_{c} } \right)_{x} + x_{c} \left( {{{W_{w} } \mathord{\left/ {\vphantom {{W_{w} } g}} \right. \kern-\nulldelimiterspace} g}} \right)\left( {a_{c} } \right)_{y} + I_{c} {\rm A} $$
(91.23)
$$ \left( {a_{c} } \right)_{x} = a_{g} - {\rm A}y_{c} - \beta^{2} x_{c} $$
(91.24)
$$ \left( {a_{c} } \right)_{y} = {\rm A}x_{c} - \beta^{2} y_{c} $$
(91.25)

where, \( a_{g} = k_{hd} g \), y c is the vertical distance from the center to toe of retaining wall, \( I_{c} \) is polar moment of inertia of the about the centroid, \( {\rm A} \)is angular acceleration.

Substituting Eqs. (91.24) and (91.25) into Eq.(91.23), we have (Choudhury and Nimbalkar 2008)

$$ \sum {M_{0} } = \left( {{{W_{w} } \mathord{\left/ {\vphantom {{W_{w} } g}} \right. \kern-\nulldelimiterspace} g}} \right)r_{c}^{2} {\rm A} - \left( {{{W_{w} } \mathord{\left/ {\vphantom {{W_{w} } g}} \right. \kern-\nulldelimiterspace} g}} \right)a_{g} y_{c} + I_{c} {\rm A} $$
(91.26)

where, \( r_{c}^{2} = x_{c}^{2} + y_{c}^{2} . \)

Combining Eqs. (91.22) and (91.26), the rotating acceleration of retaining wall about its toe can be determined by

$$ {\rm A} = \frac{{M_{e} + W_{w} x_{c} + \left( {{{W_{w} } \mathord{\left/ {\vphantom {{W_{w} } g}} \right. \kern-\nulldelimiterspace} g}} \right)a_{g} y_{c} }}{{\left( {{{W_{w} } \mathord{\left/ {\vphantom {{W_{w} } g}} \right. \kern-\nulldelimiterspace} g}} \right)r_{c}^{2} + I_{c} }} $$
(91.27)

The rotating angle velocity \( \beta \) is obtained by

$$ \beta = \int {\rm A} dt $$
(91.28)

The tilting angle can be derived as

$$ \begin{aligned} \eta_{{(t_{f} )}} = & \int\limits_{0}^{{t_{f} }} {\beta dt} \\ = & \frac{{W_{w} x_{c} + \left( {{{W_{w} } \mathord{\left/ {\vphantom {{W_{w} } g}} \right. \kern-\nulldelimiterspace} g}} \right)a_{g} y_{c} }}{{2[\left( {{{W_{w} } \mathord{\left/ {\vphantom {{W_{w} } g}} \right. \kern-\nulldelimiterspace} g}} \right)r_{c}^{2} + I_{c} ]}}t_{f}^{2} + \frac{1}{{\left( {{{W_{w} } \mathord{\left/ {\vphantom {{W_{w} } g}} \right. \kern-\nulldelimiterspace} g}} \right)r_{c}^{2} + I_{c} }}[ - \frac{1}{6}H^{3} K_{s} t_{f}^{2} \eta_{{(t_{f} - \Updelta t)}} \\ & - \frac{{Kk_{v} v_{p}^{3} \gamma }}{{\omega^{5} }}(\cos \omega t_{f} - 1) + \frac{{Kk_{v} v_{p}^{3} \gamma }}{{\omega^{5} }}(\cos m_{6} - \cos m_{7} ) \\ & + \frac{{H^{2} Kk_{v} v_{p}^{{}} \gamma }}{{2\omega^{3} }}(\cos m_{7} - \cos m_{6} ) + \frac{{H^{2} K_{s} k_{h} v_{s}^{3} \gamma }}{{G\omega^{5} }}(\cos m_{4} - \cos m_{5} ) \\ & + \frac{{H^{3} K_{s} k_{h} v_{s}^{{}} \gamma }}{{6G\omega^{3} }}(\cos m_{5} - \cos m_{4} ) - \frac{{K_{s} k_{h} v_{s}^{4} \gamma }}{{G\omega^{6} }}\sin \omega t_{f} ] \\ & - \frac{{HKk_{v} v_{p}^{2} \gamma }}{{\omega^{4} }}(\sin m_{6} + \sin m_{7} ) + \frac{{K_{s} k_{h} v_{s}^{4} \gamma }}{{G\omega^{6} }}(\sin m_{4} + \sin m_{5} ) \\ \end{aligned} $$
(91.29)

where, \( \eta \) represents the cumulative rotating angle during the time from 0 to \( t_{f} \). \( m_{4} = t_{f} \omega - \frac{H\omega }{{v_{s} }},\,m_{5} = \frac{H\omega }{{v_{s} }},\,m_{6} = t_{f} \omega - \frac{H\omega }{{v_{p} }},\,m_{7} = \frac{H\omega }{{v_{p} }}. \)

It is revealed in Eq. (91.29) that the total rotational displacement is the summation of individual rotations during the entire earthquake motion. The above procedure is repeated for each cycle of vibration.

5 Implementation of Present Model

The algorithmic implementation of present model is based on an iterative strategy. The detailed iterative scheme is plotted in Fig. 91.2 .

Fig. 91.2
figure 2

dynamic iterative strategy for the determination of rotating displacement

Full size image

Pseudo-dynamic method and free-field solution are coupled in this analysis. A simple iterative algorithmic is needed in present model and complex dynamic analysis as Newmark method is avoid. Although present method is still a pseudo-dynamic approximate one, the time-dependent seismic earth pressure and rotational displacement of retaining wall during the entire seismic process can be obtained conveniently by present model.

6 Results and Discussion

The results obtained from the numerical analyses, based on present method, are shown in this section. Comparisons have been made with the M–O method. The retaining wall is 7.0 m in height, made of concrete with a unit weight of 25 kN/m3. Moreover, the backfill is made of cohesionless soil with a unit weight of 17 kN/m3. The following parameters are used in the calculation: G = 350 MPa, H = 7.0 m, b = 1.2 m, V s = 100 m/s, V p = 187 m/s, \( \phi = 2 5 {\text{ Deg}}. \)

Figure 91.3 shows horizontal and vertical acceleration-time history response of backfill during the entire seismic process. The acceleration is time dependent, which is different from pseudo-static method. Moreover, the horizontal and vertical acceleration is independent, and the phase difference due to finite shear wave velocity is considered.

Fig. 91.3
figure 3

Horizontal and vertical acceleration-time history response of backfill with k h = 0.1, \( \delta = 20 ^\circ , \) at z = 0

Full size image

Resultant force–time response is plotted in Fig. 91.4. It is revealed that before t = 0.22 s, as the time increases, the resultant force P e acting on retaining wall also increases. But after t = 0.22 s, the resultant force P e acting on retaining wall decreases with increase in the time. Because, after t = 0.22 s, the retaining start to rotate about its toe and the relative displacement between retaining wall and backfill in the free-field decrease. Moreover, comparison between present and M–O method is carried out. It is obvious that M–O results are time-independent while present one is time-dependent. The maximum value of resultant force P e is close to the results obtained by M–O method, with 6.25 % error.

Fig. 91.4
figure 4

Resultant force–time response which acting on the retaining wall with k h = 0.1, \( \delta = 20^\circ \)

Full size image

The distribution of earth pressure is depicted in Fig. 91.5. It is revealed from Fig. 91.5 that non-linear seismic earth pressure distribution behind retaining wall in a more realistic manner compared to the pseudo-static method. It is also clear from Steedman and Zeng (1990) that the earth pressure distribution along the height is non-linear.

Fig. 91.5
figure 5

Distribution of earth pressure which varied with time

Full size image

Figure 91.6 shows the time-dependent height of the resultant forces acting on retaining wall from the base of wall. It is well known that the height of the resultant forces obtained by pseudo-static method is time-independent, and is supposed to be one-third of the height of retaining wall. However, the height obtained by present method is time dependent, ranges from 3.0 m to 5.0 m. It is higher than the pseudo-static method, so the pseudo-static method may cause some unsafe factors when the retaining wall rotating.

Fig. 91.6
figure 6

The time-dependent height of the resultant forces acting on retaining wall from the base of wall

Full size image

Figure 91.7 shows the dependence of resultant force on the wall friction angle. It is obvious that the resultant force increases with the wall friction angle increases.

Fig. 91.7
figure 7

Dependence of resultant force on the wall friction angle with k h = 0.1, \( \delta = 20^\circ \)

Full size image

7 Conclusions

In this paper, by considering the time effect and phase changes in shear and primary waves propagating in the backfill, a simple method to determine the dynamic earth pressure and rotating displacement is established. Both active and passive earth pressure are considered and it is found that earth pressure may transfer from active to passive earth pressure as the seismic intensity reach the critical value. Moreover, the rotational displacement, distribution of earth pressure along the height of retaining wall, resultant force and its height from the base of wall are time-dependent. Little iterative calculation is needed, but the time dependent process of earth pressure and displacement is obtained. Although assumptions are adopted in this paper, the proposed analysis can be used for the assessment of the safety of retaining wall under seismic condition.

In the present model only one ideal case, rotation about the toe of retaining wall, has been studied. Nevertheless, the cases for combined failure modes such as sliding and rotation can be easily extended by modify the kinetic equation. Although the method developed here is primarily for cohessionless soil, analysis for the soil with cohesion using this approach is straightforward extensions of this work.