Rapid estimation of maximum and minimum void ratios of granular soils

Abstract

Maximum and minimum void ratios (e_max and e_min) of granular soils are commonly used as indicators of many engineering properties. However, few methods, apart from laboratory tests, are available to provide a rapid estimation of both e_max and e_min. In this study, we present a theoretical model to map the densest and the loosest packing configurations of granular soils onto the void space. A corresponding numerical procedure that can predict both e_max and e_min of granular soils with arbitrary grain size distributions is proposed. The capacity of the proposed method is evaluated by predicting the maximum and minimum void ratios of medium to fine mixed graded sands with different contents of fines. The influence of the grain size distribution, characterized quantitatively by uniformity parameter and the fractal dimension, on e_max and e_min is discussed using the proposed method. Moreover, application of this method in understanding the controlling mechanism for the void ratio change during grain crushing is presented.

1 Introduction

The void ratio is commonly regarded as a comprehensive representation of the mechanical and hydromechanical properties. In the critical state theory, for example, the void ratio as well as its relationship with the mean effective stress under sufficiently large shear strain has a governing influence on the deformation and strength characteristics of granular soils [29, 33]. Due to different arrangements of the granular solids, the void ratio of a granular soil without any external stress falls within a certain range, bounded by the minimum and the maximum void ratios (e_min and e_max). Determining the minimum and maximum void ratios of granular soils is not only a preliminary step for preparing the soil specimens with certain relative densities, but also provides approximations of many material and state-dependent properties. For instance, Cubrinovski and Ishihara suggested using the void ratio range (e_max–e_min) as an indicator of some mechanical properties, such as the normalized SPT blow count [9] and the position of the critical state line [10]. In this context, geotechnical engineers may have a grasp of important properties of granular soils if the minimum and maximum void ratios can be rapidly estimated. In practical cases, however, elaborate laboratory tests are generally required to determine e_min and e_max. Needing the laboratory tests may compromise the simplicity of using e_min and/or e_max as indicators of many properties. In addition, the representative elementary volume (RVE) of some coarse-grained materials (e.g., rockfills, which may have the maximum particle size of 1 m), can be beyond the size limit of conventional laboratory apparatuses. Thus, determining e_min and e_max of such coarse-grained materials can be expensive, or imprecise if the downscaling techniques have to be adopted [15].

To address the above problems, Humphres [16] used empirical graphical method to approximately estimate the minimum void ratios of granular soils. Youd [32] proposed empirical curves to determine the maximum and minimum void ratios after analyzing the influence of particle shape, particle size range and variances in the curve shape of the grain size distribution (GSD). Despite the simplicity of these empirical methods, the essential reasonability is not elucidated. As a result, the applicability of these methods is often unclear for some particular granular soils and improvements or generalizations of these methods are not obvious.

Since the last decades, the discrete element method (DEM) has been proven to be a powerful tool in predicting the packing densities of granular soils. For example, Voivret [28] used DEM to investigate the influence of the particle size span on the packing density of polydisperse granular materials. Minh and Cheng [20] studied the influence of the “fractal dimension” of the GSD on the one-dimensional deposition properties of granular soils and found the existence of a critical fractal dimension that corresponds to the densest packing. However, the DEM simulation is far from being called a rapid method. It may take several days to simulate the packing of a moderately polydisperse granular specimen with the size of its RVE.

Regarding a possible methodology to overcome the limitations of the empirical and the numerical methods, a desirable solution would be finding an analytic expression to map the packing information onto the void space. For instance, Ouchiyama and Tanaka [23] proposed the idea of mapping the neighboring particles onto the surface of the reference particle so that the “shaded area” can be considered occupied. Using this hypothesis, Madadi et al. [18] investigated the density of densely packed granular materials with “narrowly distributed” particle sizes. Kenzi [17] proposed an analytic solution for the estimation of the minimum and maximum void ratios of binary granular mixtures. Similar analytic model for the packing density of binary mixtures was developed by Zok and Lange [34] for composite materials. Stovall et al. [26] used a linear model to predict the packing density of granular soils with multiple particle sizes. Recently, Chang et al. [4,5,6] developed the concept of active and inactive voids and proposed the packing and compression models for sand–silt mixtures. Extension of this idea from binary to polydisperse particle sizes was also presented to predict the minimum void ratio of granular materials with the effect of GSD [7]. Although these models have shed lights on the nature of the granular packing problem, they are still limited in predicting both the minimum and maximum void ratios of an arbitrary GSD.

In this study, we introduce a random close packing theory and extend it to predict the void ratios of both the densest and loosest packings. A rapid numerical procedure that can systematically determine e_min and e_max for an arbitrary GSD is developed. Moreover, the quantitative influence of the GSD on the maximum and minimum void ratios is discussed, and application of this method in understanding the controlling mechanism for the void ratio change during grain crushing is presented.

2 Model for the packing of granular soils

Before proposing a model that is capable of predicting the maximum and minimum void ratios of arbitrary granular soils, two fundamental questions should be answered: (a) How to map the topology and geometry of a granular packing onto the void space? and (b) how to define the packing configurations of the densest and loosest packings? In what follows, we will first present the outline of the dimension reduction concept proposed by Farr and Groot [14], which essentially addresses the first question. Afterward, we will answer the second question by applying this concept to both the densest and the loosest packings.

2.1 Outline of the dimension reduction concept

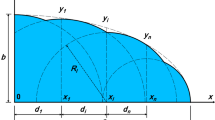
The dimension reduction concept proposed by Farr and Groot [14] is an approximate solution for the dense packing of spheres. We assume that soil particles are spherical as a starting point. The essential idea of the close packing theory is to map the 3D packing of spheres with a certain distribution P_3D(D) onto 1D rods. Here, the particle number distribution of spheres P_3D(D) is defined so that $P_{{ 3 {\text{D}}}} \left( D \right){\text{d}}D$ equals the number fraction of spheres with diameters ranging from D to D + dD. We imagine a large random but non-overlapping arrangement of spheres in 3D (see Fig. 1). If we draw a straight line through this packing and counting each portion of the line which lies within a sphere as a rod with length L, Farr and Groot argued that the rod length fraction is equal to the 3D volume fraction. The resulting distribution of rod length $P_{{ 1 {\text{D}}}} \left( L \right)$ is related to P_3D(D) by

$$ P_{{1{\text{D}}}} \left( L \right) = 2L\frac{{\int_{L}^{{D_{\text{M}} }} { P_{{3{\text{D}}}} \left( D \right){\text{d}}D} }}{{\int_{0}^{{D_{\text{M}} }} {P_{{3{\text{D}}}} \left( D \right)D^{2} {\text{d}}D} }} $$

(1)

where D_M is the maximum particle diameter. It should be noted that the dimension reduction concept is mainly valid for isotropic packings. For granular soils with special particle shapes (e.g., slate rockfill materials), the influence of anisotropy is not negligible [1] and the dimension reduction concept may not be suitable. However, the shapes of most of the granular particles in geotechnical engineering are randomly irregular, without a preferred dimension. DEM simulations [1] demonstrated that the packings of granular particles, whose geometric shapes do not have a preferred dimension, do not exhibit significant anisotropy irrespective of the packing density. Therefore, the dimension reduction concept is suitable for most granular soils.

Fig. 1

Schematic representation of the sphere-rod mapping concept

With this dimension reduction concept, it suffices to define an effective potential between the rods. By considering the size independence of the packing and the interaction of unequal particles, Farr and Groot suggested one expression for the potential that is believed to be the simplest to capture the physics of the packing of rods, which is given by

$$ V\left( h \right) = \left\{ {\begin{array}{*{20}l} \infty \hfill & {{\text{if}}\quad h < \hbox{min} (fL_{i} ,fL_{j} ),} \hfill \\ 0 \hfill & {{\text{if}}\quad h \ge \hbox{min} (fL_{i} ,fL_{j} )} \hfill \\ \end{array} } \right. $$

(2)

where V is the value of the potential, which is either zero or infinite, because the rods are considered to be rigid; h is the gap between the nearest approaching ends of rods L_i and L_j; f is the “free volume” parameter, which corresponds to the tolerable free volume between particles. In this study, we should distinguish the value of f for the densest and the loosest packings, denoted as $f_{\text{D}}$ and $f_{\text{L}}$, respectively. The values of $f_{\text{D}}$ and $f_{\text{L}}$ are considered to be related to the particle shape. Thus, we consider them as two fitting parameters in the model. It is worth mentioning that as small particles (illustrated by particle B in Fig. 1) may rattle around two contacting particles (B and C in Fig. 1) in a 3D packing, the potential defined in Eq. (2) should also be effective for non-neighboring rods (B′ and C′ in Fig. 1) to enable large rods to reach through small ones.

2.2 Configurations of the loosest and densest packings

Although the dimension reduction concept was initially proposed for the close random packing problem, we remark that the close packing configuration is not a necessary condition for this concept. That is to say, it is possible to map both the densest and the loosest packings of spheres onto a problem of the packing of rods on a line, where we should search the ordering of rods as well as their separations.

In practices, the preparation of loose granular soil samples requires a static deposition step, namely, pouring the soils into a container. Due to the gravity, soil particles will fall and possibly roll until a local stable state is reached. The falling of a single soil particle, as illustrated in Fig. 2a, can be assumed to satisfy the following conditions: (a) The falling particle can barely influence the overall arrangement of the deposited soil particles in the container, and (b) the final position of the falling particle will correspond to a local minimum potential. By analogy, we anticipate the following configurations for 1D loose packing of rods: (a) Adding a new rod will not change the overall ordering of the pre-placed rods. Without losing generality, the new rod can be placed at the extremity of the pre-placed rods. (b) And the new rod will, however, try to reach the local minimum potential. In other words, the adding rod L_i will approach the pre-placed rods until its gap between one of the pre-placed rods, designated as L_j, becomes $h = \hbox{min} (fL_{i} ,fL_{j} )$.

Fig. 2

Illustration of different packing procedures: a loosest packing; b densest packing

The densest granular soil samples are often prepared by the dynamic method (e.g., using a vibratory table suggested by ASTM [3]) in laboratory tests. Falling of a new soil particle into a vibrating granular soil sample results in the rearrangement of the soil particles until reaching a global minimum potential state (see Fig. 2b). In 1D packing of rods, the vibration process can be interpreted as the reordering of all the rods and minimization of the gaps between the rods to reach the global minimum potential.

3 Numerical procedure

3.1 Overall flowchart

Figure 3 presents the flowchart for the numerical estimation of e_min and e_max. The simulation procedure is divided into three successive steps, which can be represented by three functionals. The first functional $\mathcal{F}_{1}$ relates the cumulated mass distribution (CMD) M(D), which is commonly used in geotechnical engineering, to the particle number distribution of spheres P_3D(D). The second functional $\mathcal{F}_{2}$ maps P_3D(D) into 1D packing of rods using Eq. (1). The third functional ($\mathcal{F}_{3 - 1}$ or $\mathcal{F}_{3 - 2}$) maps eventually the 1D rods onto the void space by virtue of the densest and loosest packing configurations established previously in Sect. 2.

Fig. 3

Flowchart for the estimation of the maximum and minimum void ratios

3.2 From CMD to the particle number distribution

In order to establish the first functional, we should distinguish the definitions of the two following descriptions for the GSD of a granular soil. The CMD M(D) is defined as the percentage of mass equal or finer against the particle size

$$ M(D) = \frac{{M_{(L \le D)} }}{{M_{\text{T}} }} $$

(3)

where $M_{{\left( {L \le D} \right)}}$ is the mass of particles with diameter smaller than D; $M_{\text{T}}$ is the total mass of the soil sample. An alternative description to reflect the GSD is particle number distribution P_3D(D), as defined previously. The definition of P_3D(D) can be expressed as

$$ P_{{3{\text{D}}}} \left( D \right) = \frac{{{\text{d}}N_{(L \le D)} }}{{N_{\text{T}} {\text{d}}D}} $$

(4)

where $N_{(L \le D)}$ is the number of particles with diameter equal or smaller than D; N_T is the total number of particles.

According to Eq. (3), the mass fraction of particles with diameter ranging from D to D + dD is ${\text{d}}M(D)$. The number of particles corresponding to this mass fraction is thus calculated to be

$$ {\text{d}}N(L \le D) = \frac{{M_{\text{T}} {\text{d}}M\left( D \right)}}{\rho V(D)} $$

(5)

where $\rho$ is the average density of the grain material and V(D) is the volume of a single particle with diameter D. For spherical particles, we have

$$ V\left( D \right) = \frac{1}{6}\pi D^{3} $$

(6)

By virtue of Eq. (5), the total particle number N_T is easily integrated to be

$$ N_{\text{T}} = \int_{{D_{\text{m}} }}^{{D_{\text{M}} }} {{\text{d}}N(L \le D) = } \int_{{D_{\text{m}} }}^{{D_{\text{M}} }} {\frac{{M_{\text{T}} }}{\rho V(D)}} \frac{{{\text{d}}M\left( D \right)}}{{{\text{d}}D}}{\text{d}}D $$

(7)

Substituting Eqs. (5) and (7) into Eq. (4) eventually yields

$$ P_{{3{\text{D}}}} \left( D \right) = {{\frac{{{\text{d}}M(D)}}{{{\text{d}}D}}} \mathord{\left/ {\vphantom {{\frac{{{\text{d}}M(D)}}{{{\text{d}}D}}} {V\left( D \right)}}} \right. \kern-0pt} {V\left( D \right)}}\int_{{D_{\text{m}} }}^{{D_{\text{M}} }} {\frac{1}{V(D)}} \frac{{{\text{d}}M(D)}}{{{\text{d}}D}}{\text{d}}D $$

(8)

Thus, for a given granular soil, we can derive the particle number distribution P_3D(D) from its CMD $M(D)$ using Eq. (8).

3.3 Algorithms for the packing of rods

Now the rod number distribution P_1D(L) can be derived based on $\mathcal{F}_{1}$ (Eq. 8) and $\mathcal{F}_{2}$ (Eq. 1), respectively. In order to further map P_1D(L) onto the void space, one should (a) generate random variables that obey the distribution given by P_1D(L) and (b) optimize the ordering and/or the minimum gaps for the packing of rods.

In this study, the acceptance–rejection method [12] is adopted to generate the lengths of rods $\left\{ {L_{i} } \right\}$ that obey P_1D(L). The generation procedure is summarized as follows:

• 1) Choose a parameter $\lambda$ that $\lambda P_{{1{\text{D}}}} (L) \le 1$, $\forall L \in \left[ {0,D_{\text{M}} } \right]$.

• 2) Generate uniformly distributed pseudo-random numbers $r_{1}$ and $r_{2}$ that $r_{1} ,r_{2} \in \left( {0,1} \right)$. Let $y = D_{\text{M}} r_{1}$.

• 3) Compare $r_{2}$ and $\lambda P_{{1{\text{D}}}} (y)$. If $r_{2} \le \lambda P_{{1{\text{D}}}} (y)$, let $L = y$ and output $L$. Otherwise, abandon $r_{1}$ and $r_{2}$, then return to step (2).

Repeat the above procedure to generate the random number sequence $L_{1}$, $L_{2}$,…,$L_{n}$. The generated random number sequence corresponds to different lengths of rods.

Once the lengths of rods are generated, we use an efficient “greedy algorithm” suggested by Farr and Groot [14] to estimate the minimum void ratio. The main idea is to insert rods in decreasing order so that we can avoid calculating the two-body potential between the inserted rod and all the rods pre-placed in the packing. The algorithm is summarized as:

• 1) Label the lengths of the rods in decreasing order such that $L_{1} \ge L_{2} \ge L_{3} \cdots \ge L_{n}$. Then, these rods will be inserted in decreasing order.

• 2) Maintain a set of gaps $\left\{ {g_{i} } \right\}$, equal in number to the number of rods in the packing. The length of the first gap is $g_{1} = fL_{1}$. To insert rod j, we should identify and delete the largest gap $g_{\hbox{max} }$ in the packing. Then, we add two new gaps in the set of gaps, namely $fL_{i}$ and $\hbox{max} [g_{\hbox{max} } - (1 + f)L_{j} ,fL_{j} ]$.

For the loosest packing of rods, the inserted rod is assumed to be unable to change the overall ordering of the pre-placed rods, as discussed in the previous section. Thus, we can choose to let the rods inserted in a random order of size and simply put the inserted rod at the extremity of the pre-placed rods packing. Imagine we have i − 1 pre-placed rods and now are inserting the rod i. It suffices to put the rod i at the end of rod i − 1 with a certain gap g_i. As the potential defined in Eq. (2) exists between rod i and all the pre-placed rods, at first sight, it seems we have to find the minimum g_i that satisfies the following i − 1 conditions:

$$ \begin{aligned} & \left\{ {\begin{array}{*{20}l} {g_{i} \ge \hbox{min} \left( {fL_{i} ,fL_{i - 1} } \right)} \hfill \\ {g_{i} + D_{k} \ge \hbox{min} \left( {fL_{i} ,fL_{i - k - 1} } \right),\quad k = 1,2, \ldots ,i - 2} \hfill \\ \end{array} } \right. \\ & {\text{with}}\quad D_{k} = \sum\limits_{j = 1}^{k} {\left( {L_{i - j} + g_{i - j} } \right)} \\ \end{aligned} $$

(9)

However, if we verify each condition in (9) in an increasing order of the index k, the process can be terminated when the left term is greater than $fL_{i}$. The remaining conditions (for k + 1, k + 2,…i −2) will be satisfied automatically because (a) the left terms in (9) increase monotonically with the increase in k and (b) the right terms in (9) are bounded by $fL_{i}$.

Therefore, we propose the following algorithm for the estimation of the loosest packing of rods:

• 1) Let the lengths of rods generated in a random order. Insert $L_{1}$, $L_{2}$, $g_{1} = fL_{1}$ and $g_{2} = \hbox{min} (fL_{1} ,fL_{2} )$.

• 2) In order to insert L_i, first let $g_{i} = \hbox{min} (fL_{i} ,fL_{i - 1} )$, k = 1 and D = 0. Then, do the following: ① $D = D + g_{i - k} + L_{i - k}$; ② $g_{i} = \hbox{max} (g_{i} ,\hbox{min} (L_{i} ,L_{i - k - 1} ) - D)$; ③ k = k + 1 until $k > i - 2$ or $D > fL_{i}$.

With the above algorithms, we can eventually calculate the maximum or the minimum void ratio of the packing by

$$ e_{{{{\hbox{min} } \mathord{\left/ {\vphantom {{\hbox{min} } {\hbox{max} }}} \right. \kern-0pt} {\hbox{max} }}}} = \frac{{\sum {g_{i} } }}{{\sum {L_{i} } }} $$

(10)

4 Results and discussions

4.1 Verification of the method

There are two parameters in the proposed model, namely, $f_{\text{D}}$ and $f_{\text{L}}$. For uniform spherical particles, we find that $f_{\text{D}} = 0.7654$ and $f_{\text{L}} = 0.9881$ will lead to the minimum and maximum void ratios of $e_{\hbox{min} } = 0.5504$ and $e_{\hbox{max} } = 0.8018$, respectively. These void ratios agree with the random close and loose packings of uniform spheres in the literature [22]. The values of $f_{\text{D}}$ and $f_{\text{L}}$ for non-spherical particles are generally greater than those for spherical particles. In practice, $f_{\text{D}}$ and $f_{\text{L}}$ can be experimentally obtained by measuring the maximum and minimum void ratios of one soil sample with any GSD. Then, the proposed method will enable geotechnical engineers to predict e_max and e_min of the same soils with other GSDs. A major advantage of this method compared to other explicit dynamic simulations (e.g., DEM simulation) is the computational efficiency: The proposed method can estimate e_max and e_min in several seconds on an ordinary PC, while the DEM simulations may take hours or days.

Experimental data for the maximum and minimum void ratios of medium to fine mixed graded sands after Yilmaz [31] are used to verify the proposed method. Figure 4 presents the GSDs of 10 artificially graded sands in the tests by changing the fines content (FC) from 0 to 100%. The particle size of coarse-grained sand ranges from 1 to 1.18 mm and the particle size of fines from 0.3 to 0.6 mm. Figure 5 shows their corresponding particle number distributions P_3D(D) and rod number distributions P_1D(L), which are calculated through the methods presented in the previous section. As can be seen, both P_3D(D) and P_1D(L) increase with the increase in FC for small particle/rod sizes and decrease for big particle/rod sizes. We also remark that the rod number distribution P_1D(L) does not equal to zero for rod sizes from 0.6 to 1 mm, which contrasts with the particle number distribution P_3D(D). This is because the length of a rod “cut” by a sphere may range from zero to the diameter of the sphere. Figure 6 compares the numerically estimated maximum and minimum void ratios of these granular mixtures with the experimental results. In the simulation, the values of f_D and f_L are fitted to be 0.9583 and 1.2577, respectively. The numerical prediction is in good agreement with the experimental data. Both the minimum and maximum void ratios of the mixtures decrease as the fine content increases from 0% to approximately 30%. Further increase in the fine content results in the increase in the maximum and minimum void ratios.

Fig. 4

GSDs of medium to fine mixed graded sands with different contents of fines after [31]

Fig. 5

Probability density distributions calculated for mixed graded sands with different contents of fines: a particle number distribution P_3D(D); b rod number distribution P_1D(L)

Fig. 6

Comparison of the predicted maximum and minimum void ratios with experimentally obtained results by [31]

4.2 Influence of GSDs

The proposed method has been verified previously for artificially graded granular soils. However, unlike artificially graded granular mixtures, the particle size of natural granular soils is often continuously distributed within a certain range. In the following, the proposed method is adopted to investigate the influence of the GSDs of natural granular soils on their maximum and minimum void ratios. To this end, one should first quantify the GSDs of naturally graded granular soils. It has been repeatedly observed that granular soils undergoing sufficiently large energy (e.g., landslides) will lead to the emergence of a fractal distribution of particle sizes (e.g., Turcotte [27], McDowell et al. [19], Altuhafi and Coop [2]). In this context, Einav [13] proposed an expression for the CMD of arbitrary naturally graded granular soils, given by

$$ M\left( D \right) = \frac{{\Lambda ^{3 - d} - \left( {{D \mathord{\left/ {\vphantom {D {D_{\text{M}} }}} \right. \kern-0pt} {D_{\text{M}} }}} \right)^{3 - d} }}{{\Lambda ^{3 - d} - 1}} $$

(11)

where $\Lambda$ is the ratio of the minimum particle size $D_{\text{m}}$ to the maximum particle size $D_{\text{M}}$, given as $\Lambda = {{D_{\text{m}} } \mathord{\left/ {\vphantom {{D_{\text{m}} } {D_{\text{M}} }}} \right. \kern-0pt} {D_{\text{M}} }}$; d is a constant parameter for a given GSD. If $D_{\text{m}}$ tends toward zero, the GSD becomes a fractal distribution and the parameter d is the fractal dimension of the GSD. Figure 7 gives three examples of the GSDs using Eq. (11) in semi-log axes. It is seen that an arbitrary GSD can be uniquely determined by three parameters: the parameter $\Lambda$, which is related to the uniformity of particle size, the fractal dimension d and the maximum particle size D_M.

Fig. 7

Three typical GSDs of granular soils described by Eq. (11)

Although some test results showed that greater particle sizes tend to decrease the maximum and minimum void ratios (see Cubrinovski and Ishihara [11] for instance), Youd [32] demonstrated experimentally that the effect of particle size on the packing densities is negligible if we control elaborately the shape of the particle, the particle size range and the gradational-curve shape. Furthermore, from the point of view of packing configurations, the maximum and minimum void ratios should be unchanged if all the particles are magnified by an equal amount. As a result of the size independence of e_max and e_min, there are only two influencing parameters in Eq. (11), namely $\Lambda$ and d. Figure 8 shows the simulated maximum and minimum void ratios of both narrowly distributed ($\Lambda \to 1$) and polydisperse ($\Lambda \to 0$) granular soils. To eliminate the influence of particle shape, we use spherical particles in the simulation, namely, $f_{\text{D}} = 0.7654$ and $f_{\text{L}} = 0.9881$. For narrowly distributed granular soils (see Figs. 8a, b), the maximum void ratio follows the same overall trend as the minimum void ratio when changing the GSD of granular soils: Both the maximum and minimum void ratios increase with the increase in the uniformity parameter $\Lambda$. The fact that increasing the particle size range (decreasing $\Lambda$) results in smaller void ratio was also found experimentally [32] and numerically by DEM simulation [28]. We can also remark that the influence of the fractal dimension d on e_max and e_min is not significant for narrowly distributed cases. However, for polydisperse soils, both the fractal dimension d and the uniformity parameter $\Lambda$ influence significantly the maximum and minimum void ratios (see Figs. 8c, d). In addition, it is also interesting to remark that for a given value of $\Lambda$, both e_max and e_min may attain the minimum values. e_max attains its minimum value at the fractal dimension d of about 2.6, which coincides with the ultimate fractal dimension of granular soils under substantial grain crushing [8, 13]. Contrasting with the maximum void ratio, e_min attains its minimum value at about d = 2.3. Similar results were also found by Minh and Cheng [20], who simulated the one-dimensional compression of granular materials by DEM and found that the specific volume of the granular materials approaches its minimum value when d = 2.3.

Fig. 8

Influence of the GSD on the maximum and minimum void ratios. ae_max for narrowly distributed soils, be_min for narrowly distributed soils, ce_max for polydisperse soils and de_min for polydisperse soils

The above results show the interesting similarity between the packings of polydisperse granular soils and the ultimate crushing states of granular soils. Inspired by the above results, we anticipate that the evolution of the GSD plays an important role in the change in the packing density of granular materials, which may be the governing factor for the change in the void ratio during grain crushing. In the following, the proposed method will be used to evaluate the role that the evolution of the GSD plays in the void ratio change during grain crushing.

Nakata et al. [21] have provided sufficient details in one-dimensional high-pressure compression tests on crushable silica sand. The maximum and minimum void ratios for the prior compression sand sample are 0.632 and 0.881, respectively. Figure 9 shows the experimentally obtained GSD curves at different vertical stresses, plotted in semi-logarithmic scale. The stress levels at which the GSDs were measured are labeled in the figure. Thanks to the experimentally measured GSDs, we are able to obtain the maximum and minimum void ratios at different GSDs (and at different stress levels) using the proposed method. In the simulation, the values of $f_{\text{D}}$ and $f_{\text{L}}$ are fitted to be 0.8726 and 1.0888, respectively. For the sake of simplicity, the change in the particle shape during grain crushing is ignored in this study. Thus, the values of $f_{\text{D}}$ and $f_{\text{L}}$ are assumed to be constants for the silica sand samples irrespective of the grain crushing with increasing the stress. The estimated e_max and e_min at different stress levels (estimated $e_{\hbox{min} } - \sigma_{v}$ and $e_{\hbox{max} } - \sigma_{v}$ relationships) are compared with the experimentally obtained compression curve ($e - \sigma_{v}$ relationship) of densely prepared sample ($e_{0} = 0.6 \pm 0.03$) in Fig. 10a. If we consider the fact that the volume change in granular soils under compression is not only contributed to the evolution of the packing configuration (i.e., the grain crushing and the subsequent rearrangement), but also to the elastic deformation of the soil skeleton [24], the agreement between the experimentally obtained $e - \sigma_{v}$ curve and the estimated $e_{\hbox{min} } - \sigma_{v}$ relationship is surprisingly good. The compression curve only deviated slightly from the estimated minimum void ratio under high compressive pressure. This good agreement suggests that the volume change due to the elastic deformation of the soil skeleton is relatively small compared to the contribution of the crushing and the subsequent rearrangement. Furthermore, as the compression curve for granular samples at different initial void ratios will converge toward a unique “limit compression curve” under sufficiently high pressure [24, 25, 30], the agreement between $e - \sigma_{v}$ curve and the estimated $e_{\hbox{min} } - \sigma_{v}$ relationship under high pressure should also be valid for granular soils prepared at other initial densities (see the conceptual illustration in Fig. 10b). It is thus plausible to conclude that a crushable granular soil under compression, irrespective of its initial relative density, will evolve toward its densest packing configuration. The densest state is probably achieved through the grain crushing and the subsequent rearrangement of the fragments.

Fig. 9

Evolution of the GSD curves for the one-dimensional compression test of the silica sand from [21]

Fig. 10

Compression curve bounded by the minimum and maximum void ratios: a compression test result together with the estimated maximum and minimum void ratios; b conceptual illustration of the compression of crushable granular soils

The relationship between the estimated e_min and e_max for the crushable silica sand at different GSDs is given in Fig. 11. The e_min–e_max relationship for the silica sand is compared with experimental data from Cubrinovski and Ishihara [11] for a variety of soils. We note that as the GSD of the silica sand evolves from a relatively uniform distribution to a highly polydisperse distribution due to grain crushing, the estimated e_min–e_max relationship for the tested silica sand covers a very broad range of granular materials. Evidently, the estimated correlation between e_min and e_max agrees basically with the data for different granular soils. Both the experimental data and the estimated result for the silica sand indicate that there is a pronounced correlation between the minimum and maximum void ratios. In addition, if the e_min–e_max is fitted by a linear function, both the estimation for the crushable silica sand and the test results for different kinds of granular soils indicate that when e_min tends toward zero, there is a “residual” maximum void ratio. As e_max–e_min characterizes the deformation potential of granular soils [11], the existence of the “residual” maximum void ratio implies the capacity of dilatancy for granular materials with low packing densities (e.g., highly polydisperse granular soils).

Fig. 11

Relationship between estimated e_min and e_max for crushable silica sand compared with experimental data from [11]

5 Conclusion

The maximum and minimum void ratios of granular soils are related to many mechanical and hydromechanical properties. However, apart from experimental tests, few methods are available to estimate the maximum and minimum void ratios. In this study, we propose a numerical method to provide rapid predictions of both the maximum and minimum void ratios. The proposed method uses the dimension reduction concept to simplify the 3D packing problem into 1D ordering of rods, which was originally proposed in the random close packing of spheres and is extended to both dense and loose cases in this study. Numerical procedures that allow efficient and systematic predictions of the maximum and minimum void ratios of granular soils with arbitrary GSDs (including gapped, uniform and polydisperse distributions), are also presented. The developed method is verified using experimental data on 10 mixed graded sands with different contents of fines. The estimated results show good agreement with test data if we consider the fact that the particle sizes of sand and fines mixtures are very complex, which are both polydisperse and poorly graded.

The effect of the GSD on the maximum and minimum void ratios is discussed using the proposed method. Results show that both the maximum and minimum void ratios tend to decrease with increasing polydispersity of the particle sizes. The effect of the fractal dimension d is non-significant for narrowly distributed granular soils, and becomes more and more pronounced with increasing polydispersity of particle sizes. For polydisperse granular soils, both e_max and e_min may attain their minimum value at certain values of d. e_max attains its minimum value at approximately d = 2.6, while e_min attains its minimum value at about d = 2.3.

The one-dimensional compression of the crushable silica sand is also discussed in this study as an example of using the proposed method. Results show that the estimated minimum void ratios at different stress levels agree well with the compression curve for densely prepared silica sample. Further analysis suggests that a crushable granular soil under compression, irrespective of its initial density, will evolve toward its densest packing configuration. The densest state is probably achieved through the grain crushing and the subsequent rearrangement of the fragments. In addition, the estimated relationship between the minimum and maximum void ratios for the silica sand under crushing follows the same overall trend as the experimental data for a variety of granular soils. Both estimated and experimental results imply that there is a residual maximum void ratio when e_min tends toward zero. Such residual e_max allows the potential dilatancy of granular soils that has low minimum void ratios (e.g., polydisperse granular soils).

The influence of the particle shape is characterized by the parameters f_D and f_L. In our future work, quantitative correlation between these parameters and the roundness of particles will be investigated to refine the proposed model. In addition, the estimation of packing densities of granular materials with particular particle shapes needs further investigation.