Propagation and coalescence of quasi-static cracks in Brazilian disks: an insight from a phase field model

Abstract

The phase field model represents sharp cracks by diffusive mushy-zone and can simulate crack propagation automatically. Propagation and coalescence of quasi-static cracks in Brazilian disks are investigated by a phase field model. The phase field modeling is implemented in Comsol Multiphysics and initially verified by a benchmark of three-point bending test. The Brazilian disk specimens containing no initial crack, a single and two pre-existing cracks subjected to compression are then tested by the phase field model. Crack propagation patterns along with the load–displacement curves are fully discussed. Meanwhile, the effects of length scale parameter and critical energy release rate on crack propagation are evaluated. In addition, the effect of crack inclination angle on the pre-cracked Brazilian disk specimens is also investigated. The numerical results obtained by the phase field model are in good agreement with previous experimental and numerical results.

1 Introduction

In recent years, rock fracture mechanics has been developed with the application of fracture mechanics in geology and rock engineering. Various rock engineering problems such as rock cutting, hydraulic fracturing, explosive fracturing, underground excavation and rock stability [22] can be solved effectively by rock fracture mechanics because it focuses on the initiation and propagation of a single crack or multiple cracks in geomaterials subjected to loads [63]. Two leading bases of rock fracture mechanics are the Griffith’s theory in 1920 and Irwin’s modification in 1957, which stressed the stress intensity factor (SIF) near a crack tip [22, 28] to reflect the ability of material to resist fracture propagation. The SIF, also known as the fracture toughness, thereby becomes a widely used parameter of rock fracture.

Depending on the applied load on a crack, the crack propagation shows three modes: Mode I fracture (crack opening), Mode II fracture (crack in-plane shear), and Mode III fracture (crack out-plane tearing) [7]. In addition, the crack can also propagate according to a combination of different modes, while Mode I fracture is most frequently observed [28]. Even for some macroscopic shear or mixed-mode failure in rocks, researchers still found microscopic fractures of Mode I. During crack propagation in rocks and rock-like materials, the cracks initiating from the tips of pre-existing cracks are commonly typed into two categories: wing cracks and secondary cracks [63]. The wing cracks usually result from tensile damage, while the secondary cracks are caused by shear damage evolution. Because the fracture toughness of rock for tension is lower than that for shear, propagation of wing cracks is more frequently observed than the secondary cracks in rocks.

Many contributions have been made to study crack propagation and coalescence in rocks. For example, experimental tests were conducted to show crack propagation in rock-like materials [17, 41, 47, 48, 57, 59, 60, 62]. In particular, many novel and targeting tests were designed and implemented to test rock fracture property and discover crack patterns under compressive loads including notched semicircular bending tests (NSCB) [2, 3, 24, 27, 40], cracked chevron notched semicircular bending method (CCNSCB) [39], and Brazil splitting tests (Brazilian disk tests) [1,2,3, 63]. The Brazilian disk test on an intact specimen with no pre-existing crack is commonly used to determine tensile strength of rocks or rock-like materials. Furthermore, the Brazilian disk test on a rock or rock-like specimen with a central pre-existing crack is one of the most suitable tests to determine static and dynamic fracture toughness of materials [63]. For example, Awaji and Sato [15] and Atkinson et al. [14] have used cracked straight through Brazilian disk (CSTBD) specimens to evaluate the Mode I fracture and mixed Mode I/II fracture toughness of rocks. Therefore, considering the importance and engineering significance, it is essential to conduct further study on the mechanism of crack propagation and coalescence in the Brazilian disk test.

Researchers have to use numerical tools to conduct the research on crack propagation if the experimental tests are difficult or even impossible to conduct. For example, Firme et al. [31] used the multi-mechanism deformation model to conduct numerical simulations of triaxial creep tests on Brazilian salt rocks. Meng et al. [42] applied the mathematical programming methods to obtain a discrete description of the failure mode in a Brazilian test. In the realm of fracture mechanics, most of the numerical methods treat crack topology in discrete setting and introduce discontinuities in the displacement field such as the discrete crack models [37], extended finite element method (XFEM) [23, 46], generalized finite element method (GFEM) [32], cohesive element methods [51, 61], element-erosion method [16, 38] and the phantom-node method [21, 52]. More specifically, the discrete crack model [37] reconstructs the mesh to freshly create new crack surfaces. XFEM [46] enhances the displacement by introducing additional discontinuous shape functions in the cracked elements. Cohesive element methods [51, 61] require a displacement jump on the element boundary. The element-erosion method [16, 38] considers elements with zero stress as the cracks and cannot simulate crack branching correctly [58]. Recently, some continuous methods are also used to study crack propagation, e.g., meshless methods [50, 66], peridynamics (PD) [64], dual-horizon peridynamics (DH-PD) [54, 55], cracking particle method (CPM) [49, 53], screened-poisson equation models [11, 12], remeshing techniques [8,9,10]. Besides, for the Brazilian disk tests, simulations based on the finite element method (FEM), discrete element methods (DEM), or meshless method have been conducted [20, 28, 63]. However, the inherent disadvantages of the above-mentioned numerical methods in fracture mechanics, such as complicated implementation and special treatments for complex crack topology, have also led to the difficulty in crack problems, especially when encountering multiple cracks.

In this paper, a more effective numerical method for crack propagation, the phase field method (PFM) [5, 13, 35] is adopted. Crack propagation and coalescence in Brazilian disk tests are simulated by a phase field model. As a recently emerged and developed approach, PFM has attracted considerable attention [18, 36, 44, 45]. The phase field model uses a scalar field (phase field) to represent the sharp crack. The shape of the crack is controlled by a length scale parameter, and crack propagation is governed by the evolution equation of the phase field. The advantages of PFM over other approaches are manifold: (i) the implementation is relatively easier because all the simulations are conducted in a fixed topology; (ii) PFM does not require external criterion for fracture, and the crack propagation path is automatically determined without special algorithmic treatments [18]; (iii) PFM deals well with complex crack propagation such as branching and merging in 3D; (iv) PFM also can easily simulate crack propagation in heterogeneous materials; and (v) PFM can be coupled to some existing commercial software.

We also show our implementation details of the phase field model in this paper. The phase field model is accomplished in the commercial FEM software, Comsol Multiphysics, and verified by a benchmark of three-point bending test. In addition, the Brazilian disk specimens of rocks with no initial crack, a single or two pre-existing cracks are investigated using the PFM. Meanwhile, the effect of length scale parameter and critical energy release rate on crack propagation is evaluated. The numerical results obtained by the phase field model are in good agreement with previous experimental and numerical results, indicating the accuracy and applicability of the phase field modeling.

This paper is organized as follows. The theory of phase field modeling for brittle fracture by the variational approach is stated in Sect. 2. Subsequently, the numerical implementation details of the phase field model are described in Sect. 3. Then, we initially verify the phase field modeling by a benchmark of three-point bending test in Sect. 4. Initiation, propagation, and coalescence of cracks in Brazilian disk specimens are simulated and analyzed in Sect. 5. The examples include specimens containing no initial crack, a single and two pre-existing cracks subjected to compression. Finally, Sect. 6 summarizes the whole paper.

2 Theory of phase field modeling

2.1 Theory of brittle fracture

Let us consider an elastic body $\varOmega \subset {\mathbb {R}}^d$ ($d\in \{1,2,3\}$) as shown in Fig. 1. The external boundary and internal discontinuity boundary of the body $\varOmega$ are denoted as $\partial \varOmega$ and $\varGamma$, respectively. Denoting $\varvec{x}$ as the position vector, the displacement of body $\varOmega$ at time t is $\varvec{u}(\varvec{x},t)\subset {\mathbb {R}}^d$. As depicted in Fig. 1, the body $\varOmega$ satisfies the time-dependent Dirichlet boundary conditions, $u_i(\varvec{x},t)=g_i(\varvec{x},t)$, on $\partial \varOmega _{g_i} \in \varOmega$, and also the time-dependent Neumann conditions on $\partial \varOmega _{h_i} \in \varOmega$. A body force $\varvec{b}(\varvec{x},t)\subset {\mathbb {R}}^d$ that acts throughout the body $\varOmega$ and a traction $\varvec{f}(\varvec{x},t)$ on the boundary $\partial \varOmega _{h_i}$ are likewise considered in this paper.

Fig. 1

Phase field approximation of the crack surface

The classical Griffith’s theory [6] for brittle fracture states that the stored elastic energy can be transformed into dissipative forms of energy. The crack starts to propagate when the stored energy is sufficient to overcome the fracture resistance of the material. Thus, the crack propagation can be regarded as a process to minimize a free energy that composes the elastic energy, fracture energy, and other forms of energy. Based on this, a variational approach for fracture was proposed in Bourdin et al. [19]. In this approach, the required energy to create a fracture surface per unit area is equal to the critical fracture energy density $G_c$, which is also known as the critical energy release rate [18]. In this paper, we define the total potential energy $\varPsi _{{\mathrm{opt}}}(\varvec{u},\varGamma )$ as the sum of the elastic energy $\psi _{\varepsilon }(\varvec{\varepsilon })$, fracture energy, and energy due to external forces:

$$\begin{aligned} \varPsi _{{\mathrm{opt}}}(\varvec{u},\varGamma ) = \int _{\varOmega }\psi _{\varepsilon }(\varvec{\varepsilon }) {\mathrm{d}}{\varOmega }+\int _{\varGamma }G_c {\mathrm{d}}S-\int _{\varOmega } \varvec{b}\cdot {\varvec{u}}{\mathrm{d}}{\varOmega } - \int _{\partial \varOmega _{h_i}} \varvec{f}\cdot {\varvec{u}}{\mathrm{d}}S \end{aligned}$$

(1)

with the linear strain tensor $\varvec{\varepsilon } = \varvec{\varepsilon }(\varvec{u})$ given by

$$\begin{aligned} \varvec{\varepsilon }=\frac{1}{2} \left[ \nabla \varvec{u}+(\nabla \varvec{u})^{\mathrm { T} }\right] \end{aligned}$$

(2)

Based on the constitutive law for an isotropic linear elastic material, the elastic energy density $\psi _{\varepsilon }(\varvec{\varepsilon })$ is given by [44]

$$\begin{aligned} \psi _{\varepsilon }(\varvec{\varepsilon }) = \frac{1}{2}\lambda [{\mathrm {tr}}(\varvec{\varepsilon })]^2+\mu {\mathrm {tr}}(\varvec{\varepsilon }^2) \end{aligned}$$

(3)

where $\lambda >0$ and $\mu >0$ are Lamé constants.

2.2 Phase filed approximation for fracture energy

The first feature of a phase field method is the definition of a scalar field, the so called phase field [18, 44, 45]. The phase field indicates the phase state of point $\varvec{x}$ at time t. In this paper, we define a phase field $\phi (\varvec{x},t)\in [0,1]$ to approximate the fracture surface $\varGamma$ in Fig. 1. The phase field $\phi (\varvec{x},t)$ satisfies

$$\begin{aligned} \phi = {\left\{ \begin{array}{ll} 0,&{}\, \text {if\;material\;is\;intact}\\ 1,&{}\,\text {if\;material\;is\;cracked} \end{array}\right. } \end{aligned}$$

(4)

The second feature of the phase field method is a smooth representation of a crack. Therefore, $\phi (\varvec{x},t)\in [0,1]$ represents naturally a diffusive crack shape (the mushy-zone in Fig. 1). A typical one-dimensional phase field approximated by the exponential function is given by [44]

$$\begin{aligned} \phi (x)= e^{-|x|/l_0} \end{aligned}$$

(5)

with $l_0$ the length scale parameter. $l_0$ controls the transition region of the phase field from 0 to 1 and reflects the shape of a crack. The distribution of the one-dimensional phase field is shown in Fig. 2. The crack region will have a larger width with a larger $l_0$ and the phase field will represent a sharp crack again as $l_0$ approaches zero.

Fig. 2

Distribution of the one-dimensional phase field across a crack

Using the length scale parameter $l_0$, the crack surface density per unit volume of the solid is given by [44]

$$\begin{aligned} \gamma (\phi ,\bigtriangledown \phi )=\frac{\phi ^2}{2l_0}+\frac{l_0}{2}|\nabla \phi |^2 \end{aligned}$$

(6)

Applying Eq. (6), we have $\int _{\varGamma } {\mathrm {d}}S \approx \int _{\varOmega }\gamma {\mathrm {d}}{\varOmega }$. Thus, the fracture energy is approximated by

$$\begin{aligned} \int _{\varGamma }G_c {\mathrm {d}}S=\int _{\varOmega }G_c\left( \frac{\phi ^2}{2l_0}+\frac{l_0}{2}|\nabla \phi |^2 \right) {\mathrm {d}}{\varOmega } \end{aligned}$$

(7)

The variational approach [19] states that the crack surface energy is transformed from the elastic energy and thereby evolution of the phase field is driven by the elastic energy. To ensure cracking only under tension, it is essential to decompose the elastic energy into tensile and compressive parts [45]. In this paper, we follow the decomposition of Miehe et al. [45] and ensure that evolution of the phase field is only related to the positive elastic energy. Thus, crack propagation under compression is not allowed. Therefore, the strain tensor $\varvec{\varepsilon }$ is first decomposed as follows:

$$\begin{aligned} \varvec{\varepsilon }_{\pm }=\sum _{a=1}^d \langle \varepsilon _a\rangle _{\pm }\varvec{n}_a\otimes \varvec{n}_a \end{aligned}$$

(8)

where $\varvec{\varepsilon }_+$ and $\varvec{\varepsilon }_-$ are the tensile and compressive strain tensors, respectively. In addition, $\varepsilon _a$ is the principal strain and $\varvec{n}_a$ the principal strain direction. The operator $\langle \centerdot \rangle _{\pm }$ is defined as: $\langle \centerdot \rangle _{\pm }=(\centerdot \pm |\centerdot |)/ 2$.

Applying the decomposed strain tensor, the positive and negative elastic energy densities are represented as follows:

$$\begin{aligned} \psi _{\varepsilon }^{\pm }(\varvec{\varepsilon }) = \frac{\lambda }{2}\langle {\mathrm {tr}}(\varvec{\varepsilon })\rangle _{\pm }^2+\mu {\mathrm {tr}} \left( \varvec{\varepsilon }_{\pm }^2\right) \end{aligned}$$

(9)

It is assumed that the phase field affects only the positive elastic energy density and gives rise to a stiffness reduction as [18]

$$\begin{aligned} \psi _{\varepsilon }(\varvec{\varepsilon })=\left[ (1-k)(1-\phi )^2+k\right] \psi _{\varepsilon }^+(\varvec{\varepsilon })+\psi _{\varepsilon }^-(\varvec{\varepsilon }) \end{aligned}$$

(10)

where $0<k\ll 1$ is a model parameter that prevents the positive elastic energy density from disappearing and avoids numerical singularity when phase field $\phi$ approaches 1.

2.3 Governing equations

For quasi-static crack problems, the kinetic energy of body is neglected. Thus, we construct a Lagrange energy functional composing the phase field approximation for the fracture energy (7), the elastic energy (10), and the external potential energy by the external loads:

$$\begin{aligned} L= & {} \varPsi _{{\mathrm{opt}}}(\varvec{u},\varGamma )=\int _{\varOmega }\left\{ \left[ (1-k)(1-\phi )^2+k\right] \psi _{\varepsilon }^+(\varvec{\varepsilon })+\psi _{\varepsilon }^-(\varvec{\varepsilon })\right\} {\mathrm {d}}{\varOmega }\nonumber \\&+\int _{\varOmega }G_c\left( \frac{\phi ^2}{2l_0}+\frac{l_0}{2}|\nabla \phi |^2 \right) {\mathrm {d}}{\varOmega }-\int _{\varOmega } \varvec{b} \cdot \varvec{u} {\mathrm {d}}{\varOmega }- \int _{\partial \varOmega _{h_i}} \varvec{f} \cdot \varvec{u} {\mathrm {d}}S \end{aligned}$$

(11)

As mentioned previously, the variational approach emphasizes that crack propagation is a process to minimize the energy functional. Here, we calculate the variation of the functional L and set the first variation of the functional as zero, giving rise to the governing equations given by

$$\left\{ \begin{array}{l} \text {Div}(\varvec{\sigma })+\varvec{b}=0 \\ \left[ \frac{2l_0(1-k)\psi _{\varepsilon }^+}{G_c}+1\right] \phi -l_0^2\nabla ^2\phi =\frac{2l_0(1-k)\psi _{\varepsilon }^+}{G_c} \end{array}\right.$$

(12)

where $\varvec{\sigma }$ is Cauchy stress tensor given by

$$\begin{aligned} \varvec{\sigma }=\partial _{\varvec{\varepsilon }} \psi _{\varepsilon }=\lambda \langle tr(\varvec{\varepsilon })\rangle _- \varvec{I}+ 2\mu \varvec{\varepsilon }_-+\left[ (1-k)(1-\phi )^2+k \right] \left[ \lambda \langle tr(\varvec{\varepsilon })\rangle _+ \varvec{I}+ 2\mu \varvec{\varepsilon }_+ \right] \end{aligned}$$

(13)

with $\varvec{I}$ a unit tensor $\in {\mathbb {R}}^{d\times d}$.

In addition, the irreversibility condition $\varGamma (\varvec{x},s)$$\in$$\varGamma (\varvec{x},t)$ ($s<t$) must be satisfied during compression or unloading. That is, a crack cannot be recovered to the uncracked state once the crack initiates. To ensure a monotonically increasing phase field, we introduce a strain-history field $H(\varvec{x},t)$ [44, 45] defined by

$$\begin{aligned} H(\varvec{x},t) = \max \limits _{x\in [0,t]}\psi _\varepsilon ^+\left( \varvec{\varepsilon }(\varvec{x},s)\right) \end{aligned}$$

(14)

Replacing $\psi _\varepsilon ^+$ by $H(\varvec{x},t)$ in Eq. (12), the strong form is rewritten as

$$\left\{ \begin{array}{l} \text {Div}(\varvec{\sigma })+\varvec{b}=0\\ \left[ \frac{2l_0(1-k)H}{G_c}+1\right] \phi -l_0^2\nabla ^2\phi =\frac{2l_0(1-k)H}{G_c} \end{array}\right.$$

(15)

The necessary boundary conditions of the phase field modeling are given by

$$\begin{aligned} \left\{ \begin{array}{ll}\varvec{u} = \varvec{g} \,\, & {\mathrm{on}} \quad \partial \varOmega _{g_i}\\ \varvec{\sigma } \cdot \varvec{n} = \varvec{f} & {\mathrm{on}} \quad \partial \varOmega _{h_i} \\ \nabla \phi \cdot \varvec{n} = 0 & {\mathrm{on}} \quad \partial \varOmega \end{array}\right. \end{aligned}$$

(16)

with $\varvec{n}$ the outward-pointing normal vector of the boundary.

Finally, initial conditions for the crack propagation problems are also needed:

$$\begin{aligned} \left\{ \begin{array}{ll}\varvec{u}(\varvec{x},0)=\varvec{u}_0(\varvec{x})\,\,&\quad \varvec{x}\in \varOmega \\ \phi (\varvec{x},0)=\phi _0(\varvec{x})\,\,&\quad \varvec{x}\in \varOmega \end{array}\right. \end{aligned}$$

(17)

3 Implementation details

3.1 Finite element method

We use the finite element method to solve the governing Eq. (15), and the weak forms of the phase field modeling are given by

$$\begin{aligned} \int _{\varOmega }\left( -\varvec{\sigma }:\delta \varvec{\varepsilon }\right) {\mathrm {d}}\varOmega +\int _{\varOmega }\varvec{b} \cdot \delta \varvec{u} {\mathrm {d}}\varOmega +\int _{\varOmega _{h_i}}\varvec{f} \cdot \delta \varvec{u} {\mathrm {d}}S=0 \end{aligned}$$

(18)

and

$$\begin{aligned} \int _{\varOmega }-2(1-k)H(1-\phi )\delta \phi {\mathrm {d}}\varOmega +\int _{\varOmega }G_c\left( l_0\nabla \phi \cdot \nabla \delta \phi +\frac{1}{l_0}\phi \delta \phi \right) {\mathrm {d}}\varOmega =0 \end{aligned}$$

(19)

We denote the nodal values as $\varvec{u}_i$ and $\phi _i$. Applying the standard notation in a 2D setting, the nodal variables are discretized as

$$\begin{aligned} \varvec{u} = \sum _i^{n}N_i \varvec{u}_i,\qquad \phi = \sum _i^{n}N_i \phi _i \end{aligned}$$

(20)

where n is the total number of nodes in one element and $N_i$ is the shape function of node i. Thus, the gradients are calculated by

$$\begin{aligned} \varvec{\varepsilon } = \sum _i^{n}\varvec{B}_i^u \varvec{u}_i,\qquad \nabla \phi = \sum _i^{n}\varvec{B}_i^{\phi } \phi _i \end{aligned}$$

(21)

where $\varvec{B}_i^u$ and $\varvec{B}_i^\phi$ are the derivatives of the shape functions defined by

$$\begin{aligned} \varvec{B}_i^u=\left[ \begin{array}{cc} N_{i,x}&{}0\\ 0&{}N_{i,y}\\ N_{i,y}&{}N_{i,x} \end{array}\right] , \qquad \varvec{B}_i^u=\left[ \begin{array}{cc} N_{i,x}\\ N_{i,y} \end{array}\right] \end{aligned}$$

(22)

Because of arbitrariness of the test functions, the external force $\varvec{F}_i^{u,ext}$ and inner force $\varvec{F}_i^{u,int}$ are described by

$$\left\{ \begin{array}{l} \varvec{F}_i^{u,ext}= \int _{\varOmega }N_i\varvec{b} {\mathrm {d}}\varOmega + \int _{\varOmega _{h_i}}N_i\varvec{f} {\mathrm {d}}S\\ \varvec{F}_i^{u,int}= \int _{\varOmega }[\varvec{B}_i^u]^{{\mathrm {T}}}\varvec{\sigma } {\mathrm {d}}\varOmega \end{array} \right. $$

(23)

The inner force term of the phase field is also obtained by

$$\begin{aligned} F_i^{\phi ,{\mathrm{int}}} = \int _{\varOmega } -2(1-k)(1-\phi )H N_i+G_c\left( l_0{[\varvec{B}_i^{\phi }]^{{\mathrm T}}}\nabla \phi +\frac{1}{l_0}\phi N_i \right) {\mathrm {d}}\varOmega \end{aligned}$$

(24)

Thus, according to Eqs. (18) and (19), contribution of node i to the residual of the discrete equations of stress equilibrium and evolution of phase field is given as

$$\begin{aligned} \varvec{R}_i^{u}=\varvec{F}_i^{u,{\mathrm{ext}}}-\varvec{F}_i^{u,{\mathrm{int}}},\qquad R_i^{\phi }=- F_i^{\phi ,{\mathrm{int}}} \end{aligned}$$

(25)

We use the segregated scheme to solve the displacement and phase field. Thus, the Newton–Raphson approach is adopted to obtain $\varvec{R}_i^{u}=0$ and $R_i^{\phi }=0$, respectively. The tangents on the element level are thereby calculated by

$$\left\{ \begin{array}{l} {\varvec{K}}_{ij}^{uu}=\frac{\partial {\varvec{F}}_i^{u,{\mathrm{int}}}}{\partial {\varvec{u}}_j}=\int _{\varOmega }[{\varvec{B}}_i^u]^{{\mathrm{T}}}{\varvec{D}} [{\varvec{B}}_j^u] {\mathrm {d}} \varOmega \\ {\varvec{K}}_{ij}^{\phi \phi }=\frac{\partial F_i^{\phi ,{\mathrm{int}}}}{\partial \phi _j}=\int _{\varOmega }\left\{ [{\varvec{B}}_i^\phi ]^{{\mathrm{T}}} G_cl_0 [{\varvec{B}}_j^\phi ]+N_i\left( 2(1-k)H+\frac{G_c}{l_0}\right) N_j\right\} {\mathrm {d}} \varOmega \end{array}\right.$$

(26)

and D is the elasticity tensor of fourth order given by

$$\begin{aligned}\varvec{D}&= \frac{\partial \varvec{\sigma }}{\partial \varvec{\varepsilon }}\\&=\lambda \left\{ \left[ (1-k)(1-\phi )^2+k \right] H_\varepsilon (tr(\varvec{\varepsilon }))+H_\varepsilon (-tr(\varvec{\varepsilon }))\right\} \varvec{J}\\&\quad+ 2\mu \left\{ \left[ (1-k)(1-\phi )^2+k \right] \varvec{P}^++\varvec{P}^- \right\} \end{aligned}$$

(27)

where $H_\varepsilon \langle x \rangle$ is a Heaviside function with $H_\varepsilon \langle x \rangle$ = 1 for $x>0$ and $H_\varepsilon \langle x \rangle =0$ for $x\le 0$ and $J_{ijkl}=\delta _{ij}\delta _{kl}$ with $\delta _{ij}$ and $\delta _{kl}$ the Kronecker symbols. In addition, $\varvec{P}^\pm ={\partial \varvec{\varepsilon }_\pm }/{\partial \varvec{\varepsilon }}$. According to the algorithm for fourth-order isotropic tensor [43], the component $P_{ijkl}^{\pm }$ is calculated based on the following equation:

$$\begin{aligned} P_{ijkl}^\pm= & {} \sum _{a=1}^3\sum _{b=1}^3 H_\varepsilon (\varepsilon _a)\delta _{ab}n_{ai}n_{aj}n_{bk}n_{bl}\nonumber \\&+\sum _{a=1}^3\sum _{b\ne a}^3 \frac{1}{2} \frac{\langle \varepsilon _a\rangle _\pm - \langle \varepsilon _b\rangle _\pm }{\varepsilon _a-\varepsilon _b}n_{ai}n_{bj}(n_{ak}n_{bl}+n_{bk}n_{al}) \end{aligned}$$

(28)

where $n_{ai}$ denotes the ith component of vector $\varvec{n}_a$.

Note that Eq. (28) cannot be evaluated if $\varepsilon _a=\varepsilon _b$ and thereby a “perturbation” technology for the principal strains [33] is adopted with an unchanged $\varepsilon _2$:

$$\begin{aligned} \left\{ \begin{array}{ll}\varepsilon _1 = \varepsilon _1(1+\delta )&\qquad if\,\varepsilon _1 = \varepsilon _2 \\ \varepsilon _3 = \varepsilon _3(1-\delta ) &\qquad if\,\varepsilon _2 = \varepsilon _3 \end{array}\right. \end{aligned}$$

(29)

with the perturbation $\delta =1\times 10^{-9}$ for this paper.

3.2 Comsol implementation

The above procedures for phase field modeling are implemented in Comsol Multiphysics, a commercial FEM software for multi-field modeling. By adding application-specific modules, Comsol can handle mathematical or physical modeling easily. Therefore, three main modules are established first including the Solid Mechanics Module, History-strain Module and Phase Field Module. These modules are utilized to solve the three fields: $\varvec{u}$, H and $\phi$, respectively. These modules are solved based on the standard finite element discretization in space domain as described in Sect. 3.1. In addition, we establish a pre-set Storage Module to evaluate and store the intermediate field variables in a time step such as the positive elastic energy and principal strains.

Specifically, the Solid Mechanics Module is set up based on a linear elastic material library. The boundary and initial conditions shown in Sect. 2 are added in the Solid Mechanics Module. However, the nonlinear stress–strain relationship is considered. That is, the elasticity matrix in a time step is modified automatically. Thus, the stiffness matrix in Comsol is rewritten as

$$\begin{aligned} \varvec{D}_e= \left[ \begin{array}{cccccc} D_{1111} &{} D_{1122} &{} D_{1133} &{} D_{1112} &{} D_{1123} &{} D_{1113}\\ D_{2211} &{} D_{2222} &{} D_{2233} &{} D_{2212} &{} D_{2223} &{} D_{2213}\\ D_{3311} &{} D_{3322} &{} D_{3333} &{} D_{3312} &{} D_{3323} &{} D_{3313}\\ D_{1211} &{} D_{1222} &{} D_{1233} &{} D_{1212} &{} D_{1223} &{} D_{1213}\\ D_{2311} &{} D_{2322} &{} D_{2333} &{} D_{2312} &{} D_{2323} &{} D_{2313}\\ D_{1311} &{} D_{1322} &{} D_{1333} &{} D_{1312} &{} D_{1323} &{} D_{1313} \end{array} \right] \end{aligned}$$

(30)

A pre-defined module governed by the Helmholtz equation is utilized to construct the Phase Field Module by revising some corresponding coefficients to match the governing Eq. (15). Moreover, the boundary condition Eq. (16) and initial condition (17) are implemented in this module. The distributed ODEs and DAEs interface is used to construct the History-strain Module in Comsol. However, the history-strain field is not solved directly. We use a “previous solution” solver to record the results in the previous time step and obtain the field H by the following format in Comsol:

$$\begin{aligned} \left\{ \begin{array}{ll}H-\psi _\varepsilon ^+=0,\,&\quad \text {if}\,\, \psi _\varepsilon ^+>H\\H-H=0,\,&\quad \text {if} \,\,\psi _\varepsilon ^+\le H \end{array}\right.\end{aligned}$$

(31)

Initial conditions are also needed for the History-strain Module. We commonly set $H_0(\varvec{x})$ = 0 unless pre-existing cracks are modeled under the initial history-strain field by Borden et al. [18]. Figure 3 shows the relationship between all the established modules. The mechanical responses such as the principal strains, directions of principal strain, and the elastic energy are naturally exported from the Solid Mechanics Module and stored in the Storage Module. The positive elastic energy is then adopted in the History-strain Module to update the local history-strain field H. The Phase Field Module uses the updated H to solve the phase field. In a time step, the updated phase field and the stored principal strains as well as the directions are used to modify the stiffness matrix of the Solid Mechanics Module. The mechanical responses are subsequently obtained.

As discussed in Sect. 3.1, a segregated scheme is used to solve the coupled system. The segregated scheme will be helpful to obtain converged solution. The procedure of the segregated scheme is depicted in Fig. 4. The equations of displacement, history strain and phase field are solved independently. To ensure unconditional stability, an implicit Generalized-$\alpha$ method for time integration [25] is used. For a new time step, linear extrapolation of the previous solution is used to construct the initial guess for the present time step. Then, the Newton–Raphson approach is used to solve each module sequentially. Finally, the total relative error between the previous and present iteration steps is evaluated. If the error is less than the tolerance $\varepsilon _t$, the calculation is finished for current time step and then a new time step starts. Otherwise, another iteration step is required until the tolerance requirement is met. In addition, the iteration is different to converge for phase field modeling and requires more iteration steps when cracks initiate. Therefore, Anderson acceleration is adopted to accelerate convergence [25]. The dimension of iteration space field is chosen as more than 50. To end this section, a flowchart of our implementation of phase field modeling in Comsol is shown in Fig. 5.

Fig. 3

Relationship between all the modules established

Fig. 4

Segregated scheme for the coupled calculation in phase field modeling

Fig. 5

Comsol implementation of the phase field modeling

4 Verification of the phase field simulation

We simulate the three-point bending test to verify the phase field modeling. This test was also simulated by Miehe et al. [44, 45]. The geometry and boundary conditions are shown in Fig. 6. A simply supported beam with a vertical notch is used. The elastic parameters are chosen as $\lambda = 12\hbox { kN/mm}^2$ and $\mu = 8\hbox { kN/mm}^2$. The critical energy release rate $G_c = 0.5\hbox { N/mm}$. Most of the beam is discretized into elements with size of $h= 0.015$ mm, whereas the discretization is refined in the expected crack propagation region. The element size in the refined region is $1.9\times 10^{-3}$ mm. The calculation is conducted in a displacement-driven context. We choose constant displacement increment $\varDelta u = 1\times 10^{-4}$ mm in the first 360 time steps, afterward, $\varDelta u = 1\times 10^{-5}$ mm in the remaining time steps.

Figure 7 shows the crack patterns of the simply supported notched beam under loading for a length scale $l_0 = 0.06$ and 0.03 mm. Red and blue regions represent the fully cracked and undamaged material, respectively. As expected, the crack has a larger width for the length scale of $l_0 = 0.06$ mm. Figure 8 gives the resulting reaction force on the top of the beam with the increase in the displacement. Results in Fig. 8a for a length scale $l_0 = 0.06$ mm and in Fig. 8b for $l_0 = 0.03$ mm are compared with the results of Miehe et al. [44]. As observed, the results by the present work are in good agreement with those by Miehe et al. [44]. Only a little difference exists because different algorithm and implementation methods are used. The consistency of the crack pattern and load–displacement curve indicates the feasibility and practicability of the presented phase field modeling approach. Therefore, the phase field modeling in Comsol can be used subsequently in Brazil splitting tests.

Fig. 6

Geometry and boundary conditions of the three-point bending test

Fig. 7

Three-point bending test. Crack pattern at a displacement of a$u = 4.15\times 10^{-2}$ mm, b$u = 4.35\times 10^{-2}$ mm, c$u = 9.4\times 10^{-2}$ mm for a length scale $l_0$ of $6\times 10^{-2}$ mm and d$u = 4.25\times 10^{-2}$ mm, e$u = 4.4\times 10^{-2}$ mm and f$u = 7.1\times 10^{-2}$ mm for a length scale $l_0$ of $3.5\times 10^{-2}$ mm

Fig. 8

Load–displacement curves of the three-point bending test for a length scale a$l_0 = 6\times 10^{-2}$ mm and b$l_0 = 3\times 10^{-2}$ mm

5 Crack propagation and coalescence in Brazilian disks

5.1 Brazilian disk with no initial crack

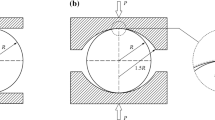
The Brazil splitting tests are often used to obtain the tensile strength of rock and many researchers simulated crack propagation in a Brazilian disk under compression [20, 63, 65]. Crack propagation in a disk with no initial crack is simulated first. The diameter of the disk is 100 mm, and we apply displacement on the upper and lower ends of the disk. Because in laboratory tests steel bars are set on the ends of the Brazilian disk, we set flat end boundaries for the disk to match the size of steel bars. The elastic parameters are $\rho = 2630\hbox { kg/m}^3$, $E = 120\hbox { GPa}$, and $\nu = 0.3$. A total of 24696 6-node quadratic triangular elements are used to discretize the disk. We set the maximum element size $h=1$ mm. To avoid numerical singularity, $k = 1 \times 10^{-9}$ is chosen. In each time step, we chose the displacement increment $\varDelta u=1\times 10^{-5}$ mm. Thus, we simulate the crack propagation in the Brazilian disk under different $G_c$: 10, 20, 30, 40, and $50\hbox { J/m}^2$ and under different length scale parameter $l_0$: 1, 2, 3, and 4 mm.

Our simulation shows that $G_c$ has no influence on the crack propagation pattern. Figure 9 shows the crack initiation and propagation in the Brazil splitting tests with no initial crack for $G_c = 30\hbox { J/m}^2$ and $l_0=2\hbox { mm}$. When the displacement u reaches to $2.2\times 10^{-2}$ mm, the crack occurs in the center of the disk. This is in good agreement with some previous work [14, 29]. The experimental tests and analytical solution indicate that the maximum tensile stress occurs in the disk center. The crack continues to propagate and becomes wider when u reaches to $2.202\times 10^{-2}$ mm. Then, when u reaches to $2.208\times 10^{-2}$ mm, the crack tips move quite close to the upper and bottom ends of disk and crack branching is observed. There is no penetration of the crack deep into the ends of the disk because the two ends are locally compressed. We compare the final crack patterns obtained by the phase field model and the experimental tests in Fig. 10. The crack pattern by the phase field model is well consistent with the experimental test, also indicating the correctness of the phase field modeling.

Fig. 9

Crack propagation in the Brazilian disk with no initial crack at a displacement of a$u = 2.2\times 10^{-2}$ mm, b$u = 2.202\times 10^{-2}$ mm, c$u = 2.208\times 10^{-2}$ mm for $G_c=30\hbox { J/m}^2$ and $l_0=2$ mm

Fig. 10

Comparison of the final crack patterns by the experimental test and phase field method. a Experimental test. b Phase field model

Figure 11 gives the curves of the reaction force on the upper end of the Brazilian disk versus the displacement u for different $G_c$ and $l_0=2$ mm. The simulated load–displacement curves, which reflect the brittle failure in a Brazilian test, are often observed in experimental tests [30, 65]. We show a sudden drop of the load after the load peak when the phase field approaches 1. Furthermore, the peak load increases with the increase in $G_c$. In the Brazil splitting test, the tensile strength $\sigma _t$ of rock is obtained by

$$\begin{aligned} \sigma _t=\frac{2P_{{\mathrm{peak}}}}{\pi D L} \end{aligned}$$

(32)

where $P_{{\mathrm{peak}}}$ is the peak load, and D and L are the diameter and length of the Brazilian disk. Figure 12 compares the tensile strength by our simulation and the 1D critical stress by Borden et al. [18]. The simulated strength increases with the increase in $G_c$ and the rate decreases. The 1D critical stress has the same trend, but the critical stress is far larger than the simulated one. Therefore, there is a limit in extending the critical stress in 1D to 2D or 3D. But the critical stress can be still regarded as a initial reference of the tensile strength.

Fig. 11

Load–displacement curves of the Brazil disk with no crack for different $G_c$ and $l_0 = 2\hbox { mm}$

Fig. 12

Comparison of simulated tensile strength and critical stress for 1D under different $G_c$

When the scale parameter $l_0$ varies from 1 mm to 4 mm, the final crack patterns keep unchanged and only a little difference in the crack width. An obvious example is the crack distribution at crack initiation for $l_0 = 1$ mm and $l_0=2$ mm with $G_c=30$ J/m$^2$ (Fig. 13). Figure 14 gives the load–displacement curves of the disk for different $l_0$ and $G_c=30$ J/m$^2$. At a fixed $G_c$, the curves move toward left and the peak load decreases with the increase in $l_0$. In addition, Fig. 15 shows both the simulated tensile strength and the 1D critical stress for different $l_0$. The simulated tensile strength decreases with the increase in $l_0$. The 1D critical stress has the same trend but is far larger than the tensile strength.

Fig. 13

Crack pattern at crack initiation for a$l_0=1$ mm and b$l_0=2$ mm

Fig. 14

Load–displacement curves of the Brazil disk with no crack for different $l_0$ and $G_c = 30\hbox { J/m}^2$

Fig. 15

Comparison of simulated tensile strength and critical stress for 1D under different $l_0$

5.2 Brazilian disk with a vertical crack

We now consider a Brazilian disk with a vertical pre-existing crack. The diameter of the rock specimen is $D=100$ mm, and the crack length is $2a=30$ mm. a is half length of the crack. The elastic parameters are $E=120$ GPa and $\nu =0.3$. The width of the pre-existing crack is set as $l_0$. 6-node quadratic triangular elements are also used to discretize the disk, and the maximum element size is fixed as $h=1$ mm. Vertical displacements are then applied on the top and bottom boundaries to promote the crack propagation. In each time step, we chose the displacement increment $\varDelta u=1\times 10^{-5}$ mm.

Figure 16 shows the progressive propagation of the pre-existing crack for $G_c=30$ J/m$^2$ and $l_0=2$ mm. As shown in Fig. 16a, the crack initiates from the two ends of the pre-existing crack under the loading. Then, the crack propagates along the direction of loading in Fig. 16b. Finally, the crack propagates to the top and bottom ends of the disk and the specimen fails, as shown in Fig. 16c. The final crack pattern is in good agreement with the results of peridynamics simulation [63] and experimental tests [26]. Comparison of the final crack patterns by the experimental tests and the phase field modeling is shown in Fig. 17.

To test the influence of critical energy release rate $G_c$ on the crack propagation in the Brazilian disk specimen, we conduct the simulation again at a fixed $l_0= 2$ mm and under different $G_c$: 10, 20, 30, 40, and 50 J/m$^2$. As expected, $G_c$ has no effect on the final crack pattern, which is the same as that in Fig. 16. In addition, Fig. 18 gives the load–displacement curves for the specimens with a vertical pre-existing crack under different $G_c$. As observed, the peak load and corresponding displacement increase with the increase in $G_c$. Furthermore, the peak load and displacement of the specimens with a vertical pre-existing crack are smaller than those of the specimens with no initial crack in Fig. 14 due to damage effect of the pre-existing crack.

Fig. 16

Crack propagation in the Brazilian disk with a vertical pre-existing crack for $G_c=30\hbox { J/m}^2$ and $l_0=2$ mm

Fig. 17

Comparison of the final crack patterns of the Brazilian disk with a vertical pre-existing crack. a Experimental test. b Phase field model

Fig. 18

Load–displacement curves of the specimens with a vertical pre-existing crack under different $G_c$

Another four numerical Brazilian specimens with the diameter $D=100$ mm containing a vertical pre-existing crack are simulated to test the influence of length scale parameter. The maximum element size is also 1 mm, and $G_c$ is fixed as $30\hbox { J/m}^2$ while the length scale $l_0$ is chosen as 1, 2, 3, and 4 mm, respectively. Fig. 19 illustrates the final crack patterns of the Brazilian disk specimens with a vertical pre-existing crack under different length scale parameter $l_0$. The crack patterns are similar only with difference in crack width. A larger $l_0$ causes a wider crack band in the specimen. This indicates the length scale parameter must be small enough to achieve a suitable crack width. Additionally, Fig. 20 shows the load–displacement curves of the numerical specimens with a vertical pre-existing crack under different $l_0$. The obtained load–displacement curves are similar, while the peak load and corresponding strain decrease as the length scale parameter $l_0$ increases. Furthermore, Fig. 20 also reflects the influence of the pre-existing crack and the peak load at a fixed $l_0$ is smaller than that of an intact specimen.

Fig. 19

Final crack patterns in the Brazilian disk with a vertical pre-existing crack under different $l_0$. a$l_0=0.001$ m. b$l_0=0.002$ m. c$l_0=0.003$ m. d$l_0=0.004$ m

Fig. 20

Load–displacement curves of the specimens with a vertical pre-existing crack under different $l_0$

5.3 Brazilian disk with an inclined pre-existing crack

Now, we test a Brazilian disk specimen with an inclined pre-existing crack. The similar experimental test was conducted by Ghazvinian et al [33], and numerical tests were conducted by Haeri et al. [34] and Zhou and Wang [63]. The pre-cracked Brazilian disk specimen is 100 mm in diameter, and the pre-existing crack intersects the vertical direction at an angle $\alpha$. Meanwhile, the center of the crack coincides with the center of the disk specimen. Seven groups of tests are conducted for different inclination angles of the pre-existing crack. The angles are set as $\alpha =0$, $\alpha =15^\circ$, $\alpha =30^\circ$, $\alpha =45^\circ$, $\alpha =60^\circ$, $\alpha =75^\circ$, and $\alpha =90^\circ$. The pre-existing crack has a length of 30 mm and a width of $l_0$ in the simulation. The elastic parameters are $E=120$ GPa and $\nu = 0.3$. $G_c = 30$ J/m$^2$ and $l_0$ are fixed as 2 mm. In each time step, we chose the displacement increment $\varDelta u=1\times 10^{-5}$ mm.

The final crack patterns of the pre-cracked Brazilian disk specimens with different inclination angles are depicted in Fig. 21. The crack patterns obtained by the phase field model are in good agreement with the experimental tests [63], the peridynamics simulation [63], the PFC simulation [33], and the BEM simulation [34]. Comparison of the final crack patterns by the experimental tests [63], the PFC simulation [33], the BEM simulation [34], and the phase field simulation for the inclination angle of $\alpha = 45^\circ$ and $\alpha =90^\circ$ is shown in Figs. 22 and 23, respectively. The consistency of the phase field model with the experimental tests and other numerical methods also shows the applicability of the phase field modeling in the Brazilian disk tests.

Fig. 21

Final crack patterns in the pre-cracked Brazilian disk with different inclination angles of crack. a$\alpha =0$. b$\alpha =15^\circ$. c$\alpha =30^\circ$. d$\alpha =45^\circ$. e$\alpha =60^\circ$. f$\alpha =75^\circ$. g$\alpha =90^\circ$

Fig. 22

Comparison of the final crack patterns in the pre-cracked Brazilian disk with inclination angle of $\alpha =45^\circ$. a Experimental test. b PFC. c BEM. d PFM

Fig. 23

Comparison of the final crack patterns in the pre-cracked Brazilian disk with inclination angle of $\alpha =90^\circ$. a Experimental test. b BEM. c PFM

Figure 21 shows that wing cracks initiate from the tips of the pre-existing crack when $\alpha \le 60 ^\circ$. The cracks propagate at a small angle with the direction of the applied load, and the propagation path is related to the inclination angle $\alpha$. Therefore, failure of the Brazilian disk specimens with $\alpha \le 60^\circ$ results from propagation of the pre-existing crack. However, for the specimens containing a pre-existing crack with $\alpha \ge 75^\circ$, cracks initiate at the position close to the tips of the pre-existing crack or even at the center of the pre-existing crack ($\alpha = 90 ^\circ$). The failure of the Brazilian disk specimens with $\alpha \ge 75^\circ$ is driven in a tensile splitting mode, which is in good agreement with the numerical and experimental results by Zhou and Wang [63]. In addition, for $\alpha = 90 ^\circ$, the BEM simulation [34] obtained a different crack pattern from the phase field simulation and cracks initiated from the tips of the pre-existing crack. The tensile splitting mode thereby cannot be simulated by BEM.

Figure 24 shows the load–displacement curves of the Brazilian disk specimen containing a pre-existing crack under different crack inclination angles. The load–displacement curves are similar with those in the previous examples. The simulated curves have three obvious crack propagation stages: (i) elastic stage, (ii) crack initiation and stable crack propagation, and (iii) unstable crack propagation and failure. In addition, the peak loads of the specimens are highly related to the crack inclination angle because the inclined pre-existing crack changes the stress distribution in the Brazilian disks. Therefore, Fig. 25 depicts the relationship between the normalized peak load and the crack inclination angle. The normalized peak load is obtained by the peak load divided by that of the specimen with no initial crack. Additionally, the normalized peak loads obtained from the peridynamics simulation [63] are also added to Fig. 25. Figure 25 shows a groove-shaped curve, and the normalized peak load decreases with the increase in the crack inclination angle for $\alpha \le 45^\circ$. While $\alpha \ge 45^\circ$, the normalized peak load increases with the increase in $\alpha$. The maximum peak load occurs when $\alpha =45^\circ$. The peridynamics simulation has the similar trend with the phase field simulation and only a little difference exists for $\alpha =30^\circ$. In addition, all the normalized peak loads are less than 1 because presence of a pre-existing crack reduces the strength of the specimen. The quite far gap occurs between the results of the PFM and peridynamics because they are two different fracture modeling methods that use different inner model parameters. For example, the particle spacing and horizon size are used in peridynamics [54,55,56] and have a great effect on the failure of a specimen. No relationship was also found between the parameters used by PFM and peridynamics. In addition, the peridynamics simulation of Brazilian disk tests [63] used a shear failure evolution, which is not included in the PFM used in this paper.

Fig. 24

Load–displacement curves of the Brazilian disk specimen containing a pre-existing crack under different inclination angles

Fig. 25

Normalized peak load versus the crack inclination angle

The Brazilian disk specimen containing a pre-existing crack can also be used to evaluate the mixed Mode I/II fracture toughness. The Mode I/II fracture toughness is related to length and inclination of the crack and is calculated by [14]

$$\begin{aligned} K_I = \frac{P\sqrt{a}}{\sqrt{\pi }RL}N_I \end{aligned}$$

(33)

and

$$\begin{aligned} K_{{\text{II}}} = \frac{P\sqrt{a}}{\sqrt{\pi }RL}N_{{\text{II}}} \end{aligned}$$

(34)

$K_{\text{I}}$ and $K_{II}$ are the Mode I and Mode II stress intensity factors, respectively; R is the radius of the specimen; P is the peak load; $N_{\text{I}}$ and $N_{{\text{II}}}$ are two non-dimensional coefficients. $N_{\text{I}}$ and $N_{{\text{II}}}$ are functions of ratio of the half length to radius (a / R) and the inclination angle $\alpha$ [14]:

$$\begin{aligned} N_{\text{I}} = 1-4\sin ^2\alpha +4\sin ^2\alpha (1-4\cos ^2\alpha )\left( \frac{a}{R}\right) ^2 \end{aligned}$$

(35)

and

$$\begin{aligned} N_{{\text{II}}} = \left[ 2+(8\cos ^2\alpha -5)\left( \frac{a}{R}\right) ^2\right] \sin 2\alpha \end{aligned}$$

(36)

Figure 26 shows the mixed Mode I/II fracture toughness estimated by the phase field simulation. The Mode I fracture toughness decreases with the increase in the crack angle. The Mode II fracture toughness increases as the inclination angle increases for $\alpha \le 30^\circ$ while the Mode II fracture toughness decreases with the increase in $\alpha$ for $\alpha \ge 30^\circ$. As a reference, the fracture toughness calculated from the peridynamics simulation [63] is also added to Fig. 26. As observed, the trend of the mixed Mode I/II fracture toughness from the PFM is the same as that estimated by the peridynamics simulation [63]. The values of the fracture toughness from the phase field and peridynamics simulations are different because the peridynamics simulation [63] used different model parameters and its fracture parameters cannot be directly transformed into those in the PFM.

Fig. 26

Mixed Mode I/II fracture toughness estimated by the phase field modeling

5.4 Brazilian disk with two pre-existing cracks

In this example, a Brazilian disk with two pre-existing cracks is tested. Crack propagation and coalescence are simulated by the phase field model. The geometry and boundary conditions of the specimen are shown in Fig. 27. The crack propagation in a Brazilian disk with two cracks was simulated by the BEM [34] and peridynamics[63]. To compare their work better, we also simulate a Brazilian disk with a diameter D of 100 mm. The elastic parameters are $E=15$ GPa and $\nu =0.21$. The critical energy release rate $G_c = 30\hbox { J/m}^2$. As shown in Fig. 27, the two pre-existing cracks in the specimen are labeled as ➀ and ➁, respectively. The crack ➀ is placed along the horizontal direction, while the crack ➁ intersects the horizontal direction at an inclination angle $\alpha$. The two cracks have a length of $2a=30$ mm, while the centers of the cracks are placed in the centerline of the specimen and also have a spacing of 30 mm. In this simulation, we only test four groups of inclination angle $\alpha$: $\alpha =0$, $\alpha =30^\circ$, $\alpha =60^\circ$, and $\alpha =90^\circ$.

Fig. 27

Geometry and boundary conditions of the Brazilian disk containing two pre-existing cracks

In the phase field simulation, the specimen is discretized into elements with maximum size h of 1 mm and the length scale parameter is chosen as $l_0=2$ mm. We set the displacement increment $\varDelta u = 2\times 10^{-4}$ mm in each time step and the progressive crack propagation and coalescence in the Brazilian disk specimen containing two pre-existing cracks are shown in Fig. 28 for different inclination angles. Comparison of the final crack patterns obtained by the experimental test [34], the BEM simulation [34], and the phase field simulation for $\alpha =60^\circ$ and $\alpha =90^\circ$ is shown in Figs. 29 and 30. Compared with the previous experimental results [34] and numerical simulations [34, 63], the present phase field simulation is in good agreement with the experimental observations , especially for $\alpha =90^\circ$. With an angle of $60^\circ$ between the two pre-existing cracks, the same crack patterns are observed from the two tips of the crack ➁ for the experimental results and phase field simulation, respectively, although the experimental results show that a crack initiates to propagate at the right end of the upper horizontal notch, while presented phase field results show that the upper crack starts at the middle location. Furthermore, for $\alpha =90^\circ$, the phase field simulation obtains more accurate results than the simulated results by BEM [34] and peridynamics [63]. The wing crack initiates from the center of crack ➀ and propagates along the direction of applied load in the phase field simulation. However, a crack initiates from the tip of crack ➀ when BEM is used, which is not in agreement with the experimental observations [63]. In addition, the peridynamics obtains several secondary cracks around the top and bottom ends of the specimen, which are not observed in the experimental tests [63] and the present phase field simulation.

Fig. 28

Progressive crack propagation and coalescence in the Brazilian disk specimen containing two pre-existing cracks for different inclination angle. a$\alpha =0$. b$\alpha =30^\circ$. c$\alpha =60^\circ$. d$\alpha =90^\circ$

Fig. 29

Comparison of the final crack patterns in the pre-cracked Brazilian disk containing two pre-existing cracks for $\alpha =60^\circ$. a Experimental test. b BEM. c PFM

Fig. 30

Comparison of the final crack patterns in the pre-cracked Brazilian disk containing two pre-existing cracks for $\alpha =90^\circ$. a Experimental test. b BEM. c PFM

Figure 31 shows the load–displacement curves of the Brazilian disk containing two pre-existing cracks. The load–displacement curves are similar with those of the specimens containing only one single crack but have a relatively smoother peak period and a gentler decent period after peak. In particular, the specimen of $\alpha =0$ has a long peak period. Thus, the presence of the two pre-existing cracks reduces brittleness of the specimen. We choose some characteristic points labeled as A, B, C, and D in the load–displacement curves and show the corresponding crack patterns in Fig. 28. For different inclination angle of the crack ➁, the crack patterns of the Brazilian disk specimens are different.

For $\alpha =0$, cracks initiate from the centers of cracks ➀ and ➁ when the displacement u increases to A1. When the displacement comes to B1, new wing cracks initiate near the tips of cracks ➀ and ➁, while the cracks from the centers of the two pre-existing cracks continue to propagate. At point C1, cracks ➀ and ➁ are connected by two curved new cracks. Then, cracks from the centers of cracks ➀ and ➁ propagate and approach the top and bottom ends of the Brazilian disk specimen at point D1. For $\alpha =30^\circ$, a crack first initiates near the left tip of crack ➁ at point A2. Then, new cracks initiate from the right tip of crack ➁ and the center of crack ➀ when the displacement increases to B2. At point C2, all the formed and pre-existing cracks coalesce and the cracks from the left tip of ➁ and the center of ➀ propagate and approach the top and bottom ends at D2.

The crack patterns for $\alpha = 60^\circ$ are similar with those for $\alpha = 30^\circ$ with a little difference. The first crack initiates from the center of crack ➀ rather than the left tip of crack ➁ at A3. In addition, a new crack initiates not exactly from the right tip of ➀ at B3. For $\alpha = 90^\circ$, a new crack initiates from the center of crack ➀ at A4 and a new crack connects cracks ➀ and ➁ at C4. All the freshly formed cracks propagate to the top and bottom ends of the specimen at D4. In summary, when the inclination angle of crack ➁ is 0 or $90^\circ$, the Brazilian disk specimen containing two pre-existing cracks shows a tensile splitting failure with the increase in the applied load. However, when the inclination angle of crack ➁ is equal to $30^\circ$ or $60^\circ$, the final failure of the Brazilian disk specimen results from coalescence of the cracks initiating from the right tips of cracks ➀ and ➁. Moreover, the failure mode obtained by the phase field modeling is in good agreement with the experimental observations and numerical simulations [63].

Fig. 31

Load–displacement curves of the Brazilian disk specimen containing two pre-existing cracks for different inclination angle. a$\alpha =0$. b$\alpha =30^\circ$. c$\alpha =60^\circ$. d$\alpha =90^\circ$

Fig. 32 compares the normalized peak load of the Brazilian disk specimen containing two pre-existing cracks from the phase field simulation and those from the peridynamics simulation [63] and experimental tests [34]. The peak load obtained from the phase field simulation has an approximately linear decreasing trend with the increase in the inclination angle $\alpha$. However, the peak loads from the peridynamics simulation and experimental tests show a groove-shaped trend. The difference in the normalized peak loads from the three methods lies in the heterogeneous nature of the experimental rock specimens and that the numerical specimens are homogeneous in this paper. Another reason is that the practical rock is also shear-resisting and a shear evolution was involved in the peridynamics simulation [63]. Only the elastic energy induced cracks are considered and the shear strengths of cracks are not used in the PFM. In addition, some details of the experimental tests [34] are lacking such as the load–displacement curves, thereby reducing the possibility for better fitting of the PFM to the experimental results.

Fig. 32

Normalized peak load of the Brazilian disk specimen containing two pre-existing cracks for different inclination angle

6 Conclusions

A phase field model for quasi-static fracture is used to investigate crack propagation and coalescence in Brazilian disk specimens subjected to compression. The phase field model is implemented in Comsol Multiphysics, and a benchmark of three-point bending test is used initially to verify the feasibility and applicability of the phase field modeling in Comsol. Then, numerical simulations of crack propagation and coalescence in Brazilian disk specimen with no initial crack, a single and two pre-existing cracks are conducted, respectively. Crack propagation patterns along with the load–displacement curves are fully discussed. Meanwhile, the effects of length scale parameter and critical energy release rate on crack propagation are evaluated. In addition, the effect of crack inclination angle on the pre-cracked Brazilian disk specimens is also investigated. Our simulation shows that the numerical results obtained by the phase field model are in good agreement with previous experimental and numerical results.

All the presented numerical examples show that the initiation, propagation, and coalescence of cracks are autonomous without external criterion for fracture. Thus, there is no need for the phase field modeling to set propagation path in advance. In addition, some adaptive technologies and remeshing are also unwanted. These advantages make the phase field model more attractive, and the numerical approach in this paper can be extended to other rock problems. In future research, more numerical methods will be used to compare and verify our simulations in this paper, such as the XFEM and enriched meshless methods [4].