XLME interpolants, a seamless bridge between XFEM and enriched meshless methods

Abstract

In this paper, we develop a method based on local maximum entropy shape functions together with enrichment functions used in partition of unity methods to discretize problems in linear elastic fracture mechanics. We obtain improved accuracy relative to the standard extended finite element method at a comparable computational cost. In addition, we keep the advantages of the LME shape functions, such as smoothness and non-negativity. We show numerically that optimal convergence (same as in FEM) for energy norm and stress intensity factors can be obtained through the use of geometric (fixed area) enrichment with no special treatment of the nodes near the crack such as blending or shifting.

1 Introduction

Maximum entropy shape functions are a relatively new class of approximation functions, as they were first introduced in [1] in the context of polygonal interpolation. The idea of these functions is to maximize the Shannon entropy [2] of the basis functions, which gives a measure of the uncertainty in the approximation scheme. The principle of maximum entropy (max-ent) was developed by Jaynes [3, 4], who showed that there is a natural correspondence between statistical mechanics and information theory. In particular, max-ent offers the least-biased statistical inference when the shape functions are viewed as probability distributions subject to the approximation constraints (such as linear reproducing properties). However, without additional constraints, the basis functions are non-local, which due to increased overlapping makes them unsuitable for analysis using Galerkin methods. The increased overlapping of the basis functions generally leads to more expensive numerical integration due to the large number of evaluation points. It also produces a non-sparse stiffness matrix, resulting in a linear system that is much more expensive to solve.

The local maximum-entropy (LME) approximation schemes were developed in [5] using a framework similar to meshfree methods. Here the support of the basis functions is introduced as a thermalization (or penalty) parameter $\beta$ in the constraint equations. When $\beta = 0$, then the max-ent principle is fully satisfied and the basis functions will be least biased. For example, if only zero-order consistency is required, the shape functions are Shepard approximants [6] with Gaussian weight function. When $\beta$ is large, then the shape functions have minimal support. In particular, they become the usual linear finite element functions defined on a Delaunay triangulation of the domain associated with the given node set. In [5] it was shown that for some values of $\beta$, the approximation properties of the maximum-entropy basis functions are greatly superior to those of the finite element linear functions, even when the added computational cost due to larger support is taken into account.

Subsequent studies, such as [7–9], show that maximum entropy shape functions are suitable for solving a variety of problems such as thin shell analysis, compressible and nearly-incompressible elasticity and incompressible media problems. Higher order approximations can also be obtained using the max-ent framework, as shown in [10]. This class of methods is therefore related to the MLS-based meshless methods (due to the node-based formulation) and isogeometric analysis (with whom it shares features such as weak Kronecker delta and non-negativity), inheriting some advantages from both.

In this work, we propose a coupling of the LME shape functions with the extrinsic enrichments used in partition of unity enriched methods for fracture, such as the extended finite element method (XFEM), see [11–13].

There is a growing interest in modeling fracture mechanics with enrichment functions combined with meshless methods [14–16], isogeometric analysis [17], or strain-smoothed XFEM [18, 19]. Advantages of the meshless and isogeometric methods include the possibility to model curved boundaries through higher order shape functions and to resolve the gradient fields more accurately than with low order Lagrange elements. This higher regularity of the basis functions is also particularly advantageous when the model problem requires it, such as for the Kirchhoff–Love theory. Also in some enriched meshless methods, no representation of the crack’s topology is needed as this is handled through cracking particles as in [20] or weight-function enrichments as in [21, 22].

Here, we show that the enriched maximum entropy shape functions are suitable for this class of problems. Moreover, this method is more accurate than standard XFEM and does not require the so-called blending elements (the elements near the crack tip). When compared to usual meshfree methods for crack propagation, such as Element Free Galerkin (EFG), the method presented here can more easily deal with essential boundary conditions, due to the fact that the shape functions satisfy a weak Kronecker delta property. The shape functions are also very smooth ($C^\infty$), which results in an accurate numerical integration with a relatively low number of integration points, especially for Gauss–Legendre quadrature [5, 8, 10]. Moreover, smooth and non-negative basis functions, such as those used in isogeometric analysis are gaining impetus.

The paper is organized as follows: in the next section we will briefly describe the LME approximants. Then we will introduce the coupling between LME and XFEM, with particular reference to implementation issues such as numerical integration. Next we examine the accuracy of the method through several numerical examples, which indicate that the convergence rates for the energy norm of the error and the stress-intensity factors, are $O(h)$ and $O(h^2)$ respectively. Some concluding remarks are stated in the last section.

2 Local maximum entropy (LME) approximants

Local maximum entropy meshfree approximants, introduced in [5], are related to other convex approximation schemes, such as natural neighbor approximants [23], subdivision approximants [24], or B-spline and NURBS basis functions [25]. The LME basis functions will be denoted by $p_a(\mathbf{x}), a=1,\ldots ,N$ with $\mathbf{x}\in \mathbb R ^d, d$ is the dimension of the physical domain. They are non-negative and are required to satisfy the zeroth-order and first-order consistency conditions:

$$\begin{aligned}&p_a(\mathbf{x})\ge 0,\end{aligned}$$

(1)

$$\begin{aligned}&\sum _{a=1}^N p_a(\mathbf{x}) = 1, \end{aligned}$$

(2)

$$\begin{aligned}&\sum _{a=1}^N p_a(\mathbf{x})\mathbf{x}_a = \mathbf{x}. \end{aligned}$$

(3)

In the last equation, the vector $\mathbf{x}_a$ identifies the positions of the nodes associated with each basis function. Consider a set of nodes $X=\{\mathbf{x}_a\}_{a=1,\ldots ,N}$, which we will call the node set. The convex hull of $X$ is the set

$$\begin{aligned} \text{ conv }X := \{ \mathbf{x}\in \mathbb R ^d| \mathbf{x} = \mathbf{X} \lambda ,\lambda \in \mathbb R ^{N}_+,\mathbf{1}\cdot \lambda =1\} \end{aligned}$$

(4)

Here $\mathbb R ^{N}_+$ is the non-negative orthant, $\mathbf{1}$ denotes the vector in $\mathbb R ^{N}$ whose entries are one, and $\mathbf{X}$ is the $d\times N$ matrix whose columns are the co-ordinates of the position vectors of the nodes in the node set $X$ [5]. Convex approximants, which are in the span of convex basis functions, can only exist within the convex hull of $X$(or subsets of it) and satisfy a weak Kronecker delta property at the boundary of the convex hull of the nodes. This means that the shape functions corresponding to the interior nodes vanish on the boundary. With this property, the imposition of essential boundary conditions in the Galerkin method is straightforward.

The principle of maximum entropy comes from statistical physics and information theory, which consider the measure of uncertainty or information entropy [2]. Consider a random variable $\chi :I\rightarrow \mathbb R ^d$, where $I$ is the index set $I=\left\{ 1,\ldots ,N\right\}$ and $\chi (a)=\mathbf{x}_a$ gives to each index the position vector of its corresponding node. Since the shape functions of a convex approximation scheme are non-negative and add to one, we regard $\left\{ p_{1}(\mathbf{x}),\ldots ,p_{N}(\mathbf{x})\right\}$ as the corresponding probabilities. The statistical expectation or average of this random variable, as regarding Eq. (3), is $\mathbf{x}$. According to this interpretation, the approximation of a function $u(\mathbf{x})\approx \sum _{a=1}^N p_a(\mathbf{x})u_a$ from the nodal values $\{u_a\}_{a\,=\,1,\ldots ,N}$ is understood as an expected value $u(\mathbf{x})$ of a random variable $\mu :I\rightarrow \mathbb R$ where $\mu (a)=u_a$.

The main idea of max-ent is to maximize the Shannon’s entropy, $H(p_1,p_2,\ldots ,p_N)$, subject to the consistency constraints as follows:

$$\begin{aligned}&\text {(ME)}\quad \text {For a fixed } \mathbf{x}\text { maximize} \\&\quad H(p_1,p_2,\ldots ,p_N)= -\sum _{a=1}^N p_a \log (p_a)\nonumber \\&\qquad \quad \text {subject to}\quad p_a \ge 0,\quad a=1,...,N\nonumber \\&\qquad \quad \,\,\,\qquad \qquad \quad \sum _{a=1}^N p_a = 1\nonumber \\&\qquad \quad \,\,\,\qquad \qquad \quad \sum _{a=1}^N p_a\mathbf x _a = \mathbf x \nonumber \end{aligned}$$

(5)

Solving the (ME) problem produces the set of basis functions, $p_a:=p_a(\mathbf{x}), a=1,\ldots ,N$. However, these basis functions are non-local, i.e. they have support in all of conv$X$, and are not suitable for use in a Galerkin approximation because it would lead to a full, non-banded matrix. Nevertheless, they have been used in [1] as basis functions for polygonal elements.

Another optimization problem which takes into account the locality of the shape functions is Rajan’s form of the Delaunay triangulation [26]. This can be stated as the following linear program:

$$\begin{aligned}&\text {(RAJ)}\quad \text {For a fixed }\mathbf{x}\text { minimize} \\&\quad U(\mathbf{x},p_1,p_2,\ldots ,p_N)= \sum _{a=1}^N p_a \left| \mathbf{x}-\mathbf{x}_a\right| ^2\nonumber \\&\qquad \qquad \qquad \qquad \quad \,\,\, \text {subject to}\quad p_a \ge 0,\quad a=1,\ldots ,N\nonumber \\&\qquad \qquad \qquad \qquad \quad \,\,\,\qquad \qquad \quad \sum _{a=1}^N p_a = 1\nonumber \\&\qquad \qquad \qquad \qquad \quad \,\,\,\qquad \qquad \quad \sum _{a=1}^N p_a\mathbf{x}_a = \mathbf{x} \nonumber \end{aligned}$$

(6)

It is easy to see that $U(\mathbf{x},p_1,p_2,\ldots ,p_N)$ is minimized when the shape functions $p_1,\ldots ,p_N$ decay rapidly as the distance from the corresponding nodes $\mathbf{x}_a$ increases. There, the shape functions that satisfy (RAJ) problem will have small supports, where the support can be defined up to a small tolerance $\epsilon$ by

$$\begin{aligned} \text{ supp } (p_a)=\left\{ \mathbf{x}:p_{a}(\mathbf{x})>\epsilon \right\} \end{aligned}$$

The main idea of LME approximants is to compromise between the (ME) problem and the (RAJ) problem by introducing parameters $\beta _{a}$ that control the support of the $p_a$. Therefore we write:

$$\begin{aligned}&\text {For a fixed } \mathbf{x} \text { minimize}\quad \\&\sum _{a=1}^N \beta _a p_a \left| \mathbf{x}-\mathbf{x}_a\right| ^2 +\sum _{a=1}^N p_a \log (p_a) \nonumber \\&\qquad \qquad \qquad \qquad \quad \,\,\, \text { subject to }\quad p_a \ge 0,\quad a=1,\ldots ,N\nonumber \\&\qquad \qquad \qquad \qquad \quad \,\,\,\qquad \qquad \quad \sum _{a=1}^N p_a = 1\nonumber \\&\qquad \qquad \qquad \qquad \quad \,\,\,\qquad \qquad \quad \sum _{a=1}^N p_a\mathbf{x}_a = \mathbf{x} \nonumber \end{aligned}$$

(7)

The non-negative parameters $\beta _a$ can in general be functions of the position $\mathbf{x}$. This convex optimization problem is solved efficiently by a duality method as described in [5]. Finally, the shape functions are written in the form:

$$\begin{aligned}&p_a (\mathbf{x}) \!=\! \frac{1}{Z(\mathbf{x},\lambda ^* (\mathbf{x}))} \exp [\!-\!\beta _a \left| \mathbf{x}\!-\!\mathbf{x}_a\right| ^2 \!+\! \lambda ^* (\mathbf{x})\cdot (\mathbf{x}-\mathbf{x}_a) ] \end{aligned}$$

where

$$\begin{aligned}&Z(\mathbf{x},\lambda ) = \sum _{b=1}^N \exp [-\beta _b \left| \mathbf{x}-\mathbf{x}_b\right| ^2 + \lambda \cdot (\mathbf{x}-\mathbf{x}_b) ] \end{aligned}$$

is a function associated with the node set X and $\lambda ^* (\mathbf{x})$ is defined by

$$\begin{aligned}&\lambda ^* (\mathbf{x}) = \arg \,\, \min _{\lambda \in \mathbb R ^d} \,\, \log \,\, Z(\mathbf{x},\lambda ) \end{aligned}$$

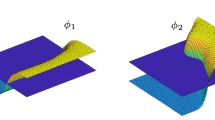
The local max-ent shape functions are as smooth as $\beta (\mathbf{x})$ and $p_{a}(\mathbf{x},\beta _{a})$ is a continuous function of $\beta \in [0, +\infty )$ [5]. For example LME shape functions are $C^{\infty }$ if $\beta$ is constant. In this paper we choose $\beta = \frac{\gamma }{h^2}$, where $h$ is a measure of the nodal spacing and $\gamma$ is constant over the domain. In this case the shape functions are smooth and their degree of locality is controlled by the parameter $\gamma$. A plot of the LME functions for $\gamma = 1.8$ and a particular choice of nodes is given in Fig. 1. In general, the optimal $\beta$ is not obvious and this will be discussed later in this paper.

Fig. 1

Local max-ent shape functions in 2D

As we mentioned before, LME shape functions satisfy a weak Kronecker delta property at the boundary of the convex hull of the nodes. Therefore, the shape functions that correspond to interior nodes vanish on the boundary.

3 Brief on extrinsic enrichments for partition of unity methods

3.1 Description

The main idea of partition of unity (PU) enrichment as used here is to extend the max-ent approximation space with some additional enrichment functions. The proposed method is based on a local PU and uses an extrinsic enrichment to model the discontinuity. The max-ent approximation can be decomposed into a standard part and an enriched part:

$$\begin{aligned}&u^{h}(\mathbf{x}) = \sum _{I\in W} p_I(\mathbf{x}) u_I +\sum _{J\in W_{b}} p_J(\mathbf{x}) \chi (\phi (\mathbf{x})) a_J\\&\quad \qquad \qquad +\sum _{K\in W_{s}} p_K(\mathbf{x}) \sum _{k\,=\,1}^4 B_{k}(\mathbf{x}) b_{kK} \end{aligned}$$

Here the first term is the standard approximation part and the second and the third terms are the enriched parts. $W$ is the set of nodes in the entire discretization and $W_b$ and $W_s$ are the sets of enriched nodes. $p_I$ are the shape functions and $\chi$ and $B_k$ are the enrichment functions. Normally, $\chi$ is selected as a step or Heaviside function and is used to enrich the nodes where the supports of the LME shape functions are completely cut by the crack. $B_k$ are branch functions and are used to enrich the shape functions whose supports include the crack tip. In this paper we use a geometric (fixed area) enrichment, and therefore we obtain optimal convergence rate [$O(h^2)$] without a special treatment of the so-called ”blending” area around the crack tip. Branch functions are defined as follows (in polar coordinate relative to the crack tip, denoted by $\mathbf{x }^{{\textit{tip}}}$):

$$\begin{aligned}&B_1(r,\theta ) = \sqrt{r}\sin \frac{\theta }{2} \end{aligned}$$

(8)

$$\begin{aligned}&B_2(r, \theta ) = \sqrt{r}\cos \frac{\theta }{2} \end{aligned}$$

(9)

$$\begin{aligned}&B_3(r, \theta ) = \sqrt{r}\sin \frac{\theta }{2}\cos \theta \end{aligned}$$

(10)

$$\begin{aligned}&B_4(r, \theta ) = \sqrt{r}\cos \frac{\theta }{2}\cos \theta , \end{aligned}$$

(11)

where $r=\left| \mathbf{x}-{\mathbf{x}}^{tip}\right|$.

$\phi (\mathbf{x})$ is the signed distance from the point $\mathbf{x}$ to the crack segment and $a_I$ and $b_{kI}$ are additional degrees of freedom [27]. The signed distance function is defined as:

$$\begin{aligned}&\phi (\mathbf{x}) = \min _{{{\mathbf{x}_{\varGamma }} \in \varGamma }}\left| \mathbf{x}-{\mathbf{x}}_{\varGamma }\right| \text{ sign }(\mathbf{n}\cdot (\mathbf{x}-{\mathbf{x}}_{\varGamma })) \end{aligned}$$

Here $\varGamma$ is the curve of discontinuity, ${\mathbf{x}}_{\varGamma }$ is an arbitrary point on $\varGamma$ and $\mathbf{n}$ is normal vector to $\varGamma$ (see Fig. 2). If we choose $\chi$ as a Heaviside function, then

$$\begin{aligned} H(\phi (\mathbf{x})) = {\left\{ \begin{array}{ll} 1 &{}\text { if } \phi (\mathbf{x})>0 \\ -1 &{}\text { if } \phi (\mathbf{x})<0 \end{array}\right. } \end{aligned}$$

(12)

This enrichment function captures the jump across the crack faces.

Fig. 2

Signed distance function

In order to model a curved crack, the signed distance function can be approximated by the same shape functions as the displacement. Assume $\mathbf{{t}}$ is a vector tangent to the curved crack, directed towards the crack tip. We approximate $\phi$ by:

$$\begin{aligned} \tilde{\phi }(\mathbf{x}) = \sum _{I}p_{I}(\mathbf{x})\phi _{I},\quad \mathbf{x}\in \varOmega _{\phi } \end{aligned}$$

(13)

Here $\phi _{I}$ are the nodal values of $\phi , p_{I}$ are the shape functions and $\varOmega _{\phi }$, is the domain of definition for $\phi$, given by:

$$\begin{aligned} \varOmega _{\phi }:= \{\mathbf{x} | \mathbf{{t}}\cdot \nabla r(\mathbf{x}) > 0 \} \end{aligned}$$

(14)

So, the approximated crack position is considered as:

$$\begin{aligned} \varGamma := \{\mathbf{x} | \tilde{\phi }(\mathbf{x}) = 0, \mathbf{x}\in \varOmega _{\phi }\} \end{aligned}$$

(15)

In this case, $\tilde{\phi }(\mathbf{x})$ is not defined beyond the crack tip. So, two possibilities are considered for the angle $\theta$ of the Branch functions. If $\mathbf{{t}}\cdot \nabla r\le 0$, then the regular polar angle from $-\mathbf{{t}}$ is computed. If $\mathbf{{t}}\cdot \nabla r > 0, \theta$ is considered as in [28]:

$$\begin{aligned} \theta =\arctan (\frac{-\phi }{\sqrt{r^2 - \phi ^{2}}}) \end{aligned}$$

(16)

3.2 Numerical integration

3.2.1 Numerical integration for LME

The numerical integration of LME shape functions poses similar challenges as that of the shape functions used in meshless methods. In particular, the integrands used in the assembly of the stiffness matrix are non-polynomial and (depending on the values of the parameter $\gamma$) the supports of the shape functions overlap more than in standard finite elements. However, the shape functions are smooth so only a relatively small number of integration points are required.

In the examples we considered, we used quadrilateral background integration cells for integrating the shape functions whose support does not intersect the crack. For the values of $\gamma$ between 4.8 and 1.8, and for uniformly spaced nodes and square we found that the $4\times 4$ Gauss quadrature rule is sufficient to ensure optimal convergence. Moreover, a quadrature rule with $8 \times 8$ Gauss points provides close to exact integration (i.e. the results change by less than $10^{-6}$ when the number of Gauss points is further increased).

3.3 Numerical integration for enriched LME

The usual numerical integration methods, for example Gauss quadrature, are less accurate for PU-enriched methods for fracture. This happens due to the discontinuity along the crack, and the singularity at the crack tip. The usual rule is to use a simple splitting of integration cells crossed by the crack [29]. In [30], a method was proposed in which each part of the elements that are cut or intersected by a discontinuity is mapped onto the unit disk using a conformal Schwarz–Christoffel map. However, for straight cracks, a triangulation of the elements cut by the crack which takes into account the location of the discontinuity is relatively easy to implement and was used in this work.

For the integration cells that contain the crack tip, special care has to be taken. These cells contain the discontinuity and a singularity together. So, simply refining the triangles that make up the integration cells leads to less accurate numerical results. A simple solution is to refine locally each split triangle, until an acceptable estimate of the integrands is achieved. Unfortunately, this method is expensive. To solve this problem, the almost polar integration was introduced in [29]. The main idea is to build a quadrature rule on a triangle from a quadrature rule on the unit square (see Fig. 3). The map is:

$$\begin{aligned}&T : (x,y)\longrightarrow (xy,y) \end{aligned}$$

which maps a square into a triangle. By looking at the integrands which contain the derivatives of the branch functions, we notice that the Jacobian of the transformation $T$, will cancel the $r^{-1/2}$ singularity. This integration method gives excellent results with a low number of integration points and is used on the sub-triangles having the crack tip as a vertex. In the other integration cells, we found it is sufficient to use standard Gauss quadrature over a background mesh (such as the Delaunay triangulation of the nodes that takes in to account the discontinuity for the cells cut by the crack).

Fig. 3

Transformation of an integration method on a square into an integration method on a triangle for crack tip functions

An important distinction between meshless methods and standard finite elements is that, in the former, the numerical integration is almost never exact. Recent work [31] has shown that integration errors in meshless methods negatively impact the stability of the method when a large number of degrees of freedom is involved. In particular, as the value of the discretization parameter $h$ decreases, the accuracy of the numerical integration should increase proportionally, so that optimal convergence can be obtained. We have conducted a detailed study on the effect of approximate integration for one of the numerical examples shown below.

3.4 Condition number

There are two ways to choose the enrichment area: topological enrichment in which the area of enrichment shrinks with the nodal spacing $h$, and geometric enrichment which uses a fixed enrichment area. In topological enrichment, the branch functions are multiplied by shape functions on a small set of nodes around the crack tip. These singular functions live on a compact support vanishing as $h$ goes to zero. In the context of meshless methods, only topological enrichment has been studied, which leads to non-optimal convergence rate. However, the numerical results of this paper show that the enrichment area should have a size independent of the mesh parameter (i.e. it should be geometric) to obtain optimal convergence, as seen for standard XFEM in [29, 32]. Unfortunately, adding singular functions on all the nodes within a fixed area around the crack tip leads to an increase in the number of degrees of freedom and an increase in the condition number (see Fig. 4).

Fig. 4

The condition number of geometric and topological enrichment for $\gamma =1.8$ and $\gamma =4.8$, using a direct solver and the preconditioning method

Some methods were proposed to improve the condition number of the stiffness matrix, such as preconditioning schemes. Here we use a method introduced in [32] which relies on a Cholesky decomposition of the diagonal blocks of the stiffness matrix corresponding to enriched nodes. This method noticeably improves the condition number (see Fig. 4), but not the rate of increase as the mesh is refined. A robust preconditioning scheme for XFEM was proposed in [33], which is based on a domain decomposition and results in a condition number close to the finite element matrices without enrichment. Another promising development for improving the condition number of geometric enrichment has been developed in [34]. This improvements will be discussed in a future work.

4 Numerical examples

4.1 Infinite plate with a horizontal crack

Consider an infinite plate containing a straight crack of length $2a$ under a remote uniform stress field $\sigma$ as shown in Fig. 5. The analytical solution near crack tip for stress fields and displacement in terms of local polar coordinates from the crack tip are [14]

$$\begin{aligned}&\sigma _{xx}(r,\theta )= \frac{K_I}{\sqrt{r}} \cos \frac{\theta }{2}\left( 1-\sin \frac{\theta }{2}\sin \frac{3\theta }{2}\right) \\&\sigma _{yy}(r,\theta )= \frac{K_I}{\sqrt{r}} \cos \frac{\theta }{2}\left( 1+\sin \frac{\theta }{2}\sin \frac{3\theta }{2}\right) \\&\sigma _{xy}(r,\theta )= \frac{K_I}{\sqrt{r}} \sin \frac{\theta }{2}\cos \frac{\theta }{2}\cos \frac{3\theta }{2}\\&u_{x}(r,\theta )= \frac{2(1+\upsilon )}{\sqrt{2\pi }}\frac{K_I}{E} \sqrt{r}\cos \frac{\theta }{2}\left( 2-2\upsilon -\cos ^{2}\frac{\theta }{2}\right) \\&u_{y}(r,\theta )= \frac{2(1+\upsilon )}{\sqrt{2\pi }}\frac{K_I}{E} \sqrt{r}\sin \frac{\theta }{2}\left( 2-2\upsilon -\cos ^{2}\frac{\theta }{2}\right) \end{aligned}$$

where $K_I = \sigma \sqrt{\pi a}$ is the stress intensity factor (SIF), $\upsilon$ is Poisson’s ratio and $E$ is Young’s modulus. The analytical solution is valid for region close enough to the crack tip. We consider a square ABCD of length $10 \hbox { mm}\times 10 \text{ mm } , a=100 \hbox { mm}, E=10^7 \hbox { N/mm}^2, \upsilon = 0.3, \sigma =10^4 \hbox { N/mm}^2$ and the modeled crack length is $5\hbox { mm}$. In all problems of this paper, plane strain state is assumed. We use Dirichlet boundary conditions on the bottom, right and top edges and Neumann boundary conditions on the left edge which includes the crack. As we mentioned in Sect. 2, LME shape functions satisfy a weak Kronecker delta property. This property allows us to impose Dirichlet boundary conditions by computing a node-based interpolant or an $L^2$ projection of the boundary data. The latter can also be used for edges that contain enriched nodes. Numerical integration is performed on a background mesh of rectangular elements and the almost polar integration is used on the elements containing a crack tip.

Fig. 5

Infinite plate with a center crack under uniform tension and modeled geometry ABCD

Approximation errors in $L^2$ norm and energy norm are illustrated in Figs. 6 and 7 for different values of $\gamma$. Figure 8 shows the percentage error for SIFs. It is obvious from these figures that in this case there is an optimal value for the parameter $\gamma$ of around $1.8$ for which accuracy is maximized. For very low values of $\gamma$, convergence is degraded. This is due to numerical integration. With a higher number of Gauss points and $\gamma =0.8$, the optimal rate of convergence for a plane elasticity problem was recovered in [5]. But in that case, the method is very expensive. The LME results converge to the standard XFEM results as $\gamma$ increases.

Fig. 6

Error in the $L^2$ norm for the horizontal crack problem

Fig. 7

Error in the energy norm for the horizontal crack problem

Fig. 8

Percentage error of stress intensity factor for horizontal crack

As shown in Figs. 6 and 7, the rate of convergence for different values of $\gamma$, the parameter that controls the support of the shape functions, is $2$ for $L^2$ norm and 1 for the energy norm. This agrees with the a priori error estimates for XFEM established in the literature (see [35]). For a fixed number of nodes, when $\gamma$ decreases the error also decreases. For example, for $n=36\times 36$ we see from Table 1 that the error becomes smaller as $\gamma$ decreases to $0.8$. However, as $\gamma$ decreases, because the support of the LME shape functions becomes larger, we also need to consider a larger radius of influence (the distance of the neighbor search between the nodes), which leads to more function evaluations and increases the computational cost. In this study, we found that choosing $\gamma = 1.8$, which corresponds to a radius of influence of three nodes, provides a reasonable balance between accuracy and computational cost.

Table 1 Error for energy norm and SIF together with the running time and efficiency ratio (17) for a problem discretized with $36\times 36$ nodes.

We note from Table 1 that LME is significantly slower than XFEM for the same number of nodes, and that the computational cost increases as $\gamma$ decreases due to larger radius of influence. However, especially for $\gamma = 1.8$, the method is much more accurate than XFEM, which makes up for some of the computational cost. This is particularly true for the computation of the SIF, where the error is almost nine times smaller (although the method is 7 times slower). For $\gamma = 0.8$ and $36 \times 36$ nodes the method is even more accurate, but unfortunately as was discussed before, the method becomes prohibitively expensive.

In Table 1, we also show the computational efficiency of the method which we define by:

$$\begin{aligned} \text {efficiency} = \frac{\mathrm{\% \,improvement \,in\, accuracy}}{\mathrm{\% \,increase \,in \,total \,computational \,time}} \end{aligned}$$

(17)

We note that an efficiency index of 1 indicates the method is as efficient as XFEM, an index $>$1 indicates the method is more efficient than XFEM, and an index $<$1 indicates the method is less efficient. Because of the additional overhead required (Newton iterations, neighbor node search, less-sparse stiffness matrix), XLME in the current implementation is generally less efficient than XFEM. The ratios showed in Table 1 are representative for any number of nodes and for the other model problems considered later in this paper. In general, the results agree with other findings in literature, which show that LME is more efficient than MLS but less efficient than FEM [36].

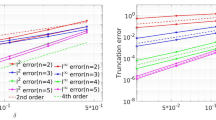
For the problems studied in this work, even in the cases of standard XFEM, the integration is not exact. This is because the Branch enrichment functions (8)–(11) are non-polynomial in nature. To study the effect of approximate integration on the accuracy and stability of the solution, we have considered Gauss quadratures with a varying number of evaluation points. The relative errors in energy norm obtained for XFEM and for XLME with $\gamma = 1.8$ are shown in Fig. 9. The figure shows the convergence study for a larger number of nodes (up to $n = 196 \times 196$). We observe that for both XFEM and XLME, a $3\times 3$ Gauss quadrature is not sufficient for a stable solution and the results diverge in the case of XFEM, or become unstable in the case of XLME. However, with a Gauss quadrature of $4 \times 4$ or more points, the error in XFEM remains constant and optimal convergence is achieved (the lines corresponding to $4 \times 4, 5 \times 5$ and $6 \times 6$ Gauss points overlap and have slope $m=1.00$).

Fig. 9

Error in the energy norm for XLME and XFEM and different quadrature rules.

For XLME with $\gamma = 1.8$ and with a $4 \times 4$ Gauss quadrature, the convergence rate becomes sub-optimal as the number of degrees of freedom increases (the slope is $m=0.83$). However, the lines corresponding to $5 \times 5$ and $6 \times 6$ Gauss points overlap almost completely, with only a slight difference that appears when the number of degrees of freedom exceeds 100,000. The slope of the convergence line that best fits the data points is $m=0.95$ in both cases. This indicates that the error due to numerical integration when $5 \times 5$ or more Gauss points are used is very small. It is possible that as the number of degrees of freedom increases, an even larger number of Gauss points per integration element will be needed, in line with the results obtained by [31]. In such cases, an adaptive numerical quadrature method may be needed. However, the LME shape functions are very smooth ($C^\infty$), so in general the integration should be less problematic in comparison to other meshless methods.

We compute the SIFs by the interaction integral method, where the domain form of the interaction integral is given by [37]

$$\begin{aligned} I^{(1,2)}=\int _{A}\left[ \sigma _{ij}^{(1)} \frac{\partial u_{i}^2}{\partial x_{1}}-\sigma _{ij}^{(2)} \frac{\partial u_{i}^1}{\partial x_{1}}-W^{(1,2)}\delta _{1j}\right] \frac{\partial q}{\partial x_{j}} dA \end{aligned}$$

The domain of integration, A, is set to be the union of all the elements which have a node within a ball of radius $r_{d}$ around the crack tip (see Fig. 10). Since we use a fixed area enrichment, $r_d$ is also a fixed distance. We found that most accurate results are obtained when $r_d$ is half of the modeled crack length. This results in a superconvergent ($O(h^2)$) rate for $K_I$, as also reported for XFEM in [29] and [32].

Fig. 10

Elements which have a node within a ball of radius $r_{d}$ around the crack tip

The weight function $q$ is taken to have a value of unity for all nodes within the ball $r_d$, and zero on the outside of the ball. Hence, the bilinear shape functions are used as the weight functions. $W^{(1,2)}$ is the interaction strain energy density

$$\begin{aligned}&W^{(1,2)}=\sigma _{ij}^{(1)} \epsilon _{ij}^{(2)}=\sigma _{ij}^{(2)} \epsilon _{ij}^{(1)} \end{aligned}$$

$\sigma _{ij}^{(1)}$ and $\epsilon _{ij}^{(1)}$ are computed stresses and strains and $\sigma _{ij}^{(2)}$ and $\epsilon _{ij}^{(2)}$ are auxiliary stresses and strains derived by Westergaard and Williams, corresponding to mode $1$ and mode $2$ as described in [37].

4.2 Edge crack under shear traction

The second problem investigated in this paper, is a finite dimensional plate subjected to uniform shear on the top of the plate $\tau = 1.0\, \text{ N/mm }^2$ and the bottom is fixed, as shown in the Fig. 11. We choose Young’s modulus $E=3\times 10^7$ Pa and Poisson’s ratio $\nu =0.25$.

Fig. 11

Edge-cracked plate under shear stress

The SIFs $K_I$ and $K_{II}$, are calculated by the extended LME method and compared to the reference solutions [38]:

$$\begin{aligned}&K_{I}^{ref}=34.0 \\&K_{II}^{ref}=4.55 \end{aligned}$$

We note that these values were calculated using a boundary collocation method and are given with an accuracy of 3 significant digits. The SIFs $K_I$ and $K_{II}$ calculated by the extended LME method on a fine mesh converge to the following values (accurate to 4 significant digits):

$$\begin{aligned}&K_I^0=34.04 \\&K_{II}^0=4.537 \end{aligned}$$

We note that there is a very good agreement between the reference solution and our computed solution. To study the convergence of the method we calculated the percentage error between the computed SIFs at various levels of refinement and $K_I^0$ and $K_{II}^0$.

Figures 12 and 13 illustrate the percentage error for $K_I$ and $K_{II}$. As evident from these figures, the smallest error for this problem is obtained by $\gamma =1.8$ and $\gamma =2.8$. We note that for these values of $\gamma$ the error becomes $<$0.01 %, which is equal to $K_I^0$ and $K_{II}^0$ up to the given significant digits. For values of $\gamma$ that are lower than $1.8$, computing the SIF accurately becomes expensive due to the large support of the shape functions. Therefore, we will not consider the case $\gamma =0.8$ in the following examples.

Fig. 12

Percentage error of $K_I$ for edge-cracked plate under shear stress

Fig. 13

Percentage error of $K_{II}$ for edge-cracked plate under shear stress

4.3 Slanted crack in an infinite plate

Consider an infinite plate containing an angled crack as shown in Fig. 14a. This problem is a mixed mode I–II problem. The analytical near-tip field solution for this problem in polar coordinates is given in [39]

$$\begin{aligned}&\sigma _{xx}(r,\theta )= \frac{K_I}{\sqrt{2\pi r}} \cos \frac{\theta }{2}\left( 1-\sin \frac{\theta }{2}\sin \frac{3\theta }{2}\right) \\&\quad \qquad \qquad \quad -\frac{K_{II}}{\sqrt{2\pi r}}\sin \frac{\theta }{2}\left( 2+\cos \frac{\theta }{2}\cos \frac{3\theta }{2}\right) \\&\sigma _{yy}(r,\theta )= \frac{K_I}{\sqrt{2\pi r}} \cos \frac{\theta }{2}\left( 1+\sin \frac{\theta }{2}\sin \frac{3\theta }{2}\right) \\&\quad \qquad \qquad \quad +\frac{K_{II}}{\sqrt{2\pi r}}\sin \frac{\theta }{2}\cos \frac{\theta }{2}\cos \frac{3\theta }{2}\\&\sigma _{xy}(r,\theta )= \frac{K_I}{\sqrt{2\pi r}} \sin \frac{\theta }{2}\cos \frac{\theta }{2}\cos \frac{3\theta }{2}\\&\quad \qquad \qquad \quad +\frac{K_{II}}{\sqrt{2\pi r}}\cos \frac{\theta }{2}\left( 1-\sin \frac{\theta }{2} \sin \frac{3\theta }{2}\right) \\&u_{x}(r,\theta )=\frac{K_I}{2\mu }\sqrt{\frac{r}{2\pi }} \cos \frac{\theta }{2}\left( \kappa -1+2\sin ^2\frac{\theta }{2}\right) \\&\quad \qquad \qquad \quad +\frac{K_{II}}{2\mu }\sqrt{\frac{r}{2\pi }}\sin \frac{\theta }{2} \left( \kappa +1+2\cos ^2\frac{\theta }{2}\right) \\&u_{y}(r,\theta )= \frac{K_I}{2\mu }\sqrt{\frac{r}{2\pi }}\sin \frac{\theta }{2}\left( \kappa +1-2\cos ^2\frac{\theta }{2}\right) \\&\quad \qquad \qquad \quad -\frac{K_{II}}{2\mu }\sqrt{\frac{r}{2\pi }}\cos \frac{\theta }{2} \left( \kappa -1-2\sin ^2\frac{\theta }{2}\right) \end{aligned}$$

Here $\mu$ is the shear modulus, $\kappa =3-4\upsilon$ for plane strain. The angle $\theta$ and the distance $r$ from the crack tip are indicated in Fig. 14b.

Fig. 14

a Slanted crack in an infinite plate where the principal stress is not perpendicular to the crack. b An infinite plate rotated with respect to the crack’s angle

We redefine the $x$-coordinate axis to coincide with the crack orientation [40], see Fig. 14b. The applied stress is decomposed into normal and shear components. The stress normal to the crack, $\sigma _{yy}$, produces pure mode I loading, while $\sigma _{xy}$ applies mode II loading to the crack. The stress intensity factors for the plate, can be computed by the relationship between $\sigma _{yy}$ and $\sigma _{xy}$ relative to $\sigma$ and $\alpha$ through Mohr’s circle [41]

$$\begin{aligned}&K_I=\sigma _{yy}\sqrt{\pi a} = \sigma \cos ^{2}\alpha \sqrt{\pi a}\\&K_{II}=\sigma _{xy}\sqrt{\pi a} = \sigma \sin \alpha \cos \alpha \sqrt{\pi a} \end{aligned}$$

In this problem, we again modeled a square region around the crack tip, the gray square in Fig. 14b, and chose different values for crack’s angle. The same tendency as for the 1st example is observed for this mixed mode problem. Again, $\gamma =1.8$ gives the most accurate results and this method has a convergence rate of approximately 2.

As shown in Table 2 when $\gamma$ decreases to the optimal value, in this case $\gamma =1.8$, the error decreases, however the computational cost increases due to a larger radius of influence of the shape functions. Nevertheless, we note that the error is much smaller (almost an order of magnitude) between $\gamma = 4.8$, which is virtually the same as standard XFEM, and $\gamma = 1.8$. We note that there is only a very small difference between the $\alpha = 15^\circ$ and $\alpha = 30^\circ$. This can be explained by the fact that the discretization is identical, the only difference being the size of the forces applied to the boundaries, as can been seen from Fig. 14. The log-log plots indicating the convergence rates of $K_{I}$ and $K_{II}$ with $\alpha = 30^\circ$ are shown in Figs. 15 and 16. We also computed the errors for $K_I$ and $K_{II}$ for angles $\alpha = 45^\circ , 60^\circ , 75^\circ$ with similar results.

Table 2 Error and the average running time when the number of nodes is $36\times 36$, the number of Gauss points is $16, \alpha =15^{\circ },30^{\circ }$ and radius of influence is 2 for $\gamma = 4.8$ and $\gamma = 3.8$, 3 for $\gamma = 2.8$ and $\gamma = 1.8$

Fig. 15

Percentage error of $K_{I}$ for slanted crack in an infinite plate with $\alpha =30^{\circ }$

Fig. 16

Percentage error of $K_{II}$ for slanted crack in an infinite plate with $\alpha =30^{\circ }$

5 Conclusions

We have developed a LME approximation scheme for fracture using enrichment functions to allow the approximation to reproduce near-tip fields and the jumps through the crack faces. The LME shape functions are non-negative which improves stability, and they possess a weak Kronecker delta property which makes it easy to impose the boundary conditions. With a fixed area (geometric) enrichment, optimal convergence is obtained. The LME basis functions are in general not polynomials but rather particle-based smooth functions, whose support is dictated by a non-dimensional parameter $\gamma$. When $\gamma$ decreases, the LME shape functions have better approximation properties compared to standard FEM shape functions, but the size of their support increases. Hence, accurate numerical integration using standard Gauss quadrature requires a greater number of function evaluations. We conclude that there is an optimal value of $\gamma$ of around 1.8 that maximizes the accuracy in relation to computational cost.

For computation of SIFs, this method is competitive in terms of costs compared to XFEM. Very likely, it is possible to improve the computational efficiency further. In particular, we plan to investigate the development of an efficient integration scheme, goal-oriented adaptivity for the parameter $\gamma$ and the enrichment radius, as well as methods to improve the condition number of the stiffness matrix. The proposed approximation also shows a lot of potential for other problems which will be examined in the future, such as crack growth and fracture in thin shell bodies.