1 Introduction

Failure of rocks is considered to occur or be initiated at the peak strength (Jaeger and Cook 1979). Hence, determination of strength of rock under different loading conditions is of great importance in the design of rock structures. While the rock mechanics literature is rich with numerous failure criteria and comparative studies (see, e.g., Colmenares and Zoback 2002; Benz and Schwab 2008; Rafiei 2011), only two relatively old criteria with very simple equations namely, the Mohr–Coulomb and the Hoek–Brown criteria are most frequently used in rock engineering practice (Al-Ajmi and Zimmerman 2005; Benz et al. 2008). In other words, most of the recently proposed criteria are of academic interest only and have not been suitable for practical applications either because of their complex forms which could not be conveniently used in analysis or involving too many parameters which could not be easily determined. Therefore, in spite of having so many criteria, there is still a great need to find new criteria which could be used in real-world applications. The suitable criterion for practical rock engineering purposes should satisfy the following conditions:

  1. (a)

    It should have a relatively simple mathematical form which can be understood and trusted by practitioners and can be conveniently implemented in numerical analysis by experts

  2. (b)

    It should have a small number of parameters which can be determined from relatively easy and well-established tests

  3. (c)

    It should give good agreement with the experimentally determined strength values of rocks under different loading conditions

Recently, a new failure criterion was introduced to the rock mechanics community and it was suggested to be probably “an answer to true representative modeling of intact rock failure” (Hammah and Carvalho 2011). The criterion was initially introduced by Christensen in 1997, and has been described in several publications (Christensen 1997, 2000, 2004, 2005, 2006a, b, 2007).

This criterion satisfies the first two conditions outlined above. It has a simple mathematical form expressed in terms of stress invariants which can be conveniently implemented in numerical methods. It also has only two parameters, the uniaxial compressive and tensile strength, which can be determined from the well-established tests. Unfortunately, Hammah and Carvalho (2011) did not apply the Christensen criterion to rock failure data. The objective of this study was to evaluate the accuracy of the Christensen criterion in prediction of rock strength and examine whether it satisfies the third condition.

A comprehensive set of strength data for four rock types under a wide range of loading conditions is compiled and the Christensen criterion is used to fit the data. As a first step, only the strength of intact rock is considered in this study and no attempt has been made to deal with the complex behavior of rock masses. In order to put the accuracy of the Christensen criterion into perspective, the well-established Hoek–Brown criterion is also applied to the same strength data. Consistent with approach taken by Christensen (2004) and Hoek and Brown (1980), only the peak strength corresponding to ultimate failure is considered in this paper and no attempt has been made to address the crack initiation or unstable crack growth thresholds.

In the next sections, a complete description of the Christensen criterion and its mathematical components are presented. The results of the application of the criterion to intact rock data are given, and the overall consistency of the Christensen criterion with observed failure characteristics of rock material is examined. Finally, the applicability of the Christensen criterion for rock failure is discussed.

2 The Christensen Criterion

In this section, the Christensen criterion and its components are introduced. The criterion has two parameters, and is proposed for failure of homogeneous isotropic materials with uniaxial compressive strength equal to or greater than the tensile strength. The criterion was developed using the mechanics sign convention for stresses, and for the purposes of this paper has been modified to the geomechanics sign convention, i.e., compression positive.

In order to fully understand the Christensen criterion, the complete derivation of the criterion is presented. In addition, explicit equations for strength under general and special loading conditions are derived.

2.1 Derivation of the Main Parabolic Criterion

The general form of a failure criterion is:

$$f\left( {\sigma_{ij} } \right) = 0$$
(1)

where σ ij represents the six components of the stress tensor specifying the magnitude and direction of principal stresses relative to the coordinate system. For isotropic material, strength is independent of the direction. Hence, the failure criterion can be expressed only in terms of the magnitude of the principal stresses:

$$f\left( {\sigma_{1} ,\sigma_{2} ,\sigma_{3} } \right) = 0$$
(2)

where σ 1, σ 2, and σ 3 are the major, intermediate and minor principal stresses, respectively. The principal stresses can also be expressed in terms of the stress invariants which are more convenient for analytical and numerical implementations:

$$f\left( {I_{1} ,J_{2} ,J_{3} } \right) = 0$$
(3)

where I 1 is the first invariant of the stress tensor, J 2 is the second invariant of the deviatoric stress tensor, and \(J_{ 3}\) is the third invariant of the deviatoric stress tensor given by:

$$I_{1} = \left( {\sigma_{1} + \sigma_{2} + \sigma_{3} } \right)$$
(4)
$$J_{2} = \frac{1}{6}\left[ {\left( {\sigma_{1} - \sigma_{2} } \right)^{2} + \left( {\sigma_{2} - \sigma_{3} } \right)^{2} + \left( {\sigma_{3} - \sigma_{1} } \right)^{2} } \right]$$
(5)
$$J_{3} = \left( {\sigma_{1} - \frac{{I_{1} }}{3}} \right)\left( {\sigma_{2} - \frac{{I_{1} }}{3}} \right)\left( {\sigma_{3} - \frac{{I_{1} }}{3}} \right)$$
(6)

Using the polynomial expansion and terminating at the second order terms, Eq. (3) can be expressed as:

$$a_{0} + a_{1} I_{1} + a_{2} I_{1}^{2} + a_{3} J_{2} = 0$$
(7)

where a 0, a 1, a 2 and a 3 are constants. Note that J 3 is eliminated in Eq. (7) because it is a third order term. In Eq. (7), the parameter a 0 merely establishes a datum and can be chosen arbitrarily. Considering the fact that homogeneous isotropic materials do not fail under hydrostatic compression (Christensen 1997), the parameter a 2 must be equal to zero. Hence, Eq. (7) can be re-written as:

$$a_{1} I_{1} + a_{3} J_{2} = 1$$
(8)

By satisfying Eq. (8) for uniaxial compression and tension conditions, the two remaining constants can be easily found as:

$$a_{1} = \frac{1}{{\sigma_{c} }} - \frac{1}{{\sigma_{t} }}$$
(9)
$$a_{3} = \frac{3}{{\sigma_{c} \sigma_{t} }}$$
(10)

where σ c and σ t are the absolute values of uniaxial compressive and tensile strength. Hence, the final criterion expressed in terms of principal stresses can be given by:

$$\left( {\frac{1}{{\sigma_{c} }} - \frac{1}{{\sigma_{t} }}} \right)\left( {\sigma_{1} + \sigma_{2} + \sigma_{3} } \right) + \left( {\frac{1}{{\sigma_{c} }}.\frac{1}{{\sigma_{t} }}} \right)\left\{ {\frac{1}{2}\left[ {\left( {\sigma_{1} - \sigma_{2} } \right)^{2} + \left( {\sigma_{2} - \sigma_{3} } \right)^{2} + \left( {\sigma_{3} - \sigma_{1} } \right)^{2} } \right]} \right\} = 1$$
(11)

This is the main parabolic part of the failure criterion proposed by Christensen (1997). However, the first term on the left hand side of Eq. (11) has the opposite sign from that originally proposed. This is because of the different sign conventions adopted in mechanics and geomechanics where compressive stresses are considered negative in the mechanics sign convention and positive in the geomechanics sign convention.

The criterion derived above bears some similarities to criteria based on elastic energy considerations (Christensen 2004). The first and second terms on the left hand side of Eq. (11) are directly related to volumetric and distortional energy terms, respectively. For the case of σ c  = σ t , the first term vanishes and the criterion is reduced to the von Mises criterion which is based on the concept of maximum distortional energy.

2.2 Explicit Forms of the Criterion

The criterion proposed by Christensen provides an implicit relationship between the principal stresses at failure. However, derivation of an explicit form is useful in the application of the criterion to measured strength data.

In the general case of a polyaxial state of stress where the three principal stresses are different, solving Eq. (11) for σ 1 gives two roots. The root with the higher value is by definition the major principal stress:

$$\sigma_{1} = \frac{1}{2}\left[ {\left( {\sigma_{2} + \sigma_{3} } \right) + \left( {\sigma_{c} - \sigma_{t} } \right) + \sqrt {\left( {\sigma_{c} + \sigma_{t} } \right)^{2} + 6\left( {\sigma_{2} + \sigma_{3} } \right)\left( {\sigma_{c} - \sigma_{t} } \right) - 3\left( {\sigma_{2} - \sigma_{3} } \right)^{2} } } \right]$$
(12)

Equation (12) can be used in analysis of the results of polyaxial tests.

In a triaxial state of stress, two principal stresses are equal to the confining pressure p, and the third principal stress is equal to the axial stress σ ax . For triaxial compression tests, the axial stress is higher than the confining pressure, σ 1 = σ ax and σ 2 = σ 3 = p. Hence, Eq. (12) reduces to:

$$\sigma_{1} = \sigma_{3} + \frac{1}{2}\left[ {\left( {\sigma_{c} - \sigma_{t} } \right) + \sqrt {\left( {\sigma_{c} + \sigma_{t} } \right)^{2} + 12\sigma_{3} \left( {\sigma_{c} - \sigma_{t} } \right)} } \right]$$
(13)

For triaxial extension tests on the other hand, the confining pressure is higher than the axial stress, σ 1 = σ 2 = p and σ 3 = σ ax . Hence, Eq. (12) gives:

$$\sigma_{1} = \sigma_{3} + \left[ {\left( {\sigma_{c} - \sigma_{t} } \right) + \sqrt {\left( {\sigma_{c} - \sigma_{t} } \right)^{2} + 3\sigma_{3} \left( {\sigma_{c} - \sigma_{t} } \right) + \sigma_{c} \sigma_{t} } } \right]$$
(14)

In a biaxial state of stress, one of the principal stresses is zero. By putting σ 3 = 0 in Eq. (12), the strength can be calculated as:

$$\sigma_{1} = \frac{1}{2}\left[ {\sigma_{2} + \left( {\sigma_{c} - \sigma_{t} } \right) + \sqrt {\left( {\sigma_{c} + \sigma_{t} } \right)^{2} + 6\sigma_{2} \left( {\sigma_{c} - \sigma_{t} } \right) - 3\sigma_{2}^{2} } } \right]$$
(15)

2.3 Tension Cut-Off

Although the Christensen parabolic criterion derived above has some similarities with the elastic energy concept, it is simply based on a polynomial expansion of stress invariants up to the second order terms and satisfies uniaxial compression and tension conditions. This approach leads to a problem under tensile stress. For materials with σ c  > 2σ t , which includes all rock types, Eq. (11) leads to tensile stresses higher than the tensile strength of the material. Hence, a tension cut-off is required in these cases:

$$\sigma_{3} = - \sigma_{t}$$
(16)

This expression for the tension cut-off is also different from the one originally proposed (Christensen 2004) because the largest principal tensile stress according to the geomechanics sign convention is σ 3 while σ 1 is the largest tensile stress in the mechanics sign convention.

2.4 Brittle to Ductile Transition

In the context of the Christensen criterion, brittle and ductile behaviors are closely related to the ratio of uniaxial compression strength to tensile strength. Materials with similar uniaxial compression and tension strengths such as steel are considered ductile while materials with uniaxial compression strength much higher than uniaxial tensile strength such as rocks may show brittle behavior (Christensen 2005).

The brittle to ductile transition criterion is defined by a plane in principal stress space which connects the three points in each principal stress plane where the main failure surface given by Eq. (11) intersects the tension cut-off (Christensen 2005). For example, the coordinate of the point of intersection in the \(\sigma_{2} - \sigma_{1}\) plane can be found by putting σ 2 = − σ t in Eq. (15) which gives σ 1 = σ c  − 2σ t . The plane of brittle to ductile transition which encompasses the three intersection points can be given by (Christensen 2005):

$$\left( {\sigma_{1} + \sigma_{2} + \sigma_{3} } \right) = \sigma_{c} - 3\sigma_{t}$$
(17)

Again, there is an opposite sign in this equation compared to the one originally proposed because of different sign conventions. According to the Christensen criterion, for a given material, the brittle or ductile behavior depends only on the volumetric stress, and there is a threshold of volumetric compressive stress above which the behavior is completely ductile.

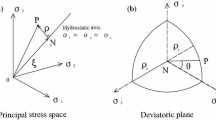
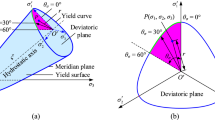
The Christensen failure surface in three-dimensional principal stress space for a typical rock material with σ c /σ t  = 12 is shown in Fig. 1a. The main parabolic surface and the three tension cut-off planes which have truncated the surface can be observed. Figure 1b shows the biaxial plane section of the failure surface where one of the principal stresses is zero. It can be observed that the tension cut-off in effect eliminates tensile stresses higher than the tensile strength. In addition, the trace of the brittle to ductile transition plane passes through the points of intersection of the parabolic surface and the tension cut-off. The section of the failure surface in the triaxial plane, where two principal stresses are equal is shown in Fig. 1c. It is worth noting that the trace of the brittle to ductile transition plane does not pass through the points of intersection of the main surface and the tension cut-off except for the case of biaxial planes. According to Fig. 1b, c, the mode of failure in most of the compressive region is ductile. More specifically, it can be observed that the predicted mode of failure in triaxial compression tests is ductile failure. Figure 1d shows the cross section of the failure surface in the π-plane. It can be observed that the Christensen criterion gives circular sections because the third invariant of the deviatoric stress tensor which is related to the Lode angle and the angular coordinate in the π-plane is eliminated in Eq. (8). Therefore for each value of the first stress invariant, the second invariant of the deviatoric stress tensor which is directly related to the radial coordinate in the π-plane is constant and independent of the angular coordinate producing circular cross sections.

Fig. 1
figure 1

The Christensen failure envelopes for a material with \(\sigma_{c} /\sigma_{t} = 12\) in a three dimensional principal stress space, b the biaxial plane σ 3 = 0, c the triaxial plane σ 2 = σ 3 = p, d the π-plane (the radius r of the circles is given for different values of I 1/σ c )

Full size image

3 The Hoek–Brown Criterion

This criterion was first proposed for the failure of intact rock and rock masses by Hoek and Brown (1980). Since then, it has undergone several stages of development (Hoek 1983, 1990; Hoek et al. 1992, 2002; Hoek and Brown 1997) and has been widely used in rock engineering. The latest version of the criterion known as the generalized Hoek–Brown criterion can be expressed as (Hoek et al. 2002):

$$\sigma_{1} = \sigma_{3} + \sigma_{c} \left( {m\frac{{\sigma_{3} }}{{\sigma_{c} }} + s} \right)^{a}$$
(18)

where m, s, and a are the parameters of this criterion, and σ c is the uniaxial compressive strength of intact rock. For an undamaged intact rock, s = 1 and a = 0.5, resulting in a two-parameter criterion. To make it consistent with the Christensen criterion, it is useful to express the Hoek–Brown parameter m is terms of σ c and σ t . By putting σ 1 = 0 into Eq. (18), the absolute value of tensile strength for intact rock can be given by:

$$\sigma_{t} = \frac{{\sigma_{c} }}{2}\left| {m - \sqrt {m^{2} + 4} } \right|$$
(19)

Hence, the parameter m for intact rock can be expressed as:

$$m = \frac{{\sigma_{c} }}{{\sigma_{t} }} - \frac{{\sigma_{t} }}{{\sigma_{c} }}$$
(20)

The Hoek–Brown criterion is fundamentally different from the Christensen criterion. While the Christensen criterion is proposed for all homogeneous isotropic materials with uniaxial compressive strength equal to or greater than the tensile strength, the Hoek–Brown criterion is specifically proposed for rocks. In addition, the intermediate principal stress has never appeared in any versions of the Hoek–Brown criterion proposed by the original developers (Hoek 1983, 1990; Hoek et al. 1992, 2002; Hoek and Brown 1980, 1997). However, the intermediate principal stress is present in the equations of the Christensen criterion.

Some researchers (e.g., Benz et al. 2008; Pan and Hudson 1988; Priest 2005; Zhang and Zhu 2007) have proposed modified version of the Hoek–Brown criterion to take into account the effect of the intermediate principal stress. However, the authors consciously decided to use the original form given in Eq. (18) partly because this form is in keeping with the first premise of simplicity and is most frequently-used for practical purposes. As it will be shown in the subsequent sections, this decision will not change the final outcome of this study.

4 Analysis of Strength Data

In order to examine the applicability of the any criterion to rock materials, it is crucial to utilize a reliable set of strength data for a wide range of loading conditions. In this study, four data sets obtained from high quality laboratory tests are compiled. The tests have been carried out on intact rock specimens under different states of stress including uniaxial tension, uniaxial compression, triaxial compression, triaxial extension, and polyaxial compression. While there are is no comprehensive set of data for strength of rock masses under these varying loading conditions, only the results of tests on intact rock have been used in this study. As it will be shown in the following sections, these data are sufficient to explore the merit of the Christensen criterion for rock material.

Two general scenarios are followed in the following analyses. In the first scenario, no fitting process is involved and the measured values of uniaxial compressive and tensile strength are used to predict the failure envelopes. This approach examines how accurate the failure criteria are when only the measured values for the parameters σ c and σ t are used. In the second scenario, date fitting analysis using the Least Squares Method is involved to find the optimized values for parameters σ c and σ t which best fit the data and minimizes the model errors. In this approach, the ultimate capacity of the criteria to fit the data is examined. These two approaches are complementary and provide a complete picture of both criteria.

In order to quantify the accuracy of the criteria, it is necessary to use an error index. In this study, the Root Mean Squared Error (RMSE) in the prediction of the major principal stresses at failure is selected as the error index:

$$RMSE = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^{n} {\left( {\sigma_{1,i}^{p} - \sigma_{1,i}^{m} } \right)^{2} } }$$
(21)

where \(\sigma_{1,i}^{p}\) and \(\sigma_{1,i}^{m}\) are the predicted and measured values of σ 1 for i’th data, respectively, and n is the number of data points.

4.1 Application of the Criteria to Synthetic Rock

Nguyen et al. (2011) prepared a granular synthetic rock which shows the main characteristics of real rocks such as cohesion, friction, and dilation. However, the synthetic rock had incredibly low strength and rigidity. A comprehensive and careful testing program was carried out on samples of the synthetic rock. The triaxial compression and extension test results are used in this study. More details about the testing procedure in given by Nguyen et al. (2011).

The measured average values of uniaxial compressive and tensile strength for the synthetic rock are 0.57 and 0.07 MPa, respectively (Nguyen et al. 2011). Figure 2 shows the Christensen and Hoek–Brown failure envelopes with these measured values for the parameters. It can be observed that the Christensen failure envelope is more accurate for triaxial compression while the Hoek–Brown envelope is more accurate for triaxial extension. However, both criteria have overestimated the strength of the synthetic rock.

Fig. 2
figure 2

The failure envelopes based on the measured values of the uniaxial compressive and tensile strength for the synthetic rock compared to the measured triaxial and extension dataset

Full size image

If only the results of triaxial compression tests are used for determination of the parameters of the two criteria, the obtained values of uniaxial compressive and tensile strength are 0.56 and 0.12 MPa for the Christensen criterion and 0.57 and 0.18 MPa for the Hoek–Brown criterion. It can be observed that the obtained values for uniaxial compressive strength are very close to the measured values while the obtained values for uniaxial tensile strength are much higher than the measured value.

Using results of triaxial extension tests for determination of the parameters, the obtained values of uniaxial compressive and tensile strength are 0.38 and 0.07 MPa for the Christensen criterion and 0.53 and 0.10 MPa for the Hoek–Brown criterion. It can be observed that for the Christensen criterion, the obtained value for uniaxial tensile strength is very close to the measured value while the obtained value for the uniaxial compressive strength is much less than the measured value. On the other hand, for the Hoek–Brown criterion, the obtained value for uniaxial tensile strength is slightly higher than the measured value and the obtained values for uniaxial compressive strength is slightly less than the measured value.

If the results of both triaxial compression and extension tests are used, the obtained values of uniaxial compressive and tensile strength are 0.43 and 0.07 MPa for the Christensen criterion and 0.52 and 0.11 MPa for the Hoek–Brown criterion. It can be observed that for the Christensen criterion, the obtained value for uniaxial tensile strength is very close to the measured value while the obtained values for uniaxial compressive strength is much less than the measured value. On the other hand, for the Hoek–Brown criterion, the obtained value for uniaxial tensile strength is higher than the measured value and the obtained values for uniaxial compressive strength is slightly less than the measured value. The failure envelopes fitted to the results of both triaxial compression extension tests are shown in Fig. 3.

Fig. 3
figure 3

The failure envelopes fitted to the results of both triaxial compression and extension tests for the synthetic rock

Full size image

Table 1 gives a summary of the results of the analyses on the synthetic rock. It can be observed that the Christensen criterion gives more accurate estimates of the uniaxial tensile strength. However, in all cases, the Hoek–Brown criterion gives closer estimates of the uniaxial compressive strength and lower values of RMSE.

Table 1 The results of application of failure criteria for the synthetic rock
Full size table

4.2 Application of the Criteria to Chert Dyke

Although the strength data for the synthetic rock were comprehensive and reliable, analyses were also carried out using careful triaxial compression tests on a highly siliceous fine grained rock known as chert dyke (Hoek 1965). This material was chosen because it is free from major geological features and is close to an ideal isotropic elastic solid (Hoek 1965). More details about the testing procedure in given by Hoek (1965).

The measured values of uniaxial compressive and tensile strength for the chert dyke are 586 and 34.5 MPa, respectively (Hoek 1965). Figure 4a shows the Christensen and Hoek–Brown failure envelopes with these measured values for the parameters. It can be observed that the Christensen failure envelope significantly underestimates the triaxial strength of the chert dyke while the Hoek–Brown envelope gives a good fit to the measured data.

Fig. 4
figure 4

The failure envelopes for the chert dyke a using the measured values, b optimized for the uniaxial compressive and tensile strength

Full size image

Using the results of triaxial compression tests, the obtained value of uniaxial compressive strength for the Christensen criterion is 865 MPa while the obtained tensile strength is zero. For the Hoek–Brown criterion, the obtained values of uniaxial compressive and tensile strength are 591 and 30.7 MPa, respectively. Figure 4b shows the Christensen and Hoek–Brown failure envelopes with these optimized values for the parameters. It can be observed that the Hoek–Brown envelope essentially has not changed. On the other hand, although the Christensen envelope is closer to the measured values, it still underestimates the triaxial compressive strength significantly. The surprising points are the zero values of uniaxial tensile strength obtained from the fitting process and the low slope of the failure envelope.

Table 2 provides a summary of the results of analyses on the chert dyke. It can be observed that in both scenarios, the Hoek–Brown criterion gives more accurate estimates of the uniaxial compressive and tensile strengths. In addition, the RMSE values for the Christensen criterion are more than double the values for the Hoek–Brown criterion.

Table 2 The results of application of failure criteria for chert dyke
Full size table

4.3 Application of the Criteria to Carrara Marble

The next set of data used in this study was obtained from careful triaxial extension tests on Carrara marble which captured the hybrid fracture and transition from extension fracture to shear fracture (Ramsey and Chester 2004). The marble is a relatively homogeneous and isotropic material with extremely low porosity and little crystal-lattice preferred orientation (Ramsey and Chester 2004). More details about the testing procedure in given by Ramsey and Chester (2004).

The measured values of uniaxial compressive and tensile strength for the Carrara marble are 94 and 6.9 MPa, respectively (Haimson and Chang 2000; Howarth and Rowlands 1987). Figure 5a shows the Christensen and Hoek–Brown failure envelopes with these measured values for the parameters. It can be observed that the Hoek–Brown criterion underestimates the triaxial extension strength and the Christensen criterion significantly overestimates it.

Fig. 5
figure 5

The failure envelopes for the Carrara marble a using the measured values, b optimized for the uniaxial compressive and tensile strengths

Full size image

Using the results of triaxial extension tests, the obtained values of uniaxial compressive and tensile strength are 70 and 8.5 MPa for the Christensen criterion and 119 and 13.2 MPa for the Hoek–Brown criterion. Figure 5b shows the Christensen and Hoek–Brown failure envelopes with these optimized values for the parameters. It can be observed that in this case, the Christensen envelope is closer to the measured data points. However, it should be noted that the slope of the Hoek–Brown envelope in intermediate to high ranges of confining pressure is very similar to that of the data points. However, the slope of the Christensen envelope in that range is not representative of the data points and it will underestimate the strength at high levels of confining pressure not included in this data set.

Table 3 gives a summary of the results of the analyses on the Carrara marble. It can be observed that in the first scenario, the Christensen criterion gives higher values of RMSE. However, in the second scenario, the Christensen criterion gives more accurate estimates of the uniaxial compressive and tensile strengths and slightly lower values of RMSE compared to the Hoek–Brown criterion.

Table 3 The results of application of failure criteria for Carrara marble
Full size table

4.4 Application of the Criteria to Westerly Granite

The final set of data used in this study is obtained from careful polyaxial tests on Westerly granite (Haimson and Chang 2000) to explore the accuracy of the Christensen criterion in polyaxial states of stresses where the intermediate principal stress varies between the major and minor principal stresses. The important properties of the granite include very low porosity, high strength, and almost complete linear elasticity, homogeneity, and isotropy (Krech et al. 1974). More details about the testing procedure in given by Haimson and Chang (2000).

The measured values of uniaxial compressive and tensile strength for the Westerly granite are 201 and 12 MPa, respectively (Johnson et al. 1987; Krech et al. 1974). Figure 6 shows the Christensen and Hoek–Brown failure envelopes with these parameters. As expected, the Christensen criterion is capable of producing the strengthening effect of the intermediate principal stress while the Hoek–Brown criterion ignores this effect. Although both criteria considerably underestimate the strength of Westerly granite, the predictions of the Christensen criterion are less accurate than those of the Hoek–Brown criterion.

Fig. 6
figure 6

The failure envelopes for Westerly granite based on measured values of uniaxial compressive and tensile strength using a the Christensen criterion, b the Hoek–Brown criterion, compared to the measured polyaxial dataset

Full size image

If the polyaxial strength data are used for determination of the parameters, the obtained value of uniaxial compressive strength for the Christensen criterion is 453 MPa while the obtained tensile strength is zero as in the case of chert dyke. For the Hoek–Brown criterion, the obtained values of uniaxial compressive and tensile strength in this case are 292 and 9.2 MPa, respectively. Figure 7 shows the Christensen and Hoek–Brown failure envelopes with these parameters. It can be observed that although the Hoek–Brown criterion does not capture the strengthening effect of the intermediate principal stress, it provides a high slope for the triaxial compression condition and gives a reasonable average strength at each level of minor principal stress. On the other hand, the Christensen criterion shows a very poor fit to the measured data. Again, the zero values of uniaxial tensile strength obtained from the fitting process and the low slope of the triaxial failure envelope are worth noting.

Fig. 7
figure 7

The failure envelopes for Westerly granite fitted to the results of polyaxial tests using a the Christensen criterion, b the Hoek–Brown criterion

Full size image

Table 4 gives a summary of the results of the analyses on the Westerly granite. It can be observed that in both scenarios, the RMSE values for the Christensen criterion are higher than those for the Hoek–Brown criterion. In addition, the obtained values of uniaxial compressive and tensile strength for the Hoek–Brown criterion are more accurate.

Table 4 The results of application of failure criteria for Westerly granite
Full size table

5 Discussion

The average values of RMSE under different scenarios for each rock type are given in Table 5. The results show that for all rock types, the RMSE values of the Christensen criterion are higher than those of the Hoek–Brown criterion. On average, the Hoek–Brown criterion is 65 % more accurate than the Christensen criterion. In addition, in all cases except for the triaxial extension of the Carrara marble, the values of the uniaxial compressive strength obtained from the fitting analyses for the Hoek–Brown criterion were more accurate than those for the Christensen criterion.

Table 5 The average error values for the Christensen criterion, RMSE Ch and the Hoek–Brown criterion, RMSE HB
Full size table

However, the results for tensile strength are more complicated. For the synthetic rock and Carrara marble, the values of tensile strength for the Christensen criterion obtained from the analyses of data were more accurate. In contrast, the fitting analyses of the results of tests on chert dyke and Westerly granite led to zero values of tensile strength for the Christensen criterion.

Another notable point is the low slope of the Christensen failure envelopes obtained for the chert dyke, Carrara marble and Westerly granite. In order to find the reason for the obtained zero values for the tensile strength and the low slopes of the failure envelopes, it is useful to derive expressions for the slopes of the failure envelopes.

The slope of failure envelope in triaxial compression can be obtained from Eq. (13) as:

$$\frac{{d\sigma_{1} }}{{d\sigma_{3} }} = 1 + \frac{{3\left( {\sigma_{c} - \sigma_{t} } \right)}}{{\sqrt {\left( {\sigma_{c} + \sigma_{t} } \right)^{2} + 12\sigma_{3} \left( {\sigma_{c} - \sigma_{t} } \right)} }}$$
(22)

It can be observed that, as expected, the slope of this failure envelope decreases with increasing minor principal stress. The initial slope at σ 3 = 0 can be calculated as:

$$\left( {\frac{{d\sigma_{1} }}{{d\sigma_{3} }}} \right)_{{\sigma_{3} = 0}} = 1 + 3\frac{{\left( {\sigma_{c} /\sigma_{t} - 1} \right)}}{{\left( {\sigma_{c} /\sigma_{t} + 1} \right)}}$$
(23)

Obviously, the initial slope increases with an increasing ratio of uniaxial compressive strength to tensile strength. However, the limit of the initial slope as this ratio tends to infinity is 4.

Following the same procedure, the slope of the failure envelope in triaxial extension can be calculated from Eq. (14) as:

$$\frac{{d\sigma_{1} }}{{d\sigma_{3} }} = 1 + \frac{{3\left( {\sigma_{c} - \sigma_{t} } \right)}}{{2\sqrt {\left( {\sigma_{c} - \sigma_{t} } \right)^{2} + 3\sigma_{3} \left( {\sigma_{c} - \sigma_{t} } \right) + \sigma_{c} \sigma_{t} } }}$$
(24)

and the initial slope at σ 3 = 0 is given by:

$$\left( {\frac{{d\sigma_{1} }}{{d\sigma_{3} }}} \right)_{{\sigma_{3} = 0}} = 1 + \frac{3}{2}\frac{{\left( {\sigma_{c} /\sigma_{t} - 1} \right)}}{{\sqrt {\left( {\sigma_{c} /\sigma_{t} - 1} \right)^{2} + \sigma_{c} /\sigma_{t} } }}$$
(25)

In the case of triaxial extension, the limit of the initial slope as the uniaxial compressive to tensile strength ratio tends to infinity is 2.5.

Hence, regardless of the ratio of uniaxial compressive strength to tensile strength, the initial slope of the Christensen failure envelope is always <4 in triaxial compression and <2.5 in triaxial extension. However, as it was shown in Figs. 4 and 7 for chert dyke and Westerly granite, the measured strength data can be along a curve with much higher slopes. In these cases, the Christensen criterion cannot capture the trend of data.

In order to put the problem in context, it is useful to determine the slope of the well-established Hoek–Brown failure envelope. The initial slope of the Hoek–Brown envelope for intact rock at σ 3 = 0 in triaxial compression and extension states of stress can be calculated from Eq. (18) as:

$$\left( {\frac{{d\sigma_{1} }}{{d\sigma_{3} }}} \right)_{{\sigma_{3} = 0}} = 1 + \frac{m}{2}$$
(26)

Substituting Eq. (20) into Eq. (26) gives:

$$\left( {\frac{{d\sigma_{1} }}{{d\sigma_{3} }}} \right)_{{\sigma_{3} = 0}} = 1 + \frac{1}{2}\left[ {\frac{{\sigma_{c} }}{{\sigma_{t} }} - \frac{{\sigma_{t} }}{{\sigma_{c} }}} \right]$$
(27)

Hence, there is no mathematical upper bound for the initial slope of the Hoek–Brown criterion.

Table 6 shows the calculated values of initial slope for the Christensen and Hoek–Brown criteria using the σ c and σ t values obtained from fitting to all strength data for each rock type. It can be seen that for the cases of chert dyke and Westerly granite, the Christensen criterion has reached the maximum values of 4 and 2.5 for triaxial compression and extension, respectively. On the other hand, the Hoek–Brown criterion has been able to produce the high initial slopes of 10.65 and 16.89 required to fit the data for the chert dyke and Westerly granite, respectively. This explains the significantly lower error values of the Hoek–Brown criterion for these rocks (Table 5).

Table 6 The initial slope of the best fit failure envelopes for different rock types
Full size table

The reason for obtaining zero values of tensile strength from fitting analyses of the strength data for chert dyke and Westerly granite is closely related to the limitation of the slope of the failure envelope for the Christensen criterion. While no tensile strength data for these rock types are used in the fitting analyses, the criterion tries to reproduce the trend of data with high slopes by decreasing the value of the tensile strength to zero. As discussed, even a tensile strength of zero, equivalent to an infinite ratio of uniaxial compressive strength to tensile strength, is not sufficient to produce the required high slopes of the failure envelopes. The reason why this problem is not encountered in fitting the triaxial compression data for the synthetic rock is that the Christensen criterion is able to reproduce the required slope for that weak material. However, this is not the case for many real rock types simply because of the inherent limitations in the formulation.

As noted above, for the synthetic rock and Carrara marble, the values of tensile strength for the Christensen criterion obtained from the analyses of data were more accurate than those of the Hoek–Brown criterion. This is because of the tension cut-off which implies the determination of tensile strength based on a few data in the tensile region rather than the whole data set. In other words, since two fitting process are required for the Christensen criterion, one for the linear tension cut-off part and one for the main parabolic part, the tensile strength obtained from the fitting process is quite accurate provided that enough data are available in the tensile region.

The results of analysis of data for Westerly granite shows an interesting point about how the Christensen and Hoek–Brown criteria handle the effect of intermediate principal stress in polyaxial loading condition. As mentioned before, while the intermediate principal stress is included in the equations of the Christensen criterion, the original form of Hoek–Brown criterion used in this study does not take into account the effect of intermediate principal stress. Considering that the strength data for Westerly granite (Fig. 7) clearly show the significant effect of intermediate principal stress on strength, it may be concluded that the Christensen criterion has an obvious advantage and can better fit the polyaxial data. However, as shown in Fig. 7, this is not the case.

Similar results have been reported by Colmenares and Zoback (2002) who conducted a comprehensive comparative study between seven different failure criteria. They showed for example that the criteria such as Mohr–Coulomb or Hoek–Brown which are independent of the intermediate principal stress can better predict the polyaxial strength of some rocks compared to the criteria which do take into account the effect of intermediate principal stress such as the Drucker-Prager (1952) criterion.

The key to understanding the reason for such seemingly surprising outcome lies in the way different criteria deal with the intermediate principal stress. The Christensen or Drucker-Prager criteria, for example, are expressed solely in terms of the stress invariants I 1 and J 2, and the σ 2 term is included in these invariants. For such criteria, the cross sections of the failure surface in the π-plane are circles. However, it is long-established that the experimentally determined π-plane representations of failure surfaces for rocks are triangular with smoothly rounded edges (e.g., Kim and Lade 1984). As an example, π-plane representations of the results of polyaxial tests carried out by Mogi (1971) on samples of Mizuho trachyte are presented in Fig. 8. It shows the experimental envelope as well as the circumscribed and inscribed Christensen envelopes fitted to triaxial compression and extension data, respectively. It can be seen that the data points are aligned on a rounded triangular failure envelope and the Christensen criterion with circular cross sections cannot adequately reproduce the trend of data.

Fig. 8
figure 8

The results of polyaxial test on Mizuho trachyte at I1 = 506 MPa, experimental envelope (rounded triangular) and the Christensen envelopes (circular)

Full size image

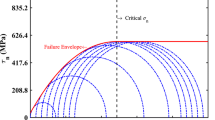
Finally, the reliability of the brittle to ductile transition condition for the Christensen criterion should be examined. As described in Sect. 2, according to the Christensen criterion the brittle or ductile behavior of a given material depends only on the volumetric stress, and there is a threshold of volumetric compressive stress above which the behavior is completely ductile. However, this contradicts the observed behavior of rocks. By studying the failure characteristics of different rock types, Mogi (1971) showed that as long as the ratio of \( \sigma_{1} /\sigma_{3} \) at failure is less than about 3.4, brittle failure occurs in triaxial compression. In other words, the brittle to ductile transition threshold of rock materials depends on the ratio of principal stresses rather than on the volumetric stress, and brittle failure is the dominant mode of failure in triaxial compression with low to intermediate levels of confining pressure.

As an example, the results of triaxial tests carried out by Schwartz (1964) on Indiana limestone are shown in Fig. 9. The measured values of uniaxial compressive and tensile strength for this rock are 41.4 and 2.5 MPa, respectively. It can be observed that the brittle to ductile transition line proposed by Mogi (1971) accurately predicts the brittle and ductile failure of Indiana limestone. On the other hand, the brittle to ductile transition condition proposed by Christensen predicts ductile mode of failure in triaxial compression with confining pressure greater than zero. Contrary to the experimental observations, the Christensen criterion makes no provision for the brittle failure of rocks under compressive stresses.

Fig. 9
figure 9

The results of triaxial test on Indiana limestone, observed behavior of rock and the brittle to ductile transition lines proposed by Mogi and Christensen

Full size image

The reason for this contradiction may be attributed to different definitions of brittle and ductile failure. The brittle failure in the context of the Christensen criterion is closely related to tensile failure and the intersection of the tension cut-off with the main failure surface. However, brittle failure in rock mechanics is related to post-failure strain softening behavior in compressive stress fields.

6 Conclusions

The Christensen criterion was discussed in detail and explicit equations were derived for biaxial, triaxial compression, triaxial extension, and polyaxial loading conditions. The results laboratory tests on a synthetic rock, chert dyke, Carrara marble and Westerly granite were used to evaluate the accuracy of the Christensen criterion compared to the well-established Hoek–Brown criterion.

On average, the Christensen criterion led to 65 % higher errors compared to the Hoek–Brown criterion. The slope of the Christensen failure envelope was found to be significantly lower than the experimental data. It was proved that the maximum initial slope for the Christensen failure envelope is 4 in triaxial compression and 2.5 in triaxial extension. However, the initial slopes of over 16 were produced by the Hoek–Brown criterion to replicate the trend of experimental data.

Although the intermediate principal stress appears in the equations of the Christensen criterion, it did not fit the polyaxial strength data of Westerly granite as well as the Hoek–Brown criterion which does not take into account the effect of intermediate principal stress. The reason for such phenomenon was discussed in terms of the circular cross sections of the Christensen failure surface in the π-plane which is inconsistent with the smooth triangular shapes obtained from experiments.

The brittle to ductile transition condition predicted by the Christensen criterion was also found to be inconsistent with the observed behavior of rocks. It was concluded that the Christensen criterion has some inherent mathematical characteristics which limits its potential for predicting the strength of rocks in compression.