On the simulation of multidimensional cyclic loading with intergranular strain

Abstract

A sample of soil is subjected to multidimensional cyclic loading when two or three principal components of the stress or strain tensor are simultaneously controlled to perform a repetitive path. These paths are very useful to evaluate the performance of models simulating cyclic loading. In this article, an extension of an existing constitutive model is proposed to capture the behavior of the soil under this type of loading. The reference model is based on the intergranular strain anisotropy concept and therefore incorporates an elastic locus in terms of a strain amplitude. In order to evaluate the model performance, a modified triaxial apparatus able to perform multidimensional cyclic loading has been used to conduct some experiments with a fine sand. Simulations of the extended model with multidimensional loading paths are carefully analyzed. Considering that many cycles are simulated ($N>30$), some additional simulations have been performed to quantify and analyze the artificial accumulation generated by the (hypo-)elastic component of the model. At the end, a simple boundary value problem with a cyclic loading as boundary condition is simulated to analyze the model response.

1 Introduction

Structures subjected to cyclic loading experience irreversible displacements resulting from the accumulated strains within the underlying soil. When the soil is fully saturated and subjected to rapid loading cycles, the resulting undrained condition is then accompanied with the reduction in the effective stresses. This event would compromise the overall stability of the structure, especially when a liquefaction zone is produced, e.g., by vibrating machines founded on soils [20, 30, 47, 48, 56] or seismic loading on structures [15, 36]. On the other hand, “slow” loading cycles under drained behavior cause irreversible displacements which may affect the long-term structure serviceability, e.g., by storage tanks [4, 13, 14] or off-shore structures [1–3, 8]. It is therefore of high importance the prediction of these undesirable events. A large number of experimental works aimed to analyze the soil behavior under cyclic loading have been performed to reproduce this complicated behavior. Two types of cyclic loading are mostly conducted on soil samples, namely one-dimensional loading and multidimensional loading [57]. The first concerns to those in which cycles are generated with the variation of a single principal component of the strain or the stress tensor, while other principal components remain constant [57]. Examples of one-dimensional loading are cyclic oedometric unloading–reloading test, cyclic undrained and drained triaxial test and cyclic shear test. These experiments have been extensively used to calibrate a vast number of constitutive models for cyclic loading, e.g., [11, 12, 35, 40, 43, 51]. On the other hand, multidimensional loading cycles are those in which two or several principal components of the strain or stress tensor are simultaneously controlled to conduct a repetitive path within the stress or strain space [57]. A closed circular loop on the stress space being several times repeated would be a particular example of this loading type. These experiments are not commonly found in the literature probably because they require more sophisticated laboratory techniques and are time-consuming. Consequently, their results are barely used to calibrate constitutive models. From the engineering perspective, this fact is very disappointing considering the three-dimensional nature of most cycles occurring in real life [7, 23, 26, 27, 44–46], or even in some boundary value problems simulating cyclic phenomena [37, 41].

Several constitutive models have been proposed in the literature to capture the accumulated strains among a number of cycles. Most of them are rate-type formulations, whereby the (effective) stress rate tensor $\dot{{\varvec{\sigma }}}$ is interrelated with the strain rate tensor $\dot{{{\varvec{\varepsilon }} }}$, as, for example, [11, 12, 17, 25, 33, 34, 40, 43, 50, 62] only to mention a few. All these models have been carefully calibrated and have shown to be very competent in many simulations. Hence, users expect them to work well on boundary value problems related to cyclic phenomena, whereby the number of cycles is still manageable under normal computational effort, e.g., $N<100$. This expectation is, however, debatable if one consider some aspects: first of all, many of these models have been calibrated with one-dimensional cyclic loading tests. Hence, it is still not known whether they perform well on the simulation of multidimensional cyclic loading. Furthermore, most of their formulations do not consider the dependence of the accumulation rate with the number of consecutive cycles as shown by many experiments. It is clear that the accumulation rate reduces for increasing number of consecutive cycles when stress loops are performed away from the critical state line [57]. Lastly, many of them exhibit artificial accumulation due to (hypo-)elastic nature of their stiffness tensor under elastic conditions. This last effect has not been properly quantified when analyzing the simulative capabilities. To the authors knowledge, a model for cyclic loading calibrated and evaluated with monotonic and multidimensional cyclic loading considering at the same time the influence of consecutive cycles in the accumulation rate has not been proposed in the literature. Furthermore, the artificial accumulation on the simulations has not been properly analyzed and quantified. It is clear that more investigation in this direction is needed.

In this work, an existing constitutive model is extended to simulate monotonic and multidimensional loading on sands accounting the effect of consecutive cycles. The reference model is based on the intergranular strain concept proposed by Niemunis and Herle [40], but following the recent formulation of Fuentes and Triantafyllidis [16, 17]. The novel interganular strain approach, also referred as intergranular strain anisotropy (ISA), is now written in an elastoplastic form to enable the description of a material elastic locus in terms of a strain amplitude. Similar to the original formulation of Niemunis and Herle [40], one can show that its mathematical structure yields to a hypoplastic equation (as in [28, 59]) when performing monotonic loading. In order to evaluate the proposed model, an experimental work has been conducted in which sand samples are subjected to multidimensional cyclic loading. Besides this, the artificial accumulation produced by the proposed model will be carefully quantified and analyzed to detect how large is its influence on the simulations. It will be shown that this component should be carefully considered under some simulations. At the end, some relevant conclusions related to the development of models for cyclic loading are given. This article is structured as follows: at the beginning, the material, the experimental testing and results are described. Subsequently, some simulations are performed and analyzed with the reference model. Then, a simple extension is proposed to improve the reference model for multidimensional loading. Finally, an example of a simple boundary value problem involving a cyclic load as boundary condition is considered to analyze the proposed development.

The notation of this article is as follows. Scalar quantities are denoted with italic fonts (e.g., a, b), second-rank tensors with bold fonts (e.g., $\mathbf {A}$, ${\varvec{\sigma }}$) and fourth-rank tensors with Sans Serif type (e.g., $\mathsf{E}, \mathsf{L}$). Multiplication with two dummy indices, also known as double contraction, is denoted with a colon “ : ” (e.g., $\mathbf {A}{:}\mathbf {B}=A_{ij}B_{ij}$). When the symbol is omitted, it is then interpreted as a dyadic product (e.g., $\mathbf {A}\mathbf {B}=A_{ij}B_{kl}$). The deviatoric component of a tensor is symbolized with an asterisk as superscript $\mathbf {A}^*$. The effective stress tensor is denoted with ${\varvec{\sigma }}$ and the strain tensor with ${\varvec{\varepsilon }}$. The Roscoe invariants are defined as $p=-\mathrm {tr}{\varvec{\sigma }}/3$, $q=\sqrt{3/2}\parallel {\varvec{\sigma }}^*\parallel$, $\varepsilon _v=-\mathrm {tr}{{\varvec{\epsilon }}}$ and $\varepsilon _s=\sqrt{2/3}\parallel {{\varvec{\epsilon }}}^*\parallel$.

2 Tested material and experimental procedure

The experiments conducted in this work are aimed to analyze the behavior under multidimensional cyclic loading. The employed material corresponds to the Karlsruhe fine sand with the following properties: the mean grain size $d_{50}$ and the uniformity coefficient $C_u=d_{60}/d_{10}$ are equal to $d_{50}=0.14$ mm and $C_u=1.5$, respectively. The grain shape is subangular, and the minimum and maximum void ratios are $e_\mathrm{min}=0.677$ and $e_{\max }=1.054$, respectively. A solid density equal to $\rho _s=2.65$ g/cm$^3$ has been determined. The grain size distribution curve of the Karlsruhe fine sand is presented in Fig. 1.

Fig. 1

Grain size distribution of the Karlruhe fine sand

Fig. 2

Components of the modified triaxial apparatus for multidimensional loading

The experimental procedure is described in the following lines. A modified triaxial apparatus able to perform multidimensional cyclic loading has been employed for all experiments. The components of the device are depicted in Fig. 2. The vertical force is applied through a vertical propulsion system placed on the bottom which moves the base plate of the sample. The applied vertical force is measured above the top plate of the specimen. The controller for the cell pressure is dynamic and able to apply cyclic loading with frequencies up to 0.5 Hz. A special software is responsible for the loading control and able to perform monotonic, sinusoidal and customized cyclic loading.

The samples show a diameter equal to 10 cm and a height equal to 20 cm. They are pluviated out of a funnel into the split mold under dry state. A thin film of grease is applied on the end plates (Fig. 3a) to reduce the interface friction and to achieve homogeneous distribution of the applied stress. The employed sample membrane is thin (thickness $t_M=0.3$ mm) to reduce the membrane effect. It was pulled over the specimen base plate and sealed on the end plates with O-rings (Fig. 3c). Subsequently, the split molds (Fig. 3d) are assembled and the dry sand is pluviated into the molds. Once the sample is prepared, the membrane is sealed to the top cap using O-rings and the specimen is stabilized through vacuum (Fig. 3e). During this procedure, the top cap is fixed with a special metallic device to avoid loading the sample and causing inhomogeneities. Then, the molds are removed and the geometry of the sample is carefully measured. Once the sample is ready, the triaxial cylinder is assembled and the cell is filled with water. Lastly, the vacuum within the specimen is gradually replaced with the cell pressure in order to keep the effective stress constant. Membrane penetration effects are neglected due to the small size of the sand particles [58].

Fig. 3

Preparation of a specimen for a cyclic triaxial test a latex membrane at the end plates, b latex membrane (thickness $t_M=0.3$ mm) sealed with O-rings, c, d split molds, e stabilized specimen by vacuum of 30 kPa, f Plexiglas cylinder, g and h specimen top cap

Samples were initially flushed with carbon dioxide (CO$_2$) and subsequently saturated with distilled water with a backpressure of $p_{w0}=500$ kPa. A B-value greater than $B\ge 0.98$ was always obtained after this procedure. Specimens were then consolidated till the desired effective stress $\sigma _3$ is achieved. Subsequently, the sample is loaded as under conventional drained triaxial conditions till the start stress point ($\sigma _{10}$, $\sigma _{30}$) of the loading path is reached. Finally, the cyclic loading is applied through the control of the principal stresses $\sigma _{1}$ and $\sigma _{3}$. The details of the applied loading paths are provided within the following section.

3 Description of the conducted loading paths

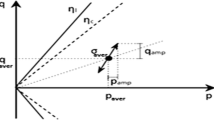
The tested loading paths are closed stress loops, having elliptical or flower-shaped form within the space of the invariants $P=\sqrt{3} p$ versus $Q=\sqrt{2/3}q$. The stress loops are performed under triaxial conditions by controlling the two principal components of the stress tensor ($\sigma _1$ and $\sigma _2=\sigma _3$). An example of multidimensional cyclic loading under triaxial conditions is depicted in Fig. 4.

Fig. 4

Example of multidimensional loading under triaxial conditions: axial and radial effective stresses. They are simultaneously controlled to perform a multidimensional loading

For this work, three different loading cases have been conducted and are shown in Fig. 5. The names of the loading cases follow from their shape in the P versus Q space and correspond to “small circle,” “big circle” and “flower” test. Their description is as follows:

• Small circle stress closed path with circular shape in the P versus Q space, with center $P=200 \sqrt{3}$ and $Q=100 \sqrt{2/3}\,\hbox {kPa}$ (or $p=200\,\hbox {kPa}$ and $q=100\,\hbox {kPa}$) and radius equal to 20 kPa. The loop is performed clockwise (see Fig. 5a).

• Big circle similar to the small circle but with radius equal to 40 kPa. The loop is performed counterclockwise (see Fig. 5a).

• Flower a flower-shaped loop with center $P=200 \sqrt{3}$ and $Q=100 \sqrt{2/3}\,\hbox {kPa}$ (or $p=200\,\hbox {kPa}$ and $q=100\,\hbox {kPa}$). While the size of the petals is comparable to the small circle, the size of the circle formed by points at the center of each petal is comparable to the big circle. The petals are performed clockwise, and the flower is performed counterclockwise (see Fig. 5b; Table 1).

Fig. 5

Cyclic loading paths considered within this work. a “Flower” test, b “big circle” test (blue) and “small circle” test (red) (color figure online)

Table 1 Description of the loading cases

For the description of the loading cases, a parametric representation of the desired curve is defined through the invariants Q and P as functions of time t with the following general form:

$$\begin{aligned} F(t) =F_0 + A_{1}\sin \left( \frac{2\pi }{T}N_{1}t + \theta _1\right) + A_{2}\sin \left( \frac{2\pi }{T}N_{2}t+\theta _2\right) \end{aligned}$$

(1)

whereby F is the stress invariant of interest ($=Q$ or P), t is the time, $F_0$ represents the magnitude of F at a reference time, $A_{1}$ and $A_{2}$ control the amplitudes, $N_{1}$ and $N_{2}$ control the frequencies, $\theta _1$ and $\theta _2$ are the phases and T is the time of a cycle (period). Particularly, the small circle is described through the parametric functions:

$$\begin{aligned} P(t)&= 200\sqrt{3} + 20 \sin \left( \frac{2\pi }{200}t + \pi /2\right) \nonumber \\ Q(t)&=100\sqrt{2/3} + 20 \sin \left( \frac{2\pi }{200}t\right) \end{aligned}$$

(2)

Notice that a circular shape is achieved through the use of a single term in Eq. 1, i.e., $A_2=0$. Similarly, for the big circle test the following parametric representation is used:

$$\begin{aligned} P(t)&=200\sqrt{3} + 40 \sin \left( \frac{2\pi }{200}10 t\right) \nonumber \\ Q(t)&= 100\sqrt{2/3} + 40 \sin \left( \frac{2\pi }{200}10t + \pi /2\right) \end{aligned}$$

(3)

Finally, the parametric representation of the flower test reads:

$$\begin{aligned} P(t)&=200\sqrt{3} + 40 \sin \left( \frac{2\pi }{200}t + \pi /2\right) + 20 \sin \left( \frac{2\pi }{200}10 t\right) \nonumber \\ Q(t)&= 100\sqrt{2/3} + 40 \sin \left( \frac{2\pi }{200}t\right) + 20 \sin \left( \frac{2\pi }{200}10t + \pi /2\right) \end{aligned}$$

(4)

In cyclic behavior, it is convenient to analyze the trend of a variable among the number cycles N. For this purpose, some plots show only the points at the end of each cycle. An arbitrary variable $\cup$ evaluated with this method is denoted with the superindex $\cup ^\mathrm{acc}$ and referred as “accumulated $\cup$,” e.g., $\varepsilon _1^\mathrm{acc}$ represents the accumulated vertical strain, see the example in Fig. 6. The resulting curve is often called “average curve” or “accumulated curve.”

Fig. 6

Example of the computation of the accumulated vertical strain $\varepsilon ^\mathrm{acc}_1$

All the conducted stress loops, namely the small circle, big circle and flower test, present a center at $p=200\,\hbox {kPa}$ and $\eta =q/p=0.5$. The experimental results for the tree different loading cases are given in Fig. 7.

Fig. 7

Experimental results for: a–c “small circle path,” d–f “big circle path,” g–i “flower path”

4 Description of the ISA + hypoplasticity model (ISA + HP)

The current work selects as constitutive model the hypoplastic model by Wolffersdorff [59] rewritten according to the ISA-plasticity constitutive platform [16, 17]. Hereinafter, this model is refereed as the ISA + HP model (ISA + hypoplasticity). The model is aimed to simulate the behavior of sands under monotonic and cyclic loading. A brief description of the model is given in the following lines.

The hypoplasticity alone can be considered as a family of constitutive models capable of simulating the mechanical behavior of soils under monotonic loading [28, 37]. The literature offers several versions of hypoplasticity for sands [6, 28, 37, 59, 60] and also for clays [22, 31, 55]. The performance of hypoplasticity in engineering problems has been also studied [29, 49]. Detailed discussion of these models is out of the scope of the present work but can be found in [18, 37, 61]. One of the most used hypoplastic constitutive models is the one proposed by Wolffersdorff, probably due to its availability as material subroutine for different finite element softwares, e.g., Tochnog, Plaxis or Abaqus and to its performance in different applications [37]. Among many features, the model can simulate some experimental observations, such as the maximum and minimum void ratio [6], a Matsuoka–Nakai critical state surface within the stress space [32] and a dilatancy–contractancy behavior according to the material state (density and pressure). The general constitutive equation can be rewritten as:

$$\begin{aligned} \dot{{\varvec{\sigma }}}=\bar{\mathsf{E}}:(\dot{{{\varvec{\varepsilon }} }}- \dot{\bar{{\varvec{\varepsilon }}}}^p) \end{aligned}$$

(5)

whereby $\bar{\mathsf{E}}$ is the “linear ”stiffness tensor [59] and $\bar{{\varvec{\varepsilon }}}^p$ is the hypoplastic strain rate. In contrast to elastoplastic models, the hypoplastic strain rate $\bar{{\varvec{\varepsilon }}}^p$ is always active, i.e., $\parallel \dot{\bar{{\varvec{\varepsilon }}}}^p \parallel >0$, because the model lacks of a yield surface. Therefore, it cannot be directly interpreted as the plastic strain rate $\dot{{{\varvec{\varepsilon }}}}^p$. A summary of the constitutive equations of this model is provided in Appendix 1 and are explained with more details in [59].

It is well known that simulations with hypoplasticity (Eq. 5) show good agreement with the material behavior under monotonic loading, but delivers an excessive plastic accumulation (ratcheting) upon cyclic loading [18, 40]. In order to encompass this shortcoming, the constitutive equation can be rewritten according to the ISA constitutive platform [17]. This recent formulation introduces a yield surface in terms of a strain amplitude and simulates some small strain effects, such as the increase in stiffness after reversal loading and the reduction in the plastic strain rate. The intergranular strain is actually a state variable, originally proposed by Niemunis and Herle [40], which provides information about the recent strain history. It is therefore able to detect whether the material has been subjected to monotonic or cyclic loading. Its mechanism is simple and can be easily illustrated as follows.

Consider the following 1D evolution equation of the intergranular strain h:

$$\begin{aligned} \dot{h}=R\dot{\varepsilon }-h{\mid } \dot{\varepsilon }{\mid } \end{aligned}$$

(6)

whereby R is a material parameter bounding the intergranular strain, i.e., ${\mid } h {\mid } \le R$. This evolution equation implies that the intergranular strain grows in the direction of $\dot{\varepsilon }$ till the bounding condition ${\mid } h {\mid } \le R$ is reached. Hence, if one performs 1D cycles with increasing strain amplitude, as shown in Fig. 8, the intergranular strain h evolves toward the direction of the current strain rate, denoted as $h \sim \mathrm{sign}(\dot{\varepsilon })$, while its rate $\dot{h}$ decreases when approaching to the limit ${\mid } h {\mid } = R$ (red lines in Fig. 8b). The bounding condition ${\mid } h {\mid } \le R$ (red lines in Fig. 8b) is only reached after performance of a large strain amplitude, or equivalently after monotonic loading. Hence, if h lies at the limit and in the same direction of the strain rate $\dot{\varepsilon }$, i.e., $h=R \mathrm{sign}(\dot{\varepsilon })$, the material has experienced monotonic loading. This particular state is also called “mobilized state” [17]. On the other hand, if ${\mid } h {\mid } = R$ but the strain rate $\dot{\varepsilon }$ points in the opposite direction, i.e., $h\approx -R \mathrm{sign}(\dot{\varepsilon })$, then a reversal loading can be detected. In that case, small strain effects, such as increase in the stiffness and reduction in the plastic strain rate, should be considered by the model. This can be regarded as the basic idea of the intergranular strain approach.

Fig. 8

One-dimensional example of the behavior of the intergranular strain. a Strain (input) versus time, b resulting intergranular strain according to Eq. 6 (color figure online)

Two different intergranular strain approaches are encountered in the literature, namely the version of Niemunis and Herle [40] and the recently proposed “ISA”-plasticity by Fuentes and Triantafyllidis [17]. The main difference is, that in contrast to the ISA plasticity [17], the first formulation [40] lacks of an elastic locus. For simulations with multidimensional cyclic loading, the existence of an elastic locus is essential because it allows to control the elastic threshold strain wherein no plastic accumulation occurs and the secant shear modulus remains constant [42]. Some details of the ISA plasticity are provided in the next section.

4.1 Description of the ISA plasticity

The ISA plasticity proposes a yield surface within the intergranular strain space to describe the elastic locus of the material in terms of a strain amplitude. This amplitude is denoted by $\parallel \Delta {\varvec{\varepsilon }}\parallel =R$ and defined by the user, e.g., $R= 5 \times 10^{-5}$, such that cycles having strain amplitudes lower than $\parallel \Delta {\varvec{\varepsilon }}\parallel < R$ deliver an elastic response.

As mentioned before, the main objective of the intergranular strain $\mathbf {h}$ is to provide information about the recent strain history. Similarly to the 1D version from Eq. 6, this state variable is proposed to evolve with the strain rate $\dot{{{\varvec{\varepsilon }} }}$ independently of the stress tensor ${\varvec{\sigma }}$. Its evolution equation according to ISA is more complicated than the 1D version to incorporate the elastic locus: it is based on an elastoplastic relation considering a yield surface within the intergranular strain space. The yield function is denoted with $F_H=F_H(\mathbf {c},\mathbf {h})$, whereby $\mathbf {c}$ is an additional hardening variable defined in the sequel. The following statements are considered for the formulation of the intergranular strain equation:

• Under elastic conditions $F_H<0$, the intergranular strain evolves identically as the strain $\dot{\mathbf {h}}=\dot{{{\varvec{\varepsilon }} }}$. With simpler words, under elastic conditions, an increment of the strain produces an identical increment of the intergranular strain $\Delta {\varvec{\varepsilon }}=\Delta \mathbf {h}$.

• At plastic conditions $F=0$, the intergranular strain evolves with a slower rate than under elastic conditions. Its rate $\dot{\mathbf {h}}$ decreases as it approaches to its bounding condition $\mathbf {h}=R\overrightarrow{\dot{{{\varvec{\varepsilon }} }}} \Leftrightarrow \dot{\mathbf {h}}=\mathbf {0}$.

The aforementioned conditions are suitably considered though the following evolution equation:

$$\begin{aligned} \dot{\mathbf {h}}=\dot{\varvec{\epsilon }}-\dot{\lambda }_H \mathbf {N}\end{aligned}$$

(7)

whereby $\lambda _H \ge 0$ is the consistency parameter (or plastic multiplier) and $\mathbf {N}$ is the flow rule ($\parallel \mathbf {N}\parallel =1$) considered as associative (normal to the yield surface). Obviously, the consistency parameter is equal to $\lambda _H=0$ under elastic conditions.

In order to relate the elastic locus with a small strain amplitude, the ISA formulation chooses a spherical yield surface $F_H=0$ within the principal space of the intergranular strain. The yield function reads:

$$\begin{aligned} F_H=\parallel \mathbf {h}-\mathbf {c}\parallel -\frac{R}{2} \end{aligned}$$

(8)

whereby R is the material parameter describing the maximum elastic strain amplitude and $\mathbf {c}$ is the hardening tensor describing the center of the surface. Considering that under elastic conditions the relation $\Delta {\varvec{\varepsilon }}=\Delta \mathbf {h}$ holds, the yield surface can be directly interpreted with a specific strain amplitude $\parallel \Delta {\varvec{\varepsilon }}\parallel =R$. This surface turns simply into a circle when plotting it within the space of the invariants $h_v=-{\text {tr}}(\mathbf {h})$ and $h_s=\sqrt{2/3}\Vert \mathbf {h}^*\Vert$ where $\mathbf {h}^*$ is the deviatoric intergranular strain, see Fig. 9. Its center $\mathbf {c}$ is also called the backintergranular strain due to its similarity with backstress tensors in conventional elastoplasticity [24].

The bounding surface limits the space wherein the intergranular strain may exist, i.e., $\mathbf {h}$ cannot lie outside of this surface. Its shape is also (hyper-)spherical and described through the function:

$$\begin{aligned} F_{Hb}=\parallel \mathbf {h}\parallel -R \end{aligned}$$

(9)

Fig. 9

Adapted from Fuentes [16]

Yield and bounding surface of the intergranular strain $\mathbf {h}$.

The formulation of the plastic component in Eq. 7 is based on some simple bounding surface plasticity relations to fulfill the condition $\parallel \mathbf {h}\parallel \le R$, see Eq. 9. For this purpose, an image of the tensor $\mathbf {c}$ is projected at the bounding surface and denoted with $\mathbf {c}_b$ according to the following mapping rule:

$$\begin{aligned} \mathbf {c}_b=(R/2)\overrightarrow{\dot{{{\varvec{\varepsilon }} }}} \end{aligned}$$

(10)

Having this, the hardening function $\bar{\mathbf {c}}=\dot{\mathbf {c}}/{\dot{\lambda }}$ is proposed such that the rate of $\mathbf {c}$ decays when $\mathbf {c}$ approaches to $\mathbf {c}_b$. The hardening function reads:

$$\begin{aligned} \bar{\mathbf {c}}=\beta _h(\mathbf {c}_b-\mathbf {c})/R\quad {\text with}\quad \dot{\mathbf {c}}=\dot{\lambda }_H{\bar{\mathbf {c}}} \end{aligned}$$

(11)

From the consistency equation $\dot{F_H}=0$, the expression for the consistency parameter $\dot{\lambda }_H$ is derived:

$$\begin{aligned} \dot{\lambda }_H=\dfrac{\langle \mathbf {N}:\dot{\varepsilon }\rangle }{1-\left( \dfrac{\partial F_H}{\partial \mathbf {c}}\right) :\bar{\mathbf {c}}} \end{aligned}$$

(12)

The ISA formulation permits to detect whether small strain effects should be considered. Similar to the 1D analysis, if the bounding condition $\mathbf {h}=R \overrightarrow{\dot{{{\varvec{\varepsilon }} }}}$ is reached, it is understood that the material has recently experienced monotonic loading $(\parallel \Delta {\varvec{\varepsilon }}\parallel \ge 10^{-3})$. Under this event, no small strain effects such as increase in the stiffness or reduction in plastic strain rate should be simulated by the model. The particular case is referred as “mobilized state” as in the 1D version. On the other hand, if the material has recently performed cyclic loading, the intergranular strain would lie somewhere within the bounding surface. In that case, small strain effects should be certainly simulated. To consider all these observations, a projection of the intergranular strain at the bounding surface is performed under the consideration of the following mapping rule:

$$\begin{aligned} \mathbf {h}_b= R\mathbf {N}\end{aligned}$$

(13)

where $\mathbf {h}_b$ is the projection and $\mathbf {N}\approx \overrightarrow{\dot{{{\varvec{\varepsilon }} }}}$ under mobilized states. Thus, while the case $\parallel \mathbf {h}_b-\mathbf {h}\parallel =2R$ means that a reversal loading path has been initialized, the case $\parallel \mathbf {h}_b-\mathbf {h}\parallel =0$ means that the mobilized state has been reached. Considering the aforementioned statement, a suitable scalar function $\rho$ is defined to detect how close is the current state to the mentioned cases and is defined as:

$$\begin{aligned} \rho =1-\dfrac{\Vert \mathbf {h}_b-\mathbf {h}\Vert }{2R} \end{aligned}$$

(14)

In this manner, $\rho =0$ implies reversal loading, while $\rho =1$ implies “mobilized states.” In the next section, the mechanical model will be briefly described.

4.2 Description of the mechanical model

The mechanical model relates the (effective) stress rate $\dot{{\varvec{\sigma }}}$ with the strain rate $\dot{{{\varvec{\varepsilon }} }}$ through a constitutive equation. The constitutive equation is elastoplastic and consistent with the formulation of the intergranular strain. Thus, an elastic response of the intergranular strain is accompanied with an elastic response of the mechanical model. Similarly, a plastic response is simultaneously delivered by both models as well. The mathematical structure of the ISA formulation has been proposed to enable the simulation of the small strain effects by increasing the stiffness and reducing the plastic strain rate through the incorporation of some scalar functions:

$$\begin{aligned} \dot{\varvec{\sigma }}=m\bar{\mathsf{E}}:(\dot{{{\varvec{\varepsilon }} }}-y_h \dot{\bar{\varvec{\varepsilon }}}^p) \end{aligned}$$

(15)

where m and $y_h$ are scalar functions and $\bar{\mathsf{E}}$ and $\dot{\bar{\varvec{\varepsilon }}}^p$ are now called “mobilized” stiffness tensor and “mobilized” plastic strain rate, respectively, and follow the relations of the Wolffersdorff hypoplastic model, see Appendix 1. The factor $y_h$ guarantees the continuity between the elastic and plastic response and reduces the plastic strain rate upon cyclic loading. This function is defined as:

$$\begin{aligned} y_h=\rho ^{\chi }\langle \mathbf {N}:\overrightarrow{\dot{{{\varvec{\varepsilon }} }}} \rangle \end{aligned}$$

(16)

where $\chi$ is an exponent considered as material parameter. Notice that if $y_h=0$, the behavior is elastic, whereas $y_h=1$ delivers the maximum plastic strain rate for a given state (${\varvec{\sigma }},e$). Hence, somehow the scalar $y_h$ expresses the plastic intensity of the material.

On the other hand, the scalar factor m is responsible for the stiffness increase after reversal loading. The formulation allows to define a maximum factor of $m=m_R>1$ which is rendered under elastic conditions $y_h=0$. Under mobilized states $y_h=1$, the model adopts the value of $m=1$. Therefore, a simple interpolation function is adopted for m:

$$\begin{aligned} m=m_R+(1-m_R)y_h \end{aligned}$$

(17)

One can show that under the elastic condition $F_H<0$, the scalar factor gives $y_h=0$ and the constitutive model reduces to:

$$\begin{aligned} \dot{{\varvec{\sigma }}}=m_R \bar{\mathsf{E}}:\dot{{{\varvec{\varepsilon }} }}\quad \quad \text{(under elastic conditions}\;F_H<0) \end{aligned}$$

(18)

The consideration of all the mentioned statements allows to illustrate schematically the behavior of the ISA model upon a secant shear stiffness degradation curve, as shown in Fig. 10. In this figure, the behavior of the ISA model is compared to a sketch of a typical experimental curve. The secant shear stiffness $G^\mathrm{sec}$ is normalized with respect to the maximum shear stiffness $G^{\max }$ for the sake of simplicity. At the beginning, when the strain amplitude is lower than R, elastic conditions are obtained and a constant stiffness is simulated through the relation $\dot{{\varvec{\sigma }}}=m_R \bar{\mathsf{E}}:\dot{{{\varvec{\varepsilon }} }}$, see Eq. 18. Subsequently, when the strain amplitude is larger than R, the model simulates a transition regime whereby the scalar factors deliver $y_h<1$ and $m>1$. When the strain amplitudes are large enough and reach the mobilized state, the scalar factors render $y_h=1$ and $m=1$ and the constitutive equation turns into hypoplastic $\dot{\varvec{\sigma }}=\bar{\mathsf{E}}:(\dot{{{\varvec{\varepsilon }} }}-\bar{\dot{{{\varvec{\varepsilon }} }}}^p)$.

Fig. 10

Schematic illustration of the ISA + HP model peformance in a secant shear modulus degradation curve. For cycles under small strain amplitudes $\parallel \dot{\varepsilon }\parallel <R$, the behavior is (hypo-)elastic. At mobilized states, the constitutive equation turns into hypoplastic. Between these two states, a smooth transition is simulated trough the functions $0\le m\le m_R$ and $0\le y_h\le 1$

4.3 Numerical integration and material parameters

The numerical implementation is based on a substepping scheme whereby very small strain subincrements $\Delta \varepsilon \approx 10^{-5}$ are applied to achieve numerical convergence. The programming code was written in Fortran under the syntax of the material subroutine UMAT of the software Abaqus Standard. The numerical integration was performed with a modified version of the software Incremental Driver [38]. This software is fully compatible with the subroutine UMAT and allows their numerical integration without using the software Abaqus Standard. Some modifications were made by the authors to the software Incremental Driver to enable the simulation of multidimensional cyclic loading paths.

The parameters of the ISA + HP model can be grouped in those from the hypoplastic model by Wolffersdorff [59] and those rising from the ISA plasticity [17]. The first set from the Wolffersdorff Hypoplasticity are in total 8 parameters, namely $h_s$, $n_B$, $e_{i0}$, $e_{c0}$, $e_{d0}$, $\alpha$ and $\beta$ and are briefly described in Appendix 2. These parameters can be calibrated with monotonic tests such as oedometric and triaxial tests. Details for their determination can be found in the work of Herle and Gudehus [21], while an explanation of their physical meaning can be found in the work of Niemunis [37]. The parameters of the Karlsruhe fine sand were previously calibrated in the work of Triantafyllidis et al. [52], and the reported values are adopted for the simulations within this work. Some simulations of monotonic undrained triaxial tests are presented at the end of this section to evaluate the performance of the reported parameters.

The ISA-plasticity parameters are in total four, namely $m_R$, R, $\beta _h$ and $\chi _h$. In general, these parameters can be fitted to data of cyclic triaxial experiments following the brief description given in Appendix 2. Additional details for their determination can be found in [17]. The values adopted for this work correspond to those calibrated in [16] for the Karlsruhe fine sand, except for the parameter $\beta _h$ which has been herein recalibrated to simulate a larger effect of the intergranular strain. This parameter controls the strain amplitude needed to reach mobilized states $y_h=1$, or in other words, the strain amplitude wherein the intergranular strain effects are active. In all the experiments, the deviatoric strain amplitudes were lower than $\Delta \varepsilon _s< 2\times 10^{-3}$. Using the recommended equation from Appendix 2, $\beta _h=\left( \sqrt{6}R(\log (4)-2\log (1-r_h))\right) /\left( 6\Delta \varepsilon _s-\sqrt{6} R(3+r_h)\right)$ with $\Delta \varepsilon _s= 2\times 10^{-3}$ and $r_h=0.99$ renders $\beta _h\approx 0.35$. The last value is adopted as parameter for the current work.

Table 2 summarizes the parameters of the ISA + HP model. For each of them, the units, suggested range and some useful experiments for their determination are also recommended. The suggested range and the useful experiments follow from the experience of the authors after calibrating different sands.

Table 2 Material constants of the ISA + HP model

The predictive capabilities of the constitutive model under monotonic behavior were checked through the simulation of undrained triaxial tests with Karlsruhe fine sand, as shown in Fig. 11. The experiments include triaxial compression and extension paths for different void ratios $e=${0.819, 0.742, 0.814, 0.946, 0.827, 0.853} and confining pressures $p_0=\{100, 200\}\,\hbox {kPa}$. Six undrained triaxial paths named from A1 to A6 were considered for simulation purposes as shown in Fig. 11. One may check with these simulations the performance of the 8 parameters of the Wolffersdorff hypoplastic model considering that no cyclic loading has been performed. Although some small discrepancies can be observed, in general the monotonic behavior is fairly well simulated.

Summary of constitutive relations

Constitutive equation

$\dot{\varvec{\sigma }}=m\bar{\mathsf{E}}:(\dot{{{\varvec{\varepsilon }} }}-y_h \dot{\bar{\varvec{\varepsilon }}}^p)$

with the scalar functions according to ISA plasticity:

$\begin{array}{ll} m=m_R+(1-m_R)y_h&{} \text {(function to increase stiffness upon cycles)}\\ y_h= \rho ^{\chi }\langle \mathbf {N}:\overrightarrow{\dot{{{\varvec{\varepsilon }} }}} \rangle &{}\text {(function to reduce plastic strain rate upon cycles)} \end{array}$

and the hypoplastic relations by Wolffersdorff [59] for mobilized states:

$\begin{array}{ll} \bar{{\mathsf{E}}}=f_{b}f_{e}\frac{1}{\hat{{\varvec{\sigma }}} {:}\,\hat{{\varvec{\sigma }}}} (F^2{\mathsf{I}}+a^2\hat{{\varvec{\sigma }}}\hat{{\varvec{\sigma }}})&{}\text {(Mobilized stiffness, hypo-elastic relation by [59])} \\ \dot{\bar{\varvec{\varepsilon }}}^p=-\bar{{\mathsf{E}}}^{-1} : \bar{{\mathbf {N}}} \parallel \dot{{{\varvec{\varepsilon }} }}\parallel &{}\text {(Mobilized plastic strain rate)}\\ \bar{\mathbf {N}}=f_{{d}}f_{{b}}{f}_{e}\dfrac{Fa}{\hat{{\varvec{\sigma }}}:\hat{{\varvec{\sigma }}}}(\hat{{\varvec{\sigma }}}+\hat{{\varvec{\sigma }}}^*)&{} \text {(non-linear hypoplastic stiffness [59])}\\ \end{array}$

Other relations defined in Appendix 1 and Sect. 4.1.

Yield surface

$F_H=\parallel \mathbf {h}-\mathbf {c}\parallel -\dfrac{R}{2}$

Evolution equation for the internal variables

$\begin{array}{ll} \dot{\mathbf {h}}=\dot{\varvec{\epsilon }}-\dot{\lambda }_H \mathbf {N}&{} \text {(evolution of intergranular strain)}\\ \dot{\mathbf {c}}=\dot{\lambda }_H \beta _h(\mathbf {c}_b-\mathbf {c})/R& \text {(evolution of the center of the yield surface) }\\ \end{array}$

with the Kuhn–Tucker conditions $\dot{\lambda }_H\ge 0$, $F_H \le 0$ and $\dot{\lambda }_H F_H=0$

Extension to the plastic accumulation rate under consecutive cycles

$\begin{array}{ll} \dot{\varepsilon }_a=\dfrac{C_a}{R}(1-y_h-\varepsilon _a)\parallel \dot{{\varvec{\varepsilon }}}\parallel &{} \text {(evolution of internal variable for cyclic history)}\\ &{}\\ \chi =\chi _0+{\varvec{\varepsilon }}_a(\chi _\mathrm{max} -\chi _0)& \text {(modification to exponent of intergranular strain effect) }\\ \end{array}$

Details of this extension are given in Sect. 6, see Eqs. 19 and 20

Fig. 11

Simulations of undrained triaxial tests for the calibration of parameters under monotonic loading

5 Simulations with the ISA + HP model and evaluation of its artificial accumulation

The experiments described in Sect. 3, namely the “small circle test,” “big circle test” and “flower test,” are in this Section simulated. The ISA + HP model is employed using the parameters of Table 2. Besides this, it is also of interest the quantification of the artificial accumulation due to the large number of cycles. Two cases of simulations are therefore considered in the present analysis:

• Case 1 the constitutive model corresponds to the ISA + HP model according to the relations explained in Sect. 4.

• Case 2 the constitutive model corresponds to the (hypo-)elastic component of the ISA + HP model. The model is expressed according to Eq. 18 whereby $\dot{{\varvec{\sigma }}}=m_R\bar{\mathsf{E}} :\dot{{{\varvec{\varepsilon }} }}$.

The simulations are shown in Fig. 12 (blue lines) and compared to the average curves (accumulated curves) of the experiments (red lines). It is recalled that “average curve” means that a point at the end of each cycle is plotted, as shown in Fig. 6. As mentioned before, the experimental results show a drastic reduction in the accumulation rate for increasing number of cycles N, see, for example, the results in Fig. 7. Unfortunately, this reduction is not simulated by the ISA + HP model (case 1). Instead, the model simulates an excessive accumulation rate which seems not to be reduced with the increasing number of cycles N. This fact shows a weakness of this formulation when dealing with a number of cycles and motivates to propose an extension of the model described in the next section.

Fig. 12

Case 1: Simulations with conventional ISA + HP model (color figure online)

Fig. 13

Case 2: Simulations with (hypo-)elastic model. Evaluation of the artificial accumulation (color figure online)

The artificial accumulation of the ISA + HP model is evaluated through the simulations of case 2. The source of the artificial accumulation comes from the (hypo-)elastic nature of tensor $\bar{\mathsf{E}}$ which depends on the stress ${\varvec{\sigma }}$ and the void ratio e, i.e., $\bar{\mathsf{E}}=\bar{\mathsf{E}}($ ${\varvec{\sigma }}$, e). The simulations show whether the resulting artificial accumulation is negligible or not. The simulations are plotted in Fig. 13 and once more compared to the average curves of the experiments (red lines). The results in Fig. 13 show that the accumulation exhibited by the (hypo-)elastic relation is not negligible compared to the experiment. In fact, the artificial accumulation of the small circle produces a larger reduction in the void ratio compared to the experimental curve. This is a very important or even disappointing result, since many constitutive models claiming to simulate well the cyclic behavior of sands are based on (hypo-)elastic relations which might produce a similar result. Notice that the artificial accumulation of the void ratio e presents a contractive behavior in the case of the small circle and the flower test, but a dilative (expansive) behavior in the case of the big circle. This is of course attributed to the polarization of the loading path (clockwise or counterclockwise) which do not agree with experimental observations.

In the following section, an extension to the ISA + HP model will be proposed to simulate the reduction in the plastic accumulation with increasing number of cycles for the given experiments.

6 Extended model for the simulation of multidimensional cyclic loading

According to the experiments, when the number of cycles N increases, and the current stress ${\varvec{\sigma }}$ lies away from the critical state surface, the rate of the plastic accumulation reduces. In other words, for a given strain amplitude, the plastic accumulation rate depends not only on the average stresses ${\varvec{\sigma }}^\mathrm{ave}$ and void ratio e, but also on the number of cycles previously performed. Defining a variable which counts the number of consecutive cycles is not feasible considering the three-dimensional nature of the current modeling framework. Furthermore, under multidimensional cyclic loading, the definition of a cycle or even an amplitude is not very clear because the loading paths may be smooth and no reversal points can be identified. Therefore, another strategy is herein followed to extend the ISA formulation toward the simulation of this effect.

An additional state variable is introduced to identify paths whereby the material remains under cyclic loading during a larger time period. The new variable would identify whether the soil has recently experienced a few or several consecutive cycles. The provided information is then considered by the model to decrease the plastic accumulation rate according to the experiments. The new state variable is denoted with $\varepsilon _a$ and is proposed to be bounded by the values $0\le \varepsilon _a \le 1$. If $\varepsilon _a\approx 0$, the model assumes that the material has experienced monotonic loading or only a few consecutive cycles. On the other hand, if $\varepsilon _a\approx 1$, it means that the model has performed a large number of consecutive cycles and a reduction in the plastic accumulation should be rendered. To achieve this, the following evolution equation is proposed:

$$\begin{aligned} \dot{\varepsilon }_a=\dfrac{C_a}{R}(1-y_h-\varepsilon _a)\parallel \dot{\varvec{\epsilon }}\parallel \end{aligned}$$

(19)

whereby $C_a$ is a new material parameter controlling the rate of $\varepsilon _a$ and $y_h$ is the scalar factor defined in Eq. 16. The desired behavior of the variable $\varepsilon _a$ is achieved because the scalar function gives $y_h=0$ under elastic conditions and $y_h=1$ upon monotonic loading.

The information of $\varepsilon _a$ is now considered in the mechanical model. The main idea is to increase the intergranular strain effect for increasing values of $\varepsilon _a\rightarrow 1$. It is known that increasing values of $\chi$ (see Eq. 16) reduces the plastic accumulation rate upon the cycles [17]. Actually, this effect has been already shown by an intergranular strain-based model by Wegener and Herle [54]. Hence, for the present work, it is proposed to make $\chi$ dependent with the internal variable $\varepsilon _a$, such that the desired effect is simulated. A suitable interpolation function is proposed to increase $\chi$ between the values $\chi _0 \le \chi \le \chi _{\max }$, whereby the boundaries $\chi _0$ and $\chi _{\max }$ are now material parameters:

$$\begin{aligned} \chi =\chi _0+\varepsilon _a(\chi _{\max } -\chi _0) \end{aligned}$$

(20)

Notice the introduction of the two additional parameters $C_a$ and $\chi _{\max }$. These parameters can be calibrated through a cyclic undrained triaxial test as shown in Fig. 14a. The experiment was conducted with Karlsruhe fine sand and performed cycles on an isotropically consolidated sample ($p_0=100\,\hbox {kPa}$, $e=0.798$) with a deviator stress amplitude of $q^\mathrm{amp}=25\,\hbox {kPa}$. The accumulated pore water pressure $p_{w}^\mathrm{acc}$ is plotted in Fig. 14c before failure. The obtained experimental curve can be divided in two portions as expected: the first one in which $p_{w}^\mathrm{acc}$ suddenly increases ($N<15$ in Fig. 14c) and the rest ($N>15$ in Fig. 14c) wherein the plastic accumulation shows approximately a constant rate. The parameter $C_a$ controls how fast the plastic accumulation rate reduces and therefore can be adjusted to the first portion of the accumulation curve. To show this, three different values of $C_a$ have been tested for a given value of $\chi _{\max }$ in Fig. 14c. On the other hand, the parameter $\chi _{\max }$ controls the accumulation rate when the number of consecutive cycles is large. Therefore, one can fit this parameter with the behavior of the second portion of the curve ($N>15$ in Fig. 14d). The best simulations were obtained with $C_a=0.015$ and $\chi _{\max }=25$ and hence are selected as parameters. In the next sections, some simulations of multidimensional cyclic loading tests are performed and analyzed with the proposed extension and the selected parameters.

Fig. 14

Simulation of the accumulated pore water pressure in a cyclic undrained triaxial test with Karlsruhe fine sand. Extended ISA + HP model. Variation of parameters

7 Simulations with extended ISA + HP model

The simulations from Sect. 5 showed two issues related to the plastic accumulation: the first is the inability in this model to simulate the dependence of the plastic accumulation rate with the cyclic history. This issue has been overcome through the proposed Eq. 20 in the extended ISA + HP model. The second is the artificial accumulation produced by the stiffness tensor $\mathsf{E}$ when the plastic strain rate is deactivated (case 2). These issues motivated to simulate once more the experimental results with two additional cases.

• Case 3 The constitutive model corresponds to the extended ISA + HP model considering Eq. 20.

• Case 4 The constitutive model corresponds to the extended ISA + HP model but with a constant (hypo-)elastic stiffness $\bar{\mathsf{E}}$. The stiffness $\bar{\mathsf{E}}$ is evaluated with the stress at the center of the loops ${\varvec{\sigma }}_0$ ($p=200\,\hbox {kPa}$ and $q=100\,\hbox {kPa}$) and the initial void ratio $e_0$, i.e., $\bar{\mathsf{E}}=\bar{\mathsf{E}}({\varvec{\sigma }}_0, e_0)$. It remains constant during the whole simulation, such that the only source of accumulation is the plastic strain rate. This modification is not a constitutive model itself and has only been considered for analysis purposes.

Although case 4 does not propose a formal constitutive model, it permits to eliminate the artificial accumulation with a simple modification. Other alternatives, such as incorporating hyperelastic or paraelastic functions, were not evaluated in the present work. The simulations with case 3 are given in Fig. 15. Compared to the results of cases 1 and 2, the new simulations show a significant improvement. The extended version achieved to reduce the plastic accumulation with the number of cycles. Some small inaccuracies are, however, observed and deserve to be mentioned: concerning to the behavior of the void ratio e for the big circle test, see, e.g., Fig. 15e, the simulation showed a dilatant (expansive) behavior for increasing number of cycles. This contrasts to the experiments and is attributed to the artificial accumulation already exhibited in the simulations of case 2.

The simulations of case 4 eliminate the artificial accumulation with the incorporation of a constant stiffness $\bar{\mathsf{E}}$ to the model. The results are compared to the experiments in Fig. 16. The accuracy seems to be in general improved, and the issue of the dilative behavior in the big circle test has been overcome. Hence, it has been shown that for these tests, the artificial accumulation is not negligible and should be carefully analyzed to avoid mistaken interpretations of the simulations.

Fig. 15

Case 3: Simulations with the extended ISA + HP model

Fig. 16

Case 4: Simulations with extended ISA + HP and constant $\mathsf{E}$

8 Simulation of a boundary value problem with FE

The performance of the proposed constitutive model is evaluated with a simple boundary value problem dealing with cyclic loading: a strip foundation (width equal to 2 m and embedment = 1 m) is simulated using finite elements under plane strain conditions. A rectangular domain with 20 m $\times$ 10 m is considered. The horizontal displacements $U_x$ are restricted at the left and right boundaries. Similarly, the vertical displacement $U_y$ is restricted at the boundary of the bottom. The mesh is regular using 4-noded finite elements (linear interpolation). The material is under dry conditions, with a unit weight of $\gamma =15$ kN/m$^3$. A constant vertical stress equal to $\sigma _y=15\,\hbox {kPa}$ is applied on the top boundary to simulate the additional material above the foundation base (embedment = 1 m). The geometry and mesh are depicted in Fig. 17a.

A sinusoidal normal stress $f_n$ with a maximum amplitude of 5 kPa is applied at the center of the top boundary as depicted in Fig. 17a to simulate the foundation. The load has a width of 2 m and follows the function:

$$\begin{aligned} f_n(t)=5 \left( 0.5 \sin (\omega t)+0.5\right)\;(\text {kPa}) \end{aligned}$$

(21)

where t is the time ($t=0$ at the beginning of the step) and $\omega =0.0188495$. The load performs 45 cycles among a total time of $15\times 10^3$ segs, see Fig. 17b. In addition, a sinusoidal tangential stress $f_t$ is considered with an amplitude of 5 kPa as schematically illustrated in Fig. 17b. The tangential stress $f_t$ satisfies the following equation:

$$\begin{aligned} f_t(t)=5 \left( \sin (\omega t)\right)\;(\text {kPa}) \end{aligned}$$

(22)

The simulations were performed considering all the cases studied before, i.e., cases 1–4.

Fig. 17

Geometry and boundary conditions of the FE problem

Fig. 18

Magnitude of displacements $\parallel \mathbf {U}\parallel$ for the 4 cases. Note that different contour scales are used in each plot.

The contours of the magnitude of the displacements $\parallel \mathbf {U}\parallel$ are plotted in Fig. 18 at the end of the simulation. As expected, the largest displacements after 45 cycles were obtained for case 1 (Fig. 18a) with $\parallel \mathbf {U}\parallel \approx 2.2$ mm. The artificial accumulation (case 2, Fig. 18b) produced displacements in the order of $\parallel \mathbf {U}\parallel \approx 0.2$ mm, i.e., a tenth of the case 1. With the extended ISA + HP model (case 3, Fig. 18c), the accumulation is reduced to almost the half of the first case. Small differences were observed between case 4 and case 3. In the next lines, the vertical displacement $U_y$ and horizontal displacement $U_x$ are carefully analyzed.

The results of the vertical displacement $U_y$ at the middle of the foundation (Point A, see Fig. 17a) are plotted in Fig. 19. Each figure corresponds to a different case. The results show a similar pattern than those obtained in the previous sections. The ISA + HP model (case 1) simulates an excessive accumulation as shown in Fig. 19a. The artificial accumulation is small as shown in Fig. 19b but not negligible. It will be shown that this component turns out to be important for the horizontal displacement $U_x$. The results of cases 3 and 4 show a reduction the accumulation for increasing number of cycles similar to the simulations in the previous section.

Fig. 19

Vertical displacements $U_y$ at the point A for the 4 cases

The behavior of the horizontal displacement $U_x$ is plotted in Fig. 20. Surprisingly, the artificial accumulation (case 2, Fig. 20b) is the predominating mechanism if one compares it with the results of the other cases (Fig. 20a, b, d). Moreover, in the simulation of case 4, in which the artificial accumulation has been eliminated, the direction of the accumulation seems to be reversed. Hence, the artificial accumulation is producing horizontal displacements $U_x$ in a different direction than those from the general model and are actually governing the behavior of this variable. This issue is attributed to the fact that in this boundary value problem the accumulated horizontal displacements are very small but comparable to those obtained with the artificial accumulation.

Fig. 20

Horizontal displacements $U_x$ at the point A for the 4 cases

9 Conclusions

In the computational geomechanics, the constitutive modeling of the plastic accumulation under complicated cyclic loading paths is not an easy task. Some relevant issues related to the simulation of cyclic loading has been pointed out within this work. The first concerns to the experimental observation that under multidimensional cyclic loading performing stress loops away from the critical state line, the accumulation rate drastically reduces. The direct implication is that constitutive models should depend on an additional information to distinguish whether the tested path has been simulating a few or a large number of consecutive cycles. To overcome this issue, an extension has been proposed to the ISA plasticity wherein an additional state variable has been introduced to capture some information about the cyclic history. In this way, the extended version of the model achieved to reduce the plastic accumulation upon increasing cycles as observed. Currently, further investigation is being performed to evaluate the model in a wider range of strain amplitudes.

The second issue recalls the importance of the artificial accumulation on cyclic loading. The artificial accumulation delivered by the simulations is in fact comparable in some cases with the amount of plastic accumulation recorded in the experiments. This is an important drawback, considering that the artificial accumulation is not an adjustable magnitude: for example, running a closed circular loop clockwise or counterclockwise would return a different (artificial) accumulation contrasting to the experimental results. The finite element simulation performed within this work showed also that this component is not negligible. The usage of (hypo-)elastic tensors in the constitutive modeling of cyclic loading is in many cases not recommended. Most of the published models for cyclic loading do not consider this fact except by a few, e.g., [9, 10, 19, 39, 53]. The next generations of constitutive models should be aware of this undesirable effect.

The precision of simulating cyclic phenomena in boundary value problems may be compromised if the aforementioned shortcomings are not properly overcome. Researchers developing constitutive models to simulate cyclic behavior should be aware of the aforementioned issues. More research in this direction is recommended to find appropriate formulations enabling us to simulate this complicated behavior.

Appendices

Appendix 1: Hypoplastic model from Wolffersdorff

The general equation of the hypoplastic model by Wolffersdorff [59] can be written as:

$$\begin{aligned} \dot{{\varvec{\sigma }}}=\bar{\mathsf{E}}:(\dot{{{\varvec{\varepsilon }} }}- \dot{\bar{\varvec{\varepsilon }}}^p) \end{aligned}$$

(23)

whereby $\bar{\mathsf{E}}$ is the “linear” stiffness and $\bar{{\varvec{\varepsilon }}}^p$ is the hypoplastic strain rate defined in the sequel. According to the ISA + HP nomenclature, the tensor $\mathsf{E}$ is referred as the mobilized stiffness and $\bar{{\varvec{\varepsilon }}}^p$ as the mobilized plastic strain rate. The definition of $\bar{\mathsf{E}}$ reads [59]:

$$\begin{aligned} \bar{\mathsf{E}}=f_bf_e\dfrac{1}{\hat{{\varvec{\sigma }}} :\hat{{\varvec{\sigma }}}} (F^2\mathsf{I}+a^2\hat{{\varvec{\sigma }}}\hat{{\varvec{\sigma }}}) \end{aligned}$$

(24)

whereby $\hat{{\varvec{\sigma }}}= {\varvec{\sigma }}/\mathrm{tr}{\varvec{\sigma }}$ is the relative stress, $f_b$, $f_e$, F and a are scalar factors and $\mathsf{I}$ is the fourth-order tensor for symmetric second-order tensors. The scalar factor F is responsible for the Matsuoka–Nakai shape of the critical state surface and is defined as:

$$\begin{aligned} F=\sqrt{\dfrac{1}{8}\tan ^2(\psi )+\dfrac{2-\tan ^2(\psi )}{2+2\sqrt{2}\tan (\psi )\cos (3\theta )}}-\dfrac{1}{2\sqrt{2}\tan (\psi )} \end{aligned}$$

(25)

whereby the factors a, $\theta$ and $\psi$ are defined as:

$$\begin{aligned} a&=\dfrac{\sqrt{3}(3-\sin (\varphi _c))}{2\sqrt{2}\sin (\varphi _c))}\nonumber \\ \tan \psi&=\sqrt{3} \Vert \hat{{\varvec{\sigma }}}^* \Vert \nonumber \\ \cos (3\theta ) &= \sqrt 6 \frac{{{\text{tr}}(\widehat{\sigma }^{*} \widehat{\sigma }^{*} \widehat{\sigma }^{*} )}}{{(\widehat{\sigma }^{*} :\widehat{\sigma }^{*} )^{{3/2}} }} \end{aligned}$$

(26)

The tensor ${\varvec{\sigma }}^*$ is the deviator stress tensor and $\varphi _c$ is the critical state friction angle. The model incorporates the characteristic void ratios corresponding to the maximum $e_i$, minimum $e_d$ and critical $e_c$, respectively. They follow the function proposed by Bauer [5] depending on the mean pressure p:

$$\begin{aligned} e_i&=e_{i0}\exp \left( -\left( 3p/h_s\right) ^{n_B}\right) \nonumber \\ e_d&=e_{d0}\exp \left( -\left( 3p/h_s\right) ^{n_B}\right) \nonumber \\ e_c&=e_{c0}\exp \left( -\left( 3p/h_s\right) ^{n_B}\right) \end{aligned}$$

(27)

where $e_{i0}$, $e_{d0}$ and $e_{c0}$ are parameters representing the characteristic void ratios at $p=0$ and $h_s$ and $n_B$ are additional parameters to fit these curves. The scalar functions $f_e$ and $f_b$ read:

$$\begin{aligned} f_e&=\left( \dfrac{e_c}{e}\right) ^\beta \nonumber \\ f_b&=\dfrac{h_s}{n}\left( \dfrac{1+e_i}{e_i}\right) \left( \dfrac{e_{i0}}{e_{c0}}\right) ^\beta \left( -\dfrac{\mathrm{tr{\varvec{\sigma }}}}{h_s}\right) ^{1-n}\left[ 3+a^2-\sqrt{3}a\left( \dfrac{e_{i0}-e_{d0}}{e_{c0}-e_{d0}}\right) ^\beta \right] ^{-1} \end{aligned}$$

(28)

whereby $\beta$ and $\alpha$ are material parameters The mobilized plastic strain rate $\dot{\bar{\varvec{\varepsilon }}}^p$ is defined as:

$$\begin{aligned} \dot{\bar{\varvec{\varepsilon }}}^p=-\bar{\mathsf{E}}^{-1} : \bar{\mathbf {N}} \parallel \dot{{{\varvec{\varepsilon }} }}\parallel \end{aligned}$$

(29)

whereby tensor $\bar{\mathbf {N}}$ reads:

$$\begin{aligned} \bar{\mathbf {N}}=f_df_bf_e\dfrac{Fa}{\hat{{\varvec{\sigma }}}:\hat{{\varvec{\sigma }}}}(\hat{{\varvec{\sigma }}}+\hat{{\varvec{\sigma }}}^*) \end{aligned}$$

(30)

and the factor $f_d$ follows the relation:

$$\begin{aligned} f_d=\left( \dfrac{e-e_d}{e_c-e_d}\right) ^\alpha \end{aligned}$$

(31)

Details of these functions are explained in [37]. The required parameters are briefly described in the following appendix.

Appendix 2: Short guide to determine the ISA + HP parameters

The ISA + HP model (without the proposed extension) requires the calibration of 12 parameters. In this appendix, a short guide for their determination is provided.

• The critical state friction angle $\varphi _c$ can be adjusted with points of a triaxial compression test after a vertical strain of $\varepsilon _1>25\,\%$. The critical state slope within the $p-q$ space can be calibrated with the relation $q/p=6\sin \varphi _c/(3-\sin \varphi _c)$ for these points.

• The maximum void ratio at $p=0$ denoted with $e_{i0}$ can be obtained through the standardized minimum density test (ASTM D4254-14).

• The exponent $n_B$ can be adjusted to match the elastic stiffness dependence with the mean pressure $G\sim p^{1-n_B}$ through the results of resonant column test for different confining pressures. If the experiments are scarce, some values from the literature can be adopted, e.g., $n_B=0.5$ [47].

• The granular hardness $h_s$ can be adjusted to simulate the oedometric compression stiffness under very loose states $e\approx e_i$ where $e_i=e_i(p)$ is the maximum void ratio curve. A method to determine $h_s$ given some oedometric results is described by Herle and Gudehus [21].

• The critical state void ratio at $p=0$ denoted with $e_{c0}$ can be adjusted from points lying at the critical state ($\varepsilon _1>25\,\%$ with triaxial compression) in the $e-p$ space with very low pressure $p<20\hbox { kPa}$. When data are scarce, one may adopt the approximation $e_{c0}\approx 0.9 e_{i0}$.

• The dilatancy exponent $\alpha$ is calibrated with the behavior of medium-dense and dense samples sheared through drained triaxial compression. This parameter controls the dilatancy rate of the volumetric strains after reaching the phase of transformation line. A relation to determine $\alpha$ with drained triaxial test is described by Herle and Gudehus [21].

• The barotropy exponent $\beta$ is adjusted to dense samples compressed under oedometric conditions. Herle and Gudehus [21] provided an equation to determine this parameter.

• The parameter R defines the size of the elastic locus in terms of strain increments. For the secant shear stiffness $G^\mathrm{sec}$, this can be interpreted as the strain range at which no degradation occurs. Many experiments point a value of approximately $\parallel \Delta {\varvec{\varepsilon }}\parallel \approx 10^{-5}$ for sands, but as mentioned in [17], a small value of this parameter may lead to numerical difficulties when dealing with finite element simulations. Hence, a value of $\parallel \Delta {\varvec{\varepsilon }}\parallel > 5\times 10^{-5}$ is recommended.

• The parameter $\beta _h$ controls the needed strain increment to eliminate the influence of the intergranular strain effect in the model. In other words, it controls the size of the strain amplitude at which no “small strain effects” is simulated by the model. The equation relating this strain amplitude with the parameter $\beta _h$ was provided in [17] and reads:

  $$\begin{aligned} \beta _h=\dfrac{\sqrt{6}R(\log (4)-2\log (1-r_h))}{6\Delta \varepsilon _s-\sqrt{6} R(3+r_h)} \end{aligned}$$

  (32)

  where $\Delta \varepsilon _s$ is the deviatoric strain amplitude and $r_h\approx 0.99$ is a factor which defines how close is tensor $\mathbf {c}$ to its bounding condition $r_h=\parallel \mathbf {c}\parallel /\parallel \mathbf {c}_b\parallel$.

• The parameter $\chi$ controls the degradation curve shape of the secant shear modulus $G^\mathrm{sec}$. Its calibration can be performed simulating some cycles of triaxial test as explained in [17].

• The parameter $C_a$ controls how fast the plastic accumulation rate reduces upon the cycles. It can be adjusted with a cyclic undrained triaxial test with the behavior of the accumulated pore pressure $p^\mathrm{acc}_w$ versus the number of cycles N. The first portion of this curve, with approximately $N<10$, can be adjusted through parameter $C_a$ by trial and error. An example of its calibration is given in Fig.14c.

• The parameter $\chi _{\max }$ controls the accumulation rate when the number of consecutive cycles is large, of about $N>10$. It can be adjusted with a cyclic undrained triaxial test with the behavior of the accumulated pore pressure $p^\mathrm{acc}_w$ versus the number of cycles N. An increasing number of $\chi _{\max }$ would return a lower value of N to reach failure at the critical state line. It can be adjusted by trial and error after fixing $C_a$. An example of its calibration is given in Fig. 14d.