Evaluating the Performance of an ISA-Hypoplasticity Constitutive Model on Problems with Repetitive Loading

Abstract

The ISA-plasticity is a useful theory to propose constitutive models for soils accounting for small strain effects. It uses the intergranular strain concept, previously proposed by Niemunis and Herle (1997) to enhance the capabilities of some existing hypoplastic models under cyclic loading. In contrast to its predecessor, the ISA-plasticity presents a completely different formulation to incorporate an elastic locus depending on a strain amplitude. However, it keeps similar advantages and brings other new ones such as the elastic locus and improved simulations of the plastic accumulation upon a number of cycles. In the present article, some numerical investigations are made to evaluate the performance of an ISA-plasticity based model on simulations with repetitive loading. We have chosen to couple the ISA-plasticity with the hypoplastic model by Wolfferdorff to simulate some experiments. At the beginning of the article, the theory of the ISA-plasticity is briefly explained. Subsequently, its numerical implementation is step by step detailed. A semi-explicit algorithm is proposed and some hints are given to allow the coupling with other models. At the end, some simulations of experiments with the Karlsruhe fine sand are shown in which the performance of the model under repetitive loading is evaluated. The behavior of the plastic accumulation is examined upon a number of cycles and some remarks are given about the current investigation.

1 Introduction

The ISA-Plasticity is a useful mathematical platform to develop constitutive models for the simulation of cyclic loading in soils. This theory considers the fact that the simulation of cyclic behavior is improved when accounting for the effect of the recent strain history [16, 17]. Therefore, it incorporates the intergranular strain concept, originally proposed by Niemunis and Herle [13] to consider this information. The mathematical formulation of the ISA-Plasticity is however different from the one of Niemunis and Herle [13]: to start, the evolution equation of the intergranular strain is elastopolastic, and its formulation is based on a simple bounding surface approach. Furthermore, it considers an elastic locus related to a specific strain amplitude which can be adjusted to the elastic threshold strain amplitude [18, 20]. Finally, its yield surface presents a kinematic hardening similar to some “bubble” models for clay (e.g. [1]) to simulate a smooth transition between the elastic and plastic behavior.

Since the work of Fuentes and Triantafyllidis [6], the ISA-plasticity has been used to extend some existing models. Recently, an ISA-plasticity model was coupled with the hypoplastic model by Wolffersdorff [21] to examine its behavior under complex loading [15]. It was concluded that the model needed to be extended in order to simulate well the plastic accumulation under repetitive loading. The proposed extension in [15] is based on a simple mechanism: if the model experiences subsequent cycles away from the critical state line, it reduces the rate of plastic accumulation. With this, the proposed extension achieved a good performance in some simulations with cyclic loading. However, this version is recent and should be carefully inspected with additional examples in order to study its advantages and disadvantages. Beside this, the procedure for its numerical integration has not been well detailed and discussed. Hence, more description is expected by some users for the implementation of an ISA-plasticity based model on finite element codes to solve boundary value problems.

In the present work, we evaluate an ISA-plasticity based model under repetitive loading. We include some simulations of element test under monotonic and cyclic loading to analyze the behavior of the plastic accumulation upon a number of cycles. Furthermore, we analyze the performance of the model in a finite element simulation of a shallow foundation subjected to cyclic loading. Additional descriptions for the numerical implementation of the model were also included. The structure of the present article is as follows. We begin with an outline of the ISA-plasticity and give some hints to link it with some existing models. Then, a numerical integration scheme is detailed. Finally, the mentioned simulations are shown and carefully analyzed. The notation of this article is as follows. Scalar quantities are denoted with italic fonts (e.g. a, b), second rank tensors with bold fonts (e.g. $\mathbf {A}$, ${\varvec{\sigma }}$), and fourth rank tensors with Sans Serif type (e.g. $\mathsf{E}, \mathsf{L}$). Multiplication with two dummy indices, also known as double contraction, is denoted with a colon “:” (e.g. $\mathbf {A}:\mathbf {B}=A_{ij}B_{ij}$). A dyadic product between two second rank tensors is symbolized with $\mathbf {A}\otimes \mathbf {B}$ and results in a fourth order tensor $C_{ijkl}=A_{ij}B_{kl}$. The deviatoric component of a tensor is symbolized with an asterisk as superscript $\mathbf {A}^*$. The effective stress tensor is denoted with ${\varvec{\sigma }}$ and the strain tensor with ${\varvec{\varepsilon }}$. The Roscoe invariants are defined as $p=-\text {tr}{\varvec{\sigma }}/3$, $q=\sqrt{3/2}\,{\parallel } {\varvec{\sigma }}^*{\parallel }$, $\varepsilon _v=-\text {tr}{{\varvec{\epsilon }}}$ and $\varepsilon _s=\sqrt{2/3}\,{\parallel } {{\varvec{\epsilon }}}^*{\parallel }$.

1.1 Brief Description of the ISA-plasticity

In this section the formulation of the ISA-plasticity is outlined. Details and additional information of the model are found in [5, 6]. We use the same notation of the variables as in former publications [5, 6].

According to this theory, cycles under small strain amplitudes (${\parallel } \varDelta {\varvec{\varepsilon }}{\parallel }<10^{-4}$) deliver an elastic response while those with larger strain amplitudes render plastic behavior. The transition from elastic to plastic is demarcated by the strain amplitude ${\parallel } \varDelta {\varvec{\varepsilon }}{\parallel }=R\approx 10^{-4}$. To capture this, the ISA-plasticity uses the information of the intergranular strain which is a strain-type state variable, proposed by Niemunis and Herle [13] to detect recent changes of the strain rate direction. Having this information, we may improve existing models for the simulation of cyclic loading and eliminate the excessive plastic accumulation (racheting). The ISA-plasticity featured an alternative evolution equation for the intergranular strain $\mathbf{h }$, with a special characteristic: under elastic conditions, the intergranular strain $\mathbf{h }$ evolves identically with the strain ${\varvec{\varepsilon }}$:

$$\begin{aligned} \dot{\mathbf{h }}=\dot{{{\varvec{\varepsilon }} }}\quad \quad \text {(under elastic conditions)} \end{aligned}$$

(1)

The latter condition makes simple the formulation of a yield surface with the desired property. It should present a spherical shape within the principal space of the intergranular strain to guarantee an elastic locus with a specific strain amplitude ${\parallel } \varDelta {\varvec{\varepsilon }}{\parallel }=R$. Therefore, the yield function denoted with $F_H$, is defined as:

$$\begin{aligned} F_H= {\parallel }\mathbf{h }-\mathbf{c }{\parallel }-\frac{R}{2} \end{aligned}$$

(2)

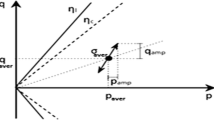
whereby R is a material parameter representing the strain amplitude and $\mathbf{c }$ is a tensor representing the center of the yield surface and therefore called the back-intergranular strain. The value of R may be adjusted to the elastic amplitude observed on shear modulus degradation curves, with typical values around $R\approx 10^{-5} {-} 10^{-4}$. The yield surface presents a kinematic hardening which follows some hardening rules from the bounding surface plasticity. Therefore, the model considers an additional bounding surface as depicted in Fig. 1. Its movement is ruled by the kinematic hardening of its center, i.e. the back-intergranular strain $\mathbf{c }$.

Fig. 1.

Yield surface and bounding surface within the intergranular strain principal space. (a) Names and notation. (b) Example of a bounding condition for the intergranular strain

The evolution law of the intergranular strain ${\mathbf{h }}$ is elastoplastic. Its formulation was basically proposed considering two facts: the first is that under elastic conditions its evolution equation gives $\dot{\mathbf{h }}=\dot{{{\varvec{\varepsilon }} }}$. The second is the assumption of an associated flow rule $\mathbf{N }=({\partial F_H}/{\partial \mathbf{h }})$ to make its formulation simple. Hence, the following evolution law has been proposed [6]:

$$\begin{aligned} \dot{\mathbf{h }}=\dot{\varvec{\epsilon }}-\dot{\lambda }_H \mathbf{N }\end{aligned}$$

(3)

whereby $\lambda _H \ge 0$ is the consistency parameter (or plastic multiplier) and $\mathbf{N }$ is the flow rule (${\parallel } \mathbf{N }{\parallel }=1$) which reads:

$$\begin{aligned} \mathbf{N }=\dfrac{\partial F_H}{\partial \mathbf{h }}=\dfrac{\mathbf{h }-\mathbf{c }}{R/2} \end{aligned}$$

(4)

The consistency parameter vanishes under elastic conditions $\lambda _H=0$ and takes its maximum value $\dot{\lambda }_H = {\parallel } \dot{\varvec{\epsilon }}{\parallel }$ at the bounding surface of the intergranular strain. The shape of the bounding surface is also spherical but with fixed center at $\mathbf{h }=\mathbf {0}$ and diameter equal to 2R, i.e. it presents twice the size of the yield surface. The bounding surface function $F_{Hb}$ reads:

$$\begin{aligned} F_{Hb}={\parallel } \mathbf{h }{\parallel }-R \end{aligned}$$

(5)

The hardening rule for the back-intergranular strain $\mathbf{c }$ uses similar ideas to the bounding surface plasticity. For this purpose, we project an image tensor of $\mathbf{c }$ at the bounding surface with the following mapping rule:

$$\begin{aligned} \mathbf{c }_b=(R/2)\overrightarrow{\dot{{{\varvec{\varepsilon }} }}} \end{aligned}$$

(6)

whereby $\mathbf{c }_b$ is the projected tensor. The hardening function $\bar{\mathbf{c }}=\dot{\mathbf{c }}/{\dot{\lambda }}$ reads:

$$\begin{aligned} \bar{\mathbf{c }}=\beta _h(\mathbf{c }_b-\mathbf{c })/R\quad \text {with}\quad \dot{\mathbf{c }}=\dot{\lambda }_H\bar{\mathbf{c }} \end{aligned}$$

(7)

where $\beta _h$ is an additional parameter to control the rate of $\mathbf{c }$. Notice that if $\mathbf{c }_b=\mathbf{c }$ then the rate $\bar{\mathbf{c }}=\mathbf {0}$ vanishes. Hence for very large strains, the model gives $\mathbf{h }=\mathbf{h }_b$, $\mathbf{c }=\mathbf{c }_b$, see Fig. 1b. The expression for the consistency parameter is deduced by simple plasticity relations from the consistency equation $\dot{F_H}=0$ and reads:

$$\begin{aligned} \dot{\lambda }_H=\dfrac{\langle \mathbf{N }:\dot{\varepsilon }\rangle }{1-\left( \dfrac{\partial F_H}{\partial \mathbf{c }}\right) :\bar{\mathbf{c }}} \end{aligned}$$

(8)

whereby the operator $\langle x\rangle =x$ when $x>0$ and $\langle x\rangle =0$ if $x\le 0$. The Eqs. 2–8 conform the model of the intergranular strain alone. This model evolves in parallel with the mechanical model but independently because it does not depend on the stress tensor ${\varvec{\sigma }}$. The ISA-plasticity introduces some additional scalar factors to use the information provided by the intergranular strain model. These scalar factors depend on the projection of the intergranular strain $\mathbf{h }$ at the bounding surface using the flow rule $\mathbf{N }$ as the mapping tensor:

$$\begin{aligned} \mathbf{h }_b= R\mathbf{N }\end{aligned}$$

(9)

where $\mathbf{h }_b$ is the projected tensor. Aided by tensor $\mathbf{h }_b$, one may detect some recent movements in the loading history. For example, if ${\parallel } \mathbf{h }_b-\mathbf{h }{\parallel }=0$, it means that the current intergranular strain lies at its bounding condition. According to the model, this condition is only reached under large strain amplitudes and is therefore called “mobilized states”. On the other hand, greater values of ${\parallel } \mathbf{h }_b-\mathbf{h }{\parallel }>0$ represent a reversal loading which has been recently performed. Hence, the model proposes the function $\rho$ as:

$$\begin{aligned} \rho =1-\dfrac{\Vert \mathbf{h }_b-\mathbf{h }\Vert }{2R} \end{aligned}$$

(10)

In this manner, $\rho =0$ implies reversal loading while $\rho =1$ implies “mobilized states”. In the next section, the mechanical model will be briefly described.

1.2 Description of the Mechanical Model

The mechanical model relates the stress rate $\dot{\varvec{\sigma }}$ with the strain rate $\dot{{{\varvec{\varepsilon }} }}$ through a constitutive equation. For this theory, the constitutive equation presents the following general form:

$$\begin{aligned} \dot{\varvec{\sigma }}=m\bar{\mathsf{E}}:(\dot{{{\varvec{\varepsilon }} }}-y_h \dot{\bar{\varvec{\varepsilon }}}^p) \end{aligned}$$

(11)

where m and $y_h$ are scalar functions, $\bar{\mathsf{E}}$ and $\dot{\bar{\varvec{\varepsilon }}}^p$ are called “mobilized” stiffness tensor and “mobilized” plastic strain rate respectively. Tensors $\bar{\mathsf{E}}$ and $\dot{\bar{\varvec{\varepsilon }}}^p$ can be adjusted to existing relations of hypoplastic models, e.g. [8, 10, 21]. Actually, when the intergranular strain lies under mobilized states, the scalar functions render $m=1$ and $y_h=1$ and the model yields to:

$$\begin{aligned} \dot{\varvec{\sigma }}=\bar{\mathsf{E}}:(\dot{{{\varvec{\varepsilon }} }}- \dot{\bar{\varvec{\varepsilon }}}^p)\quad \quad \text {(for mobilized states)} \end{aligned}$$

(12)

This mathematical form is actually not recognized as a formal hypoplastic model [9]. Users of the Hypoplasticity family are rather familiar with the equation:

$$\begin{aligned} \dot{\varvec{\sigma }}=\mathsf{L}^\mathrm{hyp}:\dot{{{\varvec{\varepsilon }} }}+\mathbf{N }^\mathrm{hyp}\,{\parallel } \dot{{{\varvec{\varepsilon }} }}{\parallel }\quad \quad \text {(for mobilized states)} \end{aligned}$$

(13)

whereby $\mathsf{L}^\mathrm{hyp}$ is the “linear” stiffness and $\mathbf{N }^\mathrm{hyp}$ is the “non-linear” stiffness [8, 10, 21, 22]. The existing relations for tensors $\mathsf{L}^\mathrm{hyp}$ and $\mathbf{N }^\mathrm{hyp}$ can be adopted for the present theory when setting the following equivalencies:

$$\begin{aligned} \mathsf{L}^\mathrm{hyp}=&\bar{\mathsf{E}}\end{aligned}$$

(14)

$$\begin{aligned} \mathbf{N }^\mathrm{hyp}=&-(\mathsf{E}:\dot{\bar{\varvec{\varepsilon }}}^p)/{{\parallel } \dot{{{\varvec{\varepsilon }} }}{\parallel }} \end{aligned}$$

(15)

We have selected the hypoplastic model by Wolffersdorff [21] for the present work considering that our interest is the simulation of sand.

The scalar function $y_h$ is a factor which ranges between $0\le y_h\le 1$ and aims to reduce the plastic strain rate after reversal loading. The function $y_h$ reads:

$$\begin{aligned} y_h=\rho ^{\chi }\langle \mathbf{N }:\overrightarrow{\dot{{{\varvec{\varepsilon }} }}} \rangle \end{aligned}$$

(16)

where $\chi$ is an exponent which can be set as a material constant [6], or improved to account for the effect of repetitive loading within the plastic accumulation rate [14]. The function m aims to increase the stiffness upon reversal loading. This function reads:

$$\begin{aligned} m=m_R+(1-m_R)y_h \end{aligned}$$

(17)

where $m_R$ is a material constant to increase the stiffness under elastic conditions. The consideration of these equations allows to illustrate schematically the response of the ISA model under different strain amplitudes, as depicted in Fig. 1. For instance, let us suppose an elastic strain amplitude of $R=10^{-4}$. For small strain amplitudes $({\parallel } \varDelta {\varvec{\varepsilon }}{\parallel }<10^{-4})$, the behavior is elastic and the constitutive equation yields to $\dot{{\varvec{\sigma }}}=m_R \bar{\mathsf{E}}:\dot{{{\varvec{\varepsilon }} }}$. For very large strain amplitudes $({\parallel } \varDelta {\varvec{\varepsilon }}{\parallel }>10^{-2})$, also called “mobilized states”, the intergranular strain lies at its bounding condition $\mathbf{h }=\mathbf{h }_b$ and the scalar factors give $y_h=1$ and $m=1$. Therefore, the model coincides with the hypoplastic equation $\dot{\varvec{\sigma }}=\bar{\mathsf{E}}:(\dot{{{\varvec{\varepsilon }} }}- \dot{\bar{\varvec{\varepsilon }}}^p)$ or $\dot{\varvec{\sigma }}=\mathsf{L}^\mathrm{hyp}:\dot{{{\varvec{\varepsilon }} }}+\mathbf{N }^\mathrm{hyp}\,{\parallel } \dot{{{\varvec{\varepsilon }} }}{\parallel }$. Between these two states, a “transition” phase exists in which the model operates with the equation $\dot{\varvec{\sigma }}=m\bar{\mathsf{E}}:(\dot{{{\varvec{\varepsilon }} }}- y_h\dot{\bar{\varvec{\varepsilon }}}^p)$, see Fig. 2.

The recent modification by Poblete et al. [15] included the modification of exponent $\chi$ to improve the simulations under repetitive loading. In order to detect whether a few or a number of subsequent cycles have been performed, they proposed an additional state variable $\varepsilon ^\mathrm{acc}$ with the following evolution law:

$$\begin{aligned} \dot{\varepsilon }_\mathrm{acc}=\dfrac{C_a}{R}(1-y_h-\varepsilon _\mathrm{acc})\,{\parallel } \dot{{{\varvec{\varepsilon }} }}{\parallel } \end{aligned}$$

(18)

whereby $C_a$ is a material parameter controlling the rate of $\dot{\varepsilon }_\mathrm{acc}$ [15]. Notice that if one performs subsequent cycles, the function $y_h$ reduces its value $y_h\rightarrow 0$ and the state variable ${\varepsilon }_\mathrm{acc}$ starts to increase. Hence, one can use this information to reduce the plastic strain rate upon subsequent cycles which are now detected with the condition ${\varepsilon }_\mathrm{acc}>0$. To achieve this, the exponent $\chi$ is reduced according to the relation:

$$\begin{aligned} \chi = \chi _0+\varepsilon _\mathrm{acc}(\chi _\mathrm{max}-\chi _0) \end{aligned}$$

(19)

whereby $\chi _0$ and $\chi _\mathrm{max}$ are material constants. The first should be adjusted for small number of cycles $N<3$ and the other for large number of cycles (e.g. $N>15$).

We now end this section with the deduction of the continuum (explicit) stiffness $\mathsf{M}=(\partial \dot{{\varvec{\sigma }}}/\partial \dot{{{\varvec{\varepsilon }} }})$ of the model. This can be deduced after derivation of the constitutive equation such that it reduces to:

$$\begin{aligned} \dot{{\varvec{\sigma }}}=\mathsf{M}:\dot{{{\varvec{\varepsilon }} }}\end{aligned}$$

(20)

whereby the continuum stiffness $\mathsf{M}$ reads:

$$\begin{aligned} \mathsf{M}= \left\{ \begin{array}{lllll} [ m_{R} + (1-m_{R})y_{h} ] (\mathsf{L}^\mathrm{hyp} + \rho ^{\chi } \mathbf{N }^\mathrm{hyp}\otimes \mathbf{N }) &{} {\text {for}}\;F_H\ge 0\\ m_{R}\mathsf{L}^\mathrm{hyp}&{} {\text {for}} \; F_H < 0 \end{array} \right. \end{aligned}$$

(21)

Fig. 2.

For cycles under small strain amplitudes ${\parallel } \dot{\varepsilon }{\parallel }<R$, the behavior is elastic. At mobilized states, the constitutive equation turns into hypoplastic. Between these two states, a smooth transition is simulated through the functions $0\le m\le m_R$ and $0\le y_h\le 1$

1.3 Numerical Implementation

A numerical implementation for finite element codes has been performed in a Fortran subroutine following the syntax of Abaqus. The simulations were made using the open-source software Incremental Driver [12] created by Niemunis but modified by the authors of this work to improve the code for cyclic loading. The algorithm is semi-explicit, meaning that most equations were solved explicitly except by a few which will be mentioned in the sequel. The integration strategy is similar to classical implementations of elastoplastic models, in which an elastic predictor is made to detect whether an elastic or plastic step should be performed. For this implementation, a subincrementation algorithm is recommended to avoid numerical convergence difficulties. A subincrement size of about ${\parallel } \varDelta \varepsilon {\parallel }\approx 10^{-5}$ is recommended. The implementation is split in two parts, the first related to the intergranular strain model and the second to the mechanical model. The subroutine structure is typical of finite elements code, in which the strain increment together with the current state (stress, state variables) are given as input and the subroutine delivers the state at the end of the increment, see Table 1. The jacobian $J_{ijkl}=\partial \varDelta \sigma _{ij}/\partial \varDelta \varepsilon _{kl}$ is provided at the end of the implementation for its use in the global finite element matrix. The integration presented in the subsequent sections is based on the equations from Sect. 1.1.

1.4 Integration of the Intergranular Strain Model

The implementation begins with the intergranular strain model. The fact that the model does not depend on the stress ${\varvec{\sigma }}$ makes its implementation easier because is not coupled with the mechanical model. In other words, the intergranular strain may be integrated independently from the mechanical model. The integration scheme begins with the computation of a trial elastic step to evaluate the yield function. In the following lines, a step-by-step guide is given using the index notation to make simpler the interpretation of the tensorial operations.

Table 1. Input and ouput variables of the numerical implementation.

The first step is to define the strain rate $\dot{\varepsilon }_{ij}$ and the unit strain rate $\hat{\dot{\varepsilon }}_{ij}$:

$$\begin{aligned} \begin{aligned} \dot{\varepsilon }_{ij}&=\varDelta \varepsilon _{ij}/\varDelta t\\ \hat{\dot{\varepsilon }}_{ij}&=\dfrac{\dot{\varepsilon }_{ij}}{ \sqrt{\dot{\varepsilon }_{ij}\dot{\varepsilon }_{ij}} } \end{aligned} \end{aligned}$$

(22)

Then, the trial intergranular strain variable $h^\mathrm{trial}_{ij}$ and trial back-intergranular strain $c^\mathrm{trial}_{ij}$ are computed assuming elastic conditions:

$$\begin{aligned} \begin{aligned} h^\mathrm{trial}_{ij}&=h_{ij} + \varDelta {\varepsilon }_{ij}\\ c^\mathrm{trial}_{ij}&= c_{ij} \end{aligned} \end{aligned}$$

(23)

The trial yield surface $F^\mathrm{trial}$ is then computed:

$$\begin{aligned} F^\mathrm{trial} = [ (h^\mathrm{trial}_{ij} - c^\mathrm{trial}_{ij}) (h^\mathrm{trial}_{ij} - c^\mathrm{trial}_{ij})]^{1/2} - \dfrac{R}{2} \end{aligned}$$

(24)

In case that $F^\mathrm{trial}<0$, an elastic step is performed. For that case, we take the trial variables $h^\mathrm{trial}_{ij}$ and $c^\mathrm{trial}_{ij}$ as the solution:

$$\begin{aligned} \begin{aligned} h_{ij}&= h^\mathrm{trial}_{ij} \\ c_{ij}&= c^\mathrm{trial}_{ij} \end{aligned} \end{aligned}$$

(25)

In case that $F^\mathrm{trial}\ge 0$, a plastic step is performed. In the plastic case, we begin with the computation of the flow rule. For our implementation, we use the approximation $N_{ij}\approx N_{ij}^\mathrm{trial}$:

$$\begin{aligned} {N}_{ij} = \dfrac{(h^\mathrm{trial}_{ij}- c^\mathrm{trial}_{ij})}{ \sqrt{(h^\mathrm{trial}_{ij}- c^\mathrm{trial}_{ij})(h^\mathrm{trial}_{ij}- c^\mathrm{trial}_{ij}) }} \end{aligned}$$

(26)

Subsequently, the consistency parameter is computed $\dot{\lambda }$ as a function of the image tensor $c^\mathrm{max}_{ij}$ and the hardening function $\bar{c}_{ij}$:

$$\begin{aligned} c^\mathrm{max}_{ij} =&\dfrac{R}{2} \hat{\dot{\varepsilon }} \nonumber \\ \bar{c}_{ij} =&\dfrac{\beta _{R}}{R} (c^\mathrm{max}_{ij} - c_{ij})\nonumber \\ \dot{\lambda }=&\dfrac{{N}_{ij} \dot{\varepsilon }_{ij}}{\bar{c}_{ij} {N}_{ij} +1 } \end{aligned}$$

(27)

Finally, the back-intergranular strain $c_{ij}$ and the intergranular strain $h_{ij}$ are deduced implicitly from Eqs. 3 and 7 respectively:

$$\begin{aligned} \begin{aligned} c_{ij}&=c_{ij}+\dfrac{\beta _R/R(c^\mathrm{max}_{ij} -c_{ij})\dot{\lambda }\varDelta t}{1+\beta _R/R\dot{\lambda }\varDelta t} \\ h_{ij}&= h_{ij} + \dfrac{\left[ \dot{\varepsilon }_{ij} \varDelta t - \dfrac{\dot{\lambda }\varDelta t}{R/2} (h_{ij} - c_{ij}) \right] }{ \left( 1+ \dfrac{ \dot{\lambda } \varDelta t}{R/2} \right) } \end{aligned} \end{aligned}$$

(28)

At the end of the plastic step, we recommend to use a simple correction to ensure the condition $F_H=0$. We compute the flow rule $N_{ij}$ with the actualized variables of the tensors $h_{ij}$ and $c_{ij}$ and then we correct $c_{ij}$ as follows:

$$\begin{aligned} \begin{aligned} N_{ij}&= \dfrac{(h_{ij} - c_{ij})}{\sqrt{(h_{ij} - c_{ij})(h_{ij} - c_{ij})}}\\ c_{ij}&= h_{ij} - \dfrac{R}{2} N_{ij} \end{aligned} \end{aligned}$$

(29)

Notice that with the latter correction the yield function gives $F_H=0$. Some minor refinements may be introduced to the code to ensure that $h_{ij}$ and $c_{ij}$ never cross beyond the bounding surface, but these corrections are not discussed in the present work. In the next section, the numerical integration of the mechanical model is detailed.

1.5 Integration of the Mechanical Model

We now present an integration procedure for the mechanical model. In contrast to the previous section, the mechanical model is coupled with the response of the intergranular strain. An implicit implementation is troublesome in view of the large amount of derivatives to be considered. Therefore, we perform an explicit integration and let the numerical convergence to be achieved by selecting an appropiated subincrement size. In the following lines, the code sequence for the mechanical model is explained.

We begin with the computation of exponent $\chi$ according to Eq. 19:

$$\begin{aligned} \chi = \chi _0+\varepsilon _\mathrm{acc}(\chi _\mathrm{max}-\chi _0) \end{aligned}$$

(30)

Then, the flow rule $N_{ij}$ is once more actualized with the variables $h_{ij}$ and $c_{ij}$ calculated within the intergranular strain model:

$$\begin{aligned} N_{ij} = \dfrac{( h_{ij} - c_{ij})}{ \sqrt{( h_{ij} - c_{ij})( h_{ij} - c_{ij})} } \end{aligned}$$

(31)

Subsequently, the scalar factors $\rho$ and $y_h$ are evaluated:

$$\begin{aligned} \begin{aligned} \rho&=1-\dfrac{\sqrt{(R N_{ij}-h_{ij})(R N_{ij}-h_{ij})}}{2R}\\ y_h&=\rho ^{\chi }\langle N_{ij} \hat{\dot{\varepsilon }}_{ij} \rangle \end{aligned} \end{aligned}$$

(32)

Once the scalar functions and the intergranular model are actualized, we proceed to compute the stiffness tensor $M_{ijkl}$. For this purpose, tensors $N^\mathrm{hyp}_{ij}$ and $L^\mathrm{hyp}_{ijkl}$ ought to be defined. For our code, we have used some additional Fortran subroutines to compute these tensors according to the hypoplastic equation by Wolfferdorff [21], see Appendix A. We recall that the user is free to select the hypoplastic model with its respective definitions for tensors $N^\mathrm{hyp}_{ij}$ and $L^\mathrm{hyp}_{ijkl}$. In general, these tensors do not depend on the intergranular strain model variables, but only on the current stress ${\varvec{\sigma }}$ and void ratio e. Hence, we recommend their implementation with a simple explicit procedure with the appropriate subincrement size. The user may improve this integration with automatic subincrementation with error control [3, 4].

Having tensors $N^\mathrm{hyp}_{ij}$ and $L^\mathrm{hyp}_{ijkl}$ defined, we compute the stiffness tensor $M_{ijkl}$. The computation of the stiffness tensor $M_{ijkl}$ depends whether an elastic ($F^\mathrm{trial}\ge 0$) or plastic step ($F^\mathrm{trial} < 0$) has been performed within the intergranular strain model and reads:

$$\begin{aligned} M_{ijkl} = \left\{ \begin{array}{lllll} [ m_{R} + (1-m_{R})y_{h} ] (L^\mathrm{hyp}_{ijkl} + \rho ^{\chi } N^\mathrm{hyp}_{ij}N_{kl}) &{} {{\text {for}}} \; F^\mathrm{trial}\ge 0\\ m_{R}L_{ijkl} &{} {{\text {for}}}\; F^\mathrm{trial} < 0 \end{array} \right. \end{aligned}$$

(33)

The stress ${\sigma _{ij}}$ is actualized with the equation:

$$\begin{aligned} {\sigma _{ij}}= {\sigma _{ij}}+ M_{ijkl} \varDelta {\epsilon } _{kl} \end{aligned}$$

(34)

Finally, the void ratio e and the state variable $\varepsilon _\mathrm{acc}$ are actualized:

$$\begin{aligned} \begin{aligned} \varepsilon _\mathrm{acc}&=\varepsilon _\mathrm{acc}+\dfrac{C_a}{R}(1-y_h-\varepsilon _\mathrm{acc})\sqrt{\varDelta \varepsilon _{ij}\varDelta \varepsilon _{ij}}\\ e&=e+(1+e)(\varDelta \varepsilon _{ii}) \end{aligned} \end{aligned}$$

(35)

For the sake of simplicity, we approximate the jacobian with $J_{ijkl}\approx M_{ijkl}$ at the end of the subroutine. Simulations have shown that this approximation leads to numerical convergence.

1.6 Material Parameters

In this section a brief description of the material parameters is given. A summary of the model parameters with their respective names is given in Table 2. In this table, we have also included their suggested range and some useful experiments for their determination.

We basically distinguish three types of parameters: the first related to the behavior of the material under monotonic loading. These parameter are the one from tensors $\mathsf{L}^\mathrm{hyp}$ and $\mathbf{N }^\mathrm{hyp}$, see Appendix A. The hypoplastic model by Wolfferdorff adopted incorporates 8 parameters very well studied in the literature [7, 11]. They correspond to $h_s$, $n_B$, $e_{i0}$, $e_{c0}$, $e_{d0}$, $\alpha$ and $\beta$ and are calibrated using routine tests under monotonic loading, especially oedometric and triaxial tests. A comprehensive guide for their determination can be found in [7, 15]. The second group corresponds to those incorporated in the evolution law of the intergranular strain model. They correspond to $m_R$, R, $\beta _h$ and $\chi _0$ and can be adjusted with cyclic triaxial test. Notice that some of these parameters, such as $m_R$ and R, were already introduced in the intergranular strain model by Niemunis and Herle [11, 13] and therefore their calibration experience can be also used for the present model. A procedure for their determination is explained in some recent works [5, 6, 15]. Lastly, the parameters $C_a$ and $\chi _\mathrm{max}$ are aimed to control the behavior of the model for a large number of repetitive cycles (e.g. $N>15$). They were explained in the work of [15] including some remarks for their calibration. In order to analyze the influence of the parameter $C_a$, we have included some simulations of a cyclic undrained triaxial test in Figs. 3 and 4. These simulations borrow the parameters of the Karlsruhe fine sand (see Table 2) but vary the parameter $C_a=\{0.005,0.015,0.025\}$. The void ratio was set to $e=0.8$ and the initial consolidation pressure to $p_0=100$ kPa. Cycles with a stress amplitude of $q^\mathrm{amp}=50$ kPa were applied. The results shows how increasing values of $C_a$ increases the number of cycles required to reach the critical state line, see e.g. Fig. 4. Hence, in some way the parameter $C_a$ represents how fast the model increases its stiffness due to the application of subsequent cycles. We will show that a similar pattern is observed in finite element simulations of cyclic phenomena.

Table 2. Material constants of the model

Fig. 3.

Simulations of cyclic undrained triaxial test. Parameters of Karlsruhe fine sand. Variation of parameter $C_a$

Fig. 4.

Simulations of cyclic undrained triaxial test. Parameters of Karlsruhe fine sand. Variation of parameter $C_a$

2 Simulations of Experiments

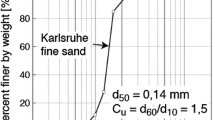
In this section, we present the simulations of some triaxial tests to analyze the model. These simulations consider an element test condition, meaning that homogeneous fields of stress and strain are assumed. The selected material corresponds to the Karlsruhe fine sand, which has been previously calibrated in a former work [15]. This sand presents a mean grain size of $d_{50}=0.14$ and a uniformity coefficient equal to $C_u=d_{60}/d_{10}=1.5$. The grain size is catalogued as sub-angular, and seems not to produce an inherent anisotropy on air pluviated samples due to its roundness [5]. The minimum and maximum void ratios are $e_\mathrm{min}=0.677$ and $e_\mathrm{max}=1.054$ respectively and a specific gravity of $G_s=2.65$ has been determined.

The first simulations correspond to six different undrained triaxial tests under monotonic loading. All these tests were consolidated isotropically to the same initial mean stress $p=200$ kPa and sheared under triaxial conditions. Three of them were sheared under compression while the other three under extension. The void ratios e range between $e={0.698{-}0.964}$ and are indicated in Fig. 5. All tests were simulated with the proposed model and showed in general a good agreement, except by the lack of a quasi-steady state in the simulations. The latter shortcoming is related to the performance of the Wolffersdorff hypoplastic model.

Fig. 5.

Undrained triaxial test under compression and extension. Variation of initial void ratios. Experiments using Karlsruhe fine sand, data from [19]

The next experiments consist on two different cyclic undrained triaxial tests. The first is shown in Fig. 6. The sample was isotropically consolidated to a mean stress of $p_0=200$ kPa and ended with a void ratio of $e=0.800$. Then, stress cycles with an amplitude of $q^\mathrm{amp}=120$ kPa were applied. The experiment exhibited 8 cycles before reaching failure at the critical state line. The simulations also showed the same number of cycles. The post-failure behavior may present some discrepancies. At that state, some other effects such as the cyclic mobility are of importance, but this analysis is out of the scope of the present article. The second cyclic test presents a similar density $e=0.798$ after consolidation but a different stress amplitude $q^\mathrm{amp}=50$ kPa. The sample has been isotropically consolidated to a pressure of $p=100$ kPa. Considering the smaller value of the stress amplitude, a larger number of cycles before reaching failure is expected. The experiment showed about 90 cycles while the simulation showed about 83 cycles (Fig. 7). This is discrepancy is somehow small and may be improved by selecting more appropriated parameters. The accumulated pore pressure $u^\mathrm{acc}$ against the number of cycles N of the two cyclic triaxial tests are plotted in Fig. 8.

Fig. 6.

Undrained triaxial test under cyclic loading. Deviator stress amplitude of $q^\mathrm{amp}=120$ kPa. Experiment using Karlsruhe fine sand, data from [19]

Fig. 7.

Undrained triaxial test under cyclic loading. Deviator stress amplitude of $q^\mathrm{amp}=50$ kPa. Experiment using Karlruhe fine sand, data from [19]

Fig. 8.

Accumulated pore pressure $u^\mathrm{acc}$ against number of cycles N. Experiment using Karlruhe fine sand, data from [19]

Fig. 9.

Geometry and boundary conditions of the finite element simulation

3 Simulations with Finite Elements

We now evaluate the constitutive model in a boundary value problem solved with finite elements. The problem corresponds to a circular shallow foundation subjected to cyclic loading. The finite element model was made by [23] to simulate a scaled model of a shallow foundation constructed in the laboratory of the Institute of Soil Mechanics and Rock Mechanics from the Karlsruhe Institute of Technology [23]. The geometry and the boundary conditions are depicted in Fig. 9. The main objective is to analyze the influence of the parameter $C_a$ in the simulations. Axial-symmetric finite elements with two degrees of freedom per node (only displacements) were employed. The soil corresponds to the Karlsruhe fine sand in dry conditions, i.e. no pore water pressure were included. The problem has been simulated using the software Abaqus Standard. A contact formulation solved by the penalty method has been employed to simulate the frictional interaction between the foundation and the soil with a friction coefficient of 0.5. The foundation material is steel and is simulated with an isotropic elastic model with a Young modulus equal to $E=2.1\times 10^{8}$ kPa and Poisson ratio $\nu =0.3$. The density of the foundation has been neglected on the current analysis.

Fig. 10.

Displacements contours for each case ($C_a=0$, $C_a=0.025$ and $C_a=0.05$)

Fig. 11.

Vertical displacement of the foundation ($C_a=0$, $C_a=0.025$ and $C_a=0.05$)

A geostatic condition has been initially applied assuming a lateral earth coefficient of $K_0=0.5$ and a dry density of the sand equal to $\rho _d=1500$ kg/m$^3$. The initial void ratio has been set to $e=0.8$ and the intergranular strain has been initialized assuming mobilized states in the vertical direction, i.e. $h_{22}=-R$ and $c_{22}=-R/2$, where the subindex 2 points in the vertical direction.

After the geostatic step, a sinusoidal load is applied on the top of the foundation. The load is schematized in Fig. 9 and presents 45 cycles with maximum value equal to $P=0.5$ kN. We consider a very slow load velocity to ignore any dynamic effect. Three different simulations were performed considering the variation of parameter $C_a=\{0,0.025,0.05\}$. The cases with $C_a>0$ consider the extension proposed in [15] to account for repetitive loading. The Fig. 10 presents the contours of the displacements for the three cases at the end of the simulation. The results clearly show an increasing settlement of the foundation with decreasing value of $C_a$. Hence in some way, the parameter $C_a$ simulates the overall increase of the stiffness upon the subsequent cycles. The plots of the vertical displacements $U_y$ on the top of the foundation are shown in Fig. 11.

4 Closure

We have performed some simulations of some experiments to evaluate the accuracy of an ISA-plasticity based model. For large strain ampltiudes ${\parallel } \delta {\varvec{\varepsilon }}{\parallel }>10^{-2}$, the model delivers the hypoplastic relation by Wolffersdorff [21]. The extension by [15] was herein considered to simulate the reduction of the plastic accumulation for increasing number of subsequent cycles. The simulations of element test with cyclic loading under undrained triaxial conditions showed satisfactory results. The model was able to capture approximately the number of cycles required to reach the critical state line. We have also inspected the performance of the model in a boundary value problem of scaled shallow foundation subjected to cyclic loading. With the simulations, we have proved that the current model is able to increase its overall stiffness when it experiences repetitive loading. Currently, some other issues are investigated to improve the model, as for example the cyclic mobility effect and the post-liquefaction behavior.

A Hypoplastic Model from Wolffersdorff

The hypoplastic model by Wolffersdorff has been explained in several works [7, 11, 15, 21]. We outline here the equations required to implement the model. The general equation reads:

$$\begin{aligned} \dot{{\varvec{\sigma }}}={\mathsf{L}}^\mathrm{hyp}:\dot{{{\varvec{\varepsilon }} }}+\mathbf{N }^\mathrm{hyp}\,{\parallel } \dot{{{\varvec{\varepsilon }} }}{\parallel } \end{aligned}$$

(36)

whereby ${\mathsf{L}}^\mathrm{hyp}$ is the “linear” stiffness and $\mathbf{N }^\mathrm{hyp}$ is the “non-linear” stiffness. The linear stiffness ${\mathsf{L}}^\mathrm{hyp}$ reads [21]:

$$\begin{aligned} \dot{{\varvec{\sigma }}}={\mathsf{L}}^\mathrm{hyp}=f_bf_e\dfrac{1}{\hat{{\varvec{\sigma }}} :\hat{{\varvec{\sigma }}}} (F^2\mathsf{I}+a^2\hat{{\varvec{\sigma }}}\hat{{\varvec{\sigma }}}) \end{aligned}$$

(37)

whereby $\hat{{\varvec{\sigma }}}= {\varvec{\sigma }}/\mathrm{tr}{\varvec{\sigma }}$ is the relative stress [11], $\mathsf{I}$ is a unit fourth order tensor for symmetric tensors and the other quantities $f_b$, $f_e$, F and a are scalar functions. The scalar function F is defined as:

$$\begin{aligned} F=\sqrt{\dfrac{1}{8}\tan ^2(\psi )+\dfrac{2-\tan ^2(\psi )}{2+2\sqrt{2}\tan (\psi )\cos (3\theta )}}-\dfrac{1}{2\sqrt{2}\tan (\psi )} \end{aligned}$$

(38)

whereby the factors a, $\theta$ and $\psi$ are defined as:

(39)

and depends on the deviator stress ${\varvec{\sigma }}^*$ and the critical state friction angle $\varphi _c$. The remaining scalar functions $f_b$, $f_e$ and $f_d$ are dependent on the characteristic void ratios proposed by Bauer [2]:

$$\begin{aligned} \begin{aligned} e_i&=e_{i0}\exp \left( -\left( 3p/h_s\right) ^{n_B}\right) \\ e_d&=e_{d0}\exp \left( -\left( 3p/h_s\right) ^{n_B}\right) \\ e_c&=e_{c0}\exp \left( -\left( 3p/h_s\right) ^{n_B}\right) \end{aligned} \end{aligned}$$

(40)

These curves introduces the parameters $e_{i0}$, $e_{d0}$, $e_{c0}$, $h_s$ and $n_B$. The scalar functions $f_e$ and $f_b$ are called picnotropy and barotropy factors and read:

(41)

with the parameter $\beta$. The non-linear stiffness is defined as:

$$\begin{aligned} {\mathbf{N }}^\mathrm{hyp}=f_df_bf_e\dfrac{Fa}{\hat{{\varvec{\sigma }}}:\hat{{\varvec{\sigma }}}}(\hat{{\varvec{\sigma }}}+\hat{{\varvec{\sigma }}}^*) \end{aligned}$$

(42)

with the density factor:

$$\begin{aligned} f_d=\left( \dfrac{e-e_d}{e_c-e_d}\right) ^\alpha \end{aligned}$$

(43)

with the parameter $\alpha$ controlling the model dilatancy.