Abstract
A new three-scale model to describe the coupling between electro-chemistry and hydrodynamics in non-swelling kaolinite clays in steady-state conditions is proposed. The medium is characterized by three separate nano-micro and macroscopic length scales. At the pore (micro)-scale the portrait of the clay consists of micro-pores saturated by an aqueous solution containing four monovalent ions (Na+, H+, Cl−, OH−) and charged solid particles surrounded by thin electrical double layers. The movement of the ions is governed by the Nernst–Planck equations and the influence of the double layers upon the hydrodynamics is modeled by a slip boundary condition in the tangential velocity governed by the Stokes problem. To capture the correct form of the interface condition we invoke the nanoscopic modeling of the thin electrical double layer based on Poisson–Boltzmann problem with varying surface charge density ruled by the protonation/deprotonation reactions which occur at the surface of the particles. The two-scale nano/micro model is homogenized to the macroscale leading to a precise derivation of effective governing equations. The macroscopic model is discretized by the finite volume method and applied to numerically simulate desalination of a clay sample induced by an external electrical field generated by the placement of electrodes. Numerical results indicate strong pH-dependence of the electrokinetics.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Electrokinetic phenomena in electrically charged porous media have received considerable attention with an enormous variety of applications in different fields of science and engineering. Among the broad range of applications, particular emphasis has been given in the current literature to the modeling of subsurface contamination phenomena. In this area the correct description of the electrokinetic couplings involved is of utmost importance in predicting the effectiveness of some clean up technologies [67]. In this context, the strong coupling between hydraulic and charge transport gives rise to electroosmotic flows in contaminated fine-grained soils and slurries which pose a significant issue to the environment giving rise to major technological challenges. Applications of electroosmosis in geotechnical engineering are widespread involving dewatering of clay mineral waste tailings [63], clean up by electrokinetic remediation techniques [67] and contaminant transport mitigation in the sub-surface environment [52]. It is well known that classical clean up techniques such as soil flushing, chemical treatment and bioremediation have been found ineffective when applied to clayey soils with low permeability [42]. Electrokinetic remediation is a promising decontamination technique which exhibits high efficiency in low-permeable media demonstrated in both laboratory tests and field scale applications [1, 3]. The effectiveness of this method, particularly its low operation cost, degree of control over the movement of the contaminants and potential applicability to a wide range of contaminant types has been extensively discussed in the current literature [67]. In recent years, a number of laboratory-scale and field-scale studies have shown the technical feasibility of electrokinetic processes in removing various contaminants from fine-grained soils [17].
Electro-osmotic technology involves application of an external electric field across a pair of electrodes placed in a contaminated soil. As the surface of the colloidal particles immersed in water is electrically charged due to the isomorphous substitutions or broken bonds at particle edges, the applied electric field plays the role of the driving force for electro-osmotic flow and also creates strong interactions between the charged colloidal particles and the aqueous solution. Such complex interactions give rise to many other macroscopically observed electrochemical phenomena such as chemico-osmosis, streaming potential, streaming current, electromigration, electrophoresis and electroviscous effects (see, e.g., [45, 46]).
During the past few decades a significant amount of research has been developed towards the derivation of models capable of capturing coupled electro-chemo-hydro-mechanical effects in charged porous media (see, e.g., [27, 44]). While the basic principles of electrokinetics have been studied for many years, great effort has been made to provide a theoretical description of contaminant migration processes in soils under electric field as a background for subsequent mathematical modeling (see, e.g., [5, 56, 57, 59]). Nevertheless, the accuracy of phenomenological studies to describe electrochemical and physicochemical processes in porous media is questionable because of the numerous couplings involving hydrodynamics, transport phenomena, chemical reactions and electrical effects which bring additional complexity and may lead to inaccurate predictions when using oversimplified models [36, 37]. Coupled phenomena in porous media has also been described by the framework of the mixture theory and thermodynamics of irreversible processes. In this approach, under near-equilibrium isothermal conditions, the interaction between flow, solute flux and electric charge are linearly coupled with the conjugated gradients of hydraulic head, concentration and electric potentials through Onsager’s reciprocity relations (see, e.g., [35, 38, 69]). This framework aims at enhancing the thermodynamic foundation of the macroscopic model by establishing a rational methodology embedded in the second principle of thermodynamics [28].
Despite the widespread development of the aforementioned macroscopic models for electrically charged media, very little information has been available to identify some of the macroscopic electrokinetic coefficients with the clay morphology and local electrical double layer (EDL) properties [43]. Owing to the complexity and variety of chemical and colloid electrochemical processes taking place in such complicated geological media, the correct interpretation of the macroscopic results and constitutive laws of the effective parameters becomes quite difficult [58]. As mixture theoretic approaches are directly conducted at the macroscale, the complex microstructural solid-fluid interactions are overlooked and the magnitude of the electrokinetic coefficients is obtained based on experimental evidence. On the other hand it has been advocated that clay microstructure plays an important role in many macroscopic observed physicochemical and electro-chemical phenomena [4, 6, 49]. Whence, establishing correlations between coupled phenomena at different scales is a crucial issue and may bring substantial improvement in the macroscopic predictions of colloidal systems.
When attempting at bridging electrochemical phenomena at different length scales, multiscale modeling offers an alternative procedure to the purely macroscopic approaches. This framework has been able to capture, in an accurate manner, the coexistence of several strong couplings of different physicochemical and electrochemical nature occurring at disparate space and time scales. Historically, attempts at correlating the morphology of charged porous media with the magnitude of the effective coefficients began by considering idealized stratified microstructures (see, e.g., [23, 29]). Subsequently the up-scaling procedure was generalized to random nano-pore geometries composed of charged particles saturated by an electrolyte solution using averaging procedures [30] and homogenization based on two-scale asymptotic expansions [43, 47, 48]. Two-scale approaches have provided a more realistic macroscopic description of the clay clusters wherein phenomena such as electro-osmosis and electro-migration naturally appear in the homogenized forms of the convection-diffusion equations and Darcy’s law. Recently in [50], for a clay composed of two levels of porosity (nano and micro pores), the homogenized two-scale electro-chemo-mechanical model for the clay aggregates derived in [48] was coupled with the equations governing flow and solute transport in the bulk solution lying in the micro-pore system and a three scale model of dual porosity type was derived wherein the clay clusters act as sources and sinks of mass to the conservation equations of the bulk phase water. In particular, under quasi steady state conditions this approach was capable of reconstructing directly from the nanoscopic numerical description the constitutive laws of the partition coefficient and isotherms of adsorption which govern the immobilization of solutes in the clay clusters.
The above-mentioned approaches were developed for aqueous saline solutions composed of two fully dissociated monovalent ions Na+ and Cl− and constant pH = 7. In addition, electro-chemical phenomena at the finest scale was described by a non-equilibrium version of the electrical double layer theory wherein the net electric potential (total potential subtracted by the streaming potential) is governed by the Poisson–Boltzmann problem with a constant surface charge density arising from the isomorphous substitutions appearing in the Neumann boundary condition at particle surface (see [47, 48] for details). The extension of the multiscale procedure to incorporate partially dissociated H+ and OH− ions in the aqueous solution along with the pH-dependent protonation/deprotonation chemical reactions giving rise to a nonlinear behavior of the surface charge density remains an open issue (see, e.g., [18, 24]). The aim of this paper is to fill this gap. A first attempt at incorporating pH effects within the framework of two-scale homogenization was pursued in [40] considering one-dimensional flow and transport in a smectitic clay composed of parallel particles of face-to-face contact with overlapping between adjacent EDLs. The model proposed herein generalizes this approach to a three-dimensional kaolinite with three disparate length scales (nano, micro and macro) with matrix composed of particles surrounded by thin EDLs (Fig. 1).
In order to characterize more precisely the hierarchy of scales we begin by reviewing kaolinite’s fabric and electro-chemistry [46, 54]. Kaolinite’s mineralogy is characterized by phyllosilicate minerals composed of stacked silicate sheets (Si2O5) linked through oxygen atoms to aluminum oxide/hydroxide layers (Al(OH)3) also called gibbsite layers. The result of this 1:1 arrangement is a flat hexagonal composite layered particle with attraction forces between the two sheets which preclude water hydration consequently mitigating swelling capacity. In contrast to smectites, wherein the chemistry is dominated by the permanent negative surface charge imbalance, a consequence of the isomorphous substitutions of higher valence ions by lower valence ions within the interior of the crystal lattice, the surface charge in kaolinite is dominated by the broken bonds where protonation/deprotonation chemical reactions take place at pH-dependent charged sites located at particle edges [9, 46]. In this picture ion concentrations in the counterion cloud, including the Stern inner compact layer adjacent to the solid surface and the outer Gouy diffuse mobile layer, are ruled by the surface charge and the electric potential at particle surface (zeta potential) whose magnitude depend strongly on the protonation/deprotonation reactions and consequently on the pH [18, 66].
The finest level of the hierarchy of length scales is the nanoscale, wherein the portrait of the soil fabric is an assembly of particles with thin EDLs surrounding each particle (Fig. 1). A typical characteristic length associated with this scale is the Debye’s screening length L D of O(10−9) m which measures the effective thickness of the EDL surrounding each particle [34, 54] and assumed much smaller than the characteristic length of the micropores L D << l (Fig. 2). At this scale chemical reactions take place at particle surface and are coupled with electrical phenomena in the electrolyte solution lying in the thin sharp EDL in the vicinity of the solid. Assuming that the characteristic time scale of the reactions is much smaller than the one associated with the hydrodynamics in the micropores, local thermodynamic equilibrium can be enforced and consequently the electric potential in the electrolyte solution is ruled by the Poisson–Boltzmann problem with a pH-dependent surface charge in the Neumann interface condition [11].
Description of the microscopic and nanoscopic domains
At the microscale (the homogenized nanoscale), whose typical length scale is the averaged size of the micro pores (herein considered O(10−6 m)), the highly heterogeneous solid–fluid surface interactions are represented in an averaged fashion through effective slip boundary conditions on the fluid velocity with the slip ruled by the magnitude of the zeta potential according to the Helmholtz–Smoluchowski model (see, e.g., [21, 31, 50]). In addition, owing to the coarser structure of the micro-pores with larger size void spaces and characteristic length much greater than the EDL thickness, the equations governing the bulk solution (Stokes problem and Nernst–Planck equations [59]) are free of EDL effects. This particular feature distinguishes properties of a bulk fluid from an electrolyte solution and further implies a pointwise form of the electroneutrality condition with local equality between co- and counter-ion concentrations [50, 53].
Assuming local periodicity of the microscopic particle/micro pore arrangement we then adopt the homogenization procedure based on formal matched asymptotic expansion techniques [60] to upscale the microscopic model to the macroscale, wherein the clay and bulk fluid are envisioned as overlaying continua with averaged properties defined at every point of the mixture (Fig. 1). By exploring the closure problems arising from the homogenization procedure we provide nanoscopic representations for the effective coefficients, such as hydraulic and electro-osmotic conductivities in Darcy’s law along with the effective diffusivities which appear in the macroscopic Nernst–Planck equations. Among the features of the model we highlight the three-scale representation of the electroosmotic conductivity in the modified Darcy’s law which was obtained herein from a double averaging procedure of the nanoscopic zeta potential. This allows for a precise numerical reconstruction of the constitutive law of this parameter dependent on salinity and pH of the bulk water.
The three-scale model is discretized by the finite volume method [55] and applied to numerically simulate an electro osmotic experiment of desalination of a kaolinite sample under steady state conditions. The numerical results obtained in the simulations suggest the characterization of different acid and basic regimes of electrokinetic remediation. Depending on the range of pH (above or below the point of zero charge), reverse electroosmotic flow may occur leading to the appearance of anomalous patterns.
Throughout the manuscript we concentrate our analysis on steady state flow and transport where our aim is the accurate three-scale representation of the diffusivities and conductivities. The extension of our study to transient phenomena requires a more elaborate description of the partition coefficients involved in order to capture time-dependent adsorption of the ions in the EDL and on the solid surface [8]. This will be accomplished in future work. The backbone of our research is to illustrate the potential of our three-scale approach in providing a first step towards the derivation of reliable effective constitutive laws arising from bridging nano, micro and macroscopic electrochemical phenomena in chemically active soils.
2 Nanoscale modeling
We begin by presenting the nanoscopic modeling which governs the electro-chemistry of the kaolinite particles at the finest scale. Our picture consists of a two-phase system composed of the solid phase (assumed rigid) which carries a surface charge density, saturated by a continuum dielectric aqueous solution containing four monovalent electrolytes (Na+, H+, Cl−, OH−). We assume absence of the mineral dissolution processes so that the volume fraction of the solid and fluid phases are constant in time. The solvent is considered a dilute solution so that ions are treated as point charges with hydration and steric effects neglected. We adopt the thin electrical double layer assumption wherein the Debye length L D, which measures the effective thickness of the diffuse layer [34], is assumed small compared to the characteristic length scale of the micro-pores (see Fig. 2). Under this assumption adjacent double layers do not overlap and consequently variations in the electric potential normal to the particle are much more pronounced than in the tangential one. Consequently, under local equilibrium conditions, the electric problem is governed by the Poisson–Boltzmann equation posed in a one-dimensional domain [34, 54]. In addition to the ionic concentrations in the electrical double layer (EDL), adsorption/desorption phenomena owing to protonation/deprotonation reactions involving the H+ ions also take place at the surface of the particles. Such chemical reactions have a paramount influence on the magnitude of the surface charge density and the zeta potential and therefore must be incorporated in our nanoscopic description [10, 33, 62]. In our nanoscopic development we assume ion adsorption in the Stern layer negligible so that the surface charge of the EDL is balanced by the one due to chemical reactions at particle edges.
2.1 Electrical double layer
Let {F,R,T} be the set composed of Faraday constant, universal ideal gas constant and absolute temperature and let φ be the electric potential of the EDL along with C i and C ib , i = (Na+, H+, Cl−, OH−), the molar concentration of the ionic species in the EDL and in the bulk fluid, respectively. Denoting \(\overline{\varphi}=F\varphi/RT\) the corresponding dimensionless electric potential, the ionic concentrations in the EDL and in the bulk fluid are related by the Boltzmann distribution [20, 54]
Denote \(\Omega_{*}^{l}=(0, L_{\rm D})\) the one-dimensional nanoscopic subdomain in the direction normal to the clay surface occupied by the electrolyte solution with \(L_{\rm D}:= \left({\widetilde{\epsilon}}_{0}{\widetilde{\epsilon}}_{r} RT/2F^{2}\hbox{C}_{b}\right)^{1/2}\) the Debye’s length [34], \({\widetilde{\varepsilon}}_{0}\) the permittivity of the free space, \({\widetilde{\varepsilon}}_{r}\) the dielectric constant of the solvent and C b the total concentration of cations (or anions) in the bulk fluid constrained by the electroneutrality condition [53]
In the usual fashion let E = −dφ/dz be the component of the electric field orthogonal to the surface with z the normal coordinate with origin located at the solid surface (Fig. 2). Denoting z = ℓ* a point further away from the interface between the electrolyte solution and bulk fluid (ℓ* > L D), the one-dimensional Gauss-Poisson problem reads as [39]
where \(q:= F\left(\hbox{C}_{\rm Na^{+}}+\hbox{C}_{\rm H^{+}}-\hbox{C}_{\rm Cl^{-}}-\hbox{C}_{\rm OH^{-}}\right)\) is the net charge density. Using the Boltzmann distribution (2.1) we have \(q=FC_{b}\left[\exp\left(-{\overline{\varphi}}\right)- \exp{\overline{\varphi}}\right]= -2FC_{b}\sinh{\overline{\varphi}}.\) Together with (2.3) this yields the Poisson–Boltzmann equation
The above equation is supplemented by boundary conditions at particle wall z = 0 and at the distance z = ℓ* away from the interface between the EDL and the bulk solution. For non-overlapping adjacent EDLs the electric field at z = ℓ* vanishes
whereas at the particle surface the electrical field balances the surface charge density σ
In contrast to the bulk solution, where the electroneutrality condition (2.2) is fulfilled pointwisely, in the electrolyte solution next to the kaolinite particles such constraint gives rise to a compatibility condition between surface and net charge density. Using (2.3) and (2.5) in (2.6) we have
The unidimensional Poisson–Boltzmann problem (2.4) together with boundary conditions (2.5) and (2.6) govern the local behavior of electric potential at the nanoscale around the kaolinite particle. Under the thin double layer assumptions a direct relation between φ and the zeta potential ζ: = φ(z = 0) can be obtained (see Appendix 1 for details)
Further combining (2.6), (2.7) with (7.4) (Appendix 1) along with the definition of L D we deduce the following relation between σ and ζ
The system of algebraic equations (2.7) and (2.8) establish our nanoscopic model in terms of the unknowns {φ, ζ} provided σ is known. However as the surface charge and the ζ-potential vary strongly which the pH of the electrolyte solution, the closure of the system is tied-up to the construction of the such dependence which can be accomplished by invoking the kinetics of the protonation/deprotonation reactions presented next (see also [10, 16, 25, 33]).
2.2 Protonation/deprotonation chemical reactions
In our subsequent development we analyze the chemical reactions of protonation/deprotonation nature which occur at the surface of the particle in order to quantify the dependence of σ on the pH and salinity of the electrolyte solution. Hereafter we consider the component of the surface charge density induced by isomorphous substitutions small compared to one due to broken bonds on the edges of the solid particles [13, 26, 46]. Moreover, considering hexagonal form of the kaolinite particles [15, 46] we assume that the charge excess on the basal hydroxyl and siloxane planes on the upper and lower planes of the hexagonal solid particle are small compared to the one produced on the lateral edges containing aluminol and silanol groups (Fig. 3) [14, 15].
Kaolinite particle geometry with structure composed of siloxane/hydroxyl planes and broken bond edges
2.2.1 1-pK Model
For the sake of simplicity we henceforth adopt a model based on a single protonation/deprotonation chemical reaction which takes place in a typical octahedral sheet (>M−OH) representative of the reactive groups on the lateral edges of the solid surface. The extension of the procedure below to higher order pK-models incorporating additional protonation reactions at the broken bonds of the tetrahedral sheets [10, 41] can be pursued adopting the same methodology. Likewise the underlying assumption of the EDL theory, we consider a fast characteristic time scale of the chemistry compared to the one associated with the hydrodynamics and transport so that local thermodynamic equilibrium can be enforced. In this context the protonation/deprotonation reaction is represented in the form [10]
where M represents the metallic ion lying in the tetrahedral (Si4+) or octahedral (Al3+) layers. Under equilibrium we can adopt the law of mass action and define the equilibrium constant associated with (2.9) as the ratio between the molarity product of the reagents and product constituents. Denoting γ j the surface density of the reagent/product j = M−OH, M−OH2 and \(\Upgamma_{\rm MAX}:= \gamma_{\{( > \hbox{M}-\hbox{OH}_{2})^{+\frac{1}{2}}\}} + \gamma_{\{( > \hbox{M}-\hbox{OH})^{-\frac{1}{2}}\}}\) the maximum surface density (mol/m2) and {j} = γ j /ΓMAX the dimensionless surface concentration of the j species, we have by definition
where \(\hbox{C}_{\rm H^{+}_{0}}\) denotes the H+ concentration at the kaolinite surface (mol/l). It should be noted that when combining the above definition with Boltzmann distribution \(\hbox{C}_{\rm H_{0}^{+}}=\hbox{C}_{\rm Hb^{+}}\exp(-{\overline{\zeta}})\) allows to rewrite the equilibrium constant in terms of bulk concentration and the dimensionless \({\overline{\zeta}}\) -potential which strongly depends on \(\hbox{C}_{{\rm H}b^{+}}\) in a non-linear fashion. From the above definition the excess in surface charge due to the protonic adsorption \(\gamma_{\rm H^{+}}\) is defined as
where z = 1/2 is the valence. To complete the characterization of σ one needs to postulate a constitutive law for \(\gamma_{\rm H^{+}}\) which can be obtained by rewriting (2.10) in the form
which together with the definition of the maximum surface density ΓMAX gives
Using (2.12) in (2.11) we deduce the constitutive laws
and
The above result furnishes the desired constitutive relation for the surface charge density provided experimental data are available to evaluate the pair of constants (K, ΓMAX). Such information can be incorporated in the model through the titration experiments described next.
2.2.2 Titration acid/basic experiments
The acid/basic titration experiment [13, 14] consists of a commonly adopted procedure in analytical chemistry to determinate an unknown concentration through the addition of a reacting solution with known concentration. Within this experimental technique one can construct the dependence of the protonic adsorption \(\gamma_{\rm H^{+}}\) as a function of the pH of the bulk fluid for a given salinity [25, 33].
In our subsequent development we invoke the titration experiment described in [33] who presented the constitutive dependence \(\gamma_{\rm H^+}=\gamma_{\rm H^{+}} \left(\hbox{C}_{{\rm N}ab^{+}},\hbox{C}_{{\rm H}b^{+}}\right)\) for a kaolinite clay (Fig. 4). We may observe at pH = 5.5 the existence of an isoelectric point, which coincides with the point of zero net protonic charge and the pH of immersion of the kaolinite, under the absence of other sources of surface charge such as isomorphic substitutions (see [65]). In the regime pH > 5.5, referred herein to as “basic regime”, the chemistry is governed by a deprotonation chemical reaction and a negative surface charge density. Conversely in the acid regime a protonation reaction takes place leading to anomalous positive surface charge.
Experimental acid–basic titration curve of kaolinite (from [33])
In order to compute the pair of constants (K, ΓMAX) we proceed by minimizing the distance between the solution of the algebraic equations (2.1), (2.8) and (2.14) with i = H+ and the experimental data reported in [33]. Denoting \(\Uplambda := \left(8{\widetilde{\epsilon}}_{0}{\widetilde{\epsilon}}_{r}RT\hbox{C}_{b}\right )^{1/2}\) and \({\overline{\zeta}} := F\zeta/RT\) the nanoscopic governing equations are summarized below
For each pair of bulk concentrations \((\hbox{C}_{{\rm N}ab^{+}}, \hbox{C}_{\rm Hb^{+}})\) the above system can be solved for ζ, σ and \(\hbox{C}_{\rm H_{0}^{+}}.\) By eliminating σ and \(\hbox{C}_{\rm H_{0}^{+}}\) we are left with a single nonlinear algebraic equation for the ζ-potential
The evaluation of K follows immediately by simply invoking the constraint σ = 0 and ζ = 0 at pH = 5.5. By enforcing this constraint in (2.13) and (2.14) this yields \(\gamma_{\rm H^{+}}=0\) which implies \(\gamma_{\{( > \hbox{M}-\hbox{OH}_{2})^{+\frac{1}{2}}\}} = \gamma_{\{( > \hbox{M}-\hbox{OH})^{-\frac{1}{2}}\}},\quad \hbox{C}_{\rm H^{+}_{0}}=\hbox{C}_{\rm Hb^{+}}, K\hbox{C}_{{\rm H}b^{+}}=1\) and K = 105.5 l/mol. To compute ΓMAX we perform a simple optimization procedure by choosing trial values (between 1 and 10 sites/nm2) for ΓMAX as suggested in [33] to minimize the distance between the computational results of \(\gamma_{H^{+}}=2\sigma/F\) and experimental data of Fig. 4. We then insert the values ΓMAX = 3.0, 5.5, 10 sites/nm2 along with \(\hbox{C}_{{\rm N}ab^{+}}=0.01\,\hbox{mol/l}\) and solve the algebraic non linear equation (2.16s) for ζ as a function of \(\hbox{C}_{{\rm H}b^{+}}\) using Newton’s method. For each value of the zeta potential calculated we compute \(\hbox{C}_{\rm H_{0}^{+}}\) from (2.15) and protonic adsorption from (2.13) and construct numerically the titration curve. In Figs. 5, 6 and 7, we display the numerical results for the protonic adsorption as a function of the pH for three chosen values of ΓMAX. When comparing the plots of \(\gamma_{\rm H^{+}}\) with the ones obtained in [33] this suggests that the choice ΓMAX = 3.0 sites/nm2 provides good agreement between the plots. It is worth noting that such number lies in a narrow range delimited by values obtained experimentally by other authors. For instance Leroy and Revil [41] reported Γmax = 5.5 sites/nm2 whereas Hoch and Weerasooriya [32] Γmax = 2 sites/nm2.
Computationally obtained titration curve for the choice ΓMAX = 3.0 sites/nm2
Computationally obtained titration curve for the choice ΓMAX = 5.0 sites/nm2
Computationally obtained titration curve for the choice ΓMAX = 10.0 sites/nm2
By inserting the values K = 105.5 l/mol and ΓMAX = 3.0 sites/nm2 in (2.16) we can build-up the constitutive law of the ζ-potential as a function of pH and \(\hbox{C}_{{\rm N}ab^{+}}.\) The numerical results are displayed in Figs. 8 and 9. We observe, a somewhat stronger dependence of the ζ-potential on the pH compared to that on the ionic-strength. The increase in acidification gives rise to the protonation reaction leading to an increase of ζ towards positive values and vice-versa in the basic regime. Given the ζ-potential we invoke (2.15(b)) and compute the constitutive response of surface charge density (see Figs. 10, 11).
Strong dependence of the ζ-potential on pH
Weak dependence of the ζ-potential on \(\hbox{C}_{{\rm N}ab^{+}}\)
Computationally obtained surface charge as a function of pH
Computationally obtained surface charge as a function of sodium concentration \(\hbox{C}_{{\rm N}ab^{+}}\)
To summarize our findings at the nanoscale, the main result which will be subsequently explored in the microscopic modeling is the numerical reconstruction of the constitutive law \(\zeta=\zeta(\text{C}_{\text{N}ab^{+}}, \text{C}_{\text{H}b^{+}})\) depicted in Figs. 8 and 9.
3 Microscopic modeling
Considering the thickness of the EDL small compared to the characteristic length of the micro-pores, the nanoscopic model is effectively represented through boundary conditions on the particle/micro-pore interface. Thus, to construct the microscopic description we postulate governing equations for flow and transport in the bulk fluid lying in the micro-pores and up-scale the nanoscopic results to the microscale to match conditions at the interface.
We begin by presenting a brief discussion on the electro-chemical phenomena which take place in the aqueous bulk solution, more precisely hydrolyze and electrolysis reactions which give rise to the dissociated ions Na+, H+, Cl−, OH−. Subsequently these phenomena are incorporated in the hydrodynamics and transport equations of the solutes.
3.1 Ionization reactions
The appearance of ions completely or partially dissociated in the aqueous solution is explained by the ionization theory which describes the thermodynamic equilibrium between ions and non-ionized solvent molecules [19]. For example, sodium chloride NaCl in water is completely dissociated and therefore is commonly referred to as a strong electrolyte. The corresponding ionization reaction is represented in the form
In contrast water molecules are often partially dissociated due to a weak phenomenon commonly refereed to as auto-ionization [19]. Such partial dissociation is commonly described by the chemical reaction
The degree of dissociation of the above reaction is dictated by the ionic product of water, defined by the product of the molar H+ and OH− concentrations [19].
3.2 Electrolysis reactions
The application of a continuum electric current through the anode and cathode placed in the kaolinite gives rise to electrolysis chemical reactions at the electrodes. At the anode, water oxidation takes place producing hydrogen ions H+ and oxygen gas O2 whereas at the cathode a reduction chemical reaction occurs giving rise to hydroxyl ions OH− and hydrogen gas H2. These reactions are represented in the form [3, 67]
-
Anode (+):
$${\text{2H}}_{\text{2}} {\text{O}} - 4e^{-} \to {\text{O}}_2 \uparrow + 4{\text{H}}^{+}$$ -
Cathode (−):
$$ {\text{2H}}_{\text{2}} {\text{O}} - 2e^{-} \to {\text{H}}_2 \uparrow + 2{\text{OH}}^{-}. $$
An important consequence of the production of ions at the electrodes is the appearance of acid and basic fronts toward the anode and cathode respectively [1, 3, 17]. Owing to the higher diffusivity of the H+ ions compared to the OH−, the acid front is the dominant diffusive phenomenon. In the subsequent development we incorporate the above-mentioned phenomena in the microscopic governing equations.
3.3 Microscopic governing equations
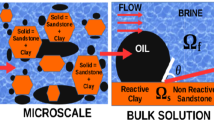
Let \(\Upomega=\Upomega_{\rm s}\cup \Upomega_{f} \subset \Re^{3}\) be the microscopic domain occupied by a biphasic porous media composed of solid particles and micro-pores filled by a bulk fluid (Fig. 2). The solid phase occupies the domain Ωs and is formed by kaolinite particles carrying the nonlinear surface charge density σ. The subdomain Ω f is occupied by the bulk solution containing four ionic monovalent solutes (Na+, H+, Cl−, OH−). In our subsequent analysis we consider steady-state flow and transport with the aqueous solution movement and ion transport governed by the classical theory of viscous fluids and Nernst-Planck equations, respectively [59].
3.3.1 Hydrodynamics
Assuming the bulk fluid an aqueous Newtonian incompressible solution, neglecting gravity and convection/inertial effects, the hydrodynamics is governed by the classical Stokes problem
where v is the fluid velocity, p the pressure and μ f the water viscosity.
3.3.2 Ion transport
In addition to the advection induced by the velocity v, ion diffusion is due to the sum of Fickian and electromigration components which govern the spreading of the ionic species under concentrations and electric potential gradients, respectively [61, 64]. Recalling the steady-state assumption, the ion concentrations in the bulk solution are governed by the Nernst–Planck equation [59]
where D i are the binary water–ion diffusion coefficients \((i=\hbox{Na}^{+}, \hbox{H}^{+}, \hbox{Cl}^{-}, \hbox{OH}^{-}), {\overline{\phi}}:= F\phi/RT\) the dimensionless microscopic electrical potential which arise from the introduction of the electrodes and \({\dot{m}}\) a source term which quantifies the mass production of H+ and OH− due to the water hydrolysis.
The set of microscopic governing equations, formulated in terms of the unknowns \(\{{\bf v}, p, \phi, \hbox{C}_{{\rm N}ab^{+}}, \hbox{C}_{{\rm H}b^{+}}, \hbox{C}_{{\rm Cl}b^{-}}, \hbox{C}_{{\rm OH}b^{-}}, {\dot{m}}\},\) is given by (3.2) and (3.3) along with the electroneutrality condition (2.2) and the ionic product of water (3.1).
3.3.3 Formulation in primary unknowns
In the analysis that follows we formulate the microscopic governing equations in primary unknowns which we select as velocity, pressure, electric potential and cation concentrations. We then proceed by eliminating the anion concentrations and the source term \({\dot{m}}.\) By subtracting (3.3(d)) from (3.3(b)) and using (3.1) we obtain
The above nonlinear steady form of the Nernst–Planck equation will be henceforth refereed to as the pH-equation. Since there are no source terms in (3.3(a)), the sodium transport equation remains invariant in the reduction of variables. Thus, it remains to derive an equation for the electric potential ϕ which follows by invoking conservation of charge. To derive this result we begin by defining the electric current I f
denotes the total convective/diffusive ionic flux of each solute. By subtracting the Nernst–Planck relations (3.3) for the anions from the cations and using the above definition together with the electroneutrality condition (2.2) and the ionic product of water (3.1) we obtain conservation of charge
with the new coefficients given by
3.3.4 Boundary conditions
The above system of microscopic equations is supplemented by boundary conditions on the particle/micropore interface Γ fs (Fig. 2). Recalling the thin double layer assumption L D ≪ l, where l is a characteristic length of the pores, the EDL is treated as a boundary layer in the vicinity of the particles and modeled microscopically by a slip condition in the tangential velocity component. Denoting n and \({\varvec{\tau}}\) the normal and tangential vectors to the interface Γ fs , the boundary conditions for the velocity in the Stokes problem read as
where V slip is a scalar field defined at the interface which governs the jump in the tangential velocity component. The slip velocity is nothing but the transversal averaging across the thin diffuse layer of the nanoscopic elecroosmotic tangential velocity governed by the modified Stokes problem including the additional body force term of Coulomb type [48]. For thin double layers such up-scaling procedure gives rise to the well known Helmholtz-Smoluchowski slip [21, 31, 50] wherein V slip is governed by the electroosmotic component of Darcy’s law with the electroosmotic permeability K E dictated by the magnitude of the ζ-potential (see Appendix 2 for details). We then have
The complete characterization of the slip velocity is accomplished by invoking the constitutive law \(\zeta=\zeta(\hbox{C}_{{\rm N}ab^{+}}, \hbox{C}_{{\rm H}b^{+}})\) reconstructed from the nanoscopic modeling (Figs. 8, 9).
Under steady state conditions and recalling the assumption of absence of mineral dissolution reaction the transient flux related to ion adsorption on the particle surface vanishes [8] and therefore homogeneous Neumann conditions for the ionic fluxes are enforced
Finally, after eliminating the anion concentrations, the above boundary conditions are rephrased in primary unknowns
and
3.4 Summary of the two scale model
The two-scale nanoscopic/microscopic steady-state model consists in: Given the constants \(\{\mu_{f}, K_{W}, D_{\rm Na^{+}}, D_{\rm H^{+}} D_{\rm Cl^{-}}, D_{\rm OH^{-}}, F, R, T, A\}\) the functions \(\{\Uptheta, {\widehat{D}}_{H}, B\}\) depending on \(\hbox{C}_{{\rm H}b^{+}},\) and the coefficient C depending on both \(\hbox{C}_{{\rm N}ab^{+}}\) and \(\hbox{C}_{{\rm H}b^{+}},\) find the microscopic fields \(\{{\bf v}, p, \hbox{C}_{{\rm N}ab^{+}}, \hbox{C}_{{\rm H}b^{+}}, \phi, {\bf I}_{\bf f}, {\bf J}_{{\bf Na}^{+}}, {\bf J}_{{\bf H}^{+}}\}\) satisfying
supplemented by boundary conditions
with the constitutive response of zeta potential \(\zeta=\zeta(\hbox{C}_{{\rm N}ab^{+}}, \hbox{C}_{{\rm H}b^{+}})\) solution of the nanoscopic relations (2.16) reconstructed numerically in Figs. 8 and 9.
4 Homogenization
In this section we apply the asymptotic homogenization theory [60] to upscale the microscopic model to the macroscale. The kaolinite is then idealized as a bounded domain characterized by a periodic structure and two characteristics length scales; the characteristic microscopic scale l of the order of the size of the micropores and the macroscopic length scale L of the overall dimension of the medium. Within the framework of homogenization introduce the perturbation parameter ɛ = l/L and adopt the assumption of scale separation ɛ ≪ 1. The family of perturbed models, referred herein to as ɛ-models, consist of properly scaled equations posed in the macroscopic domain Ωɛ, considered the union of disjoint fluid and solid sub-domains Ωɛ f and Ωɛ s along with scaled boundary conditions on the interface Γɛ fs . The perturbed domain Ωɛ is reconstructed by replication of a micro cell Y ɛ. In a similar fashion the sub-domains Ωɛ f and Ωɛ s along with the interface Γɛ fs are given by the union of adjacent cell sub-domains Y ɛ f and Y ɛ s and ∂Y ɛ fs interfaces respectively. Each cell is congruent to a standard unitary parallelepiped period Y composed of sub-domains Y f and Y s with common boundary ∂Y fs . Our starting point ɛ = 1 corresponds to our microscopic model. The basic problem consists of investigating the asymptotics as \(\varepsilon\rightarrow 0\) and obtain the homogenized limit as the scale of the heterogeneity tends to zero.
Following the classical homogenization analysis of the Stokes problem, the fluid viscosity is scaled by ɛ2 [7]. In order to estimate the Peclet number we consider typical data of an electrosmosis experiment (see, e.g., [2]). For \(D_{{\rm H}^{+}}=9.31\times 10^{-9}\hbox{m}^{2}/\hbox{s}, L=0.8\) m and electroomostic Darcy’s velocity V D = 2.5 × 10−9 m/s we have \(Pe=V_{\rm D}L/D_{{\rm H}^{+}}=0.2\approx O(1).\) Making use of the above estimates the ɛ-model reads as
and
4.1 Matched asymptotic expansions
To upscale the microscopic model to the macroscale we adopt the formal homogenization procedure based on perturbation expansions [7, 60]. Within this framework each property is considered dependent on both global and local length scales in the form f = f(x,y), where x and y denote the macroscopic and microscopic coordinates, respectively. Up to a translation x and y are related by y = x/ɛ. By the chain rule the differential operator is replaced by ∇ = ∇ x + ɛ−1∇ y . The usual procedure to obtain the homogenized problem consists in postulating asymptotic expansions for the unknowns
with the functions f i = f i(x, y) (i = 0, 1, 2, ...) y-periodic. In the subsequent notation we adopt the superscript “0” to designate the function \({{\mathcal{Y}}}=\{\Uptheta,{\widehat{D}}_{H}, B, C, \zeta, V_{\rm slip}\}\) calculated at \(\hbox{C}_{{\rm N}ab^{+}}=\hbox{C}_{{\rm N}ab^{+}}^{0}\;\hbox{and}\; \hbox{C}_{{\rm H}b^{+}}=\hbox{C}_{{\rm H}b^{+}}^{0}\) and the superscript “1” to denote the first-order component of the Taylor series expansion of \({{\mathcal{Y}}}(\hbox{C}_{{\rm N}ab})\;(\hbox{or}\;{{\mathcal{Y}}}(\hbox{C}_{{\rm H}b^{+}})),\) given by \({{\mathcal{Y}}}^{1}=\partial {{\mathcal{Y}}}/\partial \hbox{C}_{{\rm N}ab^{+}}|_{\hbox{C}_{{\rm N}ab^{+}}^{0}}\left(\hbox{C}_{{\rm N}ab^{+}}-\hbox{C}_{{\rm N}ab^{+}}^{0}\right)= \varepsilon \partial {{\mathcal{Y}}}/\partial \hbox{C}_{{\rm N}ab^{+}}|_{\hbox{C}_{{\rm N}ab^{+}}^{0}}\hbox{C}_{{\rm N}ab^{+}}^{1}.\) Inserting the ansatz into the microscopic governing equations (4.1)–(4.2) and collecting the successive power of ɛ we obtain successive equations at different orders:
whereas the successive orders of the interface conditions read as
4.2 Non-oscillatory variables
We begin by collecting our set of slow y-independent variables. From (4.7) we have \(\nabla_{y}p^{0}\left({\bf x}, {\bf y}, t\right)=0\) which implies \(p^{0}\left({\bf x}, {\bf y}, t\right)=p^{0}\left({\bf x}, t\right).\) In addition, Eqs. (4.3)–(4.5) together with the Neumann boundary conditions (4.19)–(4.21) may be rewritten in the form
where \({\varvec{\Uppsi}}^{0}:=\{\hbox{C}_{{\rm N}ab^{+}}^{0}, \hbox{C}_{{\rm H}b^{+}}^{0}, \phi^{0}\}\) and M 0 the matrix
The solution of the above homogeneous Neumann problem is simply \(\hbox{C}_{{\rm N}ab^{+}}^{0}\left({{\mathbf{x}}}, {{\mathbf{y}}}, t\right)=\hbox{C}_{{\rm N}ab^{+}}^{0}\left({{\mathbf{x}}}, t\right), \hbox{C}_{{\rm H}b^{+}}^{0}\left({{\mathbf{x}}}, {{\mathbf{y}}}, t\right)=\hbox{C}_{{\rm H}b^{+}}^{0} \left({{\mathbf{x}}}, t\right)\) and \({\overline{\phi}}^{0}\left({{\mathbf{x}}}, {{\mathbf{y}}}, t\right) = {\overline{\phi}}^{0}\left({{\mathbf{x}}}, t\right).\) Moreover, by invoking the definitions of the coefficients we also have \({{\mathcal{Y}}}^{0} ({{\mathbf{x}}},{{\mathbf{y}}},t):= \{\Uptheta^{0},{\widehat{D}}_{H}^{0}, B^{0}, C^{0}, \zeta^{0}, V_{\rm slip}^{0}\} = {{\mathcal{Y}}}^{0} ({{\mathbf{x}}},t).\) Thus our set of non-oscillatory variables is \(\{p^{0}, \hbox{C}_{{\rm N}ab^{+}}^{0}, \hbox{C}_{{\rm H}b^{+}}^{0}, {\overline{\phi}}^{0}, \Uptheta^{0}, {\widehat{D}}^{0}_{\rm H}, \zeta^{0}, B^{0}, C^{0}, V_{\rm slip}^{0}\}.\)
4.3 Microscopic closure problems
Since \(\{\hbox{C}_{{\rm N}ab^{+}}^{0}, \hbox{C}_{{\rm H}b^{+}}^{0}, \phi^{0}, \Uptheta^{0}, {\widehat{D}}^{0}_{H}\}\) are independent of the fast variable all terms containing their gradient with respect to y vanish. Thus, to establish the local closure problems for \({\varvec{\Uppsi}}^{1}=\{\hbox{C}_{{\rm N}ab^{+}}^{1}, \hbox{C}_{{\rm H}b^{+}}^{1},\phi^{1}\}\) we note that using the local incompressibility condition (4.6), only the last terms in (4.8), (4.9) and (4.10) survive. When combined with the constitutive laws (4.11)–(4.13) and boundary conditions (4.25)–(4.27) this yields the local Neumann problems
Recalling that the components of the matrix M 0 in (4.31) are y-independent, by linearity the solution can be represented in the form
with the characteristic tortuosity vectorial function f = f(y) satisfying the canonical Neumann problem
4.4 Macroscopic transport equation
To derive the macroscopic steady-state Nernst–Planck equation for the Na+ and H+ transport we begin by introducing the volume averaging operator over the periodic cell
By averaging (4.16) and (4.17) we obtain
Recalling that \(\{\hbox{C}_{{\rm N}ab^{+}}^{0}, \hbox{C}_{{\rm H}b^{+}}^{0}, {\overline{\phi}}^{0}, \Uptheta^{0}, {\widehat{D}}^{0}_{H}\}\) are y-independent defining \({\bf V}_{\bf D}^{\bf 0} := \langle {\bf v}^{\bf 0}\rangle\) the macroscopic Darcy’s velocity, using Gauss theorem and boundary conditions (4.22), (4.23), (4.28) and (4.29) we have
Using the constitutive laws for the fluxes (4.11) and (4.12) along with the closure relations in (4.32) we obtain the macroscopic results
with the effective diffusivities defined by
4.5 Macroscopic conservation of charge
The effective charge conservation equation can be obtained in a straightforward fashion. By averaging (4.18) and using boundary condition (4.30) we obtain
which furnishes
Denoting \({\bf I}_{\bf f}^{\bf eff}:= \langle{\bf I}_{\bf f}^{\bf 0}\rangle\) the effective current, by combining (4.32) for the concentration and potential fluctuations with (4.13) we obtain the macroscopic constitutive law
with the effective parameters given as
4.6 Macroscopic Darcy law
To derive the macroscopic form of Darcy’s law we begin by using the closure relation for the electric potential (4.32(c)) in (4.24) to obtain for the slip velocity
Combining the above result with the mass balance (4.6) and the momentum equation (4.15) we obtain the local Stokes problem formulated in the pair (v 0, p 1)
To derive Darcy’s law we proceed in a similar fashion to [47] and decompose velocity and pressure fluctuation into their hydraulic and electroosmotic components \({{\mathbf{v}}}^{0}={\bf v}_{\bf P}^{\bf 0}+{\bf v}_{\bf E}^{\bf 0}\) and p 1 = p 1 P + p 1 E with each one satisfying the local cell problems
and
The local system (4.34) for \(\{{{\mathbf{v}}}_{{\mathbf{P}}}^{{\mathbf{0}}}, p^{1}_{P}\}\) is nothing but the classical closure problem which gives rise to the hydraulic conductivity [7]. Denoting {e j} (j = 1, 2, 3) an orthonormal basis, define the tensorial periodic function \({{\varvec{\kappa}}_{\user2{P}}}\) and the vectorial field \({\varvec{\pi}}_{{\user2{P}}},\) with vectorial components \({\varvec{\kappa}}_{{\user2{P}}}^{{\user2{j}}}\) and scalars π j P respectively satisfying the canonical problems
By exploring linearity between (4.34) and (4.36) we obtain
Unlike (4.34), the cell problem for v 0 E is ruled by the slip boundary condition. By invoking the closure problem for the tortuosity function f one may observe that (4.35) admits a solution of the type
By adding (4.37) and (4.38) yields the following constitutive law for the total microscopic velocity
After averaging we obtain the macroscopic Darcy’s law
with the effective conductivities defined as
The macroscopic coefficients K eff P and K eff E are nothing but the macroscopic hydraulic and electroosmotic conductivities [47, 48]. It should be noted that since the closure relation for K eff E contains the zeta potential, by combining the nanoscopic constitutive law (2.16) for ζ0 with (4.40(b)) we can build-up numerically the dependency \({{\mathbf{K}}}_{{\mathbf{E}}}^{{\mathbf{eff}}}= {{\mathbf{K}}}_{{\mathbf{E}}}^{{\mathbf{eff}}} (\hbox{C}_{{\rm N}ab^{+}}^{0},\hbox{C}_{{\rm H}b^{+}}^{0}).\) This result is of utmost importance as it bridges nanoscopic/microscopic and macroscopic results. Unlike the electroosmotic permeability which depends on the pair \(\{C^{0}_{{\rm N}ab^{+}}, C^{0}_{{\rm H}b^{+}}\},\) the hydraulic permeability K eff P is only dictated by the cell geometry and fluid viscosity.
4.7 Macroscopic mass balance
The macroscopic mass conservation can easily be obtained by averaging (4.14) using the divergence theorem along with boundary condition (4.23) to obtain
which when combined with (4.39) furnishes
4.8 Summary of the three scale model
We are now ready to formulate our three-scale steady-state problem. Let Ω be the macroscopic domain occupied by the kaolinite saturated by an aqueous solution containing four monovalent ions {Na+, H+, OH−, Cl−}. Given the set of constants \(\{F, {\widetilde{\varepsilon}}_{0}, {\widetilde{\varepsilon}}_{r}, \mu_{f}, D_{\rm Na^{+}}, D_{\rm H^{+}}, D_{\rm Cl^{-}}, D_{\rm OH^{-}}, K_{W}\},\) the pair of characteristics functions \(\{{{\mathbf{f}}}, {{\varvec{\kappa}}_{P}}\},\) solution of (4.33) and (4.36), the pair of functions \(\{\Uptheta^{0}, {\widehat{D}}_{\rm H}^{0}\}\) depending on \(\hbox{C}_{{\rm H}b^{+}}^{0},\) and ζ0 depending on \(\{\hbox{C}_{Hb^{+}}^{0}, \hbox{C}_{Nab^{+}}^{0}\}\) solution of the nanoscopic problem (2.16), find the macroscopic unknowns \(\{\hbox{C}_{{\rm N}ab^{+}}^{0}, \hbox{C}_{{\rm H}b^{+}}^{0}, p^{0}, \phi^{0}, {{\mathbf{V}}}_{{\mathbf{D}}}^{{\mathbf{0}}}, {{\mathbf{J}}}_{{{\mathbf{Na}}}^{+}}^{{\mathbf{eff}}}, {{\mathbf{J}}}_{{{\mathbf{H}}}^{+}}^{{\mathbf{eff}}}, {{\mathbf{I}}}_{{\mathbf{f}}}^{{\mathbf{eff}}}\},\) functions of (x,t), satisfying
with the effective parameters \(\{{{\mathbf{K}}}_{{\mathbf{E}}}^{{\mathbf{eff}}}, {{\mathbf{K}}}_{{\mathbf{P}}}^{{\mathbf{eff}}}, {{\mathbf{D}}}_{{{\mathbf{Na}}}^{+}}^{{\mathbf{eff}}}, {\widehat{{\mathbf{D}}}}_{{{\mathbf{H}}}^{+}}^{{\mathbf{eff}}}, {{\mathbf{A}}}^{{\mathbf{eff}}}, {{\mathbf{B}}}^{{\mathbf{eff}}}, {{\mathbf{C}}}^{{\mathbf{eff}}}\}\) solution of the microscopic closure problems posed in the unit cell
In the above three-scale representation of the medium the geometry of the micropores is described by the characteristic functions \(({\bf f}, {{\varvec{\kappa}}_{P}})\) whereas the electro-chemistry at the nanoscale is propagated to the macroscale through the relation between the effective coefficients K eff E and the nanoscopic ζ0-potential depending on \(\{\hbox{C}^{0}_{{\rm N}ab^{+}}, \hbox{C}^{0}_{{\rm H}b^{+}}\}.\) Finally, after computing \(\hbox{C}^{0}_{{\rm N}ab^{+}}\;\hbox{and}\;\hbox{C}^{0}_{{\rm H}b^{+}}\) we can solve for the anion concentrations \(C^{0}_{\hbox{Cl}b^{-}}\;\hbox{and}\;\hbox{C}^{0}_{{\rm OH}b^{-}}\) within a post-processing approach considering (3.1) and the electroneutrality condition (2.2) at O(ɛ0).
5 Computational results
To illustrate the potential of the proposed three-scale approach in providing accurate numerical predictions of pH-dependent electrokinetic steady flows we simulate a one-dimensional problem of an electro-osmosis experiment for desalinization of a kaolinite sample. For simplicity we consider stratified microstructure of the clay with geometry composed of parallel particles of thickness 2δ separated by a fixed distance 2H (Fig. 12). In this form of microstructure the slow and fast coordinates x = (x,·,·) and y = (·,y,·) are parallel and orthogonal to the particle surface, respectively. Furthermore, since flow and ion transport occur only in the x-direction we only keep track of the axial components of the fluxes \(\{{{\mathbf{J}}}_{{{\mathbf{Na}}}^{+}}^{{\mathbf{eff}}}, {{\mathbf{J}}}_{{{\mathbf{H}}}^{+}}^{{\mathbf{eff}}}, {{\mathbf{I}}}_{{\mathbf{f}}}^{{\mathbf{eff}}}, {{\mathbf{V}}}_{{\mathbf{D}}}^{{\mathbf{0}}}\}\) and the tensors \(\{{{\mathbf{K}}}_{{\mathbf{E}}}^{{\mathbf{eff}}}, {{\mathbf{K}}}_{{\mathbf{P}}}^{{\mathbf{eff}}}, {{\mathbf{D}}}_{{\mathbf{Na}}}^{{\mathbf{eff}}}, {\widehat{{\mathbf{D}}}}_{{{\mathbf{H}}}^{+}}^{{\mathbf{eff}}}, {{\mathbf{A}}}^{{\mathbf{eff}}}, {{\mathbf{B}}}^{{\mathbf{eff}}}, {{\mathbf{C}}}^{{\mathbf{eff}}}\}\) denoted herein without boldface. Under these assumptions the macroscopic model reduces to the system of ordinary equations
Denoting {κ P , f} the axial and transversal components of \(\{{{\varvec{\kappa}}_{P}}, {\bf f}\}\) the simplified version of the microscopic cell problems for the tortuosity (4.33) and hydraulic conductivity (4.36) for a stratified microstructure are given by
and
The local problem (5.9) implies that f is y-independent and therefore the tortuosity df/dy vanishes. The classical solution of (5.10) is simply π = cte and κ P parabolic in y. Furthermore, in the stratified microstructure of parallel particles the cell averaging is nothing but the transversal averaging and therefore, after upscaling the local parabolic profile for κ P we obtain the local representation of hydraulic conductivity [48]
In addition, denoting n = H/(H + δ) the porosity we have the following representations for the other effective parameters in (4.42)
Stratified arrangement of face-to-face particles
5.1 Numerical examples
The macroscopic system of ODE’s (5.1)–(5.8) is discretized by the finite volume method [55] and applied to numerically simulate the one-dimensional electroosmosis experiment depicted in Fig. 13. In this example an anode and a cathode are placed at the positions x = 0 and x = L respectively wherein for simplicity the electric potential, pressure, salinity and pH are controlled and modeled by Dirichlet boundary conditions in these potentials (Fig. 13). We remark that more realistic boundary conditions of Danckwerts type have been postulated incorporating the chemistry of the reactions at the electrodes [5]. Since our aim now is the validation of the three-scale approach we save this generalization for a later occasion. In our subsequent simulation we adopt the values \(D_{\rm Na^{+}}=1.334{\times}10^{-9}, \quad D_{\rm H^{+}}=9.311{\times}10^{-9}, \quad D_{\rm Cl^{-}}=2.032{\times}10^{-9}, \quad D_{\rm OH^{-}}=5.273{\times}10^{-9} \hbox{m}^{2}/\hbox{s}\) for the diffusivities.
Boundary conditions
5.1.1 Numerical examples with constant pH
We begin by illustrating the influence of magnitude of the pH on the electroosmotic flow. In this first example we neglect the variability of the pH and concentrate our study on the different patterns dictated by pH values higher, lower and equal to 5.5 corresponding to the isoelectric point. Our simulations are then performed for three values of the pH: equal to the isoelectric point pH = 5.5; in the basic and acid regimes pH = 7.0 and pH = 4.0 respectively. In Fig. 14 we display the axial dependence of the sodium concentration parameterized by the three values of the pH. At the isoelectric point pH = 5.5 the ζ-potential vanishes and consequently from (5.12) the electroosmotic permeability is zero. Moreover, in the absence of a pressure gradient, Darcy’s velocity and convective effects vanish leading to a purely diffusive behavior of the salt concentration. In the basic regime pH = 7.0 the ζ-potential is negative (see Fig. 9) and consequently from (5.12) we have K eff E > 0 leading to electroosmotic flow induced by the Darcy’s velocity in the same direction of the applied electric field towards the cathode. Such electroosmotic coupling gives rise to a non-linear behavior of the Na+ concentration. Conversely, in the acid regime pH = 4.0 the ζ-potential is positive and from the closure relation (5.12) we have K eff E < 0 leading to electroosmotic flow in the opposite direction of the electric field. Such competition implies in a strong concentration gradient in the vicinity of the anode (see Fig. 14). The concentration profiles exhibiting boundary layers resemble in form de ones reported by Yeung and Datla [68] and Narasimhan and Ranjan [52].
Sodium concentration profiles for different pH values
We now consider the axial distribution of the electric potential in each one of the regimes. From Fig. 15 we may observe at the isoelectric point a non-linear behavior of the electric potential induced by the nonlinear coefficient C eff in (5.5) and (5.8) which appears in order to fulfill charge conservation. In the basic (pH = 7.0) and acid (pH = 4.0) regimes the non-linear behavior of the electric potential is restricted to the vicinities of the cathode and anode respectively combined with a linear behavior away from the electrodes. Similar profiles with sharp layers close to the electrodes were reported in Beddiar et al. [12]. Given the electric potential profile, the pressure field displayed in Fig. 16 develops to fulfill the incompressibility condition (5.2) and Darcy’s law (5.1). At the isoelectric point, since the electroosmotic permeability and Darcy’s velocity vanish we obtain constant pressure profile. In the basic regime the positive electroosmotic permeability together with incompressibility constraint (5.2) implies in a non-linear pressure gradient which develops in order to balance the electroosmotic component. Conversely, in the acid regime the negative electroosmotic permeability gives rise to a counter electroosmotic flow and consequently to a reflexion in the pressure field. The form of the pressure profiles, in particular their reflexion property observed for different pHs, have been previously reported in the literature (see, e.g., [22]).
Electric potential profiles for different pH values
Pressure profiles for different pH values
Finally, in Fig. 17 we display the axial behavior of the ζ-potential for the three chosen values of the pH. As mentioned before at pH = 5.5 the ζ-potential vanishes whereas at the basic/acid regimes it becomes negative and positive respectively. We also observe a weak dependence of the ζ-potential with the sodium concentration shown by the absence of significant spatial variation.
Zeta potential profiles for different pH values
5.1.2 Numerical examples with spatial variability of pH
We now perform similar numerical experiments of the previous subsection but now allowing for spatial variability of the pH to whom we enforce Dirichlet boundary conditions of same magnitude at the electrodes.
In Fig. 18 we portrait the axial distribution of the Na+ concentration. In the basic regime (pH = 7.0 at the electrodes) the negative ζ-potential produces a strong convection in the vicinity of the cathode leading to an increase of the Peclet number and giving rise to a flat profile coupled with a sharp boundary layer near the cathode. At pH = 4.0 we observe the same effect occurring near the anode due to the inversion of the electroosmotic flow consequently leading to the desalination of the clay.
Sodium concentration profiles for equal pH values prescribed at the electrodes
In Fig. 19 we plot the distribution of the pH. We may observe that despite the control of the pH at the electrodes, the influence of the convection induced by the electroosmotic velocity together with electromigration effects in (5.4) and (5.7) lead to an increase of the pH in the interior of the domain and to a consequent basification of the sample regardless of the value imposed on the boundaries. In Fig. 20 we depict the electric potential profile. The behavior is quite similar to the constant pH case with deviations from the linear profile occurring only in the vicinity of the cathode/anode in the basic/acid regimes, respectively.
pH profiles for equal pH values prescribed at the electrodes
Electric potential profiles for equal pH values prescribed at the electrodes
In Fig. 21 we display the axial behavior of the ζ-potential. Compared to the constant pH case, since \(\hbox{d}\zeta/\hbox{d}\hbox{C}_{{\rm H}b^{+}} < 0\) (Fig. 8) we may observe that the increase in pH previously reported in Fig. 19 away from the electrodes leads to a decrease of the ζ-potential. This implies in a increase of K E in the basic regime and vice-versa in the acid regime. Finally, in Fig. 22 we display the pressure field. The shape of the profiles are quite similar to the constant pH case indeed showing deviations from the linear behavior in the interior of the sample previously reported in Fig. 16. Such deviations are induced by the variability of the electroosmotic permeability due to gradients in the ζ-potential and pH.
Zeta potential profile for for equal pH values prescribed at the electrodes
Pressure profiles for same pH values prescribed at the electrodes
Lastly we depict the solution for the same aforementioned external gradients in salinity and electric potential indeed also imposing an external pH-gradient by enforcing pH = 4 and pH = 7 at the anode and cathode respectively. In this general case the sodium concentration and electric potential profiles behave in a similar fashion to the previous case (Figs. 23, 24). The behavior of the pH is advective-dominated with a sharp layer in the vicinity of the cathode (Fig. 25). It should be noted that since acidity (pH < 5.5) prevails in almost the entirely domain we have ζ > 0 and K E < 0 with implies in electroosmotic flow towards the anode. However as the nonlinear advection coefficient θ is negative, the H+-ions are convected in the opposite direction (towards the negatively charged cathode) of the Na+. In addition, we may observe a smooth layer in the vicinity of the anode due to the decrease in \({\varvec{\nabla}} \phi\) in that region (Fig. 24) with consequent reduction of the electromigration diffusive effect towards the cathode causing a decrease in H+ concentration and increase in pH. This effect is manifested by the flat profile of the pH with value greater than the one imposed on the anode. The pressure plot is displayed in Fig. 26. To ensure incompressibility with V D constant the profile oscillates around the values imposed on the boundaries with inversion of pressure gradient near the electrodes. In particular the inversion of \({\varvec{\nabla}} p\) near the cathode forces the hydraulic component of the Darcy’s velocity to counterbalance the electroosmotic component ensuring net flow toward the anode (recall that K E > 0 for pH > 5.5).
Sodium concentration profiles for different pH values prescribed at the electrodes
Electric Potential profiles for different pH values prescribed at the electrodes
pH profile for different values prescribed at the electrodes
Pressure profiles for different pH values prescribed at the electrodes
6 Conclusion
In this paper we provided a first attempt at bridging nano-micro and macroscopic electro-chemical phenomena in kaolinite under steady-state conditions. By incorporating at the nanoscale a protonation reaction coupled with the Poisson-Boltzmann model we were able to derive a microscopic slip boundary condition on the fluid velocity at the particle interface. By upscaling this slip condition in conjunction with the microscopic equations governing flow and solute transport in the bulk fluid in the micropores the homogenized electro-chemical model was rigorously derived at the macroscale. Among the three-scale results obtained herein we highlight the constitutive response of the electroosmotic permeability as a function of the ionic strength and pH which was rigorously reconstructed from a double averaging of the nanoscopic behavior of the ζ-potential. The three-scale model was applied to numerically simulate the classical electroosmotic experiment of a kaolinite sample with stratified microstructure. Different regimes of electroosmotic flow were built-up depending on pH of the bulk solution. Further work in progress to expand the three-scale model to transient phenomena including the development of complex constitutive relations for the partition coefficients and to incorporate more realistic Danckwerts’ boundary conditions at the electrodes.
References
Acar YB, Gale RJ, Alshawabkeh AN, Marks RE, Puppala S, Bricka M, Parker R (1995) Electrokinetic remediation: basic and thechnology status. J Hazard Mater 40:117–137
Acar YB, Alshawabkeh AN (1996) Electrokinetic remediation: I. Pilot-scale tests with lead spiked Kaolinite. J Geotech Eng 122:173–185
Acar YB, Alshawabkeh AN (1993) Principles of electrokinetics remediation. Environ Sci Technol 27:2638–2647
Achari G, Joshi RC, Bentley LR, Chatterji S (1999) Prediction of the hydraulic conductivity of clays using the electric double layer theory. Can Geotech J 36:783-792
Alshawabkeh AN, Acar YB (1996) Electrokinetic remediation: theoretical model. J Geotech Eng 122:186–196
Anandarajah A (1997) Influence of particle orientation on one-dimensional compression of montmorillonite. J Colloid Interface Sci 194:44–52
Auriault JL (1991) Heterogeneous media: is an equivalent homogeneous description always possible?. Int J Eng Sci 29:785–795
Auriault JL, et Lewandowska J (1996) Diffusion/adsorption/advection macrotransport in soils. Eur J Mech A Solids 15:681–704
Avena MJ, Mariscal MM, De Pauli CP (2003) Proton binding at clay surface in water. Appl Clay Sci 24:3–9
Avena MJ, De Pauli CP (1996) Modeling the interfacial properties of an amorphous aluminosilicate dispersed in aqueous NaCl solution. Colloids Surface A Physicochem Eng Aspects 118:75–87
Basu S, Shrarma MM (1997) An improved space-charge model for flow through charged microporous membranes. J Membr Sci 124:77–91
Beddiar K, Fen-Chong T, Dupas A, Berthaud Y, Dangla P (2005) Role of pH in electro-osmosis: experimental study on NaCl–water saturated Kaolinite. Aus Transport in Porous Media 61:93–107
Bolland MDA, Posner AM, Quirk JP (1976) Surface Charge on Kaolinites in aqueous suspension. Aus J Soil Res 14:197–216
Brady PV, Cygan RT, Nagy KL (1996) Molecular control on Kaolinite surface charge. J Colloid Interface Sci 183:356–364
Chi Ma, Eggleton RA (1999) Cation exchange capacity of Kaolinite. Clays Clay Miner 47(2):174–180
Chorover J, Sposito G (1995) Surface charge characteristics of kaolinite tropical soils. J Geochim Cosmochim Acta 59:875–884
Chung HI, Kang BH (1999) Lead removal from contaminated marine clay by electrokinetic soil decontamination. Eng Geol 53:139–150
Dangla P, Chong TF, Gaulard F (2004) Modelling of pH-dependent electro-osmotic flows. C R Mecanique 332:915–920
Denaro AR (1971) Elementary electrochemistry. Butterworths, London
Dormieux L, Barboux P, Coussy O, Dangla P (1995) A macroscopic model of the swelling phenomenon of a saturated clay. Euro J Mech A/Solids 14(6):981–1004
Edwards DA (1995) Charge transport through a spatially periodic porous medium: electrokinetic and convective dispersion phenomena. Phil Trans Roy Soc Lond A353:174–180
Eykholt GR (1997) Development of pore pressures by nonuniform electroosmosis in clays. J Hazard Mater 55:171–186
Fair JC, Osterlé JF (1971) Reverse electrodialysis in charged capillary membranes. J Chem Phys 54(8):3307–3316
Gajo A, Loret B (2007) The mechanics of active clays circulated by salts, acids and bases. J Mech Phys Solids 55(8):1762–1801
Ganor J, Cama J, Metz V (2003) Surface protonation data of Kaolinite-reevaluation based on dissolution experiments. J Colloid Interface Sci 264:67–75
Grim RE (1968) Clay mineralogy. McGraw-Hill Book Company, New York
Guimaraes LD, Gens A, Olivella S (2007) Coupled thermo-hydro-mechanical and chemical analysis of expansive clay subjected to heating and hydration. Transport Porous Media 66(3):341–372
de Groot SR, Mazur P (1969) Non-equilibrium thermodynamics. North-Holland, Amsterdam
Gross RJ, Osterlé JF (1968) Membrane transport characteristics of ultrafine capillaries. J Chem Phys 49(1):228–234
Gupta AK, Coelho D, Adler PM (2007) Ionic transport in porous media for high zeta potentials. J Colloid Interface Sci 314(2):733–747
Hlushkou D, Morgenstern AS, Tallarek U (2005) Numerical analysis of electroosmotic flow in dense regular and random arrays of impermeable nonconductiong spheres. Langmuir 21:6097–6112
Hoch M, Weerasooriya M (2005) Modeling interactions at the tributyltin kaolinite interface. Chemosphere 59(5):743-752
Huertas FJ, Chou L, Wollast R (1997) Mechanism of Kaolinite dissolution at room temperature an in pressure: Part 1. Surface speciation. Geochim Cosmochim Acta 62:417–431
Hunter RJ (1994) Introduction to modern colloid science. Oxford University Press, Oxford
Huyghe JM, Janssen JD (1997) Quadriphasic mechanics of swelling incompressible porous media. Int J Eng Sci 25(8):793–802
Ichikawa Y, Kawamura K, Fujii N, Kitayama K (2004) Microstructure and micro/macro-diffusion behavior of tritium in bentonite. Appl Clay Sci 26:75–90
Ichikawa Y, Prayongphan S, Kawamura K, Kitayama K (2004) Water flow and diffusion problem in bentonite: molecular simulation and homogenization analysis . Elsevier Geo-Engineering Book Series 2:457–464
Lai WM, Hou JS, Mow VC (1991) A triphasic theory for the swelling and deformation behaviors of articular cartilage. J Biomech Eng 113:245–258
Landau LD, Lifshitz EM (1960) Electrodynamics of continuous media. Pergamon Press, Oxford
Lemaire T, Moyne C, Stemmelen D (2007) Modelling of electro-osmosis in clayey materials including pH effects. Phys Chem Earth 32:441–452
Leroy P, Revil A (2004) A triple-layer model of the surface electrochemical properties of clay minerals. J Colloid Interface Sci 270(2):371–380
Li YL, Li RS (2000) The role of clay minerals and the effect of H+ ions on removal of heavy metal (Pb2+) from contaminated soils. Can Geotech J 37:296–307
Looker JR, Carnie SL (2006) Homogenization of the ionic transport equations in periodic porous media. Transport Porous Media 65:107–131
Loret B, Hueckel T, Gajo A (2002) Chemo-mechanical coupling in saturated porous media: elastic-plastic behavior of homoionic expansive clays. Int J Solids Struct 39:2773–2806
Lyklema J (1993) Fundamentals of colloid and interface science. Academic Press, London
Mitchell J (1993) Fundamentals of soil behavior. Wiley, New York
Moyne C, Murad M (2006) A two-scale model for coupled electro-chemo-mechanical phenomena and Onsager’s reciprocity relations in expansive clays: I. Homogenization analysis. Transport Porous Media 62(3):333–380
Moyne C, Murad M (2006) A two-scale model for coupled electro-chemo-mechanical phenomena and Onsager’s reciprocity relations in expansive clays: II. Computational validation. Transport Porous Media 63(1):13–56
Murad M, Moyne C (2002) Micromechanical computational modeling of expansive porous media. C R Mecanique 330:865–870
Murad M, Moyne C (2008) A dual-porosity model for ionic solute transport in expansive clays. Comput Geosci. Online first
Murray HH (1997) Applied clay mineralogy today and tomorrow. Clay Minerals 34:39–49
Narasimhan B, Sri Ranjan R (2000) Electrokinetic barrier to prevent subsurface contaminant migration: theoretical model development and validation. J Cont Hydrol 42:1–17
Newman JS (1973) Electrochemical systems. Prentice-Hall, Inc., Englewood Cliffs
Van Olphen H (1977) An introduction to clay colloid chemistry: for clay technologists, geologists, and soil scientists. Wiley, New York
Patankar SV (1980) Numerical heat transfer and fluid flow. Hemisphere Publishing Corporation, New York
Revil A (1999) Ionic diffusivity, electrical conductivity, membrane and thermoelectric potentials in colloids and granular porous media: a Unified model. J Colloid Interface Sci 212:503–522
Rosanne M, Paszkuta M, Adler PM (2006) Electrokinetic phenomena in saturated compact clays. J Colloid Interface Sci 297:353–364
Rosanne M, Paszkuta M, Thovert JF, Adler PM (2004) Electro-osmotic coupling in compact clays. Geophys Res Lett 31(18):L18614.1–L18614.5
Samson E, Marchand J, Robert J-L, Bournazel J-P (1999) Modelling ion diffusion mechanisms in porous media. Int J Numer Methods Eng 46:2043–2060
Sanchez-Palencia E (1980) Non-homogeneous media and vibration theory, Lectures Notes in Physics. Springer, Heidelberg
Sasidhar V, Ruckenstein E (1981) Electrolyte osmosis through capillaries. J Colloid Interface Sci 82(2):439–457
Schroth BK, Sposito G (1997) Surface charge properties of Kaolinite. Clays Clay Minerals 45(1):85–91
Shang JQ, Lo KY (1997) Electrokinetic dewatering of a phosphate clay. J Hazard Mater 55:117–133
Sherwood JD (1994) A model for the flow of water and ions into swelling shale. Langmuir 10:2480–2486
Sposito G (1989) The chemistry of soils. Oxford University Press
Vane LM, Zang GM (1997) Effect of aqueous phase properties on clay particle zeta potential and electro-osmotic permeability: implications for electro-kinetic soil remediation process. J Hazard Mater 55:1–22
Virkutyte J, Sillanpaa M, Latostenmaa P (2002) Electrokinetics soil remediation—critical overview. Sci Total Environ 289:97–121
Yeung AT, Subbaraju D (1995) Fundamental formulation of electrokinetic extraction of contaminants from soil. Can Geotech J 32:569–583
Yeung AT, Mitchell JK (1993) Coupled fluid, electrical and chemical flows in soil. Geotechnique 43(1):121–134
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: Analytical solution of the one-dimensional Poisson–Boltzmann equation
To derive the analytical solution (2.7) of the Poisson-Boltzmann equation we begin by rewriting (2.4) in dimensionless form
where \({\overline{z}}:= z/L_{\rm D}.\) By multiplying (7.1) by \(2\hbox{d}{\overline{\varphi}}/\hbox{d}{\overline{z}}\) and using the chain rule yields
Integrating (7.2) from an arbitrary \(\overline{z}\) inside the EDL to the point \(\overline{\ell}_{*} = \ell_{*}/L_{\rm D}\) in the bulk solution gives
Using the thin double layer assumption, the electric potential and electric field vanish at point \(\overline{\ell}_{*}\) away from the particle surface. Hence, the above expression can be rewriten in the form
Using the relation \( \hbox{sinh}\,\left({\overline{\varphi}}/2\right)= \left[\left(\hbox{cosh}\, {\overline{\varphi}}-1\right)/2\right]^{1/2}\) this yields
which can be rephrased in the form
Integrating from \(\overline{z}=0\) at particle surface to \(\overline{z}\) and denoting \({\overline{\varphi}}\left({\overline{z}}=0\right)= {\overline{\zeta}}\) the dimensionless ζ-potential we obtain
To solve the above problem we adopt the change of variables
which gives
Using the relation \(\frac{2}{t^{2}-1}=\frac{1} {\left(t-1\right)}-\frac{1}{\left(t+1\right)}\) we obtain
and
which yields
Hence, we can express the electric potential in the EDL as a function of the zeta potential ζ and Debye length L D in the form
Appendix 2: Helmholtz–Smoluchowski equation
We now show the derivation of the slip condition (3.4). Let Ωl = (0, ℓ*) × (0,l) be the two dimensional rectangular domain occupied by the electrolyte solution in the vicinity of each particle with l a characteristic length of particle width (Fig. 27). Denoting {z,y} the cartezian coordinate system normal and tangential to the particle surface and u = u(z) the tangential component of the fluid velocity unlike the bulk fluid, in the electrolyte solution, the Stokes problem is supplemented by an additional body force of Coulomb type q∇ϕ [47]. In the rectangular coordinate system the tangential component of the modified Stokes problem reads as [48]
Recalling the constitutive law for the net charge density \(q= -2F\hbox{C}_{b}\,\hbox{sinh}\,{\overline{\varphi}},\) using the Poisson–Boltzmann problem (2.4) we have, in the absence of a pressure gradient
Integrating from an arbitrary point z to z = ℓ*, where dφ/dz = du/dz = 0 yields
Hence, integrating from z = 0 to z and using the no-slip condition at z = 0 gives
Now define the microscopic slip as the averaged the velocity across the nanocell,
When the thickness of the EDL is small compared to the size of the nanocell (L D < ℓ*), the Helmholtz-Smoluchowski model can be recovered. Noting that φ(z) = 0 in the domain occupied by the bulk fluid L D < z < ℓ*, under the thin EDL assumption the second term containing the averaging of φ is small compared to the magnitude of the ζ-potential. This approximation yields
Description of the nanoscale domain
Rights and permissions
About this article
Cite this article
de Lima, S.A., Murad, M.A., Moyne, C. et al. A three-scale model for pH-dependent steady flows in 1:1 clays. Acta Geotech. 3, 153–174 (2008). https://doi.org/10.1007/s11440-008-0070-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11440-008-0070-3