Multi-scale computational modeling for pH-dependent flows and bivalent ions: application to kaolinite clays

Abstract

In this work, we present a new three-scale (nano, micro, and macroscopic) computational model to quantify $\mathrm{pH}$-dependent flows and monovalent/bivalent ion transport in clayey charged porous media. In our multi-scale approach, we consider the micropores saturated by an aqueous solution containing five ionic species ($\mathrm{Na}^+$, $\mathrm{H}^+$, $\mathrm{Cl}^-$, $\mathrm{OH}^-$, $\mathrm{X}^{2+}$, where the latter represents a generic bivalent ion). At the nanoscale, we derive a new algebraic equation in terms of the concentration of the ionic solutes that determines the zeta-potential and, consequently, the electroosmotic permeability (a macroscale parameter). At the microscale, we consider a Newtonian fluid governed by the Stokes equation and the transport of the solutes given by the Nernst–Planck equation. Applying the homogenization technique, we obtain the macroscopic model and discretize it using the Galerkin finite element method together with a staggered algorithm and the Newton–Raphson method. Our multi-scale computational model highlights the coupling among the different scales. Finally, we present numerical results considering different types of boundary conditions (Dirichlet and Danckwerts) to simulate the electroremediation applied to a kaolinite clay soil.

1 Introduction

Soil remediation became a big challenge in recent years due to its applications in the industrial and agricultural sectors (Albergaria and Nouws 2016; Meuser 2010; Reddy and Cameselle 2009). The demand for innovative approaches for treating contaminated soils has motivated the development of enhanced technologies such as soil flushing, chemical treatment, bioremediation, and phytoremediation (Meuser 2010). Among them, electrokinetic remediation (also known as electroremediation) is a very cost-effective technique for removing ionic contaminants from low hydraulic permeability charged porous media, such as clayey soils polluted by heavy metals (Acar and Alshawabkeh 1993; Reddy and Cameselle 2009).

In the field scale, since the 80’s the electrokinetic remediation has been extensively studied and has shown great potential for removing heavy metal of contaminated electrically charged soils (Cameselle et al. 2013; Reddy and Cameselle 2009). The remediation process is based on the application of an electric potential difference or a low-intensity direct current among electrodes located at the ends of the field. This electric potential difference induces the movement of the ions in the electrolyte solution and generates a fluid flow toward the electrodes, known as electroosmotic flow (Lemaire et al. 2007; Lima et al. 2008, 2010a; Olphen 1977). The solvable contaminant is then collected at the electrodes.

It is well known that the efficiency of the electrokinetic remediation strongly depends on the electrochemical phenomena occurring in the small scales of the charged porous media (Acar and Alshawabkeh 1993; Mitchell 1976; Reddy and Cameselle 2009; Sposito 1989). In this context, experiments of the electrochemical process in charged porous media were performed in laboratory scale to understand the electrokinetics of heavy metal contaminants such as Pb, Zn, Cu, Cd, Hg, Co (Acar and Alshawabkeh 1993; Alshawabkeh and Acar 1996; Angove et al. 1997, 1998; Beddiar et al. 2005; Mammar et al. 2001; Murad and Moyne 2008; Page and Page 2002; Reddy and Cameselle 2009; Rosanne et al. 2004; Vane and Zang 1997). For example, Angove et al. (1997) experimentally quantifies the protonic and heavy metal adsorption for $\mathrm{H}^+,$ $\mathrm{Co}^{2+}$, and $\mathrm{Cd}^{2+}$ using potentiometric titration and adsorption experiments where the adsorption of the cations is modeled considering Langmuir isotherms (Angove et al. 1997, 1998). Also, several researchers have studied the dependence of the zeta potential ($\zeta$-potential) on the concentration of the ions using experimental and numerical approaches (Beddiar et al. 2005; Hunter 1981; Leroy and Revil 2004; Lima et al. 2008, 2010a; Mammar et al. 2001; Vane and Zang 1997; Wang and Revil 2010). In this context, to study surface complexation models that determine the $\zeta$-potential and surface charge density in the presence of monovalent ions for charged porous media, we recommend the authors Revil and Wang (Leroy and Revil 2004; Wang and Revil 2010). Noteworthy, quantifying the $\zeta$-potential (a nanoscale parameter) accurately is important since the electroosmotic permeability (a macroscale parameter) strongly depends on it (Hunter 1981; Lima et al. 2008, 2010a; Mammar et al. 2001; Moyne and Murad 2006).

On the other hand, to better understand the electro-chemical-hydraulic phenomena occurring in charged porous media, a broad range of mathematical modeling and numerical simulations have been developed (Alshawabkeh and Acar 1996; Beddiar et al. 2005; Cameselle et al. 2013; Gupta et al. 2008; Lemaire et al. 2007; Lima et al. 2008, 2010a, b; Moyne and Murad 2006; Murad and Moyne 2008). Significant advances were provided by single-scale (macroscopic) modeling (Alshawabkeh and Acar 1996; Beddiar et al. 2005; Dormieux et al. 1995; Gupta et al. 2008). Nowadays, models based on the multi-scale approach have been widely presented in the scientific community, where we highlight the models derived from the Lattice-Boltzmann technique, such as Yang et al. (Yang et al. 2019; Yang and Wang 2019) and the models deduced using the periodic homogenization procedure (Gupta et al. 2008; Lima et al. 2008; Moyne and Murad 2006; Murad and Moyne 2008). Nevertheless, accurate models for quantifying the dependence of the $\zeta$-potential on the monovalent ions $\mathrm{Na}^+$, $\mathrm{H}^+$, $\mathrm{Cl}^-$ and $\mathrm{OH}^-$ as well as heavy metal ions such as $\mathrm{Cu}^{2+}$, $\mathrm{Cd}^{2+}$, and $\mathrm{Pb}^{2+}$, are still lacking. A broad literature review shows that the determination of the $\zeta$-potential is mainly based on empirical laws (Al-Hamdan and Reddy 2008; Alshawabkeh and Acar 1996; Beddiar et al. 2005; Hunter 1981; Rosanne et al. 2004; Vane and Zang 1997).

In this paper, we present a new multi-scale (nano/micro/macroscopic) model that provides a rigorous analytical/numerical derivation of an equation for the $\zeta$-potential in the scenario where the soil is contaminated by bivalent ions. We also derive the constitutive laws for the parameters of the macroscopic model and highlight the importance of the bivalent ion on the process. Consequently, a better understanding of the coupling between the electrochemical phenomena on the nano/microscopic level and the macroscopic response of the medium is achieved (Gupta et al. 2008; Le et al. 2013; Lemaire et al. 2007; Mainka et al. 2014; Malevich et al. 2010; Ponce et al. 2013). For multi-scale models assuming monovalent ion transport in charged porous media, we recommend (Lima et al. 2008, 2010a; Moyne and Murad 2006; Murad and Moyne 2008; Ponce et al. 2013).

In this work, we extend the work of (Igreja et al. 2017; Lima et al. 2008) by considering an electrically charged clayey soil saturated by an aqueous solution containing five ionic species ($\mathrm{Na}^+$, $\mathrm{H}^+$, $\mathrm{Cl}^-$, $\mathrm{OH}^-$, $\mathrm{X}^{2+}$) using the asymptotic homogenization method. Differently from the multi-scale models deduced by Yang et al. (2019; 2019) for the electro-diffusive transport based on the Lattice-Boltzmann technique, here we use the asymptotic homogenization method and incorporate the electroosmotic flow where $\mathrm{X}^{2+}$ represents a generic bivalent metallic ion such as the heavy metals $\mathrm{Cu}^{2+}$, $\mathrm{Cd}^{2+}$, and $\mathrm{Pb}^{2+}$. This multi-scale model highlights the influence of the bivalent ion on the electric potential of the electric double layer (EDL), on the surface charge density, and on the macroscopic parameters. In particular, the multi-scale approach models the dependence of the $\zeta$-potential on the ionic concentrations and obtains a more precise description of the electroosmotic permeability as a function of pH and salt/heavy metal concentrations. One of its novelties is a constitutive law for the electroosmotic permeability as a function of the concentration of the triple $\{ \mathrm{Na}^+, \mathrm{H}^+, \mathrm{X}^{2+}\}$.

At the nanoscale, we model the phenomena occurring at the surface of the particles via the Poisson–Boltzmann equation with Neumann boundary conditions due to the balance between electric field and surface charge density (Sposito 1989). The surface charge density, on its hand, is modeled as a function of the ionic concentration variation resulting from the $\mathrm{H}^+$ protonation/deprotonation and $\mathrm{X}^{2+}$ cationic exchange reaction at the particle surface (Angove et al. 1997, 1998). Considering the thin EDL assumption, where the double layers do not overlap, for the nanoscale problem we obtain analytical solutions determining the electric potential of the EDL, the surface charge density and, the $\zeta$-potential. At the microscale, we model the ion transport by the Nernst–Planck equations and the hydrodynamic flow via the Stokes problem. We also assume a slip boundary condition in the tangential velocity component due to the movement of the ions in the EDL (Lima et al. 2008, 2010a). The two-scale nano/micro model is then homogenized to the Darcy scale using asymptotic homogenization applied to periodic structures, which leads to the macroscopic equations.

The resulting mathematical model is a nonlinear and strongly coupled system of partial differential equations. Using data from Angove et al. (1998), we simulate the multi-scale model restricted to the stratified layers assumption (one-dimensional case) considering the Cadmium as a the bivalent ion ($X^{2+} = \mathrm{Cd}^{2+}$) and kaolinite clay as the charged porous media. The numerical simulation uses the Galerkin finite element method and the Newton–Raphson method together with a computationally efficient staggered algorithm (Kim et al. 2011). We then set realistic boundary conditions, such as Danckwerts, to simulate the hydrodynamics and ionic transport in the stationary regime of an electroosmosis experiment of heavy metal remediation.

Fig. 1

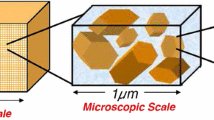
Portrait of natural length scales in a clay soil. Reproduced with permission from Lima et al. (2008)

2 Multi-scale model

Consider an electrically charged porous media composed of a clayey soil saturated with an aqueous solution containing the monovalent ionic species $\mathrm{Na}^+$, $\mathrm{H}^+$, $\mathrm{Cl}^-$, $\mathrm{OH}^-$ and an arbitrary bivalent ion denoted by $X^{2+}$. Here we improve the multi-scale model presented in Lima et al. (2008) by adding the bivalent ion $X^{2+}$ to the aqueous solution. In this section we develop the mathematical model in the three-scales considered-nano, micro and macro. The scales are illustrated in Fig. 1.

2.1 Nanoscopic model

Consider the nanoscopic domain a thin layer, $O(10^{-9}\,\,\mathrm{m}),$ surrounding the surface of the clay particles. This thin layer, known as the EDL, is composed of the electrically charged surface of the clay and an aqueous solution containing the ionic species $\mathrm{Na}^+$, $\mathrm{H}^+$, $X^{2+}$, $\mathrm{Cl}^-$, $\mathrm{OH}^-$ (see Fig. 1). We split the nanoscopic model into two subsections. In the first subsection, we solve the Poisson–Boltzmann equation to determine the electric potential of the EDL and the surface charge density, denoted by $\varphi$ and $\sigma$, respectively. Both of these quantities, $\varphi$ and $\sigma$, are derived as functions of the concentration of the ionic species at the bulk and of the electric potential of the EDL at the clay surface, commonly called the $\zeta$-potential. In the second subsection, we deduce a nonlinear algebraic expression for the $\zeta$-potential that depends only on controllable data by modeling the chemical reactions occurring at the clay surface.

Fig. 2

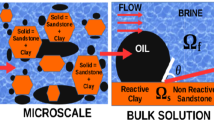
Portraits of a clay soil: a microscopic scale, b nanoscopic scale. Reproduced with permission from Lima et al. (2008)

2.1.1 The Poisson–Boltzmann equation

Let $C_i$ and $C_{i_b}$, $i = \mathrm{Na}^+$, $\mathrm{H}^+$, $X^{2+}$, $\mathrm{Cl}^-$, $\mathrm{OH}^-$, be the molar concentration of the ionic species in the EDL and in the bulk fluid, respectively. The concentrations $C_i$ and $C_{i_b}$ are related through the electric potential of the EDL via the Boltzmann distribution (Dormieux et al. 1995; Olphen 1977)

$$\begin{aligned} C_i=C_{i_b}e^{-z_i\overline{\varphi }}, \end{aligned}$$

(1)

for $i = \mathrm{Na}^+$, $\mathrm{H}^+$, $X^{2+}$, $\mathrm{Cl}^-$, $\mathrm{OH}^-$, where $\overline{\varphi }=F\varphi /RT$ and $\{z_i,F,R,T\}$ are the set composed of ion valence, Faraday constant, universal ideal gas constant and absolute temperature, respectively. Moreover, in the bulk fluid, the electroneutrality condition is satisfied pointwisely in the form

$$\begin{aligned} C_b=C_{\mathrm{Na}_b^{+}}+C_{H_b^{+}}+2C_{X_b^{2+}}=C_{\mathrm{Cl}_b^{-}}+C_{\mathrm{OH}_b^{-}}, \end{aligned}$$

(2)

where $C_b$ is the total concentration of cations (or anions) in the bulk.

Let $\Omega ^l = \left( 0,L_D \right)$ be the one-dimensional nanoscopic subdomain in the direction normal to the clay surface where $L_D$ is the Debye’s length (see Fig. 2b). Consider $z=l_{\star }$ a point further away from the interface such that $(l_{\star } \gg L_D)$. Then, assuming the surface charge is uniformly distributed on the clay surface, the electric potential of the EDL is modeled by the one-dimensional Poisson–Boltzmann equation (Landau and Lifshitz 1960; Lima et al. 2008, 2010a)

$$\begin{aligned} \dfrac{d^2 \varphi }{\mathrm{d}z^2} =-\dfrac{F}{\widetilde{\epsilon }_{0}\widetilde{\epsilon }_{r}} \sum _iz_iC_i, \qquad \qquad \text{ in } \ \ \ \Omega ^l, \end{aligned}$$

(3)

for $i = \mathrm{Na}^+, \mathrm{H}^+, X^{2+}, \mathrm{Cl}^-, \mathrm{OH}^-$, where $\widetilde{\epsilon }_{0}$ is the permittivity of the free space and $\widetilde{\epsilon }_{r}$ is the dielectric constant. Applying (1) into (3), and using the electroneutrality condition (2), we rewrite the Poisson–Boltzmann equation in terms of the electrical potential and bulk concentrations

$$\begin{aligned} \dfrac{d^2 \varphi }{\mathrm{d}z^2} =\dfrac{2F}{\widetilde{\epsilon }_{0}\widetilde{\epsilon }_{r}} \left[ C_b\sinh \left( \overline{\varphi }\right) +C_{X_b^{2+}}e^{-\overline{\varphi }} (1-e^{-\overline{\varphi }})\right] . \end{aligned}$$

(4)

In Eq. (4) is clear the influence of the bivalent ion $C_{X_b^{2+}}$ on the nanoscale model, note that for $C_{X_b^{2+}}=0$ we recover the Poisson–Boltzmann model for monovalent ions presented in Lima et al. (Lima et al. 2008).

Next, we provide boundary conditions for the new Poisson-Boltzmann problem (4). To obtain a condition at $z=0$, we assume that the electrical field balances the surface charge density $\sigma$ at the wall. For the other boundary condition, we adopt the thin EDL assumption where the clay particles are so far away from each other that adjacent double layers do not overlap (see Fig. 2a); consequently, there is no electric field at $z=l_{\star }$. Thus, the boundary conditions are

$$\begin{aligned}&\left. \dfrac{\mathrm{d} \varphi }{\mathrm{d}z} \right| _{z=0} =-\dfrac{\sigma }{\widetilde{\epsilon }_{0}\widetilde{\epsilon }_{r}}, \end{aligned}$$

(5a)

$$\begin{aligned}&\left. \quad \dfrac{\mathrm{d} \varphi }{\mathrm{d}z}\right| _{z=l_{\star }} =0. \end{aligned}$$

(5b)

Solving (4)–(5), we arrive at the analytical expression for $\varphi$ and, consequently, for $\sigma$ (see Appendix A for details)

$$\begin{aligned} \varphi= & {} \dfrac{RT}{F}\log \left[ \left( \dfrac{C_b+C_{X_b^{2+}}}{C_b}\right) \left( \dfrac{1+ \lambda _1 e^{\kappa z}}{1-\lambda _1 e^{\kappa z}}\right) ^2 - \right. \left. \dfrac{C_{X_b^{2+}}}{C_b}\right] , \end{aligned}$$

(6)

$$\begin{aligned} \sigma= & {} \beta \left[ 2C_b(\cosh \left( \overline{\zeta }\right) -1)+ C_{X_b^{2+}} \left( e^{-\overline{\zeta }}-1\right) ^2\right] ^{1/2}, \end{aligned}$$

(7)

where $\overline{\zeta } = F\zeta /RT$, with the $\zeta$-potential, $\zeta ,$ defined as the electric potential of the EDL at the clay surface, i.e., $\zeta {:=}\varphi (z=0)$, and $\beta = \text {sgn} (\overline{\zeta }) \displaystyle \sqrt{2\tilde{\varepsilon } \tilde{\varepsilon }_0 RT}$ where sgn is the sign function. Moreover,

$$\begin{aligned} \kappa= & {} -\text {sgn} (\overline{\zeta }) \sqrt{2F^2(C_{b}+C_{X_b^{2+}})/( \tilde{\varepsilon } \tilde{\varepsilon }_0 RT)} \ \ \text{ and } \end{aligned}$$

(8a)

$$\begin{aligned} \lambda _1= & {} \dfrac{\sqrt{C_{X_b^{2+}}+C_b e^{\overline{\zeta }}}-\sqrt{C_{b}+C_{X_b^{2+}}}}{\sqrt{C_{X_b^{2+}}+C_b e^{\overline{\zeta }}}+\sqrt{C_{b}+C_{X_b^{2+}}}}. \end{aligned}$$

(8b)

Equations (6)–(7) establish the nanoscopic model in terms of $\{\varphi ,\sigma \}$ provided that $C_{X_b^{2+}}$ and $\zeta$ are given. We note that in the absence of the bivalent ion ($C_{X_b^{2+}}=0$), the nanoscale model (6)–(7) reduces to the model containing only monovalent ions presented in Lima et al. (2008).

In the next subsection, we describe the chemical reactions occurring at the clay surface to determine an alternative analytical expression for $\sigma$ and then, consequently, a nonlinear algebraic equation to compute $\zeta$.

2.1.2 Chemical reactions at the clay surface

Consider that there is no mineral dissolution so that the volume fraction between the solid and fluid phase is constant. Also, assume that the component of the charge density induced by isomorphous substitutions on the basal planes is small compared to the one due to broken bonds on the lateral edges of the solid particles containing aluminol and silanol groups (Mitchell 1976; Sposito 1989). Following Angove et al. (1998), we henceforth adopt a model based on protonation/deprotonation and cationic exchange reactions which take place in the site $(>M-O^-)$, a typical representative of the reactive group on the lateral edges of the solid surface (Mitchell 1976). Moreover, we enforce local thermodynamic equilibrium by considering the chemical reactions of $\mathrm{H}^{+}$ with the clay surface given by (Angove et al. 1997, 1998)

$$\begin{aligned} (>M-\mathrm{OH}) + \mathrm{H}^+\rightleftharpoons & {} (>M-\mathrm{OH}_2)^+ , \end{aligned}$$

(9)

$$\begin{aligned} (>M-\mathrm{OH})\rightleftharpoons & {} (>M-O)^- + \mathrm{H}^+, \end{aligned}$$

(10)

where $(>M-)$ represents the metallic ion lying in the tetrahedral $(Si^{4+})$ or octahedral $(Al^{3+})$ layers (Mitchell 1976). We also assume that the bivalent ion $X^{2+}$ reacts to the clay surface via

$$\begin{aligned} 2(>M-OH) + X^{2+}\rightleftharpoons & {} (>M-O_2X) + 2\mathrm{H}^+. \end{aligned}$$

(11)

For example, Angove et al. proposes the reaction (11) for the bivalent metallic ions Cadmium and Cobalt (Angove et al. 1998).

Let $\Gamma _{\mathrm{max}}$ be the total number of sites available for adsorption per unit area associated with the Aluminol and Silanol groups defined as

$$\begin{aligned} \Gamma _{\mathrm{max}} {:=}\gamma _{\mathrm{MOH}} + \gamma _{\mathrm{MOH}_2^+} + \gamma _{\mathrm{MO}^-} + \gamma _{\mathrm{MO}_2X}, \, \end{aligned}$$

(12)

where $\gamma _{j}$, for $j=MOH$, $\mathrm{MOH}_2^+$, $\mathrm{MO}^-$, $\mathrm{MO}_2X$, is the concentration of each species on the clay surface. Applying the law of mass action, the equilibrium constants associated with the reactions (9)–(11) are, respectively,

$$\begin{aligned} K_1&{:=}&\dfrac{\overline{C}_{\mathrm{MOH}_2^+}}{\overline{C}_{\mathrm{MOH}} C_{H_0^+}} = \dfrac{\gamma _{\mathrm{MOH}_2^+}}{\gamma _{\mathrm{MOH}} C_{H_0^+} }, \end{aligned}$$

(13a)

$$\begin{aligned} K_2&{:=}&\dfrac{C_{H_0^{+}} \overline{C}_{\mathrm{MO}^-}}{\overline{C}_{\mathrm{MOH}}} = \dfrac{\gamma _{\mathrm{MO}^-} C_{\mathrm{H}^+_0} }{\gamma _{\mathrm{MOH}}}, \end{aligned}$$

(13b)

$$\begin{aligned} K_3&{:=}&\dfrac{\overline{C}_{\mathrm{MO}_2X} C_{H_0^+}^2}{\overline{C}_{\mathrm{MOH}}^2 C_{X_0^{2+}}} = \dfrac{\Gamma _{\mathrm{max}} \gamma _{\mathrm{MO}_2X} C_{H_0^+}^2 }{\gamma _{\mathrm{MOH}}^2 C_{X_0^{2+}} }, \end{aligned}$$

(13c)

where $\overline{C}_{j} = \gamma _{j} / \Gamma _\mathrm{max}$, for $j=\mathrm{MOH}$, $\mathrm{MOH}_2^+$, $\mathrm{MO}^-$, $\mathrm{MO}_2X$, is the dimensionless surface concentration of each species at the clay surface, and $C_{H_0^+}, ~C_{X_0^{2+}}$ represent the molar concentrations of $\mathrm{H}^+$ and $X^{2+}$ at the clay surface quantified using (1) with $\overline{\varphi } = \overline{\zeta }.$

We define the surface charge density $\sigma$ as the product between the Faraday constant and the sum of the weighted concentration of the charged species present at the clay surface

$$\begin{aligned} \sigma {:=}F\sum _i z_i \gamma _i = F\left( \gamma _{\mathrm{MOH}_2^+} - \gamma _{\mathrm{MO}^-} \right) . \end{aligned}$$

(14)

Substituting (13a), (13b) and the Boltzmann distribution (1) restricted to the clay surface into (14), we obtain the following expression for the charge density $\sigma$ in function of the surface concentration $\gamma _{\mathrm{MOH}}$

$$\begin{aligned} \sigma = F\left( K_1 C_{H_b^+}e^{-\bar{\zeta }} - \dfrac{K_2e^{\bar{\zeta }}}{C_{H_b^+}} \right) \gamma _{\mathrm{MOH}}. \end{aligned}$$

(15)

To fully determine $\sigma$, we next derive an expression for $\gamma _{\mathrm{MOH}}$.

Combining (12) with equations (13), we arrive at the quadratic equation

$$\begin{aligned}&\nu _1 \gamma _{\mathrm{MOH}}^2 + \nu _2\gamma _{\mathrm{MOH}} - \Gamma _\mathrm{Max} = 0 \end{aligned}$$

(16)

with

$$\begin{aligned} \nu _1 = K_3 C_{X_b^{2+}}/\left( \Gamma _\mathrm{Max} C_{H_b^+}^2\right) ,\quad \nu _2 = 1+ K_1 C_{H_b^+}e^{-\bar{\zeta }} +K_2e^{\bar{\zeta }}/ C_{H_b^+}. \end{aligned}$$

(17)

Hence, the surface concentration $\gamma _{\mathrm{MOH}}$ is given by

(18)

Equations (15) and (18) provide an analytical expression for the surface charge density $\sigma$ as a function of the $\zeta$-potential and the available experimental data ($K_1$, $K_2$, $K_3$,$\Gamma _\mathrm{Max}$, $C_{X_b^{2+}}$, $C_{H_b^+}$). Combining equations (7) and (15), we obtain the nonlinear algebraic equation for the $\zeta$-potential

$$\begin{aligned} \dfrac{ 2\varepsilon \varepsilon _0 RT}{F^2 \gamma _{\mathrm{MOH}}^2} \left[ 2C_b(\cosh \left( \overline{\zeta }\right) -1)+C_{X_b^{2+}} \left( e^{-\overline{\zeta }}-1\right) ^2\right] = \left( K_1 C_{H_b^+}e^{-\bar{\zeta }} -K_2e^{\bar{\zeta }}/C_{H_b^+} \right) ^2, \nonumber \\ \end{aligned}$$

(19)

where $\gamma _{\mathrm{MOH}}$ is given by (17)–(18).

In most of the literature, the $\zeta$-potential is obtained from experimental data (Eykholt and Daniel 1994; Vane and Zang 1997). Equation (19) provides a new algebraic way for determining the $\zeta$-potential as a function of the monovalent and bivalent ions. The $\zeta$-potential is a parameter of utmost importance since it is used to quantify the electroosmotic permeability. We highlight that the nanoscopic variables depend on the set of physical-chemical reactions considered and incorporated in the nanoscopic model, mainly by the equilibrium constants and maximum site density ($K_1,~K_2, ~K_3, \Gamma _\mathrm{Max}$). In this context, the chemical reactions postulate in Revil and Wang account for the physical–chemical parameters for monovalent ions (Leroy and Revil 2004; Wang and Revil 2010). Then, we adopt the results proposed by Angove et al. (1997; 1998) for the chemical reactions that include monovalent and bivalent ions (see Eq. (9)–(11)). Note that a set of particular physical-chemical reactions subjected to some specific experimental data may generate different values for the physical-chemical constants.

2.2 Microscopic model

Let $\Omega = \Omega _f \cup \Omega _s$ be a biphasic microscopic domain composed of rigid solid particles and micropores (bulk fluid) (Fig.2a). The solid phase $\Omega _s$ consists of the clay particles carrying the surface charge density $\sigma$ described by (15)–(18). The micropores subdomain $\Omega _f$ is occupied by the bulk fluid containing the five ionic solutes $\mathrm{Na}^+, \mathrm{H}^+, X^{2+}, \mathrm{Cl}^-, \mathrm{OH}^-$.

Here we consider the thermodynamic equilibrium between ions and non-ionized solvent molecules. In this scenario, the sodium chloride in water is completely dissociated while the water molecules are partially dissociated due to the auto ionization described by the chemical reaction

$$\begin{aligned} \mathrm{H}_{2}\mathrm{O} \rightleftharpoons \mathrm{H}^+ + \mathrm{OH}^-. \end{aligned}$$

(20)

The equilibrium constant of reaction (20) is called the ionic product of water $K_W$ given by

$$\begin{aligned} K_W {:=}C_{H_b^{+}} C_{\mathrm{OH}_b^{-}} = 10^{-14} (\mathrm{mol}/\mathrm{l})^2. \end{aligned}$$

(21)

Under a steady-state assumption, the transport of the ions in the bulk solution is governed by the Nernst–Planck equations (Alshawabkeh and Acar 1996; Lima et al. 2008). For $i=\mathrm{Na}^{+}$, $X^{2+}$, $\mathrm{Cl}^{-}$ and $j=\mathrm{H}^{+}$, $\mathrm{OH}^{-}$, we have, in $\Omega _f$

$$\begin{aligned}&\nabla \cdot \mathbf {{\widetilde{J}}_{i}} = 0, \end{aligned}$$

(22a)

$$\begin{aligned}&\nabla \cdot \mathbf {{\widetilde{J}}_{j}} = -{\dot{m}}, \end{aligned}$$

(22b)

where $\mathbf {{\widetilde{J}}_{i}}{:=}C_{i_b}{\mathbf {v}}- D_{i}\left( \nabla C_{i_b}+ z_i C_{i_b}\nabla \overline{\phi }\right)$ is the total convective/electro–diffusive ionic flux of each solute, ${\mathbf {v}}$ is the fluid velocity and $D_{i}, D_j$ are the water-ion binary diffusion coefficients. Also, ${\dot{m}}$ is the source term quantifying the mass production due to hydrolysis (20) and $\overline{\phi }{:=}F\phi /\mathrm{RT}$ is the dimensionless macroscopic electric potential. We observe that $\phi$ is the macroscopic electric potential due to the presence of electrodes while $\varphi$ represents the EDL electric potential, the nanoscopic one.

To complete the microscopic model, we consider the bulk fluid a Newtonian incompressible solution with gravity and convection/inertial effects negligible. Then, microscopic hydrodynamics is governed by the classical Stokes problem

$$\begin{aligned} \mu _{f}\varDelta {\mathbf {v}} - \nabla p = 0, \nabla \cdot {\mathbf {v}} = 0, \quad \text{ in } \ \ \Omega _{f}, \end{aligned}$$

(23)

where p is the pressure and $\mu _{f}$ is the water viscosity.

The microscopic equations are supplemented by interfacial conditions on the particle/micropore interface $\Gamma _{fs}$ (see Fig. 2a). Due to thin double layer assumption, the EDL is treated as a boundary layer in the vicinity of the particles (see Fig. 2b). Thus, the boundary condition for the velocity in the Stokes problem is given by a slip condition in the tangential velocity component. Denoting the unitary normal and tangential vectors by ${\mathbf {n}}$ and $\varvec{\tau }$, respectively, we have, on $\Gamma _{fs}$, (Edwards 1995; Eykholt and Daniel 1994)

$$\begin{aligned} {\mathbf {v}}\cdot \varvec{\tau }= & {} \dfrac{\widetilde{\epsilon }_{0}\widetilde{\epsilon }_{r} \zeta }{\mu _{f}} \nabla \phi \cdot \varvec{\tau }, \nonumber \\ {\mathbf {v}}\cdot {\mathbf {n}}= & {} 0, \end{aligned}$$

(24)

2.2.1 Formulation in primary unknowns

Now we rewrite the system of Eq. (22) as a function of the selected primary unknowns: velocity, pressure, electric potential, and concentration of the cations.

The anion concentration $C_{\mathrm{OH}^{-}_b}$ and the source term due to hydrolysis are eliminated by subtracting (22b) for $j=\mathrm{OH}^-$ from (22b) for $j=\mathrm{H}^+$ and using (21). As a result, we obtain the following nonlinear equation called the $\mathrm{pH}$-equation

$$\begin{aligned} \left. \begin{array}{l} \nabla \cdot \hat{\mathbf {J}}_\mathbf {{\mathrm{H}^{+}}} = 0, \end{array} \right. \end{aligned}$$

(25)

where

$$\begin{aligned} \hat{\mathbf {J}}_\mathbf {{\mathrm{H}^{+}}} = \Theta C_{H_b^{+}}{\mathbf {v}} - \widehat{D}_{\mathrm{H}^+}\left( \nabla C_{H_b^{+}}+C_{H_b^{+}}\nabla \overline{\phi }\right) , \end{aligned}$$

(26)

with

$$\begin{aligned} \widehat{D}_{\mathrm{H}^+}{:=}D_{\mathrm{H}^{+}}+\dfrac{D_{\mathrm{OH}^{-}}K_{W}}{(C_{H_b^{+}})^{2}} \;\; \text{ and }\;\; \Theta {:=}1-\dfrac{K_{W}}{(C_{H_b^{+}})^{2}}. \end{aligned}$$

We replace equation (22a) for $i=\mathrm{Cl}^{-}$ by an equation modeling the conservation of charge. Consider the definition of the electric current in the fluid given by

$$\begin{aligned} \left. \begin{array}{l} \mathbf {I_{f}}{:=}F \sum \limits _i z_i \mathbf {{\widetilde{J}}_{i}}, \end{array} \right. \end{aligned}$$

(27)

for $i= \mathrm{Na}^{+}$, $\mathrm{H}^{+}$, $X^{2+}$, $\mathrm{Cl}^{-}$, $\mathrm{OH}^{-}$. Applying the Nernst–Planck equations (22) and the constraints (2) and (21) in the definition (27), we obtain the conservation of charge equation

$$\begin{aligned} \nabla \cdot \mathbf {I_{f}} =0, \end{aligned}$$

(28)

with

$$\begin{aligned} \mathbf {I_{f}}= -A\nabla C_{\mathrm{Na}_b^{+}} - B \nabla C_{H_b^{+}}- C\nabla C_{X_b^{2+}} - D\nabla \overline{\phi }, \end{aligned}$$

(29)

where

$$\begin{aligned}&A {:=}F \left( D_{\mathrm{Na}^{+}}-D_{\mathrm{Cl}^{-}}\right) , \\&B {:=}F\left[ D_{\mathrm{H}^{+}}-D_{\mathrm{Cl}^{-}}+\left( D_{\mathrm{OH}^{-}}-D_{\mathrm{Cl}^{-}}\right) K_{W}/ C_{H_b^{+}}^{2}\right] , \\&C {:=}2F(D_{X^{2+}} - D_{\mathrm{Cl}^{-}}),\\&D {:=}F\left[ \left( D_{\mathrm{Na}^{+}}+D_{\mathrm{Cl}^{-}}\right) C_{\mathrm{Na}_b^{+}}+\left( D_{\mathrm{H}^{+}}+D_{\mathrm{Cl}^{-}}\right) C_{H_b^{+}}\right. \\&\left. + 2(2D_{X^{2+}} + D_{\mathrm{Cl}^{-}})C_{X_b^{2+}}+ \left( D_{\mathrm{OH}^{-}}-D_{\mathrm{Cl}^{-}}\right) K_{W}/C_{H_b^{+}}\right] . \end{aligned}$$

2.3 Summary of the nanoscopic/microscopic model

The nanoscopic/microscopic steady-state model consists in: Given the constants $\{\mu _f,K_w,$ $D_{\mathrm{Na}^{+}},D_{\mathrm{H}^{+}},D_{X^{2+}},$ $D_{\mathrm{Cl}^{-}},D_{\mathrm{OH}^{-}},F,R,T,A,C\}$, the functions $\{\Theta , \widehat{D}_H, B\}$ depending on $C_{H_b^{+}}$, and the coefficient D depending on $\{C_{\mathrm{Na}_b^{+}},C_{H_b^{+}},C_{X_b^{2+}}\}$, find the microscopic fields $\{p, {\mathbf {v}},$ $C_{\mathrm{Na}_b^{+}},C_{H_b^{+}},C_{X_b^{2+}}\}$ satisfying

$$\begin{aligned}&\nabla \cdot {\mathbf {v}} = 0, \nonumber \\&\mu _{f}\varDelta {\mathbf {v}} -\nabla p = 0, \nonumber \\&\nabla \cdot \left( C_{\mathrm{Na}^+_b}{\mathbf {v}}\right) - \nabla \cdot \left[ D_{\mathrm{Na}^+}\left( \nabla C_{\mathrm{Na}^+_b}+C_{\mathrm{Na}^+_b}\nabla \overline{\phi }\right) \right] =0, \nonumber \\&\nabla \cdot \left( C_{ X^{2+}_b}{\mathbf {v}}\right) - \nabla \cdot \left[ D_{ X^{2+}}\left( \nabla C_{ X^{2+}_b}+2C_{ X^{2+}_b}\nabla \overline{\phi }\right) \right] =0, \nonumber \\&\nabla \cdot \left( \Theta C_{H_b^{+}}{\mathbf {v}}\right) - \nabla \cdot \left[ \widehat{D}_{\mathrm{H}^+}\left( \nabla C_{H_b^{+}}+C_{H_b^{+}}\nabla \overline{\phi }\right) \right] =0, \nonumber \\&\nabla \cdot \left( A\nabla C_{\mathrm{Na}_b^{+}} + B\nabla C_{H_b^{+}}+C\nabla C_{X_b^{2+}} +D\nabla \overline{\phi } \right) =0, \end{aligned}$$

(30)

where the concentrations $C_{\mathrm{OH}_b^{-}}$ and $C_{\mathrm{Cl}_b^{-}}$ are quantified by (21) and (2), respectively. The microscopic system is subjected to the interfacial conditions (24).

Also, under steady state conditions and assuming the absence of mineral dissolution reaction, the transient flux related to ion adsorption on the particle surface vanishes. So, the microscopic interfacial conditions for the transport equations and the conservation of charge are represented by the following homogeneous Neumann conditions for the ionic fluxes

$$\begin{aligned} \mathbf {I_{f}} \cdot {\mathbf {n}} = \mathbf {J_{\mathrm{Na}^{+}}}\cdot {\mathbf {n}} = \hat{\mathbf {J}}_\mathbf {{\mathrm{H}^{+}}} \cdot {\mathbf {n}} = \mathbf {J_{X^{2+}}}\cdot {\mathbf {n}}= 0, \end{aligned}$$

(31)

where $\mathbf {I_{f}}$ is given by (29), $\hat{\mathbf {J}}_\mathbf {{\mathrm{H}^{+}}}$ by (26) and,

$$\begin{aligned} \mathbf {J_{i}}{:=}- D_i\left( \nabla C_{i_b} + z_i C_{i_b} \nabla \overline{\phi } \right) , \end{aligned}$$

for $i = \mathrm{Na}^+, X^{2+}.$

Note that the nanoscopic model is incorporated into the microscopic modeling through the $\zeta$-potential present in the tangential component of the velocity ${\mathbf {v}}$ in (24). The $\zeta$-potential is given by the solution of the nanoscopic nonlinear equation (19) that is numerically approximated in Sect. 5.1.

Fig. 3

Stratified arrangement of face-to-face particles. Reproduced with permission from Igreja et al. (2017)

In this paper, we assume the surface charge density is uniformly distributed at the clay surface. This assumption simplifies the Poisson-Boltzmann problem to the one-dimensional case allowing us to obtain its analytical solution (Liu et al. 2013; Olphen 1977; Sposito 1989). This way, the computational cost of solving the Poisson-Boltzmann problem is eliminated, reducing the overall simulation cost. Moreover, it is challenging to obtain the physical-chemical data that include bivalent ions. One source in the literature is Angove et al. (1997), where they consider fewer reactions for the monovalent ions than Leroy and Wang (2004; 2010) but include reactions for the bivalent ions. Here we describe thoroughly all the techniques used to derive the multi-scale model. In this way, incorporating new phenomena or scenarios into the nanoscopic model would be straightforward.

3 Macroscopic model

We obtain the macroscopic equations by upscaling the microscopic model using the asymptotic homogenization technique presented in Lima et al. (2010a) and detailed in Appendix B. Following this framework, we consider the clayey porous media a periodic bounded domain with two characteristics length scales, microscopic and macroscopic. The microscopic length scale, l, is of the order of the micropores diameter, $O(10^{-6}\,\, \mathrm{m})$. The macroscopic length scale, L, is of the order of the overall dimension of the sample, O(1m). Hence, the assumption of separation of scales, $\varepsilon {:=}l/L \ll 1$, is satisfied. Moreover, the periodic domain is composed of repetition of a standard periodic cell, denoted by Y. Each periodic cell is divided into the subdomains $Y_f$ and $Y_s$ that share a common boundary $\partial Y_{fs}$. Under these assumptions, $\varepsilon = 1$ corresponds to our microscopic model. The macroscopic model is obtained by investigating the asymptotics as $\varepsilon \rightarrow 0$.

We apply a procedure analogous to the one done by Lima et al. (Lima et al. 2008) to obtain the macroscopic model. The upscaling of the transport equation for the ion $X^{2+}$ is analogous to one for the transport equation of the ion $\mathrm{Na}^+$. Summarizing, the three-scale model is given by: find the macroscopic variables $C_{\mathrm{Na}_b^{+}}$, $C_{X_b^{2+}}$, $C_{H_b^{+}}$, p, $\phi$, $\mathbf {V_{D}}$, satisfying, in the macroscopic domain $\Omega$,

$$\begin{aligned}&\nabla \cdot \mathbf {V_{D}} = 0, \qquad \mathbf {V_{D}} =- \mathbf {K_{P}^{\mathrm{eff}}}\nabla p -\mathbf {K_{E}^{\mathrm{eff}}}\nabla \phi , \end{aligned}$$

(32a)

$$\begin{aligned}&\nabla \cdot \mathbf {J_{\mathrm{Na}^{+}}^{\mathrm{eff}}}= \nabla \cdot \mathbf {J_{X^{2+}}^{\mathrm{eff}}}= \nabla \cdot {\hat{\mathbf {J}}_{\mathbf {H}^{+}}^\mathrm{eff}}= \nabla \cdot \mathbf {I_{f}^{\mathrm{eff}}}=0, \end{aligned}$$

(32b)

where

$$\begin{aligned} \mathbf {J_{\mathrm{Na}^+}^{\mathrm{eff}}}= C_{\mathrm{Na}^+_b} \mathbf {V_{D}} -\mathbf {D_{\mathrm{Na}^+}^{\mathrm{eff}}}\left( \nabla C_{\mathrm{Na}^+_b}+C_{\mathrm{Na}^+_b}\nabla \overline{\phi }\right) , \end{aligned}$$

(33a)

$$\begin{aligned} \mathbf {J_{X^{2+}}^{\mathrm{eff}}}= C_{X_b^{2+}} \mathbf {V_{D}} -\mathbf {D_{X^{2+}}^{\mathrm{eff}}}\left( \nabla C_{X_b^{2+}}+2C_{X_b^{2+}}\nabla \overline{\phi }\right) , \end{aligned}$$

(33b)

$$\begin{aligned} {\hat{\mathbf {J}}_{\mathbf {H}^{+}}^\mathrm{eff}}= \Theta C_{H_b^{+}} \mathbf {V_{D}} - {\widehat{\mathbf {D}}_{{H}^{+}}^{\mathrm{eff}}}\left( \nabla C_{H_b^{+}}+ C_{H_b^{+}}\nabla \overline{\phi }\right) , \end{aligned}$$

(33c)

$$\begin{aligned} \mathbf {I_{f}^{\mathrm{eff}}}= -\mathbf {A^{\mathrm{eff}}}\nabla C_{\mathrm{Na}_b^{+}}-\mathbf {B^{\mathrm{eff}}}\nabla C_{H_b^{+}}-\mathbf {C^{\mathrm{eff}}}\nabla C_{X_b^{2+}}-\mathbf {D^{\mathrm{eff}}}\nabla \overline{\phi }. \end{aligned}$$

(33d)

In the macroscopic formulation (32)–(33), $\mathbf {K_{P}^{\mathrm{eff}}}$ represents the effective hydraulic conductivity, $\mathbf {K_{E}^{\mathrm{eff}}}$ the effective electroosmotic permeability, $\mathbf {D_{i}^{\mathrm{eff}}}$ the effective diffusivity of the ion i, for $i = \mathrm{Na}^+, X^{2+}$, $\mathbf {\widehat{D}_{\mathrm{H}^{+}}^{\mathrm{eff}}}$ the effective diffusion coefficients of the $\mathrm{H}^{+}-\mathrm{OH}^{-}$ ions, with $\mathbf {A^{\mathrm{eff}}}$, $\mathbf {B^{\mathrm{eff}}}$, $\mathbf {C^{\mathrm{eff}}}$ and $\mathbf {D^{\mathrm{eff}}}$ being the first, second, third and fourth coefficients in the Onsager sense (Coelho et al. 1996; Moyne and Murad 2006). The effective parameters of the system are given by

$$\begin{aligned}&\mathbf {K_{P}^{\mathrm{eff}}}=\dfrac{<\varvec{\kappa _{P}}>}{\mu _f}, \end{aligned}$$

(34a)

$$\begin{aligned}&\mathbf {K_{E}^{\mathrm{eff}}}= - \dfrac{\widetilde{\epsilon }_{0}\widetilde{\epsilon }_{r}\zeta }{\mu _{f}}<{\mathbf {I}} + \nabla _{y}{\mathbf {f}}>, \end{aligned}$$

(34b)

$$\begin{aligned}&\mathbf {\widehat{D}_{\mathrm{H}^{+}}^{\mathrm{eff}}}= \widehat{D}_{\mathrm{H}^{+}}<{\mathbf {I}} + \nabla _{y}{\mathbf {f}}> \end{aligned}$$

(34c)

$$\begin{aligned}&\mathbf {D_{i}^{\mathrm{eff}}}=D_{i}<{\mathbf {I}} + \nabla _{y}{\mathbf {f}}>, \quad i=\mathrm{Na}^+, X^{2+}, \end{aligned}$$

(34d)

$$\begin{aligned}&\mathbf {A^{\mathrm{eff}}}= F\left( D_{\mathrm{Na}^{+}}-D_{\mathrm{Cl}^{-}}\right) <{\mathbf {I}} + \nabla _{y}{\mathbf {f}}>, \end{aligned}$$

(34e)

$$\begin{aligned}&\mathbf {B^{\mathrm{eff}}}= F\left[ D_{\mathrm{H}^{+}}-D_{\mathrm{Cl}^{-}} \right. \nonumber \\&\quad \left. + \left( D_{\mathrm{OH}^{-}}-D_{\mathrm{Cl}^{-}}\right) K_{W}/C_{H_b^{+}}^{2}\right] <{\mathbf {I}} + \nabla _{y}{\mathbf {f}}>, \end{aligned}$$

(34f)

$$\begin{aligned}&\mathbf {C^{\mathrm{eff}}}=2F(D_{X^{2+}} - D_{\mathrm{Cl}^{-}})<{\mathbf {I}} + \nabla _{y}{\mathbf {f}}>, \end{aligned}$$

(34g)

$$\begin{aligned}&\mathbf {D^{\mathrm{eff}}} = F\left[ \left( D_{\mathrm{Na}^{+}}+D_{\mathrm{Cl}^{-}}\right) C_{\mathrm{Na}_b^{+}} \right. \nonumber \\&\quad +\left( D_{\mathrm{H}^{+}}+D_{\mathrm{Cl}^{-}}\right) C_{H_b^{+}}+ 2(2D_{X^{2+}} + D_{\mathrm{Cl}^{-}})C_{X_b^{2+}} \nonumber \\&\quad \left. + \left( D_{\mathrm{OH}^{-}}-D_{\mathrm{Cl}^{-}}\right) K_{W}/C_{H_b^{+}}\right] <{\mathbf {I}} + \nabla _{y}{\mathbf {f}}>, \end{aligned}$$

(34h)

where ${\mathbf {I}}$ is the identity matrix, $\nabla _{y}$ represents the spatial gradient with respect to the microscopic coordinate ${\mathbf {y}}$, in $Y_f$, and $<\cdot>$ is the averaging over the standard periodic cell Y defined as

$$\begin{aligned} <\chi > {:=}\dfrac{1}{|Y|} \int _{Y_f} \chi \; d{\mathbf {y}}. \end{aligned}$$

(35)

Moreover, the characteristic functions $\nabla _{y}{\mathbf {f}}$ and $\varvec{\kappa _{P}}$ satisfy the cell problems

$$\begin{aligned} \left\{ \begin{array}{ll} \varDelta _{yy}{\mathbf {f}}\left( {\mathbf {y}}\right) = 0, &{} \text{ in } Y_{f}, \\ \nabla _{y}{\mathbf {f}}\left( {\mathbf {y}}\right) {\mathbf {n}} = - {\mathbf {n}}, &{} \text{ on } \partial Y_{fs}, \end{array} \right. \end{aligned}$$

(36)

and

$$\begin{aligned} \left\{ \begin{array}{ll} \varDelta _{yy}\varvec{\kappa _{P}^{j}}-\nabla _{y}\pi _{P}^{j}=-e^{j},&{} \text{ in } Y_{f}, \\ \nabla _{y} \cdot \varvec{\kappa _{P}^{j}}= 0, &{} \text{ in } Y_{f}, \\ \varvec{\kappa _{P}^{j}}= 0, &{} \text{ on } \partial Y_{fs}, \end{array} \right. \end{aligned}$$

(37)

where $j= 1, 2, 3$, $\displaystyle \{{\mathbf {e}}^{j}\}_{j=1}^3$ is an orthonormal basis, $\varvec{\kappa _{P}}$ is the tensorial periodic function and $\varvec{\pi _{P}}$ is the vectorial field with vectorial components $\varvec{\kappa _{P}^{j}}$ and scalars $\pi _{P}^{j}$. For a periodic structure, the gradient of the vectorial function ${\mathbf {f}}$ computes the effect of the microscopic geometry on the effective parameters (34b)–(34h), commonly associated to the tortuosity of the medium. The tensor $\varvec{\kappa _{P}}$ quantifies the influence of the microstructure on the macroscopic permeability that is given by the average of $\varvec{\kappa _{P}}$ over the periodic cell (see Eq. (34a)).

Solving the multi-scale model (32)–(37) takes the following steps:

• 1. From available experimental data for the electrochemical constants, we solve the nanoscopic problem (19) to find the $\zeta$-potential.

• 2. For a given microscopic geometry (see Fig. 2a), we solve the cell problems (36)–(37).

• 3. Knowing $\zeta$, ${\mathbf {f}}$ and $\varvec{\kappa _{P}}$, we then determine the effective parameters (34).

• 4. Finally, we obtain solution the macroscopic model (32)–(33).

Note that the micro and the macro models are then coupled through the macroscopic parameters (34). Note that in the interface electrolyte solution/solid surface, the $\zeta$-potential in the EDL gives rise to the electroosmotic permeability at the macroscale (34b). Also, the electrical potential gradient applied due to the presence of electrodes in the sample is the main driven force for the fluid flow and, consequently, for the transport of the solutes induced by the convective phenomenon. The quantification of the $\zeta$-potential in the presence of monovalent/bivalent ions, its influence in the macroscopic electroosmotic permeability, and, consequently, in the Darcy velocity are among the main results presented here.

3.1 One-dimensional model

To simulate the electroremediation process, we reduce the macroscopic system (32) to a one-dimensional problem. In this scenario, the macroscopic domain is $\Omega =(0,L)$, where $x=0$ and $x=L$ are located the anode and cathode, denoted as $\Gamma _a$ and $\Gamma _c$, respectively, (see Fig. 3a). To simplify the model, we consider the clay particles have a stratified microgeometry composed of parallel particles separated from each other by a fixed distance. In this stratified geometry, denote by $\{x,y\}$ the coordinates aligned with the directions parallel and orthogonal to the particle surface, respectively. Since flow and ion transport occur just in the x-direction, we only compute the axial components of the fluxes {$\mathbf {V_{D}}$, $\mathbf {J_{i}^{\mathrm{eff}}}$, $\mathbf {\widehat{J}_{\mathrm{H}^+}^{\mathrm{eff}}}$, $\mathbf {I_{f}^{\mathrm{eff}}}$}, and tensors {$\mathbf {K_{E}^{\mathrm{eff}}}$, $\mathbf {K_{P}^{\mathrm{eff}}}$, $\mathbf {D_{i}^{\mathrm{eff}}}$, $\mathbf {\widehat{D}^{\mathrm{eff}}}$, $\mathbf {A^{\mathrm{eff}}}$, $\mathbf {B^{\mathrm{eff}}}$, $\mathbf {C^{\mathrm{eff}}}$, $\mathbf {D^{\mathrm{eff}}_{\mathrm{H}^{+}}}$}, $i=\mathrm{Na}^+, X^{2+}$ denoted without boldface. Considering these assumptions, the macroscopic system (32) is reduced to the following one-dimensional problem

$$\begin{aligned}&\frac{\mathrm{d} V_{D}}{\mathrm{d} x}=0, \end{aligned}$$

(38a)

$$\begin{aligned}&V_{D}= -K_{E}^{\mathrm{eff}} \dfrac{\mathrm{d} \phi }{\mathrm{d} x}-K_{P}^{\mathrm{eff}}\dfrac{\mathrm{d} p}{\mathrm{d} x}, \end{aligned}$$

(38b)

$$\begin{aligned}&\frac{\mathrm{d} J_{\mathrm{Na}^+}^{\mathrm{eff}}}{\mathrm{d} x}=\frac{\mathrm{d} J_{X^{2+}}^{\mathrm{eff}}}{\mathrm{d} x}= \frac{\mathrm{d} \widehat{J}_{\mathrm{H}^+}^{\mathrm{eff}}}{\mathrm{d} x}= \frac{\mathrm{d} I_{f}^{\mathrm{eff}} }{\mathrm{d} x} =0, \end{aligned}$$

(38c)

$$\begin{aligned}&J_{\mathrm{Na}^+}^{\mathrm{eff}}=C_{\mathrm{Na}^+_b} V_{D} -D_{\mathrm{Na}^+}^{\mathrm{eff}}\left( \frac{\mathrm{d} C_{\mathrm{Na}^+_b}}{\mathrm{d} x}+C_{\mathrm{Na}^+_b}\frac{\mathrm{d} \overline{\phi }}{\mathrm{d} x}\right) , \end{aligned}$$

(38d)

$$\begin{aligned}&J_{X^{2+}}^{\mathrm{eff}}=C_{X^{2+}_b} V_{D} -D_{X^{2+}}^{\mathrm{eff}}\left( \frac{\mathrm{d} C_{X^{2+}_b}}{\mathrm{d} x}+2C_{X^{2+}_b}\frac{\mathrm{d} \overline{\phi }}{\mathrm{d} x}\right) , \end{aligned}$$

(38e)

$$\begin{aligned}&\hat{J}_{\mathrm{H}^+}^{\mathrm{eff}}= \Theta C_{\mathrm{H}^{+}_b} V_{D} -\widehat{D}^{\mathrm{eff}}_{H+}\left( \frac{d C_{\mathrm{H}^{+}_b}}{\mathrm{d} x}+C_{\mathrm{H}^{+}_b}\frac{\mathrm{d} \overline{\phi }}{d x}\right) , \end{aligned}$$

(38f)

$$\begin{aligned}&I_{f}^{\mathrm{eff}}=-A^{\mathrm{eff}}\frac{\mathrm{d} C_{\mathrm{Na}_b^{+}}}{\mathrm{d} x}-B^{\mathrm{eff}}\frac{\mathrm{d} C_{\mathrm{H}^{+}_b}}{\mathrm{d} x}-C^{\mathrm{eff}}\frac{\mathrm{d} C_{X^{2+}_b}}{\mathrm{d} x}\nonumber \\&\quad -D^{\mathrm{eff}}\frac{\mathrm{d} \overline{\phi }}{\mathrm{d} x}. \end{aligned}$$

(38g)

We consider the periodic cell Y delimited by two parallel clay particles separated by a fixed distance, 2H, and particles thickness $\delta$ (see Fig. 3b). In this scenario, the porosity is given by $\eta =H/(H+\delta )$, the cell problems (36)–(37) are reduced to $\mathrm{d}f/\mathrm{d}y=0$ and $\kappa _{P}= -\left( y^{2}-\mathrm{H}^{2}\right) /2\mu _{f}$. Using (35) and replacing the previous expressions in (34) the effective parameters are rewritten as

$$\begin{aligned}&K_{E}^{\mathrm{eff}}= -\eta \widetilde{\epsilon }_{0} \widetilde{\epsilon }_{r} \zeta / \mu _{f}, \end{aligned}$$

(39a)

$$\begin{aligned}&\Theta =1-K_{W}/ C_{H_b^{+}}^2, \end{aligned}$$

(39b)

$$\begin{aligned}&K_{P}^{\mathrm{eff}}=\mathrm{H}^{3}/ \left[ 3\left( H+\delta \right) \mu _{f}\right] , \end{aligned}$$

(39c)

$$\begin{aligned}&\widehat{D}^{\mathrm{eff}}_{\mathrm{H}^{+}}= \eta \left( D_{\mathrm{H}^{+}}+K_{W} D _{\mathrm{OH}^{-}}/ C_{H_b^{+}}^{2}\right) , \end{aligned}$$

(39d)

$$\begin{aligned}&D_i^{\mathrm{eff}}=\eta D_{i}, \quad i=\mathrm{Na}^+, X^{2+}, \end{aligned}$$

(39e)

$$\begin{aligned}&A^{\mathrm{eff}}= F\eta \left( D_{\mathrm{Na}^{+}}-D_{\mathrm{Cl}^{-}}\right) , \end{aligned}$$

(39f)

$$\begin{aligned}&C^{\mathrm{eff}} = 2F\eta (D_{X^{2+}} - D_{\mathrm{Cl}^{-}}) \ \ \end{aligned}$$

(39g)

$$\begin{aligned}&B^{\mathrm{eff}}=F\eta \left[ D_{\mathrm{H}^{+}}-D_{\mathrm{Cl}^{-}}+\left( D_{\mathrm{OH}^{-}}-D_{\mathrm{Cl}^{-}}\right) \dfrac{K_{W}}{C_{H_b^{+}}^{2}}\right] , \end{aligned}$$

(39h)

$$\begin{aligned}&D^{\mathrm{eff}} = F\eta \left[ \left( D_{\mathrm{Na}^{+}}+D_{\mathrm{Cl}^{-}}\right) C_{\mathrm{Na}_b^{+}}+\right. \left( D_{\mathrm{H}^{+}}+D_{\mathrm{Cl}^{-}}\right) C_{H_b^{+}} \nonumber \\&+ 2(2D_{X^{2+}} + D_{\mathrm{Cl}^{-}})C_{X_b^{2+}}+ \left. \left( D_{\mathrm{OH}^{-}}-D_{\mathrm{Cl}^{-}}\right) K_{W}/C_{H_b^{+}}\right] , \end{aligned}$$

(39i)

We note that the effective parameters $K_{E}^{\mathrm{eff}}$, $\widehat{D}_{\mathrm{H}^{+}}^{\mathrm{eff}}$, $B^{\mathrm{eff}}$, $D^{\mathrm{eff}}$ are functions of the concentration of the cations on the bulk. Hence the system (38) is nonlinear and strongly couples the different scales. In particular, we would like to highlight that the classical effective hydraulic conductivity (39c) incorporates only microscopic parameter $\kappa _P$ associated to the microgeometry. On the other hand, the effective electroosmotic permeability $K_{E}^{\mathrm{eff}}$ (39a) incorporates the nanoscopic information (19) through the $\zeta$-potential and the microscopic information through the characteristic function ${\mathbf {f}} = \mathbf {f(y)}.$

3.2 Boundary conditions

It is a hard task to postulate boundary conditions that accurately model the electroosmotic experiments. For the convective/diffusive transport equations, boundary conditions of the first and the second type are commonly imposed. However, these boundary conditions are not suitable to model the electrokinetic of the ionic transport in the presence of charged porous media due to the existence of flux on the boundaries caused by the electrode reactions, by the prescribed electric current, and by the advection phenomenon (Parker and van Genuchten 1984; Reddy and Cameselle 2009). Another type of boundary conditions, known as Danckwerts boundary conditions, arises.

The Danckwerts boundary conditions describe more realistic scenarios of the electroosmotic experiment. They prescribe flow conditions at the interface of the sample with the bath, where the concentration is controlled. They match the total flow in the sample with the flow at the bath immediately outside, where the diffusive/dispersive effects are neglected by assuming that the solution is well-mixed (Lafolie and Hayot 1993; Parker and van Genuchten 1984).

For closing the macroscopic problem (38), we prescribe Danckwerts boundary conditions at the electrodes following (Acar and Alshawabkeh 1993; Alshawabkeh and Acar 1996):

$$\begin{aligned} \text{ For } \text{ the } \text{ anode } \ (x=0): \left\{ \begin{array}{lcl} J_{\mathrm{Na}^{+}}^{\mathrm{eff}} &{}=&{} C_{Na}^{\text {bath}} V_{D}, \\ J_{X^{2+}}^{\mathrm{eff}} &{}=&{} C_{X}^{\text {bath}} V_{D}, \\ I_{f}^{\mathrm{eff}} &{}=&{} - I_0, \\ p&{}=&{}p_{\mathrm{atm}}, \\ C_{H_b^{+}}&{}=&{}\overline{C}. \end{array} \right. \end{aligned}$$

(40a)

$$\begin{aligned} \text{ For } \text{ the } \text{ cathode } \ (x=L): \left\{ \begin{array}{lcl} J_{\mathrm{Na}^{+}}^{\mathrm{eff}} &{}=&{} C_{\mathrm{Na}_b^+} V_{D}, \\ J_{X^{2+}}^{\mathrm{eff}} &{}=&{} C_{X_b^+} V_{D}, \\ \phi &{} =&{} 0, \\ p&{}=&{}p_{\mathrm{atm}}, \\ C_{H_b^{+}}&{}= &{}\overline{C}. \end{array} \right. \end{aligned}$$

(40b)

4 Numerical method

We numerically approximate the solution of macroscopic model (38)–(40) using Galerkin finite element method together with the Newton method. The discretized model extends the validated model proposed by Igreja et al. (2017) that obtained analytical solutions to validate the numerical model considering monovalent ions, thus making the simulations reliable. To optimize the numerical computation, we apply a staggered algorithm that decouples the system into the three problems described below.

Problem I: substitute (38b) into (38a) to approximate the pressure using delayed information about the effective parameters and the electric potential.

Problem II: solve (38b) to find the Darcy velocity using the pressure obtained in Problem I.

Problem III: with the Darcy velocity computed in

Problem II, we simultaneously approximate the system (38c)–(38g) to obtain the concentration of the cations and the electric potential.

The three problems are solved sequentially at each iteration until a given tolerance is reached.

4.1 Variational formulation

Let $\mathrm{H}^1(\Omega )$ be the usual Hilbert space and $L^2(\Omega )$ be the space of square integrable functions with the inner product defined by

$$\begin{aligned} (f,g){:=}\int _{\Omega } fg \;\mathrm{d} x\,, \qquad \forall f,g \in L^2(\Omega ). \end{aligned}$$

(41)

Also, let $\mathrm{H}^1_0(\Omega )$ be the subspace of functions in $\mathrm{H}^1(\Omega )$ with zero trace on $\Gamma$. Considering the Danckwerts boundary conditions (40), we define the following subspaces of $\mathrm{H}^1(\Omega )$

$$\begin{aligned} {\mathcal {P}}(\Omega )= & {} \left\{ q \in \mathrm{H}^1(\Omega ); \ q(0)=q(L) = p_{atm}\right\} ,\\ {\mathcal {U}}(\Omega )= & {} \left\{ C \in \mathrm{H}^1(\Omega ); \ C(0) =C(L) = \overline{C}\right\} ,\\ {\mathcal {V}}(\Omega )= & {} \left\{ \phi \in \mathrm{H}^1(\Omega ); \ \phi (L) = 0 \right\} \end{aligned}$$

where $p_{atm}$ denotes the atmospheric pressure and $\overline{C}$ is the $\mathrm{H}^+$ concentration imposed at the ends of the sample.

The variational formulation of the macroscopic problem (38) is obtained by multiplying the equations by weight functions in the appropriated function space, integrating by parts and applying the boundary conditions (5). Let the index $n = 1, 2,\ldots , N$ indicate the iteration in the staggered scheme. Below, we present the resulting variational equations in the sequence that they are solved.

Problem I: given the pair $(K_{E,{n-1}}^{\mathrm{eff}}, \phi ^{n-1})$ find $p^n \in {\mathcal {P}}(\Omega )$ such that

$$\begin{aligned} \left( K_{P}^{\mathrm{eff}}\dfrac{\mathrm{d} p^n}{\mathrm{d}x},\dfrac{\mathrm{d} q}{\mathrm{d}x}\right) = -\left( K_{E,{n-1}}^{\mathrm{eff}}\dfrac{\mathrm{d} \phi ^{n-1}}{\mathrm{d}x},\dfrac{\mathrm{d} q}{\mathrm{d}x}\right) \,, \end{aligned}$$

(42)

for all $q \in \mathrm{H}^1_0$. We observe that to obtain (42) we substitute (38b) into (38a).

Problem II: given the triple $(K_{E}^{\mathrm{eff},{n-1}}, \phi ^{n-1}, p^{n})$ find $V^{n}_{D} \in L^2(\Omega )$, satisfying

$$\begin{aligned} \left( V^{n}_{D}, w\right) = -\left( K_{E,{n-1}}^{\mathrm{eff}}\dfrac{\mathrm{d} \phi ^{n-1}}{\mathrm{d}x}+K_{P}^{\mathrm{eff}}\dfrac{\mathrm{d} p^n}{\mathrm{d}x},w\right) , \end{aligned}$$

(43)

for all $w \in L^2(\Omega )$. Note that the electroosmotic component of the Darcy law is delayed in relation to hydraulic one.

Problem III: given $(C^{n-1}_{\mathrm{Na}_b^+}, C^{n-1}_{X_b^{2+}}, C^{n-1}_{H_b^+}, \phi ^{n-1},V^{n}_{D})$, find $[C^n_{\mathrm{Na}_b^+}, C^{n}_{X_b^{2+}}, C^n_{H_b^+}, \phi ^n] \in \left( \mathrm{H}^1(\Omega )\right) ^2 \times {\mathcal {U}}(\Omega )\times {\mathcal {V}}(\Omega )$, such that

$$\begin{aligned}&\left( J_{i,n}^{\mathrm{eff}},\dfrac{\mathrm{d} q_1}{\mathrm{d}x}\right) -C^n_{i_{b}} V^{n}_{D}\, q_1\bigg |_{x=L} = -C_{i}^{\text {bath}} \, V^{n}_{D}\, q_1\bigg |_{x=0}, \end{aligned}$$

(44a)

$$\begin{aligned}&\left( \hat{J}_{\mathrm{H}^{+},n}^{\mathrm{eff}},\dfrac{\mathrm{d} q_2}{\mathrm{d}x}\right) =0, \end{aligned}$$

(44b)

$$\begin{aligned}&\left( I_{f,n}^{\mathrm{eff}},\dfrac{\mathrm{d} q_3}{\mathrm{d}x}\right) = -I_0\, q_3\bigg |_{x=0}, \end{aligned}$$

(44c)

for $i=\mathrm{Na}^+, X^{2+}$ and for all $q_1 \in \mathrm{H}^1(\Omega )$, $q_2 \in \mathrm{H}^1_0(\Omega )$, $q_3 \in {\mathcal {V}}(\Omega ).$ The equations in nonlinear system (44) are solved together using the Newton–Raphson method (Quarteroni and Valli 1994).

4.2 Discrete approximation

Let $\{{\mathcal {T}}_h\}$ be a family of partitions ${\mathcal {T}}_h = \{\Omega ^e\}$ of $\Omega$ where h represents the maximum diameter of the elements $\Omega ^e \in {\mathcal {T}}_h$. Let ${\mathcal {S}}_h^k= \{\psi _h \in C^0(\Omega );\psi _h|_{\Omega ^e} \in {\mathbb {P}}_k(\Omega ^e)\}$ be the $C^0(\Omega )$ Lagrangian finite element space of degree $k \ge 1$ in each element $\Omega ^e$, where ${\mathbb {P}}_k(\Omega ^e)$ is the set of the polynomials of degree $\le k$ posed on $\Omega ^e$. The weak formulation of the system (42)–(44c) is discretized by the Galerkin finite element approximation on the conforming spaces ${\mathcal {P}}^k_h(\Omega )={\mathcal {S}}_h^k \cap {\mathcal {P}}(\Omega )$, ${\mathcal {U}}^k_h(\Omega )={\mathcal {S}}_h^k \cap {\mathcal {U}}(\Omega )$ and ${\mathcal {V}}^k_h(\Omega )={\mathcal {S}}_h^k \cap {\mathcal {V}}(\Omega )$. For the velocity $V_D$ and $C_{\mathrm{Na}_b^+}$, we define the discrete spaces ${\mathcal {S}}_h^k\cap L^2(\Omega )$ and ${\mathcal {S}}_h^k \cap \mathrm{H}^1(\Omega )$, respectively.

5 Simulation for electroremediation in kaolinite clay

To simulate the electroosmotic experiment illustrate in Fig. 3, we hereafter assume the clay soil is composed of kaolinite particles saturated by an aqueous solution where the bivalent ion is the metallic ion cadmium, i.e., $X^{2+}=\mathrm{Cd}^{2+}$ (Angove et al. 1997, 1998; Mitchell 1976). To analyze the influence of the nanoscopic variables in the behavior of the macroscopic unknowns, first, we numerically solve the nanoscopic equations (19) and (15) to construct the dependence of the $\zeta$-potential and surface charge density $\sigma$ on a given set of sodium concentration, $C_{\mathrm{Na}_b^{+}}$, cadmium concentration, $C_{\mathrm{Cd}_b^{2+}}$, and, pH. Then, considering the stratified microstructure described in Sect. 3.1, we quantify the nano and microscopic effective parameters (39a)–(39i). Finally, we simulate the electroremediation process using the finite element discretization of the macroscopic system (38) for two different cases based on the Dirichlet and Danckwerts boundary conditions.

In the first case, we propose four different scenarios for controlled variables at the electrodes. To this end, we prescribe Dirichlet boundary conditions at the electrodes for the electric potential, pressure, pH, and cationic concentrations. For the second case, we impose Danckwerts boundary conditions (40a)–(40b) to incorporate the chemistry of the reactions at the electrodes. Here, we run three simulations for different values of electric current prescribed at the anode. Table 1 displays the value of the constants used in the simulations.

Table 1 Parameters used in the numerical simulations

5.1 Numerical simulation for the nanoscopic model

Here we simulate the dependence of the nanoscopic unknowns, $\zeta$-potential and surface charge density $\sigma$, on the cationic concentrations and pH. To this end, for a given triple {$C_{\mathrm{Na}_b^{+}}$, $C_{H_b^{+}}$, $C_{\mathrm{Cd}_b^{2+}}$}, we apply the Newton–Raphson method to numerically solve the nonlinear equation (19) for the $\zeta$-potential and then use (15) to determine the surface charge density $\sigma$. In the simulations, we use the physical-chemical parameters presented in Angove et al. (1997) that are displayed in Table 1. Figures 4, 5, 6, 7 display the numerical solutions obtained for different scenarios.

Figures 4 and 5 show the surface charge density and $\zeta$-potential as functions of $\mathrm{pH}$ for different values of $C_{\mathrm{Cd}_b^{2+}}$ for $C_{\mathrm{Na}_b^{+}}=10$mol/m$^3$ and $C_{\mathrm{Na}_b^{+}}=100$mol/m$^3$, respectively. The numerical solutions clearly confirms that isoelectric point occurs in the vicinity of $\mathrm{pH}=5.0$ in accordance with the value predicted in Angove et al. (1997, 1998). We observe that for acid regimes, $\mathrm{pH}<5.0$, due to the increase of $\mathrm{H}^+$ concentration, the protonation reactions (9)–(10) dominate the electro-chemistry and, consequently, the surface charge density and $\zeta$-potential are both positive. Also, increasing the $C_{\mathrm{Cd}_b^{2+}}$ increases the surface charge density and decreases the $\zeta$-potential. Conversely, for alkaline regimes, $\mathrm{pH}>5.0$, the decrease of $\mathrm{H}^+$ concentration favors the deprotonation reaction (10) turning the surface charge density and $\zeta$-potential both negative. Moreover, for the $\mathrm{pH}>5.0$ the presence of the $\mathrm{Cd}^{2+}$ gives rise to the cationic exchange reaction (11), inhibiting the deprotonation reaction (10); consequently, the surface charge density and the $\zeta$-potential remain almost constant. In the alkaline regime, for a high value of the metallic ion concentration, the electro-chemistry is dominated by the cationic exchange reaction (11) and consequently the surface charge density and the $\zeta$-potential tend to zero. Finally, increasing the sodium concentration increases the charge density (in absolute value) and decreases the $\zeta$-potential (in absolute value).

Figures 6 and 7 display the surface charge density and $\zeta$-potential as a function of $C_{\mathrm{Cd}_b^{2+}}$ for acid and basic pH values for $C_{\mathrm{Na}_b^{+}}=10$mol/m$^3$ and $C_{\mathrm{Na}_b^{+}}=100$mol/m$^3$, respectively. For the pH values lower than the isoelectric point, $\mathrm{pH}=3$ and $\mathrm{pH}=4$, the electro-chemistry is dominated by the deprotonation reactions (9)–(10); consequently, the results show the surface charge density increasing and the $\zeta$-potential decreasing. For a pH value close to the isoelectric point, $\mathrm{pH}=5$, the charge density and $\zeta$-potential are almost independent of the ionic-strength. For $\mathrm{pH}$ values higher than the isoelectric point, $\mathrm{pH}=7$ and $\mathrm{pH}=9$, increasing the $\mathrm{Cd}^{2+}$ concentration favors the cationic exchange reaction (11); consequently the charge density and the $\zeta$-potential tend to zero. It is important to highlight that these $\zeta$-potential simulations are very important since they are used to compute the effective electroosmotic permeability, $K_E^{\mathrm{eff}},$ via (39a). The effective parameter $K_E^{\mathrm{eff}}$ appears in equation (38b) showing that, for a constant pressure prescribed at the ends of the sample, the nanoscopic parameter $\zeta$-potential dominates the behavior of the macroscopic fluid velocity profile.

Fig. 4

Charge density and $\zeta$-potential for $C_{\mathrm{Na}_b^{+}}=10$mol/m$^3$ and different values of $C_{\mathrm{Cd}_b^{2+}}$

Fig. 5

Charge density and $\zeta$-potential for $C_{\mathrm{Na}_b^{+}}=100$mol/m$^3$ and different values of $C_{\mathrm{Cd}_b^{2+}}$

Fig. 6

Charge density and $\zeta$-potential for $C_{\mathrm{Na}_b^{+}}=10$mol/m$^3$ and different values of $\mathrm{pH}$

Fig. 7

Charge density and $\zeta$-potential for $C_{\mathrm{Na}_b^{+}}=100$mol/m$^3$ and different values of $\mathrm{pH}$

Fig. 8

pH profiles for pH values fixed at the electrodes

Fig. 9

$\mathrm{Na}^+$ concentration profiles for pH values fixed at the electrodes

Fig. 10

$\mathrm{Cd}^{2+}$ concentration profiles for pH values fixed at the electrodes

Fig. 11

Electric potential profiles for pH values fixed at the electrodes

5.2 Numerical simulation for the controlled variables

Here we simulate electroosmosis experiments in a sample with length $L=0.01$ m considering controlled variables at the electrodes, i.e., Dirichlet boundary conditions for all unknowns. To analyse the influence of the $\mathrm{pH}$ on the electroosmosis process, we simulate four distinct scenarios:

• Scenario 1: $\mathrm{pH}=4$ at both electrodes;

• Scenario 2: $\mathrm{pH}=7$ at both electrodes;

• Scenario 3: $\mathrm{pH}=4$ at the anode and $\mathrm{pH}=7$ at the cathode.

• Scenario 4: $\mathrm{pH}=7$ at the anode and $\mathrm{pH}=4$ at the cathode.

The other boundary conditions are kept the same throughout the simulations. For the anode ($x=0$m), we impose $C_{\mathrm{Na}^{+}_b} = 10$mol/m$^3$, $C_{\mathrm{Cd}^{2+}_b} = 1$mol/m$^3$, $\phi = 1$V and $p=10^5$Pa. For the cathode ($x=0.01$m), we consider $C_{\mathrm{Na}^{+}_b} = 1$mol/m$^3$, $C_{\mathrm{Cd}^{2+}_b} = 0.1$mol/m$^3$, $\phi = 0$V and $p=10^5$Pa. We discretize the domain using a fine nonuniform mesh with $10^4$ elements. The resulting local Pèclet number, defined by $Pe_h {:=}h V_{\mathrm{ref}}/2D$, is low, $Pe_h={\mathbb {O}}(1)$, assuring the stability of the Galerkin scheme. In Figures 8, 9, 10, 11, 12, the results for scenarios 1, 2, 3, and, 4 are plotted in red, blue, black, and green, respectively.

Figure 8 displays the $\mathrm{pH}$ profile for the four different scenarios. In Fig. 8a, the influence of the convection given by the electroosmotic and electromigration terms together with the electrochemical phenomena in the EDL causes a tendency for basification inside the sample. For the acid regime, there is the formation of a plateau inside the sample with the $\mathrm{pH}\approx 4.5$. For the basic regime, the plateau inside the sample occurs at $\mathrm{pH}\approx 8.2$. In Fig. 8b, we observe that scenarios 3 and 4 behave similarly to scenarios 1 and 2, respectively. Note that the basification and the plateaus also occur together with a sharp boundary layer in the vicinity of the cathode to satisfy the imposed Dirichlet boundary condition.

It is important to mention that the work of Igreja et al. (2017) (see Eq. 38 of their paper) demonstrates that, for the pH profile, the range of the plateau is inversely proportional to both the gradient of the electric potential and Darcy’s velocity. Here, Figs. 4, 5, 6, 7 show that the presence of the bivalent ion lowers the range of the values for the surface charge and the $\zeta$-potential compared to those obtained on the presence of the monovalent ion only. Consequently, Eqs. (38b) and (39a) show that the Darcy velocity also assumes lower values in the presence of the bivalent ion. Getting back to Eq. (38) from (Igreja et al. 2017), the lower values for Darcy’s velocity results in a higher pH plateau. Therefore, comparing these results with the results in Lima et al. (2008), we observe that the presence of the bivalent $\mathrm{Cd}^{2+}$ ion increases the $\mathrm{pH}$ plateaus significantly.

Figures 9, 10 display the $\mathrm{Na}^+$ and $\mathrm{Cd}^{2+}$ concentration profiles considering the Dirichlet boundary conditions $C_{\mathrm{Na}_b^{+}}=10$mol/m$^3$ and $C_{\mathrm{Cd}_b^{2+}}=1$mol/m$^3$ at the anode together with $C_{\mathrm{Na}_b^{+}}=1$mol/m$^3$ and $C_{\mathrm{Cd}_b^{2+}}=0.1$mol/m$^3$ at the cathode. For the basic regime in scenario 2, with $\mathrm{pH}=7.0$ fixed at both electrodes, Fig. 8a shows that the $\mathrm{pH}>5.25$; consequently, the $\zeta$-potential is negative (see Figs. 4, 5) and $K_E^{\mathrm{eff}}>0$ (see 39a) that causes a classical electroosmotic flow in the opposite direction of the applied electric field. Thus, in this scenario, the profiles for the cation concentration exhibit a boundary layer formation close to the cathode. Conversely, for the acid regime in scenario 1, with $\mathrm{pH} = 4.0$ kept at both electrodes, the $\zeta$-potential is positive and $K_E^{\mathrm{eff}}<0$; consequently, the electroosmotic flow occurs in the same direction of the electric field, with the boundary layer now close to the anode. Finally, in Figs. 9b and 10b, we show the cations {$\mathrm{Na}^+$, $\mathrm{Cd}^{2+}$} concentration profiles considering the scenarios 3 and 4 with different $\mathrm{pH}$ values at the electrodes. In the scenario 3, the acid regime $\mathrm{pH}<5.25$ prevails in almost the entire domain (see Fig. 8b), then the $\zeta > 0$ and $K_E^{\mathrm{eff}}<0$ which implies in a convective electroosmotic flow towards the anode. In the scenario 4, the basic regime with $\mathrm{pH}>5.25$ prevails; consequently, the electroosmotic flow is towards the cathode.

Figure 11 simulates the electric potential considering $\phi =1$V at the anode and $\phi =0$V at the cathode. For the acid and basic $\mathrm{pH}$ profiles obtained in Fig. 11a, the electric potential shows a nonlinear behavior in the vicinities of the electrodes with a linear distribution inside the sample. Finally, Fig. 12 plots the simulation for the pressure $p=10^5$ Pa controlled at the electrodes. The nonlinear profile displayed for the pressure arises to fulfill the incompressibility condition (38a) along with Darcy’s law (38b).

5.3 Numerical simulation for the danckwerts boundary condition

We now impose the Danckwerts boundary condition to the discrete problems (42)–(44) to analyze more realistic scenarios of the electroremediation process where the electric current and flow for the concentration of the solutes are imposed. For the numerical simulations, we prescribe the concentrations $C_{Na}^{\text {bath}}=1.0$mol/m$^3$ and $C_{Cd}^{\text {bath}}=0.1$mol/m$^3$ at the inlet of the sample. Moreover, we set the $\mathrm{pH}=8.0$, and $p=10^5 Pa$ at both electrodes with $\phi =0$ applied at the cathode. Finally, we perform three simulations imposing the following values for the electric current at the anode: $I_0=0.1$, 0.5 e 1.5A/m$^2$. In Figs 13–15, we display the distribution of the $\mathrm{pH}$, velocity,electric potential, pressure and concentration of the cations for each value of the electric current imposed at the anode.

Figure 13a displays the $\mathrm{pH}$ profile for the different values of the electric current imposed at the anode. Considering $\mathrm{pH}=8.0$ fixed at the electrodes, we observe a acidification of the sample and the formation of a plateau close to the $\mathrm{pH}=7.6$ when the imposed electric current increases. Also, a boundary layer appears in the vicinity of the electrodes due to the Dirichlet condition for the $\mathrm{pH}$. In Fig. 13b, we display the distribution of the Darcy velocity for the three electric currents imposed. The results show that the increase of the current leads to a substantial increase in the advective effect.

Fig. 12

Pressure profiles for pH values fixed at the electrodes

Fig. 13

pH and velocity profiles for different currents prescribed at the anode

Fig. 14

Pressure and electric potential profiles for different currents prescribed at the anode

Fig. 15

Concentrations profiles for different currents prescribed at the anode

Figure 14 shows the electric potential and pressure profiles for different values of the electric current imposed at the anode. In Fig. 14a, we observe that the electric potential decreases linearly towards the cathode and grows with the current. This linear profile for the electric potential was observed experimentally in Beddiar et al. (2005). In Fig. 14b, we present the profile of the pressure for different current values. The abrupt variation counterbalances the electroosmotic component and fulfills the incompressibility constraint. This nonlinear profile for the pressure was observed experimentally in Beddiar et al. (2005).

Figure 15 shows the behavior of sodium and cadmium concentration for different values of the electric current imposed at the anode. From the potential profiles in Fig. 14a, we observe that since $\mathrm{pH} > 5.25$ throughout the sample, the $\zeta$-potential is negative (see Figs. 4, 5); consequently, $K_E^{\mathrm{eff}}>0$ which implies that the electroosmotic flow is towards the cathode. With the electroosmotic flow going in the opposite direction of the electric potential gradient towards the cathode and the Darcy velocity proportional to the electric current (see Fig. 13b), the boundary layer in the vicinity of the cathode becomes sharper as the current increases. We also point out the formation of plateaus close to 0.4 mol/m$^3$ and 0.04 mol/m$^3$ for the concentration of sodium and cadmium, respectively.

6 Conclusion

We have developed a three-scale (nano/micro/macroscopic) computational model based on the homogenization technique. The resulting model is a system of nonlinear differential equations that quantifies the hydrodynamics of an aqueous solution and the transport of monovalent/bivalent ions ($\mathrm{Na}^+$, $\mathrm{H}^+$, $X^{2+}$, $\mathrm{Cl}^-$, $\mathrm{OH}^-$) in charged porous media. The most significant results are the following:

• We derived a nanoscopic model that features the influence of the concentration of monovalent and bivalent ions on the electric potential of the EDL, on the surface charge density and on the $\zeta$-potential.

• Under the thin EDL assumption, we have obtained the analytical solution of the Poisson–Boltzmann problem considering the presence of a bivalent metallic ion.

• The nonlinear algebraic Eq. (19) determines the $\zeta$-potential and, consequently, computes the surface charge density and the electroosmotic permeability. We have numerically simulated the $\zeta$-potential and the surface charge density for different scenarios and showed their dependence on the concentration of the cations.

• The multi-scale model allows us to bridge the nano-micro and macroscopic electrochemical phenomena in clay under steady-state conditions. In particular, we highlight the dependence of the new constitutive law for the electroosmotic permeability on the $\mathrm{pH}$, sodium, and bivalent metallic ion concentration.

• The discrete model, obtained via the Galerkin finite element method, is used to numerically simulate the electroremediation process using a staggered algorithm together with the Newton–Raphson method. Due to the choice of a very fine mesh, the numerical simulations are stable and the profiles obtained are non-oscillatory. The numerical results considered Dirichlet and Danckwerts boundary conditions. The obtained profiles show the dependence of the electroremediation process on the $\mathrm{pH}$, monovalent and bivalent ions.

• The simulations with Dirichlet boundary conditions show that the presence of the bivalent ion increases the $\mathrm{pH}$ plateaus (tendency for basification of the sample). Also, when the regime changes from basic to acid, we observe an inversion of the electroosmotic flow. In the acid regime, the flow is in the same direction of the applied electric field. In the basic regime, it is in the opposite direction.

• The simulations with Danckwerts boundary conditions show a tendency for acidification of the sample when the $\mathrm{pH}$ is controlled at the electrodes. Also, for a prescribed electric current at the anode, the profile of the electric potential is linear and decreases from the anode to the cathode. Moreover, the boundary layer for the profile of the sodium and cadmium concentrations becomes sharper when we increase the prescribed current.

Appendices

Appendix A: Solution of the Poisson–Boltzmann equation

Following a similar procedure proposed in Liu et al. (2013) we derive the analytical solution (6) of the Poisson–Boltzmann equation. We begin by rewriting (4) in dimensionless form

$$\begin{aligned} \dfrac{d^2 \overline{\varphi }}{\mathrm{d}z^2}=\alpha \left[ C_{b}\sinh (\overline{\varphi }) + C_{X^{2+}_b} ( e^{-\overline{\varphi }} -e^{-2\overline{\varphi }} ) \right] \end{aligned}$$

(45)

with $\alpha =2F^2/\varepsilon \varepsilon _0 \mathrm{RT}$. Multiplying (45) by $2d\overline{\varphi }/\mathrm{d}z$ and applying the chain rule, we arrive at the differential equation

$$\begin{aligned} \dfrac{d}{\mathrm{d}z}\left( \dfrac{d\overline{\varphi }}{\mathrm{d}z}\right) ^2= & {} 2\alpha \left[ C_{b}\dfrac{d}{\mathrm{d}z}(\cosh (\overline{\varphi })) + C_{X^{2+}_b}\left( \dfrac{1}{2}\dfrac{d}{\mathrm{d}z}(e^{-2\overline{\varphi }}) \right. \right. \nonumber \\&\left. \left. - \dfrac{d}{\mathrm{d}z}(e^{-\overline{\varphi }})\right) \right] . \end{aligned}$$

(46)

Integrating (46) from $z=l\gg L_D$ where $\varphi (z)=0$ in the bulk solution to a point z inside the EDL, we obtain

$$\begin{aligned} \left( \dfrac{\mathrm{d}\overline{\varphi }}{\mathrm{d}z}\right) ^2 = \alpha \left[ 2C_{b}\left( \cosh (\overline{\varphi })- 1\right) +C_{X^{2+}_b}\left( 1-e^{-\overline{\varphi }}\right) ^2 \right] . \end{aligned}$$

Then, we have

$$\begin{aligned} \dfrac{\mathrm{d}\overline{\varphi }}{\mathrm{d}z} = \text {sgn} (\overline{\zeta }) \sqrt{\alpha } \left[ 2C_{b}\left( \cosh (\overline{\varphi })- 1\right) +C_{X^{2+}_b}\left( 1-e^{-\overline{\varphi }}\right) ^2 \right] ^{\frac{1}{2}}, \end{aligned}$$

(47)

with “sgn” the signal function. Using the fact that $2\cosh (\overline{\varphi })= e^{\overline{\varphi }}+e^{-\overline{\varphi }}$, we rearrange the terms and integrate the above expression from $z=0$, where $\overline{\varphi }(z=0)=\overline{\zeta }$ is the dimensionless $\zeta$-potential, to z to get that

$$\begin{aligned} \displaystyle \int ^{\overline{\varphi }}_{\overline{\zeta }}\dfrac{e^{\overline{\varphi }} \mathrm{d}\overline{\varphi }}{(1-e^{\overline{\varphi }})\left[ (C_{b}+C_{X^{2+}_b}) - C_b\left( 1-e^{\overline{\varphi }}\right) \right] ^{1/2}}= \text {sgn} (\overline{\zeta }) \sqrt{\alpha }z. \end{aligned}$$

(48)

To solve the integral on (48), we make the change of variables $U=1-e^{\overline{\varphi }}$ to obtain

$$\begin{aligned}&\displaystyle \int \dfrac{e^{\overline{\varphi }} \mathrm{d}\overline{\varphi }}{(1-e^{\overline{\varphi }})\left[ (C_{b}+C_{X^{2+}_b}) - C_b\left( 1-e^{\overline{\varphi }}\right) \right] ^{1/2}}=\\ \qquad&-\displaystyle \int \dfrac{1}{U\left[ {\left( C_{b}+C_{X^{2+}_b}\right) -C_{b}U}\right] ^{1/2}}\, dU. \end{aligned}$$

where for convenience the limits are omitted. Taking $T=[{(C_{b}+C_{X^{2+}_b})-C_{b}U}]^{\frac{1}{2}}$, the above expression can be rewritten in the form

$$\begin{aligned}&\displaystyle \int \dfrac{e^{\overline{\varphi }} \mathrm{d}\overline{\varphi }}{(1-e^{\overline{\varphi }})\left[ (C_{b}+C_{X^{2+}_b}) - C_b\left( 1-e^{\overline{\varphi }}\right) \right] ^{1/2}}= \nonumber \\ \qquad&2\displaystyle \int \dfrac{1}{\left( C_{b}+C_{X^{2+}_b}\right) -T^2}\, \mathrm{d}T. \end{aligned}$$

(49)

with $T=[(C_{b}+C_{X^{2+}_b})-C_{b}(1-e^{\overline{\varphi }})]^{\frac{1}{2}}$. Making the change of variables $V=T/(C_{b}+C_{X^{2+}_b})^{\frac{1}{2}}$, the expression (49) results in

$$\begin{aligned}&\displaystyle \int \dfrac{e^{\overline{\varphi }} d\overline{\varphi }}{(1-e^{\overline{\varphi }})\left[ (C_{b}+C_{X^{2+}_b}) - C_b\left( 1-e^{\overline{\varphi }}\right) \right] ^{1/2}}= \nonumber \\&\qquad \frac{2}{\left( C_{b}+C_{X^{2+}_b}\right) ^{1/2}} \displaystyle \int \dfrac{1}{1-V^2}\,\mathrm{d}V, \end{aligned}$$

(50)

with

$$\begin{aligned} V = \sqrt{\frac{\left( C_{b}+C_{X^{2+}_b}\right) -C_{b}\left( 1-e^{\overline{\varphi }}\right) }{\left( C_{b}+C_{X^{2+}_b}\right) } }. \end{aligned}$$

(51)

Using the of partial fraction method in (50) we have

$$\begin{aligned}&\displaystyle \int \dfrac{e^{\overline{\varphi }} d\overline{\varphi }}{(1-e^{\overline{\varphi }})\left[ (C_{b}+C_{X^{2+}_b}) - C_b\left( 1-e^{\overline{\varphi }}\right) \right] ^{1/2}}=\nonumber \\&\quad - \frac{1}{\left( C_{b}+C_{X^{2+}_b}\right) ^{1/2}}\log \left( \dfrac{V-1}{V+1} \right) . \end{aligned}$$

(52)

Combining the expression (48), (51) and (52) we have

$$\begin{aligned}&\log \left[ \dfrac{\sqrt{C_{X^{2+}_b}+C_b e^{\overline{\varphi }}}-\sqrt{C_b + C_{X^{2+}_b}}}{\sqrt{C_{X^{2+}_b}+C_b e^{\overline{\varphi }}}+\sqrt{C_b + C_{X^{2+}_b}}}\right] ^{\overline{\varphi }}_{\overline{\zeta }}= \nonumber \\&\quad -\text {sgn} (\overline{\zeta }) \sqrt{\alpha \left( C_b + C_{X^{2+}_b}\right) }\; z \end{aligned}$$

(53)

Rearranging the terms in (53), we derive the expression for the electric potential given by (6) and (8). Finally, to deduce expression (7) for charge density, we combine the expressions (5a) and (47) resulting in (7).

Appendix B: Homogenization procedure

Expanding the procedure proposed in previous articles, we adopt the homogenization procedure based on perturbation expansions (Lima et al. 2008). Within this framework we postulate the asymptotic expansions for the unknowns in the form

$$\begin{aligned} f^{\varepsilon }({\mathbf {x}},{\mathbf {y}})=\sum _{k=0}^{\infty }\varepsilon ^{k}f^{k}({\mathbf {x}},{\mathbf {y}}) \end{aligned}$$

where ${\mathbf {x}}$ and ${\mathbf {y}}={\mathbf {x}}/\varepsilon$ denote the macroscopic and microscopic coordinates respectively. Inserting the ansatz into the microscopic governing equations and collecting powers of $\varepsilon$ we obtain successive equations at different orders

$$\begin{aligned}&\nabla _{y} \cdot \left[ D_{i_b}\left( \nabla _{y}C_{i_b}^{0}+z_iC_{i_b}^{0}\nabla _{y}\overline{\phi }^{0}\right) \right] =0 , \end{aligned}$$

(54)

$$\begin{aligned}&\nabla _{y} \cdot {\mathbf {v}}^{0}=0, \qquad \nabla _{y} p^{0}=0, \end{aligned}$$

(55)

$$\begin{aligned}&\nabla _{y} \cdot \left( C_{i_b}^{0} {\mathbf {v}}^{0}\right) +\nabla _{x} \cdot \left[ D_{i_b}\left( \nabla _{y}C_{i_b}^{0}+z_i C_{i_b}^{0}\nabla _{y}\overline{\phi }^{0}\right) \right] + \nabla _{y} \cdot \mathbf {J_{i_b}^{0}}=0, \end{aligned}$$

(56)

$$\begin{aligned}&\mathbf {J_{i_b}^{0}}=-D_{i_b}\left[ \left( \nabla _{x}C_{i_b}^{0}+\nabla _{y}C_{i_b}^{1}\right) + z_iC_{i_b}^{0}\left( \nabla _{x}\overline{\phi }^{0}+ \nabla _{y}\overline{\phi }^{1}\right) +z_iC_{i_b}^{1}\nabla _{y}\overline{\phi }^{0}\right] , \end{aligned}$$

(57)

$$\begin{aligned}&\nabla _{x} \cdot {\mathbf {v}}^{0}+ \nabla _{y} \cdot {\mathbf {v}}^{1}=0, \qquad \mu _{f}\triangle _{yy}{\mathbf {v}}^{0}-\nabla _{y}p^{1}=\nabla _{x}p^{0}, \end{aligned}$$

(58)

$$\begin{aligned}&\nabla _{x} \cdot \left( C_{i_b}^{0} {\mathbf {v}}^{0}\right) + \nabla _{y} \cdot \left( C_{i_b}^{0} {\mathbf {v}}^{1}+C_{i_b}^{1} {\mathbf {v}}^{0}\right) +\nabla _{x} \cdot \mathbf {J_{i_b}^{0}}+ \nabla _{y} \cdot \mathbf {J_{i_b}^{1}}=0, \end{aligned}$$

(59)

whereas the successive orders of the interface conditions read as

$$\begin{aligned}&\left[ D_{i_b}\left( \nabla _{y}C_{i_b}^{0}+z_iC_{i_b}^{0}\nabla _{y}\overline{\phi }^{0}\right) \right] \cdot {\mathbf {n}}=0, \end{aligned}$$

(60)

$$\begin{aligned}&{\mathbf {v}}^{0} \cdot {\mathbf {n}}={\mathbf {v}}^{1} \cdot {\mathbf {n}}=0, \qquad {\mathbf {v}}^{0} \cdot \varvec{\tau }=\dfrac{\widetilde{\epsilon }{0}\widetilde{\epsilon }{r}}{\mu _{f}}\left[ \zeta ^{0}\left( \nabla _{x}\phi ^{0} +\nabla _{y}\phi ^{1}\right) +\zeta ^{1}\nabla _{y}\phi ^{0}\right] \cdot \varvec{\tau } \end{aligned}$$

(61)

$$\begin{aligned}&\mathbf {J_{i_b}^{0}} \cdot {\mathbf {n}}=\mathbf {J_{i_b}^{1}}=0 \end{aligned}$$

(62)

We begin by collecting our set of slow ${\mathbf {y}}$-independent variables. From (55) we have $\nabla _{y}p^{0}\left( {\mathbf {x}}, {\mathbf {y}}, t\right) =0$ implies $p^{0}\left( {\mathbf {x}}, {\mathbf {y}}, t\right) =p^{0}\left( {\mathbf {x}}, t\right)$. Moreover, from the generalized transport equation (54) together with (60) we have $C_{ib^{\pm }}^{0}\left( {\mathbf {x}}, {\mathbf {y}}, t\right) =C_{ib^{\pm }}^{0}\left( {\mathbf {x}}, t\right)$, and $\overline{\phi }^{0}\left( {\mathbf {x}}, {\mathbf {y}}, t\right) =\overline{\phi }^{0}\left( {\mathbf {x}}, t\right)$.

Since that {$C_{\mathrm{Nab}^{+}}^{0}$, $C_{\mathrm{Hb}^{+}}^{0}$, $C_{\mathrm{Cd}_b^{2+}}^{0}$, $\phi ^{0}$} is independent of the fast variable, using (55) only the last terms in the equations (56) survive. Thus, combining the constitutive laws (56)–(57) with the boundary conditions (62) we obtain

$$\begin{aligned} \left\{ \begin{array}{ll} \triangle _{yy}\mathbf {\Psi }^{1} = 0 &{} \text{ in } \ \ Y_{f} \\ \left( \nabla _{x}\mathbf {\Psi }^{0}+\nabla _{y}\mathbf {\Psi }^{1}\right) \cdot {\mathbf {n}} = 0 &{} \text{ on } \ \ \partial Y_{fs} \end{array} \right. \end{aligned}$$

Then, making use of the separation of variables we obtain the closure problem (36). To derive the macroscopic Nernst–Planck equation for the $\mathrm{Na}^{+}$, $\mathrm{H}^{+}$ and $\mathrm{Cd}^{2+}$ transport we define the volume averaging operator over the periodic cell in the form

$$\begin{aligned} < \chi >:=\frac{1}{|Y|}\int _{Y_{f}}\chi d{\mathbf {y}} \end{aligned}$$

Recalling that $C_{i_b}^{0}$ are ${\mathbf {y}}$-independent and defining $\mathbf {V_{D}^{0}} := \mathbf {<v^{0}>}$ the macroscopic Darcy’s velocity. By averaging the generalized equation (59) using boundary condition (62) we have

$$\begin{aligned}&\nabla _{x} \cdot \left( C_{i_b}^{0} \mathbf {V_{D}^{0}}\right) +\nabla _{x} \cdot <\mathbf {J_{i_b}^{0}}>=-\int _{\partial \Gamma }\mathbf {J_{i_b}^{1}}\cdot {\mathbf {n}}\mathrm{d}\Gamma =0 \end{aligned}$$

Replacing the constitutive laws for the fluxes (57) together with the closure relations (36) in the above expressions we obtain

$$\begin{aligned}&\nabla _{x} \cdot \left( C_{i_b}^{0} \mathbf {V_{D}^{0}}\right) = \nabla _{x} \cdot \left[ \mathbf {D_{i_b}^{\mathrm{eff}}}\left( \nabla _{x}C_{i_b}^{0}+ z_i C_{i_b}^{0}\nabla _{x}\overline{\phi }^{0}\right) \right] \end{aligned}$$

where the effective diffusivities are given by (34c)–(34d).

To derive Darcy’s Law we proceed in a similar fashion to Lima et al. (2010a), we decompose velocity and pressure fluctuation into their hydraulic and electroosmotic components ${\mathbf {v}}^{0}=\mathbf {v_{P}^{0}}+\mathbf {v_{E}^{0}}$ and $p^{1}=p^{1}_{P}+p^{1}_{E}$ with each one satisfying the local cell problems

$$\begin{aligned} \left\{ \begin{array}{lcrl} \mu _{f}\triangle _{yy}\mathbf {v_{P}^{0}}-\nabla _{y}p^{1}_{P}=\nabla _{x}p^{0} \\ \nabla _{y} \cdot \mathbf {v_{P}^{0}} = 0 \text{ in } \ \ \ Y_{f} \\ \mathbf {v_{P}^{0}} = 0 \text{ on } \ \ \ \partial Y_{fs} \end{array} \right. \end{aligned}$$

(63)

and

$$\begin{aligned} \left\{ \begin{array}{lcrl} \mu _{f}\triangle _{yy}\mathbf {v_{E}^{0}} -\nabla _{y}p^{1}_{E}=0 \\ \nabla _{y} \cdot \mathbf {v_{E}^{0}} = 0 \text{ in } \ \ Y_{f} \\ \mathbf {v_{E}^{0}} \cdot {\mathbf {n}}=0 \\ \mathbf {v_{E}^{0}} \cdot \varvec{\tau }=\dfrac{\widetilde{\epsilon }_{0}\widetilde{\epsilon }_{r}\zeta ^{0}}{\mu _{f}}\left( {\mathbf {I}}+\nabla _{y}{\mathbf {f}}\right) \nabla _{x}\phi ^{0} \cdot \varvec{\tau }\text{ on } \ \ \partial Y_{fs} \end{array} \right. \end{aligned}$$

(64)

The local system (63) for {$\mathbf {v_{P}^{0}}$, $p^{1}_{P}$} is nothing but the classical closure problem which gives rise to the hydraulic conductivity (37) see Auriault (1991). By exploring linearity between (63) and (37) we obtain

$$\begin{aligned} \mathbf {v_{P}^{0}} =-\varvec{\kappa _{P}}\nabla _{x}p^{0} \end{aligned}$$

(65)

Unlike (63) the cell problem for $\mathbf {v_{E}^{0}}$ is ruled by the slip boundary condition. By invoking the closure problem for the tortuosity function ${\mathbf {f}}$ one may observe that (64) admit solution of the type

$$\begin{aligned} \mathbf {v_{E}^{0}}= & {} -\varvec{\kappa _{E}^{0}}\nabla _{x}\phi ^{0} \text{ with } \varvec{\kappa _{E}^{0}}=-\dfrac{\widetilde{\epsilon }{0}\widetilde{\epsilon }{r}\zeta ^{0}}{\mu _{f}}\left( {\mathbf {I}}+\nabla _{y}{\mathbf {f}}\right) \end{aligned}$$

(66)

By adding (65) and (66) yields the constitutive law for the total microscopic velocity. Then, averaging we obtain the macroscopic Darcy’s law

$$\begin{aligned} \mathbf {V_{D}^{0}}=\mathbf {<v^{0}>} =-\mathbf {K_{P}^{\mathrm{eff}}}\nabla _{x}p^{0}-\mathbf {K_{E}^{\mathrm{eff}}}\nabla _{x}\phi ^{0} \end{aligned}$$

(67)

with the effective conductivities defined by (34a)–(34b).

The macroscopic mass conservation can easily be obtained by averaging (58) using the divergence theorem along with boundary condition (61) to obtain

$$\begin{aligned}&\nabla _{x} \cdot \mathbf {V_{D}^{0}}=-<\nabla _{y}\cdot {\mathbf {v}}^{1}>=-\dfrac{1}{|Y|}\int _{Y_{f}}\nabla _{y}\cdot {\mathbf {v}}^{1}\mathrm{d}{\mathbf {y}}= -\dfrac{1}{|Y|}\int _{\partial Y_{fs}}{\mathbf {v}}^{1} \cdot {\mathbf {n}}\mathrm{d}{\mathbf {y}} =0 \end{aligned}$$

which when combined with (67) furnishes

$$\begin{aligned} \nabla _{x} \cdot \mathbf {V_{D}^{0}}=\nabla _{x} \cdot \left( \mathbf {K_{E}^{\mathrm{eff}}}\nabla _{x}\phi ^{0}+\mathbf {K_{P}^{\mathrm{eff}}}\nabla _{x}p^{0}\right) =0. \end{aligned}$$