Dynamic modeling and CPG-based trajectory generation for a masticatory rehab robot

Abstract

Human mastication is a complex and rhythmic biomechanical process which is regulated by a brain stem central pattern generator (CPG). Masticatory patterns, frequency and amplitude of mastication are different from person to person and significantly depend on food properties. The central nervous system controls the activity of muscles to produce smooth transitions between different movements. Therefore, to rehab human mandibular system, there is a real need to use the concept of CPG for development of a new methodology in jaw exercises and to help jaw movements recovery. This paper proposes a novel method for real-time trajectory generation of a mastication rehab robot. The proposed method combines several methods and concepts including kinematics, dynamics, trajectory generation and CPG. The purpose of this article is to provide a methodology to enable physiotherapists to perform the human jaw rehabilitation. In this paper, the robotic setup includes two Gough–Stewart platforms. The first platform is used as the rehab robot, while the second one is used to model the human jaw system. Once the modeling is completed, the second robot will be replaced by an actual patient for the selected physiotherapy. Gibbs–Appell’s formulation is used to obtain the dynamics equations of the rehab robot. Then, a method based on the Fourier series is employed to tune parameters of the CPG. It is shown that changes in leg lengths, due to the online changes of the mastication parameters, occur in a smooth and continuous manner. The key feature of the proposed method, when applied to human mastication, is its ability to adapt to the environment and change the chewing pattern in real-time parameters, such as amplitudes as well as jaw movements velocity during mastication.

1 Introduction

The mastication system and its modeling have been investigated frequently in the literature [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]. Movements of the human limbs, such as the mandibular movements, are complex and hard to describe [17,18,19,20,21,22,23,24,25]. The smoothness of the movements is an important factor in modeling the human limb’s actions [18]. Previous studies indicate that chewing patterns change based on food properties such as plasticity and elasticity. Moreover, some other factors affect the chewing patterns including size, hardness and physical properties of foods [19,20,21,22,23,24], age [25], gender and number of teeth in individuals that affect the number of chewing cycle, duration of chewing sequence, chewing frequency, vertical and lateral amplitudes, and the velocity of the mandible movements [17]. Therefore, using a methodology to reproduce human jaw trajectory is required. Nature solves this problem by using the central nervous systems as the main control unit for muscle activities. The basic locomotor patterns of most biological systems, such as chewing, are generated by the central pattern generator (CPG). Variety of rhythmic motor patterns such as walking, breathing, chewing, flying and swimming are produced by neuronal circuits (called CPGs), which are located in the spinal cord of vertebrates [26,27,28,29]. Recently, the CPG-based trajectory generation approaches have gained attention in the field of biologically inspired robotics. The CPG has several advantages such as demonstrating limit cycle behavior [28]. It produces smooth trajectories even when the control parameters are abruptly changed. In the present study, these advantages are used in controlling a rehab robot for the human jaw. One of the key features of human movement is its ability to adapt to the environment and change the movement parameters in real time robustly and smoothly. Yang et al. [30] presented genetic algorithm optimized Fourier series formulation (GAOFSF) method for stable gait generation. Rigatos [31] proposed a new method for robust synchronization of coupled neural oscillators by using the derivative-free nonlinear Kalman filter. They used the standard Kalman filter recursion on the linearized equivalent model of the coupled FitzHugh–Nagumo neural oscillators. They showed the performance of the proposed synchronization control loop for the model of the coupled neural oscillators through simulation experiments. Jia et al. [32] studied propulsion mechanism of undulation locomotion by combining biological investigation, mathematical simulation and experimental validation. They implemented CPG-based control algorithm to coordinate the robot’s movement in order to produce smooth undulation pattern. Kim et al. [33] proposed a nonparametric estimation-based PSO (NEPSO) to search for the parameters of CPG needed for bipedal walking. In this article, a supervised learning method called Fourier-based automated learning CPG (FAL-CPG) is utilized to learn a periodic signal used for trajectory planning of robotic systems. In our previous work [28], the effectiveness of the FAL-CPG is shown by comparison with Gams et al. scheme, [34] Nakanishi et al. scheme [35] and Dutra et al. scheme [36]. Moreover, we demonstrated the effectiveness of the FAL-CPG and compared with harmonic trajectory, which is an online trajectory generation method [29].

Occlusion, occlusal interferences, the severity of temporomandibular disorders (TMD) or craniomandibular disorders (CMD), trismus and edentulous maxilla appear to be associated with mastication [37, 38]. Several studies regarding the treatment of these problems are considered. Studies showed that continuing and passive exercise therapy can result in relieving the pains due to musculoskeletal reasons in jaw movement [39,40,41,42,43]. Therefore, in the present medical field, there have been several studies regarding devices and robots to heal and treat patients with jaw disorder, including the TheraBite System [43, 44], the WY (Waseda-Yamanashi) series of robots [45, 46] and the Dynasplint_ Trismus System, DTS [47]. Generally, studies show that the ability of robots to produce repetitive movements and to permit increased intensity of rehabilitation makes them proper tools to implement rehabilitation exercises [42, 48]. TheraBite [43] and the DTS [47] were designed to consist of mouthpieces inserted in between the upper and lower teeth. Although TheraBite used a screw to open the mouthpieces, DTS used the internal tensioning system of the unit which is slowly adjusted to open the patient’s mouth. In both of them, the mouthpiece can be moved to the anterior or lateral positions in between the maxilla and mandible for only opening exercise in sagittal plane. Moreover, the Waseda-Yamanashi (WY) [45] series of robots are used to open and close a patient’s lower jaw by mimicking the doctors’ hand motion during a mouth opening training session. The most advanced version of WY series was the WY-5 and WY-6. These parallel robots were actuated by six linear motors through ball screw mechanisms. Here, the maxilla is clamped to the robot’s base and the mandible is the moving platform. The robot is controlled remotely by a doctor in three DOFs for open/close, forward/backward and right/left movements [12].

The rest of the manuscript is organized as follows: The main idea of the bio-inspired approach is presented in Sect. 2. Afterward, the rehab robot and the mandible model are described in Sect. 3. Next, a recent method, proposed by [28], is utilized to relate the finite Fourier series parameters with CPG parameters in Sect. 4. The experimental setup to record the four chewing patterns is discussed in Sect. 5. Finally, effectiveness and applicability of the proposed approach for the rehab robot are demonstrated through several examples in Sect. 6.

Fig. 1

Overall framework of the proposed online trajectory generation method

2 The bio-inspired approach—main idea

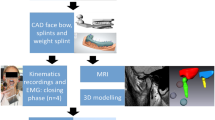
In this section, the overall framework of the proposed method is summarized and presented in Fig. 1. It should be noted that the details of the elements shown in Fig. 1 will be explained in upcoming sections of this paper. The overall method is made of offline and online processes. As shown in Fig. 2, in this paper, four main trajectories are recorded: (1) clenching movement (CM), (2) right grinding movement (RGM), (3) left grinding movements (LGM) and (4) general grinding movements (GGM) that must be predefined in offline section. These chewing patterns are recorded by a Simi Reality Motion System (GmbH, Unterschleissheim, Germany). These trajectories are defined as the trajectory of moving platform of rehab robot (box 1, Fig. 1). The inverse kinematics of rehab robot is solved to obtain the required leg lengths to pass through the corresponding trajectory (boxes 2 and 3, Fig. 1). Next, the Fourier analysis is applied to each of the six leg lengths to find the main CPG parameters (box 4). Using the Fourier-based automatic learning CPG (FAL-CPG) method [28], the main CPG parameters of the coupled oscillators were determined (box 5). CPG neurons were constructed individually for CM, LGM, GGM and RGM. CPG parameters were reduced to zeros to produce swallowing motion. For synergism, couplings between angles were made through the first oscillator of each angle (box 6). For the online section, to perform the desired trajectory, a proportional-derivative computed torque controller (PD-CTC) is utilized. In the first step, physiotherapist specified the information such as chewing patterns, velocity and amplitude of mastication process (box 7). Then, CPG parameters were modified with respect to the given information to produce the new desired actuator lengths (box 8). The controller applied an appropriate torque to the chewing robot joints (boxes 9 and 10). MATLAB/Simulink 2012b was utilized as a basic platform to develop our proposed algorithm and control the robot simultaneously.

Fig. 2

Illustration of chewing patterns

Fig. 3

Architecture of the virtual model

3 Rehab robot and jaw model

Generally, there are several robots that developed to mimic the human mastication robot, for instance, WY series robots, Wj series robots and Bite Master II [12]. Among these robots, only WY series of robotics are aimed at treating patients with jaw disorders. But these robots have a limitation that they are controlled in 3-DOF; therefore, replications of real human mastication movements are not possible for these devices. To remove this limitation, we proposed a rehab robot that covers all workspace of human mandible.

Both the rehab robot and the jaw model were developed using a Gough–Stewart approach. The Gough–Stewart platform is a parallel manipulator, which consists of a mobile platform and a stationary base, connected to each other by six linear actuators. For the rehab robot, the six linear legs were placed between a moving platform (with jaw model on top of it) and the ground. As shown in Fig. 3, to represent the geometry of human mastication, we used a general 6-universal-prismatic-spherical (UPS) Stewart–Gough platform [5, 12]. The mobile and stationary platforms represent the human mandible and skull, respectively, and the actuators represent the jaw muscles [48]. In the jaw model, each of the major chewing muscles (masseter, temporalis and pterygoid) was modeled using a linear actuator. The jaw model was developed merely to illustrate how the platform movements affected the masticatory muscles in the human jaw. This simulator generated the variations in leg lengths of both the jaw model and rehab robot and hence reproduced the movement of the robot platform as well as the masticatory motion (Fig. 3). We supposed that the chin point, CP, is adhered to moving platform of rehab robot.

3.1 Kinematics model

In this study, we employ the kinematics model that obtained by [49, 50]. For each leg, a vector loop equation can be written as:

$$\begin{aligned} {}_{~}^{B} {\mathbf{a}}_{i} +{}_{~}^{B} {\mathbf{d}}_{i} ={}_{~}^{B} {\mathbf{P}} +{}_{M}^{B} {\mathbf{R}}\, {}_{~}^{M}{\mathbf{b}}_{i} (i=1,\, 2,\ldots ,6) \end{aligned}$$

(1)

where ${}^{\varvec{B}} {\mathbf{P}}$ and ${}^{\varvec{B}} {\mathbf{a}}_{{\varvec{i}}}$ are the position vectors specifying the base of coordinate frame $\{\mathbf{M}\}$ and universal joints with respect to the fixed coordinate system, respectively. The vector ${}^{\varvec{M}} {\mathbf{b}}_{{\varvec{i}}}$ represents the position of the spherical joint with respect to the moving platform coordinate system (see Fig. 4). The magnitude of ${}^{\varvec{B}} {\mathbf{d}}_{{\varvec{i}}}$ represents the actuated leg length. The orientation of the moving platform $\{\mathbf{M}\}$ with respect to the fixed coordinates $\left\{ {\mathbf{B}} \right\}$ is referred to as the moving platform’s rotation matrix ${}_{\varvec{M}}^{\varvec{B}} {\mathbf{R}}_{\,}$. The detail of Jacobian matrix is described in “Appendix A”.

Fig. 4

a The physical model and b a closed-loop vector for ith leg of the 6-UPS parallel robot

3.2 Dynamics analysis

3.2.1 Gibbs–Appell method

In 1987, Gibbs presented Gibbs–Appell method firstly, and then, Appell completed this method in 1989 [51,52,53]. This method is similar to Lagrange method; however in Gibbs–Appell method, the acceleration variables and in Lagrange method, the velocity variables are used. Thus, in Gibbs–Appell method, we obtain the acceleration energy of each part. As compare to Lagrange method, since the implementing the Gibbs–Appell requires acceleration of a system, the calculations of complex partial derivatives were not required. Additionally, the relatively higher volume of the symbolic computation in the Lagrangian formulation increases the total execution time for the dynamic procedure [50]. Therefore, in this study the Gibbs–Appell method is employed to obtain system dynamic equation.

Acceleration energy for each part is defined as:

$$\begin{aligned} S_{i}=\frac{{1}}{{2}}m{\mathbf{a}}_{\mathrm{ci}}\cdot {\mathbf{a}}_{\mathrm{ci}}+\frac{{1}}{{2}}{\varvec{\upalpha }}_{\mathrm{i}}\cdot \frac{\delta {\mathbf{H}}_{\mathrm{ci}}}{\delta t}+{\varvec{\upalpha }}_{\mathrm{i}}\cdot (\varvec{\omega }_{i}\times {\mathbf{H}}_{\mathrm{ci}}) \end{aligned}$$

(2)

where ${\mathbf{H}}_{\mathrm{ci}}$ and ${\mathbf{a}}_{\mathrm{ci}}$ represent the angular momentum of each part about its center of gravity and linear acceleration of center of gravity of each part, respectively. Angular momentum of each part can be represented as:

$$\begin{aligned} {\mathbf{H}}_{\mathrm{ci}}=\left[ {\begin{array}{ccc} I_{xx\,i} &{}\quad -I_{xy\,i} &{}\quad {-I}_{xz\,i}\\ {-I}_{xy\,i} &{}\quad I_{yy\,i} &{}\quad {-I}_{yz\,i}\\ -I_{xz\,i} &{}\quad {-I}_{yz\, i} &{}\quad I_{zz\,i}\\ \end{array} } \right] \left[ {\begin{array}{c} \omega _{x\,i}\\ \omega _{y\,i}\\ \omega _{z\,i}\\ \end{array} } \right] \end{aligned}$$

(3)

where $\omega _{x\, i}, \omega _{y\, i}$ and $\omega _{z\, i}$ are the angular velocity of ith links about x, y and z axes, respectively. Next by taking time derivative of Eq. (3), we have

$$\begin{aligned} \frac{{{\partial \mathbf H }}_{\mathrm{ci}}}{{\partial }t}=\left[ {\begin{array}{ccc} I_{xx\,i} &{}\quad -I_{xy\,i} &{}\quad {-I}_{xz\,i}\\ {-I}_{xy\,i} &{}\quad I_{yy\,i} &{}\quad {-I}_{yz\,i}\\ -I_{xz\,i} &{}\quad {-I}_{yz\, i} &{}\quad I_{zz\,i}\\ \end{array} } \right] \left[ {\begin{array}{c} \alpha _{x\,i}\\ \alpha _{y\,i}\\ \alpha _{z\,i}\\ \end{array} } \right] \end{aligned}$$

(4)

where $\alpha _{x\, i}, \alpha _{y\, i}$ and $\alpha _{z\, i}$ are the angular accelerations of ith links about x, y and z axes, respectively. The general form of Gibbs–Appell is defined as:

$$\begin{aligned} \frac{{\partial \hbox {S}}}{{\partial }\ddot{\mathbf{x}}_{M}}={{\Gamma } ({\mathbf{x}}_{M})} \end{aligned}$$

(5)

where ${\Gamma } ({\mathbf{x}}_{M})$ represents the generalized forces and S is the Gibbs–Appell function. Here $\ddot{\mathbf{x}}_{M}=[\ddot{{x}},\ddot{y},\ddot{z},\ddot{\alpha },\ddot{\beta },\ddot{\gamma }]$. Since this model has one moving platform, six cylinders and six pistons, we have

$$\begin{aligned} S=S_{M}+\sum \limits _{i=1}^{6} S_{1i} +\sum \limits _{i=1}^{6} S_{2i} \end{aligned}$$

(6)

where ${\varvec{S}}_{\varvec{M}}, {\varvec{S}}_{\varvec{1i}}$ and ${\varvec{S}}_{\varvec{2i}}$ are energy of moving platform, cylinder and piston, respectively. Now we plan to obtain these accelerations energy, separately. It should be noted that, according to Eq. (6), we must obtain energy equations in terms of acceleration of moving platform. The detail of calculation of energy of cylinder, ${\varvec{S}}_{\varvec{1i}}$, energy of piston, ${\varvec{S}}_{\varvec{2i}}$, and energy of moving platform, ${\varvec{S}}_{\varvec{M}}$, is described in “Appendices B–D”. Therefore, based on Eq. (5), we have

$$\begin{aligned} \frac{{{\partial }S}_{M}}{{\partial }\ddot{\mathbf{x}}_{M}}= & {} \left[ {\begin{array}{cc} {\mathbf{m}}_{{3\times 3}}&{}\quad \mathbf 0 \\ \mathbf 0 &{}\quad {\varvec{I}}_{{3\times 3}}\\ \end{array}} \right] \, \ddot{\mathbf{x}}_{M}+\left[ {\begin{array}{c} {\mathbf{0}}_{{3\times 1}}\\ \left( I_{M,zz}- I_{M,yy} \right) \dot{\upbeta }{\dot{\upgamma }}\\ \left( I_{p,xx}- I_{M,zz} \right) \dot{\upalpha }\dot{\upgamma }\\ \left( I_{M,yy}- I_{M,xx} \right) \dot{\upalpha }\dot{\upbeta }\\ \end{array} } \right] \end{aligned}$$

(7)

$$\begin{aligned} \frac{{{\partial }S}_{1i}}{{\partial }\ddot{\mathbf{x}}_{M}}= & {} m_{1i}\left[ {\mathbf{J}}_{V{1}i,x}^{j\,}\cdot \dot{\mathbf{v}}_{1i} \right] \nonumber \\&+\left[ \dot{\varvec{\upomega }}_{i}\cdot \left( {}_{~}^{{i}} [I]^{1i}\cdot {\mathbf{J}}_{\omega i}^{j} \right) \right] + {\mathbf{J}}_{\omega i}^{j}\cdot K_{1i} \end{aligned}$$

(8)

$$\begin{aligned} \frac{{{\partial }S}_{2i}}{{\partial }\ddot{\mathbf{x}}_{M}}= & {} m_{2i}\left[ {\mathbf{J}}_{V{2}i,x}^{j\, }\cdot \dot{\mathbf{v}}_{2i} \right] \nonumber \\&+\left[ \dot{\varvec{\upomega }}_{i}\cdot \left( {}_{~}^{{i}} [I]^{2i}\cdot {\mathbf{J}}_{\omega i}^{j} \right) \right] + {\mathbf{J}}_{\omega i}^{j}\cdot K_{2i} \end{aligned}$$

(9)

where $\, \ddot{\mathbf{x}}_{M}=[\ddot{{x}},\ddot{y},\ddot{z},\ddot{\alpha },\ddot{\beta },\ddot{\gamma }]$, ${\mathbf{m}}_{{3\times 3}}=\hbox {diag}\left( \hbox {m, m, m} \right)$ and ${\mathbf{I}}_{\mathrm{3\times 3}}=\hbox {diag}\, (I_{M,xx},\, I_{M,yy},I_{M,zz})$. Note that j present the jth associated column and $i\,$ represent the ith actuated leg of rehab robot.

3.2.2 Equation of motion and calculation $\varvec{\varGamma }$

The principle of virtual work [50, 54] can be stated as

$$\begin{aligned} \delta {\mathbf{q}}^\mathrm{T}\tau +\delta {\mathbf{x}}_{M}^\mathrm{T}{{\mathbf{F}}}_{p}+\sum \limits _i^{6} \left( \delta ^{i} {\mathbf{x}}_{1i}^\mathrm{T} {}_{~}^{{i}}{{\mathbf{F}}}_{1i}+\delta ^{i} {\mathbf{x}}_{2i}^\mathrm{T} {}_{~}^{{i}}{{\mathbf{F}}}_{2i} \right) =0 \end{aligned}$$

(10)

In Eq. (4), ${}_{~}^{{i}} {\mathbf{F}}_{1i}$ and ${}_{~}^{{i}} {\mathbf{F}}_{2i}$ are the resultants of the applied and inertia forces and $\delta {}_{~}^{{i}} {\mathbf{x}}_{1i}^\mathrm{T}$ and $\delta {}_{~}^{{i}} {\mathbf{x}}_{2i}^\mathrm{T}$ are their corresponding virtual displacement expressed in the limb frame. Based on kinematics constraints, we can relate the virtual displacement to the set of independent generalized virtual displacement. Therefore, we have

$$\begin{aligned} \delta {\mathbf{q}}= & {} {\mathbf{J}}_{p}\delta {\mathbf{x}}_{M} \end{aligned}$$

(11)

$$\begin{aligned} \delta {}_{~}^{{i}} {\mathbf{x}}_{1i}= & {} {}_{~}^{{i}} {\mathbf{J}}_{1i} \delta {\mathbf{x}}_{M}\end{aligned}$$

(12)

$$\begin{aligned} \delta {}_{~}^{{i}} {\mathbf{x}}_{2i}= & {} {}_{~}^{{i}} {\mathbf{J}}_{2i} \delta {\mathbf{x}}_{M} \end{aligned}$$

(13)

By substituting Eqs. (11)–(13) into Eq. (10), we have

$$\begin{aligned} \delta {\mathbf{x}}_{M}^\mathrm{T}\left[ J_{p}^\mathrm{T}\varvec{\tau }+{\mathbf{F}}_{p}+\sum \limits _{i=1}^{6} \left( {}_{~}^{{i}} J_{1i}^\mathrm{T} {}_{~}^{{i}}{\mathbf{F}}_{1i}\, + {}_{~}^{{i}} J_{2i}^\mathrm{T} {}_{~}^{{i}}{\mathbf{F}}_{2i} \right) \right] =0 \end{aligned}$$

(14)

Since $\delta \hbox {w}=\sum _{j=1}^n {\Gamma }_{j} \delta {\mathbf{x}}_{M}^\mathrm{T}$, we have

$$\begin{aligned} {\Gamma }_{j}={\mathbf{J}}_{p}^\mathrm{T}\varvec{\tau }+{\mathbf{F}}_{p}+\sum \limits _{i=1}^{6} \left( {}_{~}^{{i}} {\mathbf{J}}_{1i}^\mathrm{T} {}_{~}^{{i}}{\mathbf{F}}_{1i}\, + {}_{~}^{{i}}{\mathbf{J}}_{2i}^\mathrm{T} {}_{~}^{{i}}{\mathbf{F}}_{2i} \right) \end{aligned}$$

(15)

where ${\mathbf{F}}_{p}, {}_{~}^{{i}} {\mathbf{F}}_{1i}$ and ${}_{~}^{{i}} {\mathbf{F}}_{2i}$ can be defined as

$$\begin{aligned} {\mathbf{F}}_{p}= & {} \left[ {\begin{array}{c} {\hat{\mathbf{f}}}_{p}\\ {\hat{\mathbf{n}}}_{p}\\ \end{array} } \right] =\left[ {\begin{array}{c} {\mathbf{f}}_{e}+m_{p}{\mathbf{g}}\\ {\mathbf{n}}_{e}\\ \end{array} } \right] \end{aligned}$$

(16)

$$\begin{aligned} {}_{~}^{{i}} {\mathbf{F}}_{1i}= & {} \left[ {\begin{array}{c} {\hat{\mathbf{f}}}_{1i}\\ {\hat{\mathbf{n}}}_{1i}\\ \end{array} } \right] =\left[ {\begin{array}{c} m_{1i} {}_{~}^{{i}}{\mathbf{R}}_{B}\,{\mathbf{g}}\\ {\mathbf{0}}\\ \end{array} } \right] \end{aligned}$$

(17)

$$\begin{aligned} {}_{~}^{{i}} {\mathbf{F}}_{2i}= & {} \left[ {\begin{array}{c} {\hat{\mathbf{f}}}_{2i}\\ {\hat{\mathbf{n}}}_{2i}\\ \end{array} } \right] =\left[ {\begin{array}{c} m_{2i} {}_{~}^{{i}}{\mathbf{R}}_{B}\,{\mathbf{g}}\\ {\mathbf{0}}\\ \end{array} } \right] \end{aligned}$$

(18)

where ${\mathbf{f}}_{e}$ and ${\mathbf{n}}_{e}$ are the external force and moment exerted at mass center of moving platform. Additionally, $\mathbf{g}=[0,\, 0, -9.81]$. Substituting Eqs. (7–9) and (15) into Eq. (5) and simplification, we yield

$$\begin{aligned}&{\mathbf{J}}_{p}^\mathrm{T}\varvec{\tau }+{\mathbf{F}}_{p}+\left( \sum \limits _{i=1}^{\mathbf{6}} \left( \, {}_{~}^{{i}}{\mathbf{J}}_{1i}^\mathrm{T} {}_{~}^{{i}}{\mathbf{F}}_{1i} \right) \right) +\left( \sum \limits _{i=1}^{\mathbf{6}} \left( \, {}_{~}^{{i}}{\mathbf{J}}_{2i}^\mathrm{T} {}_{~}^{{i}}{\mathbf{F}}_{2i} \right) \right) \nonumber \\&\quad =\left[ \left( \frac{{{\partial }S}_{P}}{{\partial }\ddot{{x}}_{p}} \right) +\left( \sum \limits _{i=1}^{\mathbf{6}} \left( \sum \limits _{j=1}^{6} \frac{{{\partial }S}_{1i}}{{\partial }\ddot{{x}}_{p,j}} \right) \right) \right. \nonumber \\&\qquad \left. +\left( \sum \limits _{i=1}^{\mathbf{6}} \left( \sum \limits _{j=1}^{6} \frac{{{\partial }S}_{2i}}{{\partial }\ddot{{x}}_{p,j}} \right) \right) \right] \end{aligned}$$

(19)

Equation (19) describes the dynamic of rehab robot in task space. However, to use these equations in studying control strategies, the calculation of equations in joint space is needed. Generally, to transform between the joint space and task space is not straightforward because of the complicated velocity [50]. To overcome this problem, in this study, we presented the concept of direct links Jacobian matrices are used to invert the twist vector of all rigid bodies to velocity vector of actuated joints. To do this, Eqs. (A.7) and (A.19) can be rewritten as:

$$\begin{aligned} \dot{\mathbf{x}}_{M}= & {} {\mathbf{J}}_{\varvec{p}}^{\mathrm{-T}}\dot{\mathbf{q}} \end{aligned}$$

(20)

$$\begin{aligned} \ddot{\mathbf{x}}_{M}= & {} {\mathbf{J}}_{\varvec{p}}^{ -\mathrm{T}}(\ddot{\mathbf{q}}-\mathbf O \left( {\mathbf{q}},\dot{\mathbf{q}} \right) ) \end{aligned}$$

(21)

By substituting Eqs. (20–21) into Eq. (19) and simplification, we yield

$$\begin{aligned} {\mathbf{f}}_{{\mathbf{6}\times \mathbf 1 }}+{\mathbf{J}}_{p}^\mathrm{T}\varvec{\tau }_{{\mathbf{6}\times \mathbf 1 }}+{{\mathbf{M}}\left( {\mathbf{q}} \right) }_{{\mathbf{6}\times \mathbf 6 }}\ddot{\mathbf{q}}_{{\mathbf{6}\times \mathbf 1 }} +\mathbf C \left( {\mathbf{q}}, \dot{\mathbf{q}} \right) \dot{\mathbf{q}} _{{\mathbf{6}\times \mathbf 1 }}={\mathbf{0}}_{{\mathbf{6}\times \mathbf 1 }}\nonumber \\ \end{aligned}$$

(22)

where ${\mathbf{M}}\left( {\mathbf{q}} \right)$ is the $6\times 6$ positive definite inertia matrix, ${\mathbf{C}}\left( {\mathbf{q}},\dot{\mathbf{q}} \right)$ is the $6\times 1$ matrix related to centrifugal and Coriolis terms, ${\mathbf{f}} _{{\mathbf{6}\times \mathbf 1 }}$ are $6\times 1$ matrices related to gravity vectors of moving platform/robot legs and applied external wrench exerted to moving platform. $\varvec{\uptau }$ is a $6\times 1$ matrix of input forces. Moreover, ${\mathbf{q}}, \dot{\mathbf{q}}$ and $\ddot{\mathbf{q}}$ are the vector of length, velocity and acceleration of actuators, respectively. These equations are validated by SimMechanics software and our proposed virtual works method [50]. Up to now, the dynamic equation of the rehab robot is derived. In this paper, to control the rehab robot, the computed torque control (CTC) is employed. In this method, the inverse dynamics model is needed to calculate the actuation forces resulted from a desired motion. In this method, the control rule is defined as

Fig. 5

Schematics controller loop of rehab robot

$$\begin{aligned} \varvec{\tau }={{\mathbf{M}}\left( {\mathbf{q}} \right) }\left( \ddot{\mathbf{q}}_{{\mathbf{d}}} +{\mathbf{K}}_{P}{\mathbf{e}}+{\mathbf{K}}_{D}\dot{\mathbf{e}} \right) +\mathbf V \left( {\mathbf{q}}, \dot{\mathbf{q}} \right) \end{aligned}$$

(23)

where ${\mathbf{e}}={\mathbf{q}}_{\mathrm{d}}-{\mathbf{q}}$ and ${\mathbf{K}}_{P}$ and ${\mathbf{K}}_{D}$ are the controller gains. The schematic control loop of PD-CTC is shown in Fig. 5. In Fig. 5b, the block diagram corresponding to integration of mentioned kinematic, dynamic model and control method is revealed. The implantation of computed torque expressed by Eq. (23) needs knowledge of the matrices ${\mathbf{M}}\left( {\mathbf{q}} \right)$ and ${\mathbf{V}}\left( {\mathbf{q}}, \dot{\mathbf{q}} \right)$ as well as of the desired motion trajectory ${\mathbf{q}}_{d}(t), \dot{\mathbf{q}}_{d}(t)$ and $\ddot{\mathbf{q}}_{d}(t)$ and the recorded of the positions ${\mathbf{q}}(t)$ and of the velocities $\dot{\mathbf{q}}(t)$. To obtain ${\mathbf{M}}\left( {\mathbf{q}} \right)$ and ${\mathbf{V}}\left( {\mathbf{q}}, \dot{\mathbf{q}} \right)$ the forward kinematics, Eq. (1), and inverse dynamics, Eq. (22), are needed. As shown in Fig. 5a, the desired trajectory is a modified path that is generated by CPG networks. Figure 5 shows the final experimental protocol designed to examine the ability of the proposed methodology to control the rehab robot based on the combination of CPG model and PD-CTC methods. Firstly, physiotherapist indicated the information chewing patterns. Then, CPG parameters were modified with respect to the given information to produce the new desired actuator lengths. Then controller applied an appropriate torque to the rehab robot.

4 CPG scheme

For rehab and exoskeleton robots, an important question is how to ensure smooth trajectory, while avoiding any interaction forces between robot and human in case the patients do correctly. Therefore, recently researchers attempt to find best trajectory generation method to apply for their rehabilitation robot [48, 55, 56]. In this paper, a supervised learning method, called FAL-CPG, is utilized to learn a periodic signal used for trajectory generation of robotic systems. Trajectory generation is involved in two steps. In the first step, a finite Fourier series is fitted to the desired periodic signal. In the second step, based on the Fourier series, the main parameters of the coupled oscillators are determined [28].

4.1 CPG for a single leg

Consider the CPG model presented in Eq. (24). This equation is an amplitude-controlled phase oscillator, and we can reproduce the Fourier series to obtain a desired joint angle trajectory.

$$\begin{aligned} \dot{\theta }_{i}= & {} 2\pi v_{i}\nonumber \\ \ddot{r}_{i}= & {} a_{i}\left[ \frac{a_{i}}{4}\left( R_{i}-r_{i} \right) -\dot{r}_{i} \right] \end{aligned}$$

(24)

where $v_{i}$ and $R_{i}$ determine the intrinsic frequency and amplitude of oscillator, respectively. Additionally, $a_{i}$ is a positive constant parameter. Equation (24) determines the phase $(\theta _{i})$ and amplitude $(r_{i})$ of the ith oscillator. By solving Eq. (24), output signal of the ith oscillator can be defined as

$$\begin{aligned} x_{i}(t)=r_{i}(t)\cos {(\theta _{i}(t)-\theta _{0i})} \end{aligned}$$

(25)

where $\theta _{\mathrm{0}i}$ is a constant phase lag. This equation shows that the output signal extracted from the ith oscillator is harmonics. Therefore, to obtain the output of oscillator, we can use finite Fourier series. An essential step in using a CPG as a trajectory generator is finding the parameters of the CPG to produce the desired trajectory. For detailed information on this method, please see [28]. In this study, a finite Fourier series with five parameters is needed to satisfy the time constraints as,

Fig. 6

Overall structure for the five oscillators for each leg

Fig. 7

Flowchart of the learning process

$$\begin{aligned} l_{i}(t)= & {} a_{0i}+a_{1i}\cos \left( \omega _{i}t \right) +b_{1i}\cos \left( \omega _{i}t-\frac{\pi }{2} \right) \nonumber \\&+\,a_{2i}\cos \left( 2\omega _{i}t \right) +b_{2i}\cos \left( 2\omega _{i}t-\frac{\pi }{2} \right) \end{aligned}$$

(26)

where $a_{0i}\cdots b_{2i}$ and $\omega _{i}$ are six unknown constants. By solving the inverse kinematics for each motion, six actuator’s lengths can be determined for each motion. Therefore, each leg has five oscillators that are coupled with the first oscillator. This coupling insures that all five oscillators are synchronized with each other (Fig. 6).

The proposed FAL-CPG method is indicated in Fig. 7. This figure shows the relation between kinematics problem and FAL_ CPG methodology. First, the recorded chewing patterns were defined as the trajectory of moving platform of rehab robot. Then, the inverse kinematics of rehab robot, Eq. 1, is solved to obtain the required leg lengths of the rehab robot. Then, the FAL_ CPG is applied to each of the six leg lengths to find the main CPG parameters. As it is obvious in Fig. 7, the learning process is straightforward, and the error of the learned signal depends on the accuracy of the Fourier fit. In applications where the desired signal is complex or the desired accuracy is high, the number of Fourier terms may be large. In this paper, the number of Fourier terms is $\hbox {k}=5$. This value was obtained after several trial and error simulations.

4.2 CPG network

As shown in Fig. 6, five oscillators are utilized to reproduce the desired trajectory for each leg’s length. Therefore, 30 nonlinear oscillators are required to simulate the trajectory of the moving platform of the robot. Figure 8 demonstrates the overall architecture of the CPG network.

Additionally, note that couplings between lengths are done through the first oscillator of each length. With the aid of these couplings, synchronization is achieved and synergy is formed within the leg lengths.

Fig. 8

Overall architecture of the CPG network for the rehab robot

5 Recording jaw movement

To track the jaw motion, small reflective markers, $\sim 10\hbox { mm}$ in diameter, were adhered to specific facial locations (Fig. 9). Forehead markers were used as reference points. Tracking was performed using a Simi Reality Motion System (GmbH, Unterschleissheim, Germany). Recorded data were preprocessed prior to modeling using Simi Motion software. To record jaw movement, three synchronized cameras are used. The cameras output were digitized to 250 frames/s, and frequencies above 7 Hz were removed. Then, Simi Motion system performs an automatic tracking of passive markers placed on the subject for the 3D kinematics calculations (e.g., jaw displacements) with a very high accuracy (Website: www.simi.com) [57].

Our recording consisted of four sessions of (1) three clenching movement (CM), (2) right grinding movement (RGM), (3) left grinding movements (LGM) and (4) general grinding movements (GGM). The recorded 3D mandibular trajectory is shown in Fig. 10. This figure shows the time-dependent trajectory of the mandible in a mastication process of subject.

Fig. 9

Marker position on the subject’s face

Fig. 10

Recorded chewing trajectory

6 Results

To consider the effectiveness of using CPG as a trajectory generation method, three examples are illustrated. Generally, the human jaw movements are complex and hard to describe. The smoothness of movements was effectively used for a model of human limb actions [18]. To approach this movement, CPG is used as the main controlling unit of movements.

Fig. 11

Effectiveness of CPG in case study 1: a perturbation in legs 1 and 4 trajectories, b corresponding velocity patterns in legs 1 and 4, c ability against perturbation for the central pattern generator (CPG) in legs 1 and 4, d effect of CPG in velocity patterns in legs 1 and 4. e Force of central pattern generator (CPG) trajectory for robot legs, f the zoom box for force

6.1 Case study 1

In order to investigate the capability of CPGs to cope with additive and multiplicative transient perturbation, a number between 0 and 1 are randomly added to all states $(\hbox {r}, \dot{\hbox {r}}, \uptheta )$ at time $\hbox {t}=3$–3.1 s for link 1 and at time $\hbox {t}=5$ to $\hbox {t}=5.1$ for link 4 (Fig. 11a). As shown in Fig. 11c, the CPG has stability against perturbation, and it is desirable to have smooth continuity at the perturbation points (Fig. 11a, b). In other words, Fig. 12c, d indicates that despite the sudden changes in mastication parameters at 3 and 5 s, variations in leg lengths and velocity are smooth. This characteristic, smooth transition stems from the limit cycle property of the CPG. As shown in Fig. 11d, f, despite the sudden changes in mastication parameters at 3 and 5 s, variations in forces are smooth. This characteristic, smooth transition in forces stems from the limit cycle property of the CPG.

Fig. 12

a–f Effect of modulation in leg lengths, (a$^{\prime }$–f$^{\prime }$) modulation of the leg lengths with CPG, (a$^{\prime \prime }$–f$^{\prime \prime }$) real-time-varying lengths of muscles during the chewing pattern with CPG

Fig. 13

Trajectory of chewing pattern

Fig. 14

Transition between chewing patterns

6.2 Case study 2

Properties of food such as hardness, plasticity, elasticity and food size directly influence afferent input to central nervous control system [18]. All of these factors may affect the sequence of mastication. For instance, opening and closing phase time and chewing cycle time were significantly longer when food of increased size was chewed. Therefore, modulation is another important property of a CPG. Modulation is necessary when the desired pattern is needed to change to another rhythmic pattern in an online manner. To examine this property, both frequencies and amplitudes ($v_{i}$ and $R_{i}$) of all oscillators are multiplied by number 2 at 5 s of the simulation time (Fig. 12a–f). Figure 12a$^{\prime }$–f$^{\prime }$ indicates that despite the modulation, the signal is changed in a smooth manner when the CPG is utilized. Therefore, CPG can be modulated to adapt with a dynamic environment, and trajectories are robust to perturbations. Moreover, by using jaw model, we can observe the real-time-varying lengths of muscles during the chewing pattern (Fig. 12a$^{\prime \prime }$–f$^{\prime \prime }$). This analysis provided in this study will allow researchers to characterize and study the mastication process by specifying different chewing patterns (e.g., muscle displacements) and to investigate the effect of each chewing pattern in each muscle. Figure 13 illustrates the path of reference point (the chin point (CP), placed on the end effector of rehab robot) during chewing pattern on case II. This figure confirms the CPG produces smooth trajectories even when the control parameters are abruptly changed, and it is computationally efficient. Therefore, the physiotherapists can change the velocity and amplitude of mastication based on observation of jaw model’s outputs.

6.3 Case study 3

Mastication is a rhythmic behavior, along with respiration and locomotion, in mammals. Many studies have investigated and considered the steering and controlling mechanism for chewing and swallowing. Nankali [58, 59] showed that the position of masticatory force and chewing pattern change in eating time according to mouthful characteristic and size. Therefore, the robust and smooth transitions between these patterns are essential. In rehabilitation process, physiotherapist often changes the motion patterns. Figure 14 indicates that chewing patterns can be altered and implemented based on the decision of the doctor.

Fig. 15

a–f Effect of CPG in smooth transitions of leg lengths, (a$^{\prime }$–f$^{\prime }$) effect of CPG in velocity of leg, a$^{\prime \prime }$–f$^{\prime \prime }$ real-time-varying lengths of muscles during the chewing pattern with CPG

Fig. 16

Time history of CP trajectory, a x-axis, b y-axis, c z-axis

In this case, we supposed that the doctor changes the each motion in 4 s suddenly, and CM, LGM, RGM, GGM and swallowing happened, respectively. Therefore, overall mastication time is 20 s. As shown in Fig. 15a–f, despite the sudden changes in mastication pattern, at 4-, 8-, 12- and 16-s, variations in leg lengths are smooth. This characteristic, smooth transition in leg length stems from the limit cycle property of the CPG (Fig. 15a$^{\prime }$–f$^{\prime }$). The corresponding variations of the lengths of muscles during the chewing patterns are also shown in Fig. 15 (a$^{\prime \prime }$–f$^{\prime \prime }$). As can be seen from 15 (a$^{\prime \prime }$–f$^{\prime \prime }$), the muscle length changes in a smooth manner. Stretched and suddenly contracts in muscle take place when the range of motion of corresponding limbs is changed abruptly.Therefore, Fig. 15a$^{\prime \prime }$–f$^{\prime \prime }$) shows that the proposed CPG can able to avoid happening these danger phenomena in jawmuscles.

Moreover, Fig. 16 indicates the trace path of end effector of moving platform of rehab robot or CP on jaw model. As can be seen, however, the trajectory is changed in mentioned time suddenly, but CPG manages to remove them and extract a simple rhythm from the real trajectory which is complex and polluted. These smooth trajectories can be used in healing the injured human mastication muscles.

The overall goal of this research was to develop a simple yet plausible methodology to generate a trajectory for masticatory rehabilitation purposes based on a biological concept of central pattern generator (CPG). Generally, studies showed that the ability of robots to producing repetitive movements and permitting increased intensity of rehabilitation make them perfect tools to implement rehabilitation exercises. On the other hand, errors even few in rehabilitation of mandible system can cause irreparable harm to health of the participant. But, as shown in this study, the CPG networks could generate smooth trajectories even in spite of errors. Therefore, to rehab human mandibular system, there is a real need to use the concept of CPG for development of new methodology in jaw exercises and helps increase jaw mobility and healing.

7 Conclusion

Human mastication is a rhythmic behavior with a complex biomechanical process, which is hard to reproduce. During chewing movements, frequency and the amplitude of motions change smoothly by humans.

The purpose of this study is to provide a methodology to enable physiotherapists to perform human jaw rehabilitation. In the jaw rehabilitation, there is often a need to work on a certain group of jaw muscles. Therefore, a physiotherapist needs to be able to reproduce smooth mastication patterns by means of a robotic system. Two Gough–Stewart robots are used in this study to build a rehab system. The first robot is used as the rehab robot, and the second robot is used to model the human jaw system. Once the modeling is completed, the second robot will be replaced with an actual patient for the selected physiotherapy.

To track and record chewing trajectories, six reflective markers were bonded on facial locations and the 3D motions for four chewing patterns were recorded. To do the physiotherapy, it is assumed that the human mandible is fixed to the rehab robot’s top moving platform. In other words, the path motion of the mandible and the moving platform are the same. Therefore, to reproduce the recorded human jaw trajectory, the trajectory of the rehab robot’s top platform is used as the input for the inverse kinematics of the rehab robot to obtain the rehab robot’s leg trajectories. The calculated leg trajectories were used as the input for a CPG model to produce smooth and robust rehab leg trajectories. To do this, the CPG parameters are tuned using the FAL-CPG approach. Next, to control the rehab robot, the dynamic model of the rehab robot is developed using the Gibbs–Appell method. Three case studies are presented with the goal of demonstrating that 1) the robustness of the CPG to transient perturbations, 2) speed and amplitude of chewing can be changed in a smooth way in an online process, and 3) transition pattern between chewing patterns occurs in a smooth way. As a result, a therapist can make online changes to the mastication parameters (chewing pattern, amplitude and velocity of chewing) in a smooth and continuous manner. The proposed approach enables the tele-operator to reproduce the required masticatory motion in the subject’s jaw and can independently generate new trajectories for a patient.

The main contributions of this paper are: (1) implementing an online method where mastication trajectory for a rehab robot is generated in real time by combining several concepts, tools and methods such as direct and inverse kinematics, Gibbs–Appell dynamics equations, finite Fourier series, CPG and FAL-CPG methods. Specifically, this paper contributes by (2) deriving the dynamic equations using the Gibbs–Appell method for the Stewart robot. To the best of authors’ knowledge, this has not been presented before, (3) the concept of using Gough–Stewart robot as a rehab robot and another Gough–Stewart to model the human jaw, (4) allowing a therapist to produce a smooth transition for online changes to the chewing pattern, (5) developing kinematics model of the jaw to demonstrate the time-varying behaviors of the muscle lengths of subjects in a rehabilitation process.

For our future work, a real version of this robot will be constructed and considered. This robot is controlled by a doctor, during patients’ treatments. In other words, to use this robot we need to be an experienced doctor. To remove this limitation, we will plan to use the concepts of surface electromyography signals (SEMG) to recognize chewing patterns in our rehabilitation algorithm.

Appendix

1.1 Jacobian matrix

Obtaining Jacobian matrix is the critical step in deriving equation of motion in robotics. By taking derivative of the right-hand side of Eq. (1), the velocity of spherical joint, $b_{i}$, can be obtained as:

$$\begin{aligned} {\mathbf{v}}_{bi}={\mathbf{v}}_{M}+\, {{\varvec{\upomega }}}_{M}\times {\mathbf{b}}_{i} \end{aligned}$$

(A.1)

where ${\mathbf{v}}_{M}$ and ${{\varvec{\upomega }}}_{M}$ are linear and angular velocities of mass center of moving platform, respectively. Note that ${\mathbf{v}}_{bi}={}_{~}^{B} {\mathbf{R}}_{i}{}_{~}^{{i}} {\mathbf{v}}_{bi}$. Equation (A.1) can be written as:

$$\begin{aligned} {\mathbf{v}}_{bi}=J_{bi}\dot{\mathbf{x}}_{M} \end{aligned}$$

(A.2)

where $\dot{\mathbf{x}}_{M}$ is a $1\times 6$ vector that consist of linear and angular velocity terms [49, 50]. Therefore, $J_{bi}$ can be defined as:

$$\begin{aligned} {\mathbf{J}}_{bi}=\left[ {\begin{array}{cccccc} {1} &{}\quad \mathrm {0} &{}\quad \mathrm {0} &{}\quad \mathrm {0} &{}\quad b_{i,z} &{}\quad {-b}_{i,y}\\ \mathrm {0} &{}\quad {1} &{}\quad \mathrm {0} &{}\quad {-b}_{i,z} &{}\quad \mathrm {0} &{}\quad b_{i,x}\\ \mathrm {0} &{}\quad \mathrm {0} &{}\quad {1} &{}\quad b_{i,y} &{}\quad {-b}_{i,x} &{}\quad \mathrm {0}\\ \end{array} } \right] \end{aligned}$$

(A.3)

By substituting Eq. (A.2) into ${}_{~}^{{i}}{\mathbf{v}}_{bi}={}_{~}^{{i}} {\mathbf{R}}_{B} {\mathbf{v}}_{bi}$, we have

$$\begin{aligned} {}_{~}^{{i}} {\mathbf{v}}_{bi}={}_{~}^{{i}} {\mathbf{J}}_{bi}\dot{\mathbf{x}}_{M} \end{aligned}$$

(A.4)

where

$$\begin{aligned} {}_{~}^{{i}} {\mathbf{J}}_{bi}={}_{~}^{{i}} {\mathbf{R}}_{B}\, {\mathbf{J}}_{bi}\equiv \left[ {\begin{array}{*{20}c} {}_{~}^{{i}} {\mathbf{J}}_{bi,x}\\ {}_{~}^{{i}} {\mathbf{J}}_{bi,y}\\ {}_{~}^{{i}} {\mathbf{J}}_{bi,z}\\ \end{array} } \right] ,\, {}_{~}^{{i}} {\mathbf{R}}_{B}={}_{~}^{B} {\mathbf{R}}_{i}^\mathrm{T} \end{aligned}$$

(A.5)

where ${}_{~}^{{i}} {\mathbf{J}}_{bi,x}, {}_{~}^{{i}} {\mathbf{J}}_{bi,y}$ and ${}_{~}^{{i}} {\mathbf{J}}_{bi,z}$ are the row of the ${}_{~}^{{i}} {\mathbf{J}}_{bi}$. Based on the above matrices, we have

$$\begin{aligned} \dot{d}_{i}= {}_{~}^{{i}}{\mathbf{J}}_{bi,z}\dot{\mathbf{x}}_{M} \end{aligned}$$

(A.6)

where Eq. (A.6) calculates the linear velocity of piston with respect to cylinder ith link. Since our model has six actuated legs, then the assembled form of Eq. (A.6) can be stated as:

$$\begin{aligned} \dot{\mathbf{q}}={\mathbf{J}}_{p}\, \dot{\mathbf{x}}_{M},\, {\mathbf{J}}_{p}=\left[ {\begin{array}{*{20}c} {}^{1} {\mathbf{J}}_{b\mathrm {1,}z}\\ {}^{2} {\mathbf{J}}_{b\mathrm {2,}z}\\ {\vdots }\\ {}^{\mathrm{6}} {\mathbf{J}}_{b\mathrm {6,}z}\\ \end{array}} \right] \end{aligned}$$

(A.7)

where $\dot{\mathbf{q}}$ is the velocity vector of actuated leg in their actuating direction. Moreover, ${\mathbf{J}}_{p}$ is called the manipulator Jacobian matrix [49]. Subsequently, we have [50]

$$\begin{aligned} {}_{~}^{{i}} {{\varvec{\upomega }}}_{i}= & {} \frac{{1}}{d_{i}}\left[ {\begin{array}{*{20}c} - {}_{~}^{{i}}{\mathbf{J}}_{bi,y}\\ {}_{~}^{{i}}{\mathbf{J}}_{bi,x}\\ {\mathbf{0}}_{\mathrm{1\times 6}}\\ \end{array} } \right] \,\dot{\mathbf{x}}_{M} \end{aligned}$$

(A.8)

$$\begin{aligned} {}_{~}^{{i}} {\mathbf{v}}_{1i}= & {} \frac{e_{1i}}{d_{i}}\left[ {\begin{array}{*{20}c} {}_{~}^{{i}}{\mathbf{J}}_{bi,x}\\ {}_{~}^{{i}}{\mathbf{J}}_{bi,y}\\ {\mathbf{0}}_{\mathrm{1\times 6}}\\ \end{array} } \right] \,\dot{\mathbf{x}}_{M} \end{aligned}$$

(A.9)

$$\begin{aligned} {}_{~}^{{i}} {\mathbf{v}}_{2i}= & {} \frac{{1}}{d_{i}}\left[ {\begin{array}{*{20}c} {\mathrm {(}d_{i}-e_{2i})\, {}_{~}^{{i}}{\mathbf{J}}}_{bi,x}\\ \mathrm {(}d_{i}-e_{2i})\, {}_{~}^{{i}}{\mathbf{J}}_{bi,y}\\ d_{i} {}_{~}^{{i}}{\mathbf{J}}_{bi,z}\\ \end{array} } \right] \,\dot{\mathbf{x}}_{M} \end{aligned}$$

(A.10)

By combining Eqs. (A.8), (A.9) and (A.10), we have

$$\begin{aligned} {}_{~}^{{i}} \dot{\mathbf{x}}_{1i}= & {} \, {}_{~}^{{i}}{\mathbf{J}}_{1i}\dot{\mathbf{x}}_{M} \end{aligned}$$

(A.11)

$$\begin{aligned} {}_{~}^{{i}} \dot{\mathbf{x}}_{2i}= & {} \, {}_{~}^{{i}}{\mathbf{J}}_{2i}\dot{\mathbf{x}}_{M} \end{aligned}$$

(A.12)

where

$$\begin{aligned} {}_{~}^{{i}} {\mathbf{J}}_{1i}=\frac{{1}}{d_{i}}\left[ {\begin{array}{*{20}c} e_{1i} {}_{~}^{{i}}{\mathbf{J}}_{bi,x}\\ e_{1i} {}_{~}^{{i}}{\mathbf{J}}_{bi,y}\\ {\mathbf{0}}_{{1\times 6}}\\ - {}_{~}^{{i}}{\mathbf{J}}_{bi,y}\\ {}_{~}^{{i}}{\mathbf{J}}_{bi,x}\\ {\mathbf{0}}_{{1\times 6}}\\ \end{array} } \right] \end{aligned}$$

(A.13)

and

$$\begin{aligned} {}_{~}^{{i}} {\mathbf{J}}_{2i}=\frac{{1}}{d_{i}}\left[ {\begin{array}{*{20}c} (d_{i}-e_{2i})\, {}_{~}^{{i}}{\mathbf{J}}_{bi,x}\\ (d_{i}-e_{2i})\, {}_{~}^{{i}}{\mathbf{J}}_{bi,y}\\ d_{i} {}_{~}^{{i}}{\mathbf{J}}_{bi,z}\\ - {}_{~}^{{i}}{\mathbf{J}}_{bi,y}\\ {}_{~}^{{i}}{\mathbf{J}}_{bi,x}\\ {\mathbf{0}}_{\mathrm{1\times 6}}\\ \end{array} } \right] \end{aligned}$$

(A.14)

where ${}_{~}^{{i}} {\mathbf{J}}_{1i}$ and ${}_{~}^{{i}} {\mathbf{J}}_{2i}$ are known as the link Jacobian matrices. Next, by taking time derivative of Eq. (A.6), the absolute acceleration of point, $\, b_{i}$, can be obtained as

$$\begin{aligned} \dot{\mathbf{v}}_{bi}=\dot{\mathbf{v}}_{M}+\dot{{\varvec{\upomega }} }_{M}\times {\mathbf{b}}_{i}+ {{\varvec{\upomega }}}_{M}\times \left( \, {{\varvec{\upomega }}}_{M}\times \, {\mathbf{b}}_{i} \right) \end{aligned}$$

(A.15)

where $\dot{\mathbf{v}}_{M}$ and $\dot{{\varvec{\upomega }}}_{M}$ are linear and angular acceleration of mass center of moving platform, respectively. Equation (A.15) can be rewritten as:

$$\begin{aligned} \dot{\mathbf{v}}_{bi}= & {} \left[ {\begin{array}{*{20}c} {1} &{}\quad {0} &{}\quad {0} &{}\quad {0} &{}\quad -b_{i,z} &{}\quad -b_{i,y}\\ {0} &{}\quad {1} &{}\quad {0} &{}\quad -b_{i,z} &{}\quad {0} &{}\quad b_{i,x}\\ {0} &{}\quad {0} &{}\quad {1} &{}\quad -b_{i,y} &{}\quad b_{i,x} &{}\quad {0}\\ \end{array} } \right] \left\{ {\begin{array}{*{20}c} \dot{\mathbf{v}}_{p}\\ \dot{{\varvec{\upomega }}}_{p}\\ \end{array} } \right\} \nonumber \\&+\varvec{\upomega }_{p}\times \left( {{\varvec{\upomega }}}_{p}\times {\mathbf{b}}_{i} \right) \nonumber \\= & {} {\mathbf{J}}_{bi}\left\{ {\begin{array}{*{20}c} \dot{\mathbf{v}}_{p}\\ \dot{{\varvec{\upomega }}}_{p}\\ \end{array} } \right\} +{\mathbf{D}}_{1}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) ={\mathbf{J}}_{bi}\ddot{\mathbf{x}}_{M}+{\mathbf{D}}_{1}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) \end{aligned}$$

(A.16)

By multiplying both sides of Eq. (A.16) with ${}_{~}^{B} {\mathbf{R}}_{i}$, we have

$$\begin{aligned} {}_{~}^{{i}} \dot{\mathbf{v}}_{bi}= & {} {}_{~}^{{i}}{\mathbf{R}}_{B}\dot{\mathbf{v}}_{bi}= {}_{~}^{{i}}{\mathbf{R}}_{B}{\mathbf{J}}_{bi}\ddot{\mathbf{x}}_{M}+\, {}_{~}^{{i}}{\mathbf{R}}_{B}{\mathbf{D}}_{\mathrm{1i}}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) \nonumber \\= & {} \, {}_{~}^{{i}}{\mathbf{J}}_{bi}\ddot{\mathbf{x}}_{M}+\, {}_{~}^{{i}}{\mathbf{R}}_{B}{\mathbf{D}}_{\mathrm{1i}}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) \end{aligned}$$

(A.17)

Equation (A.17) can be rewritten as:

$$\begin{aligned} {}_{~}^{{i}} \dot{\mathbf{v}}_{bi}= {}_{~}^{{i}}{\mathbf{J}}_{bi}\ddot{\mathbf{x}}_{M}+{}^{{\varvec{i}}} {\mathbf{D}}_{2i}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) \end{aligned}$$

(A.18)

where ${}^{{\varvec{i}}} {\mathbf{D}}_{2i}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) ={}_{~}^{{i}} {\mathbf{R}}_{B}{\mathbf{D}}_{1i}\left( {\mathbf{q}},\dot{\mathbf{q}} \right)$. By considering the third component of Eq. (A.18), we have the acceleration of link in the $z_{i}$ direction,

$$\begin{aligned} \ddot{\mathbf{q}}={\mathbf{J}}_{p}\ddot{\mathbf{x}}_{M}+\mathbf O \left( {\mathbf{q}},\dot{\mathbf{q}} \right) \end{aligned}$$

(A.19)

where

$$\begin{aligned} {\mathbf{O}}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) = {}_{~}^{{i}} {d}_{i}{}_{~}^{{i}} {\omega }_{i}^{2}=({}_{~}^{{i}} {v}_{bi,x}^{2}+{}_{~}^{{i}} {v}_{bi,y}^{2})/{d}_{i} \end{aligned}$$

(A.20)

On the other hand, based on [49]

$$\begin{aligned} {}_{~}^{{i}} \dot{\varvec{\upomega }}_{i}=\frac{{1}}{d_{i}}\left[ {\begin{array}{*{20}c} {- {}_{~}^{{i}}\dot{v}}_{bi,y} \\ {}_{~}^{{i}} \dot{v}_{bi,x} \\ \mathrm {0}\\ \end{array} } \right] + \underbrace{{\frac{2}{{{d}_{{i}}^{2} }}\left[ {\begin{array}{*{20}c} {{}_{~}^{{i}} {v}_{{{bi},{y}}}^{~} {}_{{}}^{{i}} {v}_{{{bi},{z}}}^{~} } \\ { - {}_{~}^{{i}} {v}_{{{bi},{x}}}^{~} {}_{{}}^{{i}} {v}_{{{bi},{z}}}^{~} } \\ 0 \\ \end{array} } \right] }}_{{{}_{~}^{{i}} {\mathbf {D}}_{{3{i}}} \left( {{\mathbf {q}},\,\dot{\mathbf{q}}} \right) }} \end{aligned}$$

(A.21)

Substituting Eq. (A.18) in Eq. (A.21), we yield

$$\begin{aligned} {}_{~}^{{i}} \dot{\varvec{\upomega }}_{i}= & {} \frac{{1}}{d_{i}}\left[ {\begin{array}{*{20}c} - {}_{~}^{{i}}{\mathbf{J}}_{bi,y}\ddot{\mathbf{x}}_{M}-{\mathbf{D}}_{2i,y}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) \\ {}_{~}^{{i}}{\mathbf{J}}_{bi,x}\ddot{\mathbf{x}}_{M}+{\mathbf{D}}_{2i,x}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) \\ {0}\\ \end{array} } \right] +{}^{{\varvec{i}}} {\mathbf{D}}_{\mathrm{3}i}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) \nonumber \\= & {} \frac{{1}}{d_{i}}\left[ {\begin{array}{*{20}c} - {}_{~}^{{i}}{\mathbf{J}}_{bi,y}\\ {}_{~}^{{i}}{\mathbf{J}}_{bi,x}\\ {0}\\ \end{array} } \right] \,\ddot{\mathbf{x}}_{M}+\frac{{1}}{d_{i}}\left[ {\begin{array}{*{20}c} {{\mathbf{-D}}}_{2i,y}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) \\ {\mathbf{D}}_{2i,x}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) \\ {0}\\ \end{array} } \right] \nonumber \\&+\,{}^{{\varvec{i}}} {\mathbf{D}}_{\mathrm{3}i}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) \nonumber \\= & {} {}_{~}^{{i}}{\mathbf{J}}_{\omega i}\, \ddot{\mathbf{x}}_{M}+{}^{{\varvec{i}}} {\mathbf{D}}_{\mathrm{4}i}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) \end{aligned}$$

(A.22)

where

$$\begin{aligned}&{}_{~}^{{i}} {\mathbf{J}}_{\omega i}\, =\frac{{1}}{d_{i}}\left[ {\begin{array}{*{20}c} - {}_{~}^{{i}}{\mathbf{J}}_{bi,y}\\ {}_{~}^{{i}}{\mathbf{J}}_{bi,x}\\ \mathrm {0}\\ \end{array} } \right] \end{aligned}$$

(A.23)

$$\begin{aligned}&{}^{{\varvec{i}}} {\mathbf{D}}_{\mathrm{4}i}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) =\frac{{1}}{d_{i}}\left[ {\begin{array}{*{20}c} {-{}^{{\varvec{i}}} {\mathbf{D}}}_{2i,y}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) \\ {}^{{\varvec{i}}} {\mathbf{D}}_{2i,x}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) \\ {0}\\ \end{array} } \right] +{}^{{\varvec{i}}} {\mathbf{D}}_{\mathrm{3}i}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) \end{aligned}$$

(A.24)

Notice that ${} \dot{\varvec{\upomega }}_{i}={}_{~}^{B} {\mathbf{R}}_{i}{}_{~}^{{i}} \dot{\varvec{\upomega }}_{i}$. Based on [49, 50], we have

$$\begin{aligned} {}_{~}^{{i}} \dot{\mathbf{v}}_{1i}=\frac{e_{1i}}{d_{i}}\left[ {\begin{array}{*{20}c} {}_{~}^{{i}}\dot{v}_{bi,x} \\ {}_{~}^{{i}} \dot{v}_{bi,y} \\ \mathrm {0}\\ \end{array} } \right] - \underbrace{{\frac{{ {e}_{1} }}{{ {d}_{ {i}}^{2} }}\left[ {\begin{array}{*{20}c} {2{}_{~}^{ {i}} {v}_{{ {bi}, {x}}}^{~} {}_{{}}^{ {i}} {v}_{{ {bi}, {z}}}^{~} } \\ {2{}_{~}^{ {i}} {v}_{{ {bi}, {y}}}^{~} {}_{{}}^{ {i}} {v}_{{ {bi}, {z}}}^{~} } \\ {{}_{{}}^{ {i}} {v}_{{ {bi}, {x}}}^{2} + {}_{~}^{ {i}} {v}_{{ {bi}, {y}}}^{2} } \\ \end{array}} \right] }}_{{{}_{~}^{ {i}} {\mathbf {D}}_{{5 {i}}} \left( {{\mathbf {q}},\,\dot{\mathbf{q}}} \right) }} \end{aligned}$$

(A.25)

Substituting Eq. (A.18) into Eq. (A.25), we yield

$$\begin{aligned} {}_{~}^{{i}}\dot{\mathbf{v}}_{1i}= & {} {\frac{e_{1i}}{d_{i}}\left[ {\begin{array}{*{20}c} {}_{~}^{{i}}{\mathbf{J}}_{bi,x}\ddot{\mathbf{x}}_{p}+{}^{{\varvec{i}}} {\mathbf{D}}_{2i,x}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) \\ {}_{~}^{{i}}{\mathbf{J}}_{bi,y}\ddot{\mathbf{x}}_{p}+{}^{{\varvec{i}}} {\mathbf{D}}_{2i,y}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) \\ {0}\\ \end{array} } \right] +{}^{{\varvec{i}}} {\mathbf{D}}_{\mathrm{5}i}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) } \nonumber \\= & {} {\frac{e_{1i}}{d_{i}}\left[ {\begin{array}{*{20}c} {}_{~}^{{i}}{\mathbf{J}}_{bi,x}\\ {}_{~}^{{i}}{\mathbf{J}}_{bi,y}\\ \mathrm {0}\\ \end{array} } \right] \ddot{\mathbf{x}}_{M}+\frac{e_{1i}}{d_{i}}\left[ {\begin{array}{*{20}c} {}^{{\varvec{i}}} {\mathbf{D}}_{2i,x}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) \\ {}^{{\varvec{i}}} {\mathbf{D}}_{2i,y}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) \\ \mathrm {0}\\ \end{array} } \right] +{}^{{\varvec{i}}} {\mathbf{D}}_{\mathrm{5}i}( {\mathbf{q}},\dot{\mathbf{q}} )}\nonumber \\= & {} {}_{~}^{{i}}{\mathbf{J}}_{V{1}i}\, \ddot{\mathbf{x}}_{M}+{}^{{\varvec{i}}} {\mathbf{D}}_{\mathrm{6}i}\left( {\mathbf{q}},\dot{\mathbf{q}}\right) \end{aligned}$$

(A.26)

where

$$\begin{aligned}&{}_{~}^{{i}} {\mathbf{J}}_{V{1}i}\, =\frac{e_{1i}}{d_{i}}\left[ {\begin{array}{*{20}c} {}_{~}^{{i}}{\mathbf{J}}_{bi,x}\\ {}_{~}^{{i}}{\mathbf{J}}_{bi,y}\\ \mathrm {0}\\ \end{array} } \right] \end{aligned}$$

(A.27)

$$\begin{aligned}&{}^{{\varvec{i}}} {\mathbf{D}}_{\mathrm{6}i}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) =\frac{e_{1i}}{d_{i}}\left[ {\begin{array}{*{20}c} {}^{{\varvec{i}}} {\mathbf{D}}_{2i,x}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) \\ {}^{{\varvec{i}}} {\mathbf{D}}_{2i,y}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) \\ {0}\\ \end{array} } \right] +{}^{{\varvec{i}}} {\mathbf{D}}_{\mathrm{5}i}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) \end{aligned}$$

(A.28)

Note that $\dot{\mathbf{v}}_{1i}={}^{S} {\mathbf{R}}_{i}{}_{~}^{{i}} \dot{\mathbf{v}}_{1i}$. Next, based on [49], we have

$$\begin{aligned} {}_{~}^{{i}} \dot{\mathbf{v}}_{2i}= & {} \frac{{1}}{d_{i}\, }\left[ {\begin{array}{*{20}c} (d_{i}-e_{2i})\, {}_{~}^{{i}}\dot{v}_{bi,x} \\ (d_{i}-e_{2i})\, {}_{~}^{{i}}\dot{v}_{bi,y} \\ d_{i} {}_{~}^{{i}}\dot{v}_{bi,z} \\ \end{array} } \right] \nonumber \\&+ \underbrace{{\frac{{ {e}_{{2 {i}}} }}{{ {d}_{ {i}}^{2} }}\left[ {\begin{array}{*{20}c} {2{}_{~}^{ {i}} {v}_{{ {bi}, {x}}}^{~} {}_{{}}^{ {i}} {v}_{{ {bi}, {z}}}^{~} } \\ {2{}_{~}^{ {i}} {v}_{{ {bi}, {y}}}^{~} {}_{{}}^{ {i}} {v}_{{ {bi}, {z}}}^{~} } \\ {\left( {{}_{~}^{ {i}} {v}_{{ {bi}, {x}}}^{2} + {}_{~}^{ {i}} {v}_{{ {bi}, {y}}}^{2} } \right) } \\ \end{array} } \right] }}_{{{}_{~}^{ {i}} {\mathbf {D}}_{7} \left( {{\mathbf {q}},\,\dot{\mathbf{q}}} \right) }} \end{aligned}$$

(A.29)

Substituting Eq. (A.18) into Eq. (A.29), we yield

$$\begin{aligned} {}_{~}^{{i}} \dot{\mathbf{v}}_{2i}= & {} \frac{{1}}{d_{i}\, }\left[ {\begin{array}{*{20}c} \left( d_{i}-e_{2i} \right) \left\{ \, {}_{~}^{{i}}{\mathbf{J}}_{bi,x}\ddot{\mathbf{x}}_{M}+{}^{{\varvec{i}}} {\mathbf{D}}_{2i,x}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) \right\} \\ \left( d_{i}-e_{2i} \right) \left\{ \, {}_{~}^{{i}}{\mathbf{J}}_{bi,y}\ddot{\mathbf{x}}_{M}+{}^{{\varvec{i}}} {\mathbf{D}}_{2i,y}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) \right\} \\ d_{i}\left\{ {}_{~}^{{i}} {\mathbf{J}}_{bi,z}\ddot{\mathbf{x}}_{M}+{}^{{\varvec{i}}} {\mathbf{D}}_{2i,z}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) \right\} \\ \end{array} } \right] \nonumber \\&+{}^{{\varvec{i}}} {\mathbf{D}}_{\mathrm{7}}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) \nonumber \\= & {} \frac{{1}}{d_{i} }\left[ {\begin{array}{*{20}c} (d_{i}-e_{2i})\, {}_{~}^{{i}}{\mathbf{J}}_{bi,x}\\ (d_{i}-e_{2i})\, {}_{~}^{{i}}{\mathbf{J}}_{bi,y}\\ d_{i} {}_{~}^{{i}}{\mathbf{J}}_{bi,z}\\ \end{array} } \right] \ddot{\mathbf{x}}_{M}\nonumber \\&+{\frac{{1}}{d_{i}\, }\left[ {\begin{array}{*{20}c} (d_{i}-e_{2i})^{{\varvec{i}}} {\mathbf{D}}_{2i,x}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) \\ (d_{i}-e_{2i})^{{\varvec{i}}} {\mathbf{D}}_{2i,y}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) \\ d_{i}^{{\varvec{i}}} {\mathbf{D}}_{2i,z}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) \\ \end{array} } \right] +{\mathbf{D}}_{\mathrm{7}}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) }\nonumber \\= & {} {}_{~}^{{i}}{\mathbf{J}}_{V{2}i}\, \ddot{\mathbf{x}}_{M}+^{{\varvec{i}}} {\mathbf{D}}_{\mathrm{8}i}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) \end{aligned}$$

(A.30)

where

$$\begin{aligned}&{}_{~}^{{i}} {\mathbf{J}}_{V{2}i}\, =\frac{{1}}{d_{i} }\left[ {\begin{array}{*{20}c} \left( d_{i}-e_{2i} \right) {}_{~}^{{i}}{\mathbf{J}}_{bi,x}\\ \left( d_{i}-e_{2i} \right) {}_{~}^{{i}}{\mathbf{J}}_{bi,y}\\ d_{i} {}_{~}^{{i}}{\mathbf{J}}_{bi,z}\\ \end{array} } \right] \end{aligned}$$

(A.31)

$$\begin{aligned} {}^{{\varvec{i}}} {\mathbf{D}}_{8i}\left( {\mathbf{q}},\dot{\mathbf{q}} \right)= & {} \frac{{1}}{d_{i} }\left[ {\begin{array}{*{20}c} (d_{i}-e_{2i})^{{\varvec{i}}} {\mathbf{D}}_{2i,x}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) \\ (d_{i}-e_{2i})^{{\varvec{i}}} {\mathbf{D}}_{2i,y}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) \\ d_{i}^{{\varvec{i}}} {\mathbf{D}}_{2i,z}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) \\ \end{array} } \right] \nonumber \\&+{}^{{\varvec{i}}} {\mathbf{D}}_{\mathrm{7}}\left( {\mathbf{q}}, \dot{\mathbf{q}} \right) \end{aligned}$$

(A.32)

Note that $\dot{\mathbf{v}}_{2i}= ^{B} {\mathbf{R}}_{i} {}_{~}^{{i}}\dot{\mathbf{v}}_{2i}$.

.

1.2 Obtain energy of moving platform, ${\varvec{S}}_{\varvec{M}}$

The Gibbs–Appell function is defined as

$$\begin{aligned} S_{M}=\frac{{1}}{{2}}m{\mathbf{a}}_{M}\cdot {\mathbf{a}}_{\mathrm{M}}+\frac{{1}}{{2}}{\varvec{\upalpha }}_{\mathrm{M}}\cdot \frac{{\partial }{\mathbf{H}}_{\mathrm{M}}}{{\partial }t}+{\varvec{\upalpha }}_{\mathrm{M}}\cdot ({{\varvec{\upomega }}}_{M}\times {\mathbf{H}}_{\mathrm{M}})\nonumber \\ \end{aligned}$$

(B.1)

where ${\mathbf{a}}_{\mathrm{M}}, {{\varvec{\upomega }}}_{\mathrm{M}}, {\varvec{\upalpha }}_{\mathrm{M}}$ and ${\mathbf{H}}_{\mathrm{M}}$ are linear acceleration, angular velocity, angular acceleration and angular momentum of mass center of moving platform, respectively. Additionally, $\frac{\delta {\mathbf{H}}_{\mathrm{M}}}{\delta t}$ represents the change of angular momentum. These variables are defined as:

$$\begin{aligned} {\mathbf{a}}_{\mathrm{M}}= & {} \ddot{{x}}\, {\mathbf{i}+}\ddot{y}\, {\mathbf{j}+}\ddot{z} {\mathbf{k}} \end{aligned}$$

(B.2)

$$\begin{aligned} {\varvec{\alpha }}_{\mathrm{M}}= & {} \ddot{\alpha }_{\,}{\mathbf{i}}+\ddot{\beta }_{\,}{\mathbf{j}}+\ddot{\gamma }_{\,}{\mathbf{k}} \end{aligned}$$

(B.3)

$$\begin{aligned} {\mathbf{H}}_{\mathrm{M}}= & {} {\mathbf{I}}_{M}{.} {{\varvec{\upomega }}}_{M}\left[ {\begin{array}{*{20}c} I_{M,xx} &{} {0} &{} {0}\\ {0} &{} I_{M,yy} &{} {0}\\ {0} &{} {0} &{} I_{M,zz}\\ \end{array} } \right] \left[ {\begin{array}{*{20}c} \dot{\alpha }_{\,}\\ \dot{\beta }_{\,}\\ \dot{\gamma }_{\,}\\ \end{array} } \right] \nonumber \\= & {} I_{M,xx}\dot{\alpha }_{{ \, }}{\mathbf{i}+} I_{M,yy}\dot{\beta }_{{ \, }}{\mathbf{j}+} I_{M,zz}\dot{\gamma }_{{ \, }}{\mathbf{k}} \end{aligned}$$

(B.4)

$$\begin{aligned} \frac{{\partial }{\mathbf{H}}_{\mathrm{M}}}{{\partial }t}= & {} I_{M,xx}\ddot{\alpha }{\mathbf{i}}+ I_{M,yy}\ddot{\beta }_{{ \, }}{\mathbf{j}}+ I_{M,zz}\ddot{\gamma }_{{ \, }}{\mathbf{k}} \end{aligned}$$

(B.5)

By substituting Eqs. (B.2)–(B.5) into Eq. (B.1), we have

$$\begin{aligned} S_{M}= & {} \frac{{1}}{{2}}m\left( \ddot{{x}}^{2}+\ddot{y}^{2}+\ddot{z}^{2} \right) \nonumber \\&+\,\frac{{1}}{{2}}\left( \, I_{M,xx}\ddot{\alpha }^{2}+ I_{M,yy}\ddot{\beta }_{{ \, }}^{2}+ I_{M,zz}\ddot{\gamma }^{2} \right) \nonumber \\&+\left( I_{M,zz}- I_{M,yy} \right) \ddot{\alpha }\dot{\beta }_{\,}\dot{\gamma }_{\,}+\left( I_{M,xx}- I_{M,zz} \right) \ddot{\beta }_{{ \, }}\dot{\alpha }_{\,}{\dot{\gamma }}_{{ \, }}\nonumber \\&+\left( I_{M,yy}- I_{M,xx} \right) \ddot{\gamma }\dot{\alpha }_{\,}\dot{\beta }_{\,} \end{aligned}$$

(B.6)

1.3 Obtain energy of cylinder, ${\varvec{S}}_{{\mathbf{1}}{\varvec{i}}}$

The Gibbs–Appell function of cylinder is defined as:

$$\begin{aligned} S_{1i}=\frac{{1}}{{2}}m_{1i}\, \dot{\mathbf{v}}_{1i}\cdot \, \dot{\mathbf{v}}_{1i}+\frac{{1}}{{2}}\, \dot{{\varvec{\upomega }}}_{i}\cdot \frac{{\partial }{\mathbf{H}}_{\mathrm{1i}}}{{\partial }t}+ \dot{{\varvec{\upomega }}}_{i}\cdot ( {{\varvec{\upomega } }}_{i}\times {\mathbf{H}}_{\mathrm{1i}})\nonumber \\ \end{aligned}$$

(C.1)

where ${} \dot{\mathbf{v}}_{1i}, {} {{\varvec{\upomega }}}_{i}, {} \dot{{\varvec{\upomega }}}_{i}$ and ${\mathbf{H}}_{\mathrm{1i}}$ are linear acceleration, angular velocity, angular acceleration and angular momentum of mass center of ith cylinder, respectively. Terms used in Eq. (C.1) can be obtained as:

$$\begin{aligned} \frac{{1}}{{2}}m_{1i} \dot{\mathbf{v}}_{1i}\cdot \dot{\mathbf{v}}_{1i}= & {} \frac{{1}}{{2}}m_{1i}\left[ \left( {\mathbf{J}}_{V{1}i,x}\, \ddot{\mathbf{x}}_{M}+ {\mathbf{D}}_{\mathrm{6}i,x}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) \right) ^{2}\right. \nonumber \\&+\,\left( {\mathbf{J}}_{V{1}i,y}\, \ddot{\mathbf{x}}_{M}+ {\mathbf{D}}_{\mathrm{6}i,y}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) \right) ^{2}\nonumber \\&\left. +\,\left( {\mathbf{J}}_{V{1}i,z}\, \ddot{\mathbf{x}}_{M}+ {\mathbf{D}}_{\mathrm{6}i,z}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) \right) ^{2} \right] \end{aligned}$$

(C.2)

where ${} {\mathbf{J}}_{V{1}i}\, = {}_{~}^{B} {\mathbf{R}}_{i} {}_{~}^{{i}}{\mathbf{J}}_{V{1}i}$ and ${} {\mathbf{D}}_{\mathrm{6}i}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) = {}_{~}^{B} {\mathbf{R}}_{i}^{{\varvec{i}}} {\mathbf{D}}_{\mathrm{6}i}\left( {\mathbf{q}},\dot{\mathbf{q}} \right)$.

$$\begin{aligned} \frac{{1}}{{2}} \dot{{\varvec{\upomega }} }_{i}\cdot \frac{{\partial }{\mathbf{H}}_{\mathrm{1i}}}{{\partial }t}= & {} \frac{{1}}{{2}}\left[ {I_{{ 11}}^{2i}\left( {\mathbf{J}}_{\omega i,x}\, \ddot{\mathbf{x}}_{M}+ {\mathbf{D}}_{\mathrm{4}i,x}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) \right) }\right. \nonumber \\&+\,{I_{\mathrm{22}}^{2i}\left( \, {\mathbf{J}}_{\omega i,y}\, \ddot{\mathbf{x}}_{M}+ {\mathbf{D}}_{\mathrm{4}i,y}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) \right) }^{2}\nonumber \\&\left. +\,{I_{\mathrm{33}}^{2i}\left( {\mathbf{J}}_{\omega i,z}\, \ddot{\mathbf{x}}_{M}+ {\mathbf{D}}_{\mathrm{4}i,z}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) \right) }^{2} \right] \end{aligned}$$

(C.3)

where ${} {\mathbf{J}}_{\omega i}\, = {}_{~}^{B} {\mathbf{R}}_{i} {}_{~}^{{i}}{\mathbf{J}}_{\omega i}$ and ${} {\mathbf{D}}_{\mathrm{4}i}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) = {}_{~}^{B} R_{i}^{{\varvec{i}}} {\mathbf{D}}_{4i}\left( {\mathbf{q}},\dot{\mathbf{q}} \right)$.

$$\begin{aligned} {} \dot{\varvec{\upomega }}_{i}\cdot \left( {{\varvec{\upomega }}}_{i}\times {\mathbf{H}}_{\mathrm{1i}} \right)= & {} \mathrm {K}_{1i,x}\left( {\mathbf{J}}_{\omega i,x}\, \ddot{\mathbf{x}}_{M}+ {\mathbf{D}}_{\mathrm{4}i,x}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) \right) \nonumber \\&+\,K_{1i,y}\left( {\mathbf{J}}_{\omega i,y}\, \ddot{\mathbf{x}}_{M}+ {\mathbf{D}}_{\mathrm{4}i,y}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) \right) \nonumber \\&+\,K_{1i,z}\left( {\mathbf{J}}_{\omega i,z}\, \ddot{\mathbf{x}}_{M}+ {\mathbf{D}}_{\mathrm{4}i,z}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) \right) \end{aligned}$$

(C.4)

where ${\mathbf{K}}_{1i}=\left( {{\varvec{\upomega }}}_{i}\times {\mathbf{H}}_{\mathrm{1ci}} \right)$.

1.4 Obtain energy of piston, ${\varvec{S}}_{{\mathbf{2}}{\varvec{i}}}$

The Gibbs–Appell function of piston is defined as:

$$\begin{aligned} S_{2i}=\frac{{1}}{{2}}m\, \dot{\mathbf{v}}_{2i}\cdot \, \dot{\mathbf{v}}_{2i}+\frac{{1}}{{2}}\, \dot{\varvec{\upomega }}_{i}\cdot \frac{{\partial }{\mathbf{H}}_{\mathrm{2i}}}{{\partial }t}+ \dot{\varvec{\upomega }}_{i}\cdot ( {{\varvec{\upomega }}}_{i}\times {\mathbf{H}}_{\mathrm{2i}}) \end{aligned}$$

(D.1)

where ${} \dot{\mathbf{v}}_{2i}, {} {{\varvec{\upomega }}}_{i}$, ${} \dot{\varvec{\upomega }}_{i}$ and ${\mathbf{H}}_{\mathrm{2i}}$ are linear acceleration, angular velocity, angular acceleration and angular momentum of mass center of ith piston, respectively. Terms of Eq. (D.1) can be obtained as:

$$\begin{aligned} \frac{{1}}{{2}}m_{2i} \dot{\mathbf{v}}_{2i}\cdot \dot{\mathbf{v}}_{2i}= & {} \frac{{1}}{{2}}m_{2i}\left[ \left( {\mathbf{J}}_{V{2}i,x}\, \ddot{\mathbf{x}}_{M}+ {\mathbf{D}}_{\mathrm{8}i,x}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) \right) ^{2}\right. \nonumber \\&+\left( {\mathbf{J}}_{V{2}i,y}\, \ddot{\mathbf{x}}_{M}+ {\mathbf{D}}_{\mathrm{8}i,y}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) \right) ^{2}\,\nonumber \\&\left. +\left( {\mathbf{J}}_{V{2}i,z}\, \ddot{\mathbf{x}}_{M}+ {\mathbf{D}}_{\mathrm{8}i,z}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) \right) ^{2} \right] \end{aligned}$$

(D.2)

where ${} {\mathbf{J}}_{V{2}i}\, = {}_{~}^{B} {\mathbf{R}}_{i} {}_{~}^{{i}}{\mathbf{J}}_{V{2}i}$ and ${} {\mathbf{D}}_{\mathrm{8}i}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) = ^{B} {\mathbf{R}}_{i}^{i} {\mathbf{D}}_{\mathrm{8}i}\left( {\mathbf{q}},\dot{\mathbf{q}} \right)$.

$$\begin{aligned} \frac{{1}}{{2}} \dot{\varvec{\upomega }}_{i}\cdot \frac{{\partial }{\mathbf{H}}_{\mathrm{1i}}}{{\partial }t}= & {} \frac{{1}}{{2}}\left[ {I_{\mathrm{11}}^{1i}\left( {\mathbf{J}}_{\omega i,x}\, \ddot{\mathbf{x}}_{M}+ {\mathbf{D}}_{\mathrm{4}i,x}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) \right) }^{2}\right. \nonumber \\&+\,{I_{\mathrm{22}}^{1i}\left( {\mathbf{J}}_{\omega i,y}\, \ddot{\mathbf{x}}_{M}+ {\mathbf{D}}_{\mathrm{4}i,y}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) \right) }^{2}\nonumber \\&\left. +\,{I_{\mathrm{33}}^{1i}\left( {\mathbf{J}}_{\omega i,z}\, \ddot{\mathbf{x}}_{M}+ {\mathbf{D}}_{\mathrm{4}i,z}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) \right) }^{2} \right] \end{aligned}$$

(D.3)

where ${} {\mathbf{J}}_{\omega i}\, = {}_{~}^{B} {\mathbf{R}}_{i} {}_{~}^{{i}}{\mathbf{J}}_{\omega i}$ and ${} {\mathbf{D}}_{\mathrm{4}i}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) = ^{\,B} {\mathbf{R}}_{i}^{{\varvec{i}}} {\mathbf{D}}_{\mathrm{4}i}\left( {\mathbf{q}},\dot{\mathbf{q}}\right)$.

$$\begin{aligned} {} \dot{\varvec{\upomega }}_{i}\cdot \left( \, {{\varvec{\upomega }}}_{i}\times {\mathbf{H}}_{\mathrm{2i}} \right)= & {} K_{2i,x}\left( {\mathbf{J}}_{\omega i,x}\, \ddot{\mathbf{x}}_{M}+ {\mathbf{D}}_{\mathrm{4}i,x}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) \right) \nonumber \\&+\,K_{2i,y}\left( {\mathbf{J}}_{\omega i,y}\, \ddot{\mathbf{x}}_{M}+ {\mathbf{D}}_{\mathrm{4}i,y}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) \right) \nonumber \\&+\,K_{2i,z}\left( {\mathbf{J}}_{\omega i,z}\, \ddot{\mathbf{x}}_{M}+ {\mathbf{D}}_{\mathrm{4}i,z}\left( {\mathbf{q}},\dot{\mathbf{q}} \right) \right) \end{aligned}$$

(D.4)

where ${\mathbf{K}}_{2i}=\left( {{\varvec{\upomega }}}_{i}\times {\mathbf{H}}_{\mathrm{2\, i}} \right)$.