1 Introduction

Recently, rehabilitation robotics are attracting higher attention by physiotherapists and robot researchers. There are many reasons for this increasing attention. The rehabilitation robots can consistently apply therapy over long periods without tiring. In addition, the use of sensors can highly improve the quality of the therapy. Moreover, it can provide various exercises that cannot be performed by a therapist and can decrease the cost of physiotherapy process. Finally, the rehabilitation robot can be easily programmed by the physiotherapist to perform the suggested exercises [1].

To perform therapeutic exercises, various control strategies such as position control, force control, hybrid position-force control, and impedance control have been proposed. Advanced control methods such as adaptive control [2], fuzzy control [3] and neural-fuzzy control [4] have been efficiently used to perform mentioned control strategies. Hybrid control and impedance control are two commonly used control methods. The hybrid control was successfully implemented on the LOKOMAT robotic system [5, 6]. Compared with other control methods, the impedance control is more effective and flexible to apply a wide range of rehabilitation exercises in the presence of uncertainties [7]. The therapeutic robots such as MIT-MANUS employ impedance control for passive and resistive exercises [8]. An impedance control law is a desired dynamics, which a rehabilitation robot should show in contact with human to perform a commanded therapeutic exercise. Because of applying impedance control, the robotic system will interact with the environment such a mass-spring-damper system in response to the applied force from the environment.

sEMG is one of the biological signals, which is often used for controlling the robots according to the user’s intention [9,10,11]. It reflects the muscle activation level in real time directly [12,13,14,15,16,17,18]. In voluntary movement, force is associated with motor unit recruitment and variations in motor unit firing frequency [19]. At the same muscle length and during isometric conditions, a greater number of recruiting motor units with greater discharge frequencies (i.e., muscle activation) lead to a greater generation of force. Therefore, a linear relationship between sEMG and muscle force is assumed. Precise estimation of muscle force based on sEMG signals in real time provides valuable information for robot in order to perform effective therapeutic exercises. Although sEMG signals are random, continuous and nonlinear in nature [20, 21]. Therefore, sEMG signals should be processed in order to get a simple model for its amplitude and then map this amplitude for the joint force. Various methods have been proposed for sEMG-based force estimation such as mathematical models, artificial neural network (ANN) and neuro-fuzzy. ANN is one of the most powerful methods of force estimation [22,23,24]. Essence of torque-based control methods forced researchers to need the precise value of human force; therefore, the majority of previous studies used complex methods for signal processing or feature extraction [25,26,27,28,29]. However, this article shows that using voltage-based methods let the researcher to use simpler signal processing or feature extraction methods.

Impedance control is basically defined as a torque control scheme. In the other words, the joint torques of the robot are commended to implement impedance control. For this purpose, the controller should overcome complex problems such as uncertainty and nonlinearity involved in the dynamics of the robotic system. Furthermore, in the torque control scheme, control system design depends on the dynamics of the patient’s limb. However, this parameter is nonlinear and time-varying. Furthermore, the majority of the proposed control approaches has ignored the dynamics of actuators, which are important in motion control. Generally, these proposed control approaches need to use estimator to estimate participant’s limb properties [30,31,32]. Also in the torque-based control approaches, it is assumed that the actuators can provide the commanded torques for the robot joints. However, this assumption may not be satisfied perfectly due to some practical problems such as the actuator dynamics, actuator saturation and sensing limitations. To overcome these problems, this paper presents a novel robust impedance control based on the voltage control strategy. The proposed control is based on the voltage control strategy, which differs from the common torque control strategy. As advantages, unlike the torque-based impedance control, the controller is not dependent on the dynamical models of the robot and the patient, so in comparison with a torque-based control approach, the voltage-based is simpler, less computational and more efficient while it considers the presence of actuators. In the proposed control approach, estimation of human force and uncertainty are both used as input in control law. To do this, first, sEMG signals with force sensor data are collected and used to train ANN. The sEMG signals as well as kinematic data, angle and angular velocity, are used as input to provide an online estimation of the limb force. Next, a novel adaptive fuzzy system based on voltage strategy is proposed to estimate uncertainties in the control approach.

The paper is organized as follows: Sect. 2 formulates the dynamics of the rehabilitation robot, explains the neural network algorithm for estimation of joint force from sEMG signals and development of the impedance control to perform therapeutic exercises. Section 3 presents the simulation results. Discussion is presented in Sect. 4.

2 Materials and methods

2.1 Force estimation

In this paper, a methodology for controlling rehabilitation robot using sEMG (for estimation of patient force) has been proposed. The estimation system architecture is divided into two phases: the training and the real-time operation, as shown id Fig. 1.

Fig. 1
figure 1

The force estimation system architecture

Full size image
Fig. 2
figure 2

The location of the sEMG electrodes

Full size image
Table 1 Muscles for each sEMG channel
Full size table

The training phase During the first phase, the users were instructed to perform the maximal (100% MVC) isometric extension contraction in a ramp fashion, gradually increase the knee extension effort over 2 s (loading), and hold the achieved moment for a further 2–3 s. The subjects had a mandatory rest period of at least 3 min between each isometric contraction. Absolute and normalized moment variations (particularly relative to body mass) were specified at each angle. Processed signals are incorporated into a neural network in order to train a set of models that will be used in real time for force estimation.

The real-time operation phase As soon as the training phase had finished, the real-time operation phase commenced. In this phase, the robust impedance control is used to perform a therapeutic exercise in real time.

Fig. 3
figure 3

Procedure of sEMG preprocessing

Full size image

2.1.1 Experimental setup and sEMG data collection

In this study, two male and two female participants were used for the data collection (the age of all participants is 27). All the participants agreed to the experimental protocol and gave permission for the publication of their photographs for scientific purposes. Four channels of sEMG signals are used as main input signals to estimate the real force of participants. The locations of sEMG electrodes are shown in Fig. 2. Each channel mainly corresponds to one muscle, as shown in Table 1. To determine the magnitude of sEMG signals of the knee extensors, our participants were seated on a dynamometer (Biodex-System3, Biodex Medical Systems Inc., USA) with hip angle of \(85{^{\circ }}\). We chose the \(85{^{\circ }}\) hip angle because in this position the contribution of the bi-articular rectus femoris, to the resultant knee moment is minimal [33,34,35]. The lever arm of the Biodex was securely attached to the shank at around 5 cm above the lateral malleolus. Velcro straps were placed firmly across the hip and trunk to restrict the participants’ movement during the knee extension contraction (Fig. 2). For the warm-up, participants exerted five submaximal and two maximum voluntary isometric concentric contractions within 2–3 min. Following this, the experimental protocol began.

The axis of rotation of the knee joint was set to be parallel to the axis of the rotation of the dynamometer, and passing through the midpoint of the line connecting the lateral and medial femoral condyles [36]. The influence of the simultaneous activation of the hamstrings, working as antagonists during the knee extension contraction, on the resultant joint moment was taken into account by establishing a relationship between hamstrings sEMG-amplitude and exerted moment, while working as agonists (described in following with more details).

For the experiment, eight sticky surface electrodes (Ag/AgCl) with an electrolytic gel interface were positioned above the midpoint of the muscle belly (with 2 cm distance on inter-electrodes) of the rectus femoris, vastus lateralis, vastus medialis and biceps femoris (Fig. 2). Moreover, reference electrodes were located on the patella bone. The skin was carefully shaved and cleaned with alcohol to reduce skin impedance. To reduce motion artifacts of the electrodes, they were further secured to the skin with an elastic tape, together with the preamplifier. Prior to the experiment, the leg was passively shaken to check mechanical artifacts of sEMG signals from each muscle. Several tests (e.g., contractions against manual resistance in knee flexion and extension) were performed to visualize whether a good signal was produced from each muscle. When artifacts or a poor signal were observed, the preparation procedure was repeated. ME6000 is used for recording the sEMG signal from the muscle in the Sport Sciences Research Institute of IRAN (SSRI). Data from sEMG sensor were sampled using 2000 Hz sampling frequency.

2.1.2 Preprocess of EMG signals

The estimated force from sEMG signals together with kinematic data, which included angle and angular velocity, is used as an input signal to the controller. Since raw sEMG signals are not suitable as input signals to the controller, the raw signal must be preprocessed. Raw sEMG processed in three steps. Step 1: Raw sEMG signal must be filtered. In this step, a fifth-ordered notch filter is used to remove the 60 Hz noise due the power supply. Step 2: Rectify sEMG signal. Step 3: The online moving average (OMA) of the preprocessed sEMG signal is calculated. The OMA calculation is written as

$$\begin{aligned} E(t)=\sqrt{\frac{1}{N}\sum _{i=0}^N {E(t-i)^{2}} } \end{aligned}$$
(1)

where N is the number of the segments (\(N=100\)) and E(t) is the voltage at its sampling point (sampling rate is 2000 Hz). At least processed sEMG (PEMG) signal is used as input for artificial neural network estimator. Signal processing is shown in Fig. 3.

2.1.3 Design neural network estimator

In this paper, the multilayer perceptron (MLP) type ANN is considered, which is consisting of three layers: input layer, tan-sigmoid hidden layer, and linear output layer. The detail structural design for feed-forward condition is depicted in Fig. 4. It is still under challenging task when it comes to deciding and select a number of neurons in the hidden layer. In addition, to store the huge numbers of network variables, the huge memory is required and hence training becomes complicated. In addition, over fitting may be occurred. Over fitting makes the network excessively complex thus, the nongeneralized network generates random error and consequently results in a very poor classification. On the other hand, the network cannot adjust the weights and biases properly during training if a very low number of neurons are selected in the hidden layer. Due to the lack of specific rule in finding the numbers of hidden neurons to obtain optimized performance of the network, particle swarm optimization (PSO) was used to find best ANN architecture. As the result of using PSO for force estimation is obtained that best condition for ANN is 6 inputs, 10 tan-sigmoid neurons in hidden layer and 8 linear neurons in the output layer. After designing the ANN with specified architecture and different hidden neurons, a suitable and efficient back-propagation training algorithm is required for the adjustment of synaptic weights and biases at different layers.

Fig. 4
figure 4

MLP neural network structure

Full size image

The relationship between the sEMG channels and the participant force is modeled as

$$\begin{aligned} \mathbf{F}_{\mathbf{h}_{\mathbf{est}} } =\left[ {{\begin{array}{c} {E_\mathrm{ch1} (t)} \\ {E_\mathrm{ch2} (t)} \\ {\begin{array}{l} E_\mathrm{ch3} (t) \\ E_\mathrm{ch4} (t) \\ \end{array}} \\ \theta \\ {\dot{\theta }} \\ \end{array} }} \right] W^{hl1}_{6\times n} W^{hl2}_{n\times m} W^{\mathrm{ol}}_{m\times 1} \end{aligned}$$
(2)

where \(\mathbf{F}_{\mathbf{h}_{\mathbf{est}} }\) is the joint force vector and \(E_{\mathrm{ch}.i} (t)\) is the joint pressed sEMG channel for each i, \(\theta \) and \(\dot{\theta }\) is angular position and velocity angular. \(W^{hl1}_{6\times n}\) and \(W^{hl2}_{n\times m}\) are the neural network’s weight matrices for the hidden layers and \(W^{\mathrm{ol}}_{m\times 1}\) is the weight matrix for the output layer. Figure 5 shows the results of force estimation from the learned neural network in real time.

Fig. 5
figure 5

Force estimation by the learned neural network

Full size image

2.2 Control system

2.2.1 Design adaptive robust impedance control

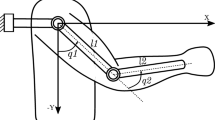
The state-space model of the electrically driven rehabilitation robot, which is shown in Fig. 6, has been obtained by Fateh and Khoshdel [33] as

$$\begin{aligned} {\dot{\mathbf{z}}}=\mathbf{f}(\mathbf{z})+\mathbf{bw} \end{aligned}$$
(3)

where \(\mathbf{w}=\left[ {{\begin{array}{c} {\mathbf{F}_\mathbf{h} } \\ \mathbf{v} \\ \end{array} }} \right] \) is considered as the inputs, \(\mathbf{z}=\left[ {{\begin{array}{ccc} {\mathbf{q}^\mathrm{T}}&{} {{\dot{\mathbf{q}}}^\mathrm{T}}&{} {\mathbf{I}^\mathrm{T}_\mathbf{a} } \\ \end{array} }} \right] ^{\mathrm{T}}\) is the state vector, \(\mathbf{b}\) and \(\mathbf{f}(\mathbf{z})\) are of the form

$$\begin{aligned}&\mathbf{f}(\mathbf{z})=\left[ {{\begin{array}{c} {\mathbf{z}_\mathbf{2} } \\ {\left( {\mathbf{J}_\mathbf{m} \mathbf{r}^{-1}+\mathbf{rM}(\mathbf{z}_1 )} \right) ^{-1}\left( {-\left( {\mathbf{B}_\mathbf{m} \mathbf{r}^{-1}\mathbf{+rC}(\mathbf{z}_1 \mathbf{,z}_2 )} \right) \mathbf{z}_2 -\mathbf{rD}(\mathbf{z}_1 )+\mathbf{K}_\mathbf{m} \mathbf{z}_3 } \right) } \\ {-\mathbf{L}^{-1}\left( {\mathbf{K}_\mathbf{b} \mathbf{r}^{-1}{} \mathbf{z}_2 +\mathbf{Rz}_3 } \right) } \\ \end{array} }} \right] ,\nonumber \\&{} \mathbf{b}=\left[ {{\begin{array}{cc} \mathbf{0}&{} \mathbf{0} \\ {\left( {\mathbf{J}_\mathbf{m} \mathbf{r}^{-1}+\mathbf{rM}(\mathbf{z}_1 )} \right) ^{-1}{} \mathbf{rJ}_\mathbf{e} ^{\mathbf{T}}(\mathbf{z}_1 )}&{} \mathbf{0} \\ \mathbf{0}&{} {\mathbf{L}^{-1}} \\ \end{array} }} \right] \end{aligned}$$
(4)

In order to obtain a task-space model, a transformation from the joint-space to the task-space should be used. This transformation is defined by manipulator Jacobian as

$$\begin{aligned} {\dot{\mathbf{x}}}=\mathbf{J}(\mathbf{q}){\dot{\mathbf{q}}} \end{aligned}$$
(5)

where \(\mathbf{x}\in R^{n}\) is the position of the end effector and \(\mathbf{J}(\mathbf{q})\in R^{n\times n}\) is the Jacobian matrix of the robot manipulator. Thus

$$\begin{aligned} {\dot{\mathbf{q}}}=\mathbf{J}^{-1}(\mathbf{q}){\dot{\mathbf{x}}} \end{aligned}$$
(6)

If the Jacobian matrix is not square, the pseudo-inverse Jacobian, \(\mathbf{J}(\mathbf{q})^{\dagger }\), is defined as

$$\begin{aligned} \mathbf{J}(\mathbf{q})^{\dagger }=\left( {\mathbf{J}(\mathbf{q})^\mathrm{T}{} \mathbf{J}(\mathbf{q})} \right) ^{-1}{} \mathbf{J}(\mathbf{q})^\mathrm{T} \end{aligned}$$
(7)
Fig. 6
figure 6

A schematic of rehabilitation robot

Full size image

Also, an impedance rule is proposed as

$$\begin{aligned} \mathbf{M}_{\mathbf{d}}(\ddot{\mathbf{x}}_{\mathbf{d}}-\ddot{\mathbf{x}})+ \mathbf{D}_{\mathbf{d}}(\dot{\mathbf{x}}_{\mathbf{d}}-\dot{\mathbf{x}})+ \mathbf{K}_{\mathbf{d}}({\mathbf{x}}_{\mathbf{d}}-{\mathbf{x}})= \mathbf{F}_{\mathbf{h}} \end{aligned}$$
(8)

where \(\mathbf{M}_\mathbf{d}\), \(\mathbf{D}_\mathbf{d}\) and \(\mathbf{K}_\mathbf{d}\) are the diagonal matrices, which include the desired impedance parameters and \(\mathbf{F}_\mathbf{h}\) is estimated force by ANN. From (8), we have

$$\begin{aligned} \dot{\mathbf{x}}=\mathbf{D}_{\mathbf{d}}^{-1}{} \mathbf{M}_\mathbf{d} (\ddot{\mathbf{x}}_{\mathbf{d}}-\ddot{\mathbf{x}})+ \dot{\mathbf{x}}_{\mathbf{d}}+ \mathbf{D}_\mathbf{d}^{-1}{} \mathbf{K}_\mathbf{d} ({\mathbf{x}}_{\mathbf{d}}-{\mathbf{x}})- \mathbf{D}_\mathbf{d}^{-1}{} \mathbf{F}_\mathbf{h}\nonumber \\ \end{aligned}$$
(9)

In addition, in order to obtain the motor voltages as the inputs of the system, we consider the electrical equation of geared permanent magnet DC motors in the matrix form,

$$\begin{aligned} \mathbf{RI}_\mathbf{a} +\mathbf{L}\dot{\mathbf{I}}_\mathbf{a} +\mathbf{K}\dot{\mathbf{q}}=\mathbf{v} \end{aligned}$$
(10)

where \(\mathbf{K}=\mathbf{K}_\mathbf{b} \mathbf{r}^{-1}\), \(\mathbf{v}\in R^{n}\) is the vector of motor voltages, \(\mathbf{I}_\mathbf{a} \in R^{n}\) is the vector of motor currents, \(\mathbf{R}\), \(\mathbf{L}\) and \(\mathbf{K}_\mathbf{b}\) represent the \(n\times n\) diagonal matrices for the coefficients of armature resistance, inductance, and back-emf constant, respectively. So, it can be obtained by using (6) and (10) that

$$\begin{aligned} \mathbf{RI}_\mathbf{a} +\mathbf{L}\dot{\mathbf{I}}_\mathbf{a} +\mathbf{KJ}^{-1}(\mathbf{q}){\dot{\mathbf{x}}}=\mathbf{v} \end{aligned}$$
(11)

Otherwise, the exact value of model’s parameters expressed by (11) is not known. So the nominal model is known and proposed based on the knowledge about the system and the nominal parameters \(\hat{{R}}\), \(\hat{{K}}\) and \(\hat{\mathbf{J}}\) are the estimations of R, K and \(\mathbf{J}\), respectively. The dynamics of the nominal model are simpler than the actual model. Since the electrical time constant of the DC geared motor is much smaller than its mechanical time constant. This implies that the effect of \(L\dot{I}_a\) being ignorable. Moreover, \(\dot{I}_a\) might be noisy thereby the measurement of \(\dot{I}_a\) is not recommended; therefore, the term \(L\dot{I}_a\) is not used in the nominal model. It is easy to write from (11)

$$\begin{aligned}&\hat{\mathbf{R}}{\mathbf{I}}_\mathbf{a} +\hat{\mathbf{K}}\hat{\mathbf{J}}^{-1}(\mathbf{q}){\dot{\mathbf{x}}}+(\mathbf{R}-\hat{\mathbf{R}}) {\mathbf{I}}_\mathbf{a}+ (\mathbf{KJ}^{-1}(\mathbf{q})\nonumber \\&\quad - \hat{\mathbf{K}}\hat{\mathbf{J}}^{-1}(\mathbf{q})){\dot{\mathbf{x}}} =\mathbf{v} \end{aligned}$$
(12)

Then, \({{\varvec{\upeta }}}\) has been defined as

$$\begin{aligned} {{\varvec{\upeta }}}=(\mathbf{R}-\hat{\mathbf{R}}) {\mathbf{I}}_\mathbf{a}+(\mathbf{KJ}^{-1}(\mathbf{q})- \hat{\mathbf{K}}\hat{\mathbf{J}}^{-1}(\mathbf{q})){\dot{\mathbf{x}}} \end{aligned}$$
(13)

Substituting (13) into (12) yields

$$\begin{aligned} \hat{\mathbf{R}}{\mathbf{I}}_\mathbf{a} +\hat{\mathbf{K}}\hat{\mathbf{J}}^{-1}(\mathbf{q}){\dot{\mathbf{x}}}+{{\varvec{\upeta }}}=\mathbf{v} \end{aligned}$$
(14)

By substituting (9) into (14), an impedance controller, which establishes the impedance rule is proposed as

$$\begin{aligned}&\hat{\mathbf{R}}{\mathbf{I}}_\mathbf{a} +\hat{\mathbf{K}}\hat{\mathbf{J}}^{-1}(\mathbf{q})(\mathbf{D}_{\mathbf{d}}^{-1}{} \mathbf{M}_\mathbf{d} (\ddot{\mathbf{x}}_{\mathbf{d}}-\ddot{\mathbf{x}})+\dot{\mathbf{x}}_{\mathbf{d}}+ \mathbf{D}_{\mathbf{d}}^{-1}\mathbf{K}_\mathbf{d} ({\mathbf{x}}_{\mathbf{d}}-{\mathbf{x}})\nonumber \\&\quad -\mathbf{D}_{\mathbf{d}}^{-1} \mathbf{F}_{\mathbf{h}})+{\hat{\varvec{\upeta }}}=\mathbf{v} \end{aligned}$$
(15)

We cannot use \({{\varvec{\upeta }}}\) in the control law since \({{\varvec{\upeta }}}\) is not known. Instead, \({\hat{{{\varvec{\upeta }}}}}\) is employed, where \({\hat{{{\varvec{\upeta }} }}}\) is the estimation of \({{\varvec{\upeta }}}\) by using an adaptive fuzzy system.

The closed-loop system is formed by substituting the control law (15) into the system (14) as

$$\begin{aligned}&\hat{\mathbf{R}}{\mathbf{I}}_\mathbf{a} +\hat{\mathbf{K}}\hat{\mathbf{J}}^{-1}(\mathbf{q})\dot{\mathbf{x}}+{{\varvec{\upeta }}}= \hat{\mathbf{R}}{\mathbf{I}}_\mathbf{a} +\hat{\mathbf{K}}\hat{\mathbf{J}}^{-1}(\mathbf{q})(\mathbf{D}_{\mathbf{d}}^{-1}{} \mathbf{M}_\mathbf{d} (\ddot{\mathbf{x}}_{\mathbf{d}}-\ddot{\mathbf{x}})\nonumber \\&\quad +\dot{\mathbf{x}}_{\mathbf{d}}+ \mathbf{D}_{\mathbf{d}}^{-1}\mathbf{K}_\mathbf{d} ({\mathbf{x}}_{\mathbf{d}}-{\mathbf{x}})-\mathbf{D}_{\mathbf{d}}^{-1} \mathbf{F}_{\mathbf{h}})+{\hat{\varvec{\upeta }}} \end{aligned}$$
(16)

In other words, (16) can be written as

$$\begin{aligned}&\mathbf{M}_{\mathbf{d}}(\ddot{\mathbf{x}}_{\mathbf{d}}-\ddot{\mathbf{x}})+\mathbf{D}_{\mathbf{d}}(\dot{\mathbf{x}}_{\mathbf{d}}-\dot{\mathbf{x}}) +\mathbf{K}_{\mathbf{d}}({\mathbf{x}}_{\mathbf{d}}-{\mathbf{x}})-\mathbf{F}_{\mathbf{h}}\nonumber \\&\quad = \hat{\mathbf{K}}^{-1}\hat{\mathbf{J}}(\mathbf{q})\mathbf{D}_{\mathbf{d}}({{\varvec{\upeta }}}-{\hat{\varvec{\upeta }}}) \end{aligned}$$
(17)

In (17) \({\hat{{{\varvec{\upeta }}}}}\) is a fuzzy system to approximate function \({{\varvec{\upeta }}}\). It can conclude from (17) that the desired impedance law has been reached if \({\hat{{{\varvec{\upeta }} }}}={{\varvec{\upeta }}}\). It is noticeable that for each degree of freedom a fuzzy adaptive system must design separately. Let us define the inputs of fuzzy system as \(x_1\), and \(x_2\)

$$\begin{aligned} x_{1}=\mathbf{I}_{\mathbf{a},}\,\,x_{2}={\dot{\mathbf{x}}} \end{aligned}$$
(18)

If three membership functions are given to each fuzzy input, the whole control space is covered by nine fuzzy rules. The linguistic fuzzy rules are proposed in the form of Mamdani type as

$$\begin{aligned} \hbox {Rule 1}: \hbox { If } x_1 \hbox { is } A_l \hbox { and } x_2 \hbox { is } B_l \hbox { Then } {\hat{{{\varvec{\upeta }}}}} \hbox { is } C_l \end{aligned}$$
(19)

where \(\hbox {Rule 1}\) denotes the lth fuzzy rule for \(l=1,2,\ldots ,9\). In the lth rule, \(A_l\), \(B_l\) and \(C_l\) are fuzzy membership functions belonging to the fuzzy variables \(x_1\), \(x_2\) and v, respectively. Three membership functions P, Z and N are given to the input \(x_1\) in the operating range of manipulator are shown in Fig. 7. They are expressed as

$$\begin{aligned}&\mu _P (x_1 )=\left\{ \begin{array}{ll} 0 &{} \quad x_1 \le 0 \\ 2x_1^{2} &{} \quad 0\le x_1 \le 0.5 \\ 1-2(x_1 -1)^{2} &{} \quad 0.5\le x_1 \le 1 \\ 1 &{} \quad x_1 \ge 1 \\ \end{array} \right. ,\nonumber \\&\mu _N (x_1 )=\left\{ \begin{array}{ll} 1 &{}\quad x_1 \le -1 \\ 1-2(x_1 +1)^{2} &{}\quad -1\le x_1 \le -0.5 \\ 2x_1 ^{2} &{} \quad -0.5\le x_1 \le 0 \\ 0 &{}\quad x_1 \ge 0 \\ \end{array} \right. \nonumber \\&\mu _Z (x_1 )=\exp \left( {-x_1 ^{2}/(2\sigma ^{2})} \right) ,\quad \sigma =0.3 \end{aligned}$$
(20)
Fig. 7
figure 7

The membership functions of the input \(x_{1}\)

Full size image

The membership functions belonging to \(x_2\) are given the same as \(x_1\). The membership functions of output u in the Gaussian shapes are expressed by

$$\begin{aligned} \mu _{C_l } ({\hat{{{\varvec{\upeta }}}}})=\exp \left( {-\left( {({ \hat{{{\varvec{\upeta }}}}}-\hat{{y}}_l )^{2}/(2\sigma ^{2})} \right) } \right) \end{aligned}$$
(21)

where \(\hat{{y}}_l\) is the center of \(C_l\). If we use the Mamdani-type inference engine, the singleton fuzzifier and the center average defuzzifier, \({\hat{{{\varvec{\upeta }}}}}\) is calculated as [33].

$$\begin{aligned} {\hat{{{\varvec{\upeta }}}}}=\sum _{l=1}^9 {\hat{{y}}_l \psi _l (x_1 ,x_2 )} ={\hat{{\mathbf{y}}}}^{\mathbf{T}}{{\varvec{\uppsi }}}(x_1 ,x_2 ) \end{aligned}$$
(22)

where \({\hat{{\mathbf{y}}}}=\left[ {{\begin{array}{ccc} {\hat{{y}}_1 }&{} {\ldots }&{} {\hat{{y}}_9 } \\ \end{array} }} \right] ^\mathrm{T}\) and \({{\varvec{\uppsi }}}=\left[ {{\begin{array}{ccc} {\psi _1 }&{} {\ldots }&{} {\psi _9 } \\ \end{array} }} \right] ^\mathrm{T}\) in which \(\psi _l\) is a positive value expressed as

$$\begin{aligned} \psi (x_{1}, x_{2})={\frac{\mu _{{A_{l}}}(x_{1})\mu _{{B_{l}}}(x_{2})}{{\mathop {\sum }\limits _{l=1}^{9}}\mu _{{A_{l}}}(x_{1})\mu _{{B_{l}}}(x_{2})}} \end{aligned}$$
(23)

Membership functions of inputs expressed by (20) take values in the interval (0, 1]. Thus \(\mu _{A_l }, \mu _{B_l } \in [0,1]\) implies that \(\left| {\psi _l (x_1 ,x_2 )} \right| \le 1\) for \(l=1,\ldots ,9\). Therefore, vector \({{\varvec{\psi }}}\) is bounded.

Result 1

Let \({\hat{{{\varvec{\upeta }}}}}\) be a fuzzy system in the form of (22). Then, the vector \({{\varvec{\psi }}}\) is bounded.

The parameters \({\hat{{\mathbf{y}}}}\) in (22) determined by adaptive rule afterward. Based on the general approximation of fuzzy systems, \({{\varvec{\upeta }}}\) can be approximated as

$$\begin{aligned} {{\varvec{\upeta }}}=\mathbf{y}^{\mathbf{T}}{{\varvec{\uppsi }}}(x_1 ,x_2 )+\varepsilon \end{aligned}$$
(24)

where \(\mathbf{y}=\left[ {{\begin{array}{ccc} {y_1 }&{} {\ldots }&{} {y_9 } \\ \end{array} }} \right] ^\mathrm{T}\) and \(\varepsilon \) is the bounded approximation error.

Fig. 8
figure 8

The block diagram of the proposed control scheme

Full size image

Substituting (22) and (24) into the closed-loop system (17) yields

$$\begin{aligned}&\mathbf{M}_{\mathbf{d}}(\ddot{\mathbf{x}}_{\mathbf{d}}-\ddot{\mathbf{x}})+ \mathbf{D}_{\mathbf{d}}(\dot{\mathbf{x}}_{\mathbf{d}}-\dot{\mathbf{x}})+ \mathbf{K}_{\mathbf{d}}({\mathbf{x}}_{\mathbf{d}}-{\mathbf{x}})- \mathbf{F}_{\mathbf{h}}\nonumber \\&\quad ={\mathbf{Kv}}(\mathbf{y}^{\mathbf{T}}-{\hat{\mathbf{y}}}^{\mathbf{T}}){\varvec{\uppsi }} (x_{1}, x_{2})+{\mathbf{Kv}}\varepsilon \end{aligned}$$
(25)
$$\begin{aligned}&{\mathbf{Kv}}=\hat{\mathbf{K}}^{-1}\hat{\mathbf{J}}(\mathbf{q})\mathbf{D}_{\mathbf{d}} \end{aligned}$$
(26)

can be written as

$$\begin{aligned} \ddot{\mathbf{e}}= & {} -{\varvec{\upalpha }}(\dot{\mathbf{e}})- {\varvec{\upbeta }}(\mathbf{e})+ \mathbf{M}_{\mathbf{d}}^{-1}{} \mathbf{F}_{\mathbf{h}}+ {\varvec{\upgamma }}(\mathbf{y}^{\mathbf{T}}-{\hat{\mathbf{y}}}^{\mathbf{T}}){\varvec{\uppsi }} (x_{1}, x_{2})+{\varvec{\upgamma }}\varepsilon \end{aligned}$$
(27)
$$\begin{aligned} {\varvec{\upalpha }}= & {} \mathbf{M}_{\mathbf{d}}^{-1}{} \mathbf{D}_{\mathbf{d}} \end{aligned}$$
(28)
$$\begin{aligned} {\varvec{\upbeta }}= & {} \mathbf{M}_{\mathbf{d}}^{-1}{} \mathbf{K}_{\mathbf{d}} \end{aligned}$$
(29)
$$\begin{aligned} {\varvec{\upgamma }}= & {} \mathbf{M}_{\mathbf{d}}^{-1}{} \mathbf{K}_{\mathbf{v}} \end{aligned}$$
(30)

The state-space equation in the tracking space is obtained using (27) as

$$\begin{aligned} {\dot{\mathbf{Z}}}=\mathbf{AZ}+\mathbf{B}w \end{aligned}$$
(31)

where

$$\begin{aligned} \mathbf{A}= & {} \left[ {{\begin{array}{cc} 0&{} 1 \\ {-{{\varvec{\upbeta }}}}&{} {-{{\varvec{\upalpha }}}} \\ \end{array} }} \right] , \mathbf{B}=\left[ {{\begin{array}{c} 0 \\ 1 \\ \end{array} }} \right] , \mathbf{Z}=\left[ {{\begin{array}{l} \mathbf{e} \\ {{\dot{\mathbf{e}}}} \\ \end{array} }} \right] ,\nonumber \\ w= & {} \mathbf{M}_\mathbf{d}^{-1} \mathbf{F}_\mathbf{h} +{{\varvec{\upgamma }}}(\mathbf{y}^{\mathbf{T}}-{\hat{{\mathbf{y}}}}^{\mathbf{T}}){{\varvec{\uppsi }}}(x_1 ,x_2 )+{{\varvec{\upgamma }}}\varepsilon \end{aligned}$$
(32)

A positive definite function V is suggested as

$$\begin{aligned} V=\frac{1}{2}Z^\mathrm{T}{} \mathbf{P}Z+\frac{{{\varvec{\upgamma }}}}{2\alpha }\left( {\mathbf{y}^\mathrm{T}-{\hat{{\mathbf{y}}}}^\mathrm{T}} \right) \left( {\mathbf{y}-{ \hat{{\mathbf{y}}}}} \right) \end{aligned}$$
(33)

where the constant \(\alpha >0\), \(\mathbf{P}\) and \(\mathbf{Q}\) are the unique symmetric, positive definite matrices satisfying the matrix Lyapunov equation

$$\begin{aligned} \mathbf{A}^\mathrm{T}{} \mathbf{P}+\mathbf{PA}=-\mathbf{Q} \end{aligned}$$
(34)

Then, \(\dot{V}\) is calculated using (31)–(33) as

$$\begin{aligned} \dot{V}= & {} -\frac{1}{2}{} \mathbf{Z}^\mathrm{T}{} \mathbf{QZ}+\mathbf{Z}^\mathrm{T}{} \mathbf{PB}\left( \mathbf{M}_\mathbf{d}^{-1} \mathbf{F}_\mathbf{h} +{{\varvec{\upgamma }}}(\mathbf{y}^{\mathbf{T}}-{\hat{{\mathbf{y}}}}^{\mathbf{T}}){{\varvec{\uppsi }}}(x_1 ,x_2 )\right. \nonumber \\&\left. +{{\varvec{\upgamma }} }\varepsilon \right) -\frac{{{\varvec{\upgamma }}}}{\alpha }\left( {\mathbf{y}^\mathrm{T}-{\hat{{\mathbf{y}}}}^\mathrm{T}} \right) {\dot{\hat{{\mathbf{y}}}}} \end{aligned}$$
(35)
$$\begin{aligned} \dot{V}= & {} -\frac{1}{2}{} \mathbf{Z}^\mathrm{T}{} \mathbf{QZ}+\mathbf{Z}^\mathrm{T}{} \mathbf{PB}\left( {\mathbf{M}_\mathbf{d}^{-1} \mathbf{F}_\mathbf{h} +{{\varvec{\upgamma }}}\varepsilon } \right) \nonumber \\&+(\mathbf{y}^{\mathbf{T}}-{\hat{{\mathbf{y}}}}^{\mathbf{T}})\left( {\mathbf{Z}^\mathrm{T}{\mathbf{PB}}{\varvec{\upgamma }} {\varvec{\uppsi }} (x_1 ,x_2 )-\frac{{{\varvec{\upgamma }}}}{\alpha }{\dot{\hat{{\mathbf{y}}}}}} \right) \end{aligned}$$
(36)

If the adaptive law is given by

$$\begin{aligned} {\dot{\hat{{\mathbf{y}}}}}=\alpha \mathbf{Z}^\mathrm{T}{\mathbf{PB}}{\varvec{\uppsi }}(x_1 ,x_2 ) \end{aligned}$$
(37)

we have

$$\begin{aligned} \dot{V}=-\frac{1}{2}{} \mathbf{Z}^\mathrm{T}{} \mathbf{QZ}+\mathbf{Z}^\mathrm{T}{} \mathbf{PB}\left( {\mathbf{M}_\mathbf{d}^{-1} \mathbf{F}_\mathbf{h} +{{\varvec{\upgamma }}}\varepsilon } \right) \end{aligned}$$
(38)

The tracking error reduces if \(\dot{V}<0\). Thus, satisfying \(\dot{V}<0\) results in

$$\begin{aligned} \mathbf{Z}^\mathrm{T}{} \mathbf{PB}\left( {\mathbf{M}_\mathbf{d}^{-1} \mathbf{F}_\mathbf{h} +{{\varvec{\upgamma }}}\varepsilon } \right) <\frac{1}{2}\mathbf{Z}^\mathrm{T}{} \mathbf{QZ} \end{aligned}$$
(39)

One can imply \(\lambda _{\min } (\mathbf{Q})\left\| \mathbf{Z} \right\| ^{2}\le \mathbf{Z}^\mathrm{T}{} \mathbf{QZ}\le \lambda _{\max } (\mathbf{Q})\left\| \mathbf{Z} \right\| ^{2}\) where \(\lambda _{\min } (\mathbf{Q})\) and \(\lambda _{\max } (\mathbf{Q})\) are the minimum and maximum eigenvalues of \(\mathbf{Q}\), respectively. To satisfy \(\dot{V}<0\) it is sufficient that

$$\begin{aligned} 2\left\| {\mathbf{PB}} \right\| .\left| {\mathbf{M}_\mathbf{d}^{-1} \mathbf{F}_\mathbf{h} +{{\varvec{\upgamma }}}\varepsilon } \right| /\lambda _{\min } (\mathbf{Q})<\left\| \mathbf{Z} \right\| \end{aligned}$$
(40)

The tracking error becomes small in the area defined by (40). As a result, the tracking error ultimately enters into the ball with the radius of \(2\left\| {\mathbf{PB}} \right\| .\left| {\mathbf{M}_\mathbf{d}^{-1} \mathbf{F}_\mathbf{h} +{{\varvec{\upgamma }}}\varepsilon } \right| /\lambda _{\min } (\mathbf{Q})\).

Therefore, \(\mathbf{Z}\) is bounded where \(\mathbf{Z}\) is expressed as, \(\mathbf{e}\) and \({\dot{\mathbf{e}}}\) as expressed by (31).

Result 2

The variables \(\mathbf{e}\) and \({\dot{\mathbf{e}}}\) are bounded.

Proposed control is shown in Fig. 8.

2.2.2 Stability analysis

A proof for the boundedness of state variables is given by stability analysis. In order to analyze the stability, the following assumptions are made:

Assumption 1

The desired trajectory in the task-space \(\mathbf{x}_\mathbf{d}\) must be smooth in the sense that \(\mathbf{x}_\mathbf{d}\) and its derivatives up to a necessary order are available and all uniformly bounded [37].

In order to avoid singularity, some constrictions are used for the joint variables. This means that the proposed workspace is nonsingular. Therefore, the following assumption is made.

Assumption 2

There is no singularity in the workspace or \(\det (\mathbf{J}(\mathbf{q}))\ne 0\).

Table 2 The parameters of the robot and patient
Full size table

Assumption 3

The rehabilitation robot has revolute joints. This follows the Jacobian matrix of the robot \(\mathbf{J}(\mathbf{q})\) is bounded. A robot which has only revolute joints, the Jacobian matrix \(\mathbf{J}(\mathbf{q})\) consists of bounded sinusoid functions.

Result 3

The Jacobian matrix \(\mathbf{J}(\mathbf{q})\) is bounded.

Using Assumption 2 and Result 2 implies that

Result 4

\(\mathbf{J}(\mathbf{q})^{-1}\) is bounded.

The desired trajectory \(\mathbf{X}_\mathbf{d}\) and its derivative \({\dot{\mathbf{X}}}_\mathbf{d}\) are assumed bounded. From result 1 Since \({\varvec{e}}={\varvec{X}}_{\varvec{d}} -{\varvec{X}}\) and \({\dot{{\varvec{ e}}}=\dot{{\varvec{X}}}}_{{\varvec{d}}} -\dot{{{\varvec{X}}}}\), thus boundedness of \(\mathbf{e}\) and \({\dot{\mathbf{e}}}\) follows boundedness of \(\mathbf{x}\) and \({\dot{\mathbf{x}}}\).

Result 5

The variables \(\mathbf{x}\), \({\dot{\mathbf{x}}}\) and \({\ddot{\mathbf{x}}}\) are bounded.

When the adaptive rule (37) is used for the adaptive fuzzy estimation so the parameters \({\hat{{\mathbf{y}}}}\) is bounded.

Result 6

The variable \({\hat{{\mathbf{y}}}}\) is bounded.

In (22) parameters \({\hat{{\mathbf{y}}}}\) and \({{\varvec{\psi }}}\) is bounded as result 1 and result 6 therefore

Result 7

The variable \({\hat{{{\varvec{\upeta }}}}}\) is bounded.

In (15) nominal parameters \({\hat{{\mathbf{R}}}}\), \({\hat{{\mathbf{K}}}}\) and \({\hat{{\mathbf{J}}}}\) are bounded. The matrices \(\mathbf{M}_\mathbf{d} (t)\), \(\mathbf{D}_\mathbf{d} (t)\) and \(\mathbf{K}_\mathbf{d} (t)\) are diagonal bounded positive matrices. From result 1, result 4 and result 7 implies that

Result 8

The variable \(\mathbf{v}\) is bounded.

According to (10), the rehabilitation robot is driven by electric motors under bounded voltages. According to a proof given by [34], the current, time derivative of current, and velocity of the motor are bounded. As result,

Result 9

\(\mathbf{I}_\mathbf{a}\), \({\dot{\mathbf{I}}}_\mathbf{a}\) and \({\dot{\mathbf{q}}}\) are bounded.

The robotic system is stable, since all system states \(\mathbf{q}\), \({\dot{\mathbf{q}}}\) and \(\mathbf{I}_\mathbf{a}\) are bounded.

3 Results

In this study, at the first, the proposed Impedance Voltage Control (IVC) strategy for a lower-limb rehabilitation robot in (11) is compared with the commonly used Impedance Torque Control (ITC) strategy presented by [1]. In this stage, it has been assumed that the exact value of model’s parameters expressed in (11) are known. This comparison shows the superiority of voltage-based control strategy. In the next stage, to present the performance of control systems in the presence of uncertainties, the proposed robust impedance voltage control (RIVC) strategy compared with the IVC.

Parameters of rehabilitation robotic system and the patient, which are obtained from Solidworks are given in Table 2 where \(m_\mathrm{r}\) is the mass of link, \(m_\mathrm{h}\) is the mass of the patient’s leg, \(l_\mathrm{r}\) is the length of link, \(l_\mathrm{p}\) is the length of the patient’s leg, and \(r_\mathrm{c} =[x_\mathrm{c} ,y_\mathrm{c} ,z_\mathrm{c} ]\) is the center of mass for the link.

Table 3 The electric motor parameters
Full size table

The inertia tensor in the center of mass is expressed as

$$\begin{aligned} I=\left( {{\begin{array}{ccc} {I_{xx} }&{} \quad {I_{xy} }&{} \quad {I_{xz} } \\ {I_{yx} }&{} \quad {I_{yy} }&{} \quad {I_{yz} } \\ {I_{zx} }&{} \quad {I_{zy} }&{} \quad {I_{zz} } \\ \end{array} }} \right) \end{aligned}$$
(41)

Parameters of the motor are given in Table 3. The parametric uncertainties \(\hat{{k}}_b\), \(\hat{{r}}\), and \(\hat{{R}}\) are assumed to be 80% of their real values which introduced in Table 3. The estimate of the Jacobian is given also as \({\hat{{\mathbf{J}}}}(\mathbf{q})=0.8\mathbf{J}(\mathbf{q})\). Depends on the type of exercise, the impedance parameters are selected. In order to have a comparison with the presented impedance control approach given by [6], the same impedance parameters \(M_\mathrm{d} =4\), \(D_\mathrm{d} =2\), \(K_\mathrm{d} =100\) has been set.

Isometric exercise For the tracking control, the desired trajectory should be sufficiently smooth such that all its derivatives up to the required order are bounded. In addition, tracking the desired trajectory in the given exercise should be suitable for the patient. The desired trajectory for the isometric exercise starts from zero and goes up to \(80{^{\circ }}\) smoothly, then stops for 10 s, and finally a desired force is applied to the patient. The force is determined by a physiotherapist. In this type of exercise, limb moves to the desired angle without applying any force by the patient. After that, the desired force is applied to the patient while the patient resists against movement. The force that applied to the patient has been selected \(F_\mathrm{d} =20\) N. Simulation results show a comparison between the proposed IVC and ITC in Fig. 9. The IVC tracks the desired trajectory better than ITC. Furthermore, Fig. 9 shows that the IVC can converge the position of robot quickly to the constant value and the controller is able to prevent oscillation of the robot’s joint.

Fig. 9
figure 9

Tracking performances of ITC and IVC for isometric exercise

Full size image
Fig. 10
figure 10

Tracking performances of RIVC and IVC in isometric exercise in the presence of uncertainties

Full size image
Fig. 11
figure 11

A comparison between ITC and IVC for isometric exercise (knee flexion-extension)

Full size image
Fig. 12
figure 12

A comparison between RIVC and IVC for isometric exercise in the presence of uncertainties

Full size image
Fig. 13
figure 13

Voltages and currents (the purple line is for uncertainty)

Full size image

The proposed RIVC and the proposed IVC are compared in Fig. 10. Figure 10 illustrates that both controllers are same in the term of tracking trajectory. The impedance control can be evaluated according to how well the impedance law is performed; therefore, to have complete comparison between controllers the applied force to the patient must be shown. The applied force to the patient is shown in Figs. 11 and 12. The art of IVC has been shown in force applied to the patient, where the ITC shows a force error with a maximum value of 6 N, the IVC shows an insignificant error. In the presence of uncertainties, the IVC and RIVC show a force error with a maximum value of 3.1 and 2.2 N, respectively. The motor voltage and motor current of robot for isometric exercise are shown in Fig.13. The voltage and currents of controllers are in valid ranges without sudden changes. Finally, to compare and contrast the performance of controllers, integral of absolute errors are shown in Table 4.

4 Discussion

In this paper, a sEMG-based robust impedance control strategy was proposed for controlling rehabilitation robot. The previous impedance control approaches were developed based on the torque control strategy, whereas the proposed impedance control is based on the voltage control strategy. In comparison with the torque-based control approaches, the proposed approach is free of manipulator dynamics and it is not dependent on the model of patient’s lower-limb dynamics. Therefore, it is simpler, more robust and requires less computation. To implement our sEMG-based robust impedance control strategy, a 1-DOF lower-limb rehabilitation robot was designed. In training phase, the sEMG signals along with force sensor data, as well as kinematic data were collected and used to train the ANN. The trained ANN used sEMG signals as well as kinematic data, angle and angular velocity as input to provide online estimation of the limb force. Experimental results showed that the ANN can effectively estimate the exerted force. Also, a novel adaptive fuzzy system was proposed to estimate uncertainties in the control approach. Simulation results show that the adaptive fuzzy system can model the uncertainty as a nonlinear function of the system states and is efficient in overcoming uncertainty and reducing the error. The adaptive fuzzy system has an advantage that does not need any additional feedback to estimate the uncertainty. Moreover, it can overcome the noises in the measured acceleration. Finally, the control approach was verified by a stability analysis. Results presented in this paper, indicate the superiority of the proposed control approach over a torque-based impedance control approach for isometric exercises.

Table 4 Integral of trajectory tracking errors in the isometric exercise
Full size table