An effective dynamic immune optimization control for the wastewater treatment process

Abstract

To resolve the conflict between multiple performance indicators in the complicated wastewater treatment process (WWTP), an effective optimization control scheme based on a dynamic multi-objective immune system (DMOIA-OC) is designed. A dynamic optimization control scheme is first developed in which the control process is divided into a dynamic layer and a tracking control layer. Based on the analysis of the WWTP performance, the energy consumption and effluent quality models are next established adaptively in response to the environment by an optimization layer. An adaptive dynamic immune optimization algorithm is then proposed to optimize the complex and conflicting performance indicators. In addition, a suitable preferred solution is selected from the numerous Pareto solutions to obtain the best set of values for the dissolved oxygen and nitrate nitrogen. Finally, the solution is evaluated on the benchmark simulation platform (BSM1). The results show that the DMOIA-OC method can solve the complex optimization problem for multiple performance indicators in WWTPs and has a competitive advantage in its control effect.

Introduction

With the continuous advancement of the economy and living standards, water consumption and wastewater supply have increased dramatically. Many wastewater treatment plants have been built to improve the state of the environment (Luna et al. 2016; Löwenberg et al. 2014). However, the typical nonlinear, multi-variable, unstable, and time-varying characteristics of wastewater treatment process (WWTPs) have resulted in for their operation and management. Energy conservation and emission reduction are two major challenges under these stricter water quality standards (Büyüközkan et al. 2021; Li et al. 2021a, 2021b; Shiek et al. 2021; Busch et al. 2013; Liu et al. 2018).

To design effective control strategies, extensive research has been conducted on process control for WWTPs (Liu et al. 2014; Cheng 2014). The focus over the past decades has been on meeting water quality standards. For example, Guerrero et al. proposed a method-based optimization method to improve the performance of control systems (Guerrero et al. 2011; Han et al. 2021). A single cost function was used to evaluate the performance of fixed and time-varying settings. The results show that the costs can be effectively reduced while improving the water quality. A generalized simplified gradient method was used to design an optimal WWTP control strategy that can effectively reduce the annual total and operation costs (Shorbaghy et al. 2011). In addition, Xie et al. developed an optimal control strategy based on an adaptive genetic algorithm to optimize the fixed residence time and the internal circulation and thereby obtain the optimal operating variables for improving the quality of the output water (Xie et al. 2011; Li et al. 2021a, 2021b; Han et al. 2021). These strategies can achieve stable WWTP operation and thus meet water quality standards (Han et al. 2021). However, the coupled relationship between energy consumption (EC) and effluent quality (EQ) has rarely been studied (Santin et al. 2015).

Multi-objective optimization control is currently a valued approach for solving the trade-off between multiple conflicting objectives (such as the EQ, EC, and operation stability in WWTPs; Han et al. 2014; Li et al. 2013). Vega et al. proposed a hierarchical optimal control strategy for WWTPs to evaluate the improvements in the EC and EQ (Li et al. 2021a, 2021b; Vega et al. 2014). They showed that this strategy can ensure the satisfaction of EQ standards and reduce costs. In addition, the ant colony algorithm has been used to better optimize the EC and ensure system stability (Schlüter et al. 2009). Although the above methods have resulted in effective improvements, the essential weight factors for transforming the multi-objective functions into single-objective problems are difficult to obtain (Cai et al. 2016).

To fundamentally resolve the conflict between the EC and EQ, Guerrero et al. proposed a multi-criteria optimal control strategy in which an appropriately controlled variable is selected as the set point and a set of solutions is generated with a Pareto optimal distribution to achieve energy-savings and emission reduction (Guerrero et al. 2012; Han et al. 2021). They proved that the control effect can be improved by optimizing the water quality, cost, and microbial action. In addition, an interactive multi-objective optimization strategy was designed to optimize several objective functions simultaneously (Hakanen et al. 2013; Han et al. 2021). This method combines control systems with interactive multi-objective optimization software to enable decision-makers to understand the interdependence between conflicting objective functions. Other multi-objective optimization control strategies were introduced in Dominic et al. (2015) and Yetilmezsoy et al. (2012). However, it is difficult to obtain reliable optimal solutions for most of these strategies.

In recent decades, intelligent optimization algorithms (Chakraborty et al. 2011; Hu et al. 2016) with good global searchability have been applied. A multi-objective genetic algorithm (MOGA) and a sensitivity analysis scheme were designed for WWTP control strategies and resulted in improved EC and EQ (Beraud et al. 2008). To further improve the MOGA convergence, a non-dominant sequencing MOGA based on an elite strategy was designed to handle the conflicting multi-objective problem in WWTPs, so that the control performance is improved while ensuring that EQ meets standards (Iqbal et al. 2009). At the same time, other MOEAs-based optimization control strategies have been successfully applied in WWTPs to generate reliable multi-objective optimization solutions with improved performance (Wang et al. 2014; Tabatabaei et al. 2015). However, different wastewater treatment plants have different cost functions and the above optimal control strategies are inevitably unable to match the actual WWTPs. A data-driven control strategy was proposed to solve the dynamic optimization of WWTPs with the support of optimized operating systems, and an adaptive multi-objective differential evolution algorithm, and an adaptive fuzzy neural network control system were also presented (Li et al. 2021a, 2021b; Qiao et al. 2018). The stability and EC of the resulting control system are better than those of the traditional control method. Sweetapple et al. developed an optimal control strategy using the non-dominated sorting algorithm II (NSGA-II) to obtain the optimal settings for the activated sludge WWTPs (Sweetapple et al. 2014). This strategy can reduce greenhouse gas emissions and operating costs (Han et al. 2021). In addition, a dynamic multi-objective optimization strategy was presented (Hreiz et al. 2015) in which precise bottom-level modelling and the NSGAII algorithm are used to optimize the relationship between the EC and EQ. However, the above methods still have the following shortcomings: (1) WWTPs are highly nonlinear. Because of the rapid fluctuations in the water inflow, limited storage space, and other difficulties, it is difficult to obtain accurate EC and EQ models in real time (Liu et al. 2019). (2) WWTPs are complex dynamic systems, with multiple goals that change over time (Li et al. 2021a, 2021b). Whether the optimal settings for the nitrate nitrogen (S_NO) and dissolved oxygen (S_O) are real-time variables or not is directly related to the EC and EQ. This presents an additional challenge to the multi-objective optimization algorithm which changes dynamically over time. (3) In WWTPs, the traditional proportional integral controller (PID) cannot sufficiently compensate for interference caused by interactions in large circuits. Therefore, the selection of an appropriate controller and the stable and accurate tracking of the optimal settings, which change with the environment, are significant issues.

To overcome the nonlinearity of the WWTP, mechanism models for the EC and EQ have been studied. However, because the parameters in these models are fixed, they cannot adapt to the operating conditions of the WWTP. Qiao et al. used a radial basis network to predict the EC and EQ and obtained the objective function for multi-objective optimization (Han et al. 2018). Hang et al. established a model relating the EC, EQ, and variables in the process using the adaptive regression kernel function method, and achieved a good prediction accuracy. However, because the input water composition and flow rate vary with time in WWTPs, prediction models with fixed structures cannot meet the requirements for high accuracy predictions of the EC and EQ (Li et al. 2021a, 2021b). In this study, a fast online self-organizing fuzzy neural network (ILM-SVDFNN) based on SVD is constructed by analysing the WWTP operation characteristics and data and combined with the improved LM algorithm. The single-sided Jacobi transformation is used to perform singular value decomposition (Qiao et al. 2017), and the rule layer neurons are grown and trimmed based on the size of the singular values of the output matrix from the rule layer. It is used to build the EC and EQ models.

To obtain the optimal setting of S_O and S_NO, Sina et al. proposed a scheme-based optimization method and defined two types of performance evaluation criteria to assess EC in various situations (Han et al. 2021). However, because the optimization results depend on the quality of the scheme, there are some limitations to this method. To overcome these limitations, Han et al. used the multi-objective particle swarm optimization algorithm to optimize the objective function and obtain the optimal settings. To obtain the optimal result with good convergence, an optimization algorithm for the multi-objective hybrid particle swarm was designed to optimize the two conflicting objectives of the EC and EQ (Zhou et al. 2017). However, because the biochemical reactions, input water components, and flow rates in WWTPs vary with time, the dynamic EC and EQ problems cannot be solved effectively by the above methods. Han et al. therefore proposed a dynamic multi-objective particle swarm optimization controller (DMOPSO-OC) and proved that the control performance can be improved while satisfying the requirements of multiple conflicting targets (Han et al. 2019). However, the uneven individual distribution in target space is a disadvantage. The accurate prediction of the location of the Pareto front in changing environments remains a challenge for the precise and dynamic determination of S_O and S_NO.

In addition, an adaptive fuzzy neural network method is used to improve the accuracy, stability, and adaptability of bottom control in WWTPs (Qiao et al. 2018; Li et al. 2021a, 2021b). A fuzzy neural network controller (FNNC) based on the second-order Begg-Marquart (L-M) approach was used to track the settings of S_O and S_NO (Han et al. 2018). WWTPs are time-varying systems in which the flow and composition of the input water are constantly changing. Therefore, a recursive fuzzy neural network with a time-varying structure is required to adapt to changes in the operating conditions.

In summary, a WWTP control strategy based on adaptive dynamic immune optimization (DMOIA-OC) is proposed to optimize the control of WWTPs. Compared to the existing control strategies, the innovations and advantages of DMOIA-OC are as follows: (1) an adaptive dynamic optimal control system for WWTPs that can reduce the EC while meeting EQ standards is designed. A fast online self-organizing fuzzy neural network based on SVD (ILM-SVDFNN) (Han et al. 2021) is constructed to model the EC and EQ of WWTPs in complex dynamic environments (Qiao et al. 2017). (2) To obtain the optimal settings for S_O and S_NO in real time, an adaptive dynamic immunization algorithm is proposed. (3) A self-organizing recursive fuzzy neural network controller is used to track the optimal settings for S_O and S_NO. To verify the effectiveness of DMOIA-OC, all the algorithms were verified using the international benchmark simulation model platform (BSM1) (Han et al. 2021). The results show that even when the flow and concentration change in time, the proposed dynamic immune optimization control method can significantly improve the control performance of the WWTP by reducing the EC while improving the outflow water quality.

The outline of the paper is as follows: “Problem formulation” describes the characteristics of the dynamic process in WWTPs. In “Framework of proposed DMOIA-OC”, the dynamic optimization control system comprising the objective function design, dynamic immune optimization algorithm, and tracking controller is discussed in detail. The simulation results and experiments to verify the effectiveness of the proposed DMOIA-OC are presented in “DMOIA-based optimization layer design”. “SORFNN control” provides a summary of the study.

Problem formulation

Dynamic characteristics of WWTPs

WWTPs are dynamic systems that are affected by different physical and biological phenomena (Han et al. 2021). They have the following characteristics: the biochemical reaction cycle in WWTPs is long, complex, and susceptible to external factors (such as the temperature and pH), and the state changes with time (Han et al. 2021). The microbial population faces indeterminate living conditions and reaction rules. The composition and flow in the process vary with time, and it is difficult to determine the pollutant content and quantity (Han et al. 2019).

In recent years, increasingly stringent environmental laws and regulations have resulted in large improvements in the operation of WWTPs. At the same time, an economic perspective, it is extremely important to reduce operation costs. However, because of the potential interactions and complex biochemical reactions that may occur, a large number of design parameters, and a variety of complex objectives (EQ, operating costs, etc.), the formulation of efficient optimal control strategies that ensure stable operation and the effective reduction of operating costs while maintaining effluent water quality is an urgent problem that remains to be solved. Therefore, the design of a dynamic optimization algorithm to optimize multiple conflicting objectives and the use of an optimal controller for stable tracking control are the basic requirements for improving the control performance of WWTPs.

Optimal control problem

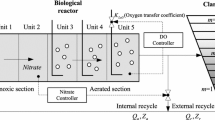
Because the inflow flow and composition in WWTPs change with time (Li et al. 2021a, 2021b), traditional models for EQ, pumping, and aeration energy consumption cannot accurately reflect the dynamic process in WWTPs. Therefore, a self-organizing fuzzy neural network is employed in which the structure and parameters can be dynamically adjusted online to determine the objective functions (Qiao et al. 2017; Li et al. 2021a, 2021b). The main input and process variables (EC, EQ, and PE) are analysed, and the soft sensing model is established based on the operational data and dynamic characteristics of the WWTP (Li et al. 2021a, 2021b). The relevant variables are the solid suspension concentration (SS), chemical oxygen demand (COD), nitrate-nitrogen concentration (S_NO), Kelvin nitrogen concentration (S_Nkj), biochemical oxygen demand on day 5 (BOD5), oxygen conversion coefficient in unit 5 (K_La5), and internal return flow (Q_a) (Han et al. 2019; Li et al. 2021a, 2021b). The optimal objective function at time t is:

$$\begin{gathered} \min \;{\mathbf{F}}\left( {f_{1} \left( {{\mathbf{X}}^{ * } ,t} \right),f_{2} \left( {{\mathbf{X}}^{ * } ,t} \right),f_{3} \left( {{\mathbf{X}}^{ * } ,t} \right)} \right)^{{\mathbf{T}}} \;\; \hfill \\ t = 1,2, \cdots \in T \hfill \\ \end{gathered}$$

(1)

$${\mathbf{X}}^{ * } = \left( {x_{1} ,x_{2} } \right)$$

(2)

where F is the objective functions vector. $f_{1} \left( {{\mathbf{X}}^{ * } ,t} \right)$, $f_{2} \left( {{\mathbf{X}}^{ * } ,t} \right)$, and $f_{3} \left( {{\mathbf{X}}^{ * } ,t} \right)$ are the AE, PE, and EQ model at time t, respectively (Li et al. 2021a, 2021b). ${\mathbf{X}}^{ * }$ is the decision vector, and x₁ and x₂ are the S_O and S_NO, respectively (Han et al. 2019; Li et al. 2021a, 2021b).

Figure 1 shows the curves of the three conflicting performance indicators comprising the AE, PE, and EQ. They are involved in controlling the WWTP through NSAGII. It can be seen that the AE, PE, and EQ have obvious nonlinear and time-varying characteristics and that there are numerous locally optimal solutions in the target space. AE and PE fluctuated greatly, which results in a complex and variable Pareto front. Therefore, additional choosing the appropriate optimization control method and obtaining precise optimized settings are proposed. The following aspects of the WTTP optimization problem are considered in depth: (1) time-varying objective function: the objective function model should be accurately and quickly established to provide a basis for the optimization process; (2) optimization of complex problems: appropriate optimization methods should be chosen to effectively coordinate the solution of complex optimization problems dynamically to achieve optimal control; (3) dissolved oxygen and nitrate nitrogen set points: the best Pareto solution should be chosen from a set of optimization results, to obtain the instantaneous optimal set point to ensure optimal control; (4) computing resources: the optimized solutions should be quickly and effectively obtained the use of computing resources reduced, and the control process made simple and efficient of the control process.

Fig. 1

The optimized control based on NSGAII. a AE value, b PE value, c EQ value

Framework of proposed DMOIA-OC

In WWTPs, the AE, PE, and EQ are coupled performance indices. They play a primary role in performance evaluation. Because these indices can be influenced by different process variables, a two-layer structure is used to establish different control objectives according to the dynamic response time. Figure 2 shows a diagram of the DMOIA-OC scheme, which consists of an upper-optimized layer, and a lower-controlled layer. The system realizes energy-saving and efficient operation of the WWTP through the optimization and tracking control layers, respectively (Li et al. 2021a, 2021b).

Fig. 2

Multi-objective optimal control chart of wastewater treatment

The optimization layer is mainly composed of two parts: B, the optimization objective function, and C, the dynamic optimization module. The module illustrated in Fig. 2B determines a sequence of objective function models (AE, PE, and EQ) that are optimized online. The dynamic optimization algorithm shown in Fig. 2C provides the best optimal solutions (the sets of S_O and S_NO settings). These sets ensure that the EC is minimized while meeting the water quality standards. The lower layer, which is shown in Fig. 2D, is mainly used to track the set values of S_O and S_NO. The self-organizing recursive fuzzy neural network (SORFNN) controller can meet the requirements for stable operation (Qiao et al. 2017). The detailed design of each control layer is presented in the following sections.

DMOIA-based optimization layer design

Owing to the complex biochemical reactions in WWTPs, a self-organizing FNN with adaptive parameters is used to calculate the time-varying objective function model for the EC and water quality to accurately obtain the mechanism model of the dynamic process. In addition, an adaptive immune optimization algorithm with improved convergence and distribution is designed to obtain the best set value of S_O and S_NO in real time, so that the optimal control target for the underlying tracking control is achieved.

Optimization objectives

Owing the strong nonlinearity and time-varying characteristics of WWTPs, traditional fixed-parameter mechanism models are insufficient for modelling the dynamic process in WWTPs. For this reason, the process variables related to the EC and EQ are first analysed based on the operation characteristics and data of WWTP.

Equations (4) and (5) show that the EC is affected by S_O, S_NO, MLSS, and other variables, while EQ is mainly related to S_O, S_NO, SS, S_NH, and other variables (Li et al. 2021a, 2021b). Therefore, S_O, S_NO, MLSS, and S_NH are selected as the model input variables and EC and EQ as the output variables because the mixed liquor solid suspended concentration (MLSS) can be measured online more easily than the SS. The relationship between the input variables, and EC and EQ is then modelled using a self-organizing fuzzy neural network (SOFNN) as follows (Qiao et al. 2017):

Step 1: Calculate the output membership value of the second layer membership function layer.

$$\varphi_{ij} = e^{{ - \frac{{\left( {x_{i} - c_{ij} } \right)^{2} }}{{\sigma_{ij}^{2} }}}} ,\;\;\;j = 1,2, \cdots ,m$$

(3)

where c_ij and σ_ij are the centre and width of the Gauss function of the jth neuron in the 2nd layer corresponding to the 1st layer of the jth neuron, and φ_ij is the output of the neuron in the corresponding membership function layer, and m is the number of neurons in regular layer.

Step 2: Operation Π and normalization are performed on the layer 2 neurons.

$$\begin{array}{*{20}c} {h_{j} = {{v_{j} } \mathord{\left/ {\vphantom {{v_{j} } {\sum\limits_{j = 1}^{m} {v_{j} } }}} \right. \kern-\nulldelimiterspace} {\sum\limits_{j = 1}^{m} {v_{j} } }} = {{e^{{ - \sum\limits_{i = 1}^{n} {\frac{{\left( {x_{i} - c_{ij} } \right)^{2} }}{{\sigma_{ij}^{2} }}} }} } \mathord{\left/ {\vphantom {{e^{{ - \sum\limits_{i = 1}^{n} {\frac{{\left( {x_{i} - c_{ij} } \right)^{2} }}{{\sigma_{ij}^{2} }}} }} } {\sum\limits_{j = 1}^{m} {e^{{ - \sum\limits_{i = 1}^{n} {\frac{{\left( {x_{i} - c_{ij} } \right)^{2} }}{{\sigma_{ij}^{2} }}} }} } }}} \right. \kern-\nulldelimiterspace} {\sum\limits_{j = 1}^{m} {e^{{ - \sum\limits_{i = 1}^{n} {\frac{{\left( {x_{i} - c_{ij} } \right)^{2} }}{{\sigma_{ij}^{2} }}} }} } }}} \\ {v_{j} = \prod\limits_{i = 1}^{n} {\varphi_{ij} } = e^{{ - \sum\limits_{i = 1}^{n} {\frac{{\left( {x_{i} - c_{ij} } \right)^{2} }}{{\sigma_{ij}^{2} }}} }} } \\ \end{array}$$

(4)

where v_j and h_j are the jth neuron output and normalized output, and n is the number of input neurons in the first input layer. ω_j is the connection weight between the regular layer and the output layer; the output of the neuron y is:

$$y = \sum\limits_{j = 1}^{m} {h_{j} w_{j} }$$

(5)

Step 3: Self-organizing optimization of network structure.

The main parameters that the FNN needs to learn are the connection weight ω_j between layers 3 and 4 and the centre c_ij and width σ_ij of the membership function of layer 2. An improved LM algorithm is used to realize the online learning of these parameters. Singular value decomposition (SVD) (Qiao et al. 2017) is used in the output matrix of the FNN rule layer. The size of the singular value is compared and the root mean square error of the training set is combined with the network learning process to realize the growth and pruning of the rule layer neurons for the online optimization of the network structure. The indexes for evaluating the growth and pruning and the root mean square error are defined as follows:

$$\begin{array}{*{20}c} {I_{g} = {{\max \left( \xi \right)} \mathord{\left/ {\vphantom {{\max \left( \xi \right)} {\sum\limits_{s = 1}^{{n_{s} }} {\xi_{s} } }}} \right. \kern-\nulldelimiterspace} {\sum\limits_{s = 1}^{{n_{s} }} {\xi_{s} } }}} \\ {I_{d} = {{\sum\limits_{s = 1}^{d} {\xi_{s} } } \mathord{\left/ {\vphantom {{\sum\limits_{s = 1}^{d} {\xi_{s} } } {\sum\limits_{s = 1}^{{n_{s} }} {\xi_{s} } }}} \right. \kern-\nulldelimiterspace} {\sum\limits_{s = 1}^{{n_{s} }} {\xi_{s} } }}} \\ \end{array}$$

(6)

$$E\left( {\Theta \left( t \right)} \right) = \sqrt {\frac{1}{{S_{a} }}\sum\limits_{{S_{a} = 1}}^{{S_{a} }} {\left( {y_{d}^{{S_{a} }} \left( t \right) - y^{{S_{a} }} \left( t \right)} \right)^{2} } }$$

(7)

where I_g is the growth indicator, I_d is the pruning indicator, singular value vector ξ is arranged from small to large, I_d is the ratio of the sum of the current d smaller singular values to all singular values, n_s is the number of current singular values, S_a is the size of sample, $y_{d}^{{S_{a} }}$ is the expected output, and $y^{{S_{a} }}$ is the actual network output. When E(Θ(t)) > E(Θ(t − 1)), and I_g > I_gth (I_gth is the preset threshold for growth), the neuron g with the largest current singular value is split to adjust the network structure to improve performance. When E(Θ(t)) < E(Θ(t − 1)) and I_d < I_dth (I_dth is the preset pruning threshold), the neurons s (s = 1, 2, …, d) corresponding to the current d smaller singular values will be deleted.

In the EC and EQ models, which are based on an online self-organizing fuzzy neural network (Qiao et al. 2017), not only can the adjust parameters be adjusted adaptively based on the error between the actual and expected outputs, but the self-organizing network structure can also be adjusted according to the root mean square error and the growth, and pruning evaluation indexes. Improving the network modeling speed, prediction accuracy, and ability is of great importance in the real-time establishment of the EC and EQ models for the WWTP.

Dynamic optimization algorithm design

Because the real-time changes of the incoming water flow and concentration occur frequently, an adaptive dynamic immune optimization algorithm (DMOIA) is designed to obtain the dynamically and adaptively changed S_O and S_NO setting values. To implement the DMOIA, the optimization problem is solved on representative individuals with good diversity and distribution when a change in the environment is detected. An efficient elite selection strategy based on a uniform distribution is proposed to solve the optimization problem. In this strategy, the number of representative individuals g is first determined as $g = \left\lceil {g_{1} + \Phi \left( t \right) * \left( {g_{2} - g_{1} } \right)} \right\rceil$, where g₁ and g₂ = 9, g₁ and g₂ the upper and lower limits of g, take the respective values of 4 and 9, and g depends on the severity of the environmental change, ɸ(t).

$$\Phi \left( t \right) = \frac{1}{{M_{o} }}\frac{1}{{N_{o} }}\sum\limits_{j = 1}^{{M_{o} }} {\sum\limits_{i = 1}^{{N_{o} }} {\left| {f_{j}^{\prime } \left( {A_{i} } \right) - \varphi_{j} \left( q \right)} \right|} }$$

(8)

$$f_{j}^{\prime } \left( {A_{i} } \right) = \frac{{f_{j} \left( {A_{i} ,q} \right) - f_{j} \left( {A_{i} ,q - 1} \right)}}{{u_{j} \left( q \right) - l_{j} \left( q \right)}}$$

(9)

Among them, M_o = 3 is the number of objectives, N_o is the population size, and $f^{\prime}_{j} \left( {A_{i} ,q} \right)$ is the jth objective function normalized value of the ith individual in the qth iteration, and $f_{j} \left( {A_{i} } \right)$ is the objective function value (Li et al. 2021a, 2021b). $l_{j} \left( q \right)$ and $u_{j} \left( q \right)$ are the minimum and maximum values of $f_{j} \left( {A_{i} ,q} \right)$, respectively. $\varphi_{j} \left( q \right)$ is the average value of $f_{j}^{\prime }$.

$$\varphi_{j} \left( q \right) = \frac{1}{{N_{o} }}\sum\limits_{j = 1}^{{N_{o} }} {\left| {\frac{{f_{j} \left( {A_{i} ,q} \right) - f_{j} \left( {A_{i} ,q - 1} \right)}}{{u_{j} \left( q \right) - l_{j} \left( q \right)}}} \right|}$$

(10)

After the number of representative solutions is calculated, a uniform distribution mechanism is used to select the representative solutions. The population is mapped to the object space, which is equally divided into g intervals. Based on the non-dominated sort, the more representative individuals are chosen from each interval. The mechanism is described as follows:

$${\mathbf{I}} = \left( {I_{1} , \cdots ,I_{i} , \cdots ,I_{g} } \right)$$

(11)

I is the set of intervals, I_i is the ith interval, i ∈ [1, g]. Within each interval D_i, in which the number of individuals $N_{{D_{i} }} \ge 1$, the individuals in the interval are sorted according to the crowding distance and the individual with the maximum crowding distance is selected. In addition, if $N_{{D_{i} }} { = }0$, the individual closest to the interval is selected for mutation. The sets of representative individuals at time t and t − 1 are then given by:

$$R^{t} = \left\{ {r_{1}^{t} , \cdots ,r_{i}^{t} , \cdots ,r_{g}^{t} } \right\}\;and\;R^{t - 1} = \left\{ {r_{1}^{t - 1} , \cdots ,r_{i}^{t - 1} , \cdots ,r_{g}^{t - 1} } \right\}$$

(12)

$r_{i}^{t}$ and $r_{i}^{{t{ - }1}}$ are the representative individual in the ith and i-1th interval, respectively. Then, the evolution direction $\Delta r_{i}^{t}$ of the individual $r_{i}^{t}$ is:

$$\Delta r_{i}^{t} = r_{i}^{t} - r_{i}^{t - 1}$$

(13)

Second, to quickly respond to environmental change and save computing resources, the new individuals $x_{i}^{t + 1}$ are generated as:

$$x_{i}^{t + 1} = x_{i}^{t} + \Delta r_{i}^{t} + \varepsilon^{t}$$

(14)

Among them, $\varepsilon^{t} \sim N\left( {0,\theta^{t} } \right)$,$\varepsilon^{t}$ is a random value with a normal distribution of variance $\theta_{t}$ and 0. In the following, to increase the diversity and improve the convergence speed (Li et al. 2021a, 2021b), the remaining N_o-g individuals are generated by the limit optimization mutation strategy (Li et al. 2018; Li et al. 2021a, 2021b).

The proposed DMOIA framework

The proposed DMOIA algorithm is presented in Algorithm 1. First, the N_o individuals in the search space are randomly initialized (lines 2 to 4). The environmental change is detected through R_g and f(R_g) (lines 6 to 11). When a change occurs, the severity of the environmental change ɸ(t) is calculated (line 12), and the number of representative individuals g is calculated (line 13). Then, the individuals are mapped to the hyperplane and clustered (line 14); the target space is evenly divided into g intervals (line 15) (Li et al. 2021a, 2021b). The crowding distance is calculated, and the individuals with the maximum distance in each interval are selected as the representative individuals R_t (line 16). If there is no individual in an interval, the individual closest to this interval is chosen to generate new representative individuals using the limit optimization mutation strategy (Qiao et al. 2020). The evolutionary trajectories are built up from the g representative individuals (line, 17). A part of the initial population is then generated for the new environment. The remaining (N_o − N_d) individuals are randomly generated (line 18), and the two parts are combined as the initial population (line 19). If a change does not occur, the crossover and variation operations on all the individuals are used to generate the initial population (lines 20 to 24). If the stopping criterion is met, the algorithm is completed and the PS is output, and the algorithm execution goes to line 7.

The proposed DMOIA algorithm allows representative individuals to be selected with good distribution and diversity. This improves the convergence and the convergence speed, and avoids falling into the local optima. At the same time, the limit optimization mutation strategy is adopted to improve the local search and exploration ability to generate the best solution for the dynamic set values of S_O and S_NO.

Best Pareto solution

To select the appropriate preferred solution from the many good Pareto solutions, a fuzzy membership function (Zhou et al., 2017) is used for intelligent decision-making. The optimal set points for S_O and S_NO are determined as follows:

$$PR_{i}^{k} = \left\{ {\begin{array}{*{20}c} 1 & {f_{i} \left( {x_{k} } \right) \le f_{i}^{\min } } \\ {\frac{{f_{i}^{\max } - f_{i} \left( {x_{k} } \right)}}{{f_{i}^{\max } - f_{i}^{\min } }}} & {f_{i}^{\min } < f_{i} \left( {x_{k} } \right) < f_{i}^{\max } } \\ 0 & {f\left( {x_{k} } \right) \ge f_{i}^{\max } } \\ \end{array} } \right.$$

(15)

Among them, $PR_{i}^{k}$ is the satisfaction degree of the non-dominant solution x_k. $f_{i}^{\max }$ and $f_{i}^{\min }$ are the maximum and minimum values of the ith objective function f_i, respectively. $f_{i} \left( {x_{k} } \right)$ is the ith objective function value of x_k.

$$PR^{k} = \frac{{\sum\limits_{i = 1}^{3} {PR_{i}^{k} } }}{{\sum\limits_{k = 1}^{\left| \varepsilon \right|} {\sum\limits_{i = 1}^{3} {PR_{i}^{k} } } }}$$

(16)

Among them, 3 is the target number and |ε| is the number of elements in external reserve set. The selected preference solution is the solution corresponding to the maximum PR^k.

SORFNN control

Owing to the frequent changes in the flow and components in WWTPs, it is difficult to ensure that a recursive fuzzy neural network (RFNN) controller with a fixed structure can adapt to all working conditions. Therefore, a SORFNN controller (Liu et al. 2018) is adopted to track the set points for S_O and S_NO. As shown in Fig. 1D, the SORFNN controller consists of the input, RBF, recursive, TSK fuzzy, and output layers. The network structure and parameters of the RFNN are adaptively adjusted over time. To adapt to changes in the set points, the structure and parameters are adjusted as follows:

1) Growth method:

To evaluate the performance of the SORFNN, the error e(t) between the actual and predicted values of the control variable is defined as:

$$e\left( t \right) \ge E_{th}$$

(17)

where E_th is a fixed constant that needs to be determined by the system requirements. In most cases, input variables do not have perfect matching rules. Therefore, the rules for structure self-organizing are:

$$Jusm < 1,\;Jsum = \sum\limits_{j = 1}^{{N_{\sigma } }} {o_{j}^{\left[ 3 \right]} }$$

(18)

Among them, Jsum(t) is the evaluation criterion of global- approximation ability (Liu et al. 2018), $o_{j}^{\left[ 3 \right]}$ is the output of the rule layer, and N_σ is the number of centres.

In the SORFNN, each rule corresponds to a set of membership functions. The Euclidean distance between the centres of two membership functions is defined as follows:

$$\begin{array}{*{20}c} {dis\left( {i,j} \right) = \left\| {c_{i} - c_{j} } \right\|,i \ne j,\;i,j = 1,2, \cdots ,N_{R} } \\ {N_{R} = \left( {\gamma - 1} \right)!;\;disc\left( i \right) = \left\| {{\mathbf{X}} - c_{i} } \right\|,i = 1,2, \cdots ,\gamma } \\ \end{array}$$

(19)

where dis(i, j) is the Euclidean distance between two membership function centres. c_i is the centre of the ith membership function, N_R is the centres number of membership function layer, γ is the number of rules, and disn(i) is the Euclidean distance to the central of all membership functions. X(t) is a new set of input data, ${\mathbf{X}}\left( t \right) = \left( {x^{\prime}_{1} \left( t \right),x^{\prime}_{2} \left( t \right), \cdots x^{\prime}_{m} \left( t \right)} \right)$. dismax and discmin are the maximum and minimum value of dis(i, j), respectively. If (25) is satisfied:

$$disn\min > dis\max$$

(20)

or formula (22) and (23) are satisfied, a rule needs to be added, and the new parameters are as follows:

$$\begin{array}{*{20}c} {\sigma^{ * } \left( {t + 1} \right) = \mathop {\min }\limits_{{1 \le j \le \gamma^{ * } \left( t \right)}} \upsilon \times \left| {x^{\prime}_{i} \left( t \right) - c_{ij}^{ * } \left( t \right)} \right|} \\ {c^{ * } \left( {t + 1} \right) = x^{\prime}_{i} \left( t \right),\;\;\omega^{ * } \left( {t + 1} \right) = \psi^{ * } ,i = 1,2, \cdots ,N_{x} \left( t \right)} \\ {\psi^{ * } { = }\frac{{\left( {a^{ * } + eb^{ * } } \right) \cdot \left( {b^{ * } + 1} \right) - a^{ * } \cdot b^{ * } }}{{\left( {N_{x} \left( t \right) + 1} \right)x^{\prime}_{i} \left( t \right)b^{ * } }}} \\ {a^{ * } = \sum\limits_{j = 1}^{\gamma } {o_{j}^{\left[ 5 \right]} \left( t \right)} ,\;b^{ * } = \sum\limits_{j = 1}^{\gamma } {o_{j}^{\left[ 4 \right]} \left( t \right)} } \\ \end{array}$$

(21)

where $c^{ * } \left( {t + 1} \right)$, $\sigma^{ * } \left( {t + 1} \right)$, and $\omega^{ * } \left( {t + 1} \right)$ are the centres, widths, and weights of the new rules at the next moment. υ ∈ (0,1) is a random value, $x^{\prime}_{i} \left( t \right)$ is the ith dimension input variable, and $c_{ij}^{ * } \left( t \right)$ is the jth centre corresponding to $x^{\prime}_{i} \left( t \right)$. N_x(t) is the size of the ith dimension-input samples, $a^{ * }$ and $b^{ * }$ are the average value of $o_{j}^{\left[ 4 \right]}$ and $o_{j}^{\left[ 5 \right]}$, respectively; $o_{j}^{\left[ 4 \right]}$ and $o_{j}^{\left[ 5 \right]}$ are the output of the jth TSK fuzzy layer and recursive layer, respectively.

2) Pruning method:

Redundancy and bad generalizations may exist when some of the rules are redundant. To address this, the overall redundancy criterion Jr(t) is defined (Liu et al. 2018) as:

$$Jr\left( t \right) = Jsum\left( t \right) - JImin\left( t \right) > 1$$

(22)

Among them, JImin(t) is the rule of the least contribute in the activation region S. The width set of S is ${{\varvec{\upsigma}}}_{{j^{\prime}}}^{ * } \left( t \right) = \left\| {\sigma_{{j^{\prime}1}}^{ * } \left( t \right),\sigma_{{j^{\prime}2}}^{ * } \left( t \right), \cdots ,\sigma_{{j^{\prime}m}}^{ * } \left( t \right)} \right\|$, the centre set is ${\mathbf{c}}^{ * }_{{j^{\prime}}} = \left( {\mu_{{j^{\prime}1}}^{ * } \left( t \right),\mu_{{j^{\prime}2}}^{ * } \left( t \right), \cdots ,\mu_{{j^{\prime}n}}^{ * } \left( t \right)} \right)$, and $\mu_{{j^{\prime}n}}^{ * } \left( t \right)$ is the nth centre of the membership function. $\sigma_{{j^{\prime}m}}^{ * } \left( t \right)$ is the nth width of the membership function. $j^{\prime}$ represents the maximum activation-intensity rule.

$$dis\left( {i,j^{\prime}} \right) = \left\| {{\mathbf{c}}_{j}^{ * } - {\mathbf{c}}_{{j^{\prime}}}^{ * } } \right\|,\;j^{\prime} \ne i,i = 1,2, \cdots ,N_{{\sigma^{ * } }}$$

$${\mathbf{dis}}\left( {j^{\prime}} \right) < {{\varvec{\upsigma}}}_{{j^{\prime}}}^{ * }$$

(23)

where dis(i,$j^{\prime}$) is the Euclidean distance between $j^{\prime}$ th and the other rule centres. ${\mathbf{dis}}\left( {j^{\prime}} \right)$ is the set of $dis\left( {i,j^{\prime}} \right)$, and ${{\varvec{\upsigma}}}_{{j^{\prime}}}^{ * }$ is the set of $dis\left( {i,j^{\prime}} \right)$. If (28) is satisfied, the $j^{\prime}$ th rule belongs to S; then Jimin = argmin(S); argmin is the minimum value of S. If (22) and (28) are satisfied, the vth rule which has the least contributing in S needs to be pruned; the weight ω_v’ of the v'th rule which is closest to the vth is adjusted as follows:

$$\omega_{{v^{\prime}}} \left( {t + 1} \right) = \omega_{{v^{\prime}}} \left( t \right) + \varepsilon$$

(24)

$$\varepsilon { = - }\frac{{a^{ * } { - }o_{{j^{ * } }}^{\left[ 5 \right]} - {{a^{ * } \left( {b^{ * } - o_{{j^{ * } }}^{\left[ 4 \right]} } \right)} \mathord{\left/ {\vphantom {{a^{ * } \left( {b^{ * } - o_{{j^{ * } }}^{\left[ 4 \right]} } \right)} {b^{ * } }}} \right. \kern-\nulldelimiterspace} {b^{ * } }}}}{{\left( {\rho + 1} \right)o_{{v^{\prime}}}^{\left[ 4 \right]} x_{i} }}$$

(25)

where ρ is the dimension of the input variable.

Experimental results and analysis

All the experiments were performed on BSM1 implemented using MATLAB 2014b running on Microsoft Windows 8. The computer used a 3.6 GHz processor and 8 GB of RAM. To objectively evaluate the performance under different conditions, the 14-day data from BSM1 was used for simulation at sampling interval of 15 min (Li et al. 2021a, 2021b). The integral of the absolute error (IAE) was used to evaluate the control performance of the system, and the proposed DMOIA-OC system was compared with other systems.

Experimental setup

The population size is 150 to compare the dynamic multi-objective optimization algorithm; the number of iterations is 100. The crossover parameter η_c = 20, the mutation parameter η_m = 20, and the crossover and mutation probabilities are 0.9 and 1/N_d, respectively. N_d = 10, it is the number of decision variables; the shape parameter N_q = 11; also, the algorithm runs 20 times independently. To test the convergence, distribution, and diversity of the algorithm, the inverse distance IGD (Lin et al. 2018) is used as the test index.

Simulation results

(1) DMOIA algorithm validation.

To evaluate the performance of DMOIA, four algorithms, dynamic population prediction strategy (PPS), dynamic non-dominant sorting genetic algorithm II (DNSGAII), decomposition-based dynamic multi-objective evolution algorithm (MOEA/D), and dynamic competitive co-evolution algorithm (DCOEA), are used to validate the performance. At the same time, to study the effect of changing frequency on the performance of the algorithm, different combinations of changing severity and frequency are used to experiment, namely (n_t, τ_t) = (5, 10), (10, 10)和(20, 10) (Li et al. 2018). Because IGD is mainly used to reflect the convergence and distribution of POF, so it is used to test the performance of the algorithm.

Table 1 gives the IGD and its standard deviation values obtained by five algorithms on FDA (Goh et al. 2008) and dMOP (Farina et al. 2004) problems to show the best results of the five algorithms in bold. From Table 1, the PPS and DCOEA algorithms show good performance for FDA4, dMOP2, and dMOP3 problems. DNSGAII performs the worst on FDA1, FDA4, FDA5, dMOP1, and dMOP3. In addition, for FDA2, FDA3, and dMOP1 problems, PPS has the worst effect. However, DMOIA performs best in most test functions of FDA and dMOP; i.e. DMOIA performs better in dynamic optimization than other comparison algorithms. The results show that DMOIA can approximate PF stably and effectively in a dynamic environment for three-dimensional problems. Because DMOIA has better population diversity and distribution, it shows better optimization performance significantly.

Table 1 Performance IGD comparison of results on the test problems

At the same time, in order to further study the performance of the algorithm under different population sizes, to evaluate the performance of DMOIA, three different population sizes were set up; they were set to 100, 150, and 200, respectively. As seen in Table 1, the DMOIA algorithm size which was set to 200 has the minimum IGD value. When set to 100, it has the maximum IGD value, and 150 was the second. Therefore, the larger the population size, the smaller the IGD value and the better the convergence, and vice versa.

(2) DMOIA-OC experimental results.

WWTPs have a non-linear change due to biochemical and nitrification reactions. When water flow changes dynamically, DMOIA-OC achieves the goal of lowering EQ before EC meets the standards. To evaluate the control performance of the DMOIA-OC, three weather conditions (dry, rainy, and storm) are experimented. It is compared with five algorithms, which are two optimization controllers: virtual reference feedback adjustment control strategy (VRFT-CS) (Roman et al. 2016), scale integral optimization controller based on non-dominant sorting genetic algorithm (NSGA + PI-OC) (Vitor et al. 2021); adaptive multi-objective particle swarm optimization algorithm based on the parallel unit coordinate system (pccsAMOPSO-OC) (Hu et al. 2015), cluster MOPSO (Zhang et al. 2012), and dynamic multi-objective particle swarm optimization control method (clusterMOPSO-OC) (Chakraborty et al. 2011). The simulation results in three kinds of weather are shown in Fig. 3, Fig. 4, and Fig. 5.

Fig. 3

a The control results of SO in the dry weather.b The control results of SNO in the dry weather. c The control errors of SO and SNO

Fig. 4

a The control results of SO in the rain weather. b The control results of SNO in the rain weather. c The control errors of SO and SNO

Fig. 5

a The control results of SO in the storm weather. b The control results of SNO in the storm weather. c The control errors of SO and SNO

1) Dry weather.

In dry weather, the control results of S_O and S_NO are shown in Fig. 3 (a) and (b). It can be seen that DMOIA-OC can generate time-varying settings based on actual input and has good tracking performance. In addition, Fig. 3 (c) shows the control error between the actual output values of S_O and S_NO and the set values. The control errors are small when they are all kept within ( +) 0.4 mg/L.

To further validate the performance of DMOIA-OC, Table 2 shows the results compared with the other five methods. It can be seen that IAE has the best control effect than other comparison methods. The AE, PE, and EQ values of DMOIA-OC are the lowest; that is, the EC and EQ of the outlet are the lowest. In addition, the concentration of SS in NSGA + PI-OC is slightly lower than that of in DMOIA-OC. However, its EC and EQ are significantly lower than that of NSGA + PI-OC. In conclusion, under dry conditions, DMOIA can output the best water quality with the least energy consumption and the best control effect.

Table 2 Comparison of different control strategies for the mean energy consumption and effluent quality with effluent parameters in three different weathers

2) Rainy weather.

In rainy weather, the S_O and S_NO control results are given in Fig. 4 (a) and (b). Seen from that, S_O settings fluctuate more than sunny days, and S_NO settings change relatively smoothly. Similarly, DMOIA-OC has good tracking performance. In addition, in order to observe the control effect of DMOIA-OC more intuitively, the control error is given in Fig. 4 (c). It can be seen that the error is also within ± 0.4 mg/L, the control error is small, and the prediction error of S_NH is greater than that of S_O.

Table 2 shows the results of DMOIA-OC compared with the other five methods. It shows that the concentration of SS is the lowest. Compared with other comparison algorithms, DMOIA-OC has the lowest AE, PE, and EQ values, NSGA + PI-OC (Jiang et al. 2004) has the lowest EQ, and cluster MOPSO-OC has the lowest AE and PE values. The control effect of DMOPSO-OC is only inferior to DMOIA-OC. Also, DMOIA-OC has the smallest IAE value. To sum up, DMOIA can output the best water quality with the least energy consumption and the best control effect under cloudy and rainy weather conditions.

3) Storm weather.

Figure 5 (a) and (b) show the control results of S_O and S_NO in rainstorm conditions. The settings for rainstorm weather fluctuate more frequently than those for sunny and rainy days, and the fluctuations in the back section are more frequent than those in the front section. In addition, to verify the control effect of DMOIA-OC more intuitively, control errors are given in Fig. 5 (c). From that, the error of the latter segment remains within ± 0.4 mg/L, and the error of the latter segment fluctuates considerably relative to the former. The prediction error of S_O is greater than that of S_NO, but the overall control error is smaller. In addition, Table 2 shows the results of DMOIA-OC compared with the other five methods. As seen that, the concentration of SS is slightly higher than that of DMOPSO-OC. The AE, PE, and EQ values of DMOIA-OC are the smallest compared with other comparison algorithms. The result of pccsAMOPSO-OC is the worst; DMOPSO-OC is second only to DMOIA-OC. VRFT-CS (Peng et al. 2007), NSGA + PI-OC (Jiang et al. 2004), and cluster MOPSO-OC (Zhang et al. 2012) ranked third to fifth, respectively, and DMOIA-OC (Lu et al. 2019) has the smallest IAE value. In summary, DMOIA can also obtain the best EQ with the least EC and the best control effect under heavy rain conditions.

Discussion on experimental results

The regularities exhibited by the experimental results can explain the factors that affected the overall performance of DMOIA-OC. These results are summarized as follows:

• 1. Excellent optimization performance: to more accurately predict the location of Pareto front, an adaptive dynamic immune optimization method is designed. When the environment changes, representative individuals are adaptively selected in the iterative process with good distribution and convergence to increase the diversity of the Pareto solutions. The multi-directional prediction strategy is used to predict the motion position of the Pareto set more accurately and improve the performance of the evolutionary algorithm in the solution of the dynamic multi-objective optimization problems. The real-time settings for S_O and S_NO are thus obtained. Meanwhile, the limit optimization mutation method (Li et al. 2018) increased the diversity of the population and improved its convergence speed. The above methods provided an excellent dynamic optimization scheme for solving complex optimization problems, as verified by the IGD results in Table 1.

• 2. Accurate tracking control: WWTP is a time-varying system, and the flow and composition of the input water are constantly changing. Therefore, a recursive fuzzy neural network with a time-varying structure is needed to adapt to the changes in operating conditions. For this reason, Zhou et al. combined the hybrid multi-objective barebones particle swarm optimization algorithm (HBBMOPSO) with a self-organizing controller to realize intelligent control of the WWTP (Zhou et al. 2017). A better control effect can be achieved by devising more effective approximations for the non-linear dynamic relationships in WWTP control. At the same time, because a recursive fuzzy neural network combines the advantages of a fuzzy system and a neural network, it has the ability to perform fuzzy inference and non-linear mapping. Therefore, a SORFNN with an adaptively adjusted structure and parameters (Qiao et al. 2017) was adopted to effectively improve the control accuracy in this study. It can be seen from Figs. 3, 4, and 5 that DMOIA-OC achieved stable and high-precision control.

Conclusion

An advanced DMOIA-OC control method was proposed to solve the multi-index coupling problem in complex WWTPs. To analyse the process variables related to EC and EQ in the WWTP operating characteristics and data, the SOFNN algorithm with a dynamically adjusted structure and parameters was adopted to establish the relationship model (between the input variables, EC, and EQ). This provides a good foundation for the WWTP optimization. The DMOIA method was also designed in this study to adaptively generate new populations with better diversity and distribution when the environment changes. This allowed the S_O and S_NO values with the lowest EC under the standard EQ to be obtained. The experimental results show that DMOIA achieved the best performance for complex dynamic optimization among the compared methods. To obtaining the best S_O and S_NO setting values, a recursive fuzzy neural network controller with high adaptive capability was used for tracking control. The experimental results show that on sunny and rainy days and under heavy rain, the proposed DMOIA-OC method achieved the best optimized control performance. The results also demonstrate the ability of DMOIA-OC to effectively optimize multiple performance indicators and achieve stable and accurate tracking and control of these indicators.