1 Introduction

Reservoir flood control operation (RFCO) is a scheduling problem which reduces flood peaks, minimizes flood damages and reserves floods by making appropriate scheduling plans on the dams’ water release sequences (Hajkowicz and Collins 2007). It is a challenging nonlinear and non-convex optimization problem in the field of water resource management, which involves multiple decision goals and interdependent decision variables (Luo et al. 2015).

At present, many research efforts have been done on RFCO problem solving from different points of view and under various assumptions. These existing research works can be divided into the following five categories: 1) Single reservoir (Kumar and Reddy 2006; Jain et al. 1992) or multiple reservoirs (Wang et al. 2014; Zhou et al. 2014). 2) Short-term scheduling (Wang et al. 2013; Li and Ouyang 2015), long-term scheduling (Li et al. 2010; Porse et al. 2015) or the mix of both in recent years (Akbari et al. 2014; Luo et al. 2015). 3) Deterministic inflow (Luo et al. 2015; Li and Ouyang 2015) or stochastic inflow (Ding et al. 2015; Hashemi et al. 2014). 4) Simulation-optimization (Chang et al. 2014; De Paes and Brandao 2013; Chou and Wu 2015) or model-optimization approaches (Wang et al. 2013; Hsu and Wei 2007). 5) Single-objective approaches (Qin et al. 2010; Chang et al. 2014; Ding et al. 2015) or multi-objectives approaches (Malekmohammadi et al. 2011; Shokri et al. 2013; Li and Ouyang 2015). In this paper, we focus on the single reservoir flood control operation problem with short-term scheduling time horizon and deterministic inflow forecasts. Following the model-optimization paradigm, a multi-objective scheduling approach is developed for RFCO problem.

For a long time, the majority of scheduling approaches which follow model-optimization paradigm for RFCO problem are single-objective ones (Nagesh Kumar et al. 2010). Optimization techniques, such as linear programming (David et al. 2000), dynamic programming (Yakowitz 1982) and non-linear programming (Unver and Mays 1990) were employed to solve this single objective RFCO problem. These approaches usually need some problem-specific settings and often obtain local optimal scheduling plans for RFCO problem. Moreover, they are time consuming when dealing with RFCO problem with large amount of decision variables. In recent years, the multi-objective optimization technique has made great progress, more and more research efforts have been devoted to solve RFCO problem by using multi-objective optimization methods directly (Fu 2008; Qin et al. 2010; Qi et al. 2012). Among exiting research works, the nature inspired optimization algorithms which known as the population based stochastic searching algorithms make up the majority of the list. With the advantage of generating a set of non-dominated solutions in a single run, these algorithms, particularly the evolutionary algorithms, have been recognized to be very successful in solving multi-objective optimization problem (MOP) (Coello Coello 2006). However, to the best of our knowledge, almost all of these approaches simply employ some existing multi-objective optimization algorithms for solving RFCO problem, few of them considers the characteristics of the RFCO problem itself.

The RFCO problem raises challenges to existing multi-objective optimization algorithms in the following two aspects. One is in the objective space. In the RFCO problem, an improvement on one objective is usually accompanied with an unstable degradation on another one. That is, the RFCO problem usually has an irregularly-shaped Pareto front (PF) which is the point set of all Pareto optimal solutions in the objective space. The complexity in PF shape raises a big challenge to most multi-objective optimization algorithms (Qi et al. 2014; Jiang and Yang 2015). The other is in the decision space. In the RFCO problem, a sequence of water release volumes which have chain-like interdependence with each other are regarded as the decision variables. The complexity of interdependence between decision variables is the major sources of complexity in many optimization problems (Omidvar et al. 2015), it also challenges the multi-objective optimization algorithms a lot. Considering the complexity of the RFCO problem in both objective space and decision space, we develop a new scheduling approaches using artificial immune algorithm for multi-objective optimization. The major contributions of this paper are as follows.

  1. 1.

    An immune inspired memetic algorithm M-NNIA2 which considers the complexity of the RFCO problem in both objective space and decision space is developed.

  2. 2.

    To cope with the complexity of the RFCO problem in the objective space, M-NNIA2 inherits the remarkable diversity preserving capability of immune inspired optimization algorithm, and manages to obtain a good representative set of non-dominated solutions that fully cover the irregularly-shaped PF of the RFCO problem and scatter evenly on it.

  3. 3.

    To cope with the complexity of the RFCO problem in the decision space, a Pareto dominance based local search operator and a differential evolution inspired local search operator are designed for the RFCO problem to guide the search of M-NNIA2 towards the and along the Pareto set respectively.

The rest of this paper is organized as follows. Section 2 gives some related backgrounds. Section 3 provides the description of the proposed M-NNIA2. Section 4 shows the experimental results on benchmark problems to validate the efficiency of M-NNIA2. Section 5 further verifies the efficiency of M-NNIA2 on multi-objective RFCO instances. Conclusions are presented in Section 6.

2 Related Backgrounds

To make it easier to understand, this section introduces some basic terms about MOP and the framework of immune inspired multi-objective optimization algorithms. A complete list of acronyms and symbols can be found in Tables 2 and 3 in the A.

2.1 Definitions and Notations of Multi-objective Optimization

The target MOP can be formally described as follows.

$$ \begin{array}{ll} \mathrm{Minimize~} \quad {\mathbf{F(x)}}=(f_{1}(\mathbf{x}),f_{2}(\mathbf{x}),\cdots,f_{m}(\mathbf{x}))^{T}\\ \mathrm{Subject~to} \quad \mathbf{x} \in {\Omega} \end{array} $$
(1)

In which Ω⊂R n is the feasible region of the decision space, and x=(x 1,x 2,⋯ ,x n )∈Ω is the decision variable vector. The target function F ( x ):x→R m consists of m real-valued objective functions f 1(x),⋯ ,f m (x) and R m is the objective space.

Suppose that x A ,x B ∈Ω are two different solutions of the target MOP. One solution x A is said to dominate the other one x B (noted as x A ≺x B ) if and only if f i (x A )≤f i (x B ), ∀i∈{1,⋯ ,m}, and there exists a j∈{1,⋯ ,m} that makes f j (x A )<f j (x B ). We say that a solution x ∗∈Ω is a Pareto optimal solution if there is no other solution x∈Ω that dominates x ∗. Then the Pareto set (PS) can be stated as P S={x ∗∣¬∃x∈Ω,x≺x ∗}. The corresponding objective vectors of the solutions in PS is named as the Pareto front (PF). The aim of a multi-objective optimization algorithm is to obtain a set of good representative solutions that uniformly scattered along the true PF.

2.2 Multi-objective Immune Algorithm and the Framework of NNIA2

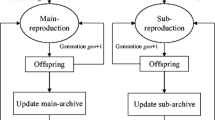
Considering the target optimization problem as antigen and the coding of its solution as antibody, the artificial immune system can be used to solve optimization problems by simulating the immunological recognition procedure. Yoo and Hajela proposed the first attempt to solve MOP using immune inspired ideas (Yoo and Hajela 1999). Coello developed the fist multi-objective immune system algorithm (MISA) based on the the immune clonal selection principle (Burnet 1959). Following the clonal selection paradigm, Gong suggested an efficient immune algorithm for MOP, the multi-objective immune algorithm with non-dominated neighbor-based selection (NNIA) (Gong et al. 2008). NNIA devotes more computing efforts to antibodies within the less-crowded regions of the current trade-off front. Experimental results have shown the good performance of NNIA, however, this algorithm might lose diversity when current non-dominated antibodies selected for proportional cloning are very few because it ignores all the dominated antibodies. To improve its robustness and adaptability, Yang developed an enhanced version, named as NNIA2, by introducing an adaptive ranks clone scheme which takes dominated antibodies into consideration and a k-nearest neighbor list strategy which help to improve the population diversity (Yang et al. 2010).

Figure 1 illustrates the workflow of NNIA2. In NNIA2, a k-nearest neighbor list (k-NNL) based diversity preserving strategy is adapted in both the steps of the adaptive selection (step 7 in Fig. 1) and the adaptive ranks clone (step 4 in Fig. 1). This diversity preserving strategy is based on the vicinity distance (Kukkonen and Deb 2006), with which the adaptive selection step trends to keep low rank and less crowded antibodies to survive. In the adaptive ranks clone step, the clone size of a certain antibody is proportional to its vicinity distance.

Fig. 1
figure 1

The workflow of NNIA2

Full size image

3 Multi-objective Optimization Model for RFCO

During floods, the most important decision goal of reservoir flood control operation (RFCO) is to guarantee the safety of both upstream and downstream of the dam by scheduling the sequence of discharge water volume. Taking the discharge water volumes during T scheduling periods Q=(Q 1,Q 2,...,Q T ) as the decision vector, a multi-objective RFCO problem can be modeled as follows (Qi et al. 2012; Qin et al. 2010).

$$ \begin{array}{ll} \mathrm{Minimize~} \quad {\mathbf{F(Q)}}=(f_{1}(\mathbf{Q}),f_{2}(\mathbf{Q}))\\ \quad \quad f_{1}(\mathbf{Q})= \max \{Z_{t}\} \\ \quad \quad f_{2}(\mathbf{Q})= \max \{Q_{t}\} \\ \mathrm{Subject~to}\\ \quad \quad Z_{min} \leq Z_{t} \leq Z_{max} \\ \quad \quad 0 \leq Q_{t} \leq Q_{max} \\ \quad \quad V_{t}=V_{t-1}+I_{t}-Q_{t} \\ \quad \quad t=1,2,...,T \end{array} $$
(2)

In which, Z t is the upstream water level of the t-th period, it has a value between its lower bound Z m i n and upper bound Z m a x . Q m a x is the upper limit of discharge water volume. V t = V t−1 + I t −Q t is the water balance equation, in this equation, V t and V t−1 are the reservoir storage of the t-th and the (t−1)-th periods, I t which is the input of the RFCO problem means the reservoir inflow volume of the t-th period. The first objective function f 1(Q) is to minimize the highest upstream water level during the T scheduling periods and ensure the safety of the dam and its upstream side. The other optimization target f 2(Q) is to minimize the largest discharge water volume during scheduling periods and protect the dam’s downstream side.

figure a

4 M-NNIA2: The Proposed Algorithm for RFCO

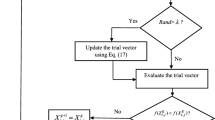
Following the main workflow of NNIA2, the Pareto dominance based local search operator and the differential evolution (DE) inspired local search operator are designed and employed to guide the search towards and along the current found PS respectively. The workflow of the proposed M-NNIA2 is summarized in Algorithm 1.

The memetic operator in step 3.2 of Algorithm 1 is the key step that the proposed M-NNIA2 enhances NNIA2. It consists of two newly designed local search operators. For each antibody A b i in clone population C t , the memetic operator performs a local search which is based on the dominance relationships between A b i and its neighbors if there are, or a local search inspired by differential evolution on it, giving rise to a new antibody \(\mathbf {Ab}_{i}^{\prime }\) which is then added into \(\mathbf {C}_{t}^{\prime }\). The details of the newly designed memetic operator can be described in Algorithm 2.

figure b

Figure 2 illustrates the basic ideas of the two newly designed local search operators. As shown in Fig. 2a, the Pareto dominance based local search operator determines a potential hill-climbing searching area according to the dominance relationships between A b i and its neighbors that dominated by it. Different from most existing hill-climbing local search methods, the developed local search operator utilizes more than one descent directions to guide the search, which is expected to provide a more accurate estimation of the potential hill-climbing area. When the searching procedure converges to a certain degree, A b i and its neighbors become incomparable. In this case, the DE inspired local search operator will play an important role. As is shown in Fig. 2b, the DE inspired local search operator guides the search towards different areas when the relative location between A b i and its neighbors A b p and A b q changes. The DE inspired local search operator is expected to provide search directions along the current found Pareto set, and thus guide the search towards even wider areas to generate more diversity.

Fig. 2
figure 2

Illustration of the two local search operators

Full size image

5 Experimental Studies on Benchmark Problems

In this section, we will compare the proposed M-NNIA2 with four other algorithms. Among which, NSGAII (Deb et al. 2002) and MOEA/D (Zhang and Li 2007) are outstanding evolutionary multi-objective optimization algorithms with different types. To illustrate the efficiency of the suggested enhancements, the original NNIA (Gong et al. 2008) and NNIA2 (Yang et al. 2010) are also included in the compared algorithm list.

5.1 Test Problems

In the experimental study, seven benchmark problems are investigated to validate the superiority of the proposed M-NNIA2. They are five widely used bi-objective ZDT problems (Zitzler et al. 2000) and two test problems with nonlinear variable linkages which are suggested by Qingfu Zhang and noted as F5 and F6 (Zhang et al. 2008). Detailed descriptions of these problems are listed in Table 1 in the A.

5.2 Performance Metrics

Two comprehensive metrics are employed to evaluate the performance of the compared algorithms. For benchmark problems whose ideal PFs can be available, the inverted generational distance (IGD) metric (Zitzler et al. 2003) is employed. For the multi-objective RFCO problem with unknown PF, the hypervolume (HV) indicator (Zitzler and Thiele 1999) is used to evaluate the performance. Given an approximation set of the PF with size n p , noted as \(\textbf {{P}} = \left ({{\textbf {{p}}_{1}},{\textbf {{p}}_{2}}, {\cdots } ,{\textbf {{p}}_{n_{\textbf {p}}}}} \right )\) , the IGD and HV metrics can be defined as follows.

IGD Metric

Suppose P ∗ is a set of evenly distributed points over the idea PF of the target MOPs, the IGD value from P ∗ to P can be calculated by the following Eq. 6.

$$ IGD(\textbf{P}^{*},\textbf{P})=\frac{{\sum}_{\nu \in \textbf{P}^{*}} d(\nu,\textbf{P})}{|\textbf{P}^{*}|} $$
(6)

In which, d(ν,P) is the minimum Euclidean distance between ν and the points in P. The IGD metric measures both the uniformity and the convergence of the approximation set P. A low value of I G D(P ∗,P) indicates that P is close to the ideal PF and covers most of the whole PF.

HV Metric

Given a reference point p R in the m-dimensional objective space, the HV indicator is a measure of the region which is simultaneously dominated by the approximation set P and bounded above by the reference point p R . A high HV value means that P is a good approximation of the unknown ideal PF. In this work, the reference point p R is set as maximum values of non-dominated solutions obtained by all the compared algorithms.

5.3 Parameter Settings

In the experimental studies, the simulated binary crossover (SBX) and polynomial mutation (PM) operators (Deb et al. 2002) are employed in all the compared algorithms. Parameters for SBX and PM are set as follows. The crossover probability p c is set as 0.8. The distribution index for SBX is set as 15. The mutation probability p m is set as 1/n, in which n is the number of decision variables. The distribution index for PM is set as 20.

For M-NNIA2, NNIA and NNIA2, the size of non-dominated population n D is set as 100, the size of active population n A is set as 20, the size of clone population n C is set as 100. For M-NNIA2 and NNIA2, the size of neighbor list is set as 20. For NSGAII, the population size is set as 100. For MOEA/D, the Tchebycheff decomposition approach is employed, the population size is set as 100, the size of neighborhood is set as 20. All the compared algorithms stop when the number of function evaluation reaches the same maximum number of 50000.

5.4 Experimental Studies on M-NNIA2 and Comparisons

This part of experiments are designed to illustrate the superiority of the proposed M-NNIA2 over the compared algorithms. The data in the following experiments are statistic results of 30 independent runs.

Figure 3 shows the plot of the non-dominated fronts with the lowest IGD value found by the compared algorithms on bi-objective ZDT problems, each group end with a box-plot of IGD values over 30 independent runs. In these box-plots, the bottom and top of the box are the first and third quartiles, the the bands inside the boxes represent robust estimates of the uncertainty about the medians for box-to-box comparison. The ends of the whiskers represent possible alternative values and the symbol ”+” denotes outliers.

Fig. 3
figure 3figure 3figure 3

The final non-dominated fronts with the lowest IGD values found by the compared algorithms on bi-objective ZDT problems

Full size image

In Fig. 3, the first and the second box-plots in each group are the non-dominated solution sets found by the compared algorithm with function evaluations of 2000 and 5000 respectively. The the third column is the final IGD box-plots of the compared algorithms over 30 independent runs.

It can be seen from Fig. 3 that the proposed M-NNIA2 converges to the ideal PFs of ZDT problems after 2000 function evaluations when the other compared algorithms have not yet converged. When the function evaluations comes to 5000, M-NNIA2 obtains non-dominated solution sets with better uniformity than the other compared algorithms. As shown by the IGD box-plots, M-NNIA2 has lower IGD values than NNIA and NNIA2 on four of the five ZDT problems except for ZDT6 problem whose Pareto-optimal solutions are non-uniformly scattered along the ideal PF. It is superior to all the compared algorithms on ZDT3 which has a discontinuous PF.

Figure 4 gives the non-dominated fronts obtained by the compared algorithms on bi-objective F5 and F6 problems. At the end of each sub-figure, a box-plot of IGD values over 30 independent runs is given. On these two complex problems with nonlinear interdependence between decision variables, the proposed M-NNIA2 significantly outperforms the compared algorithms in term of spreadability, and thus it has the lowest IGD value.

Fig. 4
figure 4figure 4

The final non-dominated fronts with the lowest IGD values found by the compared algorithms on F5 and F6 problems with nonlinear variable linkages

Full size image

To conclude, from this part of experimental studies we can come to the conclusion that the proposed M-NNIA2 converges faster than the compared algorithms. It performs as good as or superior to the compared algorithms on most of the benchmark problems, especially on complex problems with nonlinear interdependence between decision variables. The proposed M-NNIA2 has good capability of diversity preserving in the objective space and dealing whit variable interdependence in the decision space, it can be expected to be suitable for solving the RFCO problem.

6 Experimental Studies on Reservoir Flood Control Operation

After validating the superiority of the proposed M-NNIA2 on benchmark problems, this part of experimental studies are designed to investigate the performance of M-NNIA2 on the RFCO problems.

The compared algorithms are applied to deal with two typical floods at Ankang reservoir in Shanxi province of China. Figure 5a illustrates the water level to volume curve of Ankang reservoir. Figure 5b shows the design flood hydrographs for Ankang reservoir. Figures 5c and d are the reservoir inflow volumes of the two investigated floods on October 12, 2000 and August 28, 2003. According to the design flood hydrographs in Fig. 5b, the flood on October 12, 2000 is a 5 % frequency flood with return period of 20 years, and the flood on August 28, 2003 is a 20 % frequency flood with return period 5 years. Given the sequence of reservoir inflow volumes during a flood, the reservoir storage can be estimated by using the discharge water volume and the the water balance equation. After that, the dam’s upstream water level can be calculated according to the water level to volume curve.

Fig. 5
figure 5

The water level to volume curve of Ankang reservoir, the design design flood hydrograph and the inflow volumes of investigated floods

Full size image

As shown in Fig. 5, the flood on October 12, 2000 is a big flood with a single peak of more than 17000 cubic meters water inflow per second. Unlike this flood, the flood on August 28, 2003 has two flood peaks with maximum inflow water volume of more than 12000 cubic meters per second.

In this part of experimental studies, the total dispatching times of the two floods are 97 hours and 44 hours, and the dispatching time intervals are set as 6 hours and 3 hours respectively. All the compared algorithms have the same parameter setting and stopping criterion as have been described in section 4.3. The HV indicator (Zitzler and Thiele 1999) is employed to evaluate the performances of the compared algorithms.

Figure 6 illustrates the experimental results of the compared algorithms on the two multi-objective RFCO problems over 30 independent runs. In this figure, the ideal Pareto fronts of the two problems are the non-dominated solution sets obtained by running NNIA with 2,000,000 function evaluations over 30 runs.

Fig. 6
figure 6figure 6

The final non-dominated fronts with the highest HV values found by the compared algorithms on the flood on October 12, 2000 and August 28, 2003

Full size image

As shown in Fig. 6, the HV box of M-NNIA2 locate higher and are more flat than those of the compared algorithms. The final non-dominated fronts found by the compared algorithms indicate that M-NNIA2 can obtain non-dominated solution set with better convergence and uniformity. Moreover, M-NNIA2 has more stable performances on the two investigated floods, because its HV box-plots are flat.

7 Conclusions

Considering the complexity of the multi-objective reservoir flood control operation (RFCO) problem in both objective space and decision space, an immune inspired memetic algorithm, named M-NNIA2, is developed for decision making in flood control. To cope with complexity of RFCO in the objective space, M-NNIA2 inherits the remarkable diversity preserving capability of immune inspired optimization algorithm, and manages to obtain a good representative set of non-dominated solutions that fully cover the irregularly-shaped PF of the RFCO problem and scatter evenly on it. On the other hand, M-NNIA2 employs two newly developed local search operators to cope with the complexity of the RFCO problem in the decision space.

Experimental studies have been done on well-known benchmark problems with different features. The results indicate that M-NNIA2 can obtain non-dominated solution sets with better coverage and uniformity than the other four compared algorithms. In addition, it performs significantly better on complex problems with nonlinear interdependence between decision variables. We have also validated the superiority of M-NNIA2 on RFCO problems with different return periods. Experiments conducted on two typical floods at Ankang reservoir demonstrate that M-NNIA2 performs better and more stable than the compared algorithms, it is a highly competitive algorithm for solving the RFCO problems.