Introduction

Multiaxial dynamic loadings usually occur in many industrial cases such as automotive impacts [1], high-speed forming [2] or high-speed machining [3]. Multiaxial dynamic test development is therefore a crucial issue. Unfortunately, most of the dynamic tests are uniaxial. For instance, the very common Hopkinson bar test (which enables for accurate measurements at high strain rates) uses the uniaxial compression loading generated by the impact of a projectile.

In order to perform multiaxial tests, many set-ups have thus been designed to obtain multiaxial loadings from an initial uniaxial loading device. For example, a radial pressure can be applied to a cylindrical sample mounted on Hopkinson bars thanks to a confinement device. One can use a pressure vessel that enables for a controlled quasi-static pressure to be applied from a fluid [4]. Inserting the cylindrical sample inside a rigid tube can generate a dynamic radial loading even though the ratio between the radial pressure and the axial stress strongly depends on the sample material, in particular on its Poisson’s ratio [5]. Using a confinement tube made of a perfect plastic behavior material makes it possible to maintain a constant radial pressure [6]. A rigid confinement can also be imposed to a cruciform sample with a pre-loading system [7].

Another idea is to combine shear and compressive loadings. An inclined shear/compression specimen [8] or pressure bars with beveled ends [9] can be used to apply such combined loadings. The combined torsion-compression Hopkinson bar technique using torsional and compressive bars at each side of specimen was also reported [10]. It can also be carried out by blocking a brake on the input bar and by applying both compression/tension and torsion on the input boundary of the bar. Then the sudden fracture of the brake generates both torsion and tension/compression waves [11]. Unfortunately, the difference between the wave celerities does not enable simultaneous loadings to be obtained [12].

In order to apply biaxial loadings, two perpendicular Hopkinson bar devices have been built [13]. An explosive is used to obtain simultaneous loadings. The system is rather expensive and difficult to use. Recently, biaxial Hopkinson bar systems using two impactors were reported to generate biaxial compression states on samples [14], but obtaining two simultaneous impacts remains difficult. Another simple way to apply an equi-biaxial loading is the bulge-test using Hopkinson bars described in [15]. In this test, the external boundary of a circular sheet is leant against the tubular boundary of the output bar while the other side of the sheet is submitted to the pressure of a fluid compressed by the input bar. A biaxial tensile state is thus obtained at the center of the sheet. Unfortunately, only sheets can be tested and the displacement field on the sample cannot be easily measured.

From the short review above, it can be seen that the multiaxial testing design is still a tough issue. There are no commonly admitted testing set-ups and the design of such a test depend on the aimed loading state and on specimens. This paper is focused on biaxial compression and a new concept of Hopkinson bar system has been designed and tested. Its principle and its characteristics are described in Section 2. Then, Sections 3 and 4 present respectively the raw experimental results obtained from calibration tests and the analysis of a bi-axial test thanks to numerical simulations.

Design of the New Set-up

Set-up Characteristics

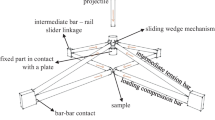
The designed bi-axial set-up uses a mechanism with intermediate parts with sliding surfaces and a cruciform specimen. This mechanism with sliding surfaces at 45° with respect to the axial direction was placed between the single input bar, the internal output bar and the co-axial external output tube (Fig. 1). After the striker impact on the input bar, the internal output bar measures the axial loading of the cross sample whereas the external output bar (the single tube that surrounds the internal output bar) measures the transversal one via the mechanism.

Fig. 1
figure 1

Schematic of the experimental configuration (cut view) with the relative motion of each part and the applied forces (up). Three-dimensional (down, left) and uncut (down, right) views without the three bars

Full size image

Using a single loading impulse avoids the difficulty due to non-simultaneous impacts occurring with perpendicular Hopkinson bar devices [13, 14]. Another advantage of such a design lies in the fact that the ratio between the axial and the transverse loadings is imposed by the ratio between the external and the internal output bar impedances and by the sliding surface angle of the mechanism.

The pressure bars are made of steel and their characteristics are given in Table 1. The external and the internal output bars have nearly the same impedance in order to ensure, on an isotropic sample, an approximate equality between the internal and the external loadings, and therefore between the axial and the transverse loadings, thanks to the mechanism. The difference between the internal radius of the external output bar (Rieo) and the internal output bar radius (Rio) is 3 mm, which is sufficient to place the gauges glued on the internal bar and their cables. These electrical cables exit from the external bar at the output end (i.e. at the opposite of the set-up). Nylon bearings are inserted between the two co-axial output bars and some of them are opened (Fig. 2g) to let a passage to the cables.

Table 1 Mass densities, tensile-compressive wave celerities, radii and lengths of the bars
Full size table
Fig. 2
figure 2

Part drawings (general tolerances: 0.1 mm); (a): parts with the sliding surfaces, (b): left-hand cylinder, (c): right-hand cylinder, (d): transverse triangular parts, e: sample, f: bearings, g: opened bearings

Full size image

The detailed drawings of the set-up parts are given in Fig. 2. The sample size (boundary to boundary) is 10 mm × 10 mm and its thickness is 5 mm (Fig. 2e). The shape of the parts with the two sliding surfaces (noted “a” in Fig. 2) has been chosen to maximize the stiffness. One of this part (the left-hand one in Fig. 1, in green) is inserted between the input bar and the two transverse triangular parts (noted “d”) and the other (the right-hand one in Fig. 1, in red) is inserted between the two transverse triangular parts and the external output bar.

The cylinder noted “b” in Fig. 2 is inserted between the input bar and the sample, and the cylinder “c” is inserted between the sample and the internal output bar (see Fig. 1). Both cylinders apply the axial loading on the cross sample and the right-hand one in Fig. 1 (the “c”) is free to have an axial motion relatively to the right-hand part with the sliding surfaces (“a”).

Forces and Velocities in the Set-up

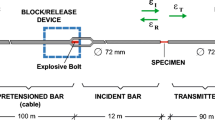
Strain gauges are glued at the middle of the input bar and on the two output bars close to the sample but far enough from the ends (at 0.374 m on the external bar and at 0.612 m on the internal one) to be within the Saint-Venant conditions.

After the striker impact, the input bar gauge measures an incident compressive wave εi followed by a reflected tensile wave εr. Moreover, the external output gauge measures a transmitted wave in the external output bar, εet and the internal output gauge also measures a transmitted wave in the internal output bar, εit. εi can be seen as a loading imposed to the biaxial set-up whereas εr, εet and εit can be seen as the set-up response to the imposed loading.

These strain waves have to be virtually transported from the gauge positions to the interfaces between the bars and the set-up presented in Fig. 1, down. Thus, εi has to be delayed and εr, εet and εit have to be shifted forward of the duration necessary for the waves to propagate from the measurement gauge to the corresponding interface. Then the Hopkinson formulae enable for the determination of the forces and of the velocities at the interfaces from these transported waves and from the bar parameters given in Table 1:

$$ {F}_i=-{\rho}_i{C_i}^2\pi {R_i}^2\left({\varepsilon}_i+{\varepsilon}_r\right) $$
(1)
$$ {V}_i={C}_i\left({\varepsilon}_r-{\varepsilon}_i\right) $$
(2)
$$ {F}_{eo}=-{\rho}_{eo}{C_{eo}}^2\pi \left({R_{eeo}}^2-{R_{ieo}}^2\right){\varepsilon}_{et} $$
(3)
$$ {V}_{eo}=-{C}_{eo}{\varepsilon}_{et} $$
(4)
$$ {F}_{io}=-{\rho}_{io}{C_{io}}^2\pi {R_{io}}^2{\varepsilon}_{it} $$
(5)
$$ {V}_{io}=-{C}_{io}{\varepsilon}_{it} $$
(6)

Fi and Vi are the force and the velocity at the interface between the input bar and the set-up shown in Fig. 1, Feo and Veo are the force and the velocity at the external output bar interface and Fio and Vio are the force and the velocity at the internal output bar interface.

Under the assumption of an equilibrium state in the set-up, the axial force in the sample can be assumed to be equal to the internal output force Fio and the transverse force Ft can be deduced from the external output force Feo. Indeed, each transverse triangular part of the mechanism is axially submitted to half Feo and by taking account of friction, the mechanical equilibrium of a transverse triangular part leads to Fig. 3.

Fig. 3
figure 3

Equilibrium of a transverse triangular part axially submitted to half Feo

Full size image

As the Fig. 3 upper triangle moves from top to bottom, the applied friction forces are oriented from bottom to top. Besides, according to the Coulomb’s laws, the friction force over normal force ratio is imposed to be equal to the friction coefficient at the mechanism sliding interfaces, noted f. The axial projection of the force transmitted by a sliding surface corresponds to half Feo (the axially applied force) and the transverse projection corresponds to Ft, which leads to:

$$ {F}_t=\frac{1-f}{1+f}{F}_{eo} $$
(7)

Experimental Results

Strain Gauge Measurement and Image Processing

Axial strain gauges are glued on each of the three bars and the measurement frequency is 500 kHz. The Hopkinson formulae (eqs. (1), (3) and (5)) permit for the calculation of the forces at the interfaces between the bars and the set-up from these measurements. The camera trigger signal is measured in the same time-basis as the gauge voltages. The image which was being recorded in the camera at the arrival of the trigger signal being known, both measurements can be time shifted.

The speckled samples are observed during the tests thanks to an SA5 high-speed camera whose frequency is 50 kHz at a definition of 512 pixels × 272 pixels. Images of the samples are acquired during the tests. The first one is called reference image and the displacement between each image and the reference is calculated thanks to Digital Image Correlation (DIC). DIC is performed by using the in-house Correli RT3 software [16, 17]. The displacement field is defined over a finite-element mesh made of triangular 3-noded elements (T3). The chosen element size is 10 pixels. The mean displacements on the four sample interfaces and the resulting axial and transverse elongations are determined from DIC. The displacement is given in pixels, which are converted into millimeters knowing the sample dimension. In order to control the uncertainty of the DIC calculation, an elastic regularization is used [16, 17].

The relative weight applied to the reference solution can be seen as the fourth power of a length called the regularization length. A too high regularization length may lead to erroneous estimations of the experimental displacement field because this field is thus constrained to be close to an elastic solution. As a result, the DIC calculations are processed with a regularization length decreasing from a value corresponding to 3 times the element size (30 pixels) to a value equal to the element size (10 pixels). DIC gives identical results when the length varies from 30 to 20 pixels but the results obtained with a 10 pixel length are sometimes a bit noisy and slightly different from the previous ones. To reduce the noise, a 20-pixel length is thus chosen for the processing.

Identification of the Sample Material Behavior

The samples are made of an AW-2017A aluminum. The material stress-strain law is identified from simple compression tests on cuboid samples (5 mm × 5 mm × 10 mm) inserted between the input bar and the internal output bar (the external output bar being removed, see Fig. 4a).

Fig. 4
figure 4

Schematics of the tests; a: cuboid sample axially compressed, b: cuboid sample transversally compressed, c: cross sample bi-axially compressed

Full size image

The compression force in the sample (Fig. 4, case a) thus corresponds to the internal output force Fio. The sample axial and transverse elongations in the image plan are determined from DIC. The real cross section (which increases because of compression), and then the true stress, can thus be calculated. Meanwhile, the axial logarithmic strain is deduced from the corresponding axial elongation. These measurements lead to repeatable axial behaviors.

Identification of the Friction at the Mechanism Sliding Interfaces

The friction coefficient in the mechanism of this new bi-axial testing device is a key parameter which has to be determined under the bi-axial test conditions. In order to reproduce the reached sliding velocities at the sliding interfaces, identical AW-2017A cuboid samples are inserted between the input bar and the external output bar, and are compressed via the mechanism (the internal output bar being removed, see Fig. 4b). The ratio between the transverse compression force Ft and the external output force Feo is thus friction dependent according to relation (7).

The set-up being far too small to insert a cell able to measure the compression force in the sample, this force will be deduced from relation (7) and from the Feo measurement. The friction coefficient f will be estimated knowing that the force-elongation laws identified during the axial (Fig. 4a) and the transverse (Fig. 4b) tests must be the same because the tested cuboid samples are the same too.

According to Fig. 5, by multiplying the external output force Feo measured during the transverse test by a constant ratio, a satisfactory fit can be obtained between the transverse and the axial tests when the displacements become high enough. However, for low displacements, the ratio should be a bit lower to obtain a satisfactory fit. It implies that the friction is first higher (adhesion phase) and then decreases when the displacements become high enough (sliding phase), which is finally consistent with the Coulomb’s law.

Fig. 5
figure 5

Friction identification by fitting the transverse test and the axial one

Full size image

Fig. 5 represents typical curves obtained from an axial test and from a transverse one, chosen as average behaviors. The transverse curve shows that the adhesion phase is not stationary, unlike the sliding one. The friction will thus be identified only during the sliding phase. The noise of the transverse force-elongation curve will lead to an uncertainty on the friction. By fitting, in the sliding phase, the transverse curve points with the minimal forces and the axial curve, a lower bound of the friction coefficient is obtained. Inversely, by fitting, in the sliding phase, the transverse curve points with the maximal forces and the axial curve, an upper bound of the coefficient is obtained. One obtains 0.05 < f < 0.09. Such values are consistent with Vaseline lubricated interfaces. It finally leads to a 0.87 average Ft/Feo ratio with a 4% relative uncertainty.

The friction coefficient magnitude and the corresponding uncertainty knowledge does not matter in itself, but it will enable for the determination of the transverse force and of the corresponding uncertainty during the bi-axial test.

Without clearances and without intermediate strains in the set-up, the corresponding interface sliding velocity should be equal to the difference between the input velocity and the external output one, or to the opposite of the transverse sample elongation rate, both divided by \( \sqrt{2} \) (because of the 45° angle):

$$ {V}_{\mathit{\operatorname{int}}, bars}=\frac{V_i-{V}_{eo}}{\sqrt{2}} $$
(8)
$$ {V}_{\mathit{\operatorname{int}}, sample}(t)=\frac{\Delta l\left(t-\Delta t\right)-\Delta l\left(t+\Delta t\right)}{2\sqrt{2}\ \Delta t} $$
(9)

Vint,bars is the interface sliding velocity estimated from the bar interface velocities (relations (2) and (4)) whereas Vint,sample is the same quantity estimated from the sample elongation Δl. Formula (9) corresponds to a numerical differentiation, t being a measurement instant and Δt the elongation acquisition time (given by the camera).

These velocity estimations show that a stationary phase with an interface sliding velocity of around 1 to 3 m/s begins for an elongation of approximately 0.1 mm, which is consistent with the beginning of the phase with a constant friction identified in Fig. 5.

Analysis of the Bi-Axial Test Measurements

An AW-2017A cross sample is tested by using the whole bi-axial mechanism and the two output bars (see Fig. 1 or Fig. 4c). The forces applied by the bars on the bi-axial set-up are determined from the strain gauge measurements and from the Hopkinson formulae and are shown in Fig. 6.

Fig. 6
figure 6

Time evolutions of the forces at the interfaces

Full size image

Fig. 6 shows that the input force and the total output force are in satisfactory equilibrium, despite of the complex 3-dimensionnal wave propagation phenomena occurring in the bi-axial mechanism. According to Section 2.2, the axial compression force in the sample corresponds to Fio whereas the transverse compression force Ft is lower than Feo but almost equal because of the low friction (in Section 3.3, the estimated Ft/Feo ratio is roughly 0.87). The obtained transverse and axial forces (Ft and Fio) being very close, Fig. 6 thus displays that the force loading path in the sample is rather equi-bi-axial.

As the external and the internal output bars have nearly the same impedance, the velocities, and thus the displacements, at the external and the internal output bar boundaries are also very similar. If there were no clearances and no strains occurring in the mechanism intermediate parts, the transverse displacement of each of the two triangular parts would be half the difference between the input bar and the external output bar displacements. The triangular parts moving symmetrically, the sample elongations, in both directions, would thus be exactly equal to the difference between the displacements at the input bar and at the output bar interfaces. It displays that the elongation loading path may be also rather equi-bi-axial.

The cross sample axial and transverse elongations are determined from the images and from DIC. The DIC reference image and the corresponding meshes on the sample are shown in Fig. 7.

Fig. 7
figure 7

Reference image (left), mesh used to determine the axial displacements (right, up) and mesh used to determine the transverse displacements (right, down)

Full size image

The obtained elongation time-evolutions and the corresponding transverse-axial loading path can be seen in Fig. 8, which clearly confirms that an almost equi-bi-axial loading is imposed to the sample. This bi-axial state can also be seen in Fig. 9, which also shows the set-up capacities in both directions.

Fig. 8
figure 8

Time-evolutions of (the opposite of) the elongations in both directions (up) and corresponding loading path (down)

Full size image
Fig. 9
figure 9

Sample force-elongation curves in axial and transverse directions

Full size image

Formulae (8) and (9) show that the sliding velocity reached at the interface during the stationary phase is of the order of 1 to 3 m/s, like during the friction identification test. It confirms the relevance of the friction coefficient value used for data processing.

Check of the Measurement Consistency Thanks to Simulations

Material Modelling

A typical result obtained from an axial compression test on a cuboidal sample (Fig. 4a), and chosen as a reference is reported in Fig. 10.

Fig. 10
figure 10

Stress-strain law identified from a test

Full size image

As there are few measurement points in the elastic phase, a 70 GPa Young modulus and a 0.3 Poisson’s ratio are assumed (AW-2017A characteristics). A yield stress - plastic strain law with a 100 MPa elastic threshold, and which exactly fits the measurements is then chosen (see retained behavior in Fig. 10). To simplify the modelling, the stress is supposed to saturate at a 268 MPa threshold value, which also well fits the measurements. In practice, the axial curves are reproducible for strains lower than 3%, but a 4% dispersion is observed for the threshold value. These parameters are implemented in a Von-Mises elastic-plastic model with an isotropic hardening. The used software is ABAQUS.

Simulation of the Sample Behavior

Because of its cross-shape, the stress and the strain states in this sample are heterogeneous. So, to check the force and elongation measurement consistency, a finite-element simulation must be performed. The calculations are performed with the Fig. 10 retained behavior. The fact that the model identification test has been carried out in the same dynamic conditions as the bi-axial test implies that the method remains valid with a strain rate dependent behavior. If any contact occurs between the arm free boundaries, it will be supposed frictionless. According to Fig. 6, the bi-axial set-up, and therefore the cross sample, are in a satisfactory equilibrium. This equilibrium state can be accurately verified by processing a dynamic explicit calculation. The chosen density is 2800 kg.m−3.

The displacements estimated thanks to DIC calculations are directly imposed to the sample interfaces (Fig. 11). Because of the image plan symmetry, only half the sample has to be modelled (Fig. 12). 8-node linear brick elements are used. The chosen brick size is 0.25 mm, which leads to the Fig. 12 mesh.

Fig. 11
figure 11

Imposed boundary displacements (axial ones oriented from left to right and transverse ones oriented from top to bottom)

Full size image
Fig. 12
figure 12

Meshed sample model accounting of the symmetry plan

Full size image

The dynamic explicit calculations display that the forces applied at opposite boundaries are almost equal until 60 μs, and become exactly the same after this duration. The sample equilibrium assumption being checked, the axial force is defined as the left and right boundary force average and the transverse force as the upper and lower boundary force average.

The numerical and the experimental forces in both directions can then be compared to check the measurement consistency. Because of the behavior dispersion (see Section 4.1), a 4% relative uncertainty must be considered for the numerical forces. The friction is taken into account by determining the measured transverse force with the 0.87 estimated Ft/Feo ratio (see end of section 3.3). The 4% relative uncertainty of this ratio also leads to a 4% uncertainty of the measured transverse force. It could be noted that the uncertainty due to friction is not so high.

In Fig. 13, the numerical forces are obtained at the displacement measurement frequency (i.e. every 20 μs). As expected, the fit is not perfect at the very beginning of the test because of the following reasons:

  • These is a too weak number of acquisition points in the elastic phase to accurately measure the brutal increase of the forces.

  • The sample equilibrium being not perfect during the first 60 μs, the axial and the transverse forces in the cross sample do not exactly correspond to measured forces at the output bar interfaces (i.e. Fio and Feo multiplied by the friction dependent ratio).

  • The transverse force is determined from the sliding friction coefficient, and as explained in section 3.3, this method overestimates the force at the very beginning of the test, i.e. in the adhesion phase.

Fig. 13
figure 13

Comparison between the experimental forces and the numerical forces obtained from the measured displacements and from the identified model

Full size image

However, during the stationary phase, the measurement consistency is clearly proven. It validates the identified sample model. Although this processing is not performed to measure the friction, it also shows that the friction coefficient used to process the data is consistent.

Simulation of the Whole Apparatus Behavior

The axial and transverse forces in the sample are both determined from the forces at the interfaces between the output bars and the set-up. This determination is based on the equilibrium assumption, which actually implies a quick enough transmission of the wave through the mechanism. A satisfactory, but not perfect, equilibrium is experimentally shown in Fig. 6. However, the incident strain wave εi and the reflected one εr being rather opposite, as shown in Fig. 15, the input force Fi determination from formula (1) is very noise sensitive. A simulation of the whole bar set-up has thus been performed to study this equilibrium. The used software is still ABAQUS in its explicit version.

The aluminum sample is supposed to have the properties given in Sections 4.1 and 4.2. The bi-axial mechanism parts are supposed to be made of the input bar steel (it is actually the case) whose Poisson’s ratio is 0.3 (density and wave celerity given in Table 1), and to remain purely elastic. The same assumptions are used to model the output bars (densities and wave celerities also given in Table 1). The striker initial velocity is 6 m.s−1, which is consistent with experimental measurements (Fig. 15). The selected friction coefficient at the contact surfaces is 0.07, as measured in Section 3.3. The static and the dynamic coefficients are supposed to be the same.

Because of the two symmetry planes (the cutting plane in Fig. 1 and the one normal to the section plane and containing the axis), only a quarter of the system is studied. The bars and the projectile are modelled by 6-node linear triangular prism elements (ABAQUS terminology) whose approximate size is 5 mm. The two parts with the sliding surfaces and the tubes inserted between the sample and the input bar and between the sample and the internal output bar are modelled by the same elements but their rough sizes are respectively 10 mm and 2.5 mm. The triangular part is composed of two triangular prism elements separated by the symmetry plane. The sample is merely composed of four 8-node linear brick elements: one corresponding to the center and three corresponding to the three arms represented in the simplified model. As shown in Fig. 15, element sizes are thin enough to roughly fit the measurements. The chosen time increment is 0.1 μs.

The experimental results display that the contacts in the bi-axial mechanism are not perfect. In Fig. 14, a non-negligible gap can be seen between the sample elongations and the differences between the input and the output bar displacements. As explained in Section 3.4, these quantities would be identical if there was neither clearances nor intermediate strains. The numerical equivalent of this gap is lower, and only due to the elastic strains of the mechanism parts. It implies that the numerical set-up is a little bit stiffer than the real one. However, the stiffness remaining in the same order, it enables to check the general relevance of the set-up.

Fig. 14
figure 14

Comparisons between the sample elongations and the differences between the bar displacements

Full size image

The gauges are glued at the middle of the input bar and on the two output bars at 0.374 m from the interface with the set-up on the external bar, and at 0.612 m on the internal one. The experimental and the numerical strain time-evolutions are compared in Fig. 15. The input gauge first measures the incident wave εi, and then the reflected wave εr. The external output gauge and the internal one measure the external transmitted wave εet and the internal transmitted wave εit. εi can be seen as a loading imposed to the bi-axial set-up whereas εr, εet and εit can be seen as the set-up response to the imposed loading. Figure 15 shows that the simulated εi (proportional to the striker initial velocity) rather fits the experimental one, despite some spurious oscillations. The numerical transmitted waves are a little bit higher than the experimental ones, which is fully consistent with a modelled set-up stiffer than the real one.

Fig. 15
figure 15

Experimental and numerical strain time evolutions at the gauge positions

Full size image

Fig. 16 finally shows that, in spite of numerical oscillations, the input force and the total output force are in mean equilibrium and that both output forces are the same.

Fig. 16
figure 16

Time evolutions of the numerical forces at the interfaces

Full size image

The finite element mesh can be seen in Fig. 17. As the contacts are not perfectly modeled, using a smaller mesh would be useless to better fit the measurements.

Fig. 17
figure 17

Finite element mesh

Full size image

Conclusion

The aim of the study was to check the relevance of a newly designed Hopkinson bi-axial compression set-up. The sample axial compression is directly generated by an internal output bar whereas the transverse compression is indirectly generated by an external output bar via a mechanism. The friction in the mechanism is identified in the relevant dynamic conditions from comparisons between axial and transverse compression tests on cuboid samples. To reproduce the sliding velocities reached at the mechanism sliding interfaces during the bi-axial test, these cuboid samples are made of the bi-axial sample material. The friction being identified, any sample can now be tested.

A calibration bi-axial test has been performed on a cross sample with a simple shape, and therefore easy to model. The measurements show that the device ensures an approximate equality between the axial and the transverse loadings, and the experimental result reliability is proven by a numerical modelling of the bi-axial sample. The set-up can therefore be used in the future for characterization on more complex samples and materials (which was not the aim of this first study).

Finally, the design of an easily buildable set-up generating and measuring a rather isotropic dynamic bi-axial loading has been achieved.