A 90-meter Split Hopkinson Tension–Torsion Bar: Design, Construction and First Tests

Abstract

This article describes the design, construction, and first experimental results of a 90 m-long Hopkinson bar which can perform high strain rate tests in a combined tension–torsion state. The system configuration is analogous to the classic Hopkinson bar technique, consisting of three bars: a pre-stressed bar, an input bar, and an output bar; the sample is placed between the input and output bar. The measurement is also based on the classical three-wave method, where the incident, transmitted and reflected waves are measured. Incident compression and torsional waves are simultaneously generated by the failure of a fragile element that connects the pre-stressed bar to electromechanical actuators; the indirect Hopkinson tension bar technique is exploited, where the compression wave reaches the end of the output bar without stressing the sample and is reflected as a tensile input wave. The length of the bars is designed so that the tensile wave reaches the sample from the output bar side at the same time as the torsion wave comes from the input bar. Void tests were carried out first, for preliminary analysis of the system behaviour. Then, successful tests have been conducted on samples made of AA7075 T6, both in combined and pure tension–torsion states; it has been possible to measure the tension–torsion stress–strain curves, from which the equivalent flow stress–strain curve has been evaluated and compared to the quasi-static ones.

Introduction

The Split Hopkinson Bar (SHB) is the most used device for carrying out dynamic compression and tensile tests on almost any type of material, with strain rates in the order of 10²–10⁴ 1/s [1]. Torsion Hopkinson bar versions have also been developed; the literature is vast on these two types of SHB, and the reader is referred to the review works [2, 3]. Typically, the apparatus is used to extract the constitutive behaviour in terms of stress–strain curve and to evaluate the strain rate hardening effect, if any of the material.

However, in recent years, growing attention has been paid to the execution of high-strain rate tests, aimed at the development and calibration of ductile damage models for the prediction of strain at failure in dynamic conditions [4, 5]. Besides the equivalent plastic strain and stress triaxiality, the most recent models consider the failure to be governed by other important parameters, such as the Lode angle or the third invariant of the deviatoric stress tensor, which give a more complete description of the state of stress [6, 7]. Therefore, in order to achieve a clear understanding of the plasticity and failure of materials, from quasi-static to dynamic conditions, it is fundamental to explore the material behaviour at high strain rate under different types of multiaxial loading conditions.

The calibration of these advanced models requires the study of the behaviour of the material in the multiaxial state of stress. The most used methods to achieve such complex stress states can be divided into 2 categories: (i) adoption of complex shapes for the samples, which are then solicited with monoaxial testing machines [8, 9]; (ii) samples of standard geometry solicited in combined tensile-torsion stress by multiaxial machines [10].

Nowadays, the first method is quite widespread for materials characterization at a high strain rate because advanced technique of image analysis and inverse identification techniques enables measuring, or predicting, plastic flows from the deformation of samples with a complex shape [11].

The second method is less common due to the complexity of test machine set-up to ensure multiaxial stress states from a direct impact loading environment. Cadoni et al. [12] proposed a multiaxial SHB where the dynamic solicitation is superimposed on a hydrostatic load. Just recently, the research group at Oxford University developed a SHB which can combine tension and torsion stress states at high strain rate​ [13, 14].

Aligned with the ongoing trend of innovation in dynamic testing, this study introduces a novel 90 m long Split Hopkinson Tension–Torsion Bar (SHTTB) which enables simultaneous tension–torsion loadings, spanning a wide range of load ratios, including pure tension and pure torsion; pure compression is also possible. The proposed SHTTB takes leverage from traditional SHB configuration for direct tension (pre-loaded, input and output bars) measuring stresses and strains in the sample according to the SHB theory. While it may appear trivial, the different propagation speeds of shear and pressure waves pose a challenge in designing an SHB that effectively acquires distinct input, transmitted, and reflected waves (both tension and torsion) and achieves simultaneous pressure-shear waves in the samples. The SHTTB proposed by the research group at Oxford University (same pre-load configuration) places the sample immediately downstream of the pre-loading system, preferring the compactness of their SHTTB and shear strain measurement via image analysis [13]. Moreover, it is noteworthy that different strategies are addressed to guarantee simultaneous pressure-shear waves on the sample: whereas Oxford’s SHTTB adopts a piezo-driven clamp release to manage the pressure-shear waves synchronisation [15], the solution here proposed is based on the failure of a sacrificial element and on waves propagation theory. An additional distinctive feature that sets apart the proposed SHTTB is the high achievable deformation induced to samples: elongations up to 30 mm and torsion angles up to π in a range of strain rates in the order of 100–1000 1/s. These features make the proposed SHTTB suitable for large tensile-torsion deformation at a high strain rate, giving it uniqueness in the literature as far as the authors are aware.

The article is organised as follows. Sect. “Working Principle” illustrates the operating principle, the Lagrangian space–time diagram and the theoretical formulas which are used to analyse the signals recorded by the strain gauges and to extract the stresses and strain experienced by the sample. Sect. “Design and Realization” illustrates the design and construction of the apparatus, with details on the requirements that led to the remarkable final system length of 87 m. Sect. “Experimental Tests” illustrates the results of the first tests carried out, which initially included void tests (without sample) for the identification of the main practical problems and the preliminary characterization of the system, in particular the possible attenuation of the waves. Four tests on AA7075-T6 aluminium are then shown, in both combined and pure tension/torsion states at an equivalent strain rate of approximately 100 1/s, the results of which are compared with quasi-static tests; furthermore, the correction of the deformation through image analysis and balance verification will be shown.

Working Principle

Split Hopkinson bars typically consist of 3 aligned rods having a diameter much smaller than their length, called striker, input and output bars, respectively. The impact of the striker bar on the input bar determines the generation and propagation in the latter of a mechanical stress wave; this wave travels at the speed of sound and reaches a sample of interest positioned between the input and output bars. As the sample is deformed, the stress wave is partially transmitted into the output bar and partially reflected back into the input bar. The measurement of these waves makes it possible to determine the stress and strain experienced by the sample, even up to large deformations and failure, while the bars remain in their elastic range.

In theory, both extensional and torsional waves can be made to travel in the bars, and the principles of operation and measurement behind longitudinal and torsional SHB are the same. However, torsional and longitudinal waves travel at different speeds, the former being slower than the latter; therefore, for the specimen to be simultaneously loaded in tension and torsion, the arrival of the two pulses on the specimen must be properly synchronised.

The fundamental principle of the device here presented is to generate an extensional and a torsion wave simultaneously, making the former travel a suitably greater distance so that their arrival on the sample is synchronized. In addition, hollow samples are used, which permit to put into direct contact the extremities of the input and output bar. Instead of launching a striker bar, a pre-stressed bar is statically loaded both in tension and in torsion; analogously to the direct tension SHB developed and today routinely used by the authors [16], the load is quickly released through the failure of a fragile element placed at the beginning of the pre-stressed bar. The sudden release generates a torsion and compression wave; the latter travelling faster reaches the sample first, but passes into the output bar which is in direct contact with the input bar, without soliciting the hollow sample. The compression wave reaches the free end of the output bar and is reflected as a tensile wave; at this point, it returns to the sample just as the torsion wave arrives from the input bar. In practice, a direct torsion SHB system is combined with an indirect tensile SHB system; note that the sample will need special terminations for applying combined traction and torque. Here follows the space–time analysis of the system.

Lagrangian Diagram

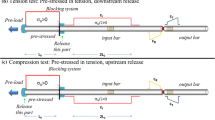
Figure 1 shows the Lagrangian space–time diagram of the system, which permits obtaining the position of the shear and normal wave fronts as a function of time. The lengths of the input and output bar are indicated with L_I and L_O, respectively, the length of the pre-loaded bar is L_pε but only a portion of length L_pγ is pre-loaded in torsion.

Fig. 1

Lagrangian space–time diagram for evaluating the position of normal and torsional waves during time

At the load release, half of the stored axial force and torque will travel towards the sample as elastic normal (blue line) and shear (red line) waves; in addition, the spatial length of the waves is twice the length of the pre-stressed bar. These are the incident waves, whose corresponding strain amplitudes are indicated as ε_I and γ_I. The normal and shear waves propagate at speeds ${C}_{\varepsilon }=\sqrt{{E}_{b}/\rho }$ and ${C}_{\gamma }=\sqrt{{G}_{b}/\rho }$, respectively, where E_b and G_b are the normal and tangential elastic moduli and ρ is the density of the bars’ material. The incident normal wave is compressive (dashed line) and is reflected as a tensile one after it has reached the free end of the output bar. A “rendezvous” between the tensile ε_I and torsional γ_I incident waves takes place at the sample location at time t_r. Then, as aforementioned, the waves are partially transmitted (ε_T and γ_T) and reflected (ε_R and γ_R).

The diagram shows 7 locations where the static preloads and the travelling waves can conveniently be measured by strain gauges. While the transmitted waves can be measured close to the sample, the incident and reflected waves must be measured at a greater distance to avoid overlaps. Note that, the measurement of the first compressive wave transit at SGax2 is redundant in real tests; however, it will be used for verification purposes in early void tests.

Design Requirements

The project aimed to meet the following requirements:

• i) synchronous arrival of tension and torsion loading waves on the sample; this implies the following relation to be satisfied: $\left({L}_{P\varepsilon }+{L}_{I}\right)/{C}_{\gamma }=\left({L}_{P\varepsilon }+{L}_{I}+{2L}_{O}\right)/{C}_{\varepsilon }$;

• ii) equal time duration of the extensional and torsional waves; this determines the further constraint ${L}_{P\varepsilon }/{C}_{\varepsilon }={L}_{P\gamma }/{C}_{\gamma }$;

• iii) avoid overlapping of the transmitted wave (ε_T) with the respective reflected wave (ε_R); this means that ${L}_{O}>2{L}_{p\varepsilon }$; given that ${L}_{P\gamma }$ is shorter than ${L}_{P\varepsilon }$, and the strain gauge SGsh3 will be installed close to the sample, this automatically prevents from overlap of γ_T with its reflection coming from the free end of the output bar;

• iv) diameter of the bars and samples for practical engineering use of the order of 20 mm;

• v) achievement of high elongations (up to 30 mm) and torsions (up to π) in the sample, in order to guarantee the rupture of ductile metallic materials with strain to failure as high as 1.5–2.5.

The Ti6Al4V alloy was selected because of its high specific strength and low elastic modulus. An elastic modulus of 110 GPa, a tangent modulus of 43 GPa, and a yield strength of 900 MPa were considered for design purposes. Considering a maximum axial and torsional preload of 100 kN and 300 Nm, respectively, the following tentative lengths were chosen for the bars: length L_Pε of the pre-stressed bar of 9.79 m (of which the first 6.00 m, L_Pγ, is subjected to both torsion and tension), output bar length L_O = 20.75 m, input bar length L_I = 55.97 m; the total system length is nearly 87 m. These values are resumed in Table 1.

Table 1 length in [m] of the designed system (* the final L_O length will be 19.85m)

Since the actual properties of the supplied titanium, and therefore of the wave velocities, could be slightly different, it was decided to initially install an output bar with an intentionally longer length than necessary (21.2 m). This would make it possible to cut to exactly the length needed to synchronize the tensile and torsion waves on the sample, once the actual wave velocities were accurately determined. In fact, after installation, it will be seen that the final length of the output bar will be 19.85 m.

Theoretical formulas

Normal and shear stress, strain and strain rate of the specimen can be computed by measuring the waves that propagate into the bars using the strain gauge rosettes appropriately placed, which convert the stress waves into proportional analogic signals. Then, the mechanical behaviour of the sample material can be evaluated by the Kolsky analysis method.

We consider the scheme of Fig. 2, where the central cylinder represents the sample in contact with the bars’ extremities; note that side 1 and side 2 of the sample are the interfaces with the 56 m long input bar and the 20 m long output bar, respectively. The displacements u₁, u₂ and rotations θ₁, θ₂ of the opposite faces of the sample can be obtained by the elementary theory of one-dimensional propagation of elastic waves:

Fig. 2

Scheme of travelling waves and displacements at specimen position in the Tension–Torsion Split Hopkinson Bar

$\left\{\begin{array}{c}{u}_{1}\left(t\right)=-{C}_{\varepsilon }{\int }_{0}^{t}{\varepsilon }_{T}\left(\tau \right)d\tau \\ {u}_{2}\left(t\right)={C}_{\varepsilon }{\int }_{0}^{t}\left[{\varepsilon }_{R}\left(\tau \right)-{\varepsilon }_{I}\left(\tau \right)\right]d\tau \end{array}\right.$

(1L)

$\left\{\begin{array}{c}{\theta }_{1}\left(t\right)=\frac{{2C}_{\gamma }}{D}{\int }_{0}^{t}\left[{\gamma }_{I}\left(\tau \right)-{\gamma }_{R}\left(\tau \right)\right]d\tau \\ {\theta }_{2}\left(t\right)=\frac{{2C}_{\gamma }}{D}{\int }_{0}^{t}{\gamma }_{T}\left(\tau \right)d\tau \end{array}\right.$

(1T)

By the same theory it is possible to also obtain the loads P₁, P₂ and torques T₁, T₂ exchanged between the sample and the bars at their interfaces:

$\left\{\begin{array}{c}{P}_{1}\left(t\right)={{A}_{b}{E}_{b}{\varepsilon }_{T}\left(t\right)}\\ \\ {P}_{2}\left(t\right)={A}_{b}{E}_{b}\left[{\varepsilon }_{R}\left(t\right)+{\varepsilon }_{I}\left(t\right)\right] \end{array}\right.$

(2L)

$\left\{\begin{array}{c}{T}_{1}\left(t\right)={G}_{b}\frac{\pi {D}^{3}}{16}\left[{\gamma }_{R}\left(t\right)+{\gamma }_{I}\left(t\right)\right]\\ \\ {T}_{2}\left(t\right)={G}_{b}\frac{\pi {D}^{3}}{16}{\gamma }_{T}\left(t\right)\end{array}\right.$

(2T)

From Eqs. (1_L), (2_L) and (1_T), (2_T) it is possible to compute the engineering average value of normal and shear stress, strain and strain rate experimented by the sample:

$\varepsilon \left(t\right)=\frac{{u}_{2}\left(t\right)-{u}_{1}\left(t\right)}{{L}_{s}}=-\frac{{C}_{0}}{{L}_{s}} {\int }_{0}^{t}\left[{\varepsilon }_{T}\left(\tau \right)-{\varepsilon }_{I}\left(\tau \right)+{\varepsilon }_{R}\left(\tau \right)\right]d\tau$	(3La)	$\gamma \left(t\right)=\frac{{C}_{t}{D}_{S}}{{L}_{s}D} {\int }_{0}^{t}\left[{\gamma }_{T}\left(\tau \right)-\left\{{\gamma }_{I}\left(\tau \right)-{\gamma }_{R}\left(\tau \right)\right\}\right]d\tau$	(3Ta)
$\dot{\varepsilon }\left(t\right)=\frac{1}{{L}_{s}}\frac{d\left[{u}_{2}\left(t\right)-{u}_{1}\left(t\right)\right]}{dt}=-\frac{{C}_{0}}{{L}_{s}} \left[{\varepsilon }_{T}\left(t \right)-{\varepsilon }_{I}\left(t \right)+{\varepsilon }_{R}\left(t \right)\right]$	(3Lb)	$\dot{\gamma }\left(t\right)=\frac{{C}_{t}{D}_{S}}{{L}_{s}D} \left[{\gamma }_{T}\left(t \right)-\left\{{\gamma }_{I}\left(t \right)-{\gamma }_{R}\left(t \right)\right\}\right]$	(3Tb)
$\sigma \left(t\right)=\frac{{P}_{1}\left(t\right)+{P}_{2}\left(t\right)}{2{A}_{S}}=\frac{{A}_{b}{E}_{b}}{2{A}_{S}}\left[{\varepsilon }_{I}\left(t \right)+{\varepsilon }_{R}\left(t \right)+{\varepsilon }_{T}\left(t \right)\right]$	(3Lc)	$\tau (t)=\frac{2{T}_{s}}{(\pi {D}_{S}^{2}){t}_{S}}=\frac{G{D}^{3}}{16{D}_{S}^{2}{t}_{S}}\left[{\gamma }_{T}\left(t\right)+{\gamma }_{I}\left(t\right)+{\gamma }_{R}\left(t\right)\right]$ ${T}_{S}\left(t\right)=\frac{1}{2}\left({T}_{1}+{T}_{2}\right)$	(3Tc)

where L_S, and A_S represent respectively the initial length and cross-sectional area of the sample, while D_s and t_s are its initial diameter and thickness, respectively. If P₁(t) is equal to P₂(t) and T₁(t) is equal T₂(t) the sample deforms uniformly and is in dynamic equilibrium, then:

${P}_{1}\left(t\right)={P}_{2}\left(t\right)\Rightarrow {\varepsilon }_{T}\left(t\right)={\varepsilon }_{I}\left(t\right)+{\varepsilon }_{R}\left(t\right)$	(4L)
${T}_{1}\left(t\right)={T}_{2}\left(t\right)\Rightarrow {\gamma }_{T}\left(t\right)={\gamma }_{I}\left(t\right)+{\gamma }_{R}\left(t\right)$	(4T)

Therefore, the engineering normal and shear stress, strain rate and strain that take place in the sample can be obtained from the classical “reduced” formulae:

$\dot{\varepsilon }(t)=-\frac{2{C}_{0}}{{L}_{s}}{\varepsilon }_{R}\left(t\right)$	(5La)	$\dot{\gamma }\left(t\right)=\frac{2{C}_{t}{D}_{S}}{{L}_{S}D} {\gamma }_{R}\left(t \right)$	(5Ta)
$\varepsilon (t)=-\frac{2{C}_{0}}{{L}_{s}}{\int }_{0}^{t}{\varepsilon }_{R}\left(\tau \right) d\tau$	(5Lb)	$\gamma \left(t\right)=\frac{2{C}_{t}{D}_{S}}{{L}_{S}D} {\int }_{0}^{t}{\gamma }_{R}\left(\tau \right)d\tau$	(5Tb)
$\sigma (t)=\frac{{A}_{b}\cdot {E}_{b}}{{A}_{s}}{\varepsilon }_{T}\left(t\right)$	(5Lc)	$\tau (t)=\frac{G{D}^{3}}{8{D}_{S}^{2}{t}_{S}}{\gamma }_{T}\left(t\right)$	(5Tc)

Excluding time from previous Eqs. (5a) to (5b), i.e., synchronizing the reflected and transmitted signals, the axial stress–strain and shear stress-shear strain laws of the material of the sample at a high strain rate are achieved. The equivalent stress and strain in a multiaxial state can be computed according to the von Mises equations:

$${\sigma }_{eqv}=\sqrt{{\sigma }^{2}+3 {\tau }^{2}}$$

(6a)

$${\varepsilon }_{eqv}=\sqrt{{\varepsilon }^{2}+{\gamma }^{2}/3}$$

(6b)

Numerical Simulation

A simple numerical model has been developed in Abaqus/Explicit software (Fig. 3a), using beam elements with solid circular section, just to analyse how the waves will look like and to evaluate the effect of lumped masses. The sample was simulated using beam elements with a tubular cross-section; for its material, a bilinear elastic–plastic constitutive model was used, just to assign a plausible behaviour, with an elastic modulus of 200 GPa, yield strength of 400 MPa and tangent modulus of 1 GPa.

Fig. 3

a Scheme of the FE model, b normal strain waves recorded by virtual strain gauges SGax2, SGax3 and SGax4, c shear strain waves recorded by virtual strain gauges SGsh2 and SGsh3

The tentative bar lengths reported in Sect. “Design Requirements”, Table 1, have been used. The pre-stressed and input bars have been simulated as tied, while the contact between the input and output bars has been mimed by a wire connector of axial type, which bears only compressive loads. Since the actual system will be obtained by joining several bars with threaded ends and collars, as will be shown in Sect. “Design and Realization”, lumped masses have been placed along the bars to simulate the effect of axial and rotary inertia of such collars; instead, the discontinuities due to contacts and threads between the bars have not been modelled.

Figure 3b shows the signals, converted to normal stress σ (S₁₁, according to Abaqus nomenclature), measured by the virtual strain gauges placed at half and at end of the input bar, named the SGax2 and SGax3 according to the scheme in Fig. 1, and at half of the output bar, named SGax4. The light blue curve refers to the SGax2, which reads the first transit of the compressive wave; the blue one refers to SGax3 which reads the first transit of the compressive wave and the transmitted tensile wave, that will used in the real experiments for accurately measuring the axial load on the sample; the dark blue curve refers to the SGax4, which read a first compressive wave transit, then the tensile input wave and the reflected compressive wave. The shape of the waves is as expected but somewhat ideal, since neither wave dispersion nor peaks or fluctuations are observed. On the one hand, this was expected both because beam elements were used instead of 3d ones and because the threaded connections between the bars were not modelled. On the other hand, the absence of any peak suggests that the axial inertia of the connecting collars has a negligible effect.

Figure 3c shows the signals, converted to shear stress τ (S₁₂, according to Abaqus nomenclature), measured by virtual strain gauges placed at half of the input bar and immediately after the specimen on the output bar, namely the SGsh2 and SGsh3 respectively, according to the scheme in Fig. 1. The brilliant red curve refers to the SGsh2, which reads the first transit of the torsional wave and the reflected wave; the dark red curve refers to the SGsh3, which reads the transmitted torsional wave. In this case, the absence of dispersion also has a physical origin since radial inertia is not involved in the deformation of the bars; nevertheless, the rotary inertia of the connecting collars can be noted in the form of small peaks. A detailed analysis was beyond the scope of the work; however, the obtained results are not surprising since the collars increase the mass towards the outer radius of the cross-section, determining a greater increase in the moment rather than axial impedance.

Design and Realization

Parts Design

All the parts that make up the system have been designed internally with CAD software and made in the workshops. The most significant components are shown here.

The static load was conceived to be applied by two actuators mounted in series: an electromechanical axial jack, equipped with a thrust bearing, pulls one end of a large rod; the latter passes through a hollow shaft which receives torque from a gear motor. Figure 4a and Fig. 4b show the CAD rendering and real installation of the loading system.

Fig. 4

Electromechanical actuators for the application of static preload. a CAD rendering (CAD section view in supplementary material), b real installation

The rod is connected at the other end to the pre-stressed bar through a sacrificial element, shown in Fig. 5a, that is specifically designed to sustain the desired amount of axial load and torque. The sacrificial element is hollow and has a sharp notch, that helps localise the failure in the section of minimum ligament t (Fig. 5b). Based on the authors’ experience with previously developed SHTB [16], the 1.2714 steel was selected for its material; by quenching at 915 °C and subsequent tempering in oil, a typical strength of 2250 MPa is achieved. This information was used in simple FE simulations for approximately predicting the combination of axial load and torque that the sacrificial element can bear withstand a sudden rupture. Figure 5c shows the estimated loads as a function of ligament thickness. All experimental tests successively shown in Sect. “Experimental Tests” were carried out with a ligament thickness t equal to 1.0 mm; the corresponding loads are reported as separate markers in Fig. 5c, denoting an acceptable level of accuracy.

Fig. 5

Sacrificial element, a real view, b CAD section view (dimensions in mm), c estimated axial load and torque combinations as a function of ligament thickness

The static torsion block system must prevent torsion at the end of the L_pγ part but must allow axial sliding; it was made using an external cam with an eccentric profile which abuts unilaterally on radially sliding supports. In this way, apart from a limited frictional interaction, the rod is free to rotate through an indefinite angle after the release of the static load. The drawing and realized parts are shown in Fig. 6a and Fig. 6b.

Fig. 6

Static torsion block, a CAD rendering (CAD section view included in supplementary material), b real installation

Given that the maximum length available among various titanium suppliers was 6 m, the system was created by joining several bars. The connection between the bars, shown in Fig. 7, is made by M12 internal threading for the transfer of axial loads. The bars are assembled by screwing one into the other until they are fully seated; the direction of the threads is such that the first torsional wave, which is of greater amplitude, acts in the direction of tightening the connections. Notably, the subsequent reflected waves act in both directions of screwing and unscrewing the connections, but they are typically smaller in amplitude than the first one because energy is absorbed by plastic deformation of the sample and by some friction at the supports. The collars have the task of preventing significant loosening due to these subsequent waves and vibrations. In addition, the collars are made of AA7075-T6 with the smallest possible section to minimize the mechanical impedance variation. The supports of the bars, the static tension block, and the end arrest at the output bar extremity are substantially identical to those used in [16] (pictures and drawings are included in the supplementary material).

Fig. 7

Bars connection a CAD section view (dimensions in mm), b real installation

Installation

Because of its relevant length, the system has been installed at the open air on the roof of the Civil Engineering building of Università Politecnica delle Marche. A protective case has been applied along the entire length. Larger cabinets were adopted at the beginning and at the end of the bars, where the electro-mechanical actuators and the end-arrest are placed. Furthermore, a test room was created with a small prefabricated shed, which contains the sample, the digital and PC acquisition system, and the high-speed camera. Figure 8 shows the final appearance of the entire rig.

Fig. 8

Facility installed on the roof of Engineering Building at Marche Polytechnic University (Lat.43.58776°N, Long.13.51667°E)

Particular attention has been paid to the alignment of the 80 supports; this phase has been accomplished by placing a laser pointer inside the first support of the pre-stressed bar and adjusting the intermediate ones so that the laser beam could reach the centre of the last support of the output bar. Any misalignment of the supports would result in strong forcing and axial blocking of the bars. After the first alignment of the supports with the laser, the entire set of interconnected bars of approximately 90 m in length could be slid axially with a limited force of the order of 200 N. Therefore, as a verification procedure, it is periodically monitored that sliding occurs with forces not exceeding 200–300 N.

Instrumentation

The system is substantially instrumented through strain gauge bridges like a classic split Hopkinson bar, except that the measurement stations are doubled in order to measure both extensional and torsional waves. In particular, according to the scheme already shown in Fig. 1, the pre-loading amplitudes (ε_P and γ_P), the incident waves (ε_I and γ_I), the transmitted waves (ε_T and γ_T), and the reflected waves (ε_R and γ_R) are measured. All measuring stations are configured as full Wheatstone bridges. The bridges for reading the longitudinal wave consist of two T-shaped rosettes with a pair of strain gauges at 0–90° each, of the MicroMeasurements® WK-00-062TT-350 type, glued on diametrically opposite points of the bars; the bridges for reading the torsion wave consist of two T-shaped rosettes with a pair of strain gauges at ± 45°, of the type MicroMeasurements® WK-00-062LV-350, glued on diametrically opposite points of the bars. In principle, this type of installation guarantees a measurement of the axial force completely decoupled from the torque, and vice versa [17]. Due to the outdoor installation which can lead to larger temperature variations compared to an internal laboratory, HBM Z70 glue was used which guarantees an operating range from -55 to 100 °C; in any case, the glue and the strain gauges are never exposed to direct solar radiation, and the temperature of the bars has been verified never to exceed 50 °C even in the summertime.

The power supply and acquisition of the strain gauge signals are performed through the HBM® Genesys 2tB system, which allows the simultaneous sampling of all the channels of interest at 500 kHz with a resolution of 16 bits. A high-speed camera, model Photron® SA4, is also used, which allows images to be acquired at a sampling frequency of 100 kfps with a resolution of 192 × 128 pixels. The start of images and signals recording is triggered on the drop of the static pretension.

Experimental Tests

Void Tests

In order to evaluate the general behaviour of the system, especially the effect of the bars connections, and to accurately measure the travelling speed and attenuation of the real waves, some void tests were first conducted without samples and without connection between input and output bars. In the first test, a handlebar (Fig. 9a) was placed at the end of the input bar to prevent indefinite rotations of the input bar, while the output bar was simply used as a momentum trap. The procedure consisted of applying slowly the axial load on the preloaded bar by means of the axial jack, up to 25 kN, and then the torque load was slowly applied by means of the gear motor. The failure of the sacrificial element (Fig. 9b) occurred at approximately 160 Nm torque. The signals recorded by the strain gauges in the input bar are converted into axial load and torque are shown in Fig. 9c.

Fig. 9

First void test on input bar only. a handlebar at the end of the input bar used to prevent indefinite rotation, b failed sacrificial element, c travelling waves measured on input bar by 0–90° (blue) and ± 45° (red) strain gauge rosettes

Some features can be observed in the load and torque signal. An evident problem in the proposed signals is given by the fluctuations and anomalous shape of the reflected waves, but this is simply due to the great inertia of the handlebar used in this first test. In subsequent tests, iron wires were rolled up 2 times around the bars and fixed to the frame to stop the indefinite rotations, while concrete absorber blocks were placed at the end of the output bar to stop the axial displacements.

The first incident waves appear to have a reasonably rectangular shape. Some peaks are visible, likely due to discontinuities and collars among the bars; they little affect the longitudinal waves (blue curve in Fig. 9c), whereas slightly larger fluctuations are observed in the torsional waves (red curve). Note that these peaks are like those estimated numerically; however, if necessary, they can be easily filtered out.

A small “precursor” is observed in the incident torsion wave; this was an undesirable effect due to the interaction of axial and torsional loads in the static blocks: it was found that when axial preload was applied, the shoulders of the eccentric collar were not in contact with the static torsion block; this meant that when the static torsional load was applied by the gearmotor, a small part of it was carried by the static axial block (because of friction) so that all 9.8 m of the preloaded bar were stressed by the static torsion. Consequently, when the axial release wave reaches the axial block, a torque wave (of limited amplitude and opposite sign to the expected torsion wave) begins to travel along the input bars. As will be shown in the next section, other problems can arise at the static torsion block, if the cam and shoulders are not efficiently lubricated.

A small limitation is represented by possible misalignments of the strain gauge rosettes with respect to the axis of the bars. Naturally, this aspect should be considered also in standard SHB systems for tension and compression, where it is easily overcome by calibration and does not represent a major problem. In the present system, if the alignment is not accurate, unintentional spurious measurements of the strain gauges are likely to occur, meaning that torsional strain gauges may read non-zero signal when they are solicited by axial waves or, on their turn, axial strain gauges may read non-zero signal when solicited by torsional waves. The latter is the case that occurred in this first test, as it can be seen in Fig. 9 that the axial strain gauge measured an apparent small axial load when it was passed through by the torsion wave; this is not possible since axial waves travel faster. Hence, axial strain gauges were re-installed with more accurate alignment for subsequent tests.

By knowing the exact position of the strain gauges, it was possible to measure the C_ε and C_γ, which turned out to be 4892 and 3027 m/s, respectively. By measuring the density of the bars with a precision balance, the physical properties were determined; they are resumed in Table 2. Further tests confirmed these values.

Table 2 Properties of bars material

With this information, it was found that the length of the output bar initially installed (21.2 m) was 1.35 m in excess; therefore, the bar was cut to the final length of 19.85 m. The strain gauges were glued on the bars at the following positions: SGax2 and SGsh2 on the input bar at 23.25 m from the beginning; SGax3 and SGsh3 approximately 0.5 m away from the sample, on the input and output bars, respectively; SGsh4 at half of the output bar, 9.93 m away from the sample.

Finally, before proceeding with the execution of tests with the samples, 2 void tests were carried out by separately applying a compression pulse and a torsion pulse in order to evaluate the possible attenuation of the waves during propagation for long distances. Again, the pulses were made to travel along the 56 m long input bar and measured by the strain gauge rosettes SGax2 and SGsh2, according to the scheme of Fig. 1. The results are shown in Fig. 10, where a nearly linear attenuation with time (i.e. with travelled distance) is found. According to the wave attenuation and dispersion theory, an exponential decay of the type ${e}^{-\gamma d}$ would be expected [18], where d is the travelled distance and $\gamma$ is a propagation coefficient which in general is a function of frequency; if the material is assumed to be simply linear-elastic, attenuation is null, and only dispersion due to geometrical effects (Pochhammer-Chree effect) is expected. The almost perfect linear decay with time can be interpreted as a predominant importance of friction on supports with respect to the internal material damping. On the other hand, considering that consecutive peaks correspond to a travelled distance of approximately 56 m, the following decrease rate can be estimated: 0.03%/m and 0.1%/m for normal and torsional waves, respectively. These attenuation factors have been considered as simple scale factors in the subsequent signals manipulation for the computation of strain amplitudes; the correction of waveform accounting for geometrical dispersion was not considered at this stage.

Fig. 10

Attenuation of waves propagating along the input bar after several reflections: a normal stress wave, b torsional wave

First Combined Test on AA7075 T6

This paragraph shows the first of two combined tension–torsion tests carried out on AA7075-T6 samples, which have been obtained by CNC machining starting from a thick plate. Such a material has been chosen since it is known to be almost insensitive to strain rate; in fact, its Johnson–Cook sensitivity parameter C is found to be in the order of 0.024–0.059 [19, 20]; in [21] a strain rate threshold of about 150 1/s was found below which the sensitivity can be neglected. In this way, the obtained curves can be compared with quasi-static ones for validation purposes.

As aforementioned, the samples are hollow in order to accommodate the ends of the input and output bars, which are in direct contact so as to allow the transit of the incident compression wave without deforming the sample itself. Special terminations were designed for transmitting axial and torsional loads, consisting of shoulders and teeth that give the peculiar shape similar to a “chess rook”. The overall geometry is shown in Fig. 11. The inner diameter is 12.1 mm, while the outer diameter is 14 mm; the constant section length is 12 mm. In addition, this design ensures an almost constant shear stress in the section.

Fig. 11

Geometry of the hollow sample: a 2D section view, b picture of a real specimen with peculiar teeth for application of torsion load, c 3D CAD section view, highlighting the connection of the sample and the direct contact between input and output bar for first compressive wave transit

The first test was conducted before cutting the output bar to 19.8 m. In this way, the tension wave was observed to come with a little delay with respect to the torsion load. Nevertheless, useful information has been recorded for determining the stress–strain curve of the material up to failure. The applied static preload was 23 kN and 190 Nm.

Figure 12 shows the acquired signals from strain gauges; for the sake of clarity, the signals are time-shifted (without dispersion correction) to the sample location. Note that the torsion strain is intended as shear strain ${\varepsilon }_{xy}={\gamma }_{xy}/2$. It is observed that, the incident axial strain wave had the typical rectangular shape. On the other hand, besides the small precursor of opposite sign as already shown in the void test, the torsional incident wave was characterized by a very smooth ramp. This further undesired effect is due to an imperfect interaction at the torsional static block, with excessive friction forces at the eccentric cam and at the sliding shoulders; this was avoided in successive tests by more efficient lubrication.

Fig. 12

Signals acquired during first combined test on AA7075 T6 sample

In addition, the tensile loading wave arrived at the sample approximately 600 μs after the torsional one. The temporal evolutions of strain and stress, as computed by Eqs. (5) are shown in Fig. 13a and Fig. 13b, respectively. It is noted that the material is close to yielding when the shear stress approaches 230 MPa; then the axial stress jumps in, determining a drop in the torsional load. Nevertheless, reasonable axial and shear stress–strain behaviours are achieved, as shown in Fig. 13c; the resulting equivalent stress–strain is reconstructed in Fig. 13d, according to von Mises theory. The equivalent strain rate was approximately 100 1/s. The fracture occurred approximately at axial strain $\varepsilon$=0.1 and shear angle ${\gamma }_{xy}$=0.18. Figure 14 shows the sample before and after the test. The video of the test is available along with the supplementary data provided with the publication.

Fig. 13

Results of first combined test. a temporal evolution of strains, b temporal evolution of stresses, c reconstructed axial and shear stress–strain curves, d reconstructed equivalent strain–stress curve

Fig. 14

Sample installed between the input and output bar. a before the test, b after the test

Second Combined Test on AA7075-T6

A second test was performed after the output bar had been cut at its final length of 19.8 m. This permitted to synchronise the arrival of axial and torsional waves at the sample location. In this test, the static preload was 25 kN and 130 Nm. The acquired signals are shown in Fig. 15. In this case, the interaction between the pre-stressed bar and the static torsional block was improved, so the incident torsional wave has a regular rectangular shape, and the precursor is almost negligible. The resulting stress and strain evolutions are reported in Fig. 16.

Fig. 15

Signals acquired during second combined test on AA 7075 T6 sample

Fig. 16

Results of second combined test. a temporal evolution of strains, b temporal evolution of stresses, c reconstructed axial and shear stress–strain curves, d reconstructed equivalent strain–stress curve

Note that in this test the maximum incident torque load is lower than in the previous test, whereas the tension wave is only slightly higher. For this reason, the sample reached 0.08 of elongation and 0.20 of shear angle, without failure. It can be stated the applied loads are barely above the yielding of the sample but not enough for achieving the failure; as a consequence, the equivalent strain rate was approximately 50 1/s, which can be considered a sort of lower bound of the achievable strain rates.

Again, pictures have been recorded during the test; Fig. 17 shows the first and last significant frame, while the video is available along with the supplementary material provided with the publication.

Fig. 17

Pictures of the sample captured by the high-speed camera. a before the test, b during the test. Note the longitudinal lines drawn on top; the edges inside the dashed green regions and the red dots are used to estimate the normal and shear strains, respectively, by image analysis

Pure tensile and Pure Torsion Tests by SHTTB

For further validation, pure tensile and pure torsion tests have been conducted with the developed Split Hopkinson Tension–Torsion System. In the pure tensile test, only axial preload was applied by means of the screw jack actuator until the failure of the sacrificial element, which occurred at 46 kN; in the pure torsion test, only static torque was applied to the pre-stressed bar by means of the gear motor until the failure of the sacrificial element, which occurred at 180 Nm. The results of these tests are shown in Fig. 18 directly in terms of equivalent stress–strain. Note that the specimen subjected to pure torsion didn’t fail.

Fig. 18

Results in terms of equivalent stress–strain curve. a pure tension test, b pure torsion tests

Equilibrium Verification

The force equilibrium can be verified for all types of tests by analysing the incident, reflected and transmitted waves, and plotting the loads at both sides of the samples in the two tests. Figure 19a and b show the measured incident, reflected and transmitted waves for pure tension and pure torsion tests, respectively. Note that these signals are unfiltered. Figure 19c shows the axial forces as computed at the input and output bar interfaces by Eqs. (2L), while Fig. 19d shows the torques as computed at the input and output bar interfaces by Eqs. (2T).

Fig. 19

Verification of dynamic equilibrium in the sample by analysis of acquired signals and comparison of loads at the input anput ba bar sides. a normal strain waves in pure tension test, b shear strain waves in pure torsion test, c forces in the pure tension test computed by Eqs. (2L), d torque in the pure torsion test computed by Eqs. (2T)

It is observed that, despite the considerable length of the SHTTB system, the situation is not much different from the typical one encountered with standard SHB, with limited additional fluctuations likely due to connections and collars. The equilibrium is very well satisfied in terms of load difference between the input and output bar side on the sample, except for small discrepancies at the very beginning of the loading part or at the steepest ramps. In any case, the signals of the transmitted waves are always pretty clear, with negligible fluctuations or ringing, meaning that they can be used to determine the loads in the sample with acceptable accuracy.

Image Analysis for Strain Correction

It is clear from Figs. 13 and 16 that the strains as evaluated from Eqs. (5b) tend to slightly overestimate the strain experienced by the specimen, especially in the early part of the loading history, across material yielding, where imperfections in experimental data compromise the accuracy of the reconstructed stress–strain curves. This is a very well-known problem also in standard SHB systems, which is related to a few causes, such as non-uniaxial stress states at the bar-sample interface, wave dispersion, force disequilibrium [1]. Furthermore, there is a transition from the sample gauge area to the gripping area, where the section is not constant so that strain will have a non-perfectly uniform distribution; it must be admitted that also this issue is typical for standard SHB systems. Therefore, image analysis, based on methods such as digital image correlation [22] or specimen silhouette determination [23], is often employed in the literature in order to improve and validate the reconstructed behaviour of the specimen at high strain rate, even in combination with recursive finite element approaches.

A thorough description of digital image post-processing is behind the scope of this paper; nevertheless, a simple but effective procedure has been implemented in Matlab® software to extract the average shear and normal strain in the gauge area of the sample. The straight lines parallel to the axis were drawn on the sample before the tests, and are used to extract the shear angle, by measuring the average slope (Fig. 17b) that they assume with respect to the undeformed configuration; knowing the focal length of the optics used and the working distance, the perspective effect due to the 3d shape of the sample was corrected with simple geometric relationships. The edges of the gripping fixture have been used within a simple DIC procedure to track their relative motion during the test thus to extract the normal strain as a sort of video-extensometer; alternatively, circumferential lines drawn on the surface of the sample have been used in the pure tension test. Even if it may not represent a robust and exhaustive approach, this method provided reasonable results considering the limited deformation of the specimens here tested. More sophisticated approaches will probably be needed for studying more ductile materials where larger deformations, and especially larger rotations, will be involved.

Figure 20 shows the comparison of the strain as measured by SHB formulas and image analysis. A good agreement is generally observed, with a small overestimation of the first method. It must be admitted that the strain correction performed by using the strain computed with image analysis is not much different from what can be obtained by manually correcting the initial slope of the stress–strain curve obtained by SHTTB formulas. However, this can be considered as a piece of validation of the experimental procedure.

Fig. 20

Comparison of strain evolution on samples as measured by SHB formulas (solid lines) and image analysis (dashed lines)

Comparison with Quasi-Static Tests

Finally, samples with the same geometry and materials as those tested with the new SHTTB system have been subjected to quasi-static tests by means of a bi-axial testing machine; an electromechanical Zwick® Z050 THW AllroundLine has been used, which is equipped with a linear crosshead with 50 kN load cell and a torque drive with 200 Nm torsiometer. The quasi-static pure tension and pure torsion tests have been performed in displacement control at strain rate of 10⁻⁻³ 1/s, while the combined tension–torsion quasi-static tests have been performed in load control, imposing a force-torque loading path analogous to the dynamic tests: considering target loads of 25 kN and 130 Nm to be reached at the same time (200 s), the speeds of loading ramps were set to 125 N/s and 0.65 Nm/s. The axial and shear strain were measured with the same image analysis method used in SHTTB tests. All tests were conducted up to specimen failure.

Figure 21a shows a picture of the sample during the combined tension–torsion, while Fig. 21b shows the equivalent stress–strain curves obtained from all quasi-static tests. A consistent behaviour is observed; it can be seen that the conversion of the pure torsion stresses to equivalent ones using Eqs. (6) is well comparable to those coming from pure tensile tests, even if a perfect overlap is not necessarily obtained.

Fig. 21

Quasi-static tension–torsion tests: a specimen installed into the Zwick Z050 THW machine, b equivalent stress–strain curves obtained with the different type of loads

The results of the dynamic tests performed with the SHTTB are compared with the quasi-static ones in Fig. 22. Note that the strains computed by image analysis are used for the dynamic tests.

Fig. 22

Comparison of equivalent flow stress curves obtained by pure tension, pure torsion, combined tension–torsion tests conducted with SHTTB and quasi-static testing machine

A general overlap of the curves is observed, with the dynamic ones substantially equal to or slightly higher than the quasi-static ones; considering the very limited sensitivity of the material to the strain rate, this can be interpreted as further validation of the system described in this work.

Conclusions and Future Work

The paper describes the main design and installation features of an innovative system for simultaneous tension and torsion testing at a high strain rate, based on Hopkinson bar technique. The system is of the pre-tensioned type, where the incident wave generation exploits the failure of a brittle sacrificial element. According to the illustrated working principle, the different speeds of longitudinal and torsional waves are compensated by forcing the former to travel for a longer path length. The design requirements led to a huge overall length of about 87m; because of its length, the system was realized by joining several titanium bars with threads and grooved collars. Finite element simulations confirmed the possibility of synchronizing the longitudinal and torsional waves’ arrival at the sample location and showed that the discontinuities and lumped masses at the bars’ connections are likely to create only small fluctuations in the travelling waves.

Even if some initial issues were experienced, especially with the static block system which alters the shape of the incident torsion wave, the wave propagation and recording appear to be acceptable for measuring the engineering deformation and stress in the specimen. A limited wave attenuation was observed, which can be attributed to the friction on the supports; however, considering the distances between the sample and the strain gauges, the attenuation is negligible for longitudinal waves and amounts to a few percent variation for torsional waves.

Two tests were conducted on hollow AA7075-T6 samples at the lower edge of the achievable strain rate. In the first test, the sample reached failure at an axial strain and a shear angle of 0.1 and 0.19, respectively; the average equivalent strain rate was in the order of 100 1/s. In a second test, the strain rate was lower, sample didn’t fail after having reached an axial strain and a shear angle of 0.06 and 0.18 at an average equivalent strain rate of 50 1/s. Pure tension and pure torsion tests were also performed with the SHTTB. The equivalent stress–strain curves for all 4 tests were compared with those obtained in quasi-static conditions with the same loading path; a very similar behaviour in terms of flow curve was found, as was expected given the limited strain rate sensitivity of the material.

Several future activities are planned, which include performing tests on materials that are more sensitive to strain rate and at higher strain rates, in order to push the SHTTB system to its upper limit. We intend to carry out a campaign of systematic tests to evaluate in detail the evolution of plastic damage, comparing different load paths. Robust and effective methods for analysing images up to high elongations and rotations will also be tested and developed.

Furthermore, by changing the length of the output bar, the developed setup provides the ability to control the loading sequence. It is therefore possible to study the behaviour of the material at high strain rates and with different loading paths, not only with synchronized tension and torsion, but also with tension followed by torsion and torsion followed by tension.