Residual Stress Measurement in Composite Laminates Using Incremental Hole-Drilling with Power Series

Abstract

Current methods for incremental hole-drilling in composite laminates have not been successfully applied in laminates of arbitrary construction or where significant variation of residual stress exists within a single ply. This work presents a method to overcome these limitations. Series expansion is applied to each ply orientation separately so that the discontinuities in the residual stresses at ply interfaces can be correctly captured. Temperature variations described by power series are used to set up eigenstrains and consequent stresses which vary in the through-thickness direction. The calibration coefficients at each incremental hole depth are calculated through the use of finite element modelling. The inverse solution employs a least-squares approach which makes the resulting solution insensitive to measurement uncertainty. Robust uncertainties in the residual stress distributions are determined using Monte Carlo simulation. The residual stress distribution is found from that combination of series orders in the different ply orientations that has the lowest RMS uncertainty, selected only from those combinations that have converged. The method is demonstrated on a GFRP laminate of [0₂/+45/−45]_s construction where it is found that transverse cracking of the plies at the inner surface of the hole may have impacted on the accuracy of the results.

Introduction

Residual stresses which originate from differences in the thermal expansion coefficients of plies of different orientation, amongst other sources, are known to appear in composite laminates during the forming process [1]. While the distribution of these stresses depends on factors such as the laminate configuration, the material properties of each ply and the forming process used, a feature of residual stresses in composite laminates is that they are typically discontinuous at the interfaces between plies of different orientation. The residual stresses can be high and can have a significant influence on the mechanical performance of the laminate. The stiffness, strength and life of a composite component can be reduced due to the negative effects caused by residual stresses such as matrix microcracking, interface debonding and warping [2].

In the case of composite laminates, non-destructive residual stress measurement methods such as X-ray and neutron diffraction cannot be applied, or have highly restricted application [3]. Measurement of the through-thickness residual stress distributions in composite laminates therefore usually demands the use of relaxation methods which involve the measurement of deformations arising from the removal of stressed material [4]. The deformations, which are typically measured in the form of displacements or strains, are used to calculate the residual stresses that existed in the material prior to its removal. Commonly used methods include layer removal [5], hole-drilling [6] and incremental slitting (crack compliance) [7].

Irrespective of the method used, relating measured deformations to the residual stresses creates a computational challenge [8] because the stresses are calculated at a different location from where the deformation measurements are taken. Additionally, all stress components throughout the volume of removed material affect the measured deformation in the adjacent material and the relationship is therefore in the form of an integral equation. The relaxation methods all differ in their material removal geometry and deformation measurement location, but the resulting integral equations are similar [8].

Determination of the residual stresses from the integral equations consists of two separate steps, namely the forward and inverse solutions [7, 8]. In the forward solution, the deformations as a function of depth of material removed, or the ‘calibration coefficients’, are determined for known through-thickness stress distributions. In many cases, the through-thickness stress distributions utilised to determine the calibration coefficients are unit pulses of uniform stress which are assumed to be released with each increment in cut or hole depth [7, 9]. Series expansion is an alternative approach, where it is assumed that the residual stresses are expandable into stress distributions defined by a series of functions [10]. While Legendre functions are the most commonly used, since they automatically satisfy the self-equilibrium requirement [11,12,13] for orders greater than 1, power series expansions [9, 14] have also been employed.

The inverse solution makes use of the calibration coefficients, obtained from the forward solution, to determine the residual stresses that would most closely approximate the measured strain response. The inverse solution in the case of unit pulses produces a strain fit that exactly matches the measured data, since the number of unknown coefficients is exactly equal to the number of material removal depths [15]. This causes the approach to be quite sensitive to measurement errors [16, 17] which places severe demands on the experimental strain measurement technique, as well as the accuracy of the results obtained from finite element (FE) calculations [18]. Tikhonov regularisation [19] is often utilised to somewhat smooth the resulting residual stress distribution by allowing a mismatch between the strain fit and the measured strain data. While this technique has been shown to be robust [20] when dealing with stress discontinuities in layered materials, it commonly requires an iterative process to determine the degree of smoothing that should be applied [8]. When series expansion is used, however, many of the problems of the unit pulse method can be avoided because the inverse solution employs a least-squares approach where the best fit of the calibration coefficients to the measured data allows the amplitude of each series order to be determined [7, 10]. Since the strain fit is not constrained to pass through all the experimentally measured data, this method is inherently tolerant of small measurement errors [15]. The least-squares approach is particularly effective when small depth increments are used such that the number of strain measurements is considerably greater than the number of unknown amplitude coefficients [15]. The most common technique is to apply surface pressure series, either power or Legendre, to the wall of the cut or hole. Series expansion of initial strain, or eigenstrain, distributions has, however, also been used to determine residual stress using the incremental slitting and hole-drilling methods [21,22,23,24,25,26,27]. The use of eigenstrain distributions is convenient in that the residual stresses are guaranteed to be in equilibrium since no external forces or moments are applied.

While all relaxation techniques require the use of inverse solutions, the hole-drilling method is probably the most widely used. It has the advantages of low cost [28], good accuracy and reliability, standardized test procedures, and convenient practical implementation [3]. The method was first introduced by Mathar [29] to determine uniform through-thickness residual stress in homogenous isotropic materials. The modern approach is to introduce a blind hole of progressively increasing depth, and is termed the incremental hole-drilling method [30]. This approach has been widely used [31,32,33] to measure the residual stress distribution in isotropic materials.

Application of the incremental hole-drilling method to composite materials and laminates has been far less frequent, however. Schajer and Yang [34] proposed a procedure to determine uniform through-thickness residual stress distributions in orthotropic materials, but this approach cannot be used with laminates because of the discontinuities in stress which exist at the interfaces between plies of different orientations. Pagliaro and Zuccarello [35] extended this technique to determine discontinuous residual stress distributions in symmetric cross-ply and angle-ply laminates. In this work, the stresses were assumed constant in each ply. Ghasemi et al. [36] made the same assumption and used the integral method to determine the residual stresses in symmetric and unsymmetric cross-ply composite laminates, as well as symmetric quasi-isotropic laminates. The calculated residual stresses compared favourably with theoretical calculations. Sicot et al. [37] adapted Lake’s model [38] to determine the through-thickness residual stress distributions in laminates using unit pulses. While only a cross-ply laminate and other simple laminates [39] have been investigated using this approach, it has been found that similar results are obtained from several different constant depth increments per ply. Akbari et al. [40] assessed the residual stress distribution through a thin-walled filament wound carbon/epoxy ring using the integral method with unit pulses. These researchers found that the hoop stress varied significantly through the thickness of each ply. Although the unit pulse method therefore appears effective in composite laminates, it requires regulated depth increments to ensure that the stress discontinuities at the interfaces between plies of different orientations can be captured. Additionally, if a steep variation in stress exists within a ply, many depth increments are required to approximate the variation as a sequence of uniform stresses, since the stress in each step is considered constant. These approaches have the potential to increase the sensitivity to measurement errors when using pulse functions, however, because the sensitivity can increase with both the number of material removal increments [9, 40, 41] and the use of regular depth increments [42, 43]. It therefore seems that current methods for incremental hole-drilling have somewhat limited utility in composite laminates where significant variation of residual stress within a single ply may exist. Series expansion would seem to offer a route to resolve this limitation.

Schajer [44] initially proposed the use of series expansion with the incremental hole-drilling method for isotropic materials in 1981, but application of this approach has been limited because numerical instabilities can arise from the use of series orders greater than one [44, 45]. Higher order Legendre series have, however, been successfully used with the slitting method [15, 25, 41, 46]. Although instability can be problematic in isotropic materials, the situation is different in composite laminates. The discontinuous nature of the residual stresses at changes in fibre orientation, coupled with the typically small thickness of individual plies, means that the residual stress distribution within each ply orientation has low complexity. It can therefore be well approximated by stress distributions of low order which are less susceptible to numerical instability.

While not discussed thus far, it is essential to know the uncertainty in a stress measurement if the significance of the measurement is to be assessed. In this regard, considerable effort has been expended by the community. Notable recent examples include the works of Peral et al. [47], Richter and Müller [48], and Scafidi et al. [28]. In the present context, the work of Prime and Hill [15] is also important. This work makes use of Monte Carlo simulations [49] to demonstrate that when series expansion is used, the uncertainties associated with the inability of the chosen series to exactly fit the actual stress variation are important and must be considered alongside the usual errors in the measured data. If this source of uncertainty is ignored, a conventional uncertainty estimate is generally non-conservative, sometimes by more than an order of magnitude.

This work presents and demonstrates the use of series expansion to address the current limitations in residual stresses measurement in composite laminates using the incremental hole-drilling method. Power series expansion functions of eigenstrain are applied to each ply orientation separately so that the discontinuities in residual stress at the interfaces between these plies can be captured correctly. The inverse solution employs a least-squares approach, where a best fit of the calibration coefficients to the measured data allows the amplitudes of each term in the eigenstrain series to be determined simultaneously in each ply, and consequently the residual stress distributions to be completely defined. Because of the use of least-squares curve fitting, the inverse solution is somewhat less sensitive to noise in the experimental data or to single erroneous measurements than that of the unit pulse approach. This reduces the uncertainty in the measured stress distributions which are estimated through the use of Monte Carlo simulations. The order of the least-squares fit to the experimental data is increased until convergence in the residual stress distribution is obtained with minimal uncertainty. The residual stress distributions determined from this method are continuous across each ply and discontinuous at the interfaces between plies of different orientation. The technique is not limited in its use, allowing the analysis of laminates with any number of plies orientated in any direction.

Proposed Method

The proposed method to determine the through-thickness variation in all three in-plane components of the residual stress is based on the following assumptions. The material is elastic, orthotropic within a single ply, and the stress component perpendicular to the surface (σ_z) is negligible. It is also assumed that removal of material does not induce significant residual stresses in the remaining laminate, which has been experimentally validated by Nobre [50]. A hole is incrementally introduced and the change in strain at each measurement location on the surface is measured relative to the undrilled laminate. The measured strains are affected by the relaxation of the x, y and in-plane shear components of the residual stress and also the geometry change of the specimen when the hole is drilled [30]. The influence of these effects on the measured strains must be determined and combined to relate the measured strains to the stress distributions in the laminate before drilling. In the case of a rectangular strain gauge rosette, this is done simultaneously for strains measured in the x, y and 45° directions. The calculation of the residual stress distribution which gives rise to the measured strain response cannot proceed directly. An indirect method is required to relate the measured strain release to the residual stress distributions by using calculated calibration coefficients.

If one considers the residual stress component in the x direction, where the variation with depth from the surface, z, is σ_x(z), the unknown stress distribution is assumed to be expandable into the stress distributions, s_nj, arising from unit power series of eigenstrain of order n in all three in-plane components with undetermined coefficients a_nj; n = 0, 1, 2, … and j = x, y, xy such that

$$ {\displaystyle \begin{array}{l}{\sigma}_x(z)={a}_{0x}{s}_{0x}(z)+{a}_{1x}{s}_{1x}(z)+{a}_{2x}{s}_{2x}(z)+\dots \\ {}\kern3em +{a}_{0y}{s}_{0y}(z)+{a}_{1y}{s}_{1y}(z)+{a}_{2y}{s}_{2y}(z)+\dots \\ {}\kern3em +{a}_{0 xy}{s}_{0 xy}(z)+{a}_{1 xy}{s}_{1 xy}(z)+{a}_{2 xy}{s}_{2 xy}(z)+\dots \end{array}}\kern3em $$

(1)

As the hole depth increases, the strain response in the x direction, ε_x(z), at a particular location can be written as

$$ {\displaystyle \begin{array}{l}{\varepsilon}_x(z)={a}_{0x}{c}_{0x}(z)+{a}_{1x}{c}_{1x}(z)+{a}_{2x}{c}_{2x}(z)+\dots \\ {}\kern3em +{a}_{0y}{c}_{0y}(z)+{a}_{1y}{c}_{1y}(z)+{a}_{2y}{c}_{2y}(z)+\dots \\ {}\kern3em +{a}_{0 xy}{c}_{0 xy}(z)+{a}_{1 xy}{c}_{1 xy}(z)+{a}_{2 xy}{c}_{2 xy}(z)+\dots \end{array}}\kern3em $$

(2)

where each c_nj(z) is the strain response at that location in the x direction to the j component of eigenstrain of order n. The coefficients a_nj can be determined by a least-squares minimisation of error between the measured strain release and that calculated using equation (2). The original stress distribution can then be determined from equation (1). In vector-matrix form, and considering all components of stress and strain, equations (1) and (2) can be expressed as equations (3) and (4) respectively.

$$ \sigma =S\cdot A $$

(3)

$$ \varepsilon =C\cdot A $$

(4)

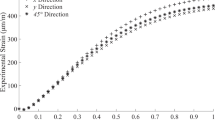
High orders of power series expansion are required if experimental strains vary abruptly or exhibit sharp turning points, but higher orders can become unstable [44]. For example, if the power series expansion method is applied to a laminate with an experimental strain variation as presented in Fig. 1, a high order series would be required to achieve a reasonable fit to the measured strain data. The consequence would be severe instabilities in the residual stress distribution which prevents this approach.

Fig. 1

Strain variation with depth

The adaption of the power series method, employed in this work, is to divide the material into multiple through-thickness regions, as presented in Fig. 1, such that multiple separate series of lower order can be used to achieve a good fit to the strain data. The material properties in composite laminates can vary abruptly at the interfaces between plies and the measured experimental strains can therefore have turning points or sharp changes in slope at the depth of such interfaces. This provides a convenient means for defining the regions to which series expansion can be separately applied. Within each of these regions a higher order power series expansion yields a better fit to the experimental data, but a certain order is reached where the benefits of an improved fit are outweighed by the inherent instability associated with a higher order series. Convergence of the calculated residual stress distributions, as the series order increases, and the magnitude of the associated uncertainty bounds can be used to determine the most appropriate order within each region.

The response of the laminate to different through-thickness stress distributions is evaluated using the FE method. The stress distributions are generated by applying separate eigenstrain distributions in each of the three in-plane strain components to each set of plies having particular material properties when observed in the global (x, y) coordinate system. Differences in material properties from one ply to the next could arise from changes in material type or, more commonly, from changes in ply orientation within a laminate of constant material type. The latter situation is assumed throughout this work.

Eigenstrain is applied by the use of through-thickness temperature variations, defined by functions with a range of [−1, 1], in conjunction with dummy coefficients of thermal expansion in each of the desired directions; α_x, α_y and α_xy. The use of temperature variation to apply eigenstrain and the use of functions with a range of [−1, 1] are used out of convenience and not necessity. The temperature variations are defined by functions ranging from 0th to 4th order according to equations (5) and (6) for even and odd orders respectively, where z is the normalised perpendicular position with respect to the midplane, i.e. z has a value of 1 on the top surface and −1 on the bottom surface.

$$ {T}_{even}(z)=2{z}^n-1 $$

(5)

$$ {T}_{odd}(z)={z}^n $$

(6)

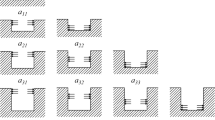
Eigenstrain in any of the three in-plane strain components causes a strain redistribution throughout the thickness of the laminate and, in turn, a through-thickness stress distribution in all the in-plane stress components. The use of eigenstrain to generate the through-thickness stress distributions maintains force and moment equilibrium in the laminate as a whole. The temperature functions are applied to each and every ply orientation separately by assigning a coefficient of thermal expansion of 1 to the ply orientation of interest and of 0 to the remaining ply orientations. It is important to note that although the eigenstrain is applied to each ply orientation independently it creates a stress distribution through the entire thickness of the laminate, i.e. in all remaining ply orientations. When material is removed from a ply to which no eigenstrain is directly applied, there are still stresses that are released and a change in strain is observed at the strain gauge locations. These released strains define a corresponding calibration coefficient and must be included in the analysis. This also applies to the stress distributions which result from eigenstrain in other directions. The total released strain variation in the x-direction, for instance, within a particular ply orientation thus also has terms associated with eigenstrain applied to other ply orientations and also those applied in the y direction and in-plane shear. Therefore calibration coefficients need to be determined for each strain gauge location for every applied eigenstrain, regardless of direction, at each incremental depth. For illustrative purposes, the balanced stress distribution in the x direction of a [0₂/90₂]_s laminate, produced by a 2nd order eigenstrain in the x direction applied to the 90° plies is presented in Fig. 2 up to the midplane.

Fig. 2

Eigenstrain and resultant stress distribution

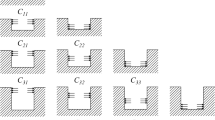
In the forward solution, the calibration coefficients are calculated using FE modelling where the depth of a blind hole is increased by incrementally removing a layer of elements defining the hole, for each applied eigenstrain. The calibration coefficients are unique for a particular laminate configuration and set of experimental parameters (length and position of strain gauges, hole diameter, depth of each increment, etc.). In the case of a rectangular strain gauge rosette, the longitudinal strain at the x, y and 45° strain gauge locations are calculated at each incremental depth within the FE model. The strain data for each successive hole depth is used to construct the calibration matrix, C, in the following form:

$$ C=\left[\begin{array}{lllllll}{C}_{1_{x_{0{x}_0}}}& \cdots & {C}_{1_{x_{0{y}_0}}}& \cdots & {C}_{1_{x_{0{xy}_0}}}& \cdots & {C}_{1_{x_{ij_n}}}\\ {}{C}_{1_{y_{0{x}_0}}}& \cdots & {C}_{1_{y_{0{y}_0}}}& \cdots & {C}_{1_{y_{0{xy}_0}}}& \cdots & {C}_{1_{y_{ij_n}}}\\ {}{C}_{1_{45_{0{x}_0}}}& \cdots & {C}_{1_{45_{0{y}_0}}}& \cdots & {C}_{1_{45_{0{xy}_0}}}& \cdots & {C}_{1_{45_{ij_n}}}\\ {}\vdots & \cdots & \vdots & \cdots & \vdots & \cdots & \vdots \\ {}{C}_{k_{p_{0{x}_0}}}& \cdots & {C}_{k_{p_{0{y}_0}}}& \cdots & {C}_{k_{p_{0{xy}_0}}}& \cdots & {C}_{k_{p_{ij_n}}}\end{array}\right] $$

(7)

where C_kpijn is the change in strain due to the presence of the hole, k is the hole depth increment, p is the strain gauge location, i is the ply orientation to which eigenstrain is applied, j is the component of the eigenstrain, and n is the order of the eigenstrain. The far-field stress distributions arising from the applied eigenstrain functions are used to create a stress matrix, S, in the following form:

$$ S=\left[\begin{array}{lllllll}{S}_{1_{x_{0{x}_0}}}& \cdots & {S}_{1_{x_{0{y}_0}}}& \cdots & {S}_{1_{x_{0{xy}_0}}}& \cdots & {S}_{1_{x_{ij_n}}}\\ {}{S}_{1_{y_{0{x}_0}}}& \cdots & {S}_{1_{y_{0{y}_0}}}& \cdots & {S}_{1_{y_{0{xy}_0}}}& \cdots & {S}_{1_{y_{ij_n}}}\\ {}{S}_{1_{45_{0{x}_0}}}& \cdots & {S}_{1_{45_{0{y}_0}}}& \cdots & {S}_{1_{45_{0{xy}_0}}}& \cdots & {S}_{1_{45_{ij_n}}}\\ {}\vdots & \cdots & \vdots & \cdots & \vdots & \cdots & \vdots \\ {}{S}_{m_{p_{0{x}_0}}}& \cdots & {S}_{m_{p_{0{y}_0}}}& \cdots & {S}_{m_{p_{0{xy}_0}}}& \cdots & {S}_{m_{p_{ij_n}}}\end{array}\right] $$

(8)

where m is the nodal position in the through-thickness direction, starting at 1 on the top surface and increasing with depth. Nodes shared by elements in the through-thickness direction have two stresses associated with them, one from each element, which allows discontinuities in stress to be captured. Subscripts p, i, j and n have the same meaning as in equation (7). The experimental strains are assembled into a strain vector, E, in the following form:

$$ E=\left[\begin{array}{l}{\varepsilon}_{1_x}\\ {}{\varepsilon}_{1_y}\\ {}{\varepsilon}_{1_{45{}^{\circ}}}\\ {}\vdots \\ {}{\varepsilon}_{k_i}\end{array}\right] $$

(9)

Once the calibration matrix is constructed, it is used with the experimental strain vector in the inverse solution to determine the amplitude vector, A, by manipulating equation (4) into the form presented in equation (10).

$$ {\displaystyle \begin{array}{l}{C}^T\cdot E={C}^T\cdot C\cdot A\\ {}A={\left({C}^T\cdot C\right)}^{-1}\cdot {C}^T\cdot E\end{array}} $$

(10)

In this equation, A is the unique set of amplitudes of the applied unit eigenstrains that best matches the experimental strain response, in the form:

$$ A=\left[\begin{array}{l}{A}_{0{x}_0}\\ {}{A}_{0{x}_1}\\ {}\vdots \\ {}{A}_{ij_n}\end{array}\right] $$

(11)

where i is the ply orientation to which eigenstrain is applied, j is the component of the eigenstrain, and n is the order of eigenstrain. The calculated amplitude vector is used to determine the though-thickness residual stress distribution vector, S_res, for the laminate using equation (12), which is presented in vector-matrix form:

$$ {S}_{res}=S\cdot A $$

(12)

Since all coefficients of A, and subsequently the residual stress distributions, are solved using a least-squares fit to the experimental strains, the method is fairly insensitive to noise in the strain measurements. The number of terms in E must be considerably greater than the number of terms in A to allow a robust least-squares fit [15]. It is therefore advantageous for the least-squares regression to have a large strain data set which is achieved by using small depth increments. This also allows the calculated residual stress distributions to vary through the thickness of a ply.

At this point, the issue of correcting for transverse sensitivity of the gauges needs to be discussed. Usually, the strain measurements in matrix E would be corrected for transverse sensitivity, but because the strain field is not uniform around the hole, the standard method of correction [51] is inaccurate and an alternative approach is required. The approach followed in this work is to leave the strains measured by the gauges as uncorrected, and instead modify the calibration coefficients determined from FE calculations. In essence, the uncorrected strain measurements are matched using calibration coefficients that are adjusted so that they reflect the strains that would be measured experimentally if transverse sensitivity was to be ignored.

An entirely new set of calibration coefficients corresponding to transverse strain is therefore required. The transverse calibration coefficients are a direct match for the longitudinal calibration coefficients and are readily obtained because all the necessary data is available from the finite element analysis required to obtain the longitudinal calibration coefficients. Each term C_kpijn in the matrix of calibration coefficients now corresponds to the change in strain that would be measured if transverse sensitivity was not accounted for, where subscripts p, i, j and n have the same meaning as in equation (7). The matrix of “uncorrected” calibration coefficients can be determined from the calibration coefficients in the longitudinal and transverse directions according to equation (13) which is found by manipulation of the standard transverse sensitivity equations given in [51]:

$$ {C}_{kpijn}=\frac{{\overline{C}}_{kpijn}+{\widehat{C}}_{kpijn}\times {K}_{tp}}{1-{v}_0{K}_{tp}} $$

(13)

where ${\overline{C}}_{kpijn}$ and ${\widehat{C}}_{kpijn}$ are the corresponding terms of the longitudinal and transverse calibration matrices, respectively, K_tp is the transverse sensitivity coefficient of the particular strain gauge of the rosette and ν₀ is the the Poisson’s ratio of the material on which the manufacturer’s gauge factor was measured.

The uncorrected C matrix found using FE calculations is then used with the uncorrected experimental strains within the strain matrix, E, to determine the coefficients of the amplitude vector, A, using equation (10). The complete residual stress distribution is found using equation (12).

Demonstration of Procedure

Experimental

The method outlined thusfar is demonstrated using a composite plate manufactured from E-glass/epoxy. The prepreg material (V_f ≈ 60%, ply thickness ≈ 200 μm) was supplied by c-m-p gmbh with manufacturer’s code T-GE-1250/635 CP002. The laminate configuration used was [0₂/+45/−45]_s with fibre alignment being carefully controlled during lay-up. The plate had dimensions 400 mm × 400 mm and was cured between two steel plates of the same dimensions and 0.9 mm thickness. The laminate was debulked at 85 °C before being cured at 6 bar and 120 °C for 3 h. The cured plate had smooth surfaces on both sides, no noticeable voids and no apparent curvature. The primary in-plane elastic properties of the composite material were determined in accordance with the ASTM D 3039 [52] and ASTM D 3518 [53] standards and are listed in Table 1. The value of v₂₃ was estimated by the hydrostatic approximation with the required bulk modulus estimated using micromechanics. The properties of the lamina are transversely isotropic in the material coordinate system and so the material properties transverse to the fibre direction are all identical. The remaining Poisson’s ratio terms are found from the reciprocal relations and the shear modulus, G₂₃, is obtained using equation (14).

$$ {G}_{23}=\frac{E_2}{2\left(1+{v}_{23}\right)} $$

(14)

Table 1 Orthotropic material properties

HBM foil strain gauge rosettes of type 1.5/350M RY61 were used for the incremental hole-drilling experiments. Each rosette has 6 strain gauge grids in total, orientated at 45° offset, and each corresponding pair is connected to one another during manufacturing. This results in a rosette which self-compensates for drilling offset errors to some extent. Strain gauges with a resistance of 350 Ω were used to reduce heating effects on the low-conductivity material. A gauge excitation voltage of 1.5 V was selected to achieve the desired sensitivity whilst keeping the power consumed by the gauge as low as possible. Each active gauge of the rosette was connected in a quarter bridge configuration with a dummy gauge to a National Instruments data acquisition system equipped with a SCXI-1520 strain gauge card. The dummy gauge used was of the same type as the active gauge and attached to the same laminate type. This reduced thermal effects over the experimental testing period which lasted approximately 35 min. Testing was performed in the basement of the laboratory where temperature fluctuations are minimal.

The Sint Technology Restan MTS 3000 incremental hole-drilling machine was used for the physical experimentation. A pneumatic turbine achieves cutting speeds of approximately 300,000 rpm which reduces the introduction of additional residual stresses during the drilling process. Drilling alignment was controlled to ensure that drilling occurred perpendicular to the surface of the laminate, and in the centre on the strain gauge rosette. A stepper motor controls the incremental drilling to a resolution of up to 1 μm, resulting in good reproducibility. The diameter and position of the hole can be determined with a resolution of 10 μm. A tungsten carbide inverted cone bur of 1.40 mm diameter was used to cut the hole which had final diameter of 1.59 mm.

The test specimen had dimensions of 40 mm × 40 mm. These dimensions were assessed using FE modelling to ensure that no edge effects were present at the hole location in the centre of the plate, or at the strain gauge locations. As a consequence of the symmetric lay-up, incremental hole-drilling was conducted up to the midplane only. The ratio between the hole radius and the inner radius of the strain gauge was found to be 0.44 which is in accordance with the recommendations of Sicot et al. [54].

The depth increment was set to 1/60th of the final hole depth to reduce the introduction of heat into the specimen as far as possible. This also means that 60 depth increments were used to populate the experimental strain vector, E. The feed rate of the MTS 3000 was set to 0.2 mm/min. Strain readings were taken 25 s after each drilling increment to allow for all thermal effects to dissipate and for steady state conditions to resume. Ten strain readings were taken over 5 s and averaged to reduce the effects of noise.

The experimentally measured variation in strain release with depth at the x, y and 45° strain gauge locations is presented in Fig. 3.

Fig. 3

Strain variation with depth in the x, y and 45° gauge directions

Computational

The calibration coefficients were calculated using MSC Nastran FE analysis. The composite laminates were modelled using HEX20 type 3D elements with orthotropic properties. The laminate was represented by 32 elements through the thickness, 4 per ply. It would be beneficial to increase the number of elements through the thickness of each ply, but the increase in computational time cannot be justified at present. The measured diameter of the hole was used in the FE modelling. Eigenstrains were applied to plies of a particular orientation by assigning to these plies a coefficient of thermal expansion of unity and to all other plies a thermal expansion coefficient of zero and then subjecting the entire laminate to a through-thickness temperature distribution corresponding to a particular order of the power series. Since no external loads were applied, the boundary conditions were simply those required to prevent rigid body motion. The longitudinal and transverse strain released at every drilling increment resulting from every eigenstrain was calculated at each strain gauge location on the top surface. These strains were used to populate the longitudinal and transverse matrices of calibration coefficients, $\overline{C}$ and $\widehat{C}$ respectively. The longitudinal strain was determined as the difference in average nodal displacement, in the gauge length direction, along the lines defining the inner and outer edges of each gauge grid, divided by the length of the grid. The transverse strain at each gauge was calculated similarly but referenced to the transverse direction. The laminate is not symmetric in the plane and must therefore be modelled in its entirety. The mesh around the hole including the strain gauge grid locations (highlighted) is presented in Fig. 4. The grid locations and sizes are included to more accurately determine the matrix of calibration coefficients. Drilling of the hole was simulated by incrementally removing elements to increase the depth of the hole. A section through the mesh is presented in Fig. 5. Elements defining each ply were assigned material properties in accordance with their ply orientation.

Fig. 4

Top view of mesh around the hole including the strain gauge grid locations

Fig. 5

Section through the mesh thickness

The application of the various eigenstrain distributions in the FE model yielded strain distributions around the hole for each incremental depth. For illustrative purposes, the strain variation in the x direction due to a 2nd order eigenstrain in the x direction applied to the 0° plies at a quarter thickness hole depth is presented in Fig. 6.

Fig. 6

Strain variation in the x direction at a quarter thickness hole depth showing also the strain gauge grid locations

The vertical dimensions of E, $\overline{C}$ and $\widehat{C}$ must agree to allow the use of equation (10). The 16 depth increments of the FE model had to be used, therefore, to find the coefficients of $\overline{C}$ and $\widehat{C}$ for the 60 measured depth increments. The strain release vs. depth relationships obtained from the FE calculations follow smooth variations, with discontinuities at the interfaces between different ply orientations. A separate spline was fitted to the calculated strain release data within each ply orientation to allow an increase in the number of calculated strain readings per ply from 4 up to 15 through interpolation. This was done for the calculated strain release data at the x, y and 45° gauge locations arising from all eigenstrain stress distributions, i.e. i × j × p × n curves were generated. This allowed the calculated strain data to be determined for 60 depth increments rather than 16, thereby ensuring that calibration coefficients could be determined for the same depth increments as for the experimentally measured strains. This procedure is presented in Fig. 7 for the calculated longitudinal strain release in the x direction resulting from a 2nd order eigenstrain in the x direction, applied to the 0° ply orientation.

Fig. 7

Determination of interpolated calibration coefficients from FE data

Although it is entirely possible to use a separate series order for each component of the eigenstrain in each ply orientation, for the sake of simplicity and illustration, the same order series was used for all three components of the eigenstrain within a particular ply orientation. Therefore, for the current laminate and for series orders ranging from 0th order to 4th order in each ply orientation, there are a total of 125 possible combinations of series expansion orders. To enable concise discussion, the abbreviation (n₀, n₄₅, n₋₄₅) is used where each value of n refers to the maximum order of the series expansion and the subscript refers to the ply orientation. This allows (1, 2, 3) to refer to the combination of 1st, 2nd and 3rd order series expansion in the 0°, +45° and −45° plies, respectively. Combinations of higher order series have the ability to better fit the experimental strain data as can be seen in Fig. 8 for the 45° strain gauge, where (1, 1, 1) and (4, 4, 4) order combinations are fitted to the experimental strain data, respectively. Combinations of higher order series can be more sensitive to measurement errors, however, which can lead to instability and greater uncertainty in the residual stresses. A thorough understanding of how uncertainty propagates through the analysis is therefore required.

Fig. 8

Least-squares fits to data at 45° strain gauge using (1, 1, 1) and (4, 4, 4) order combinations

Propagation of Uncertainties

The uncertainty in the residual stress distributions cannot be found directly using the law of propagation of uncertainty because the relationship between the measured strains and the stress is unknown and so the partial derivative terms cannot be found in a straightforward manner. The uncertainty in the stress distribution is instead estimated through the use of the Monte Carlo Method as per JCGM 101:2008 [49]. The input parameters into these calculations are provided in Table 2. Ten thousand trials were simulated for each combination of series orders.

Table 2 Input parameters and their assigned probability density functions

Uncertainties in this work can be divided into those that affect the strain matrix, E, and those that affect the calibration and stress matrices, C and S, respectively.

Uncertainties in the strain matrix are discussed first. Uncertainty propagation in the indicated strain measurements, ε_m, is calculated using the law of propagation of uncertainty as per JCGM 100:2008 [55]. Uncertainty in the measurement of the strains arose through inaccuracies in instrumentation such as strain gauges and data acquisition and from uncertainty in the average temperature during the test. The inherent noise uncertainty in the strain gauge and data acquisition system was quantified by recording strain data over a 30 min period and calculating a standard deviation from the large data set.

Within each Monte Carlo trial, the experimental strains are first adjusted for the effects of uncertainty in indicated measured strain. Since all experimental strain measurements share the same instrumentation they are considered fully correlated and so they are all varied using the same random variable. Each strain measurement is adjusted for inherent noise independently. The depths of the strain measurements are all adjusted for the uncertainty in zero depth and independently adjusted for the uncertainty in each individual depth increment. At this stage, a spline is fitted through the simulated strain distribution in each measurement direction so that the strains at the depth increments inherent to the C and S matrices can be determined and referenced to the zero depth of that trial. Finally, the uncertainty arising from the inability of the particular combination of series orders under consideration to exactly match the strain data is included. This uncertainty is calculated as the standard deviation between the experimentally measured strains and the least-squares fit within each ply orientation.

The calibration and stress matrices are affected by uncertainty in the material properties and in the ply orientations. Uncertainty in each experimentally measured material property is calculated using the law of propagation of uncertainty as per JCGM 100:2008 [55]. Uncertainty in these measurements arose through inaccuracies in instrumentation such as strain gauges, data acquisition and micrometers and from uncertainty in the average temperature during materials testing. Because the effects of misalignment are not linearly related to the angular misalignment, uncertainty due to misalignment of the plies within the material test coupons, misalignment of the strain gauges on the coupons and misalignment of the coupons within the testing machine is considered within the Monte Carlo simulation. Within each Monte Carlo trial, the material properties are first individually adjusted for the effects of measurement uncertainty. The effects on the material properties of all the possible sources of misalignment during materials testing are then incorporated. Finally, misalignment in the orientation of each ply within the hole-drilling specimen, and misalignment of the hole-drilling strain gauge rosette are included.

When including the uncertainties in material properties and the uncertainties in the orientation of individual plies within the hole-drilling specimen into the Monte Carlo simulation, it is not computationally feasible to perform a new finite element analysis for each trial. A more computationally efficient approach is therefore required. The changes in every term in the calibration and stress matrices are consequently determined for a 1% change in each material property, and a 1° change in each ply orientation. Due to the complex nature of the problem, each term of these matrices varies uniquely for each of these changes. Because of the use of a linear model, however, the variation in each of these terms can be scaled according to the uncertainty in each changed material property. In the case of angular misalignment in the hole-drilling specimen, the variation is scaled according to the square of the angular misalignment between each ply and the strain gauge rosette. For small angles, the effects of angular misalignment translate into quadratic variations in elastic constants and hence quadratic variations in the compliance and stiffness matrices. The two calibration matrices and the stress matrix within each Monte Carlo trial are then estimated according to equations (15) to (17).

$$ {\overline{C}}_j=\overline{C}+\sum \limits_{i=1}^5{r}_j\left({x}_i\right)u\left({x}_i\right)\overline{C}\left({x}_i\right)+\sum \limits_{i=6}^8{r}_j\left({x}_i\right){u}^2\left({x}_i\right)\overline{C}\left({x}_i\right) $$

(15)

$$ {\widehat{C}}_j=\widehat{C}+\sum \limits_{i=1}^5{r}_j\left({x}_i\right)u\left({x}_i\right)\widehat{C}\left({x}_i\right)+\sum \limits_{i=6}^8{r}_j\left({x}_i\right){u}^2\left({x}_i\right)\widehat{C}\left({x}_i\right) $$

(16)

$$ {S}_j=S+\sum \limits_{i=1}^5{r}_j\left({x}_i\right)u\left({x}_i\right)S\left({x}_i\right)+\sum \limits_{i=6}^8{r}_j\left({x}_i\right){u}^2\left({x}_i\right)S\left({x}_i\right) $$

(17)

where:

r(x_i) corresponds to normally distributed random numbers with standard deviations of ±1,

u(x_1–5) correspond to uncertainties in E₁, E₂, G_12,ν₁₂ and ν₂₃, respectively, including all material testing misalignment effects,

u(x_6–8) correspond to uncertainties in the orientation of the 0°, +45° and −45° plies of the hole-drilling specimen, including the misalignment of the hole-drilling rosette,

$\overline{C}\left({x}_{1-5}\right)$, $\widehat{C}\left({x}_{1-5}\right)$ and S(x_1 − 5) are the changes to the $\overline{C}$, $\widehat{C}$ and S matrices, respectively, as a result of a 1% increase in E₁, E₂, G_12,ν₁₂ and ν₂₃, respectively,

$\overline{C}\left({x}_{6-8}\right)$, $\widehat{C}\left({x}_{6-8}\right)$ and S(x_6 − 8) are the changes to the $\overline{C}$, $\widehat{C}$ and S matrices, respectively, as a result of a 1° increase in ply orientation in each of the 0°, +45° and −45° plies, respectively,

$\overline{C}$, $\widehat{C}$ and S are the original longitudinal and transverse calibration and stress matrices, respectively, and

${\overline{C}}_j$, ${\widehat{C}}_j$ and S_j are the longitudinal and transverse calibration and stress matrices, respectively, for Monte Carlo trial j.

It is important to note that the material properties are independent of each other and are therefore varied independently. A variation in a particular material property has simultaneous effects on the calibration and stress matrices and so they are varied by the same normal distribution. The same applies to variations in each ply orientation. While it must be acknowledged that this approach does not take higher order effects into account, the first order effects on the stress are of a similar magnitude to the variation in material properties. Since these are small, the higher order effects are not believed to be significant enough to justify the additional computational cost of including them.

The calculation of the two calibration matrices, $\overline{C}$ and $\widehat{C}$, depends entirely on the FE method. Since FE models cannot completely represent all the deformations that are possible in reality, some uncertainty exists in the knowledge of these matrices. The individual terms within the calibration matrices are considered to be fully correlated and so they are all varied using the same random variable [47]. The stress matrix is similarly modified.

Finally, the calibration matrix is adjusted to compensate for uncertainty in the transverse sensitivity of each gauge. Equation (13) which includes the transverse sensitivity coefficient of each gauge in that particular Monte Carlo trial, is used at this stage.

Since the hole eccentricity was measured to be close to zero, any uncertainties due to this parameter are judged to be small in comparison with the uncertainties that are considered. For the same reason, the effects of hole diameter variation are also ignored because the FE model is based on the measured hole diameter. Uncertainties due to the fillet radius are also ignored.

Once the strain matrix, E, calibration matrix, C, and the stress matrix, S, are determined for each trial, the stress variation is determined using equations (10) and (12). The uncertainties in the stress distributions are determined by evaluating the standard deviation in the 10,000 trials used in each Monte Carlo simulation at the nominal depth of each experimental datum.

Order Selection

While the experimental, computational and uncertainty propagation methods used in this work are well defined and allow the residual stress distribution and its uncertainty to be determined, the issue remains as to which combination of series orders provides the best approximation of residual stress from the experimental data. All combinations of series orders have the ability to solve the system of matrices and describe the experimental strain distributions to some degree. The approach used in this work is to select the combination of series order with the lowest RMS uncertainty from those combinations that have converged. The size of the uncertainty bounds and the convergence of every combination of series orders must therefore be investigated to quantitatively find the true, or most probable, residual stress distribution.

From the combinations that have converged, the (2, 2, 0) combination has the lowest RMS uncertainty and is consequently selected as the best solution for this laminate. Some combinations have lower uncertainty, but have not fully converged and so are not selected. Other combinations while fully converged, show the first signs of instability which leads to greater uncertainty, and so they too are not selected. It is important to emphasise that the order combination (2, 2, 0) refers to the order of eigenstrain applied to each ply orientation and not simply to the order of the residual stress distribution in each ply orientation. They are different because each and every eigenstrain function has some effect on the residual stress distributions in every ply orientation.

It is interesting to observe that in the case of the (2, 2, 0) combination, the amplitude coefficients of the 1st and 2nd order eigenstrains in the 0° and +45° plies are only 0.063 and 0.001% of the 0th order coefficient, respectively. The stress distribution of the (0, 0, 0) combination is quite different from that of the (2, 2, 0) combination, however, indicating that the higher order terms have a significant impact on the final stress result even with very small amplitude coefficients. The potential for instability in the results with several higher order terms is thus clear.

The tendency of higher order series combinations to become unstable makes them sensitive to changes in strains in the Monte Carlo simulations. This results in greater uncertainty bounds if the higher order functions are dominant within the order combination as is shown graphically in Figs. 9, 10, and 11 for the 20 most converged fits. The area between the uncertainty bounds of each fit is shaded in light grey and then superimposed. The darkest area corresponds to convergence where the uncertainty bounds of a number of combinations of orders agree. The light grey regions illustrate the divergence in uncertainty for order combinations where higher order functions are more dominant. This divergence continues to grow as the relative amplitude coefficients of the higher order terms increase. It is worth mentioning at this point, therefore, that the technique described in this work might not work well when a number of plies of the same orientation are stacked together into a thick block. In this case, the stress variation across the block might vary in a higher order fashion which would require a correspondingly high order series to match it. Instability in the resulting computational problem could prevent a valid solution from being obtained.

Fig. 9

Overlap of the ±2 standard deviation uncertainty bounds in σ_x for the 20 fits most converged to the (2, 2, 0) combination

Fig. 10

Overlap of the ±2 standard deviation uncertainty bounds in σ_y for the 20 fits most converged to the (2, 2, 0) combination

Fig. 11

Overlap of the ±2 standard deviation uncertainty bounds in τ_xy for the 20 fits most converged to the (2, 2, 0) combination

Results and Discussion

The least-squares fit and associated uncertainties (including that from the curve fit) of the (2, 2, 0) combination of series orders to the strain measurements obtained from the x, y and 45° gauges is shown in Fig. 12. The stress distributions and associated uncertainties obtained using the (2, 2, 0) combination of series orders are shown in Fig. 13. The uncertainties in these two figures correspond to ±2 standard deviations. Table 3 shows the RMS uncertainty in stress in the 0°, +45° and −45° plies, for each uncertainty source and also the combined uncertainty, u(Z).

Fig. 12

Least-squares curve fits to experimental strain data, with associated uncertainties shown as ±2 standard deviations

Fig. 13

Stress distributions and associated uncertainties obtained using the (2, 2, 0) combination of series orders. Uncertainties are shown as ±2 standard deviations

Table 3 Breakdown of RMS uncertainty in stress arising from each uncertainty source, x_i

As expected, the combined uncertainty, u(Z), in all three stress components tends to increase from the 0° ply through the +45° ply and on to the −45° ply, or as the depth increases. This reflects the decreasing sensitivity of the relaxation strains on the upper surface to internal stresses at increasing depths. It is also evident that the most important contributors to the uncertainty in the stress results are the zero depth, misalignment of the hole-drilling strain gauge rosette, the curve fit and the material properties E₂, ν₁₂ and ν₂₃. The large uncertainties in stress associated with ν₂₃ are ascribed to the large uncertainties in this parameter resulting from its estimation using micromechanics.

It is apparent from Fig. 13 that the residual stress distributions in the x and y directions have similar form: the residual stress in the 0° ply is fairly constant in tension, while the stress in the +45° and −45° plies decreases through the thickness of each ply. The residual shear stress in the 0° ply is close to zero while the distributions in the +45° and −45° plies are approximately equal and opposite. A discontinuity in stress at the interfaces between plies of different orientations is also evident for all stress components, which is required. The uncertainty in stress increases near the ply interfaces which is a consequence of using a separate curve fit within each ply orientation. The fitted curves are less constrained near their ends and as a result tend to diverge from the mean, which increases the uncertainty in these regions. Instability near the endpoints of the fitted domain, using Legendre polynomials with the slitting method, has also been reported by Shokrieh et al. [41].

While it is difficult to predict the direction and variation of the x and y components of the residual stresses in this laminate, it is known that the shear stress component of the 0° ply should have zero residual stress and that the +45 and −45° plies should have opposing stresses of equal magnitude so that they are in equilibrium. Although these conditions are not perfectly satisfied, they come close to it, and equilibrium is achieved when the uncertainty in the +45° and −45° plies is considered. When the uncertainties in the x and y components are taken into consideration, they remain unbalanced by an average of about 0.6 MPa and 4.5 MPa, respectively.

The laminate is symmetrical, and so it is expected that symmetry should exist in the residual stress distribution through the thickness of the laminate. This would imply that all three stress components should have zero slope at the mid-plane. This is clearly not the case, and we believe that the source of this unexpected behaviour can be traced to the depth of the hole being too shallow to allow the actual stress distributions in this region to emerge. While the −45° ply is continuous on the deeper side of the mid-plane, the strain data do not extend beyond this point. This means that the current stress distributions are simply those of the best possible fit using the available data. If the hole depth had been extended to provide additional data on the far side of the mid-plane, it is possible that these data would have changed the stress distributions in the −45° ply to allow zero slopes at the mid-plane. This might also have led to better convergence in the −45° ply than is currently observed in Figs. 9, 10, and 11. It therefore becomes apparent that the experiment should not have been terminated at the mid-plane, and drilling should have continued through the thickness of the −45° ply so that the best estimate of the behaviour at the mid-plane could have been obtained. This might also explain the lack of equilibrium in the x and y components as this method does not enforce equilibrium in one half of the thickness only and allows for asymmetric stress distributions to be determined. Because the method is based on eigenstrain, it does, however, enforce equilibrium in the plate as a whole.

A residual stress analysis must compare the measured stresses with allowable values. Transformation of the measured stresses into the material principal coordinate system reveals that the axial stresses and in-plane shear stresses are small in comparison with the strengths of two similar materials documented by Soden et al. [56]. The transverse stresses on the upper surfaces of all plies is, however, approaching the lower of the two transverse strengths reported by these researchers. While the strength of the laminate in this investigation is not known, it is clear that the mechanical load required to cause transverse tensile failure is significantly lower than might otherwise be expected.

Since the transverse stresses are high in comparison to the transverse strength, and since the accuracy of the hole-drilling method is clearly affected by localized transverse cracking at the hole, the effects of stress concentration must be assessed. The transverse stresses on the inner surface of the hole were consequently investigated using the finite element models employed throughout this work. The maximum stresses are, once again, located at the upper surface of each ply, with those in the 0° ply being critical. The peak stress in the 0° ply reaches nearly 58 MPa, which is about 65% higher than the lower transverse strength of 35 MPa reported by Soden et al. [56].

While transverse fracture in the internal plies might be inhibited by the transverse fibres of adjacent plies, as reported by Flaggs and Kural [57], such support does not exist on the upper surface of the 0° ply. It therefore seems probable that some transverse cracking occurred on the inner surface of the hole. The possibility of transverse cracking has also been reported by Akbari et al. [40]. We must therefore accept that the accuracy of the measured residual stresses results could have been affected by transverse failure. This is a very significant result which needs further investigation. We suspect that as hole drilling in composite laminates becomes more frequent, transverse failure may turn out to be as important a consideration in composites as plasticity effects are in metallic structures.

Conclusions

A new method for relating experimental strains from incremental hole-drilling to discontinuous stress distributions has been introduced and demonstrated. It is suitable for use on composite laminates, or any other material where discontinuous stress states could exist. The method is based on the approximation of the residual stress distribution by power series expansion of separate eigenstrain functions in each ply orientation. The unknown amplitude coefficients in each series are determined by least-squares error minimisation. The method is readily implemented and allows the uncertainty bounds of all three in-plane stress components to be robustly calculated. While the technique is not limited in its use, and allows the analysis of laminates with any number of plies orientated in any direction, instability may become a problem when several plies of the same orientation are stacked together. The transverse stresses in the [0₂/+45/−45]_s GFRP laminate under investigation were determined to be high enough that transverse cracking at the inner surface of the hole may have impacted on the accuracy of the measured residual stresses.