Use of Power Series Expansion for Residual Stress Determination by the Incremental Hole-Drilling Technique

Abstract

Background

The integral method of incremental hole-drilling is used extensively to determine the residual stress distribution in isotropic materials. When used with Tikhonov regularization, the method is robust and produces accurate results with minimal uncertainty. Alternatively, an optimal hole depth distribution can be found using the method of Zuccarello to improve the conditioning of the calibration matrices. If substantial measurement noise or a steep variation in stress exists, however, considerable uncertainty in, or distortion of, the calculated residual stress distribution can occur. Series expansion offers an alternative solution, but it has been reported to become unstable before meaningful accuracy can be achieved.

Objective

Investigate the use of series expansion to determine a rapidly changing throughthickness residual stress distribution in an aluminium alloy 7075 plate subjected to laser shock peening treatment.

Methods

Power series expansion of eigenstrains is used in finite element modelling to calculate the calibration coefficients. Monte Carlo simulation is used to determine robust uncertainties in the residual stress distributions. This allows the series order with the lowest RMS uncertainty in stress to be selected from those series orders that have converged. The best estimate of the residual stress distribution is thereby obtained.

Results

Series expansion is shown to be stable up to 8^th order and convergence to a stress solution can be found before instability dominates. The method is insensitive to measurement errors due to the least-squares approach employed by the inverse solution.

Conclusions

The use of series expansion reduces the RMS uncertainty in stress when compared to the regularized integral and Zuccarello methods.

Introduction

Laser Shock Peening (LSP) is a surface treatment technique that generates beneficial residual compressive stress that is typically greater in magnitude and reaches a greater depth [1] with less surface roughness in comparison with conventional shot peening [2]. LSP produces a steep variation in residual stress from the surface with a local minimum usually within 0.4 mm from the surface. This type of residual stress field can be challenging to measure accurately using relaxation methods.

The incremental hole-drilling technique (IHD) is one of the most widely used relaxation methods [3] because it is practical to implement, low cost and yields reliable and accurate results [4]. Another advantage of IHD is that it is only semi-destructive, unlike other relaxation methods. IHD has a standardised test procedure, ASTM E837-13a [5], and has been used extensively to measure LSP induced residual stresses in isotropic materials [6, 7]. The stress concentration around the hole may induce localised yielding which can introduce significant errors [5, 8]. According to the ASTM standard, acceptable results can be obtained if residual stresses are below 80% of the yield stress when the specimen thickness is greater than the mean diameter of the strain gauge rosette. This limit may be insufficient for highly non-uniform stress distributions due to the successive calculation nature of the integral method which means that any errors due to plasticity effects near the surface will propagate through the depth of the calculated stresses [8]. In this case, a limit of 60% of the yield stress is more appropriate [9]. A plasticity correction factor has been proposed by Beghini et al. [10] and its use has been extended by Nobre et al. [8] for the case of non-uniform stress distributions induced by surface peening, where the yield stress of the surface treated layers is also incorporated.

During IHD, strains are measured as stressed material is incrementally removed from the hole. The strain release on the measurement surface rapidly becomes insensitive to the removal of stressed material as the hole depth increases, as indicated by Saint-Venant’s Principle, and diminishes significantly once the depth of the hole surpasses half the diameter [4]. An inverse solution is required to determine the residual stress distribution from the measured strains [11] since the strain measurements occur at a different location to where the stressed material is removed. Additionally, all components of stress throughout the volume of removed material affect the measured strains at the gauge locations. Two separate steps, namely the forward and inverse solutions, are required to determine the residual stresses from the measured strains [11]. Known through-thickness stress distributions are used in the forward solution to determine the deformations, or the ‘calibration coefficients’, as a function of depth of material removed. These coefficients depend on the strain gauge rosette geometry, the hole diameter and the incremental depth. Unit pulses of uniform stress which are assumed to be released with each increment in hole depth are commonly used in the forward solution to determine the calibration coefficients [5, 12].

When unit pulses of uniform stress are used to determine the calibration coefficients, the inverse solution exactly matches the measured data [13]. This approach can be sensitive to measurement errors [14] and therefore requires a robust and accurate experimental technique and calibration coefficients determined from FE calculations [15]. Tikhonov regularization [16] is often utilised to allow a misfit between the measured strain data and that used in the inverse solution to smooth the resulting residual stress distribution. The extent of regularization must be carefully considered as it can distort the calculated stresses [5]. The sensitivity to strain measurement errors depends on the distribution of the material removal depths [17, 18]. This sensitivity can be reduced by limiting the number of depth increments used in the calculation [12, 17]. This approach, however, is limited when a steep variation in stress exists since the stress in each step is considered constant [19] and many depth increments are required to represent a rapidly varying stress field adequately. The calibration matrices, $\bar {a}$ and $\bar {b}$, of the unit pulse integral method are lower triangular and the small size of their diagonal elements reduces the matrix determinants to almost zero. The matrices of the unit pulse method are therefore numerically ill-conditioned and prone to high error sensitivity [4]. The numerical conditioning of $\bar {a}$ and $\bar {b}$ is strongly related to their diagonal elements and Zuccarello [17] has shown that the conditioning can be optimised by ensuring that the diagonal elements of $\bar {a}$ and $\bar {b}$ are constant in magnitude. This results in lower sensitivity to measurement errors and consequently reduced stress uncertainty. This approach requires progressively increasing step sizes with depth, however, with an accompanying loss of resolution. It therefore appears that the unit pulse integral method for IHD has somewhat limited utility where steep variation of residual stress exists. Series expansion is an alternative approach which could overcome these limitations.

The series expansion method assumes that the residual stress field can be expanded into stress distributions defined by a series of functions. Schajer [20] initially proposed the use of series expansion with IHD for isotropic materials in 1981 by applying power series stress distributions to the wall of the hole. However, application of this approach has been limited due to possible numerical instabilities arising from the use of series orders greater than 1 [20]. A least-squares approach is employed to determine the amplitude of each series order such that the calibration coefficients most closely match the measured strain data [21]. Series expansion is inherently tolerant of small measurement errors since the least-squares fit is not constrained to pass through all the experimentally measured strains [13]. The method is particularly effective when the number of strain measurements is considerably greater than the number of unknown amplitude coefficients. This can be achieved though the use of small depth increments [13]. While Schajer [20, 22] found numerical instabilities for series orders greater than 1, he made use of only a limited number of depth increments which may have prevented the full benefits of series expansion from being realised. Calibration coefficients can be obtained from the forward solution by applying surface pressures described by either power or Legendre series to the wall of the hole, or through the use of eigenstrain distributions [23,24,25]. Equilibrium is not a concern when eigenstrain distributions are used since no external force or moment is applied.

It is essential to know the uncertainty in any residual stress measurement so that the significance of the measurement can be assessed. A detailed approach to estimate the stress uncertainty is not included in the ASTM standard, however, numerous investigations have been conducted which propose approaches to estimate the stress uncertainty and define the main sources of uncertainty [14, 25,26,27]. The work of Prime and Hill [13] is also important in the present context. This work demonstrates that the uncertainties associated with the inability of series expansion to exactly match the measured strain data are important and must be included in the analysis. If this uncertainty is ignored, the uncertainty estimate is generally non-conservative. By the same principle, the misfit that is allowed by regularization must also be included for the unit pulse integral method.

The purpose of the present work is to investigate the use of the series expansion method with IHD when applied to a rapidly changing through-thickness stress distribution in an isotropic material. It is consequently necessary to compare results from other widely used approaches so that valid conclusions can be drawn. This work investigates the measurement of residual stresses in LSP treated aluminium, with series expansion results compared to those obtained from the regularized constant step integral method, and also the Zuccarello approach where a depth increment distribution is used such that the $\bar {a}$ matrix has constant diagonal elements. Power series expansion of eigenstrain is generated through the use of temperature variations in the forward solution. Least-squares error minimisation is employed by the inverse solution to determine the amplitudes of each term in the eigenstrain series that results in a best fit to the measured data. These amplitudes are used along with the far-field stress distributions arising from the eigenstrain series to completely define the residual stress distributions. Uncertainties are estimated through the use of Monte Carlo simulation with numerous sources of uncertainty included. The resulting stress distributions and associated uncertainties are compared against those obtained from the regularized constant step integral and Zuccarello approaches.

Method

While three different analytical approaches are used in this work, only the series expansion method is explained in some detail since the integral method [5] and Zuccarello approach [17, 28] are well known.

Series Expansion

Considering an unknown stress distribution in the x direction, σ_x(z), that is assumed to be expandable into stress distributions, s_jn, arising from power series expansion of eigenstrain of order n in all three in-plane components with undetermined coefficients a_jn; j = x,y,xy and n = 0,1,2,... such that [20]

$$ \begin{aligned} \sigma_{x}(z)&=a_{x0}s_{x0}(z)+a_{x1}s_{x1}(z)+a_{x2}s_{x2}(z)+{\dots} \\ &\quad +a_{y0}s_{y0}(z)+a_{y1}s_{y1}(z)+a_{y2}s_{y2}(z)+{\dots} \\ &\quad +a_{xy0}s_{xy0}(z)+a_{xy1}s_{xy1}(z)+a_{xy2}s_{xy2}(z)+\dots \end{aligned} $$

(1)

where z is the variation with depth from the surface. As the hole depth increases, the strain response in the x direction, 𝜖_x(z), at a particular location can be written as

$$ \begin{aligned} \epsilon_{x}(z)&=a_{x0}c_{x0}(z)+a_{x1}c_{x1}(z)+a_{x2}c_{x2}(z)+{\dots} \\ &\quad +a_{y0}c_{y0}(z)+a_{y1}c_{y1}(z)+a_{y2}c_{y2}(z)+{\dots} \\ &\quad +a_{xy0}c_{xy0}(z)+a_{xy1}c_{xy1}(z)+a_{xy2}c_{xy2}(z)+\dots \end{aligned} $$

(2)

where c_jn(z) is the strain response in the x direction at that location to the j component of eigenstrain of order n. The coefficients a_jn can be determined simultaneously using a least-squares approach. The residual stress distribution can then determined using Eq. 1. Considering all components of stress and strain, Eqs. (1) and (2) can be expressed in vector-matrix form, as Eqs. 3 and 4 respectively.

$$ \sigma=S\cdot A $$

(3)

$$ \epsilon=C\cdot A $$

(4)

The FE method is used to determine the incremental strain response to the through-thickness stress distributions caused by the redistribution of mechanical strain throughout the thickness of the specimen as a result of eigenstrain in each of the three in-plane strain components. Calibration coefficients are determined for all applied eigenstrains, for every incremental depth, at each strain gauge location to construct the calibration matrix, C, in the following form:

$$ C= \begin{bmatrix} C_{1_{x_{x_{0}}}} &{\dots} &C_{1_{x_{y_{0}}}} &{\dots} &C_{1_{x_{xy_{0}}}} &{\dots} &C_{1_{x_{j_{n}}}}\\ C_{1_{y_{x_{0}}}} &{\dots} &C_{1_{y_{y_{0}}}} &{\dots} &C_{1_{y_{xy_{0}}}} &{\dots} &C_{1_{y_{j_{n}}}}\\ C_{1_{45^{\circ}_{x_{0}}}} &{\dots} &C_{1_{45^{\circ}_{y_{0}}}} &{\dots} &C_{1_{45^{\circ}_{xy_{0}}}} &{\dots} &C_{1_{45^{\circ}_{j_{n}}}}\\ {\vdots} &{\dots} &{\vdots} &{\dots} &{\vdots} &{\dots} &\vdots\\ C_{k_{p_{x_{0}}}} &{\dots} &C_{k_{p_{y_{0}}}} &{\dots} &C_{k_{p_{xy_{0}}}} &{\dots} &C_{k_{p_{j_{n}}}}\\ \end{bmatrix} $$

(5)

where C_kpjn is the change in strain due to the presence of the hole, k is the hole depth increment, p is the strain gauge location, j is the component of eigenstrain, and n is the order of the applied eigenstrain. The far-field stress distributions arising from the applied eigenstrain functions are used to create a stress matrix, S, in the following form:

$$ S= \begin{bmatrix} S_{1_{x_{x_{0}}}} &{\dots} &S_{1_{x_{y_{0}}}} &{\dots} &S_{1_{x_{xy_{0}}}} &{\dots} &S_{1_{x_{j_{n}}}}\\ S_{1_{y_{x_{0}}}} &{\dots} &S_{1_{y_{y_{0}}}} &{\dots} &S_{1_{y_{xy_{0}}}} &{\dots} &S_{1_{y_{j_{n}}}}\\ S_{1_{xy_{x_{0}}}} &{\dots} &S_{1_{xy_{y_{0}}}} &{\dots} &S_{1_{xy_{xy_{0}}}} &{\dots} &S_{1_{xy_{j_{n}}}}\\ {\vdots} &{\dots} &{\vdots} &{\dots} &{\vdots} &{\dots} &\vdots\\ S_{m_{p_{x_{0}}}} &{\dots} &S_{m_{p_{y_{0}}}} &{\dots} &S_{m_{p_{xy_{0}}}} &{\dots} &S_{m_{p_{j_{n}}}}\\ \end{bmatrix} $$

(6)

where m is the nodal position in the through-thickness direction and p is the component of stress. Subscripts j and n have the same meaning as in Eq. 5. The experimental strain vector, E, has the following form:

$$ E= \begin{bmatrix} \epsilon_{1_{x}} \\ \epsilon_{1_{y}} \\ \epsilon_{1_{45^{\circ}}} \\ {\vdots} \\ \epsilon_{k_{p}} \\ \end{bmatrix} $$

(7)

where k and p have the same meaning as in Eq. 5.

The experimental strain vector is used with the calibration matrix in the inverse solution to determine the amplitude vector, A, by manipulating Eq. 4 into the form presented in Eq. 8.

$$ \begin{aligned} C^{T}\cdot E&=C^{T}\cdot C \cdot A\\ A&=\left( {C^{T}\cdot C}\right)^{-1} \cdot C^{T} \cdot E \end{aligned} $$

(8)

where A is the unique set of amplitudes of the applied eigenstrain functions that best matches the experimental strain response, in the form:

$$ A= \begin{bmatrix} A_{x_{0}} \\ A_{x_{1}} \\ {\vdots} \\ A_{j_{n}} \\ \end{bmatrix} $$

(9)

where j and n have the same meaning as in Eq. 5. The calculated amplitude vector is used to determine the residual stress distribution vector, S_res, for the specimen using Eq. 10, which is presented in vector-matrix form:

$$ S_{res}=S\cdot A $$

(10)

All coefficients of A, and subsequently the residual stress distributions, are solved using a least-squares approach which reduces sensitivity to strain measurement errors. The number of terms in E must be considerably greater than the number of terms in A to allow a robust least-squares fit [13]. Therefore, small depth increments must be used which also allows steep variations to be correctly captured in the calculated residual stress distributions.

The experimental strains measured during IHD in isotropic materials are generally smooth by nature without sharp turning points. However, high orders of power series expansion may still be required to ensure a reasonable fit to the measured strain data. As the order of power series expansion is increased, the least-squares fit to the experimental data will improve, but the benefits of an improved fit will be progressively outweighed by the inherent instability associated with a higher order series. It is therefore crucial that a series order which can fully describe the actual stress distribution is found before instabilities dominate.

Integral Method

The integral method is a derivation of the uniform stress calculation procedure. The method, as described in the ASTM standard [5], assumes that residual stress within each depth increment is constant.

Calibration matrices $\bar {a}$ and $\bar {b}$ relate the various stresses and strains according to Eqs. 11 and 13

$$ \bar{a}\ P=\frac{E}{1+\nu}\ p $$

(11)

$$ \bar{b}\ Q=E\ q $$

(12)

$$ \bar{b}\ T=E\ t $$

(13)

where P is the isotropic (equi-biaxial) stress, Q is the 45^∘ shear stress, T is the x-y shear stress and p, q and t are combination strain vectors [5].

The calibration matrices, $\bar {a}$ and $\bar {b}$, can be found from FE calculations where unit equi-biaxial and shear stress is applied to the surface of the hole, respectively. A physical representation of matrix $\bar {a}$ is shown in Fig. 1 [14]. Coefficient a₄₃ represents the combination strain resulting from a unit equi-biaxial stress within the third increment of a hole four increments deep.

Fig. 1

Physical interpretation of matrix coefficients $\bar {a}$ for the hole-drilling method

The number of depth increments must be carefully chosen if the residual stress varies significantly. Numerous depth increments may be required to ensure that the stress distribution can be adequately represented as a sequence of uniform stresses. However, using twenty depth increments as given in the calibration tables of the ASTM standard can lead to high error sensitivity and Tikhonov regularization [16] is used to reduce this effect. To make use of Tikhonov regularization the tri-diagonal “second derivative” matrix c is used.

$$ c= \begin{bmatrix} 0 &0 & & & \\ -1 &2 &-1 & & \\ &-1 &2 &-1 & \\ & &-1 &2 &-1 \\ & & &0 &0 \\ \end{bmatrix} $$

(14)

where the number of rows is equal to the number of hole depth increments used. Equations 11 and 13 are adjusted to implement Tikhonov second derivative regularization.

$$ \left( \bar{a}^{T}\bar{a}+\alpha_{P} \ c^{T} c\right) P=\frac{E}{1+\nu}\ \bar{a}^{T}p $$

(15)

$$ \left( \bar{b}^{T}\bar{b}+\alpha_{Q} \ c^{T} c\right) Q=E\ \bar{b}^{T}q $$

(16)

$$ \left( \bar{b}^{T}\bar{b}+\alpha_{T} \ c^{T} c\right) T=E\ \bar{b}^{T}t $$

(17)

Regularization has the effect of smoothing the stress results. The factors α_P, α_Q and α_T control the amount of regularization that is applied. Zero values for the factors yield the unregularized results. Positive values of the factors smooth the results progressively as larger factors are chosen. Insufficient regularization leads to excessive uncertainty in the calculated stress results, while excessive regularization distorts the stress results. Optimal regularization is required to balance these two tendencies. The ASTM standard suggests small regularization factors in the range 10^-4 to 10^-6. The regularized strains that correspond to the calculated stresses (P, Q and T) using Eqs. 15 and 17 do not exactly match the actual combination strains p, q and t. The extent of regularization applied can be determined by adjusting each regularization factor using Eq. 18 until the RMS of the misfit vectors, Eq. 19, are within 5% of the values of standard errors of the combination strains, Eq. 20. Shown only for p, but similarly for q and t.

$$ \left( \alpha_{P}\right)_{new}=\frac{{p_{std}}^{2}}{{p_{rms}}^{2}}\left( \alpha_{P}\right)_{old} $$

(18)

$$ {p_{rms}}^{2}=\frac{1}{n} \sum\limits_{j=1}^{n}\left( p_{misfit}\right)_{j}^{2} $$

(19)

$$ {p_{std}}^{2}= \sum\limits_{j=1}^{n-3}\frac{\left( p_{j}-3p_{j+1}+3p_{j+2}-p_{j+3}\right)^{2}}{20\left( n-3\right) } $$

(20)

where n is the number of depth increments.

The Cartesian stresses at each depth increment can be found from P, Q and T [5].

Zuccarello Approach

The conditioning of the calibration matrices can be optimised, and the sensitivity to experimental strain errors minimised, by ensuring that the diagonal elements of the calibration matrices, $\bar {a}$ and $\bar {b}$, are constant in magnitude. To achieve this, a non-uniform depth increment distribution must be used. Calibration matrices for any depth increment distribution can be obtained from cumulative calibration coefficients [12], which can be determined from the constant step matrices, $\bar {a}$ and $\bar {b}$. The non-uniform depth increment distribution which results in constant diagonal calibration coefficients can be found by iteration, following the methodology proposed by Zuccarello [17], for a particular number of depth increments or for a certain magnitude of the coefficients on the diagonal. Since biaxial stresses are dominant after the application of LSP, only the hydrostatic component, P, of the residual stress field was considered when determining the optimal depth distribution. The equi-biaxial calibration matrix for the non-uniform depth distribution is denoted as $\bar {a}_{(Zucc)}$. The same depth distribution was used to determine $\bar {b}_{(Zucc)}$.

The size of the first depth increment, and the corresponding first entry in $\bar {a}_{(Zucc)}$, defines the magnitude of all diagonal elements of $\bar {a}_{(Zucc)}$ and therefore the required depth distribution. There is scope to optimise the size of the first depth increment to find the most stable stress solution, but if this size is made too large it can lead to incorrect stress calculation when steep stress variations exist.

Demonstration of Procedure

Experimental

Samples of aluminium alloy 7075-T651 were machined from a rolled plate of 15 mm thickness. The samples were reduced to a thickness of 6 mm by machining 1 mm from the top face of the plate and 8 mm from the bottom. Individual samples of 60 mm × 60 mm were then prepared. The plate thickness of 6 mm falls within the “thick” workpiece limits prescribed by the ASTM standard. The mechanical properties of the material are shown in Table 1.

Table 1 Mechanical properties of aluminium alloy 7075-T651

The upper face of the machined plate underwent LSP treatment at the National Laser Centre (NLC) of the Council for Scientific and Industrial Research (CSIR) in Pretoria, South Africa, using a Quanta-Ray Pro Spectra Physics (QRPSP) Nd:YAG laser. The QRPSP laser specifications and the LSP parameters are shown in Table 2. An X-Y raster pattern with equidistant spot placement in the horizontal and vertical directions was used as the spot sequence strategy. A 1.5 mm spot diameter, with a spot density of 5 spots/mm² (70% spot overlap), was used to attain a power intensity of 1.5 GW/cm². LSP was applied to a region measuring 11.25 mm × 11.25 mm. In this work the LSP step and scan directions are represented by the x and y directions, respectively.

Table 2 Laser specifications and LSP parameters

IHD was conducted using the Sint Technology Restan MTS 3000 incremental hole-drilling machine equipped with a pneumatic turbine which achieves cutting speeds of approximately 300 000 rpm. IHD measurements were performed in the centre of the LSP area. A tungsten carbide inverted cone end mill with a 1.6 mm diameter was used to cut the hole which had a final diameter of 1.74 mm. The diameter and position of the hole can be determined with a resolution of 10 μ m. Incremental drilling depth is controlled to a resolution of up to 1 μ m. The feed rate of the MTS 3000 was set to 0.2 mm/min. The depth increments on the MTS Restan 3000 were set to 5 μ m for the first 0.2 mm of the test and 25 μ m for the remainder of the test up to a depth of 1.2 mm.

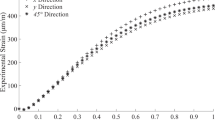
Six element rectangular HBM foil strain gauge rosettes of type 1.5/350M RY61 were used for the IHD experiment. A gauge excitation voltage of 3.5 V was selected to achieve the desired sensitivity whilst keeping the power consumed by the gauge low. To reduce thermal effects, each active gauge of the rosette was connected to dummy gauge of the same type, attached to the same specimen type, in a quarter bridge configuration using a National Instruments data acquisition system equipped with a SCXI-1520 strain gauge card. The IHD experiment lasted roughly 30 minutes and was performed in the basement of the laboratory where temperature fluctuations are minimal. The measurement uncertainty due to the temperature variation during the test is considered negligible. A 20 second delay was used after each drilling increment before strain readings were recorded to allow for all thermal effects to dissipate and for steady state conditions to resume. Ten strain readings were taken over 5 seconds and averaged to reduce the effects of noise. The experimentally measured strain variations at the x, y and 45^∘ strain gauge locations are presented in Fig. 2. Strain data are presented at depth increments of 25 μ m, which correspond to the depths used to calculate the calibration matrix. The intervening strain measurements at increments of 5 μ m over the first 0.2 mm of the test were omitted to improve the clarity of Fig. 2

Fig. 2

Strain variation with depth in the x, y and 45^∘ gauge directions

Computational

The calibration coefficients were calculated using MSC Nastran FE analysis. The specimen was modelled using HEX8 type 3D elements. The specimen was represented by 24 elements through the first 1.2 mm from the surface, and 68 elements through the remaining thickness. FE models with hole diameters of 1.70 mm, 1.75 mm and 1.80 mm were created so that any experimental hole diameter within this range could be used. This approach also allows the uncertainty of the measured hole diameter to be included in the analysis. Due to symmetry, a quarter model was used with symmetric and anti-symmetric boundary conditions applied depending on the applied loading. Eigenstrain distributions for the series expansion method were applied to elements in the first 1.2 mm below the surface of the specimen by means of through-thickness temperature variations in conjunction with dummy coefficients of thermal expansion in each of the desired directions; α_x, α_y and α_xy. The temperature variations were defined by polynomial functions according to Eqs. 21 and 22 for even and odd orders respectively, where z is the normalised perpendicular position with respect to half the maximum hole depth, i.e. z has a value of 1 on the top surface and -1 at maximum hole depth. The use of temperature variation and functions with a range of [-1, 1] to apply eigenstrain are out of convenience and not necessity. It is important to note that a stress distribution was created throughout the entire thickness of the specimen even though eigenstrain was only applied to elements in the first 1.2 mm. The boundary conditions were simply those required to prevent rigid body motion, since no external loads were applied.

$$ T_{even}(z)=2{z}^{n}-1 $$

(21)

$$ T_{odd}(z)={z}^{n} $$

(22)

The strain measurements in matrix E cannot be corrected for transverse sensitivity using the standard method of correction [29], because the strain field is not uniform around the hole. Instead, the experimentally measured strains were left uncorrected and the calibration coefficients determined from FE calculations were modified to reflect the strains that would be measured experimentally if transverse sensitivity was to be ignored [25]. The longitudinal and transverse strains at each gauge location for every drilling increment and applied eigenstrain series were used to populate the longitudinal and transverse matrices of calibration coefficients, respectively. The matrix of “uncorrected” calibration coefficients were then determined from Eq. 23 which is obtained by manipulation of the standard transverse sensitivity equations given in [29]:

$$ C_{kpjn}=\frac{\bar{C}_{kpjn}+\hat{C}_{kpjn} \times K_{tp}}{1-\nu_{0}K_{tp}} $$

(23)

where $\bar {C}$ and $\hat {C}$ are the corresponding terms of the longitudinal and transverse calibration matrices, respectively, K_tp is the transverse sensitivity coefficient of the particular strain gauge of the rosette and ν₀ is the Poisson’s ratio of the material on which the manufacturer’s gauge factor was measured.

The mesh around the hole and position of the strain gauge grid locations (highlighted) are presented in Fig. 3. The grids were not directly included in the FE model. Instead the displacements of all the nodes surrounding and including the grid locations were determined for each loading condition and a biharmonic surface spline was fitted to the nodal displacement data to calculate the displacements around the perimeter of each grid. The longitudinal strain was determined as the difference in average longitudinal displacement along the inner and outer edges of each gauge grid, divided by the length of the grid. The transverse strain at each gauge was calculated similarly but referenced to the transverse direction. Drilling of the hole was simulated by incrementally removing a layer of elements defining the hole. A section through the mesh is presented in Fig. 4.

Fig. 3

Top view of mesh around the hole including the strain gauge grid locations

Fig. 4

Section through the mesh thickness

Each applied eigenstrain distribution results in a strain distribution around the hole for each depth increment. For illustrative purposes, the strain variation in the x direction due to a 2^nd order eigenstrain in the x direction at a hole depth of 0.5 mm is presented in Fig. 5.

Fig. 5

Strain variation in the x direction at 0.5 mm hole depth showing also the strain gauge grid locations

The FE model used for series expansion was also used to determine the necessary calibration coefficients for the implementation of the integral method, as per the ASTM standard. The calibration tables provided in the standard were not used in this case since the 1.5/350M RY61 strain gauges have different geometry to those specified in the standard. Additionally, small variations in hole diameter from the nominal diameter specified in the standard [5] of 2 mm can be corrected by adjusting all calibration coefficients by a factor of (measured hole diameter/2 mm)² [12]. However, the hole diameter measured in this work was significantly lower than 2 mm and the correction given in the standard is unlikely to produce accurate results for the hole diameter of 1.74 mm. Using the same FE model and approach to calculate the calibration coefficients of the integral method also removed some expected variability in the results of the two methods due to differences arising from FE calculations. This ensures that a reasonable comparison between the computational approaches could be achieved. The necessary calibration coefficients for the integral method were determined using an equi-biaxial stress state for matrix $\bar {a}$ and a pure shear stress state for matrix $\bar {b}$ at each depth and loading increment, as shown in Fig. 1. To apply each of these loads, the equivalent radial and shear stress distributions were applied simultaneously to the hole face according to the following stress transformation equations [30]:

$$ \sigma_{x}=\sigma_{y}=1, \ \tau_{xy}=0 \rightarrow \sigma_{rr}=\cos^{2}\theta+\sin^{2}\theta, \ \tau_{r\theta}=0 $$

(24)

$$ \tau_{xy}=1, \ \sigma_{y}=\sigma_{x}=0 \rightarrow \sigma_{rr}=\sin2\theta, \ \tau_{r\theta}=\cos2\theta $$

(25)

These radial and shear stress distributions were applied to the inner surface of the hole using PLOAD4 cards applied to element faces at the appropriate depth. The strains at the relevant grid locations were calculated using the same biharmonic spline approach and correction for transverse sensitivity as used for the series expansion method. These were used to obtain the coefficients of $\bar {a}$ and $\bar {b}$. The $\bar {a}$ and $\bar {b}$ matrices obtained from the FE model were used to determine the corresponding $\bar {a}_{(Zucc)}$ and $\bar {b}_{(Zucc)}$ matrices for the Zuccarello approach.

The constant depth increment for the integral method with regularization was set to 50 μ m up to a maximum depth of 1 mm, giving twenty constant steps as in the calibration tables of the ASTM standard [5]. The first entry of $\bar {a}$ of the standard integral method was used to determine the depth distribution which results in constant diagonal values in $\bar {a}_{(Zucc)}$. Fifteen depth increments were found within 1 mm from the surface. Although this number of depth increments is greater than suggested by Zuccarello [17], the closer spacing between increments was required to correctly capture the steep variation in stress near the surface. In the case of series expansion, the depth increment was set to 25 μ m up to a maximum depth of 1.15 mm. This means that 47 depth increments, including zero depth, were used to populate the experimental strain vector, E. The additional strain data points beyond the region of interest up to 1 mm were used to help constrain the series near their end points where greater instability can occur and consequently result in greater uncertainty in stress. Equation 8 requires that E, $\bar {C}$ and $\hat {C}$ follow the same depth distribution. Therefore, $\bar {C}$ and $\hat {C}$ must be determined for the depth increments of E. The strain vs. depth relationships obtained from the FE calculations follow smooth variations. A spline was fitted to the calculated longitudinal and transverse calibration coefficients to determine $\bar {C}$ and $\hat {C}$ for the depth distribution of E through interpolation [25]. This procedure is presented in Fig. 6 for the calculated longitudinal calibration coefficients corresponding to the x direction resulting from a 2^nd order eigenstrain in the x direction.

Fig. 6

Determination of interpolated calibration coefficients from FE data

For the sake of simplicity and illustration, the same order series was used for all three components of eigenstrain. It is however possible to use a separate series order for each component of eigenstrain. Higher order series are able to more closely fit the experimental strain data as can be seen in Fig. 7 for the x direction strain gauge, where 2^nd and 6^th order series expansion are applied, respectively. Although it appears as if the 2^nd order fit is sufficient, it does not guarantee convergence to a stress solution. It has been reported that higher order series can become unstable due to increased sensitivity to measurement errors [20], resulting in greater uncertainty in calculated stresses. Therefore a thorough understanding of how uncertainty propagates through the analysis is required.

Fig. 7

Least-squares fits to data in the x direction using 2^nd and 6^th order series

Propagation of Uncertainties

The relationship between the measured strains and calculated stresses is unknown, and the partial derivative terms cannot be found in a straightforward manner. Therefore, the law of propagation of uncertainty cannot be applied directly to determine uncertainty in the residual stress distributions. Instead, uncertainty in the stress distributions was estimated through the use of Monte Carlo simulations as per JCGM 101:2008 [31]. The various experimental and computational uncertainty sources considered in this work are provided in Table 3. Ten thousand trials were simulated for each series expansion order, and for the integral and the Zuccarello approaches also.

Table 3 Uncertainty sources and their assigned probability density functions

The law of propagation of uncertainty as per JCGM 100:2008 [32] was used to calculate the indicated strain measurement uncertainty, 𝜖_m, which is due to inaccuracies in instrumentation such as strain gauges and data acquisition. The inherent noise uncertainty in the strain measurement was quantified by recording strain data over a 30 minute period and calculating a standard deviation from the large data set.

Zero depth detection is essential for any hole-drilling residual stress measurement, and can be a significant source of stress uncertainty. It is possible to use the electrical contact technique that identifies the contact between the end mill and the surface of the specimen when the electrical connection occurs. The approach used in this work, however, was to start the drilling process slightly above the sample. No relaxation response occurs while the end mill is in the air or within the thickness of the strain gauge and so the measured response is simply the scatter associated with measurement uncertainty. Since LSP induces compressive residual stress near the surface, some strain response should occur when the end mill starts to penetrate into the specimen. While this method is by no means fully robust or advisable in general (since there will be no observable or an extremely small strain response if the near surface stresses are close to zero), it does allow inclusion of the uncertainty in zero depth position when calculating the residual stresses. Incorrect zero depth position can not only alter the magnitude of the first few stress measurements, but also the entire stress distribution due to the nature of the inverse solution. After the IHD experiment, the strain variations were investigated and shifted along the x axis to find the most likely position of the surface. Using this approach, it would not be known if the first measured response occurred as the end mill was initiating contact with the specimen or whether the end mill was a full depth increment into the specimen when the data was recorded. The depth uncertainty would therefore be one half of the depth increment, or 2.5 μ m. It is, however, possible that the end mill could slightly penetrate into the specimen and the associated elastic response would be so minor that it could get lost in the scatter of the preceding data points. This would mean that the first datum point would be missed. In this case, the uncertainty would need to be increased. To be conservative, it was assumed that a datum point associated with the end mill at a full depth increment into the specimen could be missed. Additionally, the presence of surface roughness peaks from LSP or low surface stress in the specimen could impact the use of this approach. Therefore, the zero depth uncertainty in this case is taken to be two increments, or 10 μ m.

The experimental strains were first adjusted within each Monte Carlo trial for the effects of indicated strain uncertainty. Since all experimental strain measurements were recorded by the same instrumentation, they are considered fully correlated and were all varied using the same random variable. The depths of the strain measurements were independently adjusted for the uncertainty in each individual depth increment, and all adjusted for the uncertainty in zero depth. The strains at the depth increments inherent to the C, or $\bar {a}$ and $\bar {b}$, or $\bar {a}_{(Zucc)}$ and $\bar {b}_{(Zucc)}$ matrices must be determined and referenced to the zero depth of that trial for each inverse solution. This was done by means of spline interpolation, which clearly introduced some additional uncertainty, but it is believed that this uncertainty is negligible in comparison with not accounting for the effects of depth uncertainty altogether. Each interpolated strain datum was then adjusted for inherent noise independently. Lastly, the uncertainty due to the misfit between the particular series order under consideration and the experimental strain data was included at each incremental depth. The same approach was used in the case of the integral method for the misfit resulting from Tikhonov regularization.

Calibration matrices were found for the hole diameter of the current trial by spline interpolation of each coefficient obtained from the 1.70 mm, 1.75 mm and 1.80 mm FE models.

Although it is possible to use material independent calibration and stress matrices which allow variations in material properties to be included directly in the stress calculation, an alternative approach is used here where a 1% change in each material property is modelled using FE to determine the changes in every term in the calibration and stress matrices [25]. The variation in each of these terms can be scaled according to the uncertainty in each material property due to the use of a linear model. Within each Monte Carlo trial, the two calibration matrices and the stress matrix ($\bar {C}$, $\hat {C}$ and S, respectively) are determined by Eqs. 26 to 28.

$$ \bar{C_{j}}=\bar{C}+\sum\limits_{i=1}^{2}r_{j}(x_{i})u(x_{i})\bar{C}(x_{i}) $$

(26)

$$ \hat{C_{j}}=\hat{C}+\sum\limits_{i=1}^{2}r_{j}(x_{i})u(x_{i})\hat{C}(x_{i}) $$

(27)

$$ S_{j}=S+\sum\limits_{i=1}^{2}r_{j}(x_{i})u(x_{i})S(x_{i}) $$

(28)

where $\bar {C}_{j}$, $\hat {C}_{j}$ and S_j are the longitudinal and transverse calibration and stress matrices, respectively, for Monte Carlo trial j. $\bar {C}$, $\hat {C}$ and S are the original longitudinal and transverse calibration and stress matrices, respectively. Normally distributed random numbers with standard deviations of ± 1 are represented by r(x_i). Uncertainties in Young’s modulus and ν₁₂ are indicated by u(x_{1 − 2}), whilst $\bar {C}(x_{1-2})$, $\hat {C}(x_{1-2})$ and S(x_{1 − 2}) are the changes to the $\bar {C}$, $\hat {C}$ and S matrices as a result of a 1% increase in Young’s modulus and ν₁₂ respectively.

The material properties are independent of each other and were therefore varied independently. The calibration and stress matrices were varied by the same normal distribution since they are simultaneously affected by a variation in a particular material property. Uncertainty in the material properties was included in the integral method within Eqs.15 and 17 and in the Zuccarello approach within Eqs. 11 and 13.

Uncertainty exists in the calculation of the calibration and stress matrices, since FE models cannot completely represent all the deformations that are possible in reality. The individual terms of the $\bar {C}$ and $\hat {C}$ matrices were all varied by the same random variable since the matrices are considered to be fully correlated [27]. The stress matrix, S, was similarly adjusted. Finally, the calibration matrices were adjusted to compensate for uncertainty in the transverse sensitivity of each gauge through the use of Eq. 23. The longitudinal and transverse calibration matrices used to calculate the $\bar {a}$ and $\bar {b}$ matrices of the integral method were similarly modified.

The inverted cone end mill used to cut the hole during IHD results in a hole bottom that is not perfectly flat. Calibration coefficients determined by FE calculations according to the real blind hole geometry have been investigated for uniform stresses [33] and have been found to have an appreciable affect on the measured stresses, especially in the first two hole depth increments. To date, it is not possible to correct for this in non-uniform stress fields [27]. Any attempt to model the actual fillet radius in this work would have required a finite element model of such detail that it would have required impractically large computational resources. The uncertainties in fillet radius at the bottom of the hole were therefore not taken into account.

The turbine positioning in the x and y directions (i.e. the error due to the hole not being drilled exactly in the centre of the rosette) is a commonly recognised problem with the strain gauge rosette method and can have a significant effect on the calculated residual stress distribution. Correction for hole eccentricity in isotropic materials is available [34,35,36]. This effect is somewhat mitigated by the use of a 6 element strain gauge rosette, but because of the complex strain field around the hole it cannot be fully compensated for by this alone. To account for this requires correction of the calibration matrices based on the x and y offset of the hole. With respect to this investigation, the effects of hole offset in the x and y directions were minimised by meticulous experimental technique to ensure that the hole coincided with the centre of the strain gauge as accurately as possible. While the hole eccentricity for this experiment was measured to be close to zero, the effect of the small offset was corrected by changing the position of the strain gauges with respect to the hole during the biharmonic spline interpolation of the displacement data and subsequent calculation of the strain at each grid location. This process essentially eliminated any uncertainty associated with hole eccentricity.

Once the strain matrix, E, calibration matrix, C, and the stress matrix, S, were determined for each trial, the stress distribution was determined using Eqs. 8 and 10. The stress distributions for the integral and Zuccarello approaches were determined using Eqs. 15–17 and Eqs. 11– 13, respectively. The uncertainties in the stress distributions were determined at each depth increment by evaluating the standard deviation in the stress calculated at that depth across the ten thousand trials used in each Monte Carlo simulation.

Series Expansion Order Selection

Although the residual stress distribution and associated uncertainty can be determined using the series expansion method, any series order has the ability to solve the system of matrices and describe the measured strain distributions to some degree. Therefore, the issue remains as to which series order provides the best estimate of residual stress for the measured data. The approach used in this work is to determine those series orders that have converged, and from them to select the series order with the lowest RMS uncertainty [25]. Therefore, the calculated stress and uncertainty of every series order must be investigated to quantitatively determine the best estimate of the residual stress distribution.

The calculated stress and uncertainty in the x direction for 0^th to 14^th order series is shown graphically in Fig. 8. The corresponding figure for stress in the y direction is similar and is omitted in the interest of brevity. The stress uncertainty of each series order is shaded in light grey and then superimposed. The tendency of higher order series to become unstable increases their sensitivity to errors in strain measurement data within the Monte Carlo trials, resulting in greater stress uncertainty. The darkest areas correspond to convergence of a number of orders where their stress uncertainties agree. The light grey regions illustrate the divergence in uncertainty for higher order series, or the inability of low order series (0^th - 3^rd order) to describe the actual stress distribution. The 6^th order series is selected as the best solution for this experimental data set as it has the lowest RMS uncertainty of the series orders that have converged. Some orders have lower uncertainty, but have not fully converged and so are not selected. Higher orders which have converged show the first signs of instability and greater uncertainty, and were subsequently not selected either. It is important to emphasise that the 6^th order refers to the series expansion order of the temperature variations applied in each direction and not simply to the order of the residual stress distribution. They are different because each and every component of eigenstrain, resulting from the applied temperature variation, has some effect on the residual stress distributions.

Fig. 8

Overlap of the ± 2 standard deviation uncertainty bounds in σ_x for 0^th to 14^th order series

The convergence in stress results in the x direction of the 6^th, 7^th and 8^th order series is shown in Fig. 9. The results for 14^th order are also shown, where the instability in the calculated stress distribution is evident.

Fig. 9

Overlap of the ± 2 standard deviation uncertainty bounds in σ_x for converged and 14^th order series

Results and Discussion

The least-squares fits and associated uncertainties of the 6^th order series to the strain measurements obtained from the x, y and 45^∘ gauges are shown in Fig. 10. The uncertainty associated with the inability of the 6^th order power series expansion to exactly fit the measured strain data is included. The uncertainties in all figures correspond to ± 2 standard deviations. The stress distributions and associated uncertainties obtained using the 6^th order series are shown in Fig. 11. The uncertainty in all three stress components is expected to increase with depth since the sensitivity of the measured strains on the upper surface to released stresses decreases. However, stress uncertainty remains stable up to a depth of 1 mm. The maximum stress uncertainty occurs near the surface since the least-squares fits are less constrained near their endpoints and tend to diverge from the mean, resulting in increased uncertainty. The extension of the hole depth beyond 1 mm to provide additional strain data has helped improve the stability of higher order series at greater depths by providing additional data points to constrain the least-squares curve fit. The residual stress distributions in the x and y directions are similar in magnitude and form, and the residual shear stress is close to zero, as expected. A residual stress analysis must compare the measured stresses with allowable values. The peak stresses are only 55% of the bulk material yield stress and plasticity effects are therefore not included.

Fig. 10

Least-squares curve fits to experimental strain data, with associated uncertainties shown as ± 2 standard deviations

Fig. 11

Stress distributions and associated uncertainties obtained using the 6^th order series. Uncertainties are shown as ± 2 standard deviations

The residual stress distributions determined using the regularized integral and Zuccarello methods are overlaid on those determined using series expansion in Figs. 12 and 13. Only x and y stresses are shown since the shear stress is close to zero. The residual stress distributions compare favourably and the uncertainty in stress is lower overall in the case of series expansion especially at greater depths. Table 4 shows the RMS uncertainty in stress for each computational method, for each uncertainty source as well as the combined uncertainty, u(Z).

Fig. 12

Overlap of the ± 2 standard deviation uncertainty bounds in σ_x

Fig. 13

Overlap of the ± 2 standard deviation uncertainty bounds in σ_y

Table 4 Breakdown of RMS uncertainty in stress arising from each uncertainty source, x_i

It is evident that the zero depth position and noise in the experimental strains are important contributors to the stress uncertainty. While the series expansion method has a slightly greater tolerance to uncertainty in the zero depth position than the other methods, its tolerance to noise in the strain data is far greater. The uncertainty in stress associated with noise is consequently far lower in the case of series expansion. The misfit allowed by the use of Tikhonov regularization greatly improves the smoothness of the stress distribution and the overall uncertainty, but introduces its own considerable uncertainty into the stress results of the integral method. Regularization was not applied to the Zuccarello approach, and as a result it is the most adversely affected by noise in the experimental strain measurements.

Conclusions

A comprehensive study of three different computational methods for IHD in isotropic materials has been performed on an aluminium alloy 7075 specimen subjected to LSP. The use of series expansion was investigated and compared to the widely used unit pulse integral methods. A full uncertainty analysis was performed for all three computational methods using Monte Carlo simulation. Contrary to previous research, it was found that series expansion orders greater than 1 can be successfully used with IHD to calculate the residual stress distribution in isotropic materials. There is a strong correlation in calculated stress between the series expansion and integral computational methods. The uncertainty associated with the series expansion method is lower than that associated with the integral methods, especially at greater depths. The series expansion method is stable up to at least 8^th order and has lower RMS uncertainty than both the standard integral method with regularization and the Zuccarello approach. The series expansion method is also more resilient to errors in zero depth detection and noise in the experimental strain measurements than the integral methods.

It must be acknowledged, however, that at this stage in its development, the series expansion method requires more effort from practitioners than is required when using ASTM E837-13a. For this reason it is important that work be undertaken to normalise the method so that it can be more widely adopted.