The Effect of the Ill-posed Problem on Quantitative Error Assessment in Digital Image Correlation

Abstract

This work explores the effect of the ill-posed problem on uncertainty quantification for motion estimation using digital image correlation (DIC) (Sutton et al. [2009]). We develop a correction factor for standard uncertainty estimates based on the cosine of the angle between the true motion and the image gradients, in an integral sense over a subregion of the image. This correction factor accounts for variability in the DIC solution previously unaccounted for when considering only image noise, interpolation bias, contrast, and the software settings such as subset size and spacing.

Introduction

Using optical flow to estimate motion from images (as is done in DIC) leads to an ill-posed inverse problem. The ill-posed problem arises as a result of trying to recover a vector motion field from a scalar image intensity field. The nature of this deficiency has been extensively studied in references [2,3,4,5,6,7] and many methods have been developed to circumvent this issue (for example introducing regularization as proposed by Horn and Schunck [8]). While introducing regularization assuages many of the numerical issues symptomatic of the ill-posed problem, it does not fully address the resulting accuracy degradation. Regularization provides for a unique motion estimate, but regularization does not guarantee that this unique solution is the true motion. In fact, for traditional, subset-based DIC formulations, a savvy analyst needs to balance the regularization provided by increasing the subset size while avoiding the loss of accuracy due to smoothing.

While the nature of the ill-posed problem, related to optical flow and DIC, has been extensively studied, relatively few works have investigated the effect of the ill-posed problem on the accuracy of the solution in a systematic manner. In this work, we demonstrate that the accuracy of a DIC motion estimate is directly linked to directionality in the speckle pattern hearkening to the familiar axiom of optical flow, that motion can only be estimated in the direction of image gradients. In this work, we contribute a quantitative assessment of the impact of this axiom and show that all speckle patterns, regardless of how isotropic or anisotropic in orientation serve as a filter that admits only certain components of the true motion. Herein, we provide a concise means by which an analyst can estimate the accuracy of a DIC solution based on properties of the speckle pattern and the direction of the estimated motion.

Objective

The goal of this work is to provide an a posteriori error estimate for DIC based on the following two propositions:

Proposition 1

The error between a DIC motion estimate, $\hat {\mathbf {u}}(\mathbf {x})$ , and the true motion, u(x), is composed of an observable component (error which leads to a change in the residual that represents the model fit error) and an orthogonal component (error that results in no change in the residual).

Proposition 2

The total error is inversely proportional to the angle between the true motion and the image gradient (i.e. the speckle pattern).

If these propositions are correct, one can estimate the error in a DIC solution based purely upon the image data and the computed motion. This implies that our task in this work is to develop a residual-based estimate of the observable error as well as an estimate of the angle between the motion and the image gradients. These are the two necessary ingredients of the proposed error estimate.

This work also explains an additional source of variation in the DIC solution, which often exceeds the expected variation due to image noise, interpolation bias error, and approximation error. Our hypothesis is that this additional source of variation is linked to the relationship between the motion vector and the speckle pattern. We demonstrate this via formal analysis as well as numerical studies.

Investigation of quantitative error assessment in DIC has been studied in a number of works. In [9,10,11], and [12], the authors use statistical error analysis to determine the effect of common sources of error, such as interpolation bias and image noise on the resulting uncertainty in the motion estimate. In reference [13], the authors explore the effects of choices related to the subset size, speckle size, and gray level interpolation, among others on the resulting displacement field. The specific influence of the shape functions and interpolants in pattern matching is delineated in [14] and [15]. The authors of [16] show that the error in a DIC motion estimate is closely tied to the speckle size and distribution. An extension of the analysis in the works above towards material parameter identification is carried out in [17]. The effects of camera system resolution are explored in [18]. Lastly, a benchmark problem is used to capitulate the ultimate error regime in [19]. What has not been investigated in prior studies is the effect of the ill-posed problem on uncertainty, which is the primary contribution of this work.

Preliminaries

Table 5, in the Appendix, defines all of the symbols used in this work. Consider the Lebesgue space of functions, L ², on a domain, Ω, with inner product, $\langle \mathbf {a} , \mathbf {b} \rangle = {\int }_{\Omega } \mathbf {a} \cdot \mathbf {b} \, dx$, and associated norm

$$\begin{array}{@{}rcl@{}} ||\mathbf{a}||^{2}_{L^{2}({\Omega})} = ||\mathbf{a}||^{2} = \langle \mathbf{a} , \mathbf{a} \rangle\,. \end{array} $$

(1)

We define the norm of a nonzero vector, a, in the direction of a unit vector, b/|b|, as

$$\begin{array}{@{}rcl@{}} ||\mathbf{a}||^{2}_{\mathbf{b}} = \left\langle{\frac{(\mathbf{a} \cdot \mathbf{b}) \mathbf{b}}{|\mathbf{b}|^{2}} , \frac{(\mathbf{a} \cdot \mathbf{b}) \mathbf{b}}{|\mathbf{b}|^{2}}}\right\rangle = {\int}_{\Omega} \left( \frac{\mathbf{a} \cdot \mathbf{b}}{|\mathbf{b}|} \right)^{2} \, dx \,. \end{array} $$

(2)

We also define the cosine and sine of the angle between two non-zero vectors, in an integral sense, in terms of the following ratio¹

$$\begin{array}{@{}rcl@{}} &&{\cos} \, \theta (\mathbf{a}, \mathbf{b} ) = \frac{||\mathbf{a}||_{\mathbf{b}}}{||\mathbf{a}||} = \frac{||\,(\mathbf{a} \cdot \mathbf{b})\mathbf{b}/|\mathbf{b}|^{2}\,||}{||\mathbf{a}||} \,,\\&&{\sin} \, \theta (\mathbf{a}, \mathbf{b} ) = {\cos} \, \theta (\mathbf{a}, J\mathbf{b} ) \,, \end{array} $$

(3)

where J is [ 0 -1; -1 0 ]and |J b| = |b|. The cosine and sine of the angle, as defined, have the following identities:

$$\begin{array}{@{}rcl@{}} \left\{\begin{array}{llll} \qquad\qquad 0 \leq {\cos}\,\theta(\mathbf{a},\mathbf{b}) &\leq& \!1 \\ {\!\cos}^{2} \theta(\mathbf{a},\mathbf{b}) + {\sin}^{2}\theta(\mathbf{a},\mathbf{b}) &=& \!1 \\ \qquad\qquad\qquad{\cos}\,\theta(\mathbf{a},\mathbf{b}) &=& {\!\cos}\,\theta(\mathbf{b},\mathbf{a}) \\ {\!\cos}\,\left( \theta(\mathbf{a},\mathbf{b}) + \theta(\mathbf{c},\mathbf{d}) \right) &=& {\!\cos}\, \theta({\kern-.5pt}\mathbf{a},\mathbf{{\kern-.5pt}b}) \, {\cos}\, \theta(\mathbf{c},\mathbf{d}) \\&&- {\sin}\, \theta({\kern-.5pt}\mathbf{a},\mathbf{{\kern-.5pt}b{\kern-.5pt}}) \, {\sin}\, \theta({\kern-.5pt}\mathbf{c},\mathbf{{\kern-.5pt}d}) \end{array} \right. \,.\\ \end{array} $$

(4)

An a Posteriori Error Estimate

Motion Estimation using DIC

The objective of DIC is to recover a motion, v(x,t), from observations of an image intensity field, ϕ(x,t), that balances a transport model (i.e. optical flow [8]):

$$\begin{array}{@{}rcl@{}} \left\{\begin{array}{ll} \!\frac{\text{d}\phi(\mathbf{x},t)}{\text{d}t} = {\kern-.5pt}\frac{\partial \phi(\mathbf{x},t)}{\partial t} {\kern-.5pt}+{\kern-.5pt} \mathbf{v}(\mathbf{x},{\kern-.5pt}t{}) \!\cdot {\kern-.5pt}\nabla \phi{\kern-.5pt}(\mathbf{x},{\kern-.5pt}t) {}={\kern-.5pt} 0 ~~ \text{ {\kern-.5pt}over } {\kern-.5pt}{\Omega}{\kern-.5pt} \subset \mathbb{{}R}^{2}\, {\kern-.5pt},\\ \!\phi(\mathbf{x},{\kern-.5pt}0) = {\kern-.5pt}\phi_{0}(\mathbf{x}) \quad \mathbf{x} \in {\Omega}\, , \end{array}\right. \end{array} $$

(5)

where ϕ ₀(x) is the image intensity field at time, t = 0and Ωis the image domain, or a subset of the image. Assuming that the motion is independent of time (v(x,t)t ≈u(x,t)), a solution to the transport model is

$$\begin{array}{@{}rcl@{}} \phi(\mathbf{x},t) - \phi_{0}(\mathbf{x} - \mathbf{u}(\mathbf{x},t)) = 0 \, , \end{array} $$

(6)

where u(x,t) is the displacement field. A Taylor series expansion of (6) leads to

$$\begin{array}{@{}rcl@{}} \phi(\mathbf{x},t) - \phi_{0}(\mathbf{x}) + \mathbf{u}(\mathbf{x},t) \cdot \nabla \phi_{0}(\mathbf{x}) + \nu = 0 \, , \end{array} $$

(7)

where ν represents the higher-order terms of the Taylor series expansion. DIC formulations seek to find the motion, u ^∗, that minimizes some form of the correlation criteria given by (6)². For example, in a least-squares sense, u ^∗is defined as follows

$$\begin{array}{@{}rcl@{}} \mathbf{u}^{\ast} = \underset{\mathbf{u}}{\arg\min} \frac12 {\int}_{\Omega} \left( \phi - \phi_{0} + \mathbf{u} \cdot \nabla \phi_{0}\right)^{2} \, dx\,. \end{array} $$

(8)

Remark 1

Only the component of the true motion, u, in the direction of ∇ϕ ₀is observable in the transport model (7) (i.e. leads to a change in ϕ(x,t) − ϕ ₀(x)). Consequently, it is not possible to recover the true motion completely using DIC alone (unless it aligns precisely with ∇ϕ ₀).

Remark 2

Any motion vector, $\tilde {\mathbf {u}}$, orthogonal to ∇ϕ ₀, can be added to u ^∗resulting in a vector that is also a minimizer of (8).

These remarks summarize the ill-posed nature of the inverse problem underlying DIC. In regards to characterizing the accuracy of DIC, they imply that in addition to quantifying the error of the observable component of the motion, one must also determine the relationship between the true motion and the image gradient, i.e. the angle between them. When the cosine of this angle (defined below) is near zero, even if the error in the observable component is negligible, the accuracy with regards to the true motion can still be poor. This is illustrated on the right side of Fig. 1.

Fig. 1

(left) Relationship between the true motion, u, the DIC solution, $\hat {\mathbf {u}}$, and the total error, $\mathbf {u} - \hat {\mathbf {u}}$, in terms of the angles between them. (right) An illustration of two cases comparing the direction of motion with the direction of the image gradients. In the poor accuracy case, the cosine of the angle between the motion and the image gradient is small leading to a dramatic decrease in accuracy attributed to the ill-posed problem. Any point in the image for which the red motion vector is of zero length or the red and white arrows are orthogonal makes no contribution to the residual of the least squares problem (i.e. the error for this point is undetectable)

The least squares problem in (8) leads to the following set of normal equations which are solved to obtain the motion estimate.³

$$\begin{array}{@{}rcl@{}} {\int}_{\Omega} \left( \nabla\phi_{0} \otimes \nabla\phi_{0}\right)\mathbf{u} \, dx = -{\int}_{\Omega} \nabla\phi_{0}(\phi - \phi_{0}) dx \,. \end{array} $$

(9)

A Levenberg-Marquardt regularization [20] of the normal equations above can be written

$$\begin{array}{@{}rcl@{}} {\int}_{\Omega} \left( \nabla\phi_{0} \otimes \nabla\phi_{0}\right)\mathbf{u} \!+ {\!\alpha_{r}^{2}}\mathbf{u} \, dx \,=\, -{\int}_{\Omega} \nabla\phi_{0}(\phi - \phi_{0}) dx \,, \end{array} $$

(10)

where α _r is the regularization parameter. In most of the numerical examples in this work, the unregularized form of the normal equations, (9), is used, since as we discuss later, the subset-based discretization already introduces implicit regularization by means of parameterizing the motion over a subset. We use the Levenberg-Marquardt regularized form for one example to demonstrate that introducing explicit regularization, as in Eq. (10), does not circumvent the loss of accuracy due to the ill-posed problem.

Decomposition of the Error

The vectors in Fig. 1 illustrate the relationship between the true motion, u(x), the DIC solution, $\hat {\mathbf {u}}(\mathbf {x})$, and the total error $\mathbf {u}(\mathbf {x}) - \hat {\mathbf {u}}(\mathbf {x})$. We make the assumption that angle between the true motion and the DIC solution is always acute, which implies that our speckle pattern has adequate contrast for pattern matching, the images contain a reasonable amount of image noise, and that the interpolant used is at least third-order accurate (not bilinear).

Using trigonometric identities, one can prove the last identity in Eq. (4), i.e.

$$\begin{array}{@{}rcl@{}} {\cos}\, \theta(\mathbf{u} - \hat{\mathbf{u}},\nabla \phi_{0}) &=& {\cos}\left( \theta(\mathbf{u} - \hat{\mathbf{u}},\mathbf{u}) + \theta(\mathbf{u},\nabla \phi_{0}) \right) \\ &=& {\cos}\, \theta(\mathbf{u} - \hat{\mathbf{u}},\mathbf{u}) \, {\cos}\, \theta(\mathbf{u},\nabla \phi_{0})\\&& - {\sin}\, \theta(\mathbf{u} - \hat{\mathbf{u}},\mathbf{u}) \, {\sin}\, \theta(\mathbf{u},\nabla \phi_{0})\, . \end{array} $$

(11)

Noting that the sine and cosine values are bound between 0.0 and 1.0, we have

$$\begin{array}{@{}rcl@{}} {\cos}\, \theta(\mathbf{u} - \hat{\mathbf{u}},\nabla \phi_{0}) \leq {\cos}\, \theta(\mathbf{u} - \hat{\mathbf{u}},\mathbf{u}) \, {\cos}\, \theta(\mathbf{u},\nabla \phi_{0})\, , \end{array} $$

(12)

and similarly

$$\begin{array}{@{}rcl@{}} {\cos}\, \theta(\mathbf{u} - \hat{\mathbf{u}},\nabla \phi_{0}) \leq {\cos}\, \theta(\mathbf{u},\nabla \phi_{0})\, . \end{array} $$

(13)

Equation (13) leads to an estimate of the total error, $||\mathbf {u} - \hat {\mathbf {u}}||$, in terms of the observable error, $||\mathbf {u} - \hat {\mathbf {u}}||_{\nabla \phi _{0}}$, given in Eq. (2), and the angle between the true motion and the image gradients,

(14)

The expression above provides an analytical corollary to Propositions 1 and 2. What remains is to develop an estimate for the observable error and the cosine of the angle.

A Residual-based Estimate of the Observable Component of the Total Error

Consider the residuals, r and $\hat {r}$, given by

$$\begin{array}{@{}rcl@{}} r = \phi(\mathbf{x},t) - \phi_{0}(\mathbf{x} - \mathbf{u}) \approx \phi(\mathbf{x},t) - \phi_{0}(\mathbf{x}) + \mathbf{u} \cdot \nabla \phi_{0} \,, \end{array} $$

(15)

and

$$\begin{array}{@{}rcl@{}} \hat{r} = \phi(\mathbf{x},t) - \phi_{0}(\mathbf{x} - \hat{\mathbf{u}}) \approx \phi(\mathbf{x},t) - \phi_{0}(\mathbf{x}) + \hat{\mathbf{u}} \cdot \nabla \phi_{0} \,, \end{array} $$

(16)

Subtracting Eq. (16) from (15) leads to the following approximation

$$\begin{array}{@{}rcl@{}} (\hat{\mathbf{u}} - \mathbf{u}) \cdot \nabla \phi_{0} \approx \hat{r} - r \,, \end{array} $$

(17)

The observable component of the error can then be estimated as

(18)

Estimating the Cosine of the Angle

The same trigonometric analysis that led to (11) leads to a similar expression for the cosine of the angle between the true motion and the image gradient:

$$\begin{array}{@{}rcl@{}} {\cos}\, \theta(\mathbf{u},\nabla \phi_{0}) &=& {\cos}\left( \theta(\mathbf{u}, \hat{\mathbf{u}}) + \theta(\hat{\mathbf{u}},\nabla \phi_{0}) \right) \\ &=& {\cos}\, \theta(\mathbf{u},\hat{\mathbf{u}}) \, {\cos}\, \theta(\hat{\mathbf{u}},\nabla \phi_{0})\\&& - {\sin}\, \theta(\mathbf{u}, \hat{\mathbf{u}}) \, {\sin}\, \theta(\hat{\mathbf{u}},\nabla \phi_{0}) \\ &\leq& {\cos}\, \theta(\mathbf{u},\hat{\mathbf{u}}) \, {\cos}\, \theta(\hat{\mathbf{u}},\nabla \phi_{0}) \\ &\leq& {\cos}\, \theta(\hat{\mathbf{u}},\nabla \phi_{0})\,. \end{array} $$

(19)

We therefore make the approximation

(20)

for which a sufficient condition is that not only is the angle between the computed solution and the true motion acute, but also “small”.⁴ Combining Eqs. (14) and (20) leads to an error estimate based on the residual from the optical flow equations and the angle between the computed motion and the image gradients,

(21)

Note that the total error is always greater than the observable error that manifests in the residual of the least squares problem. The cosine of the angle can therefore be considered a correction to a standard error estimator that accounts for the ill-posed nature of the DIC problem.

A numerical illustration of the effect of the ill-posed problem on the error in a DIC motion estimate

To demonstrate that the total error in the estimated motion has an observable component and an orthogonal component (that does not influence the residual), we compute these quantities for a problem with a known solution imposed synthetically on an image set. We also use this numerical example to emphasize the importance of including the correction factor based on the cosine of the angle between the motion and the image gradients. The imposed motion is of the form:

$$\begin{array}{@{}rcl@{}} \mathbf{u}_{mms} = \{ 0.5\alpha {\kern-.5pt}+{\kern-.5pt} 0.5\alpha \,{\sin}\beta x \,{\cos}\beta y, 0.5\alpha {\kern-.5pt}-{\kern-.5pt} 0.5\alpha \,{\cos}\beta x \,{\sin}\beta y\}{} \, , \end{array} $$

(22)

where α is the amplitude of the motion and β is the frequency parameter. For this example, α = 1.0and β = π/50, which leads to a motion with a period of 100 pixels. Given a reference image, a corresponding deformed image was constructed by interpolating the reference image at the mapped pixel locations according to the imposed motion. For every pixel, i, in the deformed image, ϕ(x _i) = ϕ ₀(x _i −u _mms,i). A bi-quintic polynomial interpolant was used for the image manufacturing. Although the image manufacturing process introduces error (for example in the interpolation of intensity values) these errors can be fully quantified in the residual, r. The resulting effect of these errors on the total error is therefore known. A sample of the speckle pattern used in this example is shown in Fig. 2. For this example, no image noise was added to the deformed image. The software settings for this example are given in Table 1. The residual tolerance, in Table 1, was set greater than machine precision (1.0E-14) to avoid unnecessary iterations after the solution has essentially converged.

Table 1 Software settings for method of manufactured solutions example

Fig. 2

A 75×75 pixel sample of the speckle pattern used in the spatially varying imposed motion example

Since the actual motion vector is not known, the efficacy of the proposed approach lies in being able to use the angle between the estimated motion and the image gradients as a surrogate. Figure 3 shows a comparison between the estimated cosine of the angle and the exact cosine of the angle, revealing that the approximation in (20) holds, in this case. The data for this figure and the next were collected from a vertical line in the image at x = 250. Figure 4 shows the exact total error, $||\mathbf {u} - \hat {\mathbf {u}}||$, compared to the error observable in the residual of the transport model (computed using the right hand side of the approximation in Eq. (18)). Figure 4 also shows the corrected error estimate computed by multiplying the observable error by the inverse of the cosine of the angle as in (21). Note that the residual-based estimate, without the correction, underpredicts the error by roughly 20% indicating that the effect of the ill-posed problem plays a significant role in the error.

Fig. 3

Comparison of ${\cos }\, \theta (\mathbf {u},\nabla \phi _{0})$ and ${\cos }\, \theta (\hat {\mathbf {u}},\nabla \phi _{0})$, which determine the error magnification factor. This figure shows that the approximation in (20) is valid, e.g that the estimated motion can be used as a surrogate for the true motion in terms of evaluating the angle between the motion and the image intensity gradients. The data in this figure was collected along a vertical line in the image at x = 250

Fig. 4

Comparison of the exact total error, $||\mathbf {u} - \hat {\mathbf {u}}||$, the component of the error observable in the residual of the transport model (computed using the right hand side of (18)), and the corrected error estimate (computed using Eq. (21) with $||\mathbf {u} - \hat {\mathbf {u}}||_{\nabla \phi _{0}}$ computed using the right hand side of (18)). This figure shows that accounting for the orientation of the speckle pattern in relation to the motion provides for a much more accurate error estimate. The data in this figure was collected along a vertical line in the image at x = 250

Quantitative Error Assessment

The analysis above is useful for demonstrating the additional source of error related to the ill-posed problem in DIC. It also requires that the imposed motion be known so that the residual, r, can be computed. In this section, we develop an estimate for the uncertainty in a DIC measurement when the imposed motion is not known (i.e. we model the residual-based term using statistical analysis). We also use more familiar metrics such as the absolute or relative error rather than the L ²(Ω)-norm.

Consider the maximum norm of a function, f(x), in a bounded and measurable set, defined as $||f(\mathbf {x})||_{L_{\infty }} \equiv {\inf }\,\{ C \geq 0 \, : \, f(\mathbf {x}) \leq C \,\, \text {for almost every} \, \mathbf {x} \}$. A similar expression to (21) can again be developed using geometric arguments,

$$\begin{array}{@{}rcl@{}} ||\mathbf{u} - \hat{\mathbf{u}}||_{L_{\infty}} \approx \frac{1}{{\cos}\, \theta(\hat{\mathbf{u}},\nabla \phi_{0})} ||\mathbf{u} - \hat{\mathbf{u}}||_{L_{\infty},\nabla \phi_{0}}\,. \end{array} $$

(23)

Rather than use the residual of the transport model as in Section 2, to estimate the second term on the right hand side of the expression above, we follow the approach in Wang, et al. [10], in which the motion variance is treated as a linear function of the image intensity and inversely proportional to the norm of the image gradients in the reference subset,

$$\begin{array}{@{}rcl@{}} \text{Var}(\mathbf{u}\!-\hat{\mathbf{\!u}}) \!&=&\! \left[\begin{array}{ll} \text{\!Var}(u_{x}\!{\kern-.5pt}-\!\hat{u}_{x},u_{x}\,-\,\hat{u}_{x}{\kern-.5pt}) & \text{{\kern-.5pt}Var}(u_{x}\!{\kern-.5pt}-\!\hat{u}_{x},u_{y}\!{\kern-.5pt}-\!\hat{u}_{y}{\kern-.5pt}) \\ \text{\!Var}(u_{y}\,-\,\hat{u}_{y},u_{x}\,-\,\hat{u}_{x}{\kern-.5pt}) & \text{{\kern-.5pt}Var}(u_{y}\!{\kern-.5pt}-\!\hat{u}_{y},u_{y}\!{\kern-.5pt}-\!\hat{u}_{y}{\kern-.5pt}) \\ \end{array}{}\right] \\&=& 2 \eta^{2} \mathbf{\Sigma} \, , \end{array} $$

(24)

where $\mathbf {\Sigma } = ({\int }_{\Omega } \nabla \phi _{0} \otimes \nabla \phi _{0} \, dx)^{-1}$, and η is the standard deviation of the image noise. In the numerical examples below, we use the method in [21] to compute η. To get an upper bound on the variance, we employ the max norm of a matrix, $||\mathbf {A}||_{\max } = \max \limits _{ij}|A_{ij}|$.

$$\begin{array}{@{}rcl@{}} \sigma = \text{Var}(u_{i} - \hat{u}_{i}) \leq 2 \eta^{2} ||\mathbf{\Sigma}||_{\max} \,. \end{array} $$

(25)

Substituting (25) into (23) we have a corrected estimate of the displacement uncertainty, $\tilde {\sigma }$, that accounts for the variation induced by the ill-posed problem.

(26)

In words, we have developed a correction term, based on the cosine of the angle, for the uncertainty estimate in [10] that in addition to image noise, and contrast, includes the effect of the ill-posed problem.⁵ In the numerical examples below we show why including the correction factor is important.

Numerical Examples

In this section, we use a number of numerical examples to illustrate the analysis outlined above. The first example uses an unrealistically biased speckle pattern to demonstrate the role of the angle between the motion and image gradients in terms of uncertainty. In the second example, the same effect is demonstrated for a more realistic speckle pattern and a motion that is spatially varying, rather than a pixel shift. We then analyze one of the DIC Challenge data sets to show that the analysis holds for an independently generated image set. This example also shows that the correction term accurately predicts the increase in uncertainty as the subset size approaches zero. In some of the examples, a small subset size is used because this amplifies the effect of the ill-posed problem, making the correlation between the angle and uncertainty more visible. In the last example, we show that the analysis above applies to an experimental set of images and provide some quantification of the importance of the ill-posed effect on DIC in practice. All of the examples were computed using the Digital Image Correlation Engine (DICe) code, an open source DIC code available at https://github.com/dicengine/dice. The subroutines that compute the error and correction factor are located in the DICe_ObjectiveZNSSD.cpp file, in the Objective_ZNSSD::computeUncertaintyFields() method. Anyone wishing to repeat these examples or apply the same analysis to another problem of interest can freely download the software, install it and re-run these examples.

Implementation Details

The discrete DIC algorithm used for each of the examples is subset-based and includes the following details. The correlation criteria used is the zero-normalized-cross-correlation (ZNCC) criteria, C _ZNCC

$$\begin{array}{@{}rcl@{}} C_{ZNCC} = \sum\limits_{i} \left( \frac{(G_{i} - \bar{G})}{{\sum}_{j}(G_{j} - \bar{G})^{2}} - \frac{(F_{i} - \bar{F})}{{\sum}_{j}(F_{j} - \bar{F})^{2}}\right)\, , \end{array} $$

(27)

where F _i = ϕ ₀(x _i) is the reference image intensity value at pixel i,G _i = ϕ(x _i,t _n) is the deformed image intensity value at pixel $i, \bar {F}$ and $\bar {G}$ are the average intensity values over the subset for the reference and deformed images, respectively. The image gradients in x are computed using a row filter with coefficients 1/12[1,− 8,0,8,− 1]. Image gradients in y are computed using a column filter with the same coefficients. The interpolation scheme used is that of Keys [22]. A gradient-based optimization strategy is employed to determined the mapping parameters of the motion similar to the Lucas-Kanade algorithm [23]. A piecewise-linear, affine shape function is used with degrees of freedom for translation, rotation and normal stretch. The use of a subset-based method, with the motion parameterized over subregions of the image domain, leads to an inherently regularized formulation where the regularization is linked to the size of the subset. To investigate the effects of regularization, for one example, the Levenberg-Marquardt regularized form, Eq. (10), is used which includes explicit regularization in addition to the regularization provided by the subset. For the sake of simplicity, all of the numerical examples are two-dimensional. Stereo correlation was not considered.

Correlation between Variability in the DIC Solution and the Cosine of the Angle

To demonstrate a clear connection between the cosine of the angle, ${\cos }\,\theta (\hat {\mathbf {u}},\nabla \phi _{0})$, and the magnitude of the error, in this case in the x-direction, $|u_{x} - \hat {u}_{x}|$, we conduct a synthetic pixel shift experiment using a speckle pattern with a clear directional bias.⁶ The reference pattern, shown in Fig. 5, is rotated by increments of 10 degrees to create a sequence of reference patterns with a particular directional orientation. These reference images are then translated by one pixel in x-direction to create a deformed image for each case. We shift the images by a full pixel to avoid introducing interpolation bias errors. Finally, image white noise of magnitude 1% of 255, counts is added to the deformed images. The software settings used for this example are given in Table 2.

Fig. 5

A 75×75 pixel sample of the speckle pattern used for the directionality numerical example

Table 2 Software settings for the directionality numerical example

The data in Fig. 6 was generated by taking the average value, over all 40,000 subsets, of the angle between the motion and the image intensity gradients and the absolute error. This figure shows a clear anticorrelation between the magnitude of the error and the cosine of the angle. As the direction of the motion becomes closer in orientation to the gradients in the speckle pattern (in an integral sense over the subset) the error decreases nearly linearly. This correlation cannot be drawn, however, from the plot on the right hand side of Fig. 6, which shows the error compared to the sum of square of subset intensity gradients (SSSIG) criteria [24, 25]. For a given SSSIG value, the resulting error can span a large range of values. This suggests that while the SSSIG criteria does indicate the amount of gradient content in a subset, which impacts the error, it does not capture the directionality of the motion. The left plot in Fig. 6 shows that capturing the directionality is critically important for estimating the error. The right plot suggests that the SSSIG criteria cannot be used for such purposes.

Fig. 6

Accuracy results from ten speckle patterns at different predominant pattern angles. Each black dot represents the average of all subsets for one of the ten pattern orientations. (left) The average error in the displacement solution vs. the cosine of the angle between the imposed motion and the image gradients in the speckle pattern, showing a clear anticorrelation. (right) The average error in the displacement solution plotted vs. SSSIG criteria. Note that a wide range of errors are obtained for a given SSSIG value, suggesting that one cannot use the SSSIG criteria to quantitatively predict the error

The proposed error estimate highlights an additional source of error related to the orientation of the image gradients that applies to all speckle patterns, not just ones with anisotropy such as this one. An anisotropic pattern was used for this example because it clearly demonstrates the connection between the direction of motion, the direction of the image gradients, and the resulting uncertainty. In the examples that follow, the patterns are similar to those used in practice, with random sizes and orientations of speckles. The results from these patterns also support the same conclusion.

Directionality for a Spatially Varying Displacement

As opposed to the previous example that used an unconventional speckle pattern to demonstrate the effect of the directionality of the pattern and the motion, in this example we use a pattern similar to that used in practice to emphasize the same point. In this example, we impose the same spatially varying motion given in (22) to the speckle pattern shown in Fig. 2, but rotate and translate the reference pattern at random increments prior to deformation, to produce a set of reference images with a similar pattern, but a random orientation with respect to the spatially varying motion. The software settings used are given in Table 3. Figure 7 shows 100 realizations of the computed displacement along a vertical line at x = 250. The black line in the figure shows the exact solution. The dashed blue lines show the predicted uncertainty using $\tilde {\sigma }$. In general, the predicted uncertainty captures the variability in the recovered solution due to the directionality of the speckle pattern in relation to the imposed motion.

Fig. 7

100 realizations of the displacement profile for the spatially varying displacement example with a similar speckle pattern at random orientations. The data for this plot was take from a vertical line in the image at x = 250. (black line) exact solution, (grey lines) realizations of the displacement, u _y, (dashed blue lines) uncertainty bounds predicted by $\tilde {\sigma }$

Table 3 Software settings for directionality with spatially varying displacement example

DIC Challenge set 14

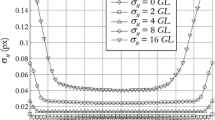
In this example, we compare the estimated uncertainty as predicted by σ and the corrected uncertainty, $\tilde \sigma$, that includes the effect of the ill-posed problem. To compute $\tilde \sigma$, we use the right hand side of the approximation in (26). The reference and deformed images for this example come from the DIC Challenge 14 data set, level 5 [26]. The software settings are given in Table 4 and a sample of the speckle pattern is shown in Fig. 8. The exact solution for this data set is known and is given by

$$\begin{array}{@{}rcl@{}} u_{x}\! =\! \left\{\begin{array}{ll} 0 & \text{if } x\!\leq\! 100\\ 0.1\, {\sin}(\beta_{14}(x\,-\,100)^{2}) & \text{otherwise} \end{array}\right. \,, \quad u_{y} \,=\, 0.0 \,, \end{array} $$

(28)

where β ₁₄ = 1.66E − 5. Figure 9 shows that the variation in the displacement error is more accurately predicted by $\tilde \sigma$ rather than than σ which underpredicts the variation. Figure 10 shows that the same trend occurs when the subset size is reduced from 35 to 11 pixels. Figure 11 shows the average displacement error in the x-direction along a vertical line at x = 1870 for various subset sizes ranging from 3 to 51 pixels. The corrected uncertainty captures the dramatic increase in the error as the subset size approaches zero. Note that the error in the motion estimation approaches an asymptote for a subset size above 20 pixels and then begins to rise again after 50 pixels. For extremely large subset sizes, the DIC solution becomes over-smoothed leading to increased errors. The range between 20 pixels and 50 pixels represents subset sizes for which all directions of motion are represented in the subset’s image gradients to some extent. One might erroneously conclude from this that the error is minimized for a threshold subset size, but in fact the error could be reduced for any subset size if the image gradients align with the direction of motion. Increasing the subset size to include more directions in the image gradients, on average decreases the portion aligned with any one particular direction of motion. This suggests that rather than adjust the subset size to ensure coverage of a wide variety of directions, one could make use of advances in pattern application to design a pattern that has image gradients in the direction of the anticipated motion (for example, as predicted by finite element analysis).

Fig. 8

A 75×75 pixel sample of the speckle pattern taken from the DIC Challenge 14 data set

Fig. 9

A comparison of the computed absolute error in u _x, the predicted uncertainty estimated by σ and the corrected uncertainty $\tilde \sigma$, which includes the effect of the ill-posed problem. In these results, a subset size of 35 pixels was used. Each dot represents a subset along a horizontal line in the image at y = 200

Fig. 10

A comparison of the computed absolute error in u _x, the predicted uncertainty estimated by σ and the corrected uncertainty $\tilde \sigma$, which includes the effect of the ill-posed problem. In these results, a subset size of 11 pixels was used. Each dot represents the error for a subset along a horizontal line in the image at y = 200

Fig. 11

A comparison of the average computed absolute error in u _xand $\tilde \sigma$, along a vertical line at x = 1870, for various subset sizes. Each dot represents the average value of all subsets along the vertical line for a given subset size

Table 4 Software settings for the DIC Challenge 14, level 5 numerical example

Regularization

Figure 12 demonstrates what happens to both the accuracy of the solution and the numerical stability (as measured by the condition number) as the amount of explicit regularization, provided by the regularization term ${\alpha _{r}^{2}}\mathbf {u}$ in Eq. (10), is increased. The data for this figure was collected by running the DIC Challenge 14 L5 data set with increasing values of α _rand comparing the resulting displacement to the known solution. Figure 12 clearly demonstrates that introducing regularization produces a linear system that is more stable (i.e. less sensitive to the input data as evidenced by a smaller condition number), but does not increase the accuracy of the formulation (the error in the solution remains constant). This subtle point motivates the importance of characterizing the error induced by the ill-posed problem even in the context of regularized formulations.

Fig. 12

Solution accuracy (left y-axis) and numerical stability (right y-axis) plotted vs. the amount of explicit regularization introduced via the parameter α _rin Eq. (10). The regularization parameter has been normalized by the area of the subset squared. In these results, a subset size of 21 pixels was used. Each marker represents the average of all subsets along a horizontal line in the image at y = 200. Notice that as the regularization increases, the condition number decreases as expected, but the accuracy remains constant

Experimental Images of a D-shaped Tensile Specimen

In the last example, we apply the uncertainty estimation methodology proposed above to an actual experiment, for which the displacement solution is not known. In this experiment, a stainless steel plate has been speckled and loaded in uniaxial tension. We analyze one time step in the load path to evaluate the efficacy of the proposed metric.⁷ Although the displacement solution is not known, given the loading and orientation of the sample we expect that the displacement in the pulling direction, x, should be relatively constant through the height of the sample (in the y-direction) throughout the initial stages of loading, prior to yielding. This is verified in the results for this example problem. Figure 13 shows a close-up of the speckle pattern applied to the plate. Figure 14 shows the overall specimen geometry.

Fig. 13

A 75×75 pixel sample of the speckle pattern taken from the D-shaped tensile specimen

Fig. 14

Reference image for the D-shaped tensile specimen showing two lines over which data is collected for other figures for this example

The uncertainty estimates σ and $\tilde {\sigma }$ are shown in Fig. 15. Notice that the corrected uncertainty increases the expected variability roughly 20 to 25% throughout the sample. This suggests that the ill-posed problem substantially impacts uncertainty and is not otherwise accounted for in the traditional uncertainty metric. This result is verified in Fig. 16 which shows the displacement variability along the line A-A in Fig. 14 for which the displacement should be nominally constant. The proposed uncertainty estimate more accurately captures the variability in the displacement solution.

Fig. 15

A comparison of the traditional displacement uncertainty, σ, (top) vs. the corrected uncertainty, $\tilde {\sigma }$, (bottom) which takes into account the effects of the ill-posed problem

Fig. 16

x-displacement data plotted along the vertical line A-A in Fig. 14 compared to the uncertainty estimated by the traditional means, σ, and the proposed uncertainty metric, $\tilde {\sigma }$. This plot shows that, even for experimental images, the proposed uncertainty metric captures the variability in the solution more accurately

Conclusions

This work presented a new perspective on quantitative error assessment in DIC that incorporates the effect of the ill-posed problem by means of a correction factor. This correction factor, based on the cosine of the angle between the true motion and the gradients in the speckle pattern, accounts for variability in the DIC solution that is not connected to interpolation bias, image noise, or contrast. Using numerical examples, we demonstrated that the error can be decomposed into an observable component and an orthogonal component that produces no change in the residual of the transport model. We also demonstrated that the cosine of the angle between the computed displacement and the gradient of the image intensity serves as a useful surrogate for the angle related to the true motion. Using this approximation, an error estimate was derived based only on computed quantities, not requiring the exact solution. Ultimately, we have demonstrated that a DIC motion estimate is closely tied to the speckle pattern and that each speckle pattern recovers only a particular component of the true motion. This emphasizes the need for further development of optimized speckle patterns that align with the predicted motion as well as including additional sources of information that can be used to augment the DIC motion estimate. This work lays the foundation for such pursuits.

Appendix

All symbols used in this work are defined in Table 5.

Table 5 Definition of all symbols used in this work