Introduction

Digital image correlation (DIC) is now being widely used in engineering disciplines, most often due to its ease of application. There have been a number of papers on the uncertainty of DIC due to the various system and mathematical processes of the technique, but a detailed analysis of how the imaging system resolution influences DIC has not been completed. This article will clarify the impact of system resolution on DIC and how to account for this in experimental work. System resolution is important because it is very common in a DIC experiment to use extension tubes to increase the magnification of the lens in order to observe smaller samples. The extension tubes can change the imaging-system resolution from being detector-limited to lens-limited. This transition is difficult to detect when viewing speckle images, and unfortunately will have deleterious effects on the DIC results. This work will demonstrate both experimentally and numerically the influence of system resolution on DIC.

Previous work to explain the sources of error in 2D DIC include: The effect of bias on DIC demonstrated by Schreier [1] that showed that the interpolation function used can have a large effect on the bias errors of the matching. The bias error and an additional variance error were calculated by Wang [2, 3]. Wang’s paper provides an analytical solution and comparison of subset size, image noise and contrast for a cubic and linear polynomial interpolation, zero-order shape function and the normalized cross-correlation (NCC) function using synthetically modified experimental images. The images in the study were experimental but modified to vary the intensity, contrast, noise, and blurring. This was extended to 3D error estimates using error propagation techniques in a paper by Wang [4] and a related paper by Ke [5]. A paper by Bornert evaluated a number of DIC algorithms and analysis choices using synthetic images [6] and a similar following article assessed different DIC codes and looked at the various errors by grouping the codes by type [7]. A study of the influence of four sum-squared difference (SSD) correlation criteria on strain errors was conducted by Tong [8] and used a bicubic spline interpolation function. Quantifying and removing lens distortions was studied by Schreier for stereo-microscope DIC [9]. Some of the influences of the modulation transfer function (MTF) have been studied by C.-H. Hwang [10] for stereo-DIC. One effect of the imaging system, namely lens distortions, has been studied by Lava [11]. This paper differs by looking at the lens resolution rather than the lens distortions.

The first section of this paper will elucidate the controlling optical components and their relevant parameters for DIC. The next section demonstrates the experimental setup and a simple method for measuring an estimate of the lower bound of the MTF. A method of simulating the aperture on existing images is then presented and used with synthetic image shifting techniques to create shifted and strained images with known results for study. These numerically produced trends are then reproduced in experiments to verify the results. Finally, conclusions for the practice of DIC are drawn to assist the experimentalist.

Definition of System Resolution

There are typically two methods of defining resolution in imaging, both related to the optical transfer function (OTF). The first one looks at the optical transfer of a point source and its output is called a point spread function (PSF) which defines the smallest possible feature that can be resolved by the system. This is illustrated in Fig. 1. A diffracted limited (ideal) system will produce an Airy disk at the image plane instead of a point, if we assume a circular aperture. The second method, used more often in the imaging world, is the modulation transfer function (MTF) and is mathematically defined as the magnitude of the OTF:

$$ \boldsymbol{MTF}\left(\boldsymbol{\xi}, \boldsymbol{\eta} \right)=\left|\boldsymbol{OTF}\left(\boldsymbol{\xi}, \boldsymbol{\eta} \right)\right|, $$
(1)

where (ξ,η) are the spatial frequencies in the x and y directions. To quantify the resolution experimentally, the MTF is preferred because it can be easily measured using a resolution target. The resolution target is either a sinusoidal pattern of varying spatial frequency or a chart with groups of different sized square waves, as in the United States Air Force (USAF) target seen in Fig. 2. Note that when using square waves the measurement is often referred to as the contrast transfer function (CTF) rather than the MTF. When using a spatially varying sinusoidal pattern, the complete MTF can be measured showing the contrast as a function of line pairs per mm (lp/mm). When using the USAF target, rather than a varying sine pattern, discrete points along the full MTF curve are sampled as illustrated in Fig. 2. The percent contrast for determining the MTF is calculated using,

$$ \%\boldsymbol{Contrast}=\left|\frac{\left({\boldsymbol{I}}_{\boldsymbol{max}}-{\boldsymbol{I}}_{\boldsymbol{min}}\right)}{\left({\boldsymbol{I}}_{\boldsymbol{max}}+{\boldsymbol{I}}_{\boldsymbol{min}}\right)}\right|\times 100, $$
(2)

where I is the intensity measured on the image. Then, at some user-determined contrast a system cutoff resolution is defined (20 % was used for this paper).

Fig. 1
figure 1

Illustration of OTF and PSF for a typical lens. Illustrated is a point source in the object space and the resulting PSF on the CCD detector in the image space

Full size image
Fig. 2
figure 2

1951 USAF Airforce target used to measure MTF. MTF Curve for the 35-mm lens with and without extension tube. Contrast image and intensity profile for the 35-mm lens with a 40-mm extension tube

Full size image

In DIC, the “optical system” is both a lens and a digital detector; both of these functioning together will define the MTF of the optical system. Often in machine vision cameras and lenses, the lens has a PSF that is typically smaller than the pixel size making the system “camera limited.” In this case, the minimum resolution can be found using the sampling theorem:

$$ \boldsymbol{MT}{\boldsymbol{F}}_{\boldsymbol{CCD}}=\frac{1}{2\cdot \left(\boldsymbol{Pixel}\ \boldsymbol{Size}\right)}\left[\mathrm{lp}/\mathrm{mm}\right]. $$
(3)

By definition the resolution calculated here is in the image space, the lens magnification can then be used to determine the pixel size and the corresponding resolution in the object space. The “2” in the denominator of equation (3) is a consequence of the sampling theorem that requires a minimum of 2 pixels to resolve any feature. The practical effect of the sampling theorem is illustrated in Fig. 3 where the PSF of a lens is superimposed on the CCD pixels (left side) along with the corresponding CCD output (right side) for both aliased and unaliased spot sizes. The spreading out of the intensity on the pixels, indicates how aliasing on the CCD will degrade the measurement. The sampling theorem therefore defines the minimum DIC speckle size for camera-limited systems: to be safe, most publications on DIC will then specify a conservative “ideal” speckle size of 3–5 pixels per speckle (in image space) in order to avoid an aliased pattern that will severely degrade the accuracy [12]. It is interesting to note that Particle Image Velocimetry (PIV), a closely related technique specifies an aliased ideal particle size of 1–2 pixels [13].

Fig. 3
figure 3

Illustration of spot size and the effect on the CCD and contrast (modified from http://www.andor.com/learning-academy/ccd-spatial-resolution-understanding-spatial-resolution)

Full size image

Now that the CCD resolution has been defined, we consider the resolution of the lens. The 35-mm Edmund Optics lens used in this experiment specifies an MTF of >100 lp/mm at f/4. This is approximately matched to the resolution of the Point Grey camera (3.45-μm pixels) with a resolution of 145 lp/mm as calculated using equation (3). This makes the optical system “camera-limited” at larger apertures (>f/4) and “lens-limited” at smaller apertures (<f/4). This is only true when the lens is used without the increased magnification of extension tubes. In this paper, the resolution of the lens was varied both by changing the aperture and by adding extension tubes to switch between camera- and lens-limited scenarios. When adding extension tubes to increase the magnification beyond the resolution of the lens, “empty magnification” will occur. Empty magnification is defined as an increase in the image size, with no added detail or contrast in the image. This emphasizes the filtering effect of a lens aperture, which acts as a low-pass spatial filter, where high-frequency content, e.g. sharp edges and small patterns, are removed. Empty magnification can be identified experimentally when speckles increase in size with added magnification, but the speckle edges seem to become less defined.

As noted above, the lens resolution is not a fixed number, but is related to the relative aperture or f-number (f/#) of the lens. The f/# Footnote 1 is defined as the ratio of the focal length to the limiting aperture:

$$ \boldsymbol{f}/\#=\frac{\boldsymbol{f}}{\boldsymbol{d}}, $$
(4)

where f is the focal length and d is the aperture diameter. The maximum resolution (available if the lens is perfect) is then often defined as the minimum resolvable point separation, χ, and is related to the aperture, d, by,

$$ \boldsymbol{\chi} =1.22\frac{\boldsymbol{\lambda} \boldsymbol{f}}{\boldsymbol{d}}, $$
(5)

where λ is the wavelength of light. This reveals that for a fixed wavelength, the lens resolution is higher for larger apertures, d (smaller f/#s, e.g. 2.8), and therefore able to resolve smaller features. Conversely, for smaller apertures (larger f/#s, e.g. 32), the resolution is lower and not able to resolve small features. For practical considerations, the f/# not only changes the resolution, but changes the depth-of-field. Depth-of-field is defined as a range of distances around the best-focus point where the object will appear in focus. Unfortunately, the resolution and the depth-of-field are inversely proportional: Increasing the lens resolution will decrease the depth-of-field and vice-versa.

Experimental Setup

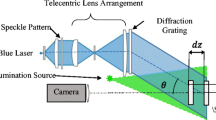
An experiment was setup to test the influence of imaging system resolution on DIC. An Edmund Optics 35-mm lens, specified at 100-lp/mm at f/4, imaged the speckle patterns onto a 5-Megapixel Point Grey Grasshopper camera, with 3.45-μm pixels. To increase the magnification, a 40-mm extension tube was added. A 2D translation stage moved the speckle patterns in-plane under the camera with subpixel motions. The MTF was measured using an Edmund Optics 1951 USAF resolution test slide. The test setup is shown in Fig. 4.

Fig. 4
figure 4

Experimental setup showing the lens and camera without extension tubes. X-Y stages for sample movement with speckle pattern. Fiber light source for illumination. Resolution target at same plane as the speckle pattern

Full size image

Imaging System Resolution

The resolution of the lens and extension tubes at different f/#s was measured using a USAF target. For the 35-mm lens, the magnification yields a pixel-size in the object space of approximately 21 μm/pixel. Figure 5 shows that Group 4/Element 1, which corresponds to a resolution of approximately 21 μm in the object space, can be resolved with 20 % contrast. This corresponds to the pixel size in the image space and indicates that the camera pixel is the resolution limiting factor.

Fig. 5
figure 5

MTF of the 35-mm lens at f/1.9 showing 20 % contrast is at Group 4/Element 1, which is a resolution of 21 μm or 16-lp/mm, making the system camera-limited

Full size image

The lens resolution is also controlled by the aperture. The effect is seen in Fig. 6 where the aperture was f/32. The image resolution is now less than the pixel-size in the object space (≈71 μm) making the imaging system “lens-limited.”

Fig. 6
figure 6

MTF of the 35 mm lens at  f/32. The contrast is 20 % at Group2/Element 5 yielding 6-lp/mm or 79 μm spot size resolution

Full size image

Figure 7 shows the USAF target with the 40-mm extension tube. The lens magnification with the extension tube yields a pixel size in the object space of 2.6 μm. Figure 7 reveals that the system is lens-limited because the resolution limit is found to be Group 6/Element 4 for a feature size of 5.5 μm (20 % contrast) in the object space. This was further confirmed by changing the aperture, where each stop decreased the resolution.

Fig. 7
figure 7

Group 6/Element 4 (90.5 lp/mm), for a spatial resolution of 5.5 μm in the object space. Making the system lens-limited

Full size image

The Lens as an Optical Fourier Transform

Considering the imaging system as a mathematical model, the lens can be viewed as a spatial filter. This is most easily modeled using Fourier optics [14]. In this paradigm shown in Fig. 8, the first lens transforms the object to the Fourier plane where the aperture functions as a mask, removing the higher frequency terms, and then the image is inverse Fourier transformed onto the detector at the image plane by the second lens. Experimentally this is seen in the USAF target images where the larger f/#s (smaller aperture) decrease the lens resolution (Fig. 6). The aperture was modeled using Fourier optics as outlined in Voelz [15]. We have made the monochromatic illumination assumption for the simulations, which varies from the experimental setup illuminated with white light. This assumption should only create small differences. The equations were coded in LabVIEW and were then applied to experimental images to create “simulated images” for the numerical simulations. For all simulated images, the experimental image to be modified was acquired with the highest resolution of f/1.9 and then modified as described above to create a “simulated” image.

Fig. 8
figure 8

Illustration of Fourier optics

Full size image

A comparison, shown in Fig. 9, was made between a simulated aperture applied to the image and an experimental image with an equivalent aperture. It can be seen that the experimental image has more filtering than the simulated image. This difference will not change the results in this paper because quantitative comparisons are only made between experiments or between simulations. Comparisons between experimental and simulated results are only qualitative showing that the approach yields physically real results. For exact matching, it is likely that the frequency content of the images should be matched. This was done by applying a numerical aperture of f/64, to the original image which clearly better matches the experimental configuration. It may be that the lens is used at a conjugate dramatically different than that for which it was designed.

Fig. 9
figure 9

Experimental versus simulated image showing the same region for all images (top images) and their respective Fourier transform (bottom images). The noise outside the aperture in the bottom-left image is due to the digitization noise during image acquisition, which does not occur in the simulated images

Full size image

Numerical Simulation of Images for DIC

To explore the influence of the MTF on DIC it is easiest to use numerically shifted images. The images were created using two methods. The first is an exact subpixel binning method using high-resolution images. The methodology for this is explained in a paper by Reu [16]. The same paper explains a Fourier image shifting technique that was used as the second method of shifting. Both methods were used to create a series of images with 0.1 pixel displacements. The results from the DIC analysis (Vic2D – Correlated Solutions) can then be compared to a known answer. The data was analyzed by calculating the mean and standard deviation of the displacement using all of the correlated points in the region-of-interest. The mean displacement will often show the well-known s-shaped bias error resulting from the interpolation [17] and the standard deviation indicates the displacement noise. The errors in DIC are controlled principally by two image attributes: noise and contrast [4, 18]. An immediate conclusion is that the filtering effect of the aperture will decrease the contrast if the speckles are not appropriately sized. This means that for an equivalent field-of-view, the speckles will need to be larger to maintain the same contrast compared to a higher resolution imaging system. There is some evidence that mild filtering of speckle images is beneficial in reducing matching errors [16]. For 2D systems this can be done using the aperture or a slight defocus of the lens. However, the filtering considered in this paper is greater than would be desired, and decreases the accuracy of DIC. Figure 10 shows the binned images used for the first numerical study. The left image is the original f/1.9 image and the right image is after numerically applying an aperture of f/64. Also shown are the resulting speckle patterns and the intensity profile along the same line illustrating the decrease in contrast due to the filtering of the aperture and the removal of the smaller speckles, leaving only the filtered large speckles.

Fig. 10
figure 10

Loss of contrast in image caused by the filtering effect of the aperture. (Left) Full resolution f/1.9 image (Right) f/64 filtered image. Green line indicates line-extract region shown in the bottom line plots. Bottom scales are identical showing a pronounced loss of contrast. The right inset FFT shows the loss of high-frequency content of the filtered image, indicated by a loss of magnitude around the edge of the FFT. σ Match (using equation (6) with noise σ = 1 count) for the left image is 0.003 pixels and 0.03 pixels for the right image. The left inset shows the gradient in the x-direction, with the corresponding histogram directly below

Full size image

Estimation of Image Quality for DIC

The concept of “image information” has been mentioned as a measure of the quality of a speckle pattern. This could possibly be measured by image entropy, however, entropy cannot differentiate between gradients caused by image noise, which has high entropy, but low information and a high-contrast fine-patterned speckle image, with low noise, which would also yield a high score, but with trackable information available for the DIC algorithms. Therefore, instead of entropy, we used a better measure, of the matching noise, σ Match , that has developed in the literature [3, 19, 20],

$$ {\boldsymbol{\sigma}}_{\boldsymbol{Match}}\propto \frac{{\boldsymbol{\sigma}}_{\boldsymbol{n}}}{\boldsymbol{n}\sqrt{\overline{\nabla {I}^2}}}, $$
(6)

where n is the subset size, σ n is the standard deviation of the noise, and \( \overline{\nabla {I}^2} \) is the average of the image gradients. For the estimates shown in the figures, the gradients were calculated using a gradient kernel (−1, 0, 1) in the x- and y-direction. The results in both directions were the same due to the random nature of the speckle. This metric, in pixels, was calculated for the images as a quality measure for comparison between images. Because the image noise was not known for all image sets, an experimentally reasonable value of σ n  = 1 was used for all results.

Simulation Results

Figure 11 shows the DIC results from the two cases in Fig. 10. In Fig. 11 and all similar figures, there are two errors that are plotted together. The solid line plots the bias error that sometimes appears as a sinusoidal-shaped curve (Fig. 13 for example), and the error bars represent the variance term of the error. The bias error was calculated by taking the mean value of all calculated subsets and subtracting from the known shift, with the variance representing the typical statistical spread around the mean value. The two errors are additive, making the total error the sum of both the bias and variance terms. For the results in Fig. 11, the bias error is much smaller, and the matching errors can be adequately represented by the variance term plotted in Fig. 14 as the standard deviation of the u-displacement. In Fig. 11, the relative size of the subset is shown overlaid on the speckle pattern to give a scale of the speckles relative to the subset size. The filtered image has no small speckles and therefore has less contrast variation within any given subset. As shown in equation (6) the matching quality is controlled by the contrast variation within a subset. The gradient is quantitatively measured by taking the derivative of the image in the x-direction using a gradient filter (3 × 3) and plotting the gradients and the histogram of the intensity distribution as shown in Fig. 10 (following figures only contain the gradient histogram). The histogram gives an indication of the pattern quality where a larger distribution of values indicates higher gradients, and therefore a better pattern. The frequency content is another measure of the information (or speckles) contained in the image. The broader spectrum of the f/1.9 image is obvious, as well as the consequence of applying the aperture seen in the f/64 image. The loss of contrast, as well as the number of speckles (information) in the image decreases the accuracy of the correlation for a given subset size as clearly seen by the larger errors in Fig. 11.

Fig. 11
figure 11

Bias and variance errors (1σ) of the binned experimental images in Fig. 10 for f/1.9 and f/64. The solid line indicates the measured bias error, with the error bars representing the variance error. The inset shows the subset overlaid on the speckle pattern

Full size image

Next, images acquired for the experimental work presented in the next section, had an aperture applied and then were numerically shifted. The original image and that with a numerical aperture of f/64 are shown in Fig. 12. The contrast along the line is plotted below the corresponding image showing the loss of both spatial resolution, frequency content and contrast due to the aperture. Using a subset size of 41 × 41 pixels, the shifted image sets were analyzed. Both the bias and variance errors are plotted together in Fig. 13. For the same reasons as above, with equivalent subset sizes, the errors are greater for the filtered image.

Fig. 12
figure 12

(Left) Original f/1.9 speckle image and contrast along line. (Right) f/64 filtered image and line contrast. σ Match (using equation (6) with noise σ = 1 count) for the left image is 0.004 pixels and 0.01 pixels for the right image

Full size image
Fig. 13
figure 13

Bias and variance errors (1σ) for numerically shifted images with apertures of f/1.9 and f/64 using the same subset size. The inset shows the subset overlaid on the speckle pattern

Full size image

Looking at the variance errors, which dominate the error term, the subset size was varied over a range of values to find at which point the f/1.9 and f/64 images would have approximately the same uncertainty. The results shown in Fig. 14 indicate that for an equivalent uncertainty, a subset size of 21 × 21 for the f/1.9 case would yield approximately the same uncertainty as a 101 × 101 pixel subset size for f/64. This clearly illustrates the loss in accuracy that occurs when the imaging system limits the spatial resolution and filters the smaller speckles. Figure 15 illustrates the errors for the “approximately equivalent” uncertainty at f/1.9 (21 × 21) and f/64  (101 × 101) and shows that the variance error is the dominant error term.

Fig. 14
figure 14

Uncertainty of the DIC results for varying subset sizes

Full size image
Fig. 15
figure 15

Bias and variance errors (1σ) for “equivalent” uncertainty for the f/1.9 (subset = 21 × 21) and f/64 (subset = 101 × 101) images

Full size image

However, if the speckles are large enough (inset in Fig. 16), the filtering of the aperture does not matter and there is no loss of contrast. In fact there is some indication that the softening of the speckle edges caused by the low-pass filtering effect of the lens has a positive effect. This is seen in Fig. 16, where the f/32 image has a lower noise floor than f/1.9. This numerical result should be interpreted with caution, as the other errors involved in DIC will almost always create errors in the 1/100th of a pixel scale, whereas these results are 1/1000th of a pixel making it difficult to draw conclusions for actual experimental situations.

Fig. 16
figure 16

Bias and variance error (1σ) for the large speckle situation. No problem with filtering of lens

Full size image

Experimental Results

Using the experimental configuration in Fig. 4, two appropriately sized speckle patterns created with spray paint were imaged. The average speckle size of the large pattern imaged with the 35-mm lens is 100 μm (Fig. 17) and 8 μm (Fig. 19) for the small pattern imaged with the same lens and a 40-mm extension tube. Because the aperture was being changed to vary the resolution of the lens, a variable intensity light source was used to ensure that the illumination between all configurations was kept approximately equal using the histogram of the image as an approximate measure. More importantly the ratio of the contrast to the noise was maintained constant for all imaging conditions. The noise was evaluated by taking five images at each configuration and measuring the pixel-by-pixel grey level standard deviation to ensure that all images had a similar noise profile. The lens distortion was also measured by looking at the shape of the displacement field of a translated rigid plate. Errors due to lens distortions were determined to be less than 0.005 pixels for a 50-pixel travel and 0.001 pixels for the 5-pixel travel, well below the errors being studied here.

Fig. 17
figure 17

Speckle image using 35-mm lens at f/1.9 (camera-limited Group 4/Element 1 at 16 lp/mm) and f/16 (lens-limited Group 3/Element 3 at 10.1 lp/mm). Line intensity profile (below) as indicated on image. σ Match (using equation (6) with noise σ = 1 count) for the left image is 0.006 pixels and 0.01 pixels for the right image

Full size image

A similar process was used to analyze the experimental images as in the numerical section. The samples were translated between 5 and 50 pixels. Figure 17 shows the speckle pattern and the contrast along a line for the low magnification case. The results in Fig. 18 indicate that there is little to no difference in the results between the two cases. This is because the system resolution is limited by the camera pixels and changing the aperture from f/1.9 to f/16 adds only a little softening to the pattern, without changing the spatial distribution or contrast as seen by the similarity of the inset contrast histograms and grey level line cuts. This confirms the numerical simulations shown above. Note that only the standard deviation of the measured displacement can be plotted because there is no “known” displacement value to recover the bias error. The variance error, however, dominates the uncertainty and will capture the largest error term as noted earlier.

Fig. 18
figure 18

Standard deviation of displacement

Full size image

Compared with the larger speckles above, the following case illustrates that selecting the speckle size based on the imaging system resolution is important. The pattern shown in Fig. 19 shows a speckle pattern with a high percentage of small speckles 2–3 pixels when camera-limited, however these small speckles are completely filtered out when the aperture is changed to f/8 making the system lens-limited. The contrast along the line profile for the image changes from 65 to 54 %. This is seen in the histogram of the gradient plot shown in the inset, where the contrast is much greater for f/1.9, and can also be seen in the grey-level line plot below. Probably more important is the FFT of the image. The wider the spread of frequencies at f/1.9 indicates that there is greater high-frequency content in the image, i.e. there are small speckles. The FFT for f/8 shows the aperture limiting the frequency content with the brighter region of frequencies in the center of the FFT (large speckles).

Fig. 19
figure 19

High-resolution speckle images showing the contrast along the green line cut. Left image is f/1.9 (camera-limited Group 6/Element 5 at 102 lp/mm) and the right image is f/8 (lens-limited Group 6/Element 1 at 64 lp/mm). σ Match (using equation (6) with noise σ = 1 count) for the left image is 0.002 pixels and 0.004 pixels for the right image

Full size image

The speckle patterns in Fig. 19 were analyzed using the same approach as in previous sections. Figure 20 shows that to obtain a similar noise floor, the subset size must be increased from 27 × 27 pixels at f/1.9 to 51 × 51 pixels at f/8. Two subset sizes for both apertures were analyzed, including the equivalent error sizes, and the results are shown in Fig. 21, which plots the displacement variance versus the u-displacement calculated over the entire analysis region. Unfortunately, bias errors cannot be calculated for these images as shown in Fig. 13 because the exact experimental displacement is unknown.

Fig. 20
figure 20

Subset size versus displacement standard deviation for f/1.9 and f/8 images using the ≈ 5-pixel shifted image

Full size image
Fig. 21
figure 21

Noise at displacements between 0 and 5 pixels for f/1.9 and f/8, for both subset sizes 27 × 27 and 51 × 51 pixels

Full size image

A Look at Aperture and Strain Resolution

An investigation on the influence of aperture on the strain resolution was also conducted. This was done by taking a high-resolution image (Fig. 22) and filtering it with a given aperture, in this case f/50. A displacement profile across the width of the image was applied using a Fourier expansion and then a final linear interpolation to find the grey value at a given shifted pixel location. The commanded position profile and the resulting displacement profile from the DIC results are shown in Fig. 23. Gaussian noise of varying levels was then numerically added to the strained image. The chosen displacement field yielded a constant strain of opposite magnitudes on each half of the image as shown in Fig. 24. Strain levels of ±500 and ±520 με where created to determine if a 20-με magnitude change could be measured over the DIC strain noise floor. The influence of the reduced image information due to the filtering is immediately obvious in the strain results and can be seen by comparing Figs. 24 and 25. Both figures have identical subset, step-size and strain window sizes. The strain window is the number of data points in both directions that are fit to smooth the displacement noise. The smoothed and fit result is then used to calculate the strain. The influence of the loss of contrast and noise are amplified in the strain results because strain is a spatial derivative of the displacement field, confirming the conclusions of the previous sections that clearly illustrated that speckle contrast reduction increases the displacement noise. To quantitatively compare the two cases, a line cut through the middle of the results was extracted, and the mean and standard deviation of the strain were calculated using 50 points along the line. Table 1 gives the results for the two apertures for five different noise levels. It indicates that a noise level of 5 counts at f/1.9 will yield the same results as 2.5 counts at f/50. Equivalent results to f/1.9 can be obtained with a very large subset of 101 × 101 pixels at f/50.

Fig. 22
figure 22

Original image and same region with f/50. σ Match (using equation (6) with noise σ = 1 count) for the left image is 0.003 pixels and 0.008 pixels for the right image

Full size image
Fig. 23
figure 23

Commanded position via FFT methods and the resulting displacement profiles. The commanded displacement yields a constant strain of opposite magnitudes on the two halves of the image

Full size image
Fig. 24
figure 24

f/1.9 image with two strain levels and two noise levels plotted

Full size image
Fig. 25
figure 25

f/50 image with identical strain and noise levels as Fig. 24

Full size image
Table 1 Strain results
Full size table

Conclusions

The resolution of the imaging system is an important parameter in determining how to setup a DIC system. For most situations where a lens is used without extension tubes, the normal assumption of the pixel as the limiting resolution factor is likely to be correct. However, when working at higher magnifications, the lens resolution must be considered. Unfortunately, the situation of the lens limiting the resolution can be difficult to identify in practice. It is recommended that when setting up an experiment with high magnifications, a USAF target should be used to determine the approximate resolution of the system. If lens-limited, it will require that the speckles be increased in size in order that the speckles are 3-times the resolution limit of the lens, rather than using the rule-of-thumb of 3-pixels per speckle. This will ensure that the speckles are fully resolved and the contrast is not compromised by the filtering of the lens. This will avoid the confusing situation where an apparently high-quality speckle pattern seems to be poorly imaged by the system.

If the speckles are not appropriately sized for the system resolution, the results will be degraded as indicated by both the experimental and numerical results. This increase in the standard deviation of the displacement can be counter-acted by increasing the subset size within certain limits. That is spatial resolution, or data point density, can be traded for better displacement resolution. A less concerning side effect is that camera pixels may be “wasted” due to the lower resolution of the lens. In these situations it may be beneficial to bin the pixels on the camera to better match the lens resolution, which will have the benefit of decreasing the image noise, helping to improve the DIC results. When the highest spatial resolution is desired for experimental reasons, i.e. when there will be large displacement gradients across the field-of-view, the experimentalist must ensure that both the lens and camera are able to resolve at small enough scales to capture the gradients. This can be a challenging optimization process as creating speckles of exact sizes at small scales can be difficult, and therefore hard to match to the imaging system minimum spot size.

The conclusions drawn in this paper apply equally to DIC measurements made through a telescope. This is an analogous situation where the lens resolution is likely to limit the image. In practice, for long distance measurements, a more severe constraint is the image distortions caused by imaging through a large body of air. This is usually indicated by the obvious atmospheric distortion seen in the images.

Another consideration for DIC is depth-of-field, which is not specifically discussed in this paper. However, when setting up an experiment in the field, a large depth of field is often desirable to be able to capture the motion of the object. The experimentalist should keep in mind when using large  f/#s that the lens resolution is inversely proportional to the depth-of-field. Again, this is most likely to be a noticeable problem when working at higher magnifications.

Most of these conclusions should extend to stereo-DIC with some added complications. These include the fact that depth-of-field is often more important for stereo, as the camera is required to be at an angle to the measured surface and the angle between the cameras often requires larger f/#s and the resulting loss in lens resolution. Furthermore, if there are resolution problems, the filtering or defocus are unlikely to be identical between the image pairs and will cause a further degradation in the results due to poor cross-correlation.

A complete analysis for measuring strain is complicated by the fact that there are an extremely large set of variables that are interacting including; contrast, noise, aperture, speckle size, subset size, step size, and strain window size. In summary the loss of resolution in the imaging system will change the ratio of the noise to the contrast and will reduce the DIC accuracy for a given subset size. The increased displacement errors can be counter-acted in the results by both increasing the subset size and increasing the strain window size, both of which negatively impact the spatial distribution of the results.