Personalized top-n influential community search over large social networks

Abstract

User-centered analysis is one of the aims of online community search. In this paper, we study personalized top-n influential community search that has a practical application. Given an evolving social network, where every edge has a propagation probability, we propose a maximal pk-Clique community model, that uses a new cohesive criterion. The criterion requires that the propagation probability of each edge or each maximal influence path between two vertices that is considered as an edge, is greater than p. The maximal clique problem is an NP-hard problem, and the introduction of this cohesive criterion makes things worse, as it mights add new edges to existing networks. To conduct personalized top-n influential community search efficiently in such networks, we first introduce a pruning based method. We then present search space refinement and heuristic based search approaches. To diversify the search result in one pass, we also propose a diversify algorithm which is based on a novel tree-like index. The proposed algorithms achieve more than double the efficiency of the the search performance for basic solutions. The effectiveness and efficiency of our algorithms have been demonstrated using four real datasets.

1 Introduction

Communities are basic structures for understanding the organization of many real-world networks, such as social, biological, and collaboration networks [17]. Recently,community search over large and evolving graphs has attracted significantly increasing attention. Different from community detection which finds all communities in an entire network, online community search aims to find communities that have certain cohesive relationships w.r.t. the query nodes in an online manner. As the communities for different vertices residing in a network may have very different characteristics, compared with general community detection, the ability for personalized community query, which online community search provides, is more meaningful.

In this paper, we study modeling and querying of the top-n influential communities to a specific query node, termed as personalized top-n influential community search. As the influential communities around a user represent the social contexts for that user, top-n influential community search provides a useful tool for other analytical tasks, such as influential social community discovery and accurate community influence modeling. The following are two examples.

Example 1

(User-centered influential community recommendation) Due to the lack of prior information from users, recommendation for new users is a key challenge and the well-known cold-start problem [29]. As we know, it is a group of users who share similar tastes to be a community. Suppose that Mr. Spike is a Twitter user and would like to join in a music fan community. Sometimes he has been surrounded by many such communities. While there are pop music, classic music and rock’n’roll music communities around him, it is difficult to tell which one influence Spike more than others. Though he does not belong to any music community yet, but one of his friends might have been in a music community. Hence, to learn the influential music communities for Spike, we conduct a top-n influential community search. In this situation, the established communities with high influence to Spike are ideal for recommendation.

Example 2

(Evaluation of community influence) Evaluating community outer influence is typically measured as the number of users influenced by the community or just to reveal the communities with the highest outer influences [22]. In counting users influenced by the community, the criterion is whether the influential probability exceeds a specified value. However, with a top-n influential community search, we have an alternative measurement, which measures the number of users involved in their top-3 influential communities. For example, a music distribution company wants to learn the influence of a music fan community among all the Twitter users. Then the company can estimate how many external users are really influenced by the influential communities to predict the trend of music. The obtained information will help the company to adjust their marketing strategies and enable more scientific decision-making.

The previous examples demonstrate the benefit of the top-n influential community search, there are challenges in this area. The first challenge is how to identify all the communities around a user in the evolving and dynamic social networks. The second is how to calculate the influence of all these communities and finds top-n efficiently. Since there are many overlapping communities, how to diversify the returned results is also challenging.

The foundation of the personalized top-n influential community search is the capability to properly measure community influence to a user. Typically, we model a social network as a graph G with vertices representing individuals and edges representing connections or relationships between any two individuals. According to a stochastic cascade model, such as Independent Cascade (IC) model [14], each edge (u, v) in the network is associated with a propagation probability w(u, v). The influence is evaluated as the probability that the community influences the external user in social networks. In addition to influence measurement, we propose the concept of a maximal pk-Clique community inspired from cliques [2]. A k-clique is a complete subgraph that includes at least k vertices, and is not contained in any other complete subgraph. A maximal pk-Clique community is a community in a social network that has edges between nodes u and v in the graph that can either be original edges in the social network or a path from u to v, and its corresponding maximum influence probability is greater than p. We argue that, with propagation probability of every edge greater than a specific value p, users are well-connected with each other in such a community. A maximal pk-Clique ensures that a discovered community is connected and cohesive. Thus a maximal pk-Clique community satisfies four desirable inner properties, i.e., society, cohesiveness, connectivity, and maximum.

The personalized top-n influential community search problem is very different from the most influential community search problem [22] and the influence maximization problem [6, 35]. The most influential community concerns the influence at the community level over entire network, and the influence maximization problem aims to select nodes as seeds in social networks such that the number of other nodes affected by the seed nodes is maximized. However, in the personalized top-n influential community, we are interested in the communities around the user which meets structural constraints, i.e., densely and cohesively connected. In other words, the personalized top-n influential community concerns the influence at the community level rather than the individual level, and the communities around a user rather than over entire network.

To find top-n influential communities efficiently, we developed a pruning and filter based search algorithm with the support of an auxiliary data structure. With the help of a priority queue, the algorithm keeps track of currently found top-n influential community. With the upper bound of the aggregated influence of maximal cliques in a subgraph, it performs pruning and filtering in the search space. We also developed a diversify method to retrieve the diversified results. A tree-based index, called D-Tree, is deliberately designed to support efficient diversified community search in one pass. And we have developed algorithms to efficiently find the top-n influential communities with the support of D-Tree. The contributions of our work can be summarized as follows:

• We propose a novel cohesive criterion to define an explicit community model in evolving and dynamic social networks;

• The method to identify the search space that contains all communities surrounding a user is proposed. Then we propose an exactly search algorithm that reduce time complexity by more than two times, while preserving the robustness of the search approaches;

• To conduct diversified top-n search in one pass, a diversify method is introduced. We design a tree-based index (D-Tree) to effectively maintain the top-n communities currently found in social networks and aid in diversifying the results;

• The experimental results of four real datasets demonstrate the correctness of our algorithms and show that the proposed algorithms significantly outperform the baseline algorithm.

The remainder of this paper is organized as follows. First, we introduce the related work in Section 2. Then we propose and formulate the personalized top-n influential community search problem in large social networks in Section 3 and present a baseline solution of the problem in Section 4. Improved algorithms are proposed to find top-n influential community with pruning and filter approach in Section 5. In Section 6, we discuss a diversify algorithm which conducts diversified search. The experimental results are analyzed in Section 7. Finally, this work is concluded in Section 8.

2 Related work

The detection of community, which is defined as natural divisions of network nodes into densely connected subgroups [25], has been widely studied in biological networks and social networks. Newman et al. [25] described a new class of algorithms for performing network clustering using a divisive technique. Ruan et al. [26] presented an efficient spectral algorithm for modularity optimization. The algorithm adopts a recursive strategy to partition networks while optimizing modularity. Instead of using a partitioning approach, Satuluri et al. [27] adopted a clustering approach and proposed a multi-level algorithm for graph clustering using flows. The graph is first successively coarsened to a manageable size, then refined, finally the algorithm is run to convergence and the high-flow regions are clustered together.

Concepts relating to graph properties like k-clique, k-core and so on have been extensively studied in random graphs. Recently, implicit community models k-core [23] and kr-Clique [22] have been proposed to discover communities. The works of Li et al. [23] focus on k-core decomposition in an evolving graph. They found that when maintaining the core number for every node in a dynamic graph, only certain nodes need to update their core numbers when the graph is changed by inserting/deleting an edge. The concept of maximal kr-Clique community [22] was introduced to search for the most influential community. A maximal kr-Clique community contains at least k nodes and any two nodes in the community can be reached in at most r hops via the shortest path in the subgraph. Huang et al. [16] propose a community model based on the k-truss concept and a compact index structure which supports the efficient search of k-truss communities with a linear cost with respect to the community size.

The online community search, which finds communities around a query vertex online, recently attracted a lot of attentions ([8, 16, 18] and [12]). Cui et al. [8] has proposed a novel approach and several algorithms for online overlapping community searches. They define a new model named α-adjacency-γ-quasi-k-clique and also provided theoretical guidelines for tuning the model. Fang et al. [11] propose attributed community query, which returns an attributed community for an attributed graph. An attributed community satisfies both structure cohesiveness and keyword cohesiveness. McAuly et al. [24] define a novel machine learning task of identifying users’ social circles which uses a model combining network structure as well as user profile information. Chen et al. [4] propose co-located community search. They developed an efficient exact algorithm with several pruning techniques and an approximation algorithm with adjustable accuracy guarantees. Fei et al. [12] propose the top-k influential communities on-line problem. They introduce an instance-optimal algorithm LocalSearch whose time complexity is linearly proportional to the size of the smallest subgraph.

In considering models for the spread of influence through a social network, a dynamic cascade model called the Independent Cascade (IC) model, was first investigated by Goldenberg et al. [14]. Granovetter et al. [15] were among the first to propose another Linear Threshold (LT) model that was based on the use of node-specific thresholds to capture such a spread process. Kempe et al. [19] discussed maximizing the spread of influence problem with these models in social network analysis. Based on these works, there appears to be a lots of proposals focusing on the spread of influence problem, for example, [5, 21], and [20]. Most of these algorithms aim to select nodes as seeds in social networks such that the number of other nodes affected by the seed nodes will be maximized.

Maximal clique enumeration is a fundamental graph problem and has been extensively studied. Most solutions for maximal clique enumeration (e.g., [2] and [1]) are backtracking search. Eppstein et al. [10] show that there exists a nearly-optimal fixed-parameter tractable algorithm for enumerating all maximal cliques in a sparse graph. A polynomial delay algorithm which enumerates all maximal cliques is given in [3]. Cheng et al. [7] propose a general framework for designing external-memory algorithms for maximal clique enumeration in large graphs. Matthew et al. [28] propose a parallel and memory-efficient algorithm for distributed high performance computing architectures. Wang et al. [31] propose an algorithm which providing a concise and complete summary of the set of maximal cliques. The diversified top-k clique search problem is studied in [33], which is to find top-k maximal cliques that can cover most number of nodes in the graph.

3 Preliminaries

In this section, we first introduce the necessary background on influence modeling, and then present our definition of community for influential community search. Finally we present the formal definition of the personalized top-n influential community search problem. The notations in this paper are shown in Table 1.

Table 1 Notations

3.1 Influence modeling in a social network

In this paper, a social network is modeled as a directed graph. Consider a directed graph G = (V, E) with an edge labeled w : E → (0, 1], where V is the set of vertices representing users of a social network and E is the set of edges connecting vertices representing user-to-user connections. For every edge (u, v) ∈ E, weight w(u, v) denotes the propagation probability of the edge, which is the probability that v is influenced by u through the edge (u, v).

To model the influence process, we adopt the widely-accepted IC (Independent Cascade) model [19] in this paper. Based on work in complex systems theory, the IC model simulates aggregate consequences concerning local interaction between individual users of a social network. This diffusion model is first investigated in the context of marketing by Goldenberg et al. [14]. It consists of a framework in which each user’s behavior is dictated by a predefined propagation probability and is a function of the state of other users with whom he interacts. When it starts with an initial active node u in step t, and is followed an activation process which unfolds in discrete steps. That is, in step t+ 1, a currently inactive neighbor v is affected by user u, in one period, change his state from “inactive” to “active” at probability w(u, v). It is worth noting that no matter u succeeds in transforming its neighbors’ state or not, it cannot make any further attempts in subsequent period. Again, the process continues until no more activations are possible in the network.

For a path P = 〈v₀, v₁, ... , v_k〉 in G, we define the propagation probability of the path as the product of the weights of its constituent edges.

$$ w(P)= \prod\limits_{i=0}^{k-1} w(v_{i},v_{i+1}) $$

(1)

There may be more than one path between one vertex and the other, and different paths may have different propagation probabilities. We use the Maximum Influence Path (MIP) to approximate the real influence from one vertex to another within the social network. A maximum influence path from vertex u to vertex v is defined as any path P with a maximal weight w(P).

3.2 Problem formulation

After introduction of graph G, influence model and MIP, we first define pk-Clique community and aggregated influence of community, then present the definition of the problem with an example followed.

Definition 1

(pk-Clique Community)

Given a graph G, and two parameters p and k, a pk-Clique community is an induced subgraph C_pk = (V_pk, E_pk) of G. It is a complete graph that satisfies the following requirements:

• Any two vertices in C_pk can be reached via an MIP between them in the subgraph C_pk, and the weight of every MIP is greater than p. And there are at least k vertices in C_pk.

• A pk-Clique community is maximal if C_pk is not a subgraph of any other pk-Clique community.

The difference in this study from previous community models [16, 22, 23] is that, for the first time, we model the relationship between users in a community with an edge as a dynamic propagation probability. We argue this is an appropriate measurement of cohesiveness in a community. For k-core model, a community is the largest subgraph within which each node has at least k connections. Since each node in the community is only required to have k neighbors, such a community may be less cohesive. The k-truss is a model based on triangle which describe the stable relationship among three nodes. With edge connectivity constraints, the induced community is connected and cohesive, and fits for communities in very small size. For kr-Clique community, it requires any two nodes can be reached at most r hops via the shortest path. Obviously there exists different propagation probabilities between any two nodes in a social network. Connections labeled “weak ties” are different from the more stable and intimate “strong ties” which have greater propagation probabilities. By taking dynamic propagation probability into consideration, the maximal pk-Clique community overcomes the drawbacks of the conventional community models

To calculate the influence of a community, the problem is that a vertex can be influenced by different vertices through different paths. Many works [22] adopt a model known as an “expectation model” to simplify the paths by supposing a dependence between paths, and mostly the MIP is the path that is adopted. In this work we are mainly concerned with the relationship between two vertices. We always assume that the paths between a different pair of vertices are independent. That is, even if two paths that share a sub-path lead to the same destination, we also assume that there are virtually two independent paths from two sources to the destination. This approximation simplifies the calculation of the aggregated influence of a community.

Definition 2

(Aggregated Influence of Community)

Aggregated influence of a maximal pk-Clique community to a vertex s, is defined as the influence probability that s is influenced by any vertices in this community, and the weight of every maximum influence path from these vertices to vertex s is greater than ε. Denote aggregated influence as Pr(v∣V (C)) by the IC model, it is calculated as

$$ Pr(v \mid V(C))= 1-\prod\limits_{v \in V(c)}(1-w(P_{v \rightarrow s}))) $$

(2)

Problem 1

(Top-n Influential Community Search)

Suppose $\mathbb {C}$ is the set of influential maximal pk-Clique communities around s. The top-n influential community search can be defined as a query to find n maximal pk-Cliques in $\mathbb {C}$, formally,

Top-n(s) = 〈C₁, C₂, ... , C_n〉 where Pr(C₁) > Pr(C₂) > ... > Pr(C_n) if $\mid \mathbb {C} \mid >n$.

Example 3

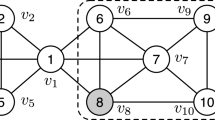
(Top-3 maximal pk-Cliques in Figure 1) Consider a small social network as shown in Figure 1. It illustrates a subgraph surrounding a query node s. Suppose the vertices residing in the dark grey area have influence over s greater than ε (say, 0.2). To simplify the illustration, we set all their influence to s with their identity number divided by 10. That is the node 2 has influence to s with 0.2, node 3 is 0.3, and so on. When calculating aggregated influence of a clique, we ignore the vertices residing in the light grey area with an influence of less than ε. But when we check whether a group of vertices is a pk-Clique, these vertices make sense, since a maximal pk-Clique may include the vertices where the influence over s is less than ε. After having completed the search, we present all maximal pk-Cliques and their aggregated influence in Table 2. We identify clique {5,6,8} as top-1, {6,8,9,7} as top 2, {2,3,5} as the top-3 result.

Figure 1

A Query Example of node s

Table 2 Maximal pk-Cliques (Example 3)

Being an NP-hard problem, the personalized top-n influential community search is a task with high challenge. So we need an algorithm try to optimize the searching process with some greedy strategy. In other words, it should exploit some specific knowledge of the problem, whose purpose is to make the result top-n(s) subject to particular constraints, with the aim of (1) reducing the algorithm search space or (2)possibly avoiding that the greedy generation of cliques not belonging to final results.

4 Basic solution

4.1 Search space

In contrast to community detection that aims to find all communities in a graph, personalized search of top-n influential communities only considers communities “near” a given vertex in the social graph. We take the word “near” to mean a vertex that can be reached by a specific community with a probability above a fixed threshold. So we only examine communities that include at least one vertex such that the MIP between this vertex and the query node is above the threshold ε.

We adopt the single-source shortest-path algorithms such as Dijkstra algorithm to find all vertices around a query node where the weight of their MIPs is above ε. A modified version of Dijkstra algorithm is used , the algorithm will stop at a vertex when the propagation probability of the MIP between this vertex and the query node is less than ε.

We denote the vertices where the propagation probability to a query node is above ε as V_in. From previous discussions we are also aware that a maximal pk-Clique community C, said to be influential to a query node, must include at least one vertex that is in V_in. If we denote this vertex as v, to determine whether C is a maximal pk-Clique, we must examine every vertex where the propagation probability of the MIP between these vertices to v is greater than p.

We derive the following lemma.

Lemma 1

(The minimum propagation probability of an MIP between a vertex in a maximal pk-Clique and the query node s.)

Given a graph G = (V, E) with influence function w : E → (0, 1], probability p, ε, and a query node s, for any vertex u, if the MIP between vertex u and node s is less than pε, u will not be included by any maximal pk-Clique that has influence on s.

Proof

Suppose u is a vertex with w(P_us) < pε. And P_us = 〈u, v₁, v₂, ... , v_k, s〉 is a maximal influential path from u to s. There will be a node v_i(1 ≤ i ≤ k) that is the last node along path P with $w(P_{v_{i}s}) \ge \varepsilon$. In other words, node v_i is the last node in set V_in along path P.

Suppose node v_i is included in a maximal pk-Clique denoted by C and path P can be decomposed into $P_{uv_{i}}$ and $P_{v_{i}s}$. We know that sub-paths of a maximal influential path are maximum influence paths. Then, paths $P_{uv_{i}}$ and $P_{v_{i}s}$ are maximum influence paths. Because with $w(P_{v_{i}s}) \ge \varepsilon$, we have $w(P_{uv_{i}})< p$. According to Definition 1, vertex u will not be included in C. □

With Lemma 1 and Definition 1, we propose Algorithm 1, that returns a candidate subgraph $G^{\prime }$, including all vertices around a query node s with influence to s greater than pε.

Algorithm 1 obtains all the vertices consisting of V_in and V_out, and any edge between these vertices remains unchanged in graph $G^{\prime }$. Since we use a modified version of Dijkstra’s algorithm to retrieve influential vertices at lines 1-2, the time complexity of identifying V_in and V_out is $O(\mid E^{\prime } \mid lg \mid V^{\prime }\mid )$.

4.2 Basic algorithm

In this and the following sections we will use the terms maximal pk-Clique and maximal clique interchangeably. Using social networks related to a query node s, the first step of a top-n Influential Community Search (ICS) is to identify the subgraph, including all candidate cliques, by executing Algorithm 1. Then the ICS enumerates all maximal cliques in this area. Among all these returned maximal cliques, we filter out those cliques whose size is less than k, calculate the integrated influence of each community, and then push it into a heap. When all the maximal cliques have been put in the heap, the algorithm selects top-n maximal cliques in the heap and returns the result list.

The procedure of the top-n influential community search is presented in Algorithm 2. Algorithm 2 calls the procedure, Maximal Cliques Enumerate (MCE), to generate all the maximal cliques in a graph. MCE is an implementation of maximal clique enumeration method proposed by Bron-Kerbosch [2]. Its performance is discussed in [30]. The basic idea of MCE is to recursively backtrack to add a vertex from the set P which consists candidate vertices, to extend the current clique C. MCE tends to produce the larger cliques first and to generate sequentially cliques having intersection. As Algorithm 3 indicates, it takes three sets as input. (1) The set P is the candidate set to be extended by a new vertex along a branch of the backtracking tree. (2) The set X is a set of vertices that have already been processed by the algorithm. (3) The set C is the set of all vertices that have already served as an extension of the present configuration of P. That is, C is a clique found along the branch of the backtracking tree. The set of vertices P ∪ X serves as search space. Once P ∪ X becomes empty, C cannot be further extend. At this point, we output C as a maximal clique. A vertex v from the search space is selected to grow the current clique C. To grow clique C, only the vertices in P ∩Γ(v) and X ∩Γ(v) can be candidates for expanding to find new larger cliques. After we finish searching in (P ∪ X) ∩Γ(v), vertex v is excluded from P and placed in X.

Algorithm 3 takes $G^{\prime }$ as input, where $G^{\prime }$ is originally obtained from Algorithm 1. Before being fed to Algorithm 2, it is transformed into an undirected graph. This searching process of MCE can be represented by a search forest, or the collection of search trees. The set of roots of the forest is exactly the same as $V^{\prime }$ of graph $G^{\prime }$. For each $v \in V^{\prime }$, all the vertices in $V^{\prime } \cap {\Gamma }(v)$ are children of v. Thus, vertices along a path from the root v to any leaf vertex of the tree constitutes a maximal clique.

After collecting all maximal cliques at line 3, Algorithm 2 pushes every maximal clique into a data structure heap. As its name implies, heap uses the heap to manage maximal cliques during the insertion. The sort key is the aggregated influence of each clique. Lines 5-6 finish this operation. After we have the ordered cliques, the next step is to output top-n results. Lines 7-9 pop cliques from heap and appended the cliques to the result list.

Algorithm 2 achieves the worst-case time complexity of O(3^{|V |/3}) for a |V |-vertex graph [30]. By using d-degenerate order in the first-round iteration, the complexity is reduced to O(|V |3^d/3) [10].

5 Efficient influential community search

Algorithm 2 is a functionally correct procedure, but we are unlikely to be satisfied with its performance, particularly with the large social networks that now exist. Since maximal clique searching is a combinatorial optimization problem, it’s well know that domain Constraint Programming (CP) has been recognized as a powerful tool for modelling and solving combinatorial optimization problems [13]. CP aims at removing from variable domains combinations of values which cannot appear in any desired solution. And when dealing with optimization problems, pruning of search trees can be performed on the basis of currently known costs or best results. Filtering can be used to remove combination of vertices which cannot lead to solutions. Following this line, in this section, we introduce pruning and filtering approach in influential community search.

5.1 A pruning approach

Domain CP usually implements a branch and bound pruning algorithm to search an optimal solution based on some domain specific knowledge. The idea is to solve a domain specific problems, each time leading to successively better results (i.e., a feasible result is get if it exists). In particular, when a feasible result r^∗ is found (whose cost or earning is f(r^∗)), a constraint f(x) < f(r^∗) is introduced to each subtree in the remaining search tree. The purpose of the introduced constraint, called upper bounding constraint, is to get rid of portions of the search space which cannot lead to better results than the best one get so far. The problems in this branch and bound pruning approach are: (1) what can be used as the the upper bounding constraint; (2) how about the monotonicity of the cost function.

The purpose of the search is to find top-n influential pk-Clique community. Algorithm 1 has identified the search space that ensures any two vertices in a found communities can be reached via an MIP with the weight greater than p. We also must ensure there are at least k vertices in any returned communities and only need to return the top-n results. To this end, we need to make sure that any candidate set of vertices used to grow a maximal pk-Clique has at least k vertices and its aggregated influence is at least greater than currently achieved the n-th maximal clique.

We consider the algorithm MCE for generating all the maximal cliques of a given graph G = (V, E)(V ≠ ∅). Suppose variable C is a set of vertices that constitutes a clique found up to this time. MCE begins by letting C be an empty set, and expands C step by step by applying a recursive procedure to V. It will induce subgraphs to achieve larger and larger cliques until they reach maximal ones.

Let C = {v₁, v₂, ... , v_d} be a clique found at some stage, and consider the set of vertices

$$ S = V \cap {\Gamma}(v_{1}) \cap {\Gamma}(v_{2}) \cap {\Gamma}(v_{3}) \cap ... \cap {\Gamma}(v_{d}) $$

(3)

where S = V and C = ∅ at the initial stage. Now, consider the smaller subgraphs G = (S_v, E_v) that are induced by new sets of vertices

$$ S_{v} = S \cap {\Gamma}(v) $$

(4)

and at this stage we have C_v. We also can denote the set of S_v with remaining candidates and finished vertices for expansion by

$$ S_{v} = P_{v} \cup X_{v} $$

(5)

So at certain stage of MCE, C_v ∪ v ∪ S_v is used to grow a possible maximal clique. We first propose Lemma 2, which constrain the lower bound of vertices in a pk-Clique.

Lemma 2

(The lower bound of vertices during MCE.)

On each recursive stage of MCE, there must exist at least k vertices in C_v ∪ v ∪ S_vto grow a pk-Clique.

Proof

It’s established from the definition of pk-Clique. □

Since we are exploring the possibility of taking the influence of the n-th maximal clique as the lower bound of to-be-found communities. Is it possible to derive an upper bound of aggregated influence of to-be-found communities in advance. And with this bound, we can prune unnecessary search branches in the graph. To obtain such an upper bound, we must prove the monotonicity of a vertex set’s aggregated influence. Recalling Definition 2, the aggregated influence of the community is defined as the probability that s is influenced by any vertex in a maximal pk-Clique community. Hence we have Definition 3, and then Lemma 3.

Definition 3

(Aggregated Influence of vertex set)

The aggregated influence of a set of vertices to a vertex s, is defined as the probability that s is influenced by any vertex in this set. The calculation is the same with that in Definition 2.

We then propose Lemma 3.

Lemma 3

(Monotonicity of the aggregated influence during MCE.)

On each recursive stage of MCE, the aggregated influence of C_v ∪ v ∪ S_vis monotone decreasing.

Proof

Suppose we have $C_{v_{i}}, v_{i}$ and $S_{v_{i}}$ at stage i, and $C_{v_{i+1}}, v_{i+1}$, $S_{v_{i+1}}$ at next stage, where 0 < i < d.

It’s obvious that

$$ C_{v_{i+1}} = C_{v_{i}} \cup \{v_{i}\} $$

(6)

$$ S_{v_{i+1}} = S_{v_{i}} \cap {\Gamma}(v_{i+1}) $$

(7)

and

$$ v_{i+1} \in S_{v_{i}} $$

(8)

Let $SC_{i} = C_{v_{i}} \cup \{v_{i}\} \cup S_{v_{i}}$ and $SC_{i+1} = C_{v_{i+1}} \cup \{v_{i+1}\} \cup S_{v_{i+1}}$.

We have

$$ SC_{i} \supseteq SC_{i+1} $$

(9)

According to equation 2, we have

$$ \begin{array}{llll} &Pr(u \mid u\in SC_{i}) - Pr(u \mid u \in SC_{i+1} \ ) \\ &= 1-\prod\limits_{u \in SC_{i}}(1-w(P_{u \rightarrow s})) -(1-\prod\limits_{u \in SC_{i+1}}(1-w(P_{u \rightarrow s}))) \\ &= \prod\limits_{u \in SC_{i+1}}(1-w(P_{u \rightarrow s}))(1-\prod\limits_{u \in SC_{i} \setminus SC_{i+1}}(1-w(P_{u \rightarrow s})))\\ &>0 \end{array} $$

(10)

Hence have the result. □

With the above lemmas, we now know the aggregated influence of a vertex set is greater than any maximal clique residing in it. We have the upper bound of the aggregated influence of maximal cliques in a subgraph. This upper bound will help us make the right decision before exploring the branch of a search tree. And we also know how to compute this upper bound.

Now we introduce Algorithm 4 which prunes unnecessary branches from a search tree in the forest.

Algorithm 4, Improved Top-n ICS, calls Algorithm 5, MCP (Maximal Cliques with Pruning), to complete the top-n influential community search. It use an efficient global priority queue to manage the found maximal cliques and returns a list of top-n influential community.

Algorithm 5 MCP takes more inputs than Algorithm 3 MCE. It takes global priority queue q, n and k to conduct branch and bound pruning.

The second main difference between MCP and MCE is lines 5-7. Vertex set T denotes a union of vertex sets, including C, {v}, and (P ∪ X) ∩Γ(v). Set C includes the vertices that are part of maximal cliques to be found. {v} is currently an expanding vertex. And (P ∪ X) ∩Γ(v) includes vertices to be extended. According to Lemma 3, the aggregate influence of set T is the upper bound of any pk-Cliques to be retrieved. Thus, if the aggregate influence of set T is less than the minimum aggregate influential pk-Cliques in the queue, which is clique q[n], there is no need to undergo further searches along this branch. For the same reason, if the size of T is less than k, there is no need to conduct further searches either. This is the pruning based top-n influential community search. When a maximal clique is found, it is also important to notice that the size of any maximal clique MCE derived is not always greater than k. Thus we also need to check if a derived maximal cliques is less than k before it is inserted into q. This operation is executed with line 2. At the end of MCP, we have a queue with n maximal pk-Cliques.

Now we analyze its time complexity. In the best case, MCP finds top-n maximal pk-Cliques first. Thus the time complexity is O(n). But in the worst case, MCP finds top-n maximal pk-Cliques at the last moment. Then the time complexity in this case is same with MCE, and is O(3^{|V |/3}) for a |V |-vertex graph.

5.2 Filtering unqualified vertex

Another main principle of CP is that every constraint is associated with a domain reduction algorithm or filtering algorithm that removes some vertices which are inconsistent with the constraint. The deletions of vertices in the search space involve a propagation mechanism that utilizes the filtering algorithm of the constraint until no more modification occurs.

In this section we use a constraint based on the degree. This constraint is imposed at the beginning of the algorithm.

Next we introduce a lemma first and then the filtering algorithm.

Lemma 4

(Degree constraint of a vertex in a pk-Clique.)

A vertex with degree less than k − 1 cannot be a member of any maximal pk-Clique.

Proof

It’s established from the definition of pk-Clique. □

The filtering algorithm uses degree to remove all vertices whose degree is too small to extend to a possible clique of size greater than k. Many core decomposition algorithms determine a vertex’s class in a bottom-up manner. That is, it sorts vertices in order of their degree and get rid of vertices whose degree is less then k. We adopt such a bottom-up approach to remove all vertices, so they will not be included in any maximal pk-Clique.

In implementation of Algorithm 6, it’s convenient to organize vertices currently under considering into min-heap, and take a vertex at the root to determine and remove at each time. With heap sort, Algorithm 6 takes time O(|V |lg|V |).

5.3 Heuristic search

According to Definition 2, the aggregated influence is calculated as the union of the influence of every vertex in a clique. If the probability distribution of each node’s influence in V_in is uniform, then the more nodes that reside in V_in for a clique, the bigger the aggregated influence it will acquire. This leads to following observation.

Observation: :

It is generally expected that a vertex u ∈ V such that V = V_in ∪ V_out and u = max{|V_in ∩Γ(u)|} has a high probability of being included in an influential maximum clique.

With above observation, we finally propose Algorithm 6, an improved version MCP, which incorporates heuristic search and vertex filtering. To minimize P ∖Γ(u), MCP chooses a pivot u ∈ P ∪ X that maximizes |P ∩Γ(u)| at line 3 of Algorithm 5. In contrast to MCP, This new version MCP chooses a pivot that maximizes |V_in ∩ P ∩Γ(u)|. That is, expending a subtree that has a high probability of leading to influential maximum cliques becomes a priority.

The main program of heuristic search based top-n ICS is almost the same as Algorithm 4, except it maintains an additional list which keeps the sets of all vertices that are in V_in and adjacent to v in $G^{\prime } = (V^{\prime },E^{\prime })$. Note that the rather time-consuming calculation at this step is carried out only at the beginning of the main program and not in HMCP. Therefore, the total time to select the pivot is very small.

Example 4

(An execution of a heuristic search) With the settings left the same as in Example 3, it is easy to find a heuristic based search that will perform the outermost recursive calls in the order of {5,7,1}, instead of {6,2,1} in MCP.

5.4 Analysis

The improvement of basic top-n influential community search focuses on filtering of unqualified vertices and brunch-bound pruning of search trees. We prove the correctness of such an approach in Theorem 1.

Theorem 1

(Correctness of algorithm Improved Top-n ICS).

Given a graph G = (V, E)(V ≠ ∅) and a query node s, the algorithm Improved Top-n ICS generates top-n maximal pk-cliques without duplication.

Proof

It has been proved in [30], that MCE generates all, and only, maximal cliques that contain all vertices in C, some vertices in P, and no vertices in X, without duplication. MCP follows MCE, and it removes some vertices in the searching space according to Lemma 4, and skips over some branches on the search tree that do not lead to top-n maximal cliques according to Lemma 2, 3. Thus MCP returns the top-n maximal cliques with input vertex sets P, X, C as well. Improved Top-n ICS call procedure MCP to finish its search of top-n maximal cliques, hence correctness is insured by MCP.

□

6 Diversified top-n search

The Improved Top-n ICS is an exact algorithm. The cohesiveness measurement used in pk-Clique is reasonable. The introduction of pk-Clique will add more new edges to a network, thus leading to an increased number and size of cliques. Though it improves the efficiency of enumerating maximal cliques in the graph, it still suffers from exploring a huge search space and a significant level of redundancy, like many existing maximal clique enumeration algorithms [31].

An exact algorithm of maximal cliques enumerating usually returns a significant level of redundancy as many maximal cliques share a large portion of common vertices. Thus, it is not very useful to report similar top-n maximal cliques since they bring about a large amount of duplicate information. Thus an approximate or diversified top-n cliques is meaningful in some circumstances. For example, the purpose of such diversification is to return the results that can best cover different possible categorizations of the query [34].

In order to compute diversified top-npk-Cliques, a straightforward solution is to enumerate all top-$n^{\prime }$ cliques first, where $n^{\prime }$ must be sufficiently great, and then pick out n diversified cliques with a specified threshold. However, since it requires two passes over created cliques, such a solution falls short to handle large amount cliques in worst-case, and might be a costly operation.

In this section, we introduce an one-pass diversify algorithm for top-n ICS. First we introduce the notion of l-diversity, which is used to ensure that every maximal clique in the result is different with each other. Then we propose a deterministic algorithm based on l-diversity. The algorithm utilizes properties of backtracking MCP algorithms for further redundancy identification and search space pruning. To compute l-diversity, we use an tree data structure to index current top-n maximal cliques to match with to be generated ones.

6.1 l-diversity

We first introduce the notion of l-diversity that measures how well each maximal clique is diversified with existing cliques.

Definition 4

(l-diversity)

Given two maximal cliques C_i, C_j in graph G and a parameter l(0 ≤ l ≤ 1). We define the diversity of two maximal cliques C_i and C_j as

$$ D(C_{i},C_{j})= 1- \frac {\mid C_{i} \cap C_{j} \mid}{\mid C_{i} \cup C_{j} \mid} $$

(11)

If D(C_i, C_j) ≥ l, then cliques C_i and C_j are l-diversified, otherwise cliques C_i and C_j are l-similar.

Because the searching process of MCP follows a depth-first order. Any two cliques’ outputs in order tend to be similar if they are near in the output sequence. Thus it’s possible to report cliques while avoiding redundant with previous ones and further pruning the search space. Specifically, such pruning is performed when the MCP process is entering a new stage of recursion.

Let $C^{\prime }$ be one of the maximal clique that previously added to top-n cliques Q. At a stage of MCP(P, X, C), let $\bar {d}$ be an upper bound depth of the to be created search tree. Then, the size of each clique C_p to be generated from P is at most $|C| + \bar {d}$.

To get the lower bound of $|C_{p} \cap C^{\prime }|$, let $Y=P \setminus C^{\prime }$, and t = |C_p ∖ C|. It’s easy to know that part of the t vertices come from Y and the rest are from $P \cap C^{\prime }$. And we also assume at most $\bar {t_{y}}$ vertices out of t come from Y. Then since C_p is extended from C, we have $|C_{p} \cap C^{\prime }| \geq |C \cap C^{\prime }| + max\{t-\bar {t_{y}}, 0\}$, where $1 \leq t \leq \bar {d}$. Similarly we also have the upper bound that $|C_{p} \cup C^{\prime }| \leq |C \cup C^{\prime }| + \bar {t_{y}}$.

We focus on whether it’s necessary to enter a new stage of MCP. We need to check if a maximal clique C currently under growing is similar with existing cliques in the queue while considering its possible growth in P at the same time. If it’s similar with some existing cliques, then we stop to extend C in candidate set P. Otherwise, we enter the new stage of MCP. We define the maximal diversity of C as following equation.

$$ \begin{array}{llll} D_{c} & = 1- \max\limits_{C^{\prime} \in Q} \frac {\mid C \cap C^{\prime} \mid}{\mid C \cup C^{\prime} \mid + \bar{t_{y}}} \\ & \ge 1- \frac {\mid C \mid}{\mid C \mid + \bar{t_{y}}} \end{array} $$

(12)

It’s easy to notice from equation 12, that we don’t need to check if a due-to-created clique is similar with existing ones. The inequation D_c < l only will be satisfied by

$$ \frac {\mid C \mid}{\mid C \mid + \bar{t_{y}}} \ge 1 - l $$

(13)

6.2 Diversified MCP

In this section, we introduce Algorithm 8 DiversifiedMCP as follows.

The algorithm DiversifiedMCP takes one more parameter $C^{\prime }$ than MCP. $C^{\prime }$ is a clique existing in q which keeps track of currently known maximal cliques. In addition to $C^{\prime }$, the algorithm defines l as the threshold of diversity of the expected results. DiversifiedMCP also uses a maximal cliques set Q, which consists of the same cliques within q but organized as a red-black tree. We will introduce the organization of Q in more details later.

Each time upon DiversifiedMCP got a maximal clique C, whether it will be inserted into the q or replace an old clique $C^{\prime }$, which would depend on $C^{\prime }$. If $C^{\prime }$ is empty, then it means exact maximal clique search. Otherwise, it is diversified search, which means C has a similar clique $C^{\prime }$ in q and the aggregated influence of C is greater than that of $C^{\prime }$. In this case, $C^{\prime }$ in q needs to be replaced the latest found clique C.

Lines 13-14 in DiversifiedMCP indicate that the algorithm would lookup in Q to make sure if there is no cliques similar with C and diversity between them is less than l when entering a new recursion. Lines 15-17 show that if there is a such clique $C^{\prime }$ and the aggregated influence of the to be generated maximal clique might be greater than $C^{\prime }$, then the algorithm must conduct diversified search on the sub-tree. Otherwise it would abandon the search.

6.3 Diversified search tree

In Algorithm 8, when entering a new stage of extending clique C, C might be tested for similarity with the existing maximal cliques in the current Q. It is costly to compare C with every clique in Q. We devise the following novel method to process efficient similarity test for every to-be found maximal clique with the maximal cliques in Q.

Let low and high be the smallest and greatest vertex id in a maximal clique C, respectively. We denote an interval[low_c, high_c] as a clique. Then the range [low_c, high_c] covers every vertices in C. Instead of comparing C with every C ∈ Q, we concern C when $[low_{c}, high_{c}] \cap [low_{c^{\prime }}, high_{c^{\prime }}]$ is nonempty. To locate such a C quickly, we augment a black-red tree to represent Q, named as Approximate Search Tree(AS-Tree), in which each node c contains an interval c.int and the key of c is the smallest vertex id, c.int.low, of the interval. In addition to the intervals themselves, each node c contains a value c.max, which is the maximum id of any vertex id in cliques stored in the subtree rooted at c. Each node also contains clique C and its sequence number in q. Figure 2 shows how an AS-Tree represents a set of maximal cliques.

Figure 2

An diversified search tree and corresponding queue

DS-Tree supports the following operations:

DS-Tree-INSERT(Q, C) creates a node c, which is assumed to contain the clique C, adds the node c to the tree Q.

DS-Tree-REPLACE($Q,C,C^{\prime }$) replaces the node c, which is assumed to contain the clique $C^{\prime }$, with a created node which contains C in the tree Q.

DS-Tree-WALK(Q, C) returns a clique contained in a node, such that the similarity of this clique with C is maximal, or ∅ if there is no such a node in the set.

The DS-Tree-INSERT(Q, C) operation is simple, since there is only one additional operation which is creating a node with input C involved, compared with general insertion in a red-black tree. The AS-Tree-REPLACE($Q,C,C^{\prime }$) operation is like deletion in a red-black tree. The different between them is AS-Tree-REPLACE($Q,C,C^{\prime }$) uses a new node to replace an old one instead of delete. It’s obvious that insertion and replacement run in O(lgn) time.

The only new operation we add is DS-Tree-WALK(Q, C), which finds a node in tree Q, whose contained clique is the most similar with C. If there is no such a node in the tree, the procedure returns ∅.

As an example of a successful search, suppose we wish to find the most similar clique with clique {1,2,3} in the tree of Figure 2. We first create a node c with c.low = 1 and c.high = 4 which also contains C, then begin with the search from the root. Since the intersection of roots clique {3,5,6} and {1,2,3,4} is {3}, we have C.this as {3}. And since Q.left.max ≤ c.low, we go left to the node {2,3,5}. As we can see, it will return c_l which is {2,3,5}. Because Q.int.low ≥ c.high, we don’t go right. We have c.r = ∅ at this point. From {{3},{2,3,5}, ∅}, we finally return the clique {2,3,5}.

Lemma 5

(Correctness of DS-Tree-WALK(Q, C).)

DS-Tree-WALK(Q, C) returns the most similar cliques in tree Q for C.

Proof

DS-Tree-WALK() follows divide-and-conquer approach and solve the problem recursively, at each level of the recursion it has three steps:

Divide the problem into three cases: I. The root is the result; II. If [c.low, c.high] overlap with ($-\infty ,Q.left.max$], then check Q’s left child; III. If [c.low, c.high] overlap with [$Q.int.low,+\infty$], then check Q’s right child.

Conquer the subproblems recursively. If Q == NULL, just return ∅.

Combine the results from above three cases into the correct result and return.

After the recursion finished, it’s obvious that it would return the most similar cliques in tree Q for C. □

6.4 Analysis

The algorithm DiversifiedMCP is invoked by Improved Top-n ICS to replace the exact algorithm MCP. The parameter q to help DiversifiedMCP track maximal cliques created. To ensure the correctness of DiversifiedMCP, we must guarantee maximal cliques in q is l-diversified. The following theorem shows its correctness.

Theorem 2

(Correctness of algorithm DiversifiedMCP ).

Given$P,X,C,C^{\prime }$, and q, the algorithm ApproximateMCP($P,X,C,C^{\prime }$) returns l-diversified maximal pk-cliques.

Proof

The recursion of DiversifiedMCP() terminates when P ∪ X == ∅ either when $C^{\prime } == \emptyset$ or not. In the latter case, it would replace $C^{\prime }$ with latest created C, and is certainly correct to maintain all cliques in the result q are l-diversified. Therefore, we focus on the first case, in which the latest created C would be inserted into q.

We use the following invariant for the recursion:

If q contains maximal cliques, then those cliques are l-diversified.

We use this invariant as follows:

Initialization::

Prior to the first recursion, q is empty, so that the invariant holds.

Maintenance::

Each recursion of the DiversifiedMCP(), after searching for the most similar clique $C^{\prime }$ in Q, if return ∅, it shows there is no clique which similar with currently extending clique C. Then it would enter next stage of recursion. In each stage of recursion, if create a maximal clique, then it would be inserted into q. So this insertion maintains the invariant.

Termination::

If the recursion terminates after traversing the entire search forest, then there is no more insertion at this point. Hence it is correct to return q.

Thus, the DiversifiedMCP procedure works correctly. □

7 Experimental study

In this section, we study the performance of the proposed algorithms over four real datasets. All the algorithms are implemented in Python2.7 and run on a CentOS server (Intel i7-7700 3.6GHz CPU with 4 cores and 32GB RAM).

• A. Data sets

We use four real social network datasets which are available at https://snap.stanford.edu/data/, as shown in Table 3. To verify performance of the proposed algorithm under different settings, we need a relatively large graph. So for each dataset, we focus on the largest subgraph. In each subgraph, we select one of the vertices with the most neighbors as the query nodes (i.e., vertex 2070 in Facebook, vertex 349932090 in Twitter, vertex 104***590 in Google+, and vertex 1 in Epinions). The degrees of chosen vertices are 12, 187, 138 and 839 in Facebook, Twitter, Google+ and Epinions, respectively. For those with no propagation probability associated with each edge in the original datasets, we set a random value which uniformly distributed in (0,1) to each edge as their propagation probabilities.

• B.Evaluation of different ε and p

Figure 3 shows the number of nodes when we vary the value of p from 0.5 to 0.9 and the value of ε from 0.1 to 0.4. To demonstrate the performance of the proposed algorithm, experiments in this work focused on the scenario when ε = 0.2 and p = 0.6. When p = 0.6, the average length of paths from source to sink is 1.0 for Twitter, 1.96 for Google+, 1.91 for Facebook, and 1.99 for Epinions.

• C.Evaluation of the maximal pk-Clique model

The Label Propagation Algorithm (LPA) is considered to be an accurate model in detecting communities in social networks [32]. Wang et al. [32] also proposed Normalized Mutual Information (NMI) [9] as a popular criterion for evaluating the accuracy of community detection models. NMI is based on defining a confusion matrix N, where the rows correspond to the “real” communities, and the columns correspond to the communities found by other method. The score of NMI stands for the agreement of two results. We identify communities using both LPA in the search space defined in Section 4.1 as the desirable communities. Then we compute the score of NMI for the results of our maximal pk-Clique model and the LPA model in this experiment. The scores we achieved were about 83% for Twttier, 58% for Google+, 67% for Facebook, and 63% for Epinions. The higher scores in the experiment demonstrate that our proposed community model is reliable in practice.

• D.Efficiency of proposed algorithms

In this and following subsections, we conduct experiments to evaluate the effectiveness of exact algorithms introduced in Section 6. We implement three versions of exact top-n search algorithm. The first one is pruning only, denoted as PS (Pruning based top-n ICS). The second is pruning and filtering, which is denoted as FS (Filtering plus pruning top-n ICS). The third is HS (Heuristic based top-n ICS including pruning and filtering). Tables 4, 5, 6 and 7 illustrate the results (time in seconds) obtained from different datasets, where BS denotes Basic Search algorithm.

It is clear that proposed pruning based PS, pruning plus filtering FS and heuristic based HS algorithms perform far more efficient than the basic solution, both in time and space costs. It also shows that the FS and HS perform better than PS in most cases. However, HS only outperforms FS in cases of searching for larger size cliques. We notice that the time cost does not decrease dramatically as vertices are progressively removed.

Tables 8, 9, 10 and 11 compare the space cost (in kbytes) of different algorithms. The results show that the PS, FS and the HS require less memory than the BS in each case.

• E.Evaluation of scalability

To further evaluate the performance of proposed algorithms, we enlarg the search space over Facebook and Epinions datasets. The results are presented in Tables 12 and 13. The cost increases as the number of vertices increases in both cases.

• F.The necessity to l-diversify

Figure 4 presents the redundancy over different maximal pk-Clique sizes. It indicates that the similarity increases as the size of maximal clique grows. The similarity is calculated according (14), where C_i and C_j represent any two maximal pk-Cliques.

In order to show the redundancy in the discovered top-n results at different values of n. We list top-8 maximal pk-Cliques found in above four datasets in Table 14, where k= 20 for Twitter and Google+, k= 8 for Facebook and Epinions. Take Twitter dataset as an example, in the second row, “1” means top-1 is the most similar to top-2 community, about 83% vertices are the same. In the eighth row, “7” means top-7 is most similar with top-8 cliques, they share about 91% common vertices. This shows the necessity to verify the query results.

$$ Similarity_{C_{ij}} = \frac {\mid C_{i} \cap C_{j} \mid}{\mid C_{i} \cup C_{j} \mid} $$

(14)

• G.Efficiency of diversified search

Figure 5 illustrates the results of exact and diversified top-n ICS. The diversify ratio is set to 0.4 in these experiments. It is observed that the cost of diversified search in those cases does not exceed 9% of exact algorithm. The cost is affordable in practice. We can take diversified top-n ICS as an optional option like heuristic search in practice.

Table 15 shows the results from different settings of l. There is no dramatically increase or decrease of time cost when vary the value of l.

• H.Case Study

We construct a co-author network from the DBLP (DataBase systems and Logic Programming) data set for this case study. The diameter of the network is 6. A vertex represents an author and an edge is added between two authors if they are co-authors. The propagation probability is calculated according to the frequency of co-authorships. We perform a top-6 influential communities (ε= 0.2, p= 0.8, k= 5) query for “Alexanderm T”, the first author in the alphabet order. The threshold of diversity is set to 0.5.

The results are shown in Figure 6. It is fortunate to obtain the same top-3 from both exact and diversified algorithms. However, for top-4 to top-6, the results area different, as shown in Tables 17 and 18. We also present aggregated influence of top-6 communities from both algorithms. The results are shown in Table 16. It is easy to find out that communities top-4th, top-5th and top-6th from exact algorithm have similar influence (about 0.77-0.78), which indicate that they share more than 60% members.

Figure 3

Evaluation of different ε and p

Figure 4

Similarity between Communities

Figure 5

Comparision between exact and diversified search

Figure 6

Top-3 influential communities for Alexanderm T

Table 3 Statistical information of the datasets

Table 4 Efficiency over Twitter

Table 5 Efficiency over Google+

Table 6 Efficiency over Facebook

Table 7 Efficiency over Epinions

Table 8 Space cost over Twitter

Table 9 Space cost over Google+

Table 10 Space cost over Facebook

Table 11 Space cost over Epinions

Table 12 Scalability over Facebook

Table 13 Scalability over Epinions

Table 14 Similarity of top-8 influential communities

Table 15 Evaluation for different l

Table 16 Aggregated influence of top-6 communities

Table 17 Top 4-6 influential communities from diversified algorithm

Table 18 Top 4-6 influential communities from exact algorithm

8 Conclusions

In this paper, we study the personalized top-n influential community search problem in social networks. This kind of search provides a useful tool for other analytical tasks.

In particular, we propose a novel community model based on the maximal pk-Clique concept which uses a new cohesive criterion. To enable efficient personalized top-n influential community searches, we first present a pruning approach which prunes vertices according an upper bound of aggregated influence and a lower bound k from the pk-Cliques definition. Then we introduce search space refinement which removes unqualified vertices in the network before searching. We also propose a heuristic search approach. To diversify the results, we propose a diversified searching algorithm which returns results in one pass. A novel tree-like index and necessary operations are devised to accelerate the search process. Extensive experiments over real social networks verify the effectiveness and efficiency of our search algorithms.