Secrecy Performance of Multi-RIS-Assisted Wireless Systems

Abstract

This paper presents a theoretical framework using multiple reconfigurable intelligent surfaces (RISs) for enhancing the secrecy performance of wireless systems. In particular, multiple RISs are exploited to support transmitter-legitimate user communication under the existence of an eavesdropper. Two practical scenarios are investigated, i.e., there are only transmitter-eavesdropper links (case 1) and there are both transmitter-eavesdropper and transmitter-RIS-eavesdropper links (case 2). We mathematically obtain the closed-form expressions of the average secrecy capacity (ASC) of the considered system in these two investigated cases over Nakagami-m fading channels. The impacts of the system parameters, such as the locations of the RISs, the number of REs, and the Nakagami-m channels, are deeply evaluated. Computer simulations are used to validate our mathematical analysis. Numerical results clarify the benefits of using multiple RISs for improving the secrecy performance of wireless systems. Specifically, the ASCs in cases 1 and 2 are significantly higher than that in the case without RISs. Importantly, when the locations of the RISs are fixed, we can arrange the larger RSIs near either the transmitter or legitimate user to achieve higher ASCs. In addition, when the numbers of reflecting elements (REs) in the RISs increase, the ASCs in cases 1 and 2 are greatly enhanced.

1 Introduction

In the age of the Internet of Things, besides coverage and capacity improvements, security and reliability enhancements of wireless communication systems are the key requirements, especially in the fifth and beyond generations (5G and B5G) of wireless systems [1, 2]. For the security requirements of the 5G and B5G wireless systems, physical layer security (PLS) has been proposed [3]. Unlike classical cryptographic algorithms, PLS utilizes the random nature of wireless channels for information security. Consequently, the PLS can provide secrecy performance without depending on the computation resources of wireless devices [3, 4]. As a result, the PLS is now widely considered and applied to enhance information security in 5G and B5G wireless systems [5,6,7].

On the other hand, the emergence of reconfigurable intelligent surfaces (RISs) used for assisting wireless systems has greatly attracted the attention of wireless researchers and designers [8, 9]. In particular, the RISs are equipped with many reflecting elements (REs) that can reflect signals transmitted from transmitter to receiver without signal processing [10, 11]. In addition, the RISs can work without power supply, decoding, encoding, and amplifying signals [12]. Consequently, the usage of RISs is much more effective than the usage of classical relays in wireless systems [13, 14]. Therefore, the RISs are promising candidates that can be deployed in B5G wireless systems. Nowadays, the RISs are widely used not only for improving capacity and reducing outage probability but also enhancing information security of the wireless systems [15, 16].

1.1 Related Works

In the literature, the secrecy performance of the RIS-assisted wireless systems has been analyzed in different scenarios such as in vehicular communications [5, 17], cognitive systems [18], and non-orthogonal multiple access networks [19]. Specifically, the key performance metrics such as secrecy outage probability (SOP) and secrecy ergodic capacity (SEC) have been derived for evaluating the security performance of the RIS-assisted wireless systems [4, 5, 16,17,18,19,20,21,22,23,24]. In [5, 20, 21], the authors investigated the case that the reflected signals generated by RIS were not arrived at an eavesdropper. Consequently, the eavesdropper only receives signals transmitted from the transmitter. Their numerical results observed the potential of the RIS for improving the secrecy performance of wireless systems.

In practice, besides receiving signals directly from the transmitter, the eavesdropper can receive signals reflected by the RIS. Thus, the works in [4, 16,17,18,19, 22,23,24] investigated the case that the reflected signals generated by RIS also arrive at the eavesdropper. The SOP expression was derived for the system performance analysis. It was shown that the SOP performance of the wireless systems is greatly improved when the number of REs increases [4, 16, 23]. In addition, the RIS-assisted wireless systems outperform the multiple-input multiple-output systems in terms of PLS [23]. However, the case of utilizing multi-RIS-assisted wireless systems for further enhancing the secrecy performance has not been analyzed yet.

1.2 Motivations and Contributions

As aforementioned, the secrecy performance of one-RIS-assisted wireless systems has been analyzed for both with and without reflected paths generated by RIS [4, 16, 18, 19, 21, 25,26,27]. Unfortunately, these works used only one RIS. The case of multiple RISs was not considered due to the computational complexity. Meanwhile, in practical scenarios, multiple RISs are often deployed in wireless systems [28]. In particular, multiple RISs are arranged in different areas; thus, either all RISs or some RISs can be used to assist the wireless systems depending on the specific goals [28, 29]. Generally, when multiple RISs are exploited, the performance of wireless systems is significantly improved compared with the case of only one RIS. However, the usage of multiple RISs to improve the secrecy performance of wireless systems was not studied. Furthermore, previous works only considered either the direct link or reflected RIS links at the legitimate users and/or eavesdroppers. The case that signals traveled on both direct link and reflected RIS links are combined at the legitimate users and/or eavesdropper was not considered. These issues motivate us to consider the secrecy performance of the wireless systems under the support of multiple RISs. Specifically, two practical scenarios where the eavesdropper receives signals either via only the transmitter-eavesdropper link or via transmitter-eavesdropper and transmitter-RISs-eavesdropper links are investigated. Also, the considered system is evaluated over Nakagami-m fading channels where the channel parameters are proposed for the 5G standard such as 3rd Generation Partnership Project [28, 30]. The main contributions of this paper can be summarized as follows:

• We consider a multi-RIS-assisted wireless system under the existence of an eavesdropper. Specifically, the eavesdropper receives signals via either direct transmitter-eavesdropper links (case 1) or both direct transmitter-eavesdropper and transmitter-RIS-eavesdropper links (case 2). Additionally, multiple RISs are arranged in different areas to enhance the secrecy performance of the considered system.

• We exploit the benefits of the traditional wireless channel and advanced RISs by combining the direct transmitter-receiver and reflect transmitter-RISs-receiver links to achieve higher signal-to-noise ratio (SNR) power at the receiver. We successfully obtain the closed-form expressions of the average secrecy capacity (ASC) of the considered system in cases 1 and 2 over Nakagami-m fading channels. We validate all derived expressions via computer simulations.

• We evaluate the ASCs of the considered system with the channel model proposed for the 5G standard¹ Numerical results show that the ASCs of the considered system in cases 1 and 2 are significantly higher than that in the case without RISs (case 3). This observation confirms the benefits of using RISs for improving the secrecy performance of wireless systems. Another important observation is that the RISs located near either transmitter or receiver can reflect signals better than the RISs located far from either transmitter or receiver. In addition, the impacts of the number of REs, the total number of REs, the locations of the RISs, and other system parameters are also studied.

Fig. 1

The system model of the considered multi-RIS-assisted wireless system with eavesdropping link

The rest of this paper is organized as follows. Section 2 describes the system and signal models, where the formulas of the received signals at the legitimate user and eavesdropper in two cases are provided in detail. Section 3 analyzes the secrecy performance of the considered system by mathematically deriving the ASC expressions in two cases. Section 4 presents the numerical results and discussions to get insights into the system behaviors. Finally, Section 5 concludes this paper.

Notations

The cumulative distribution function (CDF) and probability density function (PDF) are, respectively, denoted by F(.) and f(.); the gamma, lower, upper incomplete gamma, and Meijer functions are, respectively, denoted by $\gamma (.,.)$, $\Gamma (.)$, $\Gamma (.,.)$, and $G_{.,.}^{.,.}(.)$; the probability of an event and the expectation operator are, respectively, denoted by $\textrm{Pr}\{.\}$ and $\mathbb {E}\{.\}$; the Gaussian noise variable with zero mean and variance of $\sigma ^2$ is denoted by $C\mathcal {N}(0,\sigma ^2)$.

2 System Model

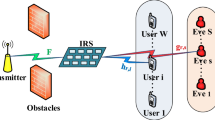
Figure 1 illustrates the multi-RIS-assisted wireless system with eavesdropper links. In particular, a base station (S) transmits signals to a legitimate user (D) via S-D direct link and S-RIS-D reflected links. Meanwhile, an eavesdropper (E) attempts to receive and decode the signals transmitted from S via S-E direct link and S-RIS-E reflected links. In the considered system, K RISs are used to assist S-D communication, where each RIS is equipped with L REs. In addition, all transceivers (S, D, and E) are equipped with a single antenna for transmitting/receiving.

Since multiple RISs are deployed to support S−D communication, the channels from RISs to E may or may not be available. As a result, we consider two scenarios: i) E only receives signals via the S-E link. The reflected links via RISs are not available at E due to blocking objects (similar to the works in [5, 20, 21]); ii) E receives signals via both S-E link and RIS reflected links.

The received signal at the legitimate user D is expressed as

$$\begin{aligned} y_d = \Big ( \hat{h}_{sd} + \sum _{k=1}^{K} \sum _{l=1}^{L_k} \hat{g}_{kl} \hat{h}_{kl} e^{j\varphi _{kl}} \Big ) x_s + z_d, \end{aligned}$$

(1)

where $\hat{h}_{sd}$, $\hat{g}_{kl}$ and $\hat{h}_{kl}$ are, respectively, the channels from S to D, from S to the lth RE of the kth RIS, and from the lth RE of the kth RIS to D; $\varphi _{kl}$ is the phase shift of the lth RE of the kth RIS; $x_s$ is the transmitted signal at S; $z_d \sim C\mathcal {N}(0,\sigma ^2_d)$ is the Gaussian noise at the D.

Using the magnitudes and phases of the complex numbers, we can represent $\hat{h}_{sd}$, $\hat{g}_{kl}$, and $\hat{h}_{kl}$ as $\hat{h}_{sd} = h_{sd} e^{-j \phi _{sd}}$, $\hat{g}_{kl} = g_{kl} e^{-j \theta _{kl}}$, and $\hat{h}_{kl} = h_{kl} e^{-j \psi _{kl}}$, where $h_{sd}$, $g_{kl}$, and $h_{kl}$ are the magnitudes and $\phi _{sd}$, $\theta _{kl}$, and $\psi _{kl}$ are the phases of $\hat{h}_{sd}$, $\hat{g}_{kl}$, and $\hat{h}_{kl}$, respectively.

Now, the received signal at D becomes

$$\begin{aligned} \nonumber y_d =&\Big ( h_{sd}e^{-j \phi _{sd}} + \sum _{k=1}^{K} \sum _{l=1}^{L_k} g_{kl} h_{kl} e^{j(\varphi _{kl}- \theta _{kl}- \psi _{kl})} \Big ) x_s + z_d \\ =&e^{-j \phi _{sd}}\Big ( h_{sd} + \sum _{k=1}^{K} \sum _{l=1}^{L_k} g_{kl} h_{kl} e^{j\zeta _{kl}} \Big ) x_s + z_d. \end{aligned}$$

(2)

where $\zeta _{kl} = \varphi _{kl} - \theta _{kl}- \psi _{kl} +\phi _{sd}$ is the phase error induced by the lth RE of the kth RIS [28].

As demonstrated in previous works on one-RIS or multi-RIS-assisted wireless systems, the phase of the RIS $\varphi _{kl}$ can be adjusted to achieve maximum received signal power [8, 13, 28, 31]. Specifically, $\varphi _{kl}$ can be chosen from a set of discrete phases so that $\zeta _{kl} = 0$ [28]. This value of $\varphi _{kl}$ is the optimal phase of the RIS, which is computed as

$$\begin{aligned} \varphi _{kl}^* = \theta _{kl} + \psi _{kl} -\phi _{sd}. \end{aligned}$$

(3)

With $\varphi _{kl}^*$ of the RISs, the received signal at D now is

$$\begin{aligned} y_d = e^{-j \phi _{sd}}\Big ( h_{sd} + \sum _{k=1}^{K} \sum _{l=1}^{L_k} g_{kl} h_{kl} \Big ) x_s + z_d. \end{aligned}$$

(4)

Since $|e^{-j \phi _{sd}}|^2 =1$, the instantaneous signal-to-noise ratio (SNR) at D is

$$\begin{aligned} \nonumber \beta _d&= \frac{\Big ( h_{sd} + \sum _{k=1}^{K} \sum _{l=1}^{L_k} g_{kl} h_{kl} \Big )^2 P_s }{\sigma ^2_d} \\&=\Big ( h_{sd} + \sum _{k=1}^{K} \sum _{l=1}^{L_k} g_{kl} h_{kl} \Big )^2 \rho _d, \end{aligned}$$

(5)

where $\rho _d = P_s/\sigma ^2_d$ is the average SNR at D.

At the eavesdropper E, the received signal is computed as

$$\begin{aligned} y_e = \Big ( \hat{h}_{se} + \sum _{k=1}^{K} \sum _{l=1}^{L_k} \hat{g}_{kl} \hat{r}_{kl} e^{j\varphi _{kl}} \Big ) x_s + z_e, \end{aligned}$$

(6)

where $\hat{h}_{se}$ and $\hat{r}_{kl}$ are, respectively, the channels from S to E and from the lth RE of the kth RIS to E; $z_e \sim C\mathcal {N}(0,\sigma ^2_e)$ is the Gaussian noise at the E.

In the literature on RIS-assisted multi-user systems, when RISs configure their phases to maximize the SNR at one user, the SNRs at other users may not be maximized [32]. However, the case that maximum SNRs at all users is often assumed [33]. This assumption has been widely used not only for legitimate users but also for eavesdroppers [4, 16, 18, 19, 21]. Similar to these works, in this paper, we assume that the received signal at E can be maximal. In other words, we consider the worst case of the secrecy performance, where maximum SNR at the E is achieved. As a result, the received signal at E can be presented as

$$\begin{aligned} y_e = e^{-j \phi _{se}} \Big ( h_{se} + \sum _{k=1}^{K} \sum _{l=1}^{L_k} g_{kl} r_{kl} \Big ) x_s + z_e, \end{aligned}$$

(7)

where $h_{se}$ and $\phi _{se}$ are, respectively, the amplitude and phase of $\hat{h}_{se}$; $r_{kl}$ is the amplitude of $\hat{r}_{kl}$.

In case 1, due to the blocking objects, the reflected paths from the RISs are not available at E. In other words, we have $r_{kl} =0$. Thus, the instantaneous SNR at E is expressed as

$$\begin{aligned} \beta _e^{c1} = \frac{ h_{se}^2 P_s}{\sigma ^2_e} = h_{se}^2 \rho _e , \end{aligned}$$

(8)

where $\rho _e = P_s/\sigma ^2_e$ is the average SNR at E.

In case 2, the reflected paths from the RISs are available at E. Thus, the instantaneous SNR at E is

$$\begin{aligned} \nonumber \beta _e^{c2}&= \frac{ \Big ( h_{se} + \sum _{k=1}^{K} \sum _{l=1}^{L_k} g_{kl} r_{kl} \Big )^2 P_s}{\sigma ^2_e} \\&= \Big ( h_{se} + \sum _{k=1}^{K} \sum _{l=1}^{L_k} g_{kl} r_{kl} \Big )^2 \rho _e . \end{aligned}$$

(9)

On the other hand, the CDF and PDF of the channel amplitudes ($h_{sd}, h_{se}, g_{kl}, h_{kl}$, and $r_{kl}$) which follow the Nakagami-m distributions are, respectively, given by

$$\begin{aligned} \nonumber F_X(x)&= \frac{1}{\Gamma (m_{X})} \gamma \Big (m_{X}, \frac{m_{X} }{\Omega _{X}}x^2\Big ) \\&= 1 - \frac{1}{\Gamma (m_{X})} \Gamma \Big (m_{X}, \frac{m_{X} }{\Omega _{X}} x^2 \Big ) , \; x \ge 0, \end{aligned}$$

(10)

$$\begin{aligned} f_X(x) = \frac{2 m_X^{m_{X}}}{\Gamma (m_{X})\Omega _{X}^{m_{X}}} x^{2m_{X} -1} \textrm{exp}\Big (-\frac{m_{X} }{\Omega _{X}}x^2\Big ) , \; x \ge 0, \end{aligned}$$

(11)

where $X \in \{sd, se, g_{k}, h_{k}, r_{k}\}$; $m_{X}$ and $\Omega _{X}$ are, respectively, the shape and spread parameters. The spread parameter calculated by the path loss model applied in the 5G standard is given as [13, 28, 30]

$$\begin{aligned} \Omega _X = G_\textrm{tx} + G_\textrm{rx} -22.7 - 26 \log (f_c) -36.7 \log (d/d_0), \end{aligned}$$

(12)

where $G_\textrm{tx}$ $(\textrm{tx} \in \{s, ris\})$ and $G_\textrm{rx}$ $(\textrm{rx} \in \{ris, d, e\})$ are, respectively, the antenna gains of the transmitter and receiver; $f_c$ is the carrier frequency; d and $d_0$ are, respectively, the transmitter-receiver and reference distances.

Furthermore, the variance of the Gaussian noise is given as [28]

$$\begin{aligned} \sigma ^2 = N_0 +10\log (\textrm{BW}) + \textrm{NF}, \end{aligned}$$

(13)

where $N_0$, $\textrm{BW}$, and $\textrm{NF}$ are, respectively, the thermal noise power density, bandwidth, and noise figure.

3 Secrecy Performance Analysis

In this section, we will derive the average secrecy capacity expression of the considered system over Nakagami-m fading channels. In particular, the ASC of the considered system is defined as the difference between the capacities of the legitimate channel and the wiretap channel. Mathematically, it is computed as [21]

$$\begin{aligned} \mathcal {C} = [\mathbb {E} \left\{ \log _2(1 + \beta _d) - \log _2(1 + \beta _e)\right\} ]^+, \end{aligned}$$

(14)

where $\beta _d$ is given in Eq. 5; $\beta _e$ is given in Eq. 8 for case 1 and Eq. 9 for case 2; $[x]^+ = \max \{x,0\}$.

From the properties of expectation [34], Eq. 14 can be rewritten as

$$\begin{aligned} \mathcal {C} = [\mathbb {E} \left\{ \log _2(1 + \beta _d) \right\} -\mathbb {E} \left\{ \log _2(1 + \beta _e) \right\} ]^+. \end{aligned}$$

(15)

We should note that in case 2, $\beta _d$ and $\beta _e$ are not independent because of $g_{kl}$; however, Eq. 15 is still correct due to the expectation properties. As a result, Eq. 15 has been widely utilized when calculating the ASC of RIS-assisted wireless systems [4, 19,20,21,22,23].

Consequently, the ASC of the considered system in these two cases can be, respectively, expressed as

$$\begin{aligned} \mathcal {C}^{c1} = \mathcal {C}_d - \mathcal {C}_e^{c1}, \end{aligned}$$

(16)

$$\begin{aligned} \mathcal {C}^{c2} = \mathcal {C}_d - \mathcal {C}_e^{c2}, \end{aligned}$$

(17)

where $\mathcal {C}_d = \mathbb {E} \left\{ \log _2(1 + \beta _d) \right\}$, $\mathcal {C}_e^{c1} = \mathbb {E} \left\{ \log _2(1 + \beta _e^{c1}) \right\}$, and $\mathcal {C}_e^{c2} = \mathbb {E} \left\{ \log _2(1 + \beta _e^{c2}) \right\}$. Notice that if $\mathcal {C}_d < \mathcal {C}_e^{c1}$, we have $\mathcal {C}^{c1} =0$. It is similar for $\mathcal {C}^{c2}$.

Based on Eqs. 16 and 17, we obtain the ASCs of the considered system in the following Theorem.

Theorem

The ASCs of the considered system in cases 1 and 2 over Nakagami-m fading channels are, respectively, given by

$$\begin{aligned} \nonumber \mathcal {C}^{c1} =&\frac{2^{\Xi _d -1}}{\sqrt{\pi } \Gamma ( \Xi _d ) \ln 2} G^{5,3}_{3,5}\left( \frac{\Psi _d^2 }{4 \rho _d} \Big |^{\quad 0, \frac{1}{2}, 1}_{\frac{\Xi _d }{2}, \frac{\Xi _d +1}{2} , 0, \frac{1}{2}, 0 } \right) \\&- \frac{1}{\Gamma ( m_{se} ) \ln 2} G^{3,1}_{2,3}\left( \frac{m_{se} }{\Omega _{se} \rho _e} \Big |^{\quad 0, 1}_{0, m_{se} , 0 } \right) , \end{aligned}$$

(18)

$$\begin{aligned} \nonumber \mathcal {C}^{c2} =&\frac{2^{\Xi _d -1}}{\sqrt{\pi } \Gamma \big ( \Xi _d \big ) \ln 2} G^{5,3}_{3,5}\left( \frac{\Psi _d^2 }{4 \rho _d} \Big |^{\quad 0, \frac{1}{2}, 1}_{\frac{\Xi _d }{2}, \frac{\Xi _d +1}{2} , 0, \frac{1}{2}, 0 } \right) \\&- \frac{2^{\Xi _e -1}}{\sqrt{\pi } \Gamma \big ( \Xi _e \big ) \ln 2} G^{5,3}_{3,5}\left( \frac{\Psi _e^2 }{4 \rho _e} \Big |^{\quad 0, \frac{1}{2}, 1}_{\frac{\Xi _e }{2}, \frac{\Xi _e +1}{2} , 0, \frac{1}{2}, 0 } \right) , \end{aligned}$$

(19)

where $\Xi _d$, $\Psi _d$, $\Xi _e$, and $\Psi _e$ are, respectively, given in Eqs. 61,62,63 and 64.

Proof

: To derive the ASCs in Eqs. 18 and 19, we must firstly derive $\mathcal {C}_d$, $\mathcal {C}_e^{c1}$, and $\mathcal {C}_e^{c2}$, then replace them into Eqs. 16 and 17.

First, $\mathcal {C}_d$, $\mathcal {C}_e^{c1}$, and $\mathcal {C}_e^{c2}$ can be calculated as

$$\begin{aligned} \mathcal {C}_d = \mathbb {E} \left\{ \log _2(1 + \beta _d) \right\} =\frac{1}{\ln 2}\int \limits _0^\infty \frac{1 - F_{\beta _d}(x)}{1 + x}dx, \end{aligned}$$

(20)

$$\begin{aligned} \mathcal {C}_e^{c1} = \mathbb {E} \left\{ \log _2(1 + \beta _e^{c1}) \right\} =\frac{1}{\ln 2}\int \limits _0^\infty \frac{1 - F_{\beta _e^{c1}}(x)}{1 + x}dx, \end{aligned}$$

(21)

$$\begin{aligned} \mathcal {C}_e^{c2} = \mathbb {E} \left\{ \log _2(1 + \beta _e^{c2}) \right\} =\frac{1}{\ln 2}\int \limits _0^\infty \frac{1 - F_{\beta _e^{c2}}(x)}{1 + x}dx. \end{aligned}$$

(22)

Next, we have to obtain the CDFs of $\beta _d$, $\beta _e^{c1}$, and $\beta _e^{c2}$ and then replace them into Eqs. 20,21 and 22. Mathematically, $F_{\beta _d}(x)$, $F_{\beta _e^{c1}}(x)$, and $F_{\beta _e^{c2}}(x)$ are, respectively, computed as

$$\begin{aligned} \nonumber F_{\beta _d}(x)&= \textrm{Pr} \left\{ \beta _d< x \right\} \\&= \textrm{Pr} \left\{ \Big ( h_{sd} + \sum _{k=1}^{K} \sum _{l=1}^{L_k} g_{kl} h_{kl} \Big )^2 \rho _d < x \right\} , \end{aligned}$$

(23)

$$\begin{aligned} F_{\beta _e^{c1}}(x) = \textrm{Pr} \left\{ \beta _e^{c1}< x \right\} = \textrm{Pr} \left\{ h_{se}^2 \rho _e < x \right\} , \end{aligned}$$

(24)

$$\begin{aligned} \nonumber F_{\beta _e^{c2}}(x)&= \textrm{Pr} \left\{ \beta _e^{c2}< x \right\} \\&= \textrm{Pr} \left\{ \Big ( h_{se} + \sum _{k=1}^{K} \sum _{l=1}^{L_k} g_{kl} r_{kl} \Big )^2 \rho _e < x \right\} . \end{aligned}$$

(25)

From these above expressions, we can obtain $F_{\beta _d}(x)$, $F_{\beta _e^{c1}}(x)$, and $F_{\beta _e^{c2}}(x)$ as (the detailed calculations are presented in Appendix)

$$\begin{aligned} F_{\beta _d}(x) = 1 - \frac{1}{\Gamma (\Xi _d)} \Gamma \Bigg ( \Xi _d, \Psi _d \sqrt{\frac{x }{\rho _d}} \Bigg ), \end{aligned}$$

(26)

$$\begin{aligned} F_{\beta _e^{c1}}(x) = 1 - \frac{1}{\Gamma (m_{se})} \Gamma \Bigg ( m_{se}, \frac{m_{se} x}{\Omega _{se} \rho _e } \Bigg ), \end{aligned}$$

(27)

$$\begin{aligned} F_{\beta _e^{c2}}(x) = 1 - \frac{1}{\Gamma (\Xi _e)} \Gamma \Bigg ( \Xi _e, \Psi _e \sqrt{\frac{x }{\rho _e}} \Bigg ). \end{aligned}$$

(28)

On the other hand, using [35, Eq. (8.4.2.5)] and [35, Eq. (8.4.16.2)], we have

$$\begin{aligned} (1+x)^{-1} = G^{1,1}_{1,1} \Big (x\Big |^0_0\Big ), \end{aligned}$$

(29)

$$\begin{aligned} \Gamma (a, x) = G^{2,0}_{1,2} \Big (x\Big |^1_{a, 0}\Big ). \end{aligned}$$

(30)

Now, $\mathcal {C}_d$, $\mathcal {C}_e^{c1}$, and $\mathcal {C}_e^{c2}$ are, respectively, calculated as

$$\begin{aligned} \nonumber \mathcal {C}_d&= \frac{1}{\Gamma (\Xi _d) \ln 2}\int \limits _0^\infty \frac{1 }{1 + x} \Gamma \Bigg ( \Xi _d, \Psi _d \sqrt{\frac{x }{\rho _d}} \Bigg ) dx \\&= \frac{1}{\Gamma (\Xi _d) \ln 2}\int \limits _0^\infty G^{1,1}_{1,1} \Big (x\Big |^0_0\Big ) G^{2,0}_{1,2} \Big (\Psi _d \sqrt{\frac{x }{\rho _d}}\Big |^1_{\Xi _d, 0}\Big ) dx, \end{aligned}$$

(31)

$$\begin{aligned} \nonumber \mathcal {C}_e^{c1}&= \frac{1}{\Gamma (m_{se}) \ln 2}\int \limits _0^\infty \frac{1 }{1 + x}\Gamma \Bigg ( m_{se}, \frac{m_{se} x}{\Omega _{se} \rho _e } \Bigg ) dx \\&= \frac{1}{\Gamma (m_{se}) \ln 2}\int \limits _0^\infty \frac{1 }{1 + x} G^{2,0}_{1,2} \Big (\frac{m_{se} x}{\Omega _{se} \rho _e }\Big |^1_{m_{se}, 0}\Big ) dx, \end{aligned}$$

(32)

$$\begin{aligned} \nonumber \mathcal {C}_e^{c2}&= \frac{1}{\Gamma (\Xi _e) \ln 2}\int \limits _0^\infty \frac{1 }{1 + x} \Gamma \Bigg ( \Xi _e, \Psi _e \sqrt{\frac{x }{\rho _e}} \Bigg ) dx \\&= \frac{1}{\Gamma (\Xi _e) \ln 2}\int \limits _0^\infty G^{1,1}_{1,1} \Big (x\Big |^0_0\Big ) G^{2,0}_{1,2} \Big (\Psi _e \sqrt{\frac{x }{\rho _e}}\Big |^1_{\Xi _e, 0}\Big ) dx. \end{aligned}$$

(33)

Applying [35, Eq. (2.24.1.1)], Eqs. 31 and 33 respectively become

$$\begin{aligned} \mathcal {C}_d = \frac{2^{\Xi _d -1}}{\sqrt{\pi } \Gamma ( \Xi _d ) \ln 2} G^{5,3}_{3,5}\left( \frac{\Psi _d^2 }{4 \rho _d} \Big |^{\quad 0, \frac{1}{2}, 1}_{\frac{\Xi _d }{2}, \frac{\Xi _d +1}{2} , 0, \frac{1}{2}, 0 } \right) , \end{aligned}$$

(34)

$$\begin{aligned} \mathcal {C}_e^{c2} = \frac{2^{\Xi _e -1}}{\sqrt{\pi } \Gamma \big ( \Xi _e \big ) \ln 2} G^{5,3}_{3,5}\left( \frac{\Psi _e^2 }{4 \rho _e} \Big |^{\quad 0, \frac{1}{2}, 1}_{\frac{\Xi _e }{2}, \frac{\Xi _e +1}{2} , 0, \frac{1}{2}, 0 } \right) . \end{aligned}$$

(35)

Using [36, Eq. (7.811.5)], Eq. 32 becomes

$$\begin{aligned} \mathcal {C}_e^{c1} = \frac{1}{\Gamma ( m_{se} ) \ln 2} G^{3,1}_{2,3}\left( \frac{m_{se} }{\Omega _{se} \rho _e} \Big |^{\quad 0, 1}_{0, m_{se} , 0 } \right) . \end{aligned}$$

(36)

Finally, replacing Eqs. 34, 36 and 35 into Eqs. 16 and 17, we obtain the ASCs of the considered system as in Eqs. 18 and 19. The proof is thus complete.

4 Numerical Results and Discussions

In this section, the secrecy performance of the considered system is examined by using the analysis expressions. Computer simulations are used to verify our numerical expressions. Besides investigating the ASCs in cases 1 and 2, the ASC in the case without RISs (denoted by “Case 3" in all below figures) is also provided to show the benefits of using RISs. Unless otherwise specified, in all scenarios, we set $K =5$ RISs and $m_{sd} = m_{se} = m_{g_k} = m_{h_k} = m_{r_k} = m$. To obtain the spread parameter and noise power given in Eqs. 12 and 13, respectively, we set $G_s = G_d = G_{ris}= 5$ dB, $G_e= 0$ dB, $f_c =3$ GHz, $d_0 = 1$ m, $d_{sd} = 100$ m, $d_{se} =150$ m, $\textrm{BW}=10$ MHz, $N_0 = -174$ dBm/Hz, and $\textrm{NF}=10$ dBm. The number of REs in each RIS is determined via vector $\textbf{L}$, i.e., $\textbf{L} =[L_1 \; L_2 \; L_3 \; L_4 \; L_5]$, where $L_k$ $(k \in \{1,2,..,5\})$ denotes the number of REs in the kth RIS. Additionally, we use the coordinate axis $(x_k,y_k)$ to indicate the location of the kth RIS, with (0, 0) is the location of S.

Fig. 2

The ASCs of the considered system in the cases 1 and case 2 in comparison with the ASC in the case without RISs for $m = 2$, $\textbf{L} = [40 \; 40 \; 40 \; 40 \;40]$, and $(x,y) = (30,10), (40,10), (50,10), (60,10)$, and (70, 10)

Figure 2 illustrates the ASCs of the considered system in cases 1 and 2 in comparison with the ASC in the case without RISs (case 3) for $m = 2$, $\textbf{L} = [40 \; 40 \; 40 \; 40 \;40]$, and $(x,y) = (30,10), (40,10), (50,10), (60,10)$, and (70, 10). We use Eqs. 18 and 19 to obtain the analysis curves in cases 1 and 2, respectively. Notice that with the investigated parameters, the numbers of REs in all RISs are equal. However, they are located in different locations, where the 1st RIS is located nearest to the S and the 5th RIS is located furthest from the S. It is easy to see in Fig. 2 that the ASC in case 1 is the best while the ASC in case 3 is the worst. This result demonstrates the benefits of using RISs for improving the ASC of wireless systems. For example, when $P_s =16$ dBm, the ASCs in the cases 1, 2, and 3 are, respectively, 4.4, 3.5, and 1.3 bit/s/Hz. That means cases 1 and 2 can achieve 3.1 and 2.2 bit/s/Hz higher ASC in comparison with case 3. As $P_s$ increases, the ASCs of three cases increase. However, the increasing rates of the ASCs in cases 2 and 3 are slow in the high transmit power regime ($P_s > 25$ dBm). Also, all ASCs gradually reach the capacity ceiling when $P_s > 30$ dBm.

Fig. 3

The ASCs of the considered system versus the distance between S and E for $P_s = 15$ and 30 dBm, $m = 2$, $\textbf{L} = [40 \; 40 \; 40 \; 40 \;40]$, and $(x,y) = (30,10), (40,10), (50,10), (60,10)$, and (70, 10)

Figure 3 investigates the effects of the distance between S and E ($d_{se}$) on the ASCs of the considered system. As shown in Fig. 3, even $d_{se} = 100$ m, the ASCs in cases 1 and 2 are still high, especially in case 1. Meanwhile, the ASC in case 3 equals zero. In other words, even though the distances between transmitter and legitimate user and between transmitter and eavesdropper are identical ($d_{sd} = d_{se} = 100$ m), the usage of RISs still significantly enhances the ASC of wireless systems. Another observation is that when $d_{se} = 100$ m, the ASCs with $P_s = 15$ and $P_s = 30$ dBm are similar for cases 2 and 3. Meanwhile, they are different for case 1. As $d_{se}$ increases, the ASCs in three cases increase for both $P_s = 15$ and $P_s = 30$ dBm. In particular, when $d_{se} = 200$ m, the ASCs in cases 1 and 2 are greatly higher than that in case 3 for both $P_s = 15$ and $P_s = 30$ dBm. Specifically, the ASCs in cases 1 and 2 with $P_s = 15$ dBm are higher than the ASC in case 3 with $P_s = 30$ dBm. Thus, besides enhancing the secrecy performance, the RISs help to reduce the power consumption of the transmitter. As a result, the usage of RISs can significantly improve the secrecy performance and energy efficiency of wireless systems.

Fig. 4

The impacts of the locations of the RISs on the ASCs of the considered system for $m = 2$ and $\textbf{L} = [40 \; 40 \; 40 \; 40 \;40]$.

Fig. 5

The ASCs of the considered system for different numbers of REs in each RIS, $m = 2$, $(x,y) = (30,10), (40,10), (50,10), (60,10)$, and (70, 10)

In Fig. 4, the impacts of the locations of the RISs on the ASCs of the considered system are investigated. Unlike Figs. 2 and 3, the locations of all RISs in Fig. 4 are similar for each investigated scenario. For example, the 1st: (50, 10) in Fig. 4 indicates that $(x,y) = (50,10), (50,10), (50,10), (50,10)$, and (50, 10). In other words, all RISs in the 1st scenario are located right in the middle between S and D. Meanwhile, all RISs in the 2nd and 3rd scenarios are located near to S and far from S, respectively. As observed in Fig. 4, the ASCs in the 3rd scenario are the best, and the ASCs in the 1st scenario are the worst among the three scenarios. On the other hand, the ASCs of the 1st and 2nd scenarios of case 2 are nearly similar. Meanwhile, they are significantly different in case 1. Hence, the locations of the RISs greatly affect the ASCs of the considered system. Additionally, we can locate RISs near either transmitter or receiver in practice to achieve higher ASCs.

Fig. 6

The ASCs of the considered system when the total number of REs in all RISs varies for $m = 2$, $(x,y) = (30,10), (40,10), (50,10), (60,10)$, and (70, 10)

In Fig. 5, three investigated scenarios such as $\textbf{L} = [40 \; 40 \; 40 \; 40 \;40]$, $\textbf{L} = [10 \; 30 \; 40 \; 55 \;65]$, and $\textbf{L} = [10 \; 20 \; 30 \; 40 \;100]$ are evaluated, where the number of REs in each RIS is varied. We should note that the total number of REs in all RISs is identical, i.e., equal to 200, in three scenarios. We also provide the ASCs in cases 1 and 2 with only one RIS (denoted by “One-RIS" in Fig. 5). Note that the ASCs with only one RIS are obtained by setting $K=1$ RIS, $L=200$ REs, and $(x,y) = (50,10)$. Figure 5 confirms the great benefits of the considered multi-RIS-assisted wireless system in comparison with one-RIS-assisted wireless systems presented in the previous works [4, 19, 20]. It is obvious from Fig. 5 that with these parameter settings, the ASCs in the 3rd scenario are the best while the ASCs in the 1st scenario are the worst. As a result, when the locations of the RISs are different, the ASCs can be higher with different numbers of REs in the RISs. In particular, when $P_s = 30$ dBm, the ASCs are 5.6, 6, and 6.8 in case 1 and 3.9, 4.4, and 4.9 bit/s/Hz in case 2 corresponding to the 1st, 2nd, and 3rd scenarios. Furthermore, when the numbers of REs in the RISs vary from the 1st to the 3rd scenarios, the ASCs increase 1.2 and 1 bit/s/Hz for cases 1 and 2, respectively. Therefore, besides locating the RISs in suitable areas, we should choose an appropriate number of REs in each RIS to improve the ASC of the wireless systems.

Unlike Fig. 5, where the total number of REs in all RISs is constant, the total number of REs in all RISs in Fig. 6 is varied, i.e., $\textbf{L} = [10 \; 10 \; 10 \; 10 \;10]$, $\textbf{L} = [20 \; 20 \; 20 \; 20 \;20]$, ..., and $\textbf{L} = [50 \; 50 \; 50 \; 50 \;50]$. As shown in Fig. 6, an increase of the number of REs in the RISs significantly enhances the ASCs of the considered system. Specifically, even when the number of REs in the RISs is small (i.e., $L=10$), the ASCs in cases 1 and 2 are still higher than that in case 3. When L increases, i.e., $L=20, 30, 40$, and 50, the ASCs in cases 1 and 2 greatly increase, especially in case 1. Another observation is that the ASCs in cases 1 and 2 are almost linearly proportional to L. Thus, we can use larger L to achieve higher ASCs of the considered system.

Fig. 7

The ASCs of the considered system for different values of Nakagami-m parameter

In Fig. 7, the severity of Nakagami-m fading is varied, i.e., $m=1,3$, and 5. Other system parameters are similar to those in Fig. 2. Notice that in the case $m=1$, the Nakagami-m fading channels become the Rayleigh fading channels. Obviously, the ASCs in the three cases remarkably increase when m increases from 1 to 3. However, when m increases from 3 to 5, these ASCs are nearly unchanged. Specifically, with high transmission power, i.e., $P_s =30$ dBm, the ASCs are similar for different m. As a result, higher values of m cannot improve the ASCs of the considered system in cases 1 and 2, even with high transmission power. Therefore, when the considered system operates in environments with higher m, we should use a suitable transmission power to exploit the benefit of these environments and avoid the ASC ceilings. On the other hand, since we set $\rho _d = \rho _e$, the ASCs of the considered system are saturated in the high transmit power regime. This feature is reasonable because $\beta _d$ and $\beta _e$ are nearly parallel when $P_s$ increases. As a result, the subtraction of $\log _2(1 + \beta _d) - \log _2(1 + \beta _e)$ becomes a constant in the high transmit power regime²

5 Conclusion

This paper exploits multiple RISs to enhance the secrecy performance of a wireless system with an eavesdropper. We successfully derived the closed-form expressions of the average secrecy capacity of the considered system over Nakagami-m fading channels in two cases, where the eavesdropper receives signals from either transmitter-eavesdropper link or both transmitter-eavesdropper and transmitter-RIS-eavesdropper links. Numerical results showed that using multiple RISs significantly increases the ASCs of the considered system compared to the case without RISs. Specifically, when the number of REs in each RIS is constant, by choosing suitable locations of the RISs, the ASCs of the considered system are significantly enhanced. When the locations of the RISs are fixed, the locations near either the base station or legitimate receiver should be used for RISs with a larger number of REs to achieve higher secrecy performance. On the other hand, using RISs with larger sizes is also a suitable method for improving the secrecy performance of the considered system.

Appendix

This appendix detailedly provides the step-by-step derivations of the CDFs of $\beta _d$, $\beta _e^{c1}$, and $\beta _e^{c2}$.

Firstly, $F_{\beta _e^{c1}}(x)$ can be derived directly by using the CDF of the channel gain following Nakagami-m fading channels [37], i.e.,

$$\begin{aligned} \nonumber F_{\beta _e^{c1}}(x)&= \textrm{Pr} \left\{ h_{se}^2 \rho _e< x \right\} = \textrm{Pr} \left\{ h_{se}^2 < \frac{x}{\rho _e} \right\} \\ \nonumber&= \frac{1}{\Gamma (m_{se})} \gamma \Bigg ( m_{se}, \frac{m_{se} x}{\Omega _{se} \rho _e } \Bigg ) \\&= 1 - \frac{1}{\Gamma (m_{se})} \Gamma \Bigg ( m_{se}, \frac{m_{se} x}{\Omega _{se} \rho _e } \Bigg ). \end{aligned}$$

(37)

Secondly, $F_{\beta _d}(x)$ and $F_{\beta _e^{c2}}(x)$ are calculated as follows. Let $\mathcal {X}_{dkl}= g_{kl} h_{kl}$, $\mathcal {Y}_{dk} = \sum _{l=1}^{L_k} \mathcal {X}_{dkl}$, $\mathcal {Z}_{d} = \sum _{k=1}^{K} \mathcal {Y}_{dk}$, $\mathcal {T}_{d} = h_{sd} + \mathcal {Z}_d$, $\mathcal {X}_{ekl}= g_{kl} r_{kl}$, $\mathcal {Y}_{ek} = \sum _{l=1}^{L_k} \mathcal {X}_{ekl}$, $\mathcal {Z}_e = \sum _{k=1}^{K} \mathcal {Y}_{ek}$, and $\mathcal {T}_e = h_{se} + \mathcal {Z}_e$ be new variables, Eqs. 23 and 25 respectively become

$$\begin{aligned} F_{\beta _d}(x) = \textrm{Pr} \left\{ \mathcal {T}_{d}^2 \rho _d < x \right\} , \end{aligned}$$

(38)

$$\begin{aligned} F_{\beta _e^{c2}}(x) = \textrm{Pr} \left\{ \mathcal {T}_e^2 \rho _e < x \right\} . \end{aligned}$$

(39)

It is obvious that $F_{\beta _d}(x)$ and $F_{\beta _e^{c2}}(x)$ have similar types. Thus, in the following parts, we focus on deriving $F_{\beta _d}(x)$, $F_{\beta _e^{c2}}(x)$ can be derived similarly as $F_{\beta _d}(x)$.

Since the Nakagami-m fading channels are considered, the nth moment of $h_{sd}$ is given by [28]

$$\begin{aligned} \mu _{h_{sd}}(n) \triangleq \mathbb {E}\{h_{sd}^n\} = \frac{\Gamma (m_{sd}+n/2)}{\Gamma (m_{sd})} \Big ( \frac{m_{sd}}{\Omega _{sd}}\Big )^{-n/2}. \end{aligned}$$

(40)

From Eq. 40, we obtain the first and second moments of $h_{sd}$ as

$$\begin{aligned} \mu _{h_{sd}}(1) = \frac{\Gamma (m_{sd}+1/2)}{\Gamma (m_{sd})} \sqrt{\frac{\Omega _{sd} }{m_{sd}}}, \end{aligned}$$

(41)

$$\begin{aligned} \mu _{h_{sd}}(2) = \frac{\Gamma (m_{sd}+1)\Omega _{sd}}{\Gamma (m_{sd})m_{sd}} = \Omega _{sd}. \end{aligned}$$

(42)

Since $\mathcal {X}_{dkl}= g_{kl} h_{kl}$, the PDF of $\mathcal {X}_{dkl}$ is calculated as

$$\begin{aligned} f_{\mathcal {X}_{dkl}}(y) = \int _{0}^{\infty } \frac{1}{x} f_{h_{kl}} \Big (\frac{y}{x}\Big ) f_{g_{kl}} (x) dx. \end{aligned}$$

(43)

Replacing the PDF given in Eq. 11 into Eq. 43, we have

$$\begin{aligned} \nonumber f_{\mathcal {X}_{dkl}}(y) =&\frac{4}{\Gamma (m_{g_k}) \Gamma (m_{h_k}) } \Big (\frac{m_{g_k}}{ \Omega _{g_k}}\Big )^{m_{g_k}} \Big (\frac{m_{h_k}}{ \Omega _{h_k}}\Big )^{m_{h_k}} \\ \nonumber&\times y^{2 m_{h_k}-1} \int _{0}^{\infty } x^{2 m_{g_k} - 2 m_{h_k} -1} \\&\times \exp \Big (- \frac{m_{g_k} x^2}{\Omega _{g_k}} -\frac{y^2 m_{h_k}}{ \Omega _{h_k} x^2} \Big ) dx. \end{aligned}$$

(44)

Applying [36, Eq. (3.478.4)], Eq. 44 becomes

$$\begin{aligned} f_{\mathcal {X}_{dkl}}(y) = \frac{4 \alpha _{kl}^{m_{g_k}+m_{h_k}} }{\Gamma (m_{g_k}) \Gamma (m_{h_k})} y^{m_{g_k}+ m_{h_k}-1} \mathcal {K}_{m_{g_k} - m_{h_k}} (2 \alpha _{kl} y), \end{aligned}$$

(45)

where $\alpha _{kl} = \sqrt{\frac{m_{g_k} m_{h_k}}{\Omega _{g_k} \Omega _{h_k}}}$.

Now, the nth moment of $\mathcal {X}_{dkl}$ is computed as

$$\begin{aligned} \mu _{\mathcal {X}_{dkl}}(n) \triangleq \mathbb {E}\{\mathcal {X}_{dkl}^n\} = \int _{0}^{\infty } y^n f_{\mathcal {X}_{dkl}}(y) dy. \end{aligned}$$

(46)

Using [36, Eq. (6.561.16)], Eq. 46 becomes

$$\begin{aligned} \mu _{\mathcal {X}_{dkl}}(n) = \alpha _{kl}^{-n} \frac{\Gamma (m_{g_k}+n/2) \Gamma (m_{h_k}+n/2) }{\Gamma (m_{g_k}) \Gamma (m_{h_k}) }. \end{aligned}$$

(47)

Then, the CDF of $\mathcal {X}_{dkl}$ is given by

$$\begin{aligned} \nonumber&F_{\mathcal {X}_{dkl}}(x) \approx \frac{1}{\Gamma \Big ( \frac{[\mu _{\mathcal {X}_{dkl}}(1)]^2 }{\mu _{\mathcal {X}_{dkl}}(2) - [\mu _{\mathcal {X}_{dkl}}(1)]^2} \Big )} \\&\times \gamma \Big ( \frac{[\mu _{\mathcal {X}_{dkl}}(1)]^2 }{\mu _{\mathcal {X}_{dkl}}(2) - [\mu _{\mathcal {X}_{dkl}}(1)]^2}, \frac{\mu _{\mathcal {X}_{dkl}}(1) x}{\mu _{\mathcal {X}_{dkl}}(2) - [\mu _{\mathcal {X}_{dkl}}(1)]^2} \Big ) \cdot \end{aligned}$$

(48)

Now, we can derive the CDF of $\mathcal {Y}_{dk} = \sum _{l=1}^{L_k} \mathcal {X}_{dkl}$ as

$$\begin{aligned} \nonumber&F_{\mathcal {Y}_{dk}}(x) \approx \frac{1}{\Gamma \Big ( \frac{L_k [\mu _{\mathcal {X}_{dkl}}(1)]^2 }{\mu _{\mathcal {X}_{dkl}}(2) - [\mu _{\mathcal {X}_{dkl}}(1)]^2} \Big )} \\&\times \gamma \Big ( \frac{L_k [\mu _{\mathcal {X}_{dkl}}(1)]^2 }{\mu _{\mathcal {X}_{dkl}}(2) - [\mu _{\mathcal {X}_{dkl}}(1)]^2}, \frac{\mu _{\mathcal {X}_{dkl}}(1) x}{\mu _{\mathcal {X}_{dkl}}(2) - [\mu _{\mathcal {X}_{dkl}}(1)]^2} \Big ) \cdot \end{aligned}$$

(49)

Based on [38], we obtain the nth moment of $\mathcal {Y}_{dk}$ as

$$\begin{aligned} \nonumber \mu _{\mathcal {Y}_{dk}}(n)&\triangleq \mathbb {E}\{\mathcal {Y}_{dk}^n\} \\ \nonumber&= \sum _{n_1=0}^{n} \sum _{n_2=0}^{n_1} \cdots \sum _{n_{L_k -1}=0}^{n_{L_k -2}} {n \atopwithdelims ()n_1} {n_1 \atopwithdelims ()n_2} \cdots {n_{L_k -2} \atopwithdelims ()n_{L_k -1}} \\&\times \mu _{\mathcal {X}_{dk1}}(n -n_1) \mu _{\mathcal {X}_{dk2}}(n_1 -n_2) \cdots \mu _{\mathcal {X}_{dkL_k}}(n_{L_k -1}), \end{aligned}$$

(50)

where ${a \atopwithdelims ()b} = \frac{a!}{b!(a-b)!}$, and the nth moment of $\mathcal {Z}_d = \sum _{k=1}^{K} \mathcal {Y}_{dk}$ is

$$\begin{aligned} \nonumber \mu _{{\mathcal {Z}_d}}(n)&\triangleq \mathbb {E}\{\mathcal {Z}_d^n\} \\ \nonumber&= \sum _{n_1=0}^{n} \sum _{n_2=0}^{n_1} \cdots \sum _{n_{K -1}=0}^{n_{K -2}} {n \atopwithdelims ()n_1} {n_1 \atopwithdelims ()n_2} \cdots {n_{K -2} \atopwithdelims ()n_{K -1}} \\&\times \mu _{\mathcal {Y}_{d1}}(n -n_1) \mu _{\mathcal {Y}_{d2}}(n_1 -n_2) \cdots \mu _{\mathcal {Y}_{dK}}(n_{K -1}). \end{aligned}$$

(51)

From Eqs. 47,50 and 51, we compute the first and second moments of ${\mathcal {Z}_d}$ as

$$\begin{aligned} \mu _{\mathcal {Z}_d}(1) = \sum _{k=1}^{K} \sum _{l=1}^{L_k} \mu _{\mathcal {X}_{dkl}}(1) , \end{aligned}$$

(52)

$$\begin{aligned} \nonumber \mu _{\mathcal {Z}_d}(2) =&\sum _{k=1}^{K} \Big [ \sum _{l=1}^{L_k} \mu _{\mathcal {X}_{dkl}}(2) +2 \sum _{l=1}^{L_k} \mu _{\mathcal {X}_{dkl}}(1) \sum _{l'=l+1}^{L_k} \mu _{\mathcal {X}_{dkl'}}(1) \Big ] \\&+ 2 \sum _{k=1}^{K} \Big [ \sum _{l=1}^{L_k} \mu _{\mathcal {X}_{dkl}}(1) \Big ] \sum _{k'=k+1}^{K} \Big [ \sum _{l=1}^{L_{k'}} \mu _{\mathcal {X}_{dk'l}}(1) \Big ] . \end{aligned}$$

(53)

Then, the nth moment of ${\mathcal {T}_{d}} = h_{sd} + {\mathcal {Z}_d}$ is calculated as

$$\begin{aligned} \nonumber \mu _{\mathcal {T}_d}(n)&\triangleq \mathbb {E}\{(h_{sd} + \mathcal {Z}_d)^n\} = \mathbb {E}\left\{ \sum _{i=0}^{n} {n \atopwithdelims ()i} h_{sd}^i \mathcal {Z}_d^{n-i} \right\} \\&= \sum _{i=0}^{n} {n \atopwithdelims ()i} \mu _{h_{sd}}(i) \mu _{\mathcal {Z}_d}(n-i). \end{aligned}$$

(54)

Consequently, the first and second moments of ${\mathcal {T}_d}$ calculated from Eq. 54 are

$$\begin{aligned} \mu _{\mathcal {T}_d}(1) = \mu _{h_{sd}}(1) + \mu _{\mathcal {Z}_d}(1), \end{aligned}$$

(55)

$$\begin{aligned} \mu _{\mathcal {T}_d}(2) = \mu _{h_{sd}}(2) + \mu _{\mathcal {Z}_d}(2) + 2 \mu _{h_{sd}}(1) \mu _{\mathcal {Z}_d}(1). \end{aligned}$$

(56)

Similarly, the first and second moments of ${\mathcal {T}_e}$ are expressed as

$$\begin{aligned} \mu _{\mathcal {T}_e}(1) = \mu _{h_{se}}(1) + \mu _{\mathcal {Z}_e}(1), \end{aligned}$$

(57)

$$\begin{aligned} \mu _{\mathcal {T}_e}(2) = \mu _{h_{se}}(2) + \mu _{\mathcal {Z}_e}(2) + 2 \mu _{h_{se}}(1) \mu _{\mathcal {Z}_e}(1). \end{aligned}$$

(58)

Therefore, the CDFs of ${\mathcal {T}_d}$ and ${\mathcal {T}_e}$ are, respectively, given by

$$\begin{aligned} \nonumber F_{\mathcal {T}_d}(x) =&\frac{1}{\Gamma \Big ( \frac{[\mu _{\mathcal {T}_d}(1)]^2 }{\mu _{\mathcal {T}_d}(2) - [\mu _{\mathcal {T}_d}(1)]^2} \Big )} \\ \nonumber&\times \gamma \Bigg ( \frac{[\mu _{\mathcal {T}_d}(1)]^2 }{\mu _{\mathcal {T}_d}(2) - [\mu _{\mathcal {T}_d}(1)]^2}, \frac{\mu _{\mathcal {T}_d}(1) x}{\mu _{\mathcal {T}_d}(2) - [\mu _{\mathcal {T}_d}(1)]^2} \Bigg ) \\ \nonumber =&\frac{1}{\Gamma (\Xi _d)} \gamma ( \Xi _d, \Psi _d x ) \\ =&1-\frac{1}{\Gamma (\Xi _d)} \Gamma ( \Xi _d, \Psi _d x ) , \end{aligned}$$

(59)

$$\begin{aligned} F_{\mathcal {T}_e}(x) = 1- \frac{1}{\Gamma (\Xi _e)} \Gamma ( \Xi _e, \Psi _e x ) , \end{aligned}$$

(60)

where

$$\begin{aligned} \Xi _d =\frac{[\mu _{\mathcal {T}_d}(1)]^2 }{\mu _{\mathcal {T}_d}(2) - [\mu _{\mathcal {T}_d}(1)]^2}, \end{aligned}$$

(61)

$$\begin{aligned} \Psi _d =\frac{\mu _{\mathcal {T}_d}(1) }{\mu _{\mathcal {T}_d}(2) - [\mu _{\mathcal {T}_d}(1)]^2}, \end{aligned}$$

(62)

$$\begin{aligned} \Xi _e = \frac{[\mu _{\mathcal {T}_e}(1)]^2 }{\mu _{\mathcal {T}_e}(2) - [\mu _{\mathcal {T}_e}(1)]^2}, \end{aligned}$$

(63)

$$\begin{aligned} \Psi _e =\frac{\mu _{\mathcal {T}_e}(1) }{\mu _{\mathcal {T}_e}(2) - [\mu _{\mathcal {T}_e}(1)]^2}. \end{aligned}$$

(64)

Next, we can calculate the CDFs of $\beta _d$ and $\beta _e^{c2}$ from Eqs.  38 and 39 as

$$\begin{aligned} F_{\beta _d}(x) = \textrm{Pr} \left\{ \mathcal {T}_{d}^2< \frac{x}{\rho _d} \right\} = \textrm{Pr} \left\{ \mathcal {T}_{d} < \sqrt{\frac{x}{\rho _d}} \right\} = F_{\mathcal {T}_{d}}\Big (\sqrt{\frac{x}{\rho _d}}\Big ), \end{aligned}$$

(65)

$$\begin{aligned} F_{\beta _e^{c2}}(x) = \textrm{Pr} \left\{ \mathcal {T}_{e}^2< \frac{x}{\rho _e} \right\} = \textrm{Pr} \left\{ \mathcal {T}_{e} < \sqrt{\frac{x}{\rho _e}} \right\} = F_{\mathcal {T}_{e}}\Big (\sqrt{\frac{x}{\rho _e}}\Big ). \end{aligned}$$

(66)

Applying Eqs. 59 and 60,65, and 66 become Eqs. 26 and 28, respectively. The proof is thus complete.