Non Orthogonal Multiple Access Using Reconfigurable Intelligent Surfaces

Abstract

In this paper, we propose the use of Reconfigurable Intelligent Surfaces (RIS) for Non Orthogonal Multiple Access (NOMA). RIS is decomposed in N sets of reflectors serving N users. The ith RIS contains $N_i$ reflectors dedicated to user i. When RIS is used, all reflections reach the ith user with the same phase. RIS has not been yet used in NOMA systems where the transmitter sends a combination of symbols dedicated to N user. The ith user $U_i$ has to detect the symbols of remaining $N-i$ users. It performs Successive Interference Cancelation and detects first the symbol of weakest user. Then, it removes the signal of weakest user and detect that of second weakest user. The process is continued until $U_i$ detects its own symbol. We suggest to optimize power allocation coefficients to all users as well as the number of reflector dedicates to each user in order to maximize the total throughput using the alternating maximization algorithm. More power and a larger number of reflectors should be allocated to weak users. An example of RIS implementation is provided in Dai et al. (IEEE Access, 8:45913–45923, 2020).

1 Introduction

Reconfigurable Intelligent Surfaces (RIS) can be used in future 6G wireless communications to ensure higher data rates. When RIS is used as reflector, the received signal at destination can be viewed as the output of a Maximum Ratio Combiner (MRC) [2] resulting in larger Signal to Noise Ratio (SNR) than conventional wireless systems without RIS. RIS can be used as a reflector or a transmitter [2]. When RIS is used as reflector, the phase of ith reflecting meta-surface of RIS is optimized to compensate the phases of product of channel gains between Base Station (BS)/RIS and RIS/destination [3]. All N reflections over RIS reach the destination with the same phase resulting in a high SNR [4,5,6]. RIS requires a perfect knowledge of channel phases of BS-RIS and RIS-Destination links [2]. When RIS is used as transmitter, RIS is illuminated with an antenna of Base Station (BS). The phase of kth reflector of RIS depends on the phase of channel gain between RIS and destination as well as the phase of transmitted Phase Shift Keying (PSK) symbol. RIS don’t consume much power and are nearly passive [2]. A hardware architecture of RIS has been proposed in [7].

Throughput maximization for wireless communications using RIS has been proposed in [8]. Non Orthogonal Multiple Access (NOMA) using RIS has been discussed in [9] where $N_1$ and $N_2$ reflectors are dedicated to weak and strong users. In [9], the authors derived the bit and symbol error probabilities of NOMA using RIS. The source sends a combination of symbols dedicated to near and far users. The transmitted signal is reflected by RIS and forwarded to far and near users [10]. RIS can be used for millimeter wave communications [10, 11]. RIS allows to increase data rates in hybrid Radio Frequency (RF) Free Space Optical (FSO) systems when one hop uses RF communications and the second one is based on FSO [12]. In practical systems, RIS can be deployed with finite phase shifts leading to non perfect RIS [13]. The asymptotic outage probability of wireless communications using RIS was derived in [14, 15]. RIS using unnamed aerial vehicle has been suggested in [16]. RIS with artificial intelligence algorithms have been discussed in [1, 17]. RIS with phase shifts optimized using machine learning was studied in [18]. RIS with transmission probability optimization was considered in [19]. RIS with imperfect channel estimation was studied in [20, 21].

The contributions of the paper are:

• We analyze and optimize the throughput at the packet level while previous studies deal with symbol or bit error probability [9].

• We maximize the total throughput of NOMA using RIS. We optimize power allocation coefficients to near and far users as well as the number of reflectors per user. Power allocation and number of reflectors optimization has not been yet proposed in the literature.

The paper contains six sections. Section 2 presents the system model. Section 3 analyze and optimize the throughput. Section 4 extends the results to mutliple users NOMA. Section 5 provides theoretical and simulation results. Finally, Sect. 6 concludes the paper.

2 System Model

Fig. 1

NOMA using Reconfigurable Intelligent Surfaces (RIS)

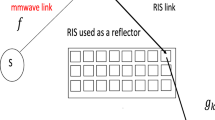
When RIS is used, the phase shift of a given reflector dedicated to kth user is optimized so that all reflections have the same phase. Different sets of reflectors are dedicated to the different users. The receiver output at kth user is similar to that of a Maximum Ratio Combiner (MRC) [2]. The system model is shown in Fig. 1. It contains a Base Station (BS) and two NOMA users $U_1$ and $U_2$. $U_1$ is the near user while $U_2$ is the far user. We denote by $\sqrt{\alpha }h_k$ the channel coefficient between BS and the kth reflecting meta-surface of RIS, $\alpha =\frac{1}{d^{\beta }}$ is the average power of channel coefficient, d is the distance between BS and RIS, $\beta$ is the path loss exponent, $h_k$ is a zero mean complex Gaussian random variable (r.v.) with variance one, i.e. $h_k\sim CN(0,1)$. We denote by $h_k=a_k e^{-j\theta _k}$ where $a_k=|h_k|$ the absolute value of $h_k$ and $\theta _k$ is the phase of $h_k$. For Rayleigh channels, $a_k$ is Rayleigh distributed with mean $E(a_k)=\frac{\sqrt{\pi }}{2}$ and second order moment $E(a_k^2)=1$ where E(X) is the expectation of X. Let $\sqrt{\lambda _i}g_k$ be the channel coefficient between kth reflecting meta-surface of RIS and user $U_i$ where $\lambda _i=\frac{1}{d_i^{\beta }}$ is the average power of channel coefficient and $d_i$ is the distance between RIS and $U_i$. $g_k=b_k e^{-j\psi _k}\sim CN(0,1)$, $b_k=|g_k|$ the absolute value of $g_k$ and $\psi _k$ is the phase of $g_k$. For Rayleigh channels, $b_k$ is Rayleigh distributed with mean $E(b_k)=\frac{\sqrt{\pi }}{2}$ and second order moment $E(b_k^2)=1$. We assume a Rayleigh block fading channel where channel coefficients $h_k$ and $g_k$ remain constant during packet duration.

It is assumed that RIS adjusts the phases $\Phi _k$ induced by the kth reflecting meta-surface such that

$$\begin{aligned} \Phi _k=\theta _k+\psi _k. \end{aligned}$$

(1)

RIS assume a perfect knowledge of channel coefficient phases $\theta _k$ and $\psi _k$. As shown in Fig. 1, $N_1$ reflectors are dedicated to user $U_1$ while $N_2$ reflectors are dedicated to user $U_2$. Let $N=N_1+N_2$ be the total number of available reflectors. Let $I_1$ and $I_2$ be the set of reflector indexes dedicated to $U_1$ and $U_2$. The number of reflectors in set $I_i$ is $|I_i|=N_i$ where |x| is the cardinality of set x. The received signals at $U_1$ and $U_2$ are equal to

$$\begin{aligned} y_1= & {} s\sqrt{2E_s\alpha \lambda _1}\sum _{k\in I_1}h_kg_ke^{j\Phi _k}+n_1, \end{aligned}$$

(2)

$$\begin{aligned} y_2= & {} s\sqrt{2E_s\alpha \lambda _2}\sum _{k\in I_2}h_kg_ke^{j\Phi _k}+n_2, \end{aligned}$$

(3)

where $E_s$ is the transmitted energy per symbol of S, s is the transmitted symbol and $n_i$ is a Gaussian noise with variance $N_0$.

The BS sends a combination of two symbols $s_1$ and $s_2$ dedicated to near and far users :

$$\begin{aligned} s=\sqrt{p_1}s_1+\sqrt{p_2}s_2, \end{aligned}$$

(4)

where $p_i$ is the power allocation coefficient to user $U_i$ such that $p_1+p_2=1$. More power is allocated to far user $U_2$: $0<p_1<p_2<1$.

Using (1–3) and the expression of $h_k=a_k e^{-j\theta _k}$ and $g_k=b_k e^{-j\psi _k}$, the received signals at $U_1$ and $U_2$ are given by [2]

$$\begin{aligned} y_1=s\sqrt{2E_s\alpha \lambda _1}\sum _{k\in I_1}a_k e^{-j\theta _k}b_k e^{-j\psi _k}e^{j\Phi _k}+n_1, \\ y_2=s\sqrt{2E_s\alpha \lambda _2}\sum _{k\in I_2}a_k e^{-j\theta _k}b_k e^{-j\psi _k}e^{j\Phi _k}e^{j\Phi _k}+n_2, \end{aligned}$$

Since $\Phi _k=\psi _k+\Phi _k$ (1), we obtain

$$\begin{aligned} y_1= & {} s\sqrt{2E_s\alpha \lambda _1} \sum _{k\in I_1}a_kb_k+n_1, \end{aligned}$$

(5)

$$\begin{aligned} y_2= & {} s\sqrt{2E_s\alpha \lambda _2} \sum _{k\in I_2}a_kb_k+n_2, \end{aligned}$$

(6)

Therefore, we can write

$$\begin{aligned} y_1= & {} \sqrt{X_1}s+n_1, \end{aligned}$$

(7)

$$\begin{aligned} y_2= & {} \sqrt{X_2}s+n_2, \end{aligned}$$

(8)

where

$$\begin{aligned} X_1= & {} 2E_s\alpha \lambda _1A_1^2, \end{aligned}$$

(9)

$$\begin{aligned} X_2= & {} 2E_s\alpha \lambda _2A_2^2, \end{aligned}$$

(10)

$$\begin{aligned} A_1= & {} \sum _{k\in I_1}a_kb_k, \end{aligned}$$

(11)

and

$$\begin{aligned} A_2=\sum _{k\in I_2}a_kb_k \end{aligned}$$

(12)

Using (4-6), we obtain

$$\begin{aligned} y_1= & {} \sqrt{X_1}[\sqrt{p_1}s_1+\sqrt{p_2}s_2]+n_1, \end{aligned}$$

(13)

$$\begin{aligned} y_2= & {} \sqrt{X_2}[\sqrt{p_1}s_1+\sqrt{p_2}s_2]+n_2. \end{aligned}$$

(14)

3 Throughput Analysis and Optimization

In (14), the second term is the useful signal containing the symbol to be detected. The first term is the interference while last term is the noise. Therefore, far user $U_2$ detects its symbol $s_2$ with Signal to Interference plus Noise Ratio (SINR) [9]:

$$\begin{aligned} \Gamma _2=\frac{p_2X_2}{p_1X_2+N_0}. \end{aligned}$$

(15)

During the first detection at near user, the first term of (13) is the interference from its own signal. The second term is the useful term of far user to be detected and the last one is noise. Therefore, near user $U_1$ detects first $s_2$ since $p_2>p_1$ with SINR [9]

$$\begin{aligned} \Gamma _{1\rightarrow 2}=\frac{p_2X_1}{p_1X_1+N_0}. \end{aligned}$$

(16)

Then, near user removes the signal of $U_2$ (the second term in (13)) and detects its own symbol $s_1$ with SINR [9]

$$\begin{aligned} \Gamma _{1\rightarrow 1}=\frac{p_1X_1}{N_0}. \end{aligned}$$

(17)

The outage probability of user $U_2$ is equal to the probability that the SINR $U_2$ is lower than SINR threshold $\Gamma _{th}$:

$$\begin{aligned} P^{outage,2}(\Gamma _{th})=P(\Gamma _2 \le \Gamma _{th})=P(\frac{p_2X_2}{p_1X_2+N_0}\le \Gamma _{th})=P_{X_2}(\frac{N_0\Gamma _{th}}{p_2-p_1\Gamma _{th}}) \end{aligned}$$

(18)

where $P_{X_2}(x)$ is the Cumulative Distribution Function of $X_2$ equal to [22]

$$\begin{aligned} P_{X_2}(x)=P(X_2\le x)=P(-\sqrt{\frac{x}{2E_s\alpha \lambda _2}} \le A_2 \le \sqrt{\frac{x}{2E_s\alpha \lambda _2}}) \end{aligned}$$

(19)

Using the Central Limit Theorem (CLT), we can approximate $A_i$ by a Gaussian r.v. with mean $m_{A_i}=\frac{N_i\pi }{4}$ and variance $\sigma _{A_i}^2=N_i(1-\frac{\pi ^2}{16})$ [2].

Therefore, we deduce

$$\begin{aligned} P_{X_2}(x)\simeq 0.5erfc\left( \frac{-\sqrt{\frac{N_0x}{2E_s\alpha \lambda _2}}-m_{A_2}}{\sqrt{2}\sigma _{A_2}}\right) -0.5erfc\left( \frac{\sqrt{\frac{N_0x}{2E_s\alpha \lambda _2}}-m_{A_2}}{\sqrt{2}\sigma _{A_2}}\right) \end{aligned}$$

(20)

There is no outage at $U_1$ when both SINRs $\Gamma _{1\rightarrow 1}$ and $\Gamma _{1\rightarrow 2}$ are greater than $\Gamma _{th}$

$$\begin{aligned} P^{outage,1}(\Gamma _{th})=1-P(\Gamma _{1\rightarrow 1}>\Gamma _{th})P(\Gamma _{1\rightarrow 2}>\Gamma _{th}) \end{aligned}$$

$$\begin{aligned} =P_{X_1}(max[\frac{N_0\Gamma _{th}}{p_2-p_1\Gamma _{th}},\frac{N_0\Gamma _{th}}{p_1}]), \end{aligned}$$

(21)

where $P_{X_1}(x)$ is the CDF of $X_1$ expressed similarly to that of $X_2$ [22]:

$$\begin{aligned} P_{X_1}(x)\simeq 0.5erfc\left( \frac{-\sqrt{\frac{N_0x}{2E_s\alpha \lambda _1}}-m_{A_1}}{\sqrt{2}\sigma _{A_1}}\right) -0.5erfc\left( \frac{\sqrt{\frac{N_0x}{2E_s\alpha \lambda _1}}-m_{A_1}}{\sqrt{2}\sigma _{A_1}}\right) \end{aligned}$$

(22)

An upper bound of Packet Error Probability (PEP) at $U_1$ and $U_2$ are deduced from the outage probability [23]

$$\begin{aligned}&PEP_1(p_1,p_2,N_1)<P^{outage,1}(T_0), \end{aligned}$$

(23)

$$\begin{aligned}&PEP_2(p_1,p_2,N_1)<P^{outage,2}(T_0), \end{aligned}$$

(24)

where $T_0$ is a waterfall threshold defined as

$$\begin{aligned} T_0=\int _0^{+\infty }PEP(x)dx, \end{aligned}$$

(25)

where

$$\begin{aligned} PEP(x)=1-[1-SEP(x)]^L, \end{aligned}$$

(26)

L is the packet length in symbols and SEP(x) is the Symbol Error Probability (SEP) for M-Quadrature Amplitude Modulation (QAM) [22]

$$\begin{aligned} SEP(x)=2(1-\frac{1}{\sqrt{M}})erfc(\sqrt{\frac{3x}{M-1}}) \end{aligned}$$

(27)

The throughput at users $U_1$ and $U_2$ are computed as

$$\begin{aligned}&Thr_1(p_1,p_2,N_1)=log_2(M)[1-PEP_1(p_1,p_2,N_1)], \end{aligned}$$

(28)

$$\begin{aligned}&Thr_2(p_1,p_2,N_2)=log_2(M)[1-PEP_2(p_1,p_2,N_2)]. \end{aligned}$$

(29)

The total throughput is the sum of throughput at $U_1$ and $U_2$:

$$\begin{aligned} Thr(p_1,p_2,N_1,N_2)=Thr_1(p_1,p_2,N_1)+Thr_2(p_1,p_2,N_2). \end{aligned}$$

(30)

In NOMA systems using RIS, more power $p_2>p_1$ and more reflectors $N_2>N_1$ should be allocated to far user $U_2$. Power allocation coefficients $p_1$, $p_2$ as well as number of reflectors $N_1$ and $N_2$ are optimized using the alternating maximization algorithm [24–26] to maximize the total throughput

$$\begin{aligned} Thr^{max}=\underset{0<p_1<p_2<1, N_1\ge 1,N_2=N-N_1}{Max[Thr(p_1,p_2,N_1,N_2)]}. \end{aligned}$$

(31)

under constraint $p_1+p_2=1$ and $N=N_1+N_2$.

4 NOMA with Multiple Users Using RIS

Fig. 2

NOMA with K users using Reconfigurable Intelligent Surfaces (RIS)

The system model of NOMA with K users is shown in Fig. 2. $N_i$ reflectors of RIS are dedicated to user $U_i$. The total number of reflectors is $N=\sum _{i=1}N_i$. $I_i$ is the index of reflectors dedicated to user $U_i$. The number of reflector dedicated to $U_i$ is $|I_i|=N_i$. When there are K users, the BS sends a linear combination of K symbols $s_i$ $i=1,\ldots ,K$ to K NOMA users:

$$\begin{aligned} s=\sum _{i=1}^K\sqrt{p_i}s_i, \end{aligned}$$

(32)

where $\sum _{i=1}^Kp_i=1$ and $0<p_1<p_2<\cdots<p_K<1$ are power allocation coefficients to users $U_1$, $U_2$,...$U_K$.

The received signal at user $U_i$ is expressed as

$$\begin{aligned} y_i=s\sqrt{KE_s\alpha \lambda _1} \sum _{k\in I_i}a_kb_k+n_i, \end{aligned}$$

(33)

We deduce

$$\begin{aligned} y_i=s\sqrt{X_i}+n_i=\sum _{j=1}^K\sqrt{p_j}s_j\sqrt{X_i}+n_i, \end{aligned}$$

(34)

where

$$\begin{aligned} X_i= & {} KE_s\alpha \lambda _2A_i^2, \end{aligned}$$

(35)

$$\begin{aligned} A_i= & {} \sum _{k\in I_i}a_kb_k, \end{aligned}$$

(36)

In (34), the Kth term is the useful signal to be detected by $U_i$ during first detection and all other terms are interference. $U_i$ detects first $s_K$ since it is transmitted with a larger power $p_K>p_{K-1}>\cdots >p_i$. The SINR at $U_i$ to detect $s_K$ is equal to [9]

$$\begin{aligned} \Gamma _{i\rightarrow K}=\frac{X_ip_K}{N_0+X_i\sum _{j=1}^{K-1}p_j} \end{aligned}$$

(37)

Then, $U_i$ removes the contribution of $s_K$ (The Kth term in (34)) and detects $s_{K-1}$ with SINR [9]

$$\begin{aligned} \Gamma _{i\rightarrow K-1}=\frac{X_ip_{K-1}}{N_0+X_i\sum _{j=1}^{K-2}p_j} \end{aligned}$$

(38)

Then, $U_i$ removes the contribution of $s_{K-1}$ (The (K-1)th term in (34)) and detects $s_{K-2}$. The process is repeated until $U_i$ detects its symbol $s_i$. All terms with indexes $K,K-1,\ldots ,i+1$ will be removed during SIC iterations When detecting $s_q$, all terms of (34) with indexes $K,K-1,\ldots ,q+1$ will be removed. The useful term is the qth term in (34) and the other indexes $q-1,q-2,\ldots ,1$ are interference from other users. The SINR at $U_i$ to detect $s_q$, $i\le q\le K$, is equal to [9]

$$\begin{aligned} \Gamma _{i\rightarrow q}=\frac{X_ip_{q}}{N_0+X_i\sum _{j=1}^{q-1}p_j}, i\le q\le K, \end{aligned}$$

(39)

There is no outage at $U_i$ if all SINRs $\Gamma _{i\rightarrow K}$, $\Gamma _{i\rightarrow K-1}$,..., $\Gamma _{i\rightarrow i}$ are larger than $\Gamma _{th}$. Therefore, the outage probability is equal to [9]

$$\begin{aligned} P^{outage,i}(\Gamma _{th})=1-P(\Gamma _{i\rightarrow K}>\Gamma _{th},\Gamma _{i\rightarrow K-1}>\Gamma _{th},\ldots ,\Gamma _{i\rightarrow i}>\Gamma _{th}) \end{aligned}$$

$$\begin{aligned} P_{X_i}\left(\underset{i\le q\le K}{max}(\frac{N_0\Gamma _{th}}{p_q-\Gamma _{th}\sum _{j=1}^{q-1}p_j})\right), \end{aligned}$$

(40)

where [22]

$$\begin{aligned} P_{X_i}(x)\simeq 0.5erfc\left( \frac{-\sqrt{\frac{N_0x}{KE_s\alpha \lambda _i}}-m_{A_i}}{\sqrt{2}\sigma _{A_i}}\right) -0.5erfc\left( \frac{\sqrt{\frac{N_0x}{KE_s\alpha \lambda _i}}-m_{A_i}}{\sqrt{2}\sigma _{A_i}}\right) \end{aligned}$$

(41)

An upper bound of PEP at user $U_i$ is deduced from the outage probability [23]

$$\begin{aligned} PEP_i(p_1,p_2,\ldots ,p_K,N_i)<P^{outage,i}(T_0), \end{aligned}$$

(42)

where $T_0$ is a waterfall threshold defined in (25).

The throughput at user $U_i$ are computed as

$$\begin{aligned} Thr_i(p_1,p_2,\ldots ,p_K,N_i)=log_2(M)[1-PEP_1(p_1,p_2,\ldots ,p_K,N_i)], \end{aligned}$$

(43)

The total throughput is the sum of throughput at all K users:

$$\begin{aligned} Thr(p_1,p_2,\ldots ,p_K,N_1,N_2,\ldots ,N_K)=\sum _{i=1}^KThr_i(p_1,p_2,\ldots ,p_K,N_i). \end{aligned}$$

(44)

In this paper, we propose to optimize power allocation coefficients $p_1$, $p_2$, ..., $p_K$ as well as number of reflectors $N_1$, $N_2$, ..., $N_K$ using the alternating maximization algorithm [24] to maximize the total throughput:

$$\begin{aligned} Thr^{max}=\underset{0<p_1<p_2<\cdots<p_K<1, N_i\ge 1}{Max[Thr(p_1,p_2,\ldots ,p_K,N_1,N_2,\ldots ,N_K)]}. \end{aligned}$$

(45)

under constraint $\sum _{i=1}^Kp_i=1$ and $N=\sum _{i=1}^KN_i$.

5 Theoretical and Simulation Results

We have plotted theoretical PEP and throughput of NOMA with and without RIS. The average power of channel coefficient between nodes X and Y as $\frac{1}{d^{\beta }}$ where $\beta =3$ is the path loss exponent and d is the distance between node X and Y. We have simulated packet containing 300 symbols and a packet is declared to be corrected only when all its symbols are correct. The Packet Error Rate (PER) measured during simulation is the percentage of erroneous packets. We did simulations until 200 packets are erroneously received. The distance between BS and RIS is $d=1$. The distance between RIS and users $U_1$, $U_2$ and $U_3$ are $d_1=1$, $d_2=1.1$, $d_3=1.3$. These are normalized distances $d_i=\frac{d_i^{effective}}{d_0}$ where $d_i^{effective}$ is the effective distance between RIS and $U_i$ in meters and $d_0$ is a reference distance.

Figures 3 and 4 show the PEP at far and near user for 16-QAM modulation and when there are $K=2$ users and $N_1=N_2=16,32,64,128$. Power allocation coefficients are $p_1=1-p_2=0.4$. As the number of reflectors is increases, as the PEP decreases. In fact, the signal at $U_i$ can be viewed as the output of a Maximum Ratio Combination (MRC) of $N_i$ signals [2]. We notice that the PEP of NOMA using RIS is lower than that of conventional NOMA without RIS.

Fig. 3

PEP at far user

Fig. 4

PEP at near user

Figures 5 and 6 show the average throughput at far and near users for 16-QAM modulation and when there are $K=2$ users and $N_1=N_2=16,32,64,128$. We observe that the throughput increases as the number of reflectors is increased : $N_1=N_2=16,32,64,128$. When NOMA is employed with RIS, the throughput at far and near users is better than conventional NOMA without RIS.

Fig. 5

Throughput at far user

Fig. 6

Throughput at near user

Figures 7 and 8 show the total throughput for 16QAM modulation and when there are $K=2$ users for 16QAM modulation. We observe that the throughput of NOMA using RIS is better than that of conventional NOMA. Besides, the throughput improved as the number of reflectors is increased $N_1=N_2=16,32,64,128$. In Fig. 7, power allocation coefficients are $p_1=1-p_2=0.4$ and the same number of reflectors were dedicated to near and far users : $N_1=N_2$. In Fig. 8, we have compared the total throughput when $p_1=1-p_2=0.4$ to Optimal Power Allocation (OPA). We also considered a total number of reflectors $N=N_1+N_2=32$. By optimizing both power allocation coefficients as well as the number of reflectors, we obtained a larger throughput than $N_1=N_2=16$ where the same number of reflectors was dedicated to far and near users with $p_1=1-p_2=0.4$. By optimizing power allocation coefficients and number of reflectors, we obtained up to 4 dB gain with respect to $N_1=N_2=16$ and $p_1=1-p_2=0.4$.

Fig. 7

Total throughput in the presence of two users

Fig. 8

Total throughput in the presence of two users with optimal number of reflectors and optimal power allocation

Figures 9 and 10 show the total throughput for 16QAM modulation and when there are $K=3$ users for 16QAM modulation. We observe that the throughput of NOMA using RIS is better than that of conventional NOMA. Besides, the throughput improved as the number of reflectors is increased $N_1=N_2=N_3=16,32,64$. In Fig. 7, power allocation coefficients are $p_1=0.2,p_2=0.3,p_3=0.5$ and the same number of reflectors were dedicated to the three users : $N_1=N_2=N_3$. In Fig. 8, we have compared the total throughput when $p_1=0.2,p_2=0.3,p_3=0.5$ to OPA. We also considered a total number of reflectors $N=N_1+N_2+N_3=48$. The number of reflectors of RIS is 48. An uniform allocation consists to use $N_1=N_2=N_3=16$ reflectors for each user. In this paper, we optimize the number of reflectors per user by allocating more reflectors to weak users in order to maximize the total throughput. By optimizing both power allocation coefficients as well as the number of reflectors, we obtained a larger throughput than $N_1=N_2=N_3=16$ where the same number of reflectors was dedicated to all three users with $p_1=0.2,p_2=0.3,p_3=0.5$. By optimizing power allocation coefficients and number of reflectors, we obtained up to 7 dB gain with respect to $N_1=N_2=N_3=16$ and $p_1=0.2,p_2=0.3,p_3=0.5$.

Fig. 9

Total throughput in the presence of three users

Fig. 10

Total throughput in the presence of three users with optimal number of reflectors and optimal power allocation

6 Conclusions

In this paper, we analyzed and optimized the throughput of Non Orthogonal Multiple Access (NOMA) using Reconfigurable Intelligent Surfaces (RIS). We optimized both power allocation coefficients as well as the number of reflectors per user to maximize the total throughput. We have shown that NOMA using RIS offers a higher throughput than conventional NOMA without RIS. By optimizing power allocation coefficients and number of reflector per user, we obtained a larger total throughput than fixed power allocation and the same number of reflectors per user.