1 Introduction

In realistic scenarios, the performance measures in wireless communication systems are strongly affected by multipath fading and shadowing effects [1,2,3] as the received signals may be of stochastic nature or be superpositioned. The shadowing effect in wireless communication is characterized through various distributions viz., Lognormal, Gamma and Inverse Gaussian [1, 3] whereas the multipath behavior is described using various models viz., Rician, Nakagami-m and Weibull distribution [1, 4]. These combined effects of fading and shadowing can be captured using composite fading/shadowed fading models and is portrayed well in the literature [5,6,7].

In wireless radio systems, the Weibull distribution has been proven to be of great importance towards capturing the effects of both indoor and outdoor fading phenomena [8, 9] in contrast to the available multipath fading models. The priority of the Weibull model in evaluating the performance measures of various communication systems have been portrayed in [10, 11]. However, it is pertinent to capture both the effects of fading and shadowing. These effects are portrayed by different mixture models viz., Rayleigh-Lognormal, Rician-Lognormal, Nakagami-Lognormal [1] and the Weibull-Lognormal (WL) distribution [12, 13]. The widely used lognormal distribution to characterize the shadowing effects however, fails to efficiently capture the tail fluctuations. In addition, the explicit solutions of these lognormal based mixture models are not analytically tractable and usually prone to errors under extreme fluctuations.

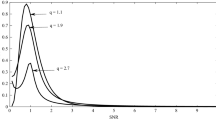
In this paper, we follow Beck-Cohen’s superstatistics framework [14], the superposition of two statistics that can characterize the composite shadowed fading channels. First statistics involves the Weibull distribution [1, 4] to describe fast fading channels. The second statistics i.e., the q-lognormal distribution is obtained by employing maximum Tsallis entropy framework [15,16,17,18] to characterize a wide range of slow fading channels for different values of the non-extensive parameter q. The dynamic range of non-extensive parameter ‘q’ characterizes the phenomenon of a variety of complex systems viz., physics, economics, bioinformatics, geography and communication systems [19]. The values of q mimics many existing well known models i.e., for \(q\rightarrow 1\), the q-lognormal model converges to the lognormal model and for \(q\rightarrow 1.5\), the q-Gaussian model captures the Student-t distribution with three degrees of freedom [15]. One important behavior (i.e., bimodality) of q-lognormal distribution is also observed for the value of \(q\ge 2.7\). The specific values of q (i.e., for \(q=1.4\) and \(q=1.5\)), the proposed model provides an excellent agreement with the generated synthetic data i.e., there is a proper balance between underfitting and overfitting.

The Tsallis entropy is maximized under the normalization constraint, first and second moment constraints of signal to noise ratio (SNR). The Lagrangian is constructed for the same and is further optimized using the Euler–Lagrange equation to obtain the proposed q-lognormal distribution. The unconditional proposed superstatistics Weibull/q-Lognormal model is obtained by conditioning the Weibull distribution over the q-lognormal distribution and is of fundamental significance due to the presence of non extensive parameter q over the mean ergodic behavior of communication channels. The parameter ‘q’ in the proposed model can capture the entire range of tail fluctuations for \(1<q<3\). Hence, it is worthwhile to characterize the wide range of wireless communication channels and correlated fading phenomena using the superstatistics Weibull/q-Lognormal model.

The closed form solution for the probability density function (PDF) corresponding to SNR is evaluated by using Holtzman technique [20]. The performance measures viz., amount of fading and outage probability are approximated and the analytical solution for these measures has been obtained. In conjunction to this, an important performance metric i.e., the average channel capacity is approximated using Meijer’s G-function in terms of Fox’s H representation [21]. Furthermore, the obtained measures are also validated through extensive Monte-Carlo simulation schemes, and since the error complexity of Monte-Carlo simulation is \(O\left( {{N^{ - 1/2}}} \right)\), to get an accurate and tight result, we average over \(O(10^8)\) simulation paths.

The rest of the paper proceeds as follows. In Sect. 2, we derive the q-Lognormal PDF using maximum Tsallis entropy framework to characterize slow fading channels. The significance of the q-Lognormal distribution is portrayed in Sect. 3. In Sect. 4, the analytical model for the generalized superstatistics Weibull/q-Lognormal is computed. The next Sect. 5, outlines the various performance metrics of the composite fading channel viz., the amount of fading, average channel capacity, outage probability (\(P_{out}\)) and the results are validated using Monte–Carlo simulation scheme. Finally, we conclude this paper in Sect. 6.

2 The q-Lognormal Distribution

In this section, the analytical expression for the non-extensive q-Lognormal pdf is derived. Let Z denote the random variable of the received average SNR (z) i.e.,

$$\begin{aligned} Z \equiv \ln (z ), \quad z>0. \end{aligned}$$
(1)

The Tsallis entropy [15, 16] in terms of the parameter q is given by

$$\begin{aligned} S_q(z) = \frac{{1 - \int _{ - \infty }^{ + \infty } {{{[g_q(z)]}^q}dz} }}{{q - 1}}. \end{aligned}$$
(2)

The constant of normalization is given as

$$\begin{aligned} \int \limits _{ - \infty }^{ + \infty } {g_q(z)dz = 1}. \end{aligned}$$
(3)

The first and second moment of SNR are defined as

$$\begin{aligned} \int \limits _{ - \infty }^{ + \infty } {{g_{es}}(z)zdz = } \mu , \end{aligned}$$
(4)

and

$$\begin{aligned} \int \limits _{ - \infty }^{ + \infty } g_{es}(z){(z - \mu )^2}dz = {\sigma ^2}, \end{aligned}$$
(5)

where

$$\begin{aligned} {g_{es}}(z) = {[g_q(z)]^q}/\int {{{[g_q(z)]}^q}dz} \end{aligned}$$
(6)

is defined as the escort probability distribution [22, 23]. The uses of the escort probability distribution over the general probability distribution is described in [22]. The Lagrangian is constructed and is given by

$$\begin{aligned} L({g_q},z) = \left( \begin{array}{l} \frac{{1 - \int _{ - \infty }^{ + \infty } {{{[{g_q}(z)]}^q}dz} }}{{q - 1}} + {\lambda _1}\left( {1 - \int \limits _{ - \infty }^\infty {{g_q}(z)dz} } \right) \\ + {\lambda _2}\left( {\mu - \int \limits _{ - \infty }^\infty {z{g_{es}}(z)dz} } \right) + {\lambda _3}\left( {{\sigma ^2} - \int \limits _{ - \infty }^\infty {{{\left( {z - \mu } \right) }^2}{g_{es}}(z)dz} } \right) \end{array} \right) , \end{aligned}$$
(7)

where \({\lambda _1}\), \({\lambda _2}\) and \({\lambda _3}\) are Lagrangian multipliers. Using Euler–Lagrange equation:

$$\begin{aligned} \frac{{\partial L}}{{\partial {g_q}}} - \frac{d}{{dz}}\left( {\frac{{\partial L}}{{\partial {g_q^{\prime }}}}} \right) = 0. \end{aligned}$$
(8)

Equation 8 together with Eqs. 1 to 7, provides the maximum entropy q-Lognormal PDF for slow fading channels as:

$$\begin{aligned} {g_q}(z) = \frac{1}{{Cz }}{\left( {1 - \frac{{1 - q}}{{\left( {3 - q} \right) {\sigma ^2}}}{{\left( {\ln (z ) - \mu } \right) }^2}} \right) ^{\frac{1}{{1 - q}}}}, \quad z>0, \end{aligned}$$
(9)

where C is the normalization constant and is given by

$$\begin{aligned} C = \sigma \sqrt{\frac{{\left( {3 - q} \right) \pi }}{{(q - 1)}}} \frac{{\varGamma \left( {\frac{{3 - q}}{{2q - 2}}} \right) }}{{\varGamma \left( {\frac{1}{{q - 1}}} \right) }},\quad 1<q<3. \end{aligned}$$
(10)

When \(q\rightarrow 1\), Eq. 9 exhibits the Lognormal model given as

$$\begin{aligned} {g}(z ) = \frac{1}{{\sqrt{2\pi }\sigma z }}{e^{ - \frac{{{{\left( {\ln (z ) - \mu } \right) }^2}}}{{2{\sigma ^2}}}}},\quad z > 0. \end{aligned}$$
(11)

3 Significance of the q-Lognormal Distribution

This section describes the impact of the proposed q-Lognormal distribution in characterizing the effects of the shadowing effects over the well known lognormal distribution. It is well known that all the slow fading channels are characterized by lognormal distribution [1, 12, 24]. However, this assumption fails to capture the outliers in the fading signal. So, in this context, we provide a new entropy based approach to capture the tail fluctuations observed in slow fading channels. The q-Lognormal model converges to lognormal distribution as \(q\rightarrow\)1. Fig. 1, illustrates the PDFs correspoding to the Lognormal and q-Lognormal distribution when q → 1. In Fig. 2, we provide the q-Lognormal PDF for different values of non-extensive parameter q, when q = 1.1, q = 1.9, and q = 2.7. But, for \(q=1\) the model cannot characterize the tail fluctuations as shown in Fig. 3. However, the parameter ‘q’ in the proposed model can capture the entire range of tail fluctuations for \(1<q<3\). The synthetic signal generated using MATLAB is well characterized by the proposed q-Lognormal model for \(q=1.4\) and \(q=1.5\) as shown in Figs. 4 and 5.

Fig. 1
figure 1

Lognormal and q-Lognormal PDF for \(q\rightarrow 1\), \(\mu =0\), \(\sigma =1\)

Full size image
Fig. 2
figure 2

q-Lognormal PDF for different values of non-extensive parameter q

Full size image
Fig. 3
figure 3

Plot of q-Lognormal distribution for \(q\rightarrow 1\) with generated signal data

Full size image
Fig. 4
figure 4

Plot of q-Lognormal distribution for \(q=1.4\) with generated signal data

Full size image
Fig. 5
figure 5

Plot of q-Lognormal distribution for \(q=1.5\) with generated signal data

Full size image

4 Analytical Model

In wireless communication systems, it is observed that the Weibull distribution provides an envelope for multipath fading channels whereas the generalized q-Lognormal model can characterize the shadowing effects. In this context, we derive an analytical expression for the generalized superstatistics Weibull/q-Lognormal model to capture the simultaneous effects of both fading and shadowing phenomena.

The conditional Weibull distribution is defined as [1, 25],

$$\begin{aligned} f(\left. \gamma \right| z) = \frac{{\beta A}}{{{z^{\beta /2}}}}{\gamma ^{\beta - 1}}\exp \left[ { - A{{\left( {\frac{{{\gamma ^2}}}{z}} \right) }^{\beta /2}}} \right] ,\quad \gamma > 0, \end{aligned}$$
(12)

where z is the received average signal to noise ratio (SNR), \(\gamma\) is the received SNR, \(A = {\left[ {\varGamma \left( {1 + \frac{2}{\beta }} \right) } \right] ^{\beta /2}}\) and \(\varGamma (.)\) represents the Gamma function. The channel condition improves as the multipath/fading parameter \(\beta \rightarrow \infty .\)

4.1 Superstatistics Weibull/q-Lognormal Model

The superstatistics distribution is obtained by superimposing the Weibull distribution and the q-Lognormal distribution. The Weibull distribution is defined in Eq. 12 whereas the PDF of a q-Lognormal distribution is defined in Eq. 9.

The composite distribution can be defined as [5]:

$$\begin{aligned} f(\gamma ) = \int \limits _0^\infty {f(\gamma |z )g(z)dz }. \end{aligned}$$
(13)

Using Eq. 13 along with Eqs. 12 and 9, we have:

$$\begin{aligned} \begin{array}{l} {f}(\gamma ) = \int \limits _0^\infty {\beta A{z^{ - \beta /2}}{\gamma ^{\beta - 1}}\exp \left[ { - A{{\left( {\frac{{{\gamma ^2}}}{z}} \right) }^{\beta /2}}} \right] }\times \frac{1}{{Cz}}{\left[ {1 - \frac{{(1 - q){{(\ln (z) - \mu )}^2}}}{{(3 - q){\sigma ^2}}}} \right] ^{\frac{1}{{1 - q}}}}dz. \end{array} \end{aligned}$$
(14)

For \(q\rightarrow 1\) Eq. 14 reduces to:

$$\begin{aligned} \begin{array}{l} f(\gamma ) = \frac{{\beta A{\gamma ^{\beta - 1}}}}{C}\int \limits _0^\infty {{z^{ - \beta /2}}\exp \left[ { - A{{\left( {\frac{{{\gamma ^2}}}{z}} \right) }^{\beta /2}}} \right] } \times \exp \left[ {\frac{{ - {{(\ln z - \mu )}^2}}}{{2{\sigma ^2}}}} \right] \frac{1}{z}dz. \end{array} \end{aligned}$$
(15)

Now substituting \(\ln (z) = t\), we have:

$$\begin{aligned} \begin{array}{l} f(\gamma ) = \beta A{\gamma ^{\beta - 1}}\int \limits _{ - \infty }^\infty {\exp {{(t)}^{ - \beta /2}}\exp \left[ { - A{{\left( {\frac{{{\gamma ^2}}}{{\exp (t)}}} \right) }^{\beta /2}}} \right] } \times \frac{1}{{\sqrt{2\pi } \sigma }}\exp \left[ {\frac{{ - {{(t - \mu )}^2}}}{{2{\sigma ^2}}}} \right] dt. \end{array} \end{aligned}$$
(16)

Applying Holtzman Three Point Distribution [20], we obtain the generalized superstatistics Weibull/q-Lognormal PDF as follows:

$$\begin{aligned} {f}(\gamma ) \simeq \frac{2}{3}\delta \left( {\gamma ;\,\mu } \right) + \frac{1}{6}\delta \left( {\gamma ;\,\mu + \sqrt{3} \sigma } \right) + \frac{1}{6}\delta \left( {\gamma ;\,\mu - \sqrt{3} \sigma } \right), \end{aligned}$$
(17)

where

$$\begin{aligned} \delta (\gamma ;\,t) = \beta A{\gamma ^{\beta - 1}}\left[ {\exp {{(t)}^{ - \beta /2}} \times \exp \left( { - A{{\left( {\frac{{{\gamma ^2}}}{{\exp (t)}}} \right) }^{\beta /2}}} \right) } \right] . \end{aligned}$$
(18)
Fig. 6
figure 6

Analytical and simulation results of Weibull/q-Lognormal PDF for \(\mu =0\), \(\sigma =1.155\), \(\beta =3\)

Full size image
Fig. 7
figure 7

Plot of Weibull/q-Lognormal distribution for \(q=1\) with generated synthetic signal

Full size image
Fig. 8
figure 8

Plot of Weibull/q-Lognormal distribution for \(q=1.8\) with generated synthetic signal

Full size image

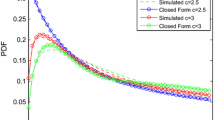
Figure 6 shows the plot of the analytical and simulation results of the Weibull/q-lognormal model. In Fig. 7 it can be seen that the well known Weibull/lognormal model [12, 13, 26] does not provide a good fit with the generated synthetic signal. The synthetic signal has been generated using MATLAB. However, in Fig. 8 it is seen that the Weibull/q-Lognormal model provides an excellent agreement with the generated synthetic signal for the value of the non extensive parameter \(q=1.8\). The plots in Figs. 7 and 8 are obtained by using Monte-carlo simulation technique on Eq. 14.

5 Performance Analysis

In this section, the various performance metrics viz., amount of fading, outage probability and average channel capacity for the superstatistics shadowed fading model are evaluated and the analytical expressions for each measures have been presented.

5.1 Amount of Fading

An important and condemnatory performance measure in fading environment is the Amount of Fading that specifies the severity of fading. It is mathematically expressed as [26]:

$$\begin{aligned} AF = \frac{{E[{\gamma ^2}]}}{{{{\{ E[\gamma ]\} }^2}}} - 1. \end{aligned}$$
(19)

The closed form expression obtained in Eq. 17 is the sum of three Weibull distributions terms and the kth moment of \(\gamma\) (SNR per symbol) is obtained as:

$$\begin{aligned} \begin{array}{l} E[{\gamma ^k}] = \int \limits _0^\infty {{\gamma ^k} \times \beta A{\gamma ^{\beta - 1}}\left( {\exp {{(t)}^{ - \beta /2}}} \right) } \times \exp \left( { - A{{\left( {\frac{{ {\gamma ^2}}}{{\exp {{(t)}^\beta }}}} \right) }^{\beta /2}}} \right) d\gamma . \end{array} \end{aligned}$$
(20)

Substituting \(\bar{\gamma } = \exp (t)\), we obtain:

$$\begin{aligned} E[{\gamma ^k}] = {\left[ {\frac{{\exp {{(t)}^{\beta /2}}}}{A}} \right] ^{\frac{k}{\beta }}} \times \varGamma \left( {1 + \frac{k}{\beta }} \right) . \end{aligned}$$
(21)

Using Eq. 21 equipped with Eq. 17, we have:

$$\begin{aligned} E[{\gamma ^k}] = \varGamma \left( {1 + \frac{k}{\beta }} \right) \left\{ \begin{array}{l} (2/3){\left[ {\frac{{\exp (\mu )}}{{\varGamma (1 + 2/\beta )}}} \right] ^{k/2}} + (1/6){\left[ {\frac{{\exp (\mu + \sqrt{3} \sigma )}}{{\varGamma (1 + 2/\beta )}}} \right] ^{k/2}}\\ + (1/6){\left[ {\frac{{\exp (\mu - \sqrt{3} \sigma )}}{{\varGamma (1 + 2/\beta )}}} \right] ^{k/2}} \end{array} \right\} . \end{aligned}$$
(22)

Finally, the analytical expression for Amount of Fading is given as:

$$\begin{aligned} \begin{array}{l} AF = \frac{{\varGamma \left( {1 + \frac{2}{\beta }} \right) }}{{{\varGamma ^2}\left( {1 + \frac{1}{\beta }} \right) }}\left[ {\frac{{\left\{ {2/3 + (1/6)\exp (\sqrt{3} \sigma ) + (1/6)\exp ( - \sqrt{3} \sigma )} \right\} }}{{{{\left\{ {2/3 + (1/6)\exp \left( {\frac{{\sqrt{3} }}{2}\sigma } \right) + (1/6)\exp \left( { - \frac{{\sqrt{3} }}{2}\sigma } \right) } \right\} }^2}}}} \right] - 1 \end{array}. \end{aligned}$$
(23)

We present the analytical and simulation results for amount of fading in Fig. 9, for σ = 6 dB, σ = 4 dB, and σ = 2 dB.

Fig. 9
figure 9

Analytical and simulation results of amount of fading for different values of \(\sigma\)

Full size image

5.2 Average Channel Capacity

The channel capacity is defined as the maximum transmission capacity that a channel is capable of achieving with a small probability of error [27]. It is significant to study the channel capacity in fading environments and hence we exploit the Meijer’s G function to derive the analytical expression of the average channel capacity.

The ergodic channel capacity is defined as [28]:

$$\begin{aligned} \frac{C}{B} = \frac{1}{{\ln (2)}}\int \limits _0^\infty {\ln (1 + \gamma ){f}(\gamma )d\gamma }, \end{aligned}$$
(24)

where B represents bandwidth of the fading channel. Using Eqs. 17, 24 we have:

$$\begin{aligned} \begin{array}{l} \frac{C}{B} = \frac{1}{{\ln (2)}}\int \limits _0^\infty \ln (1 + \gamma )\beta A{\gamma ^{\beta - 1}} \times \left( {\exp {{(t)}^{ - \beta /2}}\exp \left( { - A{{\left( {\frac{{{\gamma ^2}}}{{\exp (t)}}} \right) }^{\beta /2}}} \right) } \right) d\gamma . \end{array} \end{aligned}$$
(25)

Using Meijer’s G-functions [29] and modifying the above equations according to \(\ln (1 + x) = \mathop G\nolimits _{22}^{12} \left[ {x\left| {_{1,0}^{1,1}} \right. } \right]\) and \(\exp ( - x) = \mathop G\nolimits _{01}^{10} \left[ {x\left| {_0^.} \right. } \right]\) we obtain:

$$\begin{aligned} \begin{array}{l} \frac{C}{B} = \frac{{\beta A\exp {{(t)}^{ - \beta /2}}}}{{\ln (2)}}\int \limits _0^\infty {{\gamma ^{\beta - 1}}} \mathop G\nolimits _{01}^{10} \left[ {A{{\left( {\frac{{{\gamma ^2}}}{{\exp (t)}}} \right) }^{\beta /2}}\left| {_0^.} \right. } \right] \mathop G\nolimits _{22}^{12} \left[ {\gamma \left| {_{1,0}^{1,1}} \right. } \right] d\gamma . \end{array} \end{aligned}$$
(26)

From Eq. 26 and using the substitutions given in [21] we obtain:

$$\begin{aligned} \begin{array}{l} \frac{C}{B} = \frac{{\beta A\exp {{(t)}^{ - \beta /2}}}}{{\ln (2)}}H_{23}^{31}\left[ {\frac{A}{{\exp {{(t)}^{\beta /2}}}}\left| {_{(0,1),( - \beta , - \beta ),( - \beta ,\beta )}^{( - \beta ,\beta ),(1 - \beta ,\beta )}} \right. } \right] . \end{array} \end{aligned}$$
(27)

Thus, from Eqs. 17 and 27, the average channel capacity can be expressed in closed form as:

$$\begin{aligned} \frac{C}{B} = \sum \limits _{k = 1}^3 {\frac{\beta }{{\ln (2)}}{p_k}^{\beta /2}{q_k}} H_{23}^{31}\left[ {{p_k}^{\beta /2}\left| {_{(0,1),( - \beta , - \beta ),( - \beta ,\beta )}^{( - \beta ,\beta ),(1 - \beta ,\beta )}} \right. } \right] , \end{aligned}$$
(28)

where \({q_1}=2/3, {q_2}={q_3}=1/6,\) and \({p_k}=\frac{{\varGamma (1 + 2/\beta )}}{{\exp ({t_k})}}\) with \({t_1}=\mu , {t_2}=\mu + \sqrt{3} \sigma\) and \({t_3}=\mu - \sqrt{3} \sigma\). In Fig. 10, the analytical and simulation results corresponding to the average channel capacity for different values of β i.e., β = 2, β = 2.5, and β = 3.

Fig. 10
figure 10

Analytical and simulation results of average channel capacity for different values of \(\beta\)

Full size image

5.3 Outage Probability

For wireless communications systems functioning over fading channels the outage probability stands as an important performance measurement. It is denoted by \(P_{out}\) and is stated as the probability of the output SNR \(\gamma\), not exceeding a specified threshold value \(\gamma _{th}\) .

It is expressed mathematically as [1]:

$$\begin{aligned} {P_{out}} = \int \limits _0^{{\gamma _{th}}} {{f}(\gamma )d\gamma }. \end{aligned}$$
(29)

From Eqs. 17, 18, 29 and using [30] Eqs. (3.381.1) and (8.352.1) the analytical expression for outage probability is obtained as follows:

$$\begin{aligned} {P_{out}} = \left\{ \begin{array}{l} \frac{2}{3}\left( {1 - \exp \left[ { - \frac{{A{\gamma _{th}}^\beta }}{{\exp {{(\mu )}^{\beta /2}}}}} \right] } \right) \\ + \frac{1}{6}\left( {1 - \exp \left[ { - \frac{{A{\gamma _{th}}^\beta }}{{\exp {{(\mu + \sqrt{3} \sigma )}^{\beta /2}}}}} \right] } \right) \\ + \frac{1}{6}\left( {1 - \exp \left[ { - \frac{{A{\gamma _{th}}^\beta }}{{\exp {{(\mu - \sqrt{3} \sigma )}^{\beta /2}}}}} \right] } \right) \end{array} \right\} . \end{aligned}$$
(30)

Through Fig. 11, we provide the analytical and simulation results of the outage probability (Pout) versus threshold SNR for different values of β, viz., β = 1, β = 3, and β = 5.

Fig. 11
figure 11

Analytical and simulation results of \(P_{out}\) versus threshold SNR for different values of \(\beta\)

Full size image

6 Conclusion and Future Work

In this paper, various performance measures viz., SNR, amount of fading, outage probability and average channel capacity over the superstatistics Weibull/q-Lognormal model were expressed in closed form. As \(q \rightarrow 1\), this generalized superstatistics model provided an excellent agreement with the results of [26]. The model characterized the fast fading as well as shadowing effects of various wireless communication channels for different values of the non extensive parameter q. It has been observed that the Weibull/q-Lognormal model provided a better agreement to the generated signal for \(q=1.8\) in comparison to the well known Weibull/Lognormal model. The analytical expressions of the aforementioned performance metrics were obtained using Holtzman technique and Meijer’s G function equipped with Fox’s (H) function. Furthermore, the results were validated using extensive Monte-carlo simulation techniques.

Since, the proposed Weibull/q-Lognormal model is not analytically tractable, we follow rigorous simulation technique to validate our results. Thus, it will be an interesting and challenging task to obtain the closed form expression for the same and derive the performance measures which will be the future objective of this work.