Cooperative Relaying Protocol for Improving Physical Layer Security in Wireless Decode-and-Forward Relaying Networks

Abstract

In this paper, we consider cooperative relaying protocols for enhancing wireless physical layer security. For time-division multiple-access based cooperative protocols, we analyze achievable secrecy rates with total and individual relay power constraints and design relay beamforming weights to improve the secrecy rate, assuming that multiple cooperative relays operate in decode-and-forward mode. Numerical results are presented to compare the secrecy rates of the cooperative protocols in various secure communication environments.

1 Introduction

In modern wireless systems such as mobile cellular networks, wireless local area networks, sensor networks, and smart grid, there has been growing demand for transmission of private information such as banking information, online transactions, and private medical information. However, the broadcast nature of wireless channels is known to make it difficult to send secure information to the intended recipient without being eavesdropped by unauthorized receivers or jammed by malicious transmitters in wireless networks. Recently, physical layer security schemes have attracted growing attention to enable secure communication over wireless channel without using any encryption techniques, which rely on the upper-layer operations [1].

Exploiting the physical characteristics of wireless channels, physical layer security investigates the amount of information securely transmitted to the desired user in an information-theoretic point of view. An achievable secrecy rate is defined as a rate at which the source can transmit secure information to its intended destination, while the eavesdropper extracts nothing from the transmitted information. The maximum achievable secrecy rate is called the secrecy capacity [1]. In [2–4], it is proved that positive secrecy rate can be achieved without the need of sharing a secret key when the source–eavesdropper channel is a degraded version of the main source–destination channel.

In order to achieve positive secrecy rates even when the source–destination channel condition is worse than the source–eavesdropper channel condition, cooperative relaying schemes have been widely studied, where multiple relay nodes cooperatively operate to increase the secrecy rate [5–9]. In [5], a secure communication with the help of multiple cooperating relays is considered in the presence of one or more eavesdroppers. A set of trusted relays is assumed to perform one of three different operation modes: amplify-and-forward (AF), decode-and-forward (DF), and cooperative jamming (CJ). For AF and DF modes, the relays receive the signal from the source in the first time slot. In the second time slot, the relays forward the weighted versions of their received signals for AF mode and their re-encoded signals for DF mode. For CJ mode, the relays transmit weighted jamming signals to confuse the eavesdroppers while the source transmits the signal to the destination.

Table 1 Cooperative protocols

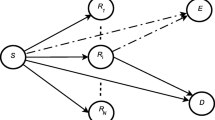
Let us consider a secure communication of one source–destination pair with the help of multiple DF relays in the presence of one eavesdropper, where each node is equipped with a single antenna. Assuming that a set of trusted relays performs the DF mode, we consider two different cooperative protocols in Table 1 [10]. In Protocol I, the source communicates with the relays and the destination, while the eavesdropper also receives the signal from the source, over the first time slot. In the second time slot, only the relays communicate with the destination and the eavesdropper also hears the relays. In Protocol II, the relays, eavesdropper, and the destination receive the signal from the source over the first time slot, whereas both the destination and eavesdropper receive the signals from both the source and the relays over the second time slot. The difference between two cooperative protocols is found in the second time slot, where Protocol I allows only the relays to send information signals, while both the source and relays are allowed to send information signals in Protocol II.

In the conventional works, the secrecy rate has been investigated only for Protocol I. In [5] and [8], the secrecy rate of Protocol I is studied under an overall power constraint, where the sum of the transmit powers of the source and all relays is restricted. In this work, we consider total relay power constraint (TRPC) and individual relay power constraint (IRPC). The TRPC indicates that the sum of the transmit powers of all the relays is restricted, whereas the peak transmit power at each relay is restricted in the IRPC. For the TRPC and IRPC, the secrecy rates of Protocol I can be obtained through a simple modification of the result in [6]. In this paper, let us focus on the achievable secrecy rate of Protocol II and design relay beamforming weights tailored for Protocol II to enhance the secrecy rate under TRPC and IRPC. Numerical results are presented to investigate the different characteristics of Protocol I and II.

2 System Model

Let us consider one source–destination pair, $M$ trusted DF relays, and one passive eavesdropper [5]. Each node is equipped with a single antenna. All channels are assumed to undergo flat fading, which is practically realizable using an orthogonal frequency-division multiplexing technique, even in frequency selective channels. Let $h_{SD}^{*}$ denote the complex channel gain between the source and the destination, $h_{SE}^{*}$ denote the complex channel gain between the source and the eavesdropper, ${\mathbf {h}}_{SR}^{\dagger }$ denote the $M \times 1$ channel vector between the source and $M$ relays, ${\mathbf {h}}_{RD}^{\dagger }$ denote the $1 \times M$ channel vector between $M$ relays and the destination, and ${\mathbf {h}}_{RE}^{\dagger }$ denote the $1 \times M$ channel vector between $M$ relays and the eavesdropper. $(.)^{*}$ and $(.)^{\dagger }$ denote the complex conjugate and the conjugated transpose, respectively. The noise at each node is assumed to be complex additive white Gaussian with zero-mean and variance $\sigma ^2$.

For Protocol II, the received signals at the destination, the eavesdropper, and $M$ relays in the first time slot are given as

$$\begin{aligned} y_{D,1}& = \sqrt{P_S}h_{SD}^{*}x_1+n_{D,1}, \\ y_{E,1}& = \sqrt{P_S}h_{SE}^{*}x_1+n_{E,1}, \\ {\mathbf {y}}_{R,1}& = \sqrt{P_S}{\mathbf {h}}_{SR}^{\dagger }x_1 +{\mathbf {n}}_{R,1}. \end{aligned}$$

(1)

where $x_1$ is the data symbol with unit power transmitted in the first time slot and $P_S$ is the transmit power of the source. In the second time slot, each relay transmits its own weighted version of $x_1$ assuming that $x_1$ is correctly decoded by all relays, whereas the source simultaneously transmits the data symbol $x_2$. Let ${\mathbf {w}}=[w_1, w_2,\ldots , w_M]^{T}$ be a $M \times 1$ beamforming weight vector to stack all weights of the relays. Then, the received signals at the destination and the eavesdropper are expressed as

$$\begin{aligned} y_{D,2} &= {\mathbf {h}}_{RD}^{\dagger }{\mathbf {w}}x_1+\sqrt{P_S}h_{SD}^{*}x_2+n_{D,2}, \\ y_{E,2} &= {\mathbf {h}}_{RE}^{\dagger }{\mathbf {w}}x_1+\sqrt{P_S}h_{SE}^{*}x_2+n_{E,2}. \end{aligned}$$

(2)

In (1) and (2), $n_{D,i}$ and $n_{E,i}$ denote additive white Gaussian noise (AWGN) at the destination and the eavesdropper in the $i\text{th}$ time slot, respectively. ${\mathbf {n}}_{R,1}$ is a $M \times 1$ vector to stack the noises at $M$ relays.

3 Achievable Secrecy Rate

Let us first evaluate the rate at the destination, $R_D$. We express the received signals at the destination in (1) and (2) as the following matrix form:

$$ {\mathbf {y}}_{D}={\mathbf {H}}_{D}{\mathbf {x}}+{\mathbf {n}}_{D},$$

(3)

where ${\mathbf {x}}=[x_1, x_2]^{T},\, {\mathbf {y}}_{D}=[{y}_{D,1}, {y}_{D,2}]^{T},\, {\mathbf {n}}_{D}=[{n}_{D,1}, {n}_{D,2}]^{T}$, and

$$ {\mathbf {H}}_{D}=\left[ \begin{array}{ll} \sqrt{P_S}h_{SD}^{*} &0\\ {\mathbf {h}}_{RD}^{\dagger }{\mathbf {w}} &\sqrt{P_S}h_{SD}^{*} \end{array} \right] . $$

(4)

For the DF mode, let us define $R^{relay},\,R_{D}^{total},\, R_{D}^{(1)}$ and $R_{D}^{(2)}$ as in [10], which are given as

$${R}^{relay}= \frac{1}{2}\log _2 \left( 1+P_S\alpha _{SR} \right) , $$

(5)

$${R}_{D}^{total}= \frac{1}{2} \log _2 \det \left( {\mathbf {I}}_2 + \frac{1}{\sigma ^2} {\mathbf {H}}_{D}{\mathbf {H}}_{D}^{\dagger } \right) , $$

(6)

$$R_{D}^{(1)}= \frac{1}{2}\log _2 \left( 1+\frac{||{\mathbf {h}}_{D}||^2}{\sigma ^2} \right) , $$

(7)

$$ R_{D}^{(2)}= \frac{1}{2}\log _2 \left( 1+P_S\alpha _{SD} \right) , $$

(8)

where ${\mathbf {I}}_k$ is a $k \times k$ identity matrix, ${\mathbf {h}}_{D}$ denotes the first column of ${\mathbf {H}}_{D}, \alpha _{SR}=\min _m \frac{ |h_{SR,m}|^2}{\sigma ^2}, h_{SR,m}$ is the $m\text{th}$ entry of ${\mathbf {h}}_{SR}$, and $\alpha _{SD}=\frac{|h_{SD}|^{2}}{\sigma ^2}$. In (5)–(8), the factor of 1/2 indicates that the information is transmitted over two time slots, which have the same duration. Note that $R_{D}^{(1)}$ and $R_{D}^{(2)}$ indicate the maximum achievable rates for $x_1$ and $x_2$, respectively. ${R}^{relay}$ is the rate at which all the relays can correctly decode $x_1$ from the source, and ${R}_{D}^{total}$ denotes the maximum sum rate of $x_1$ and $x_2$ over the two time slots. In particular, substituting (4) into (6), we obtain

$${R}_{D}^{total}= \frac{1}{2} \log _2 \left( \bar{\beta }_{D} + {\mathbf {w}}^{\dagger }{\mathbf {R}}_{RD} {\mathbf {w}} \right) , $$

(9)

where $\bar{\beta }_{D}=(1+P_S \alpha _{SD})^2$ and ${\mathbf {R}}_{RD}=\frac{{\mathbf {h}}_{RD}{\mathbf {h}}_{RD} ^{\dagger }}{\sigma ^2}$.

From the analysis given in [10], it is found that the achievable rate can be given as

$$ {R}_{D} = {\left\{ \begin{array}{ll} {R}_{D}^{total}, &R^{relay} \ge {R}_{D}^{total}-R_{D}^{(2)} \\ R^{relay}+R_{D}^{(2)}, &R^{relay} < {R}_{D}^{total}-R_{D}^{(2)}. \end{array}\right. }$$

(10)

In (10), let us first consider the case where the maximum sum rate of $x_1$ and $x_2$ is achieved (i.e., $R_D={R}_{D}^{total}$). Since $R_{D}^{(2)}$ is the maximum achievable rate for $x_2$, the achievable rate for $x_1$ becomes ${R}_{D}^{total}-R_{D}^{(2)}$. In order to guarantee that all the relays correctly decode $x_1$, we require the constraint $R^{relay} \ge {R}_{D}^{total}-R_{D}^{(2)}$. In case that $R^{relay} < {R}_{D}^{total}-R_{D}^{(2)}$, the rate for $x_1$ should be limited to $R^{relay}$ because all the relays should correctly decode $x_1$, and the achievable sum rate for $x_1$ and $x_2$ becomes ${R}_{D}=R^{relay}+R_{D}^{(2)}$ as shown in (10). Substituting (5), (8), and (9) into (10), we rewrite ${R}_{D}$ in (10) as follows:

$$\begin{aligned} {R}_{D} = {\left\{ \begin{array}{ll} \frac{1}{2}\log _2 \left( \bar{\beta }_{D} + {\mathbf {w}}^{\dagger }{\mathbf {R}}_{RD} {\mathbf {w}} \right) , &{\mathbf{w}}^{\dagger }{\mathbf {R}}_{RD} {\mathbf {w}} \le \rho _{D}\\ \frac{1}{2}\log _2 \left( 1+P_S\alpha _{SR} \right) \left( 1+P_S\alpha _{SD} \right) , &{\mathbf{w}}^{\dagger }{\mathbf {R}}_{RD} {\mathbf {w}} > \rho _{D}, \end{array}\right. } \end{aligned}$$

(11)

where $\rho _{D}=P_S(\alpha _{SR}-\alpha _{SD})(1+P_S\alpha _{SD})$.

Now, let us consider the rate at the eavesdropper, $R_E$. As in (3), the received signals at the eavesdropper in (1) and (2) can be also expressed as the matrix form ${\mathbf {y}}_{E}={\mathbf {H}}_{E}{\mathbf {x}}+{\mathbf {n}}_{E}$, where ${\mathbf {y}}_{E}=[{y}_{E,1}, {y}_{E,2}]^{T}$, ${\mathbf {n}}_{E}=[{n}_{E,1}, {n}_{E,2}]^{T}$, and

$$\begin{aligned} {\mathbf {H}}_{E}=\left[ \begin{array}{ll} \sqrt{P_S}h_{SE}^{*} &0\\ {\mathbf {h}}_{RE}^{\dagger }{\mathbf {w}} &\sqrt{P_S}h_{SE}^{*} \end{array} \right] . \end{aligned}$$

(12)

In the same way described above, we can compute $R_E$ as

$$\begin{aligned} {R}_{E} = {\left\{ \begin{array}{ll} \frac{1}{2}\log _2 \left( \bar{\beta }_{E} + {\mathbf {w}}^{\dagger }{\mathbf {R}}_{RE} {\mathbf {w}} \right) , &{\mathbf {w}}^{\dagger }{\mathbf {R}}_{RE} {\mathbf {w}} \le \rho _{E}\\ \frac{1}{2}\log _2 \left( 1+P_S\alpha _{SR} \right) \left( 1+P_S\alpha _{SE} \right) , &{\mathbf {w}}^{\dagger }{\mathbf {R}}_{RE} {\mathbf {w}} > \rho _{E}, \end{array}\right. } \end{aligned}$$

(13)

where $\bar{\beta }_{E}=(1+P_S \alpha _{SE})^2, {\mathbf {R}}_{RE}=\frac{{\mathbf {h}}_{RE}{\mathbf {h}}_{RE}^{\dagger }}{\sigma ^2}, \rho _{E}=P_S(\alpha _{SR}-\alpha _{SE})(1+P_S\alpha _{SE})$, and $\alpha _{SE}=\frac{|h_{SE}|^{2}}{\sigma ^2}$. Since the achievable secrecy rate is defined as $R_s=\max \{ 0, R_D-R_E \}$, we derive the achievable secrecy rate for Protocol II using (11) and (13) shown as

$$\begin{aligned} {R}_{s} = {\left\{ \begin{array}{ll} \max \left\{ 0, \frac{1}{2}\log _2 \frac{ \bar{\beta }_{D} + {\mathbf {w}}^{\dagger }{\mathbf {R}}_{RD} {\mathbf {w}}}{\bar{\beta }_{E} + {\mathbf {w}}^{\dagger }{\mathbf {R}}_{RE} {\mathbf {w}}} \right\} , \\ \quad \text{Case 1:}\, {\mathbf {w}}^{\dagger }{\mathbf {R}}_{RD} {\mathbf {w}} \le \rho _{D}, {\mathbf {w}}^{\dagger }{\mathbf {R}}_{RE} {\mathbf {w}} \le \rho _{E} \\ \max \left\{ 0, \frac{1}{2}\log _2 \frac{ \bar{\beta }_{D} + {\mathbf {w}}^{\dagger }{\mathbf {R}}_{RD} {\mathbf {w}}}{(1+P_S\alpha _{SR})(1+P_S\alpha _{SE})} \right\} , \\ \quad \text{Case 2:}\, {\mathbf {w}}^{\dagger }{\mathbf {R}}_{RD} {\mathbf {w}} \le \rho _{D}, {\mathbf {w}}^{\dagger }{\mathbf {R}}_{RE} {\mathbf {w}} > \rho _{E} \\ \max \left\{ 0, \frac{1}{2}\log _2 \frac{(1+P_S\alpha _{SR})(1+P_S\alpha _{SD})}{\bar{\beta }_{E} + {\mathbf {w}}^{\dagger }{\mathbf {R}}_{RE} {\mathbf {w}}} \right\} , \\ \quad \text{Case 3:}\, {\mathbf {w}}^{\dagger }{\mathbf {R}}_{RD} {\mathbf {w}} > \rho _{D}, {\mathbf {w}}^{\dagger }{\mathbf {R}}_{RE} {\mathbf {w}} \le \rho _{E} \\ \max \left\{ 0, \frac{1}{2}\log _2 \frac{1+P_S\alpha _{SD}}{1+P_S\alpha _{SE}} \right\} , \\ \quad \text{Case 4:}\, {\mathbf {w}}^{\dagger }{\mathbf {R}}_{RD} {\mathbf {w}} > \rho _{D}, {\mathbf {w}}^{\dagger }{\mathbf {R}}_{RE} {\mathbf {w}} > \rho _{E}. \end{array}\right. } \end{aligned}$$

(14)

Since both $R_D$ and $R_E$ are defined in two different cases, the achievable secrecy rate is categorized into four cases as in (14).

4 Design for Achievable Secrecy Rate Maximization

In this section, we design the relay weight vectors to maximize the achievable secrecy rate in (14) for TRPC and IRPC, assuming that the transmit power of the source $P_S$ is fixed. For each case in (14), we design the beamforming weight vector ${\mathbf {w}}$ and compute the corresponding secrecy rate $R^{(j)}_s$. Then, the final secrecy rate for Protocol II is computed as ${R}_{s}=\max _j R^{(j)}_s$.

4.1 Case 1

The optimization problem to maximize the achievable secrecy rate is given as

$$\begin{aligned} \max _{{\mathbf {w}}}& \quad \frac{ \bar{\beta }_{D} + {\mathbf {w}}^{\dagger }{\mathbf {R}}_{RD} {\mathbf {w}}}{\bar{\beta }_{E} + {\mathbf {w}}^{\dagger }{\mathbf {R}}_{RE} {\mathbf {w}}} \\ \text{s.t.}& \quad{\mathbf {w}}^{\dagger }{\mathbf {R}}_{RD} {\mathbf {w}} \le \rho _{D}, \quad {\mathbf {w}}^{\dagger }{\mathbf {R}}_{RE} {\mathbf {w}} \le \rho _{E} \\&\quad{\left\{ \begin{array}{ll} {\mathbf {w}}^{\dagger }{\mathbf {w}} \le M P_R,&\text{TRPC} \\ |w_m|^2 \le P_R \,\text{for all}\,m,&\text{IRPC}, \end{array}\right. } \end{aligned}$$

(15)

where $P_R$ denotes the peak transmit power of each relay for IRPC. For TRPC, the sum of the transmit powers of $M$ relays is restricted to $M P_R$.

4.1.1 TRPC

We solved the optimization problem for TRPC using an iterative approach. Let us define $\tilde{{\mathbf {w}}}=\frac{1}{\sqrt{P_t}}{\mathbf {w}}$, where $P_t$ denotes the sum of the transmit powers of all the relays, ${\mathbf {w}}^{\dagger } {\mathbf {w}}=P_t$, and $\tilde{{\mathbf {w}}}^{\dagger }\tilde{{\mathbf {w}}}=1$. Then, we can rewrite the optimization problem for TRPC in (15) as

$$\begin{aligned} \max _{\tilde{{\mathbf {w}}}}&\quad\frac{\tilde{{\mathbf {w}}}^{\dagger }\bar{{\mathbf {R}}}_{RD} \tilde{{\mathbf {w}}}}{\tilde{{\mathbf {w}}}^{\dagger }\bar{{\mathbf {R}}}_{RE} \tilde{{\mathbf {w}}}} \\ \text{s.t.}&\quad\tilde{{\mathbf {w}}}^{\dagger }{\mathbf {R}}_{RD} \tilde{{\mathbf {w}}} \le \frac{\rho _D}{P_t}, \quad \tilde{{\mathbf {w}}}^{\dagger }{\mathbf {R}}_{RE} \tilde{{\mathbf {w}}} \le \frac{\rho _E}{P_t}, \\&\quad P_t \le M P_R, \end{aligned}$$

(16)

where $\bar{{\mathbf {R}}}_{RD}=\bar{\beta }_D{\mathbf {I}}_{M}+{P_t}{\mathbf {R}}_{RD}$ and $\bar{{\mathbf {R}}}_{RE}=\bar{\beta }_E{\mathbf {I}}_{M}+{P_t}{\mathbf {R}}_{RE}$. As in [5], we use an iterative approach to solve (16). In (2), we first determine $\tilde{{\mathbf {w}}}$ to null out the signals at the eavesdropper shown as

$$ \tilde{{\mathbf {w}}}= \frac{({\mathbf {I}}_{M}-{\mathbf {P}}_{RE}){\mathbf {h}}_{RD}}{||({\mathbf {I}}_{M}-{\mathbf {P}}_{RE}){\mathbf {h}}_{RD}||}, $$

(17)

where ${\mathbf {P}}_{RE}={\mathbf {h}}_{RE}({\mathbf {h}}_{RE}^{\dagger }{\mathbf {h}}_{RE})^{-1}{\mathbf {h}}_{RE}^{\dagger }$ [5]. Using (17), we set the initial value of $P_t$ as

$$ P_t=\min \left\{ M P_R, \frac{\rho _D}{\tilde{{\mathbf {w}}}^{\dagger }{\mathbf {R}}_{RD} \tilde{{\mathbf {w}}} }, \frac{\rho _E}{\tilde{{\mathbf {w}}}^{\dagger }{\mathbf {R}}_{RE} \tilde{{\mathbf {w}}} } \right\} . $$

(18)

Using (18), we compute the eigenvector corresponding to the maximal eigenvalue of $\bar{{\mathbf {R}}}_{RE}^{-1}\bar{{\mathbf {R}}}_{RD}$ and use it as the initial vector of $\tilde{{\mathbf {w}}}$. Then, we perform the following steps to solve the problem iteratively.

• Step (1) Given $\tilde{{\mathbf {w}}}$, compute $P_t$ as in (18) and the secrecy rate. If the computed $P_t$ provides better secrecy rate, update $P_t$.

• Step (2) Given $P_t$, compute $\tilde{{\mathbf {w}}}$ by using the solution of the generalized eigenvector problem. If the computed $\tilde{{\mathbf {w}}}$ provides better secrecy rate, update $\tilde{{\mathbf {w}}}$.

• Step (3) Repeat Steps (1) and (2) until the secrecy rate converges or the number of iterations reaches to the predetermined number.

4.1.2 IRPC

For IRPC, the optimization problem in (15) can be equivalently rewritten as [11]

$$\begin{aligned} \max _{{\mathbf {W}},t}&\quad t \\ \text{s.t.}&\quad \text{tr}\left( {\mathbf {W}}({\mathbf {R}}_{RD}-t{\mathbf {R}}_{RE}) \right) \ge t \bar{\beta }_E-\bar{\beta }_D \\& \quad\text{tr}\left( {\mathbf {W}}{\mathbf {R}}_{RD}\right) \le \rho _D, \quad \text{tr}\left( {\mathbf {W}}{\mathbf {R}}_{RE}\right) \le \rho _E, \\&\quad\text{rank}\, {\mathbf {W}}=1, \quad {\mathbf {W}} \succeq 0, \\&\quad {\mathbf {W}}_{mm} \le P_R \, \text{for all}\, m, \end{aligned}$$

(19)

where ${\mathbf {W}}={\mathbf {w}}{\mathbf {w}}^{\dagger },\, \text{tr}(.)$ denotes the trace operation, ${\mathbf {W}}_{mm}$ is the $m$th diagonal entry of ${\mathbf {W}},{\mathbf {W}} \succeq 0$ indicates that ${\mathbf {W}}$ should be a symmetric positive semidefinite matrix, and $\text{rank}\,{\mathbf {W}}=1$ implies that the rank of ${\mathbf {W}}$ should be one. Let us use the semidefinite relaxation to ignore the rank constraint in (19). Then, we employ a bisection technique associated with the following convex feasibility problem [12]:

$$\begin{aligned} \text{find}&\quad{\mathbf {W}} \\ \text{such that}&\quad \text{tr}\left( {\mathbf {W}}({\mathbf {R}}_{RD}-t{\mathbf {R}}_{RE}) \right) \ge t \bar{\beta }_E-\bar{\beta }_D \\&\quad\text{tr}\left( {\mathbf {W}}{\mathbf {R}}_{RD}\right) \le \rho _D,\quad \text{tr}\left( {\mathbf {W}}{\mathbf {R}}_{RE}\right) \le \rho _E,\quad {\mathbf {W}} \succeq 0, \\&\quad{\mathbf {W}}_{mm} \le P_R \,\text{for all}\, m. \end{aligned}$$

(20)

The convex feasibility problem in (20) can be solved by the well-established interior-point-based package such as SeDuMi [13] and Yalmip [14], which provides a feasibility certificate if the problem is feasible. The bisection technique requires initial upper and lower values. The initial lower value is set to be zero. Since it is reasonable to assume that the secrecy rate with TRPC is larger than that with IRPC, the initial upper value is set to be the secrecy rate with TRPC. After performing the bisection technique, we can obtain the optimal solution ${\mathbf {W}}^{\star }$. If ${\mathbf {W}}^{*}$ is of rank one, the principal eigenvector of ${\mathbf {W}}^{\star }$ is used as ${\mathbf {w}}$. If the rank of ${\mathbf {W}}^{\star }$ is higher than one, we employ a randomization technique [15]. In this work, let us eigendecompose ${\mathbf {W}}^{\star }$ as ${\mathbf {W}}^{\star }={\mathbf {U}}\mathbf {\Lambda }{\mathbf {U}}^{\dagger }$, where $\mathbf {\Lambda }$ is the diagonal matrix whose diagonal elements are the eigenvalues of ${\mathbf {W}}^{\star }$, and each column of ${\mathbf {U}}$ is the eigenvector corresponding to each eigenvalue. Then, we generate a set of candidate weight vectors, ${\mathbf {w}}_k={\mathbf {U}}\mathbf {\Lambda }^{1/2}{\mathbf {v}}_k$, where ${\mathbf {v}}_k$ is a vector of zero-mean, unit-variance complex circularly symmetric uncorrelated Gaussian random variables. After checking whether each candidate weight vector satisfies the given constraints or not, we choose the best one among these candidates.

4.2 Cases 2 and 3

In these cases, we can formulate the following optimization problems:

$$\begin{aligned} \max _{{\mathbf {w}}}&\quad{\mathbf {w}}^{\dagger }{\mathbf {R}}_{RD} {\mathbf {w}} \\ \text{s.t.}&\quad{\mathbf {w}}^{\dagger }{\mathbf {R}}_{RD} {\mathbf {w}} \le \rho _{D}, \quad {\mathbf {w}}^{\dagger }{\mathbf {R}}_{RE} {\mathbf {w}} > \rho _{E}, \\&\quad{\left\{ \begin{array}{ll} {\mathbf {w}}^{\dagger }{\mathbf {w}} \le M P_R, &\text{TRPC} \\ |w_m|^2 \le P_R \,\text{for all}\, m,&\text{IRPC} \end{array}\right. } \end{aligned}$$

(21)

for Case 2 and

$$\begin{aligned} \min _{{\mathbf {w}}}&\quad{\mathbf {w}}^{\dagger }{\mathbf {R}}_{RE} {\mathbf {w}} \\ \text{s.t.}&\quad{\mathbf {w}}^{\dagger }{\mathbf {R}}_{RD} {\mathbf {w}} > \rho _{D}, \quad {\mathbf {w}}^{\dagger }{\mathbf {R}}_{RE} {\mathbf {w}} \le \rho _{E}, \\&\quad{\left\{ \begin{array}{ll} {\mathbf {w}}^{\dagger }{\mathbf {w}} \le M P_R,&\text{TRPC} \\ |w_m|^2 \le P_R \, \text{for all}\, m, &\text{IRPC} \end{array}\right. } \end{aligned}$$

(22)

for Case 3. It is seen that the optimization problems in (21) and (22) are quadratically constrained quadratic problems (QCQP) [16]. Using semidefinite relaxation as in [16], we rewrite the above problems given as

$$\begin{aligned} \max _{{\mathbf {W}}}&\quad\text{tr}\left( {\mathbf {W}}{\mathbf {R}}_{RD} \right) \\ \text{s.t.}&\quad\text{tr}\left( {\mathbf {W}}{\mathbf {R}}_{RD} \right) \le \rho _{D},\quad \text{tr}\left( {\mathbf {W}}{\mathbf {R}}_{RE} \right) > \rho _{E},\quad {\mathbf {W}} \succeq 0, \\&\quad{\left\{ \begin{array}{ll} \text{tr}\left( {\mathbf {W}} \right) \le M P_R,&\text{TRPC} \\ \text{tr}\left( {\mathbf {W}}{\mathbf {G}}_{m} \right) \le P_R \,\text{for all}\, m, &\text{IRPC}. \end{array}\right. } \end{aligned}$$

(23)

for Case 2 and

$$\begin{aligned} \min _{{\mathbf {W}}}&\quad\text{tr}\left( {\mathbf {W}}{\mathbf {R}}_{RE} \right) \\ \text{s.t.}&\quad\text{tr}\left( {\mathbf {W}}{\mathbf {R}}_{RD} \right) > \rho _{D}, \quad \text{tr}\left( {\mathbf {W}}{\mathbf {R}}_{RE} \right) \le \rho _{E}, \quad {\mathbf {W}} \succeq 0, \\&\quad{\left\{ \begin{array}{ll} \text{tr}\left( {\mathbf {W}} \right) \le M P_R, &\text{TRPC} \\ \text{tr}\left( {\mathbf {W}}{\mathbf {G}}_{m} \right) \le P_R \,\text{for all}\, m, &\text{IRPC}. \end{array}\right. } \end{aligned}$$

(24)

for Case 3, where ${\mathbf {G}}_{m}$ is a $M \times M$ matrix with all zero entries except for the $m\text{th}$ diagonal entry, which is equal to one. Note that the above problems can be also handled by SeDuMi and Yalmip. For each case, we can obtain the optimal solution when the problem is feasible. If the rank of the solution is higher than one, we employ the randomization technique.

4.3 Case 4

In this case, we have to solve the following feasibility problem:

$$\begin{aligned} \text{find}&\quad{\mathbf {w}} \\ \text{such that}&\quad{\mathbf {w}}^{\dagger }{\mathbf {R}}_{RD} {\mathbf {w}} > \rho _{D},\quad {\mathbf {w}}^{\dagger }{\mathbf {R}}_{RE} {\mathbf {w}} > \rho _{E}, \\&\quad{\left\{ \begin{array}{ll} {\mathbf {w}}^{\dagger }{\mathbf {w}} \le M P_R,&\text{TRPC} \\ |w_m|^2 \le P_R \, \text{for all}\, m,&\text{IRPC}. \end{array}\right. } \end{aligned}$$

(25)

Using semidefinite relaxation, we rewrite the above problem shown as

$$\begin{aligned} \text{find}&\quad{\mathbf {W}} \\ \text{such that}&\quad\text{tr}\left( {\mathbf {W}}{\mathbf {R}}_{RD} \right) > \rho _{D},\quad \text{tr}\left( {\mathbf {W}}{\mathbf {R}}_{RE} \right) > \rho _{E}, \quad {\mathbf {W}} \succeq 0, \\&\quad{\left\{ \begin{array}{ll} \text{tr}\left( {\mathbf {W}} \right) \le M P_R,&\text{TRPC} \\ \text{tr}\left( {\mathbf {W}}{\mathbf {G}}_{m} \right) \le P_R \,\text{for all}\, m, &\text{IRPC}. \end{array}\right. } \end{aligned}$$

(26)

If the problem in (26) is feasible, we can obtain the solution. If the rank of the solution is higher than one, we employ the randomization technique.

5 Numerical Results

In this section, we present numerical results to investigate the performance of the proposed design schemes. As in [8], a simple one-dimensional system configuration is considered, where the source, relays, destination, and eavesdropper are located in a line. It is assumed that the source–destination and source–eavesdropper distances, denoted as $d_{SD}$ and $d_{SE}$, respectively, are always larger than the source–relay distance $d_{SR}$. In the one-dimensional configuration, the relay–destination and relay–eavesdropper distances are simply given as $d_{RD}=d_{SD}-d_{SR}$ and $d_{RE}=d_{SE}-d_{SR}$, respectively. Furthermore, channels between any two nodes are assumed to follow a line-of-sight (LOS) channel model $d^{-\frac{c}{2}}e^{j\theta }$, where $d$ is the distance between the nodes, $\theta$ denotes a random phase distributed uniformly within $[0, 2\pi )$, and $c=3.5$ is the path loss exponent. We also assume that the distances between relays are much smaller than the distances between relays and source/destination/eavesdropper, such that the path losses between relays and the other nodes are taken to be the same. The average secrecy rate is evaluated for 1000 independent channel realizations. In the following simulation results, we set $M=10,\,P_S=20\,\text{dBm}$, and $\sigma ^2=-30\,\text{dBm}$.

Fig. 1

Comparison of secrecy rates as a function of $d_{SE}$ ($d_{SR}=5\,\text{m},\,d_{SD}=20\,\text{m}$, and $P_R=20\, \text{dBm}$)

Figure 1 presents the secrecy rates of Protocol I and II as a function of $d_{SE}$ when $d_{SR}=5\,\text{m},\,d_{SD}=20\,\text{m}$, and $P_R=20\,\text{dBm}$. As expected, the secrecy rate increases as the eavesdropper moves away from the source. It is favorable to secure communication that the eavesdropper is located farther from the source than the destination. It is observed that the secrecy rates of Protocol I saturate even though $d_{SE}$ increases. For TRPC, Protocol II with the proposed relay weights provides better secrecy rate than Protocol I when $d_{SE} \ge 35\,\text{m}$. For IRPC, Protocol II is more advantageous than Protocol I when $d_{SE} \ge 25\,\text{m}$. Keeping in mind that Protocol II allows the source to send information signal to the destination even in the second time slot, we can conclude that Protocol II is guaranteed to outperform Protocol I for both TRPC and IRPC when the source–destination channel is good and the channel conditions are favorable to secure communication.

Fig. 2

Comparison of secrecy rates as a function of $d_{SR}$ ($d_{SD}=20\,\text{m}, \,d_{SE}=40\,\text{m}$, and $P_R=20\, \text{dBm}$)

In Fig. 2, we compare the secrecy rates of Protocol I and II as a function of $d_{SR}$ when $d_{SD}=20\,\text{m},\,d_{SE}=40\, \text{m}$, and $P_R=20\,\text{dBm}$. The secrecy rates of Protocol I and II decrease, as the relays move away from the source (i.e., $d_{SR}$ increases). Note that the increase of $d_{SR}$ results in the decrease of the rate at which all the relays can correctly decode the signal from the source. It is remarkable that the secrecy rate of Protocol I decreases more steeply than that of Protocol II as $d_{SR}$ increases. For both TRPC and IRPC, Protocol II is found to provide better secrecy rates than Protocol I in all ranges of $d_{SR}$.

Fig. 3

Comparison of secrecy rates as a function of $d_{SD}$ ($d_{SR}=5\,\text{m},\,d_{SE}=40\,\text{m}$, and $P_R=20\, \text{dBm}$)

Figure 3 shows the secrecy rates of Protocol I and II as a function of $d_{SD}$ when $d_{SR}=5\,\text{m},\,d_{SE}=40\,\text{m}$, and $P_R=20\,\text{dBm}$. Protocol II is found to outperform Protocol I for both TRPC and IRPC when $d_{SR} \le 20\,\text{m}$. Furthermore, in the range of $d_{SD}$ less than 20 m, it is observed that the secrecy rates of Protocol I for both TRPC and IRPC are slightly improved with decreasing $d_{SD}$, whereas those of Protocol II are significantly improved with the decrease of $d_{SD}$. Since the smaller value of $d_{SD}$ makes the source–destination channel condition better, Fig. 3 also confirms that, when the source–destination channel is good, Protocol II is more beneficial than Protocol I in the viewpoint of the secrecy rate performance as discussed in Fig. 1.

Fig. 4

Comparison of secrecy rates as a function of $P_R$ ($d_{SR}=5\,\text{m},\,d_{SD}=20\,\text{m}$, and $d_{SE}=40\,\text{m}$)

In Fig. 4, we presents how the secrecy rates of Protocol I and II vary with $P_R$ when $d_{SR}=5\,\text{m},\,d_{SD}=20\,\text{m}$, and $d_{SE}=40$ m. For TRPC and IRPC, Protocol I provides slightly better secrecy rates than Protocol II when $P_R < 20\,\text{dBm}$ and $P_R < 17.5\,\text{dBm}$, respectively. However, the secrecy rates of Protocol I with both TRPC and IRPC saturate when $P_R > 17.5\,\text{dBm}$, whereas the secrecy rates of Protocol II increase almost linearly with $P_R$ until $P_R \le 22.5\,\text{dBm}$. Furthermore, it is found that Protocol II outperforms Protocol I for both TRPC and IRPC when $P_R > 20\,\text{dBm}$.

6 Conclusion

In this paper, cooperative relaying protocols have been investigated for enhancing wireless physical layer security. We derived the achievable secrecy rate and designed the relay weight vector to enhance the secrecy rate under TRPC and IRPC. The secrecy maximization problem has been solved by using a convex feasibility problem with semidefinite relaxation and a bisection technique. From numerical results, we have shown that the cooperative relaying protocol studied in this work provides better secrecy rate than the conventional protocol in favorable secure communication environments with good source–destination channel conditions. In these environments, our works can be utilized to improve secrecy rates and meet the growing demand for secure information transfer.