Spectrum Efficiency Evaluation with Diversity Combining for Fading and Branch Correlation Impairments

Abstract

In this paper, closed-form expressions for capacities per unit bandwidth for fading channels with impairments due to Branch Correlation are derived for optimal power and rate adaptation, constant transmit power, channel inversion with fixed rate, and truncated channel inversion policies for maximal ratio combining diversity reception case. Closed-form expressions for system spectrum efficiency when employing different adaptation policies are derived. Analytical results show accurately that optimal power and rate adaptation policy provides the highest capacity over other adaptation policies. In the case of errors due to branch correlation, optimal power and rate adaptation policy provides the best results. All adaptation policies suffer no improvement in channel capacity as the branch correlation is increased. This fact is verified using various plots for different policies. With increase in branch correlation, capacity gains are significantly larger for optimal power and rate adaptation policy as compared to the other policies. The outage probability for branch correlation is also derived and analyzed using plots for the same.

1 Introduction

The purpose of any communication system is to reliably transfer information between the source and the destination [1]. The wireless communication channel is dynamic and random, and at times, the received signal is not strong enough for a dependable link to exist between the transmitter and the receiver. The average signal strength received by an antenna element over local area in the propagation environment can be quite large, but during some instances, it is not uncommon for the instantaneous signal level in a multipath environment to fall 30 dB or more below its mean level. It is during these abrupt drops in local signal level, that the message is most likely to be received incorrectly. In order to compensate for fading brought upon by the channel, and to ensure that data is not erroneously decoded, the transmit power can be increased during the times a low signal strength is received by the antenna.

Most wireless communications systems, however, have low power and do not have the dynamic range available to counter the effects introduced by the propagation environment. An increase in reliability in a multipath fading environment without increasing transmit power can be efficiently achieved using a receive antenna diversity system. Multiple antennas at the receiver have been used successfully in operational systems to diminish the variance of local signal strength fluctuations using the signals on all antenna elements to reduce the incidence of severe signal degradations that occur during a fade. Using multiple antennas, the probability that one or more of the elements will receive signals with adequate signal strength increases. Reducing the occurrence of fading improves the overall reliability of the received information, and therefore allows for greater coverage distance.

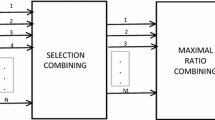
Diversity is an effective method for increasing the received Signal-to-Noise Ratio (SNR) in a flat fading environment (i.e. nearly constant fading over the bandwidth of interest). The mobile radio channel varies with time, and at times a receiver might receive a signal that is indistinguishable from noise. Diversity is meant to provide the receiver with alternative paths to the transmitted signal to ensure that the signal is reliably received. When identical elements are closely spaced, the signal envelopes received by both antennae can exhibit a large degree of correlation, or similarity. A large correlation implies that when one antenna receives a low signal level, the second antenna most likely also attains a similar degraded signal level. It is also not uncommon for an antenna diversity system to use different antennas at each diversity branch. Using non-identical elements at the receiver (e.g. antennas with different polarizations or patterns) could lead to average power imbalances between the different branches of a diversity system. Antennas that are different usually receive unequal average signal levels, depending on which antenna is better matched to the received signal environment. The performance of any diversity system also depends on the combining technique used to merge the signals received by the antenna elements. The most popular combining schemes are Selection Combining, Equal Gain Combining, and Maximal Ratio Combining. Maximal Ratio Combining technique outperforms other combining schemes under certain conditions and implementation issues.

1.1 Overview

In general, the analysis of mean SNR of the combined signal is based on the assumption that faded signals in the various branches are uncorrelated. In some cases, the antennas in the diversity array could be improperly positioned, or frequency separation between diversity signals could be too small [2]. It is thus important to examine possible deterioration in the performance of a diversity system when diversity branch signals are correlated to a certain extent. It remains to be seen if a moderate amount of correlation among diversity branches is not too damaging. Owing to the rarity of deep fades in any event, it would require a very high degree of correlation between the two faded signals to bring about a higher correspondence between the deep fades [2].

Most of the diversity combining schemes assume that combining mechanisms operate perfectly. Since information needed to operate a combiner is extracted in some way from the signals themselves, there is a possibility of making an error, thus not completely achieving the expected performance. This effect has been studied in detail in [3] for the particular case of the MRC combiner. The quantity, $\upvarepsilon$, is the correlation measure for the magnitude of complex cross-covariance of the two faded Gaussian signals (assumed also to be jointly Gaussian) [3]; Here, $\upvarepsilon ^{2}$ is very nearly equal to the normalized envelope covariance of the two signals.

1.2 Literature Review

Kong and Milstein [4] derived the closed-form expression for the average SNR of a Generalized Selection Combining scheme (GSC), which is upper bounded by that of MRC and lower bounded by conventional SC. Digham and Alouini [5] presented closed form expression for average Probability of Packet Error (PPE) for a MRC diversity scheme which encompassed arbitrarily correlated Nakagami and Rician fading channels. Novel exact expressions involving hyper-geometric functions were derived [6] for the Symbol Error Rate (SER) of M-ary Quadrature Amplitude Modulation (MQAM) for $L$-branch diversity reception in Rayleigh fading and Additive White Gaussian Noise (AWGN) for MRC and SC combining. In further work [7], error rate performance of coherent M-ary phase shift keyed signals in slow non selective Nakagami fading and AWGN channel was analysed. For real values of the Nakagami fading parameter, $m$, a simple formula was presented for the SER.

Bit error rate (BER) was analyzed theoretically [8] for diversity reception in a Nakagami fading environment using an $M$-branch MRC combiner. Coherent and non-coherent reception of Frequency Shift Keying (FSK), Coherent Phase Shift Keying (CPSK), and Differential Phase Shift Keying (DPSK) was considered using the multiple branch diversity system for both identical and different diversity branch fading parameters. Calculation of equivalent number of uncorrelated branches with equal average SNRs for a system with correlated, unequal average SNR branches was studied [9]. The technique uses eigen-decomposition of a correlation matrix estimate and calculation of diversity gain using MRC combining with unequal average SNRs.

In further work [10], using a simple finite integral representation for bivariate Rayleigh Cumulative Distribution Function (CDF) expressions for outage probability and average error probability of a dual selective diversity system with correlated slow Rayleigh fading either in closed form (in particular for binary differential phase-shift keying) or in terms of a single integral with finite limits, and an integrand composed of elementary (exponential and trigonometric) functions was presented. Simon and Alouini [11] showed that by employing alternate forms of Gaussian and Marcum functions, it is possible to unify error-probability performance of coherent, differentially coherent, and non-coherent communications in the presence of generalized fading. Bhaskar [12] presented a comprehensive closed-form expression for the evaluation of error performance in a 2-branch EGC diversity system over Generalized Rayleigh fading channels. The authors analyzed [13] the error probability performance of MRC, EGC, and SC diversity schemes with coherent BPSK signalling on Rayleigh fading channels with Gaussian channel estimation errors. It was shown that with weighting errors, the conditional probability of error is not an explicit function of SNR at the output of the diversity combiner.

Goldfield and Wulich [14] considered a diversity reception system with majority decoding and Optimal Adaptive Power Loading (ADRM) applied to a Rayleigh fading channel. It was shown that the proposed system has a lower average Bit Error Rate (BER) than Optimal Diversity Reception (ODR) with uniform power distribution for the same redundancy. Malik et al. [15] derived closed-form expressions for single-user capacity of MRC diversity systems, taking into account the effect of correlation between the different branches. A Rayleigh fading channel with two kinds of correlation: 1) equal branch SNRs and the same correlation between any pair of branches, and 2) unequal branch SNRs and arbitrary correlation between branches for the three adaptive transmission schemes were analyzed: 1) optimal simultaneous power and rate adaptation; 2) optimal rate adaptation with constant transmit power; and 3) channel inversion with fixed rate.

Dietrich [16] derived BER for binary modulation and multiple correlated Rayleigh fading diversity branches. The results provide new analytical insights into performance, design, and optimization of some known communication receivers. Bhaskar [17] derived closed-form expressions for the capacities per unit bandwidth for Generalized Rayleigh fading channels for Optimal Power and Rate Adaptation (OPRA), Optimal Rate Adaptation (ORA) with constant transmit power, Channel Inversion with Fixed Rate (CIFR), and Truncated channel Inversion with Fixed Rate (TIFR) policies. OPRA policy provides the highest capacity over other adaptation policies both with and without diversity combining. CIFR policy suffers a large capacity penalty relative to the other policies.

1.3 Organization of the Paper

Novel ergodic channel capacity expressions are derived and plotted for different adaptation policies like OPRA (where power and rate changes with channel quality) and ORA (where rate alone changes with channel quality) for branch correlation errors under (i) Low SNR Regime I (ii) Low SNR Regime II, (iii) High SNR Regime, (iv) Asymptotic Approximation, and (v) Upper Bound Case. This is the motivation of this paper. Computation of optimum cut-off SNR [18] $\upgamma _{0}$ is also performed in this paper without fixing P$_\mathrm{out}$ as constant. Simulation results for above five cases are also presented in this paper. The remainder of the paper is organized as follows: In Sect. 2, we derive closed-form expressions for spectral efficiencies of the MRC combiner with branch correlation errors for different adaptation policies. Section 3 presents the capacity statistics for branch correlation impairments. Numerical results are given in Sect. 4. Finally, Sect. 5 contains some concluding remarks.

2 Impairments Due to Branch Correlation

A base station with two receiver antennas is considered for analysis as shown in Fig. 1. The Power Controller adapts power in case of OPRA policy and Encoder/Modulator adapts rate depending on the channel feedback from channel estimator for OPRA and ORA policy. The diversity combiner is MRC type for two branches at the receiver.

Fig. 1

Block diagram of two branch MRC transceiver-Rayleigh fading

The CDF of received instantaneous SNR, $\upgamma$, at the output of a 2-branch MRC output for the case of impairments due to branch correlation between two signals is given by [2]

$$\begin{aligned} \hbox {F}_{2}^\mathrm{(BC)} (\gamma )=1-\frac{1}{2\varepsilon }\left[ {(1+\varepsilon )\exp \left( {-\frac{\gamma }{\Gamma (1+\varepsilon )}} \right) -(1-\varepsilon )\exp \left( {-\frac{\gamma }{\Gamma (1-\varepsilon )}} \right) } \right] \end{aligned}$$

(1)

where $\varepsilon$ is the magnitude of complex covariance (as fading causes change in phase and amplitude of the transmitted signal at the receiver antennas Rx1 and Rx2 as shown in Fig. 1) of two fading Gaussian signals given by $\upvarepsilon =\hbox {E}[(\hbox {R}_{\mathrm{x1}},\upeta _{\mathrm{Rx1}),} (\hbox {R}_{\mathrm{x2}},\upeta _{\mathrm{Rx2}}]$, where $\hbox {R}_{\mathrm{x1}}$, ${\hbox {R}}_{\mathrm{x2}}$ are the received signals from the two branches of MRC, BC stands for Branch Correlation, and ${\Gamma }$ is the individual branch SNR defined as ${\Gamma }=\frac{E\left( {\sum _{i=1}^2 {\left| {R_i ^{2}} \right| } } \right) }{E(N)}$. The PDF of the received instantaneous SNR, $\upgamma$, at the output of a 2-branch MRC output is given by

$$\begin{aligned} f_2^{\mathrm{(BC)}} (\gamma )=\frac{1}{2\Gamma \varepsilon }\left[ {\exp \left( {-\frac{\gamma }{\Gamma (1+\varepsilon )}} \right) -\exp \left( {-\frac{\gamma }{\Gamma (1-\varepsilon )}} \right) } \right] . \end{aligned}$$

(2)

2.1 Optimal Simultaneous Power and Rate Adaptation Policy

Under this condition known as OPRA policy, the power and rate of the transmitted signal is altered above the cut-off SNR depending on the channel. The optimal cut off must satisfy [19]

$$\begin{aligned} \int \limits _{\gamma _0 }^\infty {\left( {\frac{1}{\gamma _0 }-\frac{1}{\gamma }} \right) } \frac{1}{2\Gamma \varepsilon }\left[ {\exp \left( {-\frac{\gamma }{\Gamma (1+\varepsilon )}} \right) -(1-\varepsilon )\exp \left( {-\frac{\gamma }{\Gamma (1-\varepsilon )}} \right) } \right] d\gamma =1. \end{aligned}$$

(3)

2.2 Lemma

Given $\upvarepsilon$ and ${\Gamma }$ there exists an optimum cut-off SNR, $\gamma _0 \in (0,1)$ such that (4) is satisfied. Substituting (2) into (3) and simplifying, we find that $\upgamma _{0}$ must satisfy

$$\begin{aligned}&\frac{\Gamma }{\gamma _0 }\left[ {(1+\varepsilon )\exp \left( {-\frac{\frac{\gamma _0 }{\Gamma }}{\Gamma (1+\varepsilon )}} \right) -(1-\varepsilon )\exp \left( {-\frac{\frac{\gamma _0 }{\Gamma }}{\Gamma (1-\varepsilon )}} \right) } \right] +E_i \left( {\frac{-\frac{\gamma _0 }{\Gamma }}{1+\varepsilon }} \right) \nonumber \\&\qquad - E_i \left( {\frac{-\frac{\gamma _0 }{\Gamma }}{1-\varepsilon }} \right) =2\varepsilon \Gamma , \end{aligned}$$

(4)

where $E_i (-u)=-\int \nolimits _u^\infty {\frac{e^{-t}}{t}dt}$ is the exponential integral function, as given on p. xxxv, (Exponential and Related Integrals section) of [20]. Define

$$\begin{aligned} f(x)&= \frac{1}{x}\left[ {(1+\varepsilon )\exp \left( {-\frac{x}{\Gamma (1+\varepsilon )}} \right) -(1-\varepsilon )\exp \left( {-\frac{x}{\Gamma (1-\varepsilon )}} \right) } \right] +E_i \left( {\frac{-x}{1+\varepsilon }} \right) \nonumber \\&-E_i \left( {\frac{-x}{1-\varepsilon }} \right) -2\varepsilon \Gamma . \end{aligned}$$

(5)

Note that $\frac{\partial f(x)}{\partial x}=\left( {\frac{\Gamma }{\gamma _0 }-\frac{1}{x}} \right) \left( {\exp \left( {-\frac{x}{1-\varepsilon }} \right) -\exp \left( {-\frac{x}{1+\varepsilon }} \right) } \right) <0\quad \forall \;x>\frac{\gamma _0 }{\Gamma }.$ Moreover, from (5), $\lim _{x\rightarrow 0^{+}} f(x)=\frac{2\varepsilon \Gamma }{\gamma _0 }>0$ and $\lim _{x\rightarrow \infty } f(x)<0.$ Thus, we conclude that there is a unique $\gamma _{0}$ for which f ($\gamma _0)=0$ satisfies (6). Numerical results using MATLAB show that $\gamma _0\in$ [0, 1] as $\Gamma \rightarrow \infty$. Simplifying the spectrum efficiency for OPRA policy under branch correlation is given by

$$\begin{aligned} \frac{\mathop {\left\langle \hbox {C} \right\rangle }\nolimits _{\mathrm{OPRA}}^{\mathrm{(BC)}} }{\hbox {B}}=\hbox { }\frac{\log _2 (e)}{2\varepsilon }\left[ {(1+\varepsilon )E_1 \left( {-\frac{\frac{\gamma _0 }{\Gamma }}{(1+\varepsilon )}} \right) -(1-\varepsilon )E_1 \left( {-\frac{\frac{\gamma _0 }{\Gamma }}{(1-\varepsilon )}} \right) } \right] , \end{aligned}$$

(6)

where $E_1 (x)=\int \nolimits _1^\infty {\frac{e^{-xt}}{t}dt}$ [20]. The proof of (6) is shown in Appendix 1. Simplifying the outage probability for the case of Branch Correlation (BC), we have

$$\begin{aligned} \hbox {P}_{\mathrm{out}}^{\mathrm{(BC)}} =1-\frac{1}{2\varepsilon }\left[ {(1+\varepsilon )\exp \left( {-\frac{\frac{\gamma _0 }{\Gamma }}{(1+\varepsilon )}} \right) -(1-\varepsilon )\exp \left( {-\frac{\frac{\gamma _0 }{\Gamma }}{(1-\varepsilon )}} \right) } \right] . \end{aligned}$$

(7)

The proof of (7) is shown in Appendix 1.

2.3 Optimal Rate Adaptation with Constant Transmit Power Policy

Under this condition known as ORA policy, the rate of the transmitted signal alone is altered depending on the quality of the channel but the transmitted power is kept a constant. Simplifying the spectrum efficiency for ORA policy under branch correlation, we have

$$\begin{aligned} \frac{\mathop {\left\langle \hbox {C} \right\rangle }\nolimits _{\mathrm{ORA}}^{\mathrm{(BC)}} }{\hbox {B}}&= \frac{\log \;_2 (e)}{2\varepsilon }\left[ (1-\varepsilon )\left( {\exp \;\left( {\frac{1}{\Gamma (1-\varepsilon )}} \right) E_i \left( {-\frac{1}{\Gamma (1-\varepsilon )}} \right) } \right) \right. \nonumber \\&\left. - (1+\varepsilon )\left( {\exp \;\left( {\frac{1}{\Gamma (1+\varepsilon )}} \right) E_i \left( {-\frac{1}{\Gamma (1+\varepsilon )}} \right) } \right) \right] . \end{aligned}$$

(8)

The proof of (8) is shown in Appendix 1.

2.4 Channel Inversion with Fixed Rate policy

Under this condition known as CIFR policy, the channel characteristics are inverted (Equalised) depending on the quality of the channel. Simplifying the spectrum efficiency of CIFR policy under branch correlation, we have

$$\begin{aligned} \frac{\mathop {\left\langle \hbox {C} \right\rangle }\nolimits _{\mathrm{CIFR}}^{\mathrm{(BC)}} }{\hbox {B}}=\log _2 \left[ {1+\frac{2\varepsilon \Gamma }{\left( {\begin{array}{l} \exp \left( {\frac{\gamma _{\max } }{\Gamma (1-\varepsilon )}} \right) E_i \left( {\frac{-\gamma _{\max } }{\Gamma (1-\varepsilon )}} \right) -\exp \left( {\frac{\gamma _{\min } }{\Gamma (1-\varepsilon )}} \right) E_i \left( {\frac{-\gamma _{\min } }{\Gamma (1-\varepsilon )}} \right) + \\ \exp \left( {\frac{\gamma _{\min } }{\Gamma (1+\varepsilon )}} \right) E_i \left( {\frac{-\gamma _{\min } }{\Gamma (1+\varepsilon )}} \right) -\exp \left( {\frac{\gamma _{\max } }{\Gamma (1+\varepsilon )}} \right) E_i \left( {\frac{-\gamma _{\max } }{\Gamma (1+\varepsilon )}} \right) \\ \end{array}} \right) }} \right] . \end{aligned}$$

(9)

The proof of (9) is shown in Appendix 1.

2.5 Truncated Channel Inversion Policy

Under this condition known as TIFR policy, the channel characteristics are inverted beyond the cut-off SNR depending on the channel quality. So, outage capacity is overcome in this policy. Simplifying the spectrum efficiency of TIFR policy under branch correlation, we have

$$\begin{aligned} \frac{\mathop {\left\langle \hbox {C} \right\rangle }\nolimits _{\mathrm{TIFR}}^{\mathrm{(BC)}} }{\hbox {B}}=\log _2 \left[ {1+\frac{2\varepsilon \Gamma }{\int \nolimits _{\gamma _0 }^\infty {\left( {\frac{e^{-\frac{\gamma }{\Gamma (1+\varepsilon )}}}{\gamma }-\frac{e^{-\frac{\gamma }{\Gamma (1-\varepsilon )}}}{\gamma }} \right) d\gamma } }} \right] \left( {1-P_{\mathrm{out}}^{\mathrm{(BC)}} } \right) \end{aligned}$$

(10)

$$\begin{aligned}&= \frac{1}{2\varepsilon }\log _2 \left[ {1+\frac{2\varepsilon \Gamma }{E_i \left( {\frac{-\gamma _0 }{\Gamma (1-\varepsilon )}} \right) -E_i \left( {\frac{-\gamma _0 }{\Gamma (1+\varepsilon )}} \right) }} \right] \quad \left[ \left( {1+\varepsilon } \right) \exp \left( {\frac{-\gamma _0 }{\Gamma (1+\varepsilon )}} \right) \right. \nonumber \\&\left. -\left( {1-\varepsilon } \right) \exp \left( {\frac{-\gamma _0 }{\Gamma (1-\varepsilon )}} \right) \right] . \end{aligned}$$

(11)

The proof of (11) is shown in Appendix 1.

2.6 Asymptotic Approximation

We can obtain asymptotic approximation for $\frac{\mathop {\left\langle \hbox {C} \right\rangle }\nolimits _{\mathrm{OPRA}}^{(\infty ,\mathrm{BC})} }{B}$ using the series representation of exponential integral of first order function [20] expressed as

$$\begin{aligned} E_1 (x)=-C-\ln (x)-\sum _{i=1}^\infty {\frac{-(x)^{i}}{i.i!}} , \end{aligned}$$

(12)

where C = 0.1566557729 is the Euler-Mascheroni constant. Then, the asymptotic approximation for OPRA policy can be shown as

$$\begin{aligned} \frac{\mathop {\left\langle \hbox {C} \right\rangle }\nolimits _{\mathrm{OPRA}}^{(\infty ,\mathrm{BC})} }{\hbox {B}}&= \frac{1}{2\varepsilon \log 2}\left[ -(1+\varepsilon )\sum _{i=1}^\infty {\left( {\frac{-\gamma _0 }{\Gamma (1+\varepsilon )}} \right) } ^{i}\frac{1}{ii!}+(1-\varepsilon )\sum _{i=1}^\infty {\left( {\frac{-\gamma _0 }{\Gamma (1-\varepsilon )}} \right) } ^{i}\frac{1}{ii!}\right. \nonumber \\&\left. -\,2C\varepsilon +\ln \left( {\frac{1+\varepsilon }{1-\varepsilon }} \right) -\varepsilon \ln \left( {\frac{\gamma _0 ^{2}}{\Gamma ^{2}1-\varepsilon ^{2}}} \right) \right] . \end{aligned}$$

(13)

Following the same procedure as above, the asymptotic approximation,$\frac{\left\langle \hbox {C} \right\rangle _{\mathrm{ORA}}^{(\infty ,\mathrm{BC})} }{\hbox {B}}$can be computed as

$$\begin{aligned} \frac{\mathop {\left\langle \hbox {C} \right\rangle }\nolimits _{\mathrm{ORA}}^{(\infty , \mathrm{BC})} }{\hbox {B}}&= \frac{\log _2 e}{2\varepsilon }\left[ \left\{ {(\nu 1)(\kappa 1)+(\nu 1)\sum _{i=1}^\infty {\frac{\left( {-1} \right) ^{i}}{\Gamma (1-\varepsilon )i.i!}} } \right\} \right. \nonumber \\&\left. -\left\{ {(\nu 2)(\kappa 2)+(\nu 2)\sum _{i=1}^\infty {\frac{\left( {-1} \right) ^{i}}{\Gamma (1+\varepsilon )i.i!}} } \right\} \right] , \end{aligned}$$

(14)

where $\kappa 1=C+v1\ln \left( {\frac{1}{\Gamma (1-\varepsilon )}} \right) , \kappa 2=C+v2\ln \left( {\frac{1}{\Gamma (1+\varepsilon )}} \right)$.

2.7 Upper Bound

The channel capacity per unit bandwidth expression for OPRA policy can be upper bounded by applying Jensen’s inequality to (2) as follows:

$$\begin{aligned} \frac{\mathop {\left\langle \hbox {C} \right\rangle }\nolimits _{\mathrm{OPRA}}^{\mathrm{(UB,BC)}} }{\hbox {B}}&= \ln (E[\gamma ])\le E[\ln (\gamma )]=\frac{1}{2\varepsilon \Gamma }\int \ln (\gamma )\left( \exp \left( {-\frac{\gamma }{\Gamma \left( {1+\varepsilon } \right) }} \right) \right. \nonumber \\&\left. -\exp \left( {-\frac{\gamma }{\Gamma \left( {1-\varepsilon } \right) }} \right) \right) d\gamma .\qquad \end{aligned}$$

(15)

Making change of variables in (15) with $\hbox {t}=\frac{\gamma }{\Gamma \left( {1+\varepsilon } \right) }, \hbox {dt} =\frac{d\gamma }{\Gamma \left( {1+\varepsilon } \right) }$ in the first integral, and $\hbox {u} =\frac{\gamma }{\Gamma \left( {1-\varepsilon } \right) }, \hbox {du} =\frac{d\gamma }{\Gamma \left( {1-\varepsilon } \right) }$ in the second integral, and using Eq. (1) of section 4.331 on p. 567 of [20], we obtain

$$\begin{aligned} \frac{\mathop {\left\langle \hbox {C} \right\rangle }\nolimits _{\mathrm{OPRA}}^{\mathrm{(UB,BC)}} }{\hbox {B}}=-C+\frac{1}{2\varepsilon }\ln \left( {\frac{1+\varepsilon }{1-\varepsilon }} \right) -\ln \left( {\frac{1}{\Gamma \left( {\sqrt{1-\varepsilon ^{2}}} \right) }} \right) . \end{aligned}$$

(16)

The channel capacity per unit bandwidth expression for ORA policy under branch correlation can be upper bounded by applying Jensen’s inequality to (8) as follows:

$$\begin{aligned} \frac{\mathop {\left\langle \hbox {C} \right\rangle }\nolimits _{\mathrm{ORA}}^{\mathrm{(UB,BC)}} }{\hbox {B}}=1-C+\frac{1}{2\varepsilon }\ln \left( {\frac{1+\varepsilon }{1-\varepsilon }} \right) +\ln \left( {\Gamma \sqrt{1-\varepsilon }} \right) . \end{aligned}$$

(17)

2.8 Low SNR Region I

Ergodic capacity can be approximated in the low SNR region I by approximating $\log _2 (1+\gamma )$ as $\sqrt{\gamma }$ [17]. Using this approximation in (8) yields the approximated channel capacity per unit bandwidth (in bits/sec/Hz) at Low SNR Region I as

$$\begin{aligned}&\frac{\mathop {\left\langle \hbox {C} \right\rangle }\nolimits _{\mathrm{ORA}}^{(\mathrm{LSR}\,\mathrm{1,BC})} }{\hbox {B}}=\int \limits _0^\infty {\sqrt{\gamma }} \mathop f\nolimits _2^{\mathrm{(BC)}} (\gamma )d\gamma \nonumber \\&\quad \approx \frac{1}{2\varepsilon \Gamma }\int \limits _0^\infty {\sqrt{\gamma }\exp \;\left( {-\frac{\gamma }{\Gamma (1+\varepsilon )}} \right) } \;d\gamma -\frac{1}{2\varepsilon \Gamma }\int \limits _0^\infty {\sqrt{\gamma }\exp \;\left( {-\frac{\gamma }{\Gamma (1-\varepsilon )}} \right) } \;d\gamma .\qquad \quad \end{aligned}$$

(18)

Making change of variables in the first integral of (18), where $\hbox {t} =\frac{\gamma }{\Gamma }$ and $\hbox {dt} = \frac{d\gamma }{\Gamma }$, and making change of variables in the second integral of (18), where $\hbox {u} =\frac{\gamma }{\Gamma }$ and $\hbox {du} = \frac{d\gamma }{\Gamma }$, we have

$$\begin{aligned} \frac{\mathop {\left\langle \hbox {C} \right\rangle }\nolimits _{\mathrm{ORA}}^{(\mathrm{LSR}\,\mathrm{1,BC})} }{\hbox {B}}&= \frac{1}{2\varepsilon }\left[ {\frac{\sqrt{\pi }}{2}\left( {\sqrt{\Gamma }(1+\varepsilon )^{\frac{3}{2}}} \right) -\frac{\sqrt{\pi }}{2}\left( {\sqrt{\Gamma }(1-\varepsilon )^{\frac{3}{2}}} \right) } \right] =\frac{\sqrt{\Gamma \pi }}{4\varepsilon }\left[ \left( {1+\varepsilon } \right) ^{\frac{3}{2}}\right. \nonumber \\&\left. -\left( {1-\varepsilon } \right) ^{\frac{3}{2}} \right] . \end{aligned}$$

(19)

2.9 Low SNR Region II

Another approximation for Ergodic capacity in low SNR region II can be found by exploiting the fact that$\log _2 (1+\gamma )\approx \frac{1}{\ln 2}\left( {\gamma -\frac{\gamma ^{2}}{2}} \right)$, which results in the approximated Ergodic capacity in low SNR region II given as

$$\begin{aligned} \frac{\mathop {\left\langle \hbox {C} \right\rangle }\nolimits _{\mathrm{ORA}}^{\mathrm{(LSR2,BC)}} }{\hbox {B}}&= \int \limits _0^\infty {\frac{1}{\ln 2}\left( {\gamma -\frac{\gamma ^{2}}{2}} \right) \mathop f\nolimits _2^{\mathrm{(BC)}} \left( \gamma \right) d\gamma }\nonumber \\&\approx \frac{1}{2\Gamma \ln 2\varepsilon }\int \limits _0^\infty {\left( {\gamma -\frac{\gamma ^{2}}{2}} \right) \exp \left( {\frac{-\gamma }{\Gamma \left( {1+\varepsilon } \right) }} \right) d\gamma }\nonumber \\&- \frac{1}{2\Gamma \ln 2\varepsilon }\int \limits _0^\infty {\left( {\gamma -\frac{\gamma ^{2}}{2}} \right) \exp \left( {\frac{-\gamma }{\Gamma \left( {1-\varepsilon } \right) }} \right) d\gamma }. \end{aligned}$$

(20)

Making change of variables in the first integral of (20), where $\hbox {t} =\frac{\gamma }{\Gamma }$ and $\hbox {dt} =\frac{d\gamma }{\Gamma }$, and making change of variables in the second integral of (20), where $\hbox {u} =\frac{\gamma }{\Gamma }$ and $\hbox {du} =\frac{d\gamma }{\Gamma }$, we have

$$\begin{aligned} \frac{\mathop {\left\langle \hbox {C} \right\rangle }\nolimits _{\mathrm{ORA}}^{(\mathrm{LSR2,\,BC)}} }{\hbox {B}}=2.88539\,\Gamma \left[ {1-\Gamma +\Gamma \varepsilon } \right] . \end{aligned}$$

(21)

2.10 High SNR Region

The Ergodic capacity can be approximated at high SNR region using the fact that $\log _2 (1+\gamma )=\log _2 (\gamma )$ as $\gamma \rightarrow \infty ,$and can be expressed as

$$\begin{aligned} \frac{\mathop {\left\langle \hbox {C} \right\rangle }\nolimits _{\mathrm{ORA}}^{\mathrm{(HSR,BC)}} }{\hbox {B}}=\int \limits _0^\infty {\log _2 \left( \gamma \right) \frac{1}{2\Gamma \varepsilon }\left[ {\exp \left( {-\frac{\gamma }{\Gamma (1+\varepsilon )}} \right) -(1-\varepsilon )\exp \left( {-\frac{\gamma }{\Gamma (1-\varepsilon )}} \right) } \right] d\gamma }. \end{aligned}$$

(22)

Making change of variables in the first integral of (22), where $t=\frac{\gamma }{\Gamma (1+\varepsilon )}$ and $dt=\frac{d\gamma }{\Gamma (1+\varepsilon )}$, and making change of variables in the second integral of (22), where $u=\frac{\gamma }{\Gamma (1-\varepsilon )}$ and $du=\frac{d\gamma }{\Gamma (1-\varepsilon )}$, we have

$$\begin{aligned} \frac{\mathop {\left\langle \hbox {C} \right\rangle }\nolimits _{\mathrm{ORA}}^{\mathrm{(HSR,BC)}} }{\hbox {B}}=\frac{-C}{\ln 2}+\frac{\ln \Gamma }{\ln 2}+\frac{1}{2\varepsilon \ln 2}\left[ {\ln \left( {\frac{1+\varepsilon }{1-\varepsilon }} \right) +\varepsilon \ln \left( {1-\varepsilon ^{2}} \right) } \right] , \end{aligned}$$

(23)

where we have used the relation $\int \nolimits _0^\infty {e^{(-\mu x)}\ln x\;dx=-\frac{1}{\mu }(C+\ln \mu )\quad [\mathfrak {R}e\mu >0]}$ from Section 4.331 on p. 567 of [20].

3 Capacity Statistics

This section focuses on deriving exact analytical expressions for capacity statistics of impairments due to branch correlation, assuming perfect channel knowledge at the receiver and no channel knowledge with average input-power constraint.

3.1 Moment Generating Function (MGF)

The MGF of the capacity for impairments due to branch combining is given by

$$\begin{aligned} \Phi _{C,BC} (\tau )=\frac{1}{2\Gamma \varepsilon }\int \limits _0^\infty {\left( {1+\gamma } \right) ^{\frac{\gamma }{\ln 2}}} \left[ {\exp \left( {-\frac{\gamma }{\Gamma (1+\varepsilon )}} \right) -\exp \left( {-\frac{\gamma }{\Gamma (1-\varepsilon )}} \right) } \right] d\gamma . \end{aligned}$$

(24)

Making change of variables in the first integral of (51), where $\hbox {t}=\frac{\gamma }{\Gamma }$ and $\hbox {dt}=\frac{d\gamma }{\Gamma }$, and making change of variables in the second integral of (51), where $\hbox {u}=\frac{\gamma }{\Gamma }$ and $\hbox {du}=\frac{d\gamma }{\Gamma }$, we have

$$\begin{aligned} \Phi _C (\tau )&= \frac{\Gamma ^{1+\frac{\tau }{\ln 2}}}{2\Gamma \varepsilon }\left[ {\exp \;\left( {\frac{1}{\Gamma (1+\varepsilon )}} \right) \left( {1+\varepsilon } \right) ^{\frac{\tau }{\ln 2}}\Gamma \left( {1+\frac{\tau }{\ln 2},\frac{1}{\Gamma (1+\varepsilon )}} \right) } \right] \nonumber \\&-\frac{\Gamma ^{1+\frac{\tau }{\ln 2}}}{2\Gamma \varepsilon }\left[ {\exp \;\left( {-\frac{1}{\Gamma (1-\varepsilon )}} \right) \left( {1-\varepsilon } \right) ^{\frac{\tau }{\ln 2}}\Gamma \left( {1+\frac{\tau }{\ln 2},\frac{1}{\Gamma (1-\varepsilon )}} \right) } \right] .\qquad \end{aligned}$$

(25)

3.2 Complementary Cumulative Distribution Function (CCDF)

The CCDF of $C=\log _2 (1+\gamma )$ in the presence of impairments due to branch combining is given as

$$\begin{aligned} {\overline{\hbox {F}}}_{\overline{\mathrm{C,}} \mathrm{CE}}&= 1-\int \limits _0^{2^{C}-1} f_2 ^{\mathrm{(BC)}}(\gamma )d\gamma \nonumber \\&= 1-\frac{1}{2\varepsilon \Gamma }\int \limits _0^{2^{C}-1} {\left[ {\exp \left( {-\frac{\gamma }{\Gamma (1+\varepsilon )}} \right) -\exp \left( {-\frac{\gamma }{\Gamma (1-\varepsilon )}} \right) } \right] } d\gamma \nonumber \\&= \frac{1}{2\varepsilon }\left( {(1+\varepsilon )\exp \left( {-\frac{2^{C}-1}{\Gamma (1+\varepsilon )}} \right) -(1-\varepsilon )\exp \left( {-\frac{2^{C}-1}{\Gamma (1-\varepsilon )}} \right) } \right) . \end{aligned}$$

(26)

3.3 Probability Density Function

The PDF of the capacity is defined as the derivative of CCDF with respect to C, which can be written as

$$\begin{aligned} \hbox {P}_\mathrm{C}^{\mathrm{(BC)}} \hbox {(C)}=\frac{2^{C}\ln 2}{2\varepsilon \Gamma }\left[ {\exp \left( {-\frac{2^{C}-1}{\Gamma (1+\varepsilon )}} \right) -\exp \left( {-\frac{2^{C}-1}{\Gamma (1-\varepsilon )}} \right) } \right] . \end{aligned}$$

(27)

4 Numerical Results

Figure 2a shows channel capacity per unit bandwidth for optimal power and rate adaptation policy as a function of the Individual Branch SNR for a fading channel with impairments due to branch correlation for different correlation $\varepsilon$. Equation (6) is used to generate the numerical results of Fig. 2a, b. Figure 2a shows that the variations in correlation is more pronounced at high SNRs beyond 6 dB. The enhancement of capacity is prominent at high SNRs than at low SNRs for OPRA policy. At high received SNRs, the rate of adaptation is higher which leads to better performance. From Fig. 2a, it is also clear that as SNR increases, capacity also increases. Figure 2b shows channel capacity per unit bandwidth for optimal power and rate adaptation policy as a function of correlation $(\upvarepsilon )$ for a fading channel with impairments due to branch correlation for different correlation. The graph clearly shows that capacity increase is higher for large SNRs than at low SNRs. Also, the gap between the graphs widen at high SNRs. The dotted line in Fig. 2a shows the simulation results for capacity at ${\Gamma } = 5$ dB. The dotted line in Fig. 2b shows the simulation results for capacity at $\upvarepsilon = 0.6$. From Fig. 2a, b, it is clear that the simulation results are in close agreement with the analytical results.

Fig. 2

a Variation in capacity for OPRA policy with individual branch SNR, ${\Gamma }$, for $\upvarepsilon = 0.3, 0.6, 0.9$ and $\upgamma _{0}= 0.5$ b Variation in capacity for OPRA policy with correlation $\upvarepsilon$ for ${\Gamma }$ = 3, 5, 7 dB and $\upgamma _{0}= 0.5$

Figure 3a shows channel capacity per unit bandwidth for optimal rate adaptation policy as a function of the Individual Branch SNR for a fading channel with impairments due to branch correlation for different correlation $\upvarepsilon$. Equation (8) is used to generate the numerical results of Fig. 3a, b. Figure 3a resembles Fig. 2a but for the decrease in capacity achieved at a particular branch SNR. This decrease in capacity for ORA policy is attributed to the fact that the policy adapts only the rate and not power due to Channel State Information not known at the transmitter but known at the receiver alone. The characteristics of Fig. 3b are similar to Fig. 2b except for the decrease in capacity for a particular correlation value. The dotted line in Fig. 3a show the simulation results for capacity at ${\Gamma } = 5\hbox {dB}$ and the dotted line in Fig. 3b show the simulation results for capacity at $\upvarepsilon = 0.6$. From Fig. 3a, b, it is again clear that the simulation results are in close agreement with the analytical results.

Fig. 3

a Variation in capacity for ORA policy with individual branch SNR ${\Gamma }$ for $\upvarepsilon = 0.3, 0.6, 0.9$ and $\upgamma _{0 }= 0.5$. b Variation in capacity for ORA policy with correlation $\upvarepsilon$ for ${\Gamma }$ = 3, 5, 7 dB and $\upgamma _{0}= 0.5$

Figure 4a shows channel capacity per unit bandwidth for CIFR policy as a function of Individual Branch SNR. Equation (9) is used to generate the numerical results of Fig. 4a, b. The capacity difference for lower values of correlation ($\upvarepsilon = 0.3$ and $\upvarepsilon = 0.6$) is less pronounced compared to the capacity difference for higher values of correlation $(\upvarepsilon = 0.6$ and $\upvarepsilon = 0.9$). Further, at low SNRs the capacity increase is much lower than at high SNRs for different correlation values. Figure 4b shows the channel capacity per unit bandwidth for CIFR policy as a function of correlation $(\upvarepsilon )$ for a fading channel with impairments due to branch correlation for individual branch SNR, ${\Gamma } = 5 \hbox {dB}$. All these curves show that capacity is maximized for lower correlation, $(\upvarepsilon = 0.3)$. Also from the graphs, we find that the decrease in capacity is steeper than OPRA and ORA policies at high correlation values. The dotted line in Fig. 4a shows the simulation results for capacity at ${\Gamma } = 5 \hbox {dB}$ and the dotted line in Fig. 4b shows the simulation results for capacity at $\upvarepsilon = 0.6$. From Fig. 4a, b, it is obvious that simulation results are in close agreement with the analytical results.

Fig. 4

a Variation in capacity for CIFR policy with individual branch SNR ${\Gamma }$ for $\upvarepsilon = 0.3, 0.6, 0.9$ and $\upgamma _{0}= 0.5$. b Variation in capacity for CIFR policy with correlation $\upvarepsilon$ for ${\Gamma }$ = 3, 5, 7 dB and $\upgamma _{0 }= 0.5$

Figure 5a shows channel capacity per unit bandwidth for TIFR policy as a function of Individual Branch SNR. Equation (11) is used to generate the numerical results of Fig. 5a, b. Figure 5a resembles Fig. 4a but for the increase in capacity achieved at a particular branch SNR. The increase in capacity is due to the subtraction of outage from the channel and considering the branches with SNRs above the optimal cut-off SNR for combining. The characteristics of Fig. 5b are similar to that of Fig. 4b except for the increase in capacity for a particular correlation value. The dotted line in Fig. 5a shows the simulation results for capacity at ${\Gamma } = 5\,\hbox {dB}$ and the dotted line in Fig. 5b shows the simulation results for capacity at $\upvarepsilon = 0.6$. From both Fig. 5a, b, it is clear that the simulation results are in close agreement with the analytical results.

Fig. 5

a Variation in capacity for TIFR policy with individual branch SNR ${\Gamma }$ for $\upvarepsilon = 0.3, 0.6, 0.9$ and $\upgamma _{0}=0.5$. b Variation in capacity for TIFR policy with correlation $\upvarepsilon$ for ${\Gamma }$ $=$ 3, 5, 7 dB and $\upgamma _{0 }= 0.5$

Figure 6a shows the variation in channel capacity per unit bandwidth with Individual Branch SNR. Figure 6b shows the variation in channel capacity per unit bandwidth with correlation $(\upvarepsilon )$ for four different adaptation policies. From Fig. 6a, we observe that at low individual branch SNRs $({\Gamma })$, the correlation influences all four policies in a similar manner. But at high SNRs, the correlation $(\upvarepsilon )$ has more influence on channel inversion policies like CIFR and TIFR compared to ORA and OPRA policies. For the same bandwidth B (Hz), it can be observed that $\hbox {C}_{\mathrm{opra}} > \hbox {C}_{\mathrm{ora}} >\hbox {C}_{\mathrm{tifr}} > \hbox {C}_{\mathrm{cifr}}$. The capacity difference between $\hbox {C}_{\mathrm{opra}}$ and $\hbox {C}_{\mathrm{cifr}}$ increases rapidly as branch SNR increases compared to the capacity difference between $\hbox {C}_{\mathrm{ora}}$ and $\hbox {C}_{\mathrm{cifr}}$. The capacity difference between $\hbox {C}_{\mathrm{cifr}}$ and $\hbox {C}_{\mathrm{tifr}}$ depends on outage probability, $\hbox {P}_{\mathrm{out}}$ and the optimal cut-off SNR, $\gamma _{0}$. Figure 6b shows the channel capacity per unit bandwidth versus Correlation for four various adaptation policies. The graphs show that capacity decreases as correlation $(\upvarepsilon )$ increases which is expected. The decrease in capacity for CIFR policy is sharper with increase in correlation compared to other three policies. Increase in the individual branch SNR $({\Gamma })$ leads to improvement in capacity for all four cases. Further, from the graphs, it is inferred that a decrease in capacity is higher for high correlation values whereas at low correlation values, the decrease in capacity is less prominent.

Fig. 6

a Variation in capacity for four different adaptation policies with individual branch SNR ${\Gamma }$ for $\upvarepsilon = 0.3, 0.6, 0.9$ and $\upgamma _{0}= 0.5$. b Variation in capacity for four different adaptation policies with Correlation $\upvarepsilon$ for ${\Gamma }$ = 3, 5, 7 dB and $\upgamma _{0 }= 0.5$

Figure 7a shows outage probability for impairments due to branch correlation as a function of correlation for various values of individual branch SNR. The graph shows that outage probability decreases as SNR increases. Equation (7) is used to generate the numerical results of Fig. 7a, b. The outage is higher at lower SNRs but decreases drastically with increase in received branch SNR and is almost minimal or negligible at SNRs beyond 9 dB. Figure 7b shows the outage probability for impairments due to branch correlation as a function of correlation for various values of individual branch SNR. The graph shows that outage probability decreases as SNR increases. Further, outage probability is higher for large correlation and reduces as correlation decreases. Thus, it is can be concluded that higher the correlation between the two message signals, higher is the probability of error and outage probability.

Fig. 7

a Variation in outage probability $\hbox {P}_{\mathrm{out}}$ with individual branch SNR ${\Gamma }$ for $\upvarepsilon = 0.3, 0.6, 0.9$ and $\upgamma _{0 }= 0.5$. b Variation in outage probability $\hbox {P}_{\mathrm{out}}$ with correlation $\upvarepsilon$ for ${\Gamma }$ = 3, 5, 7 dB and $\upgamma _{0 }= 0.5$

Figure 8a, b show the asymptotic approximation for OPRA and ORA policies respectively. The closed-form expressions for OPRA and ORA capacity have the term, $\hbox {E}_{1}\hbox {(x)}$, which can be expanded into an infinite series. Equations (6) and (13) are used to generate the numerical results of Fig. 8a. Equations (8) and (14) are used to generate the numerical results of Fig. 8b. Asymptotic approximation gives an idea about the particular branch SNR above which analytical capacity converges with the asymptotic capacity. Beyond that particular SNR, analytical and asymptotic capacities converge. From Fig. 8a, b, we observe that convergence takes place for low SNRs in the case of ORA policy (i.e., around 8 dB), but in the case of OPRA policy, the asymptotic capacity converges with the analytical capacity at higher SNRs (i.e., around 10 dB).

Fig. 8

a Comparison of asymptotic capacity for OPRA policy, $\hbox {C}_{\mathrm{OPRA} }$ versus individual branch SNR ${\Gamma }$ (dB) for $\upvarepsilon = 0.7$. b Comparison of asymptotic capacity for ORA policy, $\hbox {C}_{\mathrm{ORA} }$ versus individual branch SNR ${\Gamma }$ (dB) for $\upvarepsilon = 0.7$

Figure 9a, b show the Upper bound capacity for OPRA and ORA policies, respectively. Equations (6) and (16) are used to generate the numerical results of Fig. 9a. Equations (8) and (17) are used to generate the numerical results of Fig. 9b. From these results, it is obvious that upper bounds for both policies are much tighter. The upper bound for OPRA capacity is tighter at lower SNRs than at higher SNRs. But the upper bound for ORA capacity is tighter and uniform for all SNRs.

Fig. 9

a Comparison of capacity for OPRA policy with upper bound OPRA capacity versus individual branch SNR ${\Gamma }$ (dB) for $\upvarepsilon = 0.7$. b Comparison of capacity for ORA policy with upper bound ORA capacity versus Individual Branch SNR ${\Gamma }$ (dB) for $\upvarepsilon = 0.7$

Figure 10 shows the Low SNR region I approximation of capacity for ORA policy. Equations (8) and (19) are used to generate the numerical results of Fig. 10. This approximation provides the lower bound to the branch SNR beyond which efficient transmission and adaptation is not accountable. In the case of two branch correlation, the lower bound is approximately $-$3 dB beyond which analytical capacity exceeds the LSR I capacity approximation.

Fig. 10

a Comparison of capacity for ORA policy for normal SNRs with capacity for ORA policy under low SNR Regime I versus individual branch SNR ${\Gamma }$ (dB) for $\upvarepsilon = 0.7$. b Comparison of capacity for ORA policy for normal SNRs with capacity for ORA policy under Low SNR Regime II versus individual branch SNR ${\Gamma }$ (dB) for $\upvarepsilon = 0.7$

Figure 11 shows the Low SNR region II approximation of capacity for ORA policy. Equations (8) and (21) are used to generate the numerical results of Fig. 11. This approximation provides minimum branch SNR required for adaptation to be effective. In the case of two branch correlation, the minimum branch SNR required is approximately 2 dB, beyond which the analytical capacity exceeds the LSR II capacity approximation.

Fig. 11

Comparison of capacity for ORA policy for normal SNRs with capacity for ORA policy under low SNR Regime II versus individual branch SNR ${\Gamma }$ (dB) for $\upvarepsilon = 0.7$

Figure 12 shows the High SNR region approximation of capacity for ORA policy. Equations (8) and (23) are used to generate the numerical results of Fig. 12. This approximation helps to determine the upper bound branch SNR beyond which adaptation becomes unnecessary as the channel is good and performance of the system is at its peak. In the case of two branch correlation, the upper bound Branch SNR is approximately 16 dB beyond which the analytical capacity converges with the HSR capacity approximation.

Fig. 12

Comparison of capacity for ORA policy for normal SNRs with capacity for ORA under high SNR regime versus individual branch SNR ${\Gamma }$ (dB) for $\upvarepsilon = 0.7$

5 Conclusions

The channel capacities per unit bandwidth for various adaptation policies over fading channels with impairments due to branch correlation for two branch case have been computed in this paper. Closed-form expressions for spectral efficiencies for the four adaptation policies are derived for the MRC diversity reception case.

The main contribution of the paper includes the derivation of LSR I, LSR II, HSR, Asymptotic Approximation and Upper bound capacity expressions for OPRA and ORA policies for two branch correlation impairments. The numerical results provide an insight on performance improvement of two branch MIMO system with impairments due to constant branch correlation with four types of adaptation policies. Different wireless platforms have different upper and lower bound SNR regimes with which they work on. The numerical results in our two branch MIMO wireless system provides the upper and lower bounds of SNR region suitable for our system, based on the SNR feedback from the channel to decide on the nature of the channel and which adaptation policy to be adopted. Depending upon the type of channel available any one of two optimal policies namely OPRA or ORA can be chosen. Suboptimal policies like CIFR or TIFR also provide better results for the above system. Further work would be to extend these results to an M-branch MIMO system for (i) constant correlation and (ii) Distinct eigenvalue case.

Appendices

Appendix 1

The Spectrum Efficiency for OPRA policy is obtained by substituting (2) into (7) of [18] as

$$\begin{aligned} \frac{\mathop {\left\langle \hbox {C} \right\rangle }\nolimits _{\mathrm{OPRA}}^{\mathrm{(BC)}} }{\hbox {B}}&= \hbox { }\frac{1}{2\Gamma \varepsilon }\int \limits _{\gamma _0 }^\infty {\log _2 } \left( {\frac{\gamma }{\gamma _0 }} \right) \left[ \exp \left( {-\frac{\gamma }{\Gamma (1+\varepsilon )}} \right) -\exp \left( {-\frac{\gamma }{\Gamma (1-\varepsilon )}} \right) \right] d\gamma \end{aligned}$$

(28)

$$\begin{aligned}&= \frac{\gamma _0 \log _2 (e)}{2\Gamma \varepsilon }\int \limits _1^\infty {\log _e } \left( t \right) \exp \left( {-\frac{\gamma _0 }{\Gamma (1+\varepsilon )}t} \right) dt\nonumber \\&-\frac{\gamma _0 \log _2 (e)}{2\varepsilon \Gamma }\int \limits _1^\infty {\log _e (t)} \exp \left( {-\frac{\gamma _0 }{\Gamma (1-\varepsilon )}t} \right) dt. \end{aligned}$$

(29)

Substituting $\mu _1 =\frac{\gamma _0 }{\Gamma (1+\varepsilon )}$ and $\mu _2 =\frac{\gamma _0 }{\Gamma (1-\varepsilon )}$, $t=\frac{\gamma }{\gamma _0 }$ and $\hbox {dt} =\frac{d\gamma }{\gamma _0 }$ in (29), we have

$$\begin{aligned} \frac{\mathop {\left\langle \hbox {C} \right\rangle }\nolimits _{\mathrm{OPRA}}^{\mathrm{(BC)}} }{\hbox {B}}=\hbox { }\frac{\gamma _0 }{2\Gamma \varepsilon \log (2)}\int \limits _1^\infty {\log _2 } \left( t \right) \left[ {\exp \left( {-\mu _1 t} \right) -\exp \left( {-\mu _2 t} \right) } \right] dt. \end{aligned}$$

(30)

From Eq. (2) of section 4.331 on p. 567 in [20], we have $\int _1^\infty e^{-\mu t}\ln tdt=-\frac{1}{\mu }E_i (-\mu ),[\mathfrak {R}e\mu >0].$ Substituting this expression in (30), we obtain the capacity for OPRA policy in (6). The optimal policy suffers a probability of outage, $\hbox {P}_{\mathrm{out}}^{\mathrm{(BC)}}$ given by

$$\begin{aligned} \mathop {\hbox {P}}\nolimits _{\mathrm{out}}^{\mathrm{(BC)}} =\int \limits _0^{\gamma _0 } {f_2^{\mathrm{(BC)}} (\gamma )d\gamma } =1-\int \limits _{\gamma _0 }^\infty {f_2^{\mathrm{(BC)}} (\gamma )d\gamma }. \end{aligned}$$

(31)

Making change of variables in the integral of (31), where $\eta _1 =\frac{1}{\Gamma (1+\varepsilon )}$ and $\eta _2 =\frac{1}{\Gamma (1-\varepsilon )}$, we have

$$\begin{aligned} \mathop {\hbox {P}}\nolimits _{\mathrm{out}}^{\mathrm{(BC)}} =\int \limits _0^{\gamma _0 } {\frac{1}{2\Gamma \varepsilon }\left[ {\exp \left( {-\eta _1 \gamma } \right) -\exp \left( {-\eta _2 \gamma } \right) } \right] d\gamma }. \end{aligned}$$

(32)

Substituting $\int \nolimits _0^{\gamma _0 } {\exp (-\mu x)=\frac{1-\exp (-\gamma _0 \mu )}{\mu }}$ into (32) and simplifying, we have the outage probability expression as in (7). Substituting (2) into Eq. (29) of [18], we have

$$\begin{aligned} \frac{\mathop {\left\langle \hbox {C} \right\rangle }\nolimits _{\mathrm{ORA}}^{\mathrm{(BC)}} }{\hbox {B}}=\frac{\log _2 e}{2\varepsilon \Gamma }\int \limits _0^\infty {\log _e (1+\gamma )\left( {\exp \left( {-\frac{\gamma }{\Gamma (1+\varepsilon )}} \right) -\exp \left( {-\frac{\gamma }{\Gamma (1-\varepsilon )}} \right) } \right) } d\gamma . \end{aligned}$$

(33)

From Eq. (1) of section 4.337 on p. 568 in [20], we have $\int \nolimits _0^\infty \exp (-\mu x)\log _e (\beta +x)dx=\frac{1}{\mu }[\log _e (\beta )-e^{(\mu \beta )}E_i (-\beta \mu )],\;\forall \;[\left| {\arg \beta } \right| <\pi ,\mathfrak {R}e{}\mu >0].$

Substituting $\beta = 1, \eta _1 =\frac{1}{\Gamma (1+\varepsilon )},$ and $\eta _2 =\frac{1}{\Gamma (1-\varepsilon )}$ in (33), we have

$$\begin{aligned} \frac{\mathop {\left\langle \hbox {C} \right\rangle }\nolimits _{\mathrm{ORA}}^{\mathrm{(BC)}} }{\hbox {B}}=\frac{\log _2 e}{2\varepsilon \Gamma }\int \limits _0^\infty {\log _e (1+\gamma )\left( {\exp \left( {-\eta _1 \gamma } \right) -\exp \left( {-\eta _2 \gamma } \right) } \right) } d\gamma . \end{aligned}$$

(34)

Integrating the above equation, we obtain the expression for capacity for ORA policy as in (8).

Substituting (2) into Equation (46) of [18], we have

$$\begin{aligned} \frac{\mathop {\left\langle \hbox {C} \right\rangle }\nolimits _{\mathrm{CIFR}}^{\mathrm{(BC)}} }{\hbox {B}}=\log _2 \left[ {1+\frac{2\Gamma \varepsilon }{\int \nolimits _0^\infty {\frac{\left[ {\exp \left( {-\frac{\gamma }{\Gamma (1+\varepsilon )}} \right) -\exp \left( {-\frac{\gamma }{\Gamma (1-\varepsilon )}} \right) } \right] }{\gamma }d\gamma } }} \right] . \end{aligned}$$

(35)

Since the closed-form expression is not possible for $\int \nolimits _0^\infty {\frac{\exp \left( {-\gamma } \right) }{\gamma }d\gamma }$, we find the numerical limits for $\upgamma$ through simulation, and substitute the minimum and maximum values as limits to give

$$\begin{aligned} \frac{\mathop {\left\langle \hbox {C} \right\rangle }\nolimits _{\mathrm{CIFR}}^{\mathrm{(BC)}} }{\hbox {B}}=\log _2 \left[ {1+\frac{2\Gamma \varepsilon }{\int \nolimits _{\gamma _{\min } }^{\gamma _{\max } } {\frac{\left[ {\exp \left( {-\eta _1 \gamma } \right) -\exp \left( {-\eta _2 \gamma } \right) } \right] }{\gamma }d\gamma } }} \right] . \end{aligned}$$

(36)

Using Eq. (3) of Section 3.352 in [20], we obtain the expression for capacity of CIFR policy as in (9). Substituting (35) into Eq. (47) of [18], we have

$$\begin{aligned} \frac{\mathop {\left\langle \hbox {C} \right\rangle }\nolimits _{\mathrm{TIFR}}^{\mathrm{(BC)}} }{\hbox {B}}=\log _2 \left[ {1+\frac{2\Gamma \varepsilon }{\int \nolimits _{\gamma _0 }^\infty {\frac{\left[ {\exp \left( {-\frac{\gamma }{\Gamma (1+\varepsilon )}} \right) -\exp \left( {-\frac{\gamma }{\Gamma (1-\varepsilon )}} \right) } \right] }{\gamma }d\gamma } }} \right] . \end{aligned}$$

(37)

Making change of variables in the integral of (37), we have

$$\begin{aligned} \frac{\mathop {\left\langle \hbox {C} \right\rangle }\nolimits _{\mathrm{TIFR}}^{\mathrm{(BC)}} }{\hbox {B}}=\log _2 \left[ {1+\frac{2\Gamma \varepsilon }{\int \nolimits _{\gamma _0 }^\infty {\frac{\left[ {\exp \left( {-\eta _1 \gamma } \right) -\exp \left( {-\eta _2 \gamma } \right) } \right] }{\gamma }d\gamma } }} \right] . \end{aligned}$$

(38)

From Eq. (2) of section 3.352 on p. 343 in [20], we obtain the expression for capacity of TIFR policy as in (10).

Appendix 2

Figure 2a, b through Fig. 5a, b show the simulation of the system through the steps discussed below.

Step 1: The base for the simulation is to find out numerical instantaneous SNRs ($\upgamma )$. This is obtained from the CDF of the received instantaneous SNR ($\upgamma )$ for branch correlation at the output of two branch system given in (2), i.e.

$$\begin{aligned} \hbox {F}_2^{\mathrm{(BC)}} (\gamma )=1-\frac{1}{2\varepsilon }\left[ {(1+\varepsilon )\exp \left( {-\frac{\gamma }{\Gamma (1+\varepsilon )}} \right) -(1-\varepsilon )\exp \left( {-\frac{\gamma }{\Gamma (1-\varepsilon )}} \right) } \right] . \end{aligned}$$

(39)

Step 2: The CDF is equated to a uniform random number. Then, 10$^{6}$ Uniform random numbers are generated using rand command in MATLAB.

Step 3: The maximum and minimum values of U are found out.

Step 4: The maximum value of received SNR $(\upgamma _{\mathrm{max}})$ and the minimum value of received SNR $(\upgamma _{\mathrm{min}})$ are found for different values of Individual Branch SNRs $({\Gamma })$, different values of Correlation $(\upvarepsilon )$ and different number of diversity orders (M) as tabulated below.

M $=$ 2; $\bar{\gamma }=$ 5 dB				M $=$ 2; $\upvarepsilon = 0.5$
E	$\upgamma _{\mathrm{max}}$	$\upgamma _{\mathrm{min}}$	Range	$\bar{\gamma }$	$\upgamma _{\mathrm{max}}$	$\upgamma _{\mathrm{min}}$	Range
0.1	37	0.0375	36.9625	1	18	0.0135	17.9865
0.2	38	0.037	37.963	2	22	0.0165	21.9835
0.3	40	0.036	39.964	3	28	0.0207	27.9793
0.4	42	0.0354	41.9646	4	35	0.026	34.974

Step 5: Using the maximum and minimum values of instantaneous SNRs $(\upgamma )$, the capacity for all four policies is obtained for different values of ${\Gamma }, \upvarepsilon$ and M by approximating the integral as a numerical summation from $\upgamma _{\mathrm{min}}$ to $\upgamma _{\mathrm{max}}$ in steps of 0.001.

Step 6: The simulated capacity values for all four policies for different values of correlation, $\upvarepsilon$, at ${\Gamma } = 5 \hbox {dB}$ are compared with the corresponding analytical results for the above four cases. Figure 1a, b through Fig. 4a, b show the analytical versus simulated graphs for capacity for the case of impairments due to branch correlation errors.