Ergodic Channel Capacity for Rayleigh Fading Channels with Impairments Due to Errors in M-Branch Hybrid Diversity Combining

Abstract

Novel closed-form expressions are derived for Ergodic channel capacity for fading channels with impairments due to combining errors for M-branch Rayleigh fading with Generalized Diversity Combining. Four different adaptation policies are analyzed for (1) maximal ratio combining (MRC) diversity, (2) spread spectrum (SS) diversity with MRC and Antenna diversity with selection combining (SC), and (3) SS diversity with SC and Antenna diversity with MRC diversity reception cases. Correlation is defined physically as the similarity between the channel coefficients of the pilot and the message. If the pilot and the message are highly correlated, we have a high system performance. Optimal power and rate adaptation policy yields the best spectrum efficiency, while channel inversion with fixed rate policy suffers the highest penalty in comparison to other policies.

1 Introduction

Each of the M receive antennas in a diversity array provides an independent signal to a M-branch diversity combiner which then operates on the assembly of signals to produce the most favorable result. But in practical systems, correlation between signals in different paths exists. Information-theoretic studies on spatially correlated multiple input multiple output (MIMO) channels have also considered covariance feedback systems. Since the statistics of channel realizations change more slowly than the instantaneous channel gains, it is practical for the receiver to accurately measure the channel covariance matrix and feed it back to the transmitter at a negligible cost [1]. Diversity methods require that a number of transmission paths be available, all carrying the same message, but having independent fading statistics [2]. Proper combination of the signals from these transmission paths yields a resultant received with greatly reduced severity of fading and correspondingly improved reliability of transmission.

1.1 Overview

In general, the analysis of mean signal-to-noise ratio (SNR) of the combined signal is based on the assumption that the faded signals at the various branches are uncorrelated. In some cases, the antennas in the diversity array could be improperly positioned, or frequency separation between diversity signals could be too small [2]. It is thus important to examine possible deterioration in the performance of a diversity system when diversity branch signals are correlated to a certain extent. It is observed that a moderate amount of correlation among diversity branches is not too damaging. Owing to the rarity of deep fades in any event, it would require a very high degree of correlation between the two faded signals to bring about a higher correspondence between the deep fades [2].

Most diversity combining schemes assume that combining mechanisms operate perfectly. Since information needed to operate a combiner is extracted in some way from the signals themselves, there is a possibility of making an error, thus not completely achieving expected performance. This effect has been studied in detail [3] for the particular case of the MRC combiner. This paper deals with effects of the above combining errors in Generalized Combining schemes like MRC-SC and SC-MRC. The results are compared with that of the normal MRC case and are proved to be better compared to it.

1.2 Literature Survey

In earlier work [4], the behavior of eigenmodes of a MIMO Rayleigh channel and power levels allocated to them through the water-filling algorithm with SNR and channel correlation, was analyzed. Capacity of channel eigenmodes and total channel capacity were studied to find that the strongest eigenmode of a channel matrix increases with correlation, while other channel eigenmodes correspondingly decrease with correlation. Mareef and Aissa investigated [5] how spatial fading correlation and keyhole condition affected the capacity of MIMO channels when instantaneous Channel State Information at the Transmitter (CSIT) and Channel State Information at the Receiver (CSIR) were available. Later, capacity analysis of a MIMO Rayleigh channel with spatial correlation at the receiver of multipath signals taken into account was presented [6]. The incremental improvement of a correlated Rayleigh channel is reduced by increasing spatial fading correlation. Krone and Fettvies studied [7] the capacity of orthogonal frequency division multiplexing (OFDM) systems that are impaired by transceiver I/Q imbalance of low cost mobile terminals. Closed-form expressions were derived for ergodic system capacity and outage probability, considering different types of Rayleigh fading channels.

More recently [8], the channel capacity of a dual branch MRC diversity system over correlated waveform intensity, characterized as correlated Nakagami-m distribution, was evaluated. The closed-form expressions for channel capacity performance were provided with a probability density function (PDF) based approach. Choi et al. [9] considered a severely fading MIMO channel and showed that the coefficients of channel amplitude variations predicted the mutual information on the link for different channel models. A closed-form expression for the probability of error in a coherent Binary Phase Shift Keying (BPSK) system over Generalized Rayleigh fading channels was derived [10]. An L-branch equal gain combining (EGC) diversity scheme was used. Theoretical results for the probability of error were plotted for various values of number of degrees of freedom (n) and diversity order (L).

The performance of Antenna Selection (AS) systems with imperfect CSI caused by Gaussian errors and Doppler spread was analysed [11]. Exact bit-error rate (BER) expression for the Antenna Selection system was derived using space-time coding transmission scheme. Bhaskar [12] analyzed Ergodic channel capacity for Generalized Rayleigh fading channels with MRC diversity for four types of adaptation policies. A novel virtual branch technique was proposed [13] to succinctly derive the mean and variance of the combined output SNR for hybrid SC/MRC (H-S/MRC) in a multipath-fading environment. Analytical expressions for the symbol error probability (SEP) for the H-S/MRC diversity system in multipath-fading wireless environments was derived by Win et al [14]. Calmon and Yacoub [15] presented and investigated a general diversity combining scheme, namely MRC signals (MRCS), in which maximal-ratio combined signals were chosen on a selection combining basis. The performance of diversity combining and adaptive combining schemes were investigated in [16]. Based on these results, a hybrid combining scheme was proposed for a dual smart antenna system at handsets for the 3GPP WCDMA system, and presented the performance of a hybrid combining scheme. A general expression for BER of a pre-detection EGC receiver for coherent BPSK modulation in an exponentially correlated Nakagami-m fading channel for an arbitrary number of branches was presented in [17]. Performance analysis of two hybrid SC-MRC diversity receivers over Nakagami-m fading channels with a flat multipath intensity profile was presented [18] and numerically compared with that of the conventional SC and MRC schemes. Annamalai et al. [19] examined the impact of Gaussian distributed weighting errors on both output statistics of a H-S/MRC receiver and the degradation of the average symbol error rate (ASER) performance was observed compared to the ideal case. A new diversity technique that combines SC-MRC, SC-EGC, SC-EGC, SC-MRC was presented in [20]. The proposed scheme will have a better frame error rate (FER) performance than those of SC and MRC schemes, respectively. The BER performance of a GSC receiver [21] for M-ary Non-Coherent Frequency Shift Keying (NCFSK) signals on i.i.d Rayleigh fading channels with L antennas at the receiver was proposed and analyzed (Figs. 1, 2).

Fig. 1

Block diagram of SC-MRC diversity

Fig. 2

Block diagram of MRC-SC diversity

In this paper, we discuss the impairments due to combining errors for the three cases of diversity combining, namely, (1) MRC system (2) SS diversity with MRC and Antenna diversity with SC, and (3) SS diversity with SC and Antenna diversity with MRC, and, how the effects of impairments can be reduced using the four different adaptation policies which adapt Power and Rate, known as Optimal Power and Rate Adaptation (OPRA) policy, fixing power and adapting Rate alone, known as Optimal Rate Adaptation (ORA) policy, channel inversion with fixed rate (CIFR) policy, and truncated channel inversion with fixed rate (TIFR) policies. From the results, it is confirmed that OPRA policy outperforms other three policies.

1.3 Organization of the Paper

Section 2 presents the expressions for spectral efficiencies for impairments due to combining errors for the various policies for the classic MRC case. Section 3 derives the cumulative density function (CDF), and PDF of capacity for impairments due to combining errors for SS diversity with MRC, and Antenna diversity with SC case. Section 4 derives the CDF and PDF of capacity for impairments due to combining errors for SS diversity with SC and Antenna diversity with MRC cases. Section 5 presents the results which are computed through numerical methods using MATLAB for all the three cases of impairments. Finally, Section 6 presents the conclusions.

2 Maximal Ratio Combining of Impairments in Errors

The PDF of instantaneous received SNR, γ, at the output of M-branch MRC when the correlation between the pilot and message signals are not perfect, i.e., 0 < ρ < 1. In other words, the PDF of MRC diversity of impairments in errors is expressed as (page 328 of [2])

$$ \mathop f\nolimits_{\text{M}}^{{ ( {\text{CE)}}}} (\gamma ) = \frac{{\left( {1 - \rho^{2} } \right)^{M - 1} \exp \left( { - \frac{\gamma }{{\bar{\gamma }}}} \right)}}{{\bar{\gamma }}}\sum\limits_{n = 0}^{M - 1} {\left( \begin{aligned} M - 1 \hfill \\ n \hfill \\ \end{aligned} \right)\frac{1}{n!}\left( {\frac{{\gamma \rho^{2} }}{{\bar{\gamma }\left( {1 - \rho^{2} } \right)}}} \right)^{n} } , $$

(1)

where M is the number of diversity branches, ρ is the correlation between the envelopes of two single sinusoid frequencies of the pilot and the message transmitted over a medium, $\bar{\gamma }$ is the average Individual branch SNR, and CE is an acronym for Combining Errors. The average SNR of M-branch MRC output is given by $\left\langle \gamma \right\rangle = \bar{\gamma }$ [1 + (M − 1) ρ²] as shown on page 328 of [2]. It is to be noted that if the pilot and message signals are uncorrelated, then ρ = 0, and is considered as the worst case, and if ρ = 1, the pilot and message signals are perfectly correlated which is the best case.

The CDF of the received instantaneous SNR, γ, for imperfect correlation between pilot and message is given as

$$ {\text{F}}_{\text{M}}^{{({\text{CE}})}} (\gamma ) = 1 - \exp \left( { - \frac{\gamma }{{\bar{\gamma }}}} \right)\sum\limits_{n = 0}^{M - 1} {\left( \begin{aligned} M -1 \\ n \quad \\ \end{aligned} \right)\rho^{2n} \left( {1 - \rho^{2} } \right)^{M - 1 - n} \sum\limits_{k = 0}^{n} {\frac{1}{k!}} \left( {\frac{\gamma }{{\bar{\gamma }}}} \right)}^{k} . $$

(2)

For MRC combining, the pilot signal frequency is chosen and transmitted adjacent to the message band. The phase and amplitude of the pilot signal are sensed and used to adjust the weighting factors of the individual branches [2]. In the practical scenario, the fading of the pilot is different from fading of the message which causes imperfect correlation between them. The reason for imperfect correlation is due to large frequency separation between the message and the pilot signal. In this case, the complex weighting factors would be in error, and degrades the system performance [2].

2.1 Optimal Power and Rate Adaptation (OPRA) Policy

The Ergodic channel capacity of a fading channel under average transmit power constraint, and using received SNR PDF, $f\left( \gamma \right)$, is obtained using Equation (7) of [22] as

$$ \frac{{\left\langle {\text{C}} \right\rangle_{\text{OPRA}} }}{B} = \int\limits_{{\gamma_{0} }}^{\infty } {\log_{2} \left( {\frac{\gamma }{{\gamma_{0} }}} \right)} f(\gamma )d\gamma , $$

(3)

where $\gamma_{0}$ is the optimal cut-off SNR level below which data transmission is suspended. This optimal cut-off SNR, $\gamma_{0}$, must satisfy [23].

$$ \int\limits_{{\gamma_{0} }}^{\infty } {\left( {\frac{1}{{\gamma_{0} }} - \frac{1}{\gamma }} \right)\mathop f\nolimits_{M}^{(CE)} (\gamma )d\gamma = 1} . $$

(4)

Here, $\gamma_{0}$ is computed through numerical iterative search. From Equation (14) of [22], we have $\Im_{n} \left( \mu \right) = \int\limits_{1}^{\infty } {t^{n - 1} \ln t\exp \left( { - \mu t} \right)dt,\mu > 0,\;\forall n = 1,{\kern 1pt} 2, \ldots }$. Further, from Equation (64) of [22], $\Im_{n} \left( \mu \right) = \frac{(n - 1)!}{{\mu^{n} }}\sum\nolimits_{k = 0}^{n - 1} {\frac{\varGamma (k,\mu )}{k!}}$. Using this relation in (3) and simplifying, we have

$$ \frac{{\mathop {\left\langle {\text{C}} \right\rangle }\nolimits_{\text{OPRA}}^{{({\text{CE}})}} }}{B} = \left( {1 - \rho^{2} } \right)^{M - 1} \log_{2} (e)\sum\limits_{n = 0}^{M - 1} {\left( \begin{array}{l} M - 1 \hfill \\ n \hfill \\ \end{array} \right)\left( {\frac{{\rho^{2} }}{{1 - \rho^{2} }}} \right)^{n} \sum\limits_{k = 0}^{n} {\frac{\varGamma (k,\mu )}{k!}} } , $$

(5)

where $\varGamma (x,\alpha ) = \int\limits_{x}^{\infty } {e^{ - t} t^{\alpha - 1} dt}$ is the incomplete gamma function in [23], i.e.,

$$ \frac{{\mathop {\left\langle {\text{C}} \right\rangle }\nolimits_{\text{OPRA}}^{{({\text{CE}})}} }}{B} = \left( {1 - \rho^{2} } \right)^{M - 1} \log_{2} (e)\sum\limits_{n = 0}^{M - 1} {\left( \begin{array}{l} M - 1 \hfill \\ n \hfill \\ \end{array} \right)\left( {\frac{{\rho^{2} }}{{1 - \rho^{2} }}} \right)^{n} \left( {E_{1} (\mu ) + \sum\limits_{k = 1}^{n} {\frac{{P_{k} (\mu )}}{k}} } \right)} , $$

(6)

where B [Hz] is the channel bandwidth, $E_{i} \left( x \right) = - \int\limits_{ - x}^{\infty } {\frac{{e^{ - t} dt}}{t}}$ is the exponential integral function [23], $E{}_{1}(x) = - E_{i} (x),$ P(.) is the Poisson distribution, and $\mu = \frac{{\gamma_{0} }}{{\bar{\gamma }}}$.

To adapt power, the channel fade level must be known at the transmitter, and to adapt rate, the channel fade level must be known at the receiver. Accordingly, higher power levels and rates are allocated to good channels with large γ, and lower power levels and rates are allocated to bad channels with small γ. Data transmission is suspended when $\gamma < \gamma_{0}$, and a probability of outage, $P_{out}$, equal to the probability of no transmission is obtained as

$$ {\mathbf{P}}_{\text{out}} = P\left( {\gamma < \gamma_{0} } \right) = \int\limits_{0}^{{\gamma_{0} }} {f(\gamma )d\gamma } = 1 - \int\limits_{{\gamma_{0} }}^{\infty } {f(\gamma )d\gamma } . $$

(7)

Substituting (1) into (7), we have

$$ {\mathbf{P}}_{\text{out}}^{{({\text{CE}})}} = 1 - \left( {1 - \rho^{2} } \right)^{M - 1} \sum\limits_{n = 0}^{M - 1} {\left( \begin{array}{l} M - 1 \hfill \\ n \hfill \\ \end{array} \right)\frac{{\delta^{n} }}{n!}\varGamma \left( {n + 1,\frac{{\gamma_{0} }}{{\bar{\gamma }}}} \right)} . $$

(8)

2.2 Optimal Rate Adaptation (ORA) Policy

The ergodic channel capacity for rate adaptation along with constant transmit power becomes

$$ \frac{{\mathop {\left\langle {\text{C}} \right\rangle }\nolimits_{\text{ORA}}^{{({\text{CE}})}} }}{B} = \int\limits_{0}^{\infty } {\log_{2} (1 + \gamma )f(\gamma )d\gamma } , $$

(9)

i.e.,

$$ \frac{{\mathop {\left\langle {\text{C}} \right\rangle }\nolimits_{\text{ORA}}^{{({\text{CE}})}} }}{B} = \frac{{\left( {1 - \rho^{2} } \right)^{M - 1} }}{{\bar{\gamma }}}\log_{2} (e)\sum\limits_{n = 0}^{M - 1} {\frac{1}{n!}\left( \begin{array}{l} M - 1 \hfill \\ n \hfill \\ \end{array} \right)\left( {\frac{{\rho^{2} }}{{\bar{\gamma }\left( {1 - \rho^{2} } \right)}}} \right)^{n} I_{n + 1} \left( \zeta \right)} , $$

(10)

where $I_{n} \left( \zeta \right) = \int\limits_{0}^{\infty } {t^{n - 1} \ln (1 + t)\exp ( - \zeta t)dt;\;\zeta = \frac{1}{{\bar{\gamma }}} > 0;\quad n = 1,2, \ldots }$ is given by Equation (32) of [22]. Equation (9) represents the capacity of a fading channel without transmitter feedback, i.e., with the channel fade level known at the receiver only. Using Equation (78) of [22] in (10) for $I_{n + 1} \left( . \right)$, we have

$$ \frac{{\mathop {\left\langle {\text{C}} \right\rangle }\nolimits_{\text{ORA}}^{{({\text{CE}})}} }}{B} = \left( {1 - \rho^{2} } \right)^{M - 1} \log_{2} (e)\sum\limits_{n = 0}^{M - 1} {\left( \begin{array}{l} M - 1 \hfill \\ \quad n \hfill \\ \end{array} \right)\left( {\frac{{\rho^{2} }}{{1 - \rho^{2} }}} \right)^{n} e^{\zeta } \sum\limits_{l = 0}^{n} {\varGamma ( - n - l,\zeta )} \zeta^{n - l} } . $$

(11)

2.3 Channel Inversion with Fixed Rate (CIFR) Policy

CIFR policy is a suboptimal transmitter adaptation scheme where the transmitter uses CSI to maintain a constant received power, i.e., it equalizes channel fading. The channel then appears to be a time-invariant AWGN channel to the encoder and the decoder [24]. Perfect channel estimates must be available at the transmitter and receiver to improve system performance using this scheme. Using Equation (46) of [22], the capacity per unit bandwidth with CIFR policy is obtained from

$$ \frac{{\mathop {\left\langle {\text{C}} \right\rangle }\nolimits_{\text{CIFR}}^{(CE)} }}{\text{B}} = \log_{2} \left( {1 + \frac{1}{{\int\limits_{0}^{\infty } {\frac{{f_{\text{M}}^{{ ( {\text{CE)}}}} (\gamma )}}{\gamma }d\gamma } }}} \right), $$

(12)

i.e.,

$$ \frac{{\mathop {\left\langle {\text{C}} \right\rangle }\nolimits_{\text{CIFR}}^{(CE)} }}{\text{B}} = \log_{2} \left( {1 + \frac{{\bar{\gamma }}}{{\left( {1 - \rho^{2} } \right)^{M - 1} \sum\limits_{n = 0}^{M - 1} {\frac{1}{n}\left( \begin{array}{l} M - 1 \hfill \\ n \hfill \\ \end{array} \right)\left( {\frac{{\rho^{2} }}{{1 - \rho^{2} }}} \right)^{n} } }}} \right). $$

(13)

2.4 Truncated Channel Inversion with Fixed Rate (TIFR) Policy

CIFR policy is less efficient for deep channel fading conditions as a large amount of power is required at the transmitter to compensate for deep channel fades. TIFR policy is an improved version of channel inversion policy which equalizes channel fading only above a fixed cut-off fade depth, γ₀. The ergodic channel capacity with TIFR policy is derived using Equation (47) in [22] as

$$ \frac{{\mathop {\left\langle {\text{C}} \right\rangle }\nolimits_{\text{TIFR}}^{{}} }}{\text{B}} = \log_{2} \left( {1 + \frac{1}{{\int\limits_{{\gamma_{0} }}^{\infty } {\frac{{\mathop f\nolimits_{M}^{(CE)} (\gamma )}}{\gamma }d\gamma } }}} \right)\left( {1 - {\text{P}}_{\text{out}} } \right). $$

(14)

The cut-off level SNR, $\gamma_{0}$, can be selected to achieve a specified minimum outage probability in order to maximize (14). Substituting (1) and (8) into (14) and simplifying, we have

$$ \begin{aligned} \frac{{\mathop {\left\langle {\text{C}} \right\rangle }\nolimits_{\text{TIFR}}^{{ ( {\text{CE)}}}} }}{\text{B}} & = \log_{2} \left( {1 + \frac{1}{{\frac{{\left( {1 - \rho^{2} } \right)^{M - 1} }}{{\bar{\gamma }}}\sum\limits_{n = 0}^{M - 1} {\frac{1}{n!}\left( \begin{array}{l} M - 1 \hfill \\ n \hfill \\ \end{array} \right)\left( {\frac{{\rho^{2} }}{{1 - \rho^{2} }}} \right)^{n} \varGamma \left( {n,\frac{{\gamma_{0} }}{{\bar{\gamma }}}} \right)} }}} \right) \\ & \quad \times \, \left[ {\left( {1 - \rho^{2} } \right)^{M - 1} \sum\limits_{n = 0}^{M - 1} {\left( \begin{array}{l} M - 1 \hfill \\ n \hfill \\ \end{array} \right)\frac{{\delta^{n} }}{n!}\varGamma \left( {n + 1,\frac{{\gamma_{0} }}{{\bar{\gamma }}}} \right)} } \right]. \\ \end{aligned} $$

(15)

3 SC-MRC Diversity of Impairments in Errors

Hybrid SC-MRC is a reduced-complexity diversity combining scheme, where M largest SNRs out of a total of N diversity branches are selected and combined using MRC. This technique provides improved performance over a branch MRC scheme when additional diversity is available without requiring additional electronics and/or power consumption. The main motivation behind this suboptimal hybrid scheme is to approach the performance provided by MRC with a less complex receiver. The PDF of SC combining of N branches to give a resultant signal is given as [2]

$$ f(\gamma ) = \frac{N}{{\bar{\gamma }}}\left( {1 - \exp \left( { - \frac{\gamma }{{\bar{\gamma }}}} \right)} \right)^{N - 1} \exp \left( { - \frac{\gamma }{{\bar{\gamma }}}} \right), $$

(16)

where M such resultant signals are then MRC combined, the overall resultant signal is given as

$$ \gamma_{overall} = \sum\limits_{k = 1}^{M} {\gamma_{k} } . $$

(17)

Combining (16) and (17) along with combining error conditions provides the PDF of SC-MRC combining as follows:

$$ f(\gamma ) = \frac{{(M(1 - \rho^{2} ))^{N} }}{{\bar{\gamma }^{N} }}\left( {1 - (1 - \rho^{2} )\exp \left( { - \frac{\gamma }{{\bar{\gamma }}}} \right)} \right)^{NM - 1} \exp \left( { - \frac{N\gamma }{{\bar{\gamma }}}} \right). $$

(18)

Applying the four different adaptation policies for SC-MRC combining provides the following spectrum efficiency expressions:

Substituting (18) into (3) and simplifying using Equation (2) in Section 4.331 of [23], the ergodic channel capacity for OPRA policy is given as

$$ \frac{{\mathop {\left\langle {\text{C}} \right\rangle }\nolimits_{\text{OPRA}}^{{}} }}{B} = \frac{{(M(1 - \rho^{2} ))^{N} }}{{\bar{\gamma }^{N} \log (2)\gamma_{0} }}\sum\limits_{k = 0}^{N(M - 1) - 1} {\left( \begin{array}{l} N(M - 1) - 1 \hfill \\ k \hfill \\ \end{array} \right)( - (1 - \rho^{2} ))^{k} \left[ {\frac{{\bar{\gamma }}}{{\gamma_{0} (k + N)}}} \right]} {\text{E}}_{\text{i}} \left( { - \frac{{\gamma_{0} (k + N)}}{{\bar{\gamma }}}} \right). $$

(19)

To obtain the ergodic capacity for ORA policy, we substitute (18) into (9) and simplify it using Equation (2) in Section 4.337 of [23] as

$$ \frac{{\mathop {\left\langle {\text{C}} \right\rangle }\nolimits_{\text{ORA}}^{{}} }}{B} = \frac{{(M(1 - \rho^{2} ))^{N} }}{{\bar{\gamma }^{N} \log (2)}}\sum\limits_{k = 0}^{N(M - 1) - 1} {\left( \begin{array}{l} N(M - 1) - 1 \hfill \\ k \hfill \\ \end{array} \right)( - (1 - \rho^{2} ))^{k} \left[ { - \frac{{\bar{\gamma }}}{(k + N)}} \right]\exp \left( {\frac{(k + N)}{{\bar{\gamma }}}} \right)} {\text{E}}_{\text{i}} \left( { - \frac{(k + N)}{{\bar{\gamma }}}} \right). $$

(20)

The ergodic capacity for CIFR policy is obtained by substituting (18) into (12), and simplifying using Equation (5) in Section 3.351 of [23] as given by

$$ \frac{{\mathop {\left\langle {\text{C}} \right\rangle }\nolimits_{\text{CIFR}}^{{}} }}{\text{B}} = \log \;_{2} \left( {1 + \frac{1}{{\frac{{(M(1 - \rho^{2} ))^{N} }}{{\bar{\gamma }^{N} }}\sum\limits_{k = 0}^{N(M - 1) - 1} {\left( {N(M - 1) - 1k} \right)( - (1 - \rho^{2} ))^{k} \left( {{\text{E}}_{\text{i}} \left( { - \frac{{(k + N)\gamma_{\hbox{max} } }}{{\bar{\gamma }}}} \right) - {\text{E}}_{\text{i}} \left( { - \frac{{(k + N)\gamma_{\hbox{min} } }}{{\bar{\gamma }}}} \right)} \right)} }}} \right). $$

(21)

The outage probability associated with SC-MRC diversity is obtained by substituting (18) into (6) and simplifying as

$$ {\text{P}}_{\text{out}} = \frac{{(M(1 - \rho^{2} ))^{N} }}{{\bar{\gamma }^{N} }}\sum\limits_{k = 0}^{N(M - 1) - 1} {\left( \begin{aligned} N(M - 1) - 1 \\ k \quad \\ \end{aligned} \right)( - (1 - \rho^{2} ))^{k} \left[ { - \frac{{\bar{\gamma }}}{(k + N)}} \right]} { \exp }\left( { - \frac{{\gamma_{0} (k + N)}}{{\bar{\gamma }}}} \right). $$

(22)

Now, the ergodic capacity for TIFR policy, $\frac{{\mathop {\left\langle {\text{C}} \right\rangle }\nolimits_{\text{TIFR}}^{{}} }}{\text{B}}$, is obtained by substituting (18) into (14), and simplifying using Equation (5) in Section 3.351 of [23] as given by

$$ \frac{{\mathop {\left\langle {\text{C}} \right\rangle }\nolimits_{\text{TIFR}}^{{}} }}{\text{B}} = \log_{2} \left( {1 + \frac{1}{{\frac{{(M(1 - \rho^{2} ))^{N} }}{{\bar{\gamma }^{N} }}\sum\limits_{k = 0}^{N(M - 1) - 1} {\left( \begin{array}{l} N(M - 1) - 1 \hfill \\ k \hfill \\ \end{array} \right)( - (1 - \rho^{2} ))^{k} {\text{Ei}}\left( { - \frac{{(k + N)\gamma_{0} }}{{\bar{\gamma }}}} \right)} }}} \right). $$

(23)

4 MRC-SC Diversity of Impairments in Combining Errors

In a technique named MRC-SC, the outputs of N different M_i- branch maximal ratio combiners for i = 1, 2,…, N are combined into a N-branch selection combiner. The MRC-SC scheme has two very attractive key features: (1) it can be readily applied to situations in which diversity exists, and (2) it is mathematically easily tractable. In soft handoff processes, such as, in Universal Mobile Telecommunications System (UMTS), the MRC-SC technique is already employed with the serving base stations (BSs) providing the maximal ratio combined signals received from a mobile terminal, and the serving switching center carrying out selection combining of the resultant maximal ratio combined signals [25, 26]. The main results of the current work is the derivation of an exact closed-form expression for the capacity in the presence of combining errors at the output of the MRC-SC combiner for a Rayleigh fading scenario.

The CDF of MRC combining of M branches to give a resultant signal is given as [2]

$$ F(\gamma ) = 1 - (1 - \rho^{2} )\exp \left( { - \frac{\gamma }{{\bar{\gamma }}}} \right)\sum\limits_{k = 0}^{M - 1} {\frac{1}{k!}} \left( {\frac{\gamma }{{\bar{\gamma }}}} \right)^{k} . $$

(24)

Here, N such resultant signals are then SC combined to provide the overall resultant CDF:

$$ F(\gamma_{overall} ) = \left( {F(\gamma )} \right)^{N} . $$

(25)

Now, selection combining of these N resultant signals provides a PDF as follows:

$$ f(\gamma_{overall} ) = N\left( {F(\gamma )} \right)^{N - 1} f(\gamma ), $$

(26)

i.e.

$$ \begin{aligned} f(\gamma ) & = N\left( {1 - (1 - \rho^{2} )\exp \left( { - \frac{\gamma }{{\bar{\gamma }}}} \right)\sum\limits_{k = 0}^{M - 1} {\frac{1}{k!}} \left( {\frac{\gamma }{{\bar{\gamma }}}} \right)^{k} } \right)^{N - 1} \frac{{(1 - \rho^{2} )}}{{\bar{\gamma }}}\exp \left( { - \frac{\gamma }{{\bar{\gamma }}}} \right) \\ & \quad \times \left( {\sum\limits_{k = 0}^{M - 1} {\frac{1}{k!}} \left( {\frac{\gamma }{{\bar{\gamma }}}} \right)^{k} - \sum\limits_{k = 0}^{M - 1} {\frac{k}{k!}} \left( {\frac{\gamma }{{\bar{\gamma }}}} \right)^{k - 1} } \right). \\ \end{aligned} $$

(27)

Since the above PDF becomes complicated mathematically for higher values of M and N, we limit our research to specific cases of M = 2, 3, 4 and N = 2 in this paper. The PDFs for these specific values are given as follows:

The PDF for N = 2 and M = 2 MRC-SC diversity is given as

$$ f^{2,2} (\gamma ) = \frac{{2(1 - \rho^{2} )}}{{\bar{\gamma }}}\exp \left( { - \frac{\gamma }{{\bar{\gamma }}}} \right)\frac{\gamma }{{\bar{\gamma }}} - (1 - \rho^{2} )\exp \left( { - \frac{2\gamma }{{\bar{\gamma }}}} \right)\frac{\gamma }{{\bar{\gamma }}} - (1 - \rho^{2} )\exp \left( { - \frac{2\gamma }{{\bar{\gamma }}}} \right)\left( {\frac{\gamma }{{\bar{\gamma }}}} \right)^{2} . $$

(28a)

The PDF for N = 2 and M = 3 MRC-SC diversity is given as

$$ \begin{aligned} f^{2,3} (\gamma ) & = \frac{{(1 - \rho^{2} )}}{{\bar{\gamma }}}\exp \left( { - \frac{\gamma }{{\bar{\gamma }}}} \right)\left( {\frac{\gamma }{{\bar{\gamma }}}} \right)^{2} - (1 - \rho^{2} )\exp \left( { - \frac{2\gamma }{{\bar{\gamma }}}} \right)\left( {\frac{\gamma }{{\bar{\gamma }}}} \right)^{2} \\ & \quad - (1 - \rho^{2} )\exp \left( { - \frac{2\gamma }{{\bar{\gamma }}}} \right)\left( {\frac{\gamma }{{\bar{\gamma }}}} \right)^{3} - \frac{{(1 - \rho^{2} )}}{2}\exp \left( { - \frac{2\gamma }{{\bar{\gamma }}}} \right)\left( {\frac{\gamma }{{\bar{\gamma }}}} \right)^{4} . \\ \end{aligned} $$

(28b)

The PDF for N = 2 and M = 4 MRC-SC diversity is given as

$$ \begin{aligned} f^{2,4} (\gamma ) & = \frac{{(1 - \rho^{2} )}}{{3\bar{\gamma }}}\exp \left( { - \frac{\gamma }{{\bar{\gamma }}}} \right)\left( {\frac{\gamma }{{\bar{\gamma }}}} \right)^{3} - (1 - \rho^{2} )\exp \left( { - \frac{2\gamma }{{\bar{\gamma }}}} \right)\left( {\frac{\gamma }{{\bar{\gamma }}}} \right)^{3} - (1 - \rho^{2} )\exp \left( { - \frac{2\gamma }{{\bar{\gamma }}}} \right)\left( {\frac{\gamma }{{\bar{\gamma }}}} \right)^{4} \\ & - \frac{{(1 - \rho^{2} )}}{2}\exp \left( { - \frac{2\gamma }{{\bar{\gamma }}}} \right)\left( {\frac{\gamma }{{\bar{\gamma }}}} \right)^{5} - \frac{{(1 - \rho^{2} )}}{6}\exp \left( { - \frac{2\gamma }{{\bar{\gamma }}}} \right)\left( {\frac{\gamma }{{\bar{\gamma }}}} \right)^{6} . \\ \end{aligned} $$

(28c)

Applying the four different adaptation policies for SC-MRC combining gives the following capacity expressions:

The channel capacity for OPRA policy, $\frac{{\mathop {\left\langle {\text{C}} \right\rangle }\nolimits_{\text{OPRA}}^{{}} }}{B}$, for MRC-SC diversity is obtained by substituting (28) into (3) and simplifying using Equation (2) in Section 4.331of [23] as given for N = 2 and M = 2 MRC-SC diversity as

$$ \frac{{\left\langle {\text{C}} \right\rangle_{\text{OPRA}}^{2,2} }}{B} = \frac{{(2(1 - \rho^{2} ))}}{\log (2)}\left( {\sum\limits_{k = 0}^{1} {\frac{1}{k!}\varLambda^{c} \left( {k,\frac{{\gamma_{0} }}{{\bar{\gamma }}}} \right)} - \frac{{(1 - \rho^{2} )}}{4}\sum\limits_{k = 0}^{1} {\frac{1}{k!}\varLambda^{c} \left( {k,\frac{{2\gamma_{0} }}{{\bar{\gamma }}}} \right) - } \frac{{3(1 - \rho^{2} )}}{8}\sum\limits_{k = 0}^{2} {\frac{1}{k!}\varLambda^{c} \left( {k,\frac{{2\gamma_{0} }}{{\bar{\gamma }}}} \right)} } \right), $$

(29a)

and for N = 2 and M = 3 MRC-SC diversity as

$$ \frac{{\left\langle {\text{C}} \right\rangle_{\text{OPRA}}^{2,3} }}{B} = \frac{{(1 - \rho^{2} )}}{\log (2)}\left( \begin{array}{ll} \sum\limits_{k = 0}^{2} {\frac{2}{k!}\varLambda^{c} \left( {k,\frac{{\gamma_{0} }}{{\bar{\gamma }}}} \right)} - \frac{{(1 - \rho^{2} )}}{4}\sum\limits_{k = 0}^{2} {\frac{1}{k!}\varLambda^{c} \left( {k,\frac{{2\gamma_{0} }}{{\bar{\gamma }}}} \right) - } \frac{{3(1 - \rho^{2} )}}{8}\sum\limits_{k = 0}^{3} {\frac{1}{k!}\varLambda^{c} \left( {k,\frac{{2\gamma_{0} }}{{\bar{\gamma }}}} \right)} \\ \quad- \frac{{3(1 - \rho^{2} )}}{8}\sum\limits_{k = 0}^{4} {\frac{1}{k!}\varLambda^{c} \left( {k,\frac{{2\gamma_{0} }}{{\bar{\gamma }}}} \right)} \\ \end{array} \right), $$

(29b)

and for N = 2 and M = 4 MRC-SC diversity as

$$ \frac{{\left\langle {\text{C}} \right\rangle_{\text{OPRA}}^{2,4} }}{B} = \frac{{(1 - \rho^{2} )}}{\log (2)}\left( \begin{array}{ll} \sum\limits_{k = 0}^{3} {\frac{2}{k!}\varLambda^{c} \left( {k,\frac{{\gamma_{0} }}{{\bar{\gamma }}}} \right)} - \frac{{(1 - \rho^{2} )}}{8}\sum\limits_{k = 0}^{3} {\frac{1}{k!}\varLambda^{c} \left( {k,\frac{{2\gamma_{0} }}{{\bar{\gamma }}}} \right) - } \frac{{(1 - \rho^{2} )}}{8}\sum\limits_{k = 0}^{4} {\frac{1}{k!}\varLambda^{c} \left( {k,\frac{{2\gamma_{0} }}{{\bar{\gamma }}}} \right)} \\ \quad - \frac{{5(1 - \rho^{2} )}}{16}\sum\limits_{k = 0}^{5} {\frac{1}{k!}\varLambda^{c} \left( {k,\frac{{2\gamma_{0} }}{{\bar{\gamma }}}} \right)} - \frac{{5(1 - \rho^{2} )}}{16}\sum\limits_{k = 0}^{6} {\frac{1}{k!}\varLambda^{c} \left( {k,\frac{{2\gamma_{0} }}{{\bar{\gamma }}}} \right)} \\ \end{array} \right), $$

(29c)

respectively. Substituting (28) into (9) and simplifying using Equation (2) in Section 4.337 of [23], we obtain the ergodic channel capacity for ORA policy for N = 2 and M = 2 MRC-SC diversity as

$$ \frac{{\left\langle C \right\rangle_{\text{ORA}}^{2,2} }}{B} = \frac{{(2(1 - \rho^{2} ))}}{{\bar{\gamma }\log (2)}}\left( \begin{array}{ll} \exp \left( {\frac{1}{{\bar{\gamma }}}} \right)\sum\limits_{k = 1}^{2} {\bar{\gamma }^{k - 1} \varLambda^{c} \left( { - 2 + k,\frac{1}{{\bar{\gamma }}}} \right)} - \frac{{(1 - \rho^{2} )}}{{\bar{\gamma }}}\exp \left( {\frac{2}{{\bar{\gamma }}}} \right) \\ \quad\times \sum\limits_{k = 1}^{2} {\left( {\frac{{\bar{\gamma }}}{2}} \right)^{k} \varLambda^{c} \left( { - 2 + k,\frac{2}{{\bar{\gamma }}}} \right) - } \frac{{2(1 - \rho^{2} )}}{{\bar{\gamma }^{2} }}\exp \left( {\frac{2}{{\bar{\gamma }}}} \right)\sum\limits_{k = 1}^{3} {\left( {\frac{{\bar{\gamma }}}{2}} \right)^{k} \varLambda^{c} \left( { - 3 + k,\frac{2}{{\bar{\gamma }}}} \right)} \\ \end{array} \right), $$

(30a)

and for N = 2 and M = 3 MRC-SC diversity as

$$ \frac{{\left\langle {\text{C}} \right\rangle_{\text{ORA}}^{2,3} }}{B} = \frac{{(1 - \rho^{2} )}}{{\bar{\gamma }\log (2)}}\left( \begin{aligned} \left( {\frac{2!}{{\bar{\gamma }^{2} }}} \right)\exp \left( {\frac{1}{{\bar{\gamma }}}} \right)\sum\limits_{k = 1}^{3} {\bar{\gamma }^{k} \varLambda^{c} \left( { - 3 + k,\frac{1}{{\bar{\gamma }}}} \right)} - \frac{{2!(1 - \rho^{2} )}}{{\bar{\gamma }^{2} }}\exp \left( {\frac{2}{{\bar{\gamma }}}} \right)\sum\limits_{k = 1}^{3} {\left( {\frac{{\bar{\gamma }}}{2}} \right)^{k} \varLambda^{c} \left( { - 3 + k,\frac{2}{{\bar{\gamma }}}} \right)} \hfill \\ - \frac{{3!(1 - \rho^{2} )}}{{\bar{\gamma }^{3} }}\exp \left( {\frac{2}{{\bar{\gamma }}}} \right)\sum\limits_{k = 1}^{4} {\left( {\frac{{\bar{\gamma }}}{2}} \right)^{k} \varLambda^{c} \left( { - 4 + k,\frac{2}{{\bar{\gamma }}}} \right) - \frac{{4!(1 - \rho^{2} )}}{{2\bar{\gamma }^{3} }}\exp \left( {\frac{2}{{\bar{\gamma }}}} \right)\sum\limits_{k = 1}^{5} {\left( {\frac{{\bar{\gamma }}}{2}} \right)^{k} \varLambda^{c} \left( { - 5 + k,\frac{2}{{\bar{\gamma }}}} \right)} } \hfill \\ \end{aligned} \right), $$

(30b)

and for N = 2 and M = 4 MRC-SC diversity as

$$ \frac{{\mathop {\left\langle {\text{C}} \right\rangle }\nolimits_{\text{ORA}}^{2,4} }}{B} = \frac{{(1 - \rho^{2} )}}{{3\bar{\gamma }\log (2)}}\left( \begin{aligned} \left( {\frac{3!}{{\bar{\gamma }^{3} }}} \right)\exp \left( {\frac{1}{{\bar{\gamma }}}} \right)\sum\limits_{k = 1}^{4} {\bar{\gamma }^{k} \varLambda^{c} \left( { - 4 + k,\frac{1}{{\bar{\gamma }}}} \right)} - \frac{{3!(1 - \rho^{2} )}}{{\bar{\gamma }^{3} }}\exp \left( {\frac{2}{{\bar{\gamma }}}} \right)\sum\limits_{k = 1}^{4} {\left( {\frac{{\bar{\gamma }}}{2}} \right)^{k} \varLambda^{c} \left( { - 4 + k,\frac{2}{{\bar{\gamma }}}} \right)} \hfill \\ - \frac{{4!(1 - \rho^{2} )}}{{\bar{\gamma }^{4} }}\exp \left( {\frac{2}{{\bar{\gamma }}}} \right)\sum\limits_{k = 1}^{5} {\left( {\frac{{\bar{\gamma }}}{2}} \right)^{k} \varLambda^{c} \left( { - 5 + k,\frac{2}{{\bar{\gamma }}}} \right) - } \frac{{5!(1 - \rho^{2} )}}{{2\bar{\gamma }^{5} }}\exp \left( {\frac{2}{{\bar{\gamma }}}} \right)\sum\limits_{k = 1}^{6} {\left( {\frac{{\bar{\gamma }}}{2}} \right)^{k} \varLambda^{c} \left( { - 6 + k,\frac{2}{{\bar{\gamma }}}} \right)} \hfill \\ - \frac{{6!(1 - \rho^{2} )}}{{2\bar{\gamma }^{6} }}\exp \left( {\frac{2}{{\bar{\gamma }}}} \right)\sum\limits_{k = 1}^{7} {\left( {\frac{{\bar{\gamma }}}{2}} \right)^{k} \varLambda^{c} \left( { - 7 + k,\frac{2}{{\bar{\gamma }}}} \right)} \hfill \\ \end{aligned} \right), $$

(30c)

respectively. The capacity for CIFR policy is obtained by substituting (28) into (12), and simplifying using (5) in Section 3.351 of [23] as given for N = 2 and M = 2 MRC-SC diversity by

$$ \frac{{\mathop {\left\langle {\text{C}} \right\rangle }\nolimits_{\text{CIFR}}^{2,2} }}{B} = \log_{2} \left( {1 + \frac{{2\bar{\gamma }}}{{(1 - \rho^{2} )\left[ {4 - 3(1 - \rho^{2} )} \right]}}} \right), $$

(31a)

and for N = 2 and M = 3 MRC-SC diversity as

$$ \frac{{\mathop {\left\langle {\text{C}} \right\rangle }\nolimits_{\text{CIFR}}^{2,3} }}{B} = \log_{2} \left( {1 + \frac{{16\bar{\gamma }}}{{(1 - \rho^{2} )\left[ {16 - 11(1 - \rho^{2} )} \right]}}} \right), $$

(31b)

and for N = 2 and M = 4 MRC-SC diversity as

$$ \frac{{\mathop {\left\langle {\text{C}} \right\rangle }\nolimits_{\text{CIFR}}^{2,4} }}{B} = \log_{2} \left( {1 + \frac{{48\bar{\gamma }}}{{(1 - \rho^{2} )\left[ {32 - 17(1 - \rho^{2} )} \right]}}} \right), $$

(31c)

respectively. The outage probability associated with SC-MRC diversity is obtained by substituting (28) into (6) and simplifying for N = 2 and M = 2 MRC-SC diversity as

$$ {\text{P}}_{\text{out}}^{ 2 , 2} = 2(1 - \rho^{2} )\left[ {\varLambda \left( {2,\frac{{\gamma_{0} }}{{\bar{\gamma }}}} \right) - \frac{{(1 - \rho^{2} )}}{4}\varLambda \left( {2,\frac{{2\gamma_{0} }}{{\bar{\gamma }}}} \right) - \frac{{(1 - \rho^{2} )}}{8}\varLambda \left( {3,\frac{{2\gamma_{0} }}{{\bar{\gamma }}}} \right)} \right], $$

(32a)

and for N = 2 and M = 3 MRC-SC diversity as

$$ {\text{P}}_{\text{out}}^{ 2 , 3} = (1 - \rho^{2} )\left[ {\varLambda \left( {3,\frac{{\gamma_{0} }}{{\bar{\gamma }}}} \right) - \frac{{(1 - \rho^{2} )}}{4}\varLambda \left( {3,\frac{{2\gamma_{0} }}{{\bar{\gamma }}}} \right) - \frac{{(1 - \rho^{2} )}}{16}\varLambda \left( {4,\frac{{2\gamma_{0} }}{{\bar{\gamma }}}} \right) - \frac{{(1 - \rho^{2} )}}{64}\varLambda \left( {5,\frac{{2\gamma_{0} }}{{\bar{\gamma }}}} \right)} \right] $$

(32b)

and for N = 2 and M = 4 MRC-SC diversity as

$$ {\text{P}}_{\text{out}}^{ 2 , 4} = \frac{{(1 - \rho^{2} )}}{3}\left[ {\varLambda \left( {4,\frac{{\gamma_{0} }}{{\bar{\gamma }}}} \right) - \frac{{(1 - \rho^{2} )}}{16}\varLambda \left( {4,\frac{{2\gamma_{0} }}{{\bar{\gamma }}}} \right) - \frac{{(1 - \rho^{2} )}}{32}\varLambda \left( {5,\frac{{2\gamma_{0} }}{{\bar{\gamma }}}} \right) - \frac{{(1 - \rho^{2} )}}{128}\varLambda \left( {6,\frac{{2\gamma_{0} }}{{\bar{\gamma }}}} \right) - \frac{{(1 - \rho^{2} )}}{768}\varLambda \left( {7,\frac{{2\gamma_{0} }}{{\bar{\gamma }}}} \right)} \right], $$

(32c)

respectively. To obtain the capacity with TIFR policy, $\frac{{\mathop {\left\langle {\text{C}} \right\rangle }\nolimits_{\text{TIFR}}^{{}} }}{B}$, we substitute (28) into (14) and simplify using Equation (5) in Section 3.351 of [23] for N = 2, M = 2 MRC-SC diversity as

$$\begin{aligned} \frac{{\mathop {\left\langle {\text{C}} \right\rangle }\nolimits_{\text{TIFR}}^{2,2} }}{B} &= \log_{2} \left( {1 + \frac{{\bar{\gamma }}}{{2(1 - \rho^{2} )\left[ {\exp \left( { - \frac{{\gamma_{0} }}{{\bar{\gamma }}}} \right) - \frac{{(1 - \rho^{2} )}}{2}\exp \left( { - \frac{{2\gamma_{0} }}{{\bar{\gamma }}}} \right) - \frac{{(1 - \rho^{2} )}}{4}\varLambda^{c} \left( {2,\frac{{2\gamma_{0} }}{{\bar{\gamma }}}} \right)} \right]}}} \right)\\ & \quad \times \left( { 1- {\text{ P}}_{\text{out}}^{ 2 , 2} } \right), \end{aligned}$$

(33a)

and for N = 2 and M = 3 MRC-SC diversity as

$$ \begin{aligned} \frac{{\left\langle C \right\rangle_{\text{TIFR}}^{2,3} }}{B} & = \log_{2} \left( {1 + \frac{{\bar{\gamma }}}{{(1 - \rho^{2} )\left[ {\varLambda^{c} \left( {2,\frac{{\gamma_{0} }}{{\bar{\gamma }}}} \right) - \frac{{(1 - \rho^{2} )}}{4}\varLambda^{c} \left( {2,\frac{{2\gamma_{0} }}{{\bar{\gamma }}}} \right) - \frac{{(1 - \rho^{2} )}}{8}\varLambda^{c} \left( {3,\frac{{2\gamma_{0} }}{{\bar{\gamma }}}} \right) - \frac{{(1 - \rho^{2} )}}{32}\varLambda^{c} \left( {4,\frac{{2\gamma_{0} }}{{\bar{\gamma }}}} \right)} \right]}}} \right) \\ & \quad \times \left( { 1 -{\text{P}}_{\text{out}}^{ 2 , 3} } \right), \\ \end{aligned} $$

(33b)

and for N = 2 and M = 4 MRC-SC diversity as

$$ \begin{aligned} \frac{{\left\langle C \right\rangle_{\text{TIFR}}^{2,4} }}{B} & = \log_{2} \left( {1 + \frac{{3\bar{\gamma }}}{{(1 - \rho^{2} )\left[ {\varLambda^{c} \left( {3,\frac{{\gamma_{0} }}{{\bar{\gamma }}}} \right) - \frac{{(1 - \rho^{2} )}}{8}\varLambda^{c} \left( {3,\frac{{2\gamma_{0} }}{{\bar{\gamma }}}} \right) - \frac{{(1 - \rho^{2} )}}{16}\varLambda^{c} \left( {4,\frac{{2\gamma_{0} }}{{\bar{\gamma }}}} \right) - \frac{{(1 - \rho^{2} )}}{64}\varLambda^{c} \left( {5,\frac{{2\gamma_{0} }}{{\bar{\gamma }}}} \right) - \frac{{(1 - \rho^{2} )}}{384}\varLambda^{c} \left( {6,\frac{{2\gamma_{0} }}{{\bar{\gamma }}}} \right)} \right]}}} \right) \\ & \quad \times \left( { 1 -{\text{ P}}_{\text{out}}^{2,4} } \right). \\ \end{aligned} $$

(33c)

5 Numerical Results

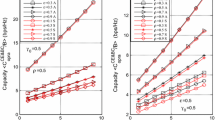
Figure 3a–c show the capacity for OPRA policy versus individual branch SNR for three types of diversity combining methods, namely MRC, MRC-SC, SC-MRC for ρ = 0.5. Figure 4a–c show the capacity for OPRA policy versus individual branch SNR for MRC, MRC-SC, SC-MRC techniques for ρ = 0.7. Figures 3a and 4 how improvement in capacity of almost 2 bps for MRC due to increase in correlation from ρ = 0.5 to ρ = 0.7 and M = 4 which is very much appreciable. Comparing Fig. 3b with Fig. 4b for MRC-SC, we find that system performance is better than MRC alone. Also, from the graphs, it is clear that the characteristics of MRC-SC resemble that of MRC except for the increase in capacity. It is also noted that for both types of combining, the gap between the graphs reduces as M increases, which imposes a threshold on the value of M beyond which M cannot be increased for a set of individual branch SNRs. Figures 3c and 4c show variations in capacity for SC-MRC versus individual branch SNR for ρ = 0.5 and ρ = 0.7. From the graphs, we can infer that the presence of more number of multipath branches aids in reducing combining errors and increases channel capacity. Also, it can be noted that for lower number of diversity branches, SC-MRC is inferior to MRC and MRC-SC. However, as M increases, SC-MRC provides the best capacity improvement. From Fig. 4c, it can be observed that a maximum of 8 bps is obtained for SC-MRC combining with ρ = 0.7 and M = 4. Also, SC-MRC combining gives best results compared to MRC and MRC-SC scheme for M > 3, as the best signals are chosen using SC diversity scheme and then combined using MRC scheme. Hence, there is a lower impact due to combining errors as ρ is higher for branches with good SNR selected through SC diversity combining.

Fig. 3

Capacity for OPRA policy versus Individual Branch SNR for ρ = 0.5 for (a) MRC (b) MRC-SC (c) SC-MRC schemes

Fig. 4

Capacity for OPRA policy versus Individual Branch SNR for ρ = 0.7 and (a) MRC (b) MRC-SC (c) SC-MRC schemes

Figure 5a–c show the capacity for ORA policy versus individual branch SNR for three types of diversity combining schemes, namely MRC, MRC-SC, SC-MRC for ρ = 0.5. Figure 6a–c show the capacity for ORA policy versus individual branch SNR for MRC, MRC-SC, SC-MRC schemes for ρ = 0.7. The capacity characteristics for ORA policy resembles that of OPRA policy except for increased capacity for OPRA policy at a particular individual branch SNR value than that of ORA policy. From Fig. 6c, it can be observed that a maximum of 6 bps/Hz is obtained for SC-MRC scheme with ρ = 0.7 and M = 4. Also, capacity increase for SC-MRC scheme is drastic for M = 4 compared to M = 2 and M = 3 for ORA policy. But in the case of OPRA policy, the increase in capacity is uniform for M = 2, 3, 4. So, it can be concluded that increase in M is more effective for ORA policy than OPRA policy. For ORA policy also, SC-MRC combining gives best results compared to MRC and MRC-SC scheme as high rates can be allocated to channels with good SNRs selected by SC diversity combining and then combined using MRC diversity combining.

Fig. 5

Capacity for ORA policy versus individual branch SNR for ρ = 0.5 for (a) MRC (b) MRC-SC (c) SC-MRC schemes

Fig. 6

Capacity for ORA policy versus individual branch SNR for ρ = 0.7 for (a) MRC (b) MRC-SC (c) SC-MRC schemes

Figure 7a–c show the capacity for CIFR policy versus individual branch SNR for the three types of diversity combining schemes namely MRC, MRC-SC, and SC-MRC for ρ = 0.5. Figure 8a–c show the capacity for CIFR policy versus individual branch SNR for MRC, MRC-SC, and SC-MRC schemes for ρ = 0.7.Compared Figs. 3 and  4, and comparing Figs. 7 and 8, capacity improvement is lower for CIFR policy than OPRA and ORA policies respectively, though the capacity characteristics of CIFR policy resembles that of the other two policies for MRC and MRC-SC cases. But, SC-MRC for CIFR policy yields the best result. The capacity improvement is exponential and is steeper at higher individual branch SNRs. At low SNRs, the capacity increase is linear and slow. From Fig. 8c, it can be observed that a maximum of 3 bps is obtained for SC-MRC combining with ρ = 0.7 and M = 4. Capacity obtained using CIFR policy is the least as it equalizes the channel characteristics.

Fig. 7

Capacity for CIFR policy versus individual branch SNR for ρ = 0.5 for (a) MRC (b) MRC-SC (c) SC-MRC schemes

Fig. 8

Capacity for CIFR policy versus individual branch SNR for ρ = 0.7 for (a) MRC (b) MRC-SC (c) SC-MRC schemes

Figure 9a–c show the capacity for TIFR policy versus individual branch SNR for three types of diversity schemes, namely MRC, MRC-SC, and SC-MRC schemes for ρ = 0.5. Figure 10a–c show the capacity for TIFR policy versus individual branch SNR for MRC, MRC-SC, and SC-MRC schemes for ρ = 0.7. The capacity characteristics resemble that of Figs. 3 and 4 for OPRA policy except that the capacity increase is lower for a particular individual branch SNR values for MRC and MRC-SC cases. For the SC-MRC case, the capacity increase is higher at larger SNRs than at smaller SNRs, where capacity is almost the same for different number of diversity branches. From Fig. 10c, it can be observed that a maximum of 5 bps is obtained for SC-MRC combining with ρ = 0.7 and M = 4. The capacity obtained using TIFR policy is better than CIFR policy due to the idea of truncation of outage probability effects.

Fig. 9

Capacity for TIFR policy versus individual branch SNR for ρ = 0.5 for (a) MRC (b) MRC-SC (c) SC-MRC schemes

Fig. 10

Capacity for TIFR policy versus individual branch SNR for ρ = 0.7 for (a) MRC (b) MRC-SC (c) SC-MRC schemes

Figures 11 and 12 show a decrease in outage probability with increase in individual branch SNR for ρ = 0.5 and ρ = 0.7for three types of diversity combining schemes, namely, MRC, MRC-SC, and SC-MRC, respectively. Comparing Fig. 11a with Fig. 12a for MRC, Fig. 11b with Fig. 12b for MRC-SC, Fig. 11c with Fig. 12c for SC-MRC, it is noted that an increase in correlation (ρ) reduces the outage probability. Also, from the graphs, we observe that an increase in M, decreases the outage probability. Outage Probability is the least for SC-MRC combining compared to MRC and MRC-SC scheme as the capacity achieved is higher for SC-MRC combining.

Fig. 11

Outage probability for individual branch SNR for ρ = 0.5 for (a) MRC (b) MRC-SC (c) SC-MRC schemes

Fig. 12

Outage probability for individual branch SNR for ρ = 0.7 for (a) MRC (b) MRC-SC (c) SC-MRC schemes

The ergodic capacity values listed in Table 1a–d follow from the results found in comparisons of graphs listed in Figs. 3, 4, 5, 6, 7, 8, 9 and 10 respectively. A fixed value of SNR (dB) = 5 dB is considered. Two different values of correlation (ρ = 0.5, 0.7) are considered. From the tabulated values, it can be observed that the hybrid combining techniques provide higher capacity values than the MRC technique, leading to the conclusion that hybrid techniques have the potential to perform better than standalone techniques. For OPRA policy, the MRC-SC technique performs better than SC-MRC technique, whereas for other policies, the relative capacity performance is comparable between the hybrid techniques.

Table 1 Comparison of ergodic capacity of (a) OPRA policy, (b) ORA policy, (c) CIFR policy, (d) TIFR policy for MRC, SC-MRC and MRC-SC schemes for a particular value of SNR (dB) and two correlation coefficients for M = 3 diversity level

Table 2 shows a comparison of outage probabilities of the hybrid and standalone techniques for a particular value of SNR (dB) and two different values of correlation coefficients. It is observed that the hybrid techniques offer a lower outage probability than the standalone technique for identical diversity levels, SNR (dB), and correlation coefficients.

Table 2 Comparison of outage probability of MRC, SC-MRC and MRC-SC schemes for a particular value of SNR (dB) and two correlation coefficients for M = 3 diversity level

6 Conclusions

In this paper, a comparison of ergodic capacity for MRC, SC-MRC and MRC-SC diversity techniques are made for various diversity levels in the case of impairments in combining. The impairments are quantified in terms of a correlation coefficient. Higher the value of the correlation coefficient, lower is the impairment and vice versa. This means that ergodic capacity values are generally higher for higher correlation coefficients. This work emphasizes the utility of hybrid combining techniques, such as SC-MRC and MRC-SC, which are proven to outperform the best standalone diversity combining technique, MRC, available in literature. The hybrid combining schemes also reduce the cost, time and linear signal processing work at the receiver compared to MRC schemes when the number of receive antennas is very large. At receive antennas where the received signals are negligible, the received signals are not considered in the overall linear processing at the receiver for the SC-MRC case. For the MRC-SC case, linear signal processing is first done with a few sets of received signals obtained from the receive antennas, and selection combining is made on a few largest signals obtained after MRC combining. Further, improvement in outage probability performance for hybrid combining schemes as compared to the MRC techniques reemphasizes the importance of hybrid schemes over standalone schemes. OPRA policy provides the highest capacity and CIFR or ORA policies (depending on different cases) provide the highest capacity penalty when compared to the other policies.