A survey on handling computationally expensive multiobjective optimization problems using surrogates: non-nature inspired methods

Abstract

Computationally expensive multiobjective optimization problems arise, e.g. in many engineering applications, where several conflicting objectives are to be optimized simultaneously while satisfying constraints. In many cases, the lack of explicit mathematical formulas of the objectives and constraints may necessitate conducting computationally expensive and time-consuming experiments and/or simulations. As another challenge, these problems may have either convex or nonconvex or even disconnected Pareto frontier consisting of Pareto optimal solutions. Because of the existence of many such solutions, typically, a decision maker is required to select the most preferred one. In order to deal with the high computational cost, surrogate-based methods are commonly used in the literature. This paper surveys surrogate-based methods proposed in the literature, where the methods are independent of the underlying optimization algorithm and mitigate the computational burden to capture different types of Pareto frontiers. The methods considered are classified, discussed and then compared. These methods are divided into two frameworks: the sequential and the adaptive frameworks. Based on the comparison, we recommend the adaptive framework to tackle the aforementioned challenges.

1 Introduction

Many practical engineering problems often involve optimizing (either minimizing or maximizing) multiple, possibly incommensurable objective functions subject to a feasible set determined by constraint functions. In such problems known as multiobjective optimization problems (MOPs), the best solution for an objective function may be the worst solution for some other objective functions. As a matter of fact, in a solution of an MOP, improvement in the value of one objective is only possible by allowing impairment in the values of at least one of the other objectives which is known as the concept of Pareto optimality (Miettinen 1999). A solution of an MOP satisfying this concept is called a Pareto optimal solution, and the set of all such solutions is referred to as a Pareto frontier (often also known as a Pareto optimal set). Mathematically, without any additional information, all Pareto optimal solutions are equally acceptable solutions of an MOP. It is, however, generally desirable to obtain one solution to be implemented. Therefore, when solving an MOP, we need a decision maker (DM) to compare several different solutions or to provide preference information in some other way and to select the most preferred one. In this survey, we define solving an MOP in two ways, i.e., finding a representation of the entire Pareto frontier to a DM or obtaining the most preferred solution based on the preferences of a DM.

In real-world MOPs, the mathematical formulas of objective and constraint functions could be either computationally expensive to evaluate and/or of a black-box type. For black-box functions, all that is known about them is the output for a given input. When dealing with these functions, mathematical properties such as convexity or continuity are not available. In some problems, objective and constraint functions are evaluated using real and/or computational experiments such as thermodynamic analysis, structural analysis, computational fluid dynamics (CFD) or reservoir simulation which involve differential equations to be solved. Numerical techniques such as finite element (FE) and finite difference methods may be applied to solve these equations. These experiments are time consuming and such problems are known as computationally expensive (intensive, costly) MOPs. For example, each objective function evaluation in reservoir simulation problems may take several days even after applying various techniques to improve the computational speed (Rezaveisi et al. 2014). The Pareto frontiers of such problems may be convex, nonconvex or disconnected. How to most efficiently solve these computationally expensive problems is an open research question in the literature.

In this paper, we present a survey of methods to handle computationally expensive MOPs. The focus of this survey is on general methods which are independent of the type of the optimization algorithms used in them. The basic idea in such methods is to introduce a computationally less expensive replacement problem known as a surrogate problem. Besides methods considered here, methods have been developed in the literature where mechanisms of nature-inspired methods such as evolutionary and particle swarm algorithms are essential elements of building the surrogates of the methods. See Tenne and Goh (2010), Jin (2011), Zhou et al. (2011) for reviews of such methods. As said, these methods are not considered here. Surveys on methods to solve computationally expensive single objective optimization problems utilizing surrogate problems are given in Simpson et al. (2001, 2004, 2008), Shan and Wang (2010), Koziel et al. 2011. In such methods, only one objective function is concerned, while in multiobjective optimization methods, at least two objectives are considered. In single objective optimization, comparing two solutions based on the concept of optimality is possible: the smaller (or larger) the objective function value, the better the solution. In multiobjective optimization problems, however, the concept of Pareto optimality is needed. In the literature, there are scalarization-based methods (Steuer 1986; Miettinen et al. 2008) that transform an MOP into a single objective optimization problem with respect to the preferences of a DM. Then, the optimal solution of the single objective optimization problem is considered as a preferred solution for the decision maker. In this survey, wherever such methods are employed to deal with computationally expensive MOPs, we discuss them.

As far as we know, this is the first survey which fully concentrates on handling computationally expensive MOPs by general methods as defined above. This survey covers 20 selected papers written in English and published in scientific journals before 2013. Besides as an overview of the methods available, one can use this survey to find a method applicable to one’s own problems.

A method where a computationally expensive MOP is handled using a surrogate problem is here termed a surrogate-based multiobjective optimization method. In what follows, for the sake of simplicity, such methods are called surrogate-based methods. Handling a computationally expensive MOP relying on a surrogate problem involves selecting sample points, building, updating and solving the surrogate problem. Based on when the surrogate problem is updated, surrogate-based methods are here classified into two frameworks: the adaptive and the sequential framework. In accordance with when the sample points are selected to update the surrogate problem, the adaptive framework is divided into types 1 and 2.

The motivation of this survey is to focus on the characteristics of the surrogate-based methods to solve a computationally expensive MOP and compare these methods in four aspects: (1) Can the methods deal with general black-box functions where information regarding mathematical properties of the functions such as convexity or continuity is not available? (2) Can the methods capture different types of Pareto frontiers? (3) How many objective and constraint functions as well as decision variables can be handled by the methods? (4) What is the role of a DM during the solution process? For this comparison, we rely on the results given by the authors of the papers considered on the employed benchmark and real-world problems.

In surrogate-based methods, the quality of the Pareto frontier of the surrogate problem depends on the accuracy of the surrogate problem and the performance of the optimization algorithm employed to solve this surrogate problem. In the literature (Wu and Azarm 2000; Okabe et al. 2003; Zitzler et al. 2003; Zitzler et al. 2008), several performance indices for measuring the quality of the Pareto frontier have been proposed. According to Okabe et al. (2003), this quality can be assessed based on the number of solutions in the Pareto frontier of the surrogate measured by e.g., overall non-dominated vector generation, the distribution and spread of these solutions measured by e.g., △ index and closeness of the surrogate’s Pareto frontier to the Pareto frontier of the computationally expensive MOP measured by e.g., generational distance, inverted generational distance and hyper-volume. If such information is given in the papers considered, we also mention it.

The rest of this paper is organized as follows. In Section 2, the basic concepts used in this survey, and a brief discussion on how a surrogate problem can be built, are addressed. In Section 3, the classification of surrogate-based methods into the sequential and the adaptive frameworks is discussed. Details of the sequential framework and the related methods are discussed in Section 4. Types 1 and 2 of the adaptive framework, and methods belonging to them are discussed in Sections 5 and 6, respectively. There is a method in which the sequential framework and type 1 of the adaptive framework are hybridized to handle computationally expensive MOPs. Therefore, it is discussed in Section 7. In Section 8, the surrogate-based methods considered in this survey are compared. Future research directions are also discussed. Finally, conclusions are drawn in Section 9.

2 Concepts

2.1 Definitions and notations

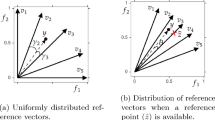
In the following, basic definitions and notations used in this survey are given (mostly from Miettinen (1999)). Some of these are illustrated in Fig. 1. In this paper, we deal with multiobjective optimization problems of the form

$$ \underset{x \in S} {\text{minimize}}\ \{f_{1}(x),\ldots,f_{k}(x)\}, $$

(1)

where the set S is called the feasible decision region (set) (often also called the feasible design space) which is a subset of the decision space $\mathbb {R}^{n}$. We have k(≥2) objective functions $f_{i} : S \rightarrow \mathbb {R}$. We denote the vector of objective functions by f(x) = (f ₁(x),…,f _k (x))^T. An example of the feasible decision region is $S=\{x \in \mathbb {R}^{n}: g_{i}(x) \leq 0, i=1,\ldots ,m, h_{j}(x)=0, j=1,\ldots ,p\}$, where $g_{i} : \mathbb {R}^{n} \rightarrow \mathbb {R},$ i = 1,…,m, and $h_{j} : \mathbb {R}^{n} \rightarrow \mathbb {R}$, j = 1,…,p, are called constraint functions. A solution $x=(x_{1},\ldots ,x_{n})^{T} \in \mathbb {R}^{n}$ is called a decision (variable) vector, where x _i , i = 1,…,n, are decision variables. A decision vector x ∈ S satisfying all the constraint functions is called a feasible decision vector. The image of the feasible decision region in the objective space $\mathbb {R}^{k}$ is called the feasible objective region (set) (often also called performance space) denoted by Z(=f(S)). The elements of Z are called feasible objective vectors denoted by f(x) or z = (z ₁,…,z _k )^T, where z _i =f _i (x), i = 1,…,k, are objective (function) values. For the sake of simplicity, we use the term a feasible solution which refers to either a feasible decision vector or a feasible objective vector. If needed, we clarify whether a feasible solution belongs to either S or Z.

Fig. 1

Some definitions in MOPs

A feasible solution x ^∗ ∈ S and the corresponding f(x ^∗) ∈ Z are said to be weakly Pareto optimal for the problem (1), if there does not exist another feasible solution x ∈ S such that f _i (x) < f _i (x ^∗) for all i = 1,…,k. Correspondingly, they are Pareto optimal for the problem (1), if there does not exist another feasible solution x ∈ S such that f _i (x) ≤ f _i (x ^∗) for all i = 1,…,k, and f _j (x) < f _j (x ^∗) for at least one index j∈{1,…,k}. Obviously, a Pareto optimal solution is a weakly Pareto optimal solution. The set of all Pareto optimal solutions in the objective space is called a Pareto frontier (often referred to as a Pareto optimal set) . We also define a feasible solution $x^{i}_{e}=\text {argmin}_{x \in S} \{f_{i}(x)\}$ for i = 1,…,k. The i-th extreme solution (also called the anchor point (Messac and Mullur 2008)) for i = 1,…,k, is defined as $z^{i}_{e}=f(x^{i}_{e})$ (see Fig. 1). A hyperplane passing through all extreme solutions is called a utopia hyperplane (Messac and Mullur 2008).

As mentioned earlier, in the process of solving an MOP, a DM may be involved, whose role is to give preference information, e.g., by comparing the obtained solutions. Based on the literature (Miettinen 1999; Luque et al. 2011; Ruiz et al. 2012), (s)he can provide his/her preferences, e.g., in the form of a reference point $\bar {z}=(\bar {z}_{1},\ldots ,\bar {z}_{k})^{T}$ where $\bar {z}_{i}$ is an aspiration level consisting of a desirable value for the i-th objective function. Another approach to elicit information about a DM’s preference during the solution process is classification, i.e., the DM classifies the objectives into classes in which the objective function values should be improved, can impair or are satisfactory. See Miettinen (1999) for further information of the roles of a DM during the solution process.

In the literature, scalarizing an MOP means formulating a single objective optimization problem such that an optimal solution for the single objective optimization problem is a (weakly) Pareto optimal solution for the MOP. The following is an example of scalarization. It involves a so-called achievement scalarizing function (Wierzbicki 1986):

$$ \underset{x \in S} {\text{minimize}} \underset{i=1,\ldots,k} {\max} \left[w_{i}(f_{i}(x)-\bar{z}_{i})\right] $$

(2)

where w _i ≥ 0 for all i = 1,…,k, are nonnegative weights, and $\bar {z}_{i}$ for all i = 1,…,k, the aspiration level for the i-th objective function provided by a DM. Different (weakly) Pareto optimal solutions can be obtained by changing the reference point. Pareto optimal solutions can be obtained by adding a so-called augmentation term to the objective function of the problem (2) (see, e.g. Miettinen (1999)).

Let us assume that the set X = {x ¹,…,x ^q} is an arbitrary subset of feasible solutions in S, and F = {f(x ¹),…,f(x ^q)} the corresponding objective vectors in Z. A solution x ⁱ (or f(x ⁱ)) for i = 1,…,q, that satisfies the definition of Pareto optimality with respect to all solutions in X (or F), is called a non-dominated solution in X (or F) (see Fig. 1). A Pareto optimal solution is a non-dominated solution, but a non-dominated solution is not necessarily a Pareto optimal solution. If X = S (or F = Z), then every non-dominated solution is a Pareto optimal solution and vice versa. Non-dominated solutions for the given set X can be identified by e.g., the Pareto fitness function (Schaumann et al. 1998) defined as

$$\begin{array}{@{}rcl@{}} G_{i}&=& 1- \underset{j \in \{1,\ldots,q\} \setminus \{i\}} {\max} \left[\min \left\{\bar{f}_{1}(x^{i})-\bar{f}_{1}(x^{j}),\ldots,\bar{f}_{k}(x^{i})\right.\right.\\ &&\left.\left.-\bar{f}_{k}(x^{j})\right\}\right],\\ i&=&1,\ldots,q, \end{array} $$

(3)

where G _i denotes the Pareto fitness of the i-th feasible solution x ⁱ, and $\bar {f}_{l}(x^{i})$ for l = 1,…,k, is the l-th normalized objective function value of the i-th feasible solution, given by:

$$ \bar{f}_{l}(x^{i})=\frac {f_{l}(x^{i})-f_{l,min}(x)} {f_{l,max}(x)-f_{l,min}(x)}, $$

(4)

where f _{l,m a x} (x) and f _{l,m i n} (x) represent the maximum and minimum values of the l-th objective function among all feasible solutions in X, respectively. When the Pareto fitness G _i is greater than 1, the corresponding feasible solution is a non-dominated solution (Shan and Wang 2004).

2.2 How to build a surrogate problem

As mentioned earlier, the basic idea in a surrogate-based method is to replace a computationally expensive MOP with a computationally less expensive surrogate problem. One approach to building a surrogate problem is to approximate each computationally expensive function using metamodeling techniques such as polynomial functions (Madsen et al. 2000), Kriging models (Kleijnen 2009), radial basis functions (RBFs) (Buhmann 2003), multivariate adaptive regression splines (MARS) (Friedman 1991), neural networks (Hagan et al. 1996) and support vector regression (SVR) (Smola and Schökopf 2004). To approximate a computationally expensive function, sample points are required. These sample points which are solutions in the decision space can be selected by sampling techniques such as Latin hypercube sampling (LHS) (Helton et al. 2006), central composite design (CCD) (Simpson et al. 2001), orthogonal array sampling (OAS) (Simpson et al. 2001) and full factorial sampling (FFS) (Simpson et al. 2001). See Simpson (2001), Queipo et al. (2005), Wang and Shan (2006), Forrester et al. (2008) and Simpson (2001), Queipo et al. (2005), Wang and Shan (2006), Forrester et al. (2008), Jin et al. (2001), Clarke et al. (2004), Forrester and Keane (2009), Nakayama et al. (2009), Li et al. (2010) for surveys of the sampling and metamodeling techniques and their characteristics, respectively.

Once a set of points is sampled, these points are evaluated with the computationally expensive function for which the metamodel is to be fitted. Sample points can also be generated by other methods such as a posteriori methods for multiobjective optimization where a subset of (weakly) Pareto optimal solutions representing the Pareto frontier is obtained. These methods are surveyed in Miettinen (1999) and Marler and Arora (2004). The obtained (weakly) Pareto optimal solutions can be considered as a set of sample points. When a set of points evaluated with the computationally expensive function is available, a metamodeling technique is employed to fit a computationally inexpensive function to the sample points known as a surrogate function (see Fig. 2). Once the surrogate functions of all computationally expensive functions are constructed, a computationally inexpensive MOP known as a surrogate problem is formulated.

Fig. 2

A surrogate function

According to Forrester and Keane (2009), in the context of surrogate-based single objective optimization, we want to build a surrogate problem to be most accurate in the region of the optimum. In surrogate-based multiobjective optimization, the accuracy of the surrogate problem in the region of the Pareto optimal solutions is desirable. Since each individual surrogate function may not be accurate in such a region, the Pareto frontier of the surrogate problem may not coincide with the Pareto frontier of the original, computationally expensive MOP. The accuracy of the surrogate functions can be evaluated with statistical measurements such as root mean square error (RMSE) (Giunta et al. 1998), predicted error sum of squares (PRESS) (Kutner et al. 2005), cross-validation method (Wang and Shan 2006) and R ² (Jin et al. 2001). See Shan and Wang (2010), Wang and Shan (2006), Jin et al. (2001) and Li et al. (2010) for surveys of commonly used criteria to evaluate the accuracy. In this survey, we study how the Pareto frontier of the surrogate problem represents the Pareto frontier of the computationally expensive MOP by the methods proposed in the papers considered.

Beside approximating each computationally expensive function, other approaches can be used to build a surrogate of a computationally expensive MOP, e.g., by approximating directly the Pareto frontier. These other approaches apply particular techniques which are discussed in the subsequent sections.

In this survey, when summarizing the methods considered we sometimes call a computationally expensive MOP as an original problem. The objective and/or constraint functions in the original and the surrogate problems are referred to as computationally expensive and surrogate functions, respectively. These functions involve models based on which functions are formed. For the sake of simplicity, we assume that all functions involved in the original problem are computationally expensive. A set of non-dominated (or Pareto optimal) solutions of the surrogate problem which may be evaluated with the computationally expensive functions is considered as the approximated Pareto frontier of the original problem. We also use the terms benchmark and application problems. The first one refers to the available test problems in the literature, e.g. ZDT problems (Deb et al. 2002), used to compare the performance of different methods. Application problems refer to the problems arising from industries which are dealt with in the papers considered in this survey. If the information regarding the characteristics of the Pareto frontiers of the benchmark and application problems like convexity, nonconvexity or discontinuity as well as performance indices to assess the quality of the surrogate’s Pareto frontier is provided by the authors of the surveyed papers, we also mention it. There are methods that have been developed to solve some particular application problems. While discussing such methods, first these problems are mentioned and then the summary of the methods is discussed. One should notice that the benchmark problems are not computationally expensive and, thus, their validity for properly testing the methods surveyed is questionable.

3 Classification of surrogate-based methods

After reviewing the journal papers considered in this survey, we have found out that two frameworks are employed to handle computationally expensive MOPs utilizing surrogates. Nevertheless, there is no unified description of the main steps involved in surrogate-based methods (see, e.g. Queipo et al. (2005), Wang and Shan (2006), Forrester and Keane (2009), Liu et al. (2008) and Kitayama et al. (2013)). Therefore, we consider two general frameworks, i.e., sequential and adaptive frameworks to classify surrogate-based methods, inspired by the classification in Wang and Shan (2006) and Liu et al. (2008), and based on when to update the surrogate problem. The key point in the sequential framework is to build an accurate surrogate problem and then to solve it. In this framework, the approximated Pareto frontier (i.e., a set of non-dominated (or Pareto optimal) solutions of the surrogate problem) is supposed to be as close as possible to the Pareto frontier of the original problem. Details of the sequential framework and methods belonging to this framework are discussed in Section 4. In the adaptive framework, however, the key point is first to construct an initial surrogate problem. As mentioned earlier, since the initial surrogate problem may not be accurate over the region of the Pareto optimal solutions of the original problem, the approximated Pareto frontier (obtained by solving the initial surrogate problem) may not represent the exact Pareto frontier of the original problem. Hence, by updating and solving the surrogate problem iteratively, the approximated Pareto frontier is supposed to coincide with the Pareto frontier of the original problem.

In order to update the surrogate problem, new sample points (which are also termed infill points in Forrester et al. (2008)) are required. These sample points can be selected from either a set of non-dominated (or Pareto optimal) solutions of the surrogate problem or unexplored regions in the decision and/or objective space. Based on when the sample points are selected to update the surrogate problem, inspired by Liu et al. (2008), we divide the adaptive framework into types 1 and 2. Details of the adaptive framework and methods in this framework are discussed in Sections 5 and 6, respectively. In addition, there is a method in which the sequential framework and type 1 of the adaptive framework are hybridized to handle computationally expensive MOPs. This method is discussed in Section 7 after describing both frameworks. All the methods considered in this survey are then compared in Section 8.

To solve a surrogate problem in both frameworks, two types of methods can be employed, i.e., sampling-based and optimization-based ones. In a sampling-based method, a surrogate problem is solved with an emphasis on a sampling process and without using any optimization algorithms. In contrast, in an optimization-based method, a surrogate problem is solved utilizing an optimization algorithm. If the aim of solving an MOP is to find the most preferred solution for a DM, depending on the way of giving the preference information, one can employ an interactive method. An overview of such methods has been presented in Miettinen (1999) and Miettinen et al. (2008). Several different solutions generated during the solution process can also be visualized for the DM to compare them. See Miettinen (2014) for a review of visualization techniques.

4 Sequential framework

4.1 General flowchart

Constructing an accurate surrogate problem is the key point in the sequential framework. The flowchart in Fig. 3 presents the main steps of methods belonging to this framework. As can be seen in this figure, in Step 1 of a method in this framework, initial points are sampled, and then evaluated with the computationally expensive functions in Step 2. After this, function values at the sample points are available. A surrogate problem is then constructed in Step 3. Evaluating the accuracy of the surrogate problem in Step 4 (highlighted in Fig. 3) is critical in this framework. As mentioned earlier, the accuracy can be evaluated by statistical measurements such as the cross-validation method, root mean square error (RMSE), predicted error sum of squares (PRESS) and R ². If the surrogate problem is not sufficiently accurate, it is updated by selecting new sample points in Step 5, and Steps 2-4 are then repeated. If the sample points are selected only once to build a surrogate problem, this is considered as a special case termed as one-stage sampling. In this case, Step 5 is not conducted. After constructing the accurate enough surrogate problem, it is solved in Step 6 with a DM, if available. As mentioned earlier, the aim of solving the surrogate problem can be to represent non-dominated (or Pareto optimal) solutions to a DM or to provide the most preferred solution based on the preferences of a DM. The solution(s) obtained by solving the surrogate problem are typically evaluated with the computationally expensive functions in Step 7. As a result, the outcome of Step 7 is considered as the approximated Pareto frontier of the original problem and/or the most preferred solution for a DM in Step 8. This outcome can also be visualized using an appropriate visualization technique. In this framework, depending on the accuracy of the surrogate problem, the approximated Pareto frontier is as close as possible to the Pareto frontier of the original problem. In Section 4.2, we summarize the methods belonging to the sequential framework. These methods are then compared in Section 8.

Fig. 3

Flowchart of the sequential framework

4.2 Summary of methods in the sequential framework

In Goel et al. (2007), an optimization-based method using polynomial functions is introduced. In Step 1 of this method, initial points are sampled with OAS and then evaluated with the computationally expensive functions in Step 2. Each computationally expensive function is approximated by a quadratic or a cubic polynomial function in Step 3, and the surrogate problem is built. The accuracy of the surrogate problem is evaluated with a cross-validation method in Step 4. If needed, new points are sampled in Step 5 to improve the accuracy, and Steps 2–4 are repeated. After constructing the accurate enough surrogate problem, highly correlated objectives among the surrogate functions may be dropped or a representative objective can be used for all the correlated objectives (applying principal component analysis) (Goel et al. 2004). In Step 6, the surrogate problem is then solved using a population-based evolutionary multiobjective optimization method called NSGA-II (Deb et al. 2002). The non-dominated solutions obtained are then locally improved by the 𝜖-constraint method (Zanakis et al. 1998). In this paper, the authors do not discuss evaluating the non-dominated solutions obtained in Step 6 with the computationally expensive functions in Step 7. In Step 8, for an MOP with less than three objective functions, the approximated Pareto frontier is visualized by fitting a polynomial function to the non-dominated solutions in the objective space. This function is accurate in a limited region of the objective space which is identified by convex hulls.

In Goel et al. (2007), besides solving a computationally expensive MOP, the authors discuss the problem of Pareto drift (losing some non-dominated solutions in each generation of the dominance based Multiobjective Evolutionary Algorithms (MOEAs)). They propose an implementation of an archiving strategy to preserve all good solutions. Regarding the issue of capturing a nonconvex Pareto frontier, the authors mention that the number of convex hulls is important. In this method, a metamodeling technique is applied for two reasons, i.e., to build the accurate enough surrogate problem, and to visualize the approximated Pareto frontier. Finding the correlated functions along with a representation of an objective as a function of the remaining objectives to visualize the approximated Pareto frontier can be a barrier of using this method for MOPs with more than three objective functions. The efficiency of this method was evaluated on an MOP of liquid-rocket single element injector with four black-box objective functions and four decision variables requiring CFD simulations. In this problem, the number of objective functions was reduced to three by applying principal component analysis. The quality of the approximated Pareto frontier was assessed based on the average and maximum distances between the non-dominated solutions in two successive iterations of the optimization algorithm employed. This application problem was also studied in Queipo et al. (2005), where a discussion on the global sensitivity analysis of the objective functions and the decision variables was considered.

In the sequential framework, there are two sampling-based methods which we discuss in the following paragraphs. In Wilson et al. (2001), a sampling-based method called efficient Pareto frontier exploration is introduced in which metamodeling techniques are employed to approximate individual computationally expensive objective and/or constraint functions. In efficient Pareto frontier exploration, first the DM provides desirable ranges for the decision variables. Then, making use of two sampling techniques (i.e., CCD and LHS), two sets of initial points are sampled within these ranges in the decision space in Step 1 and evaluated with the computationally expensive functions in Step 2. For each set, the computationally expensive functions are approximated with a second-order polynomial function and a Kriging model in Step 3 to compare the results, and the surrogate problems are constructed. In Step 4, using a cross-validation method, the accuracies of the surrogates are evaluated. If needed, new sample points are selected in Step 5, and Steps 2-4 are repeated. In order to solve the surrogate problems and to represent the corresponding non-dominated solutions in Step 6, a considerable number of points is sampled and evaluated with the surrogate functions. Then non-dominated solutions of the surrogate problems among the evaluated points are identified using the Pareto fitness function (3). These non-dominated solutions are then evaluated in Step 7 with the computationally expensive functions. The sets of evaluated non-dominated solutions are considered as the approximated Pareto frontier of the original problem in Step 8.

The efficient Pareto frontier exploration method was applied in designing a piezoelectric bimorph actuator with two black-box objective functions and five decision variables. The function evaluations involved applying the FE method using Abaqus (2013). The performance of the efficient Pareto frontier exploration method was also evaluated on two benchmark problems with convex, nonconvex and disconnected Pareto frontiers. The authors show that the surrogate problem constructed based on initial sample points of LHS and the Kriging model is more accurate than the other surrogates for these problems. The results demonstrated that, while this method can capture a nonconvex and disconnected Pareto frontier, it performs better for an MOP with a convex Pareto frontier. Since in this method, a large number of sample points is required to solve the surrogate problem, it cannot be applied to handle high-dimensional MOPs in the decision and objective spaces. The role of a DM is also to provide desirable ranges for the decision variables which does not match with the definition of a DM’s role in the literature as defined in Section 2.1.

In most of the methods discussed so far, surrogates of the computationally expensive functions are built using metamodeling techniques to approximate computationally expensive functions. In contrast, (Lotov et al. 2001) proposes a sampling-based method called Feasible Goals Method (FGM) to approximate the set Z (the feasible objective region) by means of a collection of boxes in the objective space and without using any metamodeling technique. In order to approximate the set Z with a finite number of boxes, it is assumed to be bounded. In Step 1 of this method, evenly distributed initial points are sampled randomly, and then evaluated with the computationally expensive functions in Step 2. In Step 3, a box in the neighborhood of each point in the objective space is formed. The collection of the boxes is considered as the surrogate of the feasible objective region. Utilizing the Chebyshev metric, the authors introduce a probability function to evaluate the accuracy of the surrogate in Step 4. To do this, a set of new evenly distributed points is sampled randomly in Step 5, and evaluated with the computationally expensive functions in Step 2. If the probability function value is less than a predetermined threshold, the farthest point is selected. Then, a new box in the neighborhood of the selected point is formed to update the surrogate in Step 3, and Steps 2-4 are repeated. Otherwise, that is, the surrogate is sufficiently accurate, the surrogate problem is considered in Step 6 to select the most preferred solution in the objective space by the DM. In this step, the collection of boxes is visually shown to a DM. Then, the DM identifies a preferred solution. The center of the related box is computed along with the associated decision vector value in Step 7, and displayed to the DM in Step 8. FGM was applied to a set of application problems such as pollution monitoring station problem with five nonlinear objective functions and two decision variables. The feasible objective region of this problem was nonconvex. This method can handle black-box functions, since in practice, the boundedness of Z can be assumed by considering boundaries for the decision variables. Developments of FGM to approximate both convex and nonconvex Pareto frontiers are discussed in Lotov et al. (2004).

So far, we have discussed methods involving all steps in the sequential framework. In the following paragraphs, we discuss methods involving one-stage sampling. As mentioned earlier, in one-stage sampling, sample points are selected only once. In Liao et al. (2008), an optimization-based method is developed which is applied to solve an MOP of crash safety design of vehicles with three black-box objective functions and five decision variables. LS-DYNA (Livermore Software Technology Corporation (LSTC) 2013) is employed as a simulation software. In this method, initial points are sampled with an extension of LHS called optimal Latin hypercube sampling (OLHS) in Step 1 and then evaluated with the computationally expensive functions involving the FE method in Step 2. After that, stepwise regression and a quadratic polynomial function are applied to approximate each computationally expensive function and, then the surrogate problem is built in Step 3. The accuracy of this problem is evaluated based on R ² in Step 4. Non-dominated solutions of the surrogate problem are obtained using NSGA-II in Step 6. This set of non-dominated solutions is considered as the approximated Pareto frontier of the original problem in Step 8. This set is not evaluated with the computationally expensive functions in Step 7.

In Su et al. (2011), an optimization-based method is developed, and is applied to solve a biobjective optimization problem of designing a bus body with 13 constraints and 31 decision variables. The objective and constraint functions are evaluated with the FE method using simulation software called MSC Nastran (MSC Nastran-Multidisciplinary structural analysis 2013) and LS-DYNA. In Step 1 of this method, initial points are sampled with OLHS and evaluated with the computationally expensive functions in Step 2. Then, stepwise regression is applied to approximate each objective and constraint function making use of a hybrid of a linear polynomial function and a Gaussian RBF, and the surrogate problem is constructed in Step 3. The accuracy of the surrogate problem is evaluated based on PRESS in Step 4. The surrogate problem is then solved in Step 6. The non-dominated solutions obtained are evaluated with the computationally expensive functions in Step 7. The set of evaluated solutions is considered as the approximated Pareto frontier of the original problem in Step 8. In this paper, two evolutionary algorithms, i.e., NSGA-II and AMISS-MOP (Su et al. 2011) were employed to solve the surrogate problem. The authors concluded that the spread of non-dominated solutions obtained by NSGA-II was wider than AMIS-MOP, but the convergence of AMISS-MOP was better than NSGA-II.

In Bornatico et al. (2013) steps similar to those of Liao et al. (2008) and Su et al. (2011) are followed to solve a design optimization problem of a solar thermal building system with two black-box objective functions and two decision variables involving the Polysun simulation software (Polysun 2013). In this method, the sample points are selected only once with the Poisson disk node distribution (Gamito and Maddock 2009). Each computationally expensive function is approximated with a cubic RBF. The biobjective surrogate problem is solved with NSGA-II. In this paper, the accuracies of the surrogate problems constructed with four sampling techniques, i.e., Cartesian distribution (Bornatico et al. 2011), Hexagonal distribution (Steinhaus 2011), uniform distributions (Hickernell et al. 2005) and Poisson disk node distribution were also compared. To assess the quality of the approximated Pareto front, the original problem was also solved. Then, the average Euclidean distance between the Pareto frontiers of the original problem and the surrogates was considered. The authors concluded that the surrogate problem constructed with the Poisson disk node distribution sample points and a cubic RBF outperformed the others in terms of the accuracy.

In the optimization-based methods discussed so far, a surrogate problem is constructed using metamodeling techniques to approximate each computationally expensive function. In Hartikainen et al. (2012), however, an optimization-based method called PAINT is proposed to approximate the Pareto frontier of a computationally expensive MOP directly without utilizing any metamodeling techniques. In this method, a linear mixed integer multiobjective optimization problem is introduced as a surrogate of the original problem. In PAINT, initial sample points are generated by an a posteriori method in Steps 1 and 2. These sample points are Pareto optimal solutions of the original problem. Then, a PAINT interpolation between the sample points is created in Step 3 and the surrogate problem is introduced. The accuracy of the surrogate problem is high, if a large number of well-distributed Pareto optimal solutions is used as sample points. This problem can be solved with any interactive multiobjective optimization method, and a preferred approximated solution for a DM is obtained in Step 6. After finding this solution, it is then projected to the Pareto frontier of the original problem with the achievement scalarizing function (2) in Steps 7 and 8.

In PAINT, only the objective space is considered. Although the authors claim that PAINT can represent a nonconvex Pareto frontier, it cannot capture a disconnected Pareto frontier. In addition, the approximation of the Pareto frontier loses the connection to the decision space when solving the surrogate problem. However, after projecting the preferred approximated solution to the Pareto frontier, the closest Pareto optimal solution both in the decision and objective spaces is obtained. The efficiency of this method was evaluated on a benchmark problem with a convex Pareto frontier. This method was also applied in approximating the Pareto frontier of an MOP of wastewater treatment planning with three black-box objective functions described in Hakanen et al. (2011). The number of constraint functions and decision variables was not mentioned.

All the described methods are compared in Section 8. Table 1 summarizes the characteristics of the methods in the sequential framework with respect to sampling techniques, metamodeling techniques, number of objective and constraint functions as well as decision variables in the considered benchmark and application problems, whether the methods involve one-stage sampling and whether they are optimization- or sampling-based. In this table, for every method, the most challenging MOP that was considered as a benchmark or an application problem is mentioned. Since the number of equality constraints in all problems are zero (p = 0), it is not mentioned in the table. As can be seen, most of the problems considered are limited to two or three objective functions except (Lotov et al. 2001) with five objective functions. As mentioned earlier, since the method in Messac and Mullur (2008) hybridizes both the sequential and the adaptive frameworks, we discuss it in Section 7.

Table 1 Characteristics of methods in the sequential framework (k, m, n are the number of objective functions, inequality constraint functions and decision variables, respectively)

5 Adaptive framework: type 1

5.1 General flowchart

As mentioned in Section 3, another class of surrogate-based methods is the adaptive framework. In this framework, as can be seen in the flowcharts in Figs. 4 and 6, in comparison with the sequential framework (Fig. 3), after sampling, first an initial surrogate problem is constructed. As mentioned earlier, the approximated Pareto frontier (obtained by solving the initial surrogate problem) may not represent the exact Pareto frontier of the original problem. Therefore, the surrogate problem is iteratively solved and updated by selecting new sample points such that, the approximated Pareto frontier is supposed to coincide with the Pareto frontier of the original problem. As described in Section 3, the new sample points can be selected from either a set of non-dominated (or Pareto optimal) solutions of the surrogate problem or unexplored regions in the decision and/or objective space. Based on when new sample points are employed to update the surrogate problem, we divide this framework into types 1 and 2. In type 1, the sample points generated before assessing a stopping criterion (Step 4 highlighted in Fig. 4) are utilized to update the surrogate problem. In type 2, not only the sample points generated before assessing the stopping criterion (Step 4 highlighted in Fig. 6) are considered, but also new sample points are generated and selected after assessing the stopping criterion (Step 6 highlighted in Fig. 6) to update the surrogate problem. In this section, we discuss type 1 of the adaptive framework. Type 2 is considered in Section 6.

Fig. 4

Flowchart of the adaptive framework: type 1

The flowchart in Fig. 4 shows the main steps of methods belonging to type 1 of the adaptive framework. As can be seen, in the first step of type 1, initial points are sampled, and then evaluated with the computationally expensive functions in Step 2. After this, function values of the sample points are available. In Step 3, the initial surrogate problem is constructed. In order to capture the Pareto frontier or to provide the most preferred solution based on the preferences of a DM, if available, new sample points are generated in Step 4. These points can be obtained by solving the surrogate problem and/or sampling unexplored regions in the decision and/or objective space depending on a sampling process. In accordance with a method-dependent criterion, a subset of points among the generated points is selected. In Step 5, assessing a stopping criterion may require to evaluate the selected sample points with the computationally expensive functions and/or to update the surrogate problem. There are different stopping criteria which are discussed in more detail in the following subsection. If a stopping criterion is met, the set of non-dominated (or Pareto optimal) solutions or the most preferred solution of the last surrogate problem which may have been evaluated with the computationally expensive functions are considered as the approximated Pareto frontier of the original problem or the most preferred solution for a DM in Step 6. These solutions can also be visualized using an appropriate visualization technique. Otherwise, that is, when a stopping criterion is not met, if the surrogate problem has already been updated, Steps 4–5 are repeated. If not, first the surrogate problem is updated with the evaluated sample points and then Steps 4–5 are repeated.

In Section 5.2, we describe how the above steps are conducted by methods in type 1 of the adaptive framework. We compare these methods in Section 8.

5.2 Summary of methods in the adaptive framework: type 1

In Yang et al. (2002), first an optimization-based method called adaptive approximation in single objective optimization (AASO) is developed, and then it is extended to adaptive approximation in multiobjective optimization (AAMO). AAMO is the oldest method in the literature developed based on the adaptive framework. In Step 1 of AAMO, initial points are sampled with any sampling technique (e.g., LHS) and evaluated with the computationally expensive functions in Step 2. Then in Step 3, each computationally expensive function is approximated with a Kriging model, and an initial surrogate problem is built. In Step 4, a set of non-dominated solutions of the surrogate problem is obtained by Multiobjective Genetic Algorithm (MOGA) (Goldberg 1989) and denoted by P ₀. Among these points, using the maximin distance design criterion (Johnson et al. 1990), a number of isolated points is selected. In Step 5, these points are evaluated with the computationally expensive functions, and utilized to update the surrogate problem. The solutions in the set P ₀ obtained in Step 4 are again evaluated with the updated surrogate problem. A set of non-dominated solutions among these evaluated points is identified and denoted by P _{n e w} . If the difference between the number of the non-dominated solutions in P ₀ and in P _{n e w} is less than a predetermined threshold, the set P _{n e w} is considered as the approximated Pareto frontier in Step 6. Otherwise, the set P _{n e w} is inserted into an initial population of MOGA and the method continues with Step 4.

Similar to Goel et al. (2007), the authors in Yang et al. (2002) also discuss the difficulties of GA-based algorithms in identifying extreme solutions in the Pareto frontier. To overcome these difficulties, they propose a method called combined AASO-AAMO in which the AASO and AAMO methods are combined. In combined AASO-AAMO, after obtaining a set of non-dominated solutions of the surrogate problem in Step 4, all objective functions in the surrogate problem are individually minimized. The obtained optimal solutions along with the set P _{n e w} are inserted into an initial population of MOGA. The combined AASO-AAMO method was tested on solving an I-beam design problem with two nonlinear objective functions, one nonlinear constraint function and four decision variables. The quality of the approximated Pareto frontier was assessed based on closeness of it to the Pareto frontier of the application problem. While this method can handle black-box functions, the application of combined AASO-AAMO to a practical optimization problem involving actual computationally expensive or noisy simulations is mentioned as a future research direction.

In Zhou and Turng (2007), an optimization-based method is developed which is applied to solve an MOP of injection-molding process with five black-box objective functions and three decision variables. To do this, initial points are sampled with LHS in Step 1 and evaluated with the computationally expensive functions in Step 2 involving the Moldex3D simulation software (Moldex3d: Plastic injection molding simulation software 2013). Each computationally expensive function is approximated in Step 3 with a Kriging model, and the initial surrogate problem is built. In Step 4, new sample points are selected randomly. The objective function values of these points are evaluated with the surrogate functions. The variances of the objective function values of these points are also calculated with the Kriging model. For each point, a vector consisting of these variances is considered. These vectors are sorted using the non-dominated sorting method (Deb et al. 2002) (variances are maximized). Then, a subset of points with the largest variances (at the first front) is selected randomly. In Step 5, the selected points are evaluated with the computationally expensive functions and added to the sample points set. Then, the surrogate problem is updated. In other methods in type 1 of the adaptive framework, the surrogate problem is solved in Step 4. In this method, however, the surrogate problem is solved using NSGA-II in Step 5 to assess the stopping criterion.

The authors in Zhou and Turng (2007) employ the concept of user-defined indifference threshold (Wu and Azarm 2000) as the stopping criterion in Step 5. This threshold refers to the change in each objective function value within which the non-dominated solutions are indifferent to each other. Applying the user-defined indifference thresholds, the objective space is discretized into a collection of hyperboxes. Using the method of Wu and Azarm (2000), if the distances between the boundaries of the hyperboxes are less than the predetermined threshold, the method stops. The set of non-dominated solutions of the last surrogate problem is considered as the approximated Pareto frontier of the original problem in Step 6. Otherwise, the method repeats Steps 4-5. According to the authors, the quality of the approximated Pareto frontier was assessed based on the average error percentage between the non-dominated solutions obtained by solving the surrogate and the original problems.

In Yun et al. (2009), an optimization-based method is developed to represent an approximation of the Pareto frontier as well as to identify the most preferred solution for a DM with respect to a reference point consisting of desirable aspiration levels for all objectives. In this method, initial points are sampled randomly in Step 1, and evaluated with the computationally expensive functions in Step 2. Then, each computationally expensive function is approximated with an extension of SVR called μ−ν−SVR, and the surrogate problem is built in Step 3. This surrogate problem is

then solved with an evolutionary multiobjective optimization method called SPEA2 (Zitzler et al. 2001) in Step 4. In order to approximate well a neighborhood of the closest Pareto optimal solution to the reference point provided by the DM, among the generated non-dominated solutions, thepoint with the minimum value of an order-approximating achievement function (Miettinen 1999) is selected. Moreover, to update the surrogate problem, another point is selected based on a specific parameter associated with the μ−ν−SVR. In Step 5, if the number of computationally expensive function evaluations is less than a predetermined threshold, the selected points are evaluated with the computationally expensive functions. The surrogate problem is then updated, and the method returns to Step 4. Otherwise, the set of non-dominated solutions of the last surrogate problem is considered as the approximated Pareto frontier of the original problem. The point with the minimum value of the order-approximating achievement function is also considered as the most preferred solution for the DM. The efficiency of this method was evaluated on a benchmark problem with a nonconvex and disconnected Pareto frontier, and on a welded beam design problem with two nonlinear objective functions, four nonlinear constraint functions and four decision variables.

In Jakobsson et al. (2010), an optimization-based method is developed to handle noisy black-box single objective optimization problems. This method is then extended to handle computationally expensive MOPs. The authors call both methods qualSolve. They claim that it is the first method to handle a computationally expensive noisy MOP. However, the performance of the qualSolve method for MOPs is only evaluated with deterministic benchmark problems. Here, we focus on qualSolve for MOPs. In Step 1 of qualSolve, initial points are sampled with LHS and evaluated with the computationally expensive functions in Step 2. Each computationally expensive function is approximated with a thin plate spline RBF in Step 3, and a surrogate problem is built. In Step 4, the surrogate problem is solved by a multiobjective optimization method to represent its Pareto frontier. Using this Pareto frontier, the extended Pareto frontier, i.e., the set of weakly Pareto optimal solutions in $Z_{s}+\mathbb {R}^{k}$ is represented where Z _s is the feasible objective region of the surrogate problem. Figure 5 which is a modification of a figure in Jakobsson et al. (2010) shows the extended Pareto frontier in which s ₁ and s ₂ are the approximated objective functions.

Fig. 5

Extended approximated Pareto front

To update the surrogate problem, in every iteration of the method, a sample point is selected from either the Pareto frontier of the surrogate problem or in an area near the extended Pareto frontier of the surrogate problem. This point can be a Pareto optimal solution, or a feasible solution in the objective space, near the extended Pareto frontier of the current surrogate problem. To select the new sample point, the authors introduce a quality function based on two functions, i.e., a distance and a weight function. The distance function is defined as the smallest Euclidean distance between a feasible solution in the objective space and a solution on the extended Pareto frontier of the current surrogate problem. The weight function controls the procedure of selecting new sample points from either the Pareto frontier or an area near the extended Pareto frontier in the feasible objective region of the current surrogate problem. The quality function is formulated with respect to the weight and distance functions. The point that maximizes the quality function is used to update the surrogate problem. In Step 5, if the number of computationally expensive function evaluations is less than a predetermined threshold, the selected point is evaluated with the computationally expensive functions. The surrogate problem is then updated, and the method returns to Step 4. Otherwise, the Pareto frontier of the last surrogate problem is considered as the approximated Pareto frontier of the original problem in Step 6.

The performance of this method was evaluated on a set of benchmark problems such as Kursawe (1991) and OKA1 (2006). The authors concluded that qualSolve performed well on the Kursawe problem with a nonconvex and disconnected Pareto frontier. It, however, failed to represent the convex Pareto frontier of OKA1, since OKA1 has a very strong nonlinear behavior close to the minimum solution to one of the objective functions. They note that qualSolve was developed in a project on simulation-based multiobjective optimization of the Volvo D5 diesel engine with three black-box objective functions and five decision variables (Jakobsson et al. 2010) involving CFD simulation using Star-CD (Star-CD 2013). The authors consider the execution time, as a main downside of the qualSolve method for MOPs. Because the quality function includes an integral equation, the evaluation time of this function rises exponentially with the dimension of the decision space. They mention that qualSolve is suitable for problems with less than six decision variables. They also discuss that representing the extended Pareto frontier can be hard for three or more objective functions.

In Gobbi et al. (2013), an optimization-based method called approximate normal constraint (ANC) is introduced in which the idea of employing the normal constraint method (Messac et al. 2003; Messac and Mattson 2004) is followed. In the ANC method, a neural network with a single hidden layer is used to handle computationally expensive MOPs. To do this, first one of the computationally expensive objective functions is optimized to calculate the corresponding extreme solution. The authors, however, do not provide any guideline to choose this function. In a neighborhood of the extreme solution obtained in the decision space, initial points are sampled randomly in Step 1 and evaluated with the computationally expensive functions in Step 2. These points are used to train a neural network to approximate each computationally expensive function, and to build a surrogate problem in Step 3. In Step 4, the other extreme solutions are calculated by minimizing the corresponding objective functions in the surrogate problem, and a utopia hyperplane is constructed. A set of evenly distributed points is then generated on the utopia hyperplane. For each point on the hyperplane, the surrogate problem is scalarized using the scalarizing technique introduced in the normal constraint method (Messac et al. 2003; Messac and Mattson 2004), and a single objective optimization problem is formulated.

The authors claim that by solving the single objective optimization problem, a non-dominated solution in an area near the Pareto frontier of the original problem can be obtained. Therefore, a set of non-dominated solutions can be generated near the Pareto frontier of the original problem by forming and solving the single objective optimization problem for each point on the hyperplane. In Step 5, these non-dominated solutions are evaluated with the computationally expensive functions. To keep the number of the training sample points constant, the points that are the farthest from the current utopia hyperplane are removed. The evaluated points are added to the training set, and the surrogate problem is updated. If the number of computationally expensive function evaluations is less than a threshold, the method returns to Step 4. Otherwise, the set of non-dominated solutions obtained near the Pareto frontier of the original problem is considered as the approximated Pareto frontier.

The efficiency of the ANC method was evaluated on benchmark problems with nonconvex Pareto frontiers. The efficiency was also assessed on an MOP of ground vehicle suspension design with five black-box objective functions and eleven decision variables. The authors compared the efficiency of the ANC method with MOGA and a method called Parameter Space Investigation (PSI) described in Miettinen (1999) and references therein. They provided remarks to show that the ANC outperformed the others. The authors claim that ANC can be used to refine the solutions obtained with other methods which approximate the Pareto frontier at once (i.e., genetic algorithms (Goldberg 1989) and quasi Monte Carlo method (Niederreiter 1992)).

In Kitayama et al. (2013), an optimization-based method is developed to handle computationally expensive black-box MOPs. In this method, the aim is to find the most preferred solution for a DM rather than to represent an approximation of the entire Pareto frontier. The authors introduce two sampling functions. They describe how to capture disconnected parts of the Pareto frontier by generating a set of sample points as evenly distributed as possible using the first sampling function. The second sampling function provides the most preferred solution for a DM. In addition, to approximate computationally expensive functions with RBF, they utilize a new estimation proposed in Kitayama et al. (2011a) for the width parameter of a Gaussian kernel in RBF based on the number of and distances between sample points. In Kitayama et al. (2013), a set of initial points is sampled with LHS in Step 1 and evaluated with the computationally expensive functions in Step 2. The width parameter is also calculated based on the number of sample points. In Step 3, each computationally expensive function is approximated with the Gaussian RBF, and a surrogate problem is built. The multiobjective surrogate problem is scalarized with the weighted L _p -norm function known e.g., in Miettinen (1999) as the method of weighted metrics in which a DM provides his/her preferences by the weights. In Step 4, this scalarized problem is optimized with the differential evolution algorithm (Kitayama et al. 2011b). This optimal solution is added to the sample points set and the width parameter is recalculated.

Introducing the first sampling function based on the current sample points, a set of sample points as evenly distributed as possible is obtained. These points are added to the current sample points. Then, the second sampling function is introduced and optimized based on the updated sample points and a modification of the Pareto fitness function (3). Both functions are approximated using a Gaussian RBF. In Step 5, if a stopping criterion based on the selected points is not met, the optimal solution obtained with the second sampling function is added to the current sample point. The updated sample points are evaluated with the computationally expensive functions. The width parameter is recalculated, and the surrogate problem is updated. The method then returns to Step 4. Otherwise, the last optimal solution of the second sampling function is considered as the most preferred solution for the DM.

Regarding the new estimated width parameter, the authors mention that this estimation has been obtained with a heuristic approach. Therefore, the validity of the new parameter is not proved mathematically. They also propose that this parameter can be used for SVR. The performance of this method was evaluated on a set of benchmark problems with nonconvex and disconnected Pareto frontiers. The efficiency of the method was also evaluated on an MOP of variable blank holder force trajectory in deep drawing with two nonlinear objective functions and six decision variables. The numerical simulation was done by LS-DYNA.

In the optimization-based methods discussed so far in this subsection, a surrogate problem is constructed with metamodeling techniques to approximate each computationally expensive function. In Monz et al. (2008), however, an interactive optimization-based method called Pareto Navigation method is introduced for convex problems to find the most preferred solution with respect to a DM’s preference without using any metamodeling techniques, and is applied in intensity-modulated radiation therapy planning. Based on a figure in this paper, we conclude that the application problem has six objective functions. Moreover, there is no information regarding the number of constraint functions and the decision variables. In this method, a set of initial sample points is generated with an a posteriori method (Steps 1 and 2). Then, in Step 3, convex hulls of these points are constructed in both the decision and objective spaces. The set of sample points is shown to the DM who must select one of them. The DM provides his/her preference information by specifying an aspiration level called a goal for one of the objective functions and upper bounds for the other objective functions. With respect to the given preference information, a convex scalarization problem introduced in Pascoletti and Serafini (1984) (based on a reference point) is formulated as the surrogate problem in Step 3, which is optimized in Step 4. The optimal solution of this problem is a convex combination of the Pareto optimal solutions in the sample points set in the decision and objective spaces corresponding to the given preferences. In Step 5, if the DM desires, this point can be evaluated with the computationally expensive functions. If the DM is not satisfied with this point, it can be added to the sample points set, and the surrogate problem is updated. Then, the method returns to Step 4. Otherwise, the obtained point is considered as the most preferred solution for the DM in Step 7.

In Eskelinen et al. (2010), an interactive method called Pareto navigator is introduced. In this method, conducting Steps 1 and 2, i.e., constructing a convex hull, and showing the set of sample points to the DM are similar to the Pareto navigation method (Monz et al. 2008). In Step 3 of the Pareto navigator method, however, the DM provides the preference information in a form of a classification or a reference point consisting of desirable values for all objectives. The main difference between this method and the method in Monz et al. (2008) is that in the latter, only one solution with respect to the given preference is generated whereas, in this method, multiple solutions corresponding to the given preference are available when moving from the current solution towards the reference point specified.

To be more specific, a search direction with respect to the preference information is formed. Then, based on the convex hull, the single objective optimization problem (2), where the reference point is parametrically moved along the search direction, is formulated as the surrogate problem. If the DM desires, (s)he can control the speed of movement. Pareto optimal solutions to the surrogate problem are generated by solving the single objective optimization problem for different reference points until the DM wants to stop. If the DM wishes, the corresponding Pareto optimal solution of any point generated is obtained by projecting this point to the Pareto frontier of the original problem using the achievement scalarization function (2) in Step 5. If the DM is satisfied with the projected Pareto optimal solution, it is considered as the most preferred solution for the DM in Step 7. Otherwise, the DM can change the preference information, that is, the direction of movement and/or the starting solution. If desired, it is possible to add the projected Pareto optimal solution to the sample points set in order to improve the accuracy of the surrogate problem. Then, Steps 4-5 are repeated. The performance of this method was evaluated on a simple problem with three nonlinear objective functions, three linear constraint functions, two decision variables and a simple nonconvex Pareto frontier. In the Pareto navigation method (Monz et al. 2008), the objective functions and the Pareto frontier are assumed to be convex, whereas in Pareto navigator (Eskelinen et al. 2010), a simple nonconvex Pareto frontier can be captured by the convex hull. Capturing a complex nonconvex Pareto frontier is mentioned as a future research direction in Eskelinen et al. (2010). While the Pareto navigation method keeps the connection to the decision space, Pareto navigator loses the connection with the decision space when navigating in the objective space. In the Pareto navigation method (Monz et al. 2008), convexity of the objective functions is assumed, which is an obstacle to deal with black-box functions. However, the method in Eskelinen et al. (2010) can handle black-box functions.

In Shan and Wang (2004), a sampling-based method called Pareto Set Pursuing (PSP) is introduced, which is an extension of the Mode Pursuing Sampling (MPS) method proposed in Wang et al. (2004). In Step 1 of PSP, initial points are sampled randomly. These points are evaluated with the computationally expensive functions in Step 2, and are saved in an archive based on their Pareto fitness values. In Step 3 of the method, two metamodeling techniques (a quadratic polynomial function and a linear RBF) are used to approximate the computationally expensive functions. Using the two surrogate problems, the authors introduce two functions to guide the sampling process, and devise two criteria for selecting between them during the sampling in Step 4. The first function selects sample points towards the extremes of the Pareto frontier, and the second one towards the entire Pareto frontier of the original problem. These sample points are then combined with the sample points in the archive and a subset of these is selected with the help of the second function. The selected points are evaluated in Step 5 with the computationally expensive functions and added to the archive. The authors have two criteria to stop the sampling process. If the stopping criteria are not met, the surrogate problem is updated. Then, the method returns to Step 4. Otherwise, the non-dominated solutions in the archive are considered as the approximated Pareto frontier. The authors claim that PSP can capture a nonconvex and disconnected Pareto frontier. Similar to Goel et al. (2007) and Yang et al. (2002), the authors also discuss the difficulties of GA-based algorithms in identifying extreme solutions in the Pareto frontier. They claim that the first function can overcome this difficulty. As far as the accuracy of the surrogate problem is concerned, the authors claim that the accuracy of their method is not critical when solving an MOP. The efficiency of PSP was evaluated on solving an MOP of fuel cell component design with one nonlinear objective function, one black-box objective function, one black-box constraint function and three decision variables.

In Khokhar et al. (2010), the PSP method (Shan and Wang 2004) is modified for mixed integer MOPs as the MV-PSP method. In the MV-PSP method, the basic idea of employing a surrogate problem is similar to the PSP method. To deal with discrete variables, however, random sampling in PSP would most likely generate infeasible discrete sample points (Khokhar et al. 2010). In order to rectify this issue, the authors use a method to sample feasible discrete points during the sampling process. The performance of the MV-PSP method was evaluated on solving an MOP of welded beam design with two nonlinear objective functions, four nonlinear constraint functions and four decision variables. In this paper, the performance of the MV-PSP method was also compared with the performance of six evolutionary multiobjective optimization algorithms, i.e., AbYSS (Nebro et al. 2008), CellDE (Durillo et al. 2008), FastPGA (Eskandari and Geiger 2008), NSGA-II (Deb et al. 2002), OMOPSO (Reyes and Coello 2005) and SPEA2 (Zitzler et al. 2002). These evolutionary algorithms, however, have not been developed to deal with computationally expensive MOPs. To compare these methods, a set of benchmark problems with convex, nonconvex and disconnected Pareto frontiers was considered. Since the basic idea of MV-PSP and PSP is the same, for MOPs with real-valuated and discrete decision variables, PSP and MV-PSP were applied, respectively. In this comparison, spread, generational distance, inverted generational distance, hyper-volume, generalized spread and percentage of the Pareto optimal solutions were considered as the performance indices to assess the quality of the solutions obtained by these methods. Based on this comparison, the authors claim to be relatively safe to mention that with a limited number of computationally expensive function evaluations, the PSP and MV-PSP methods outperform the compared methods for MOPs with two to three objective functions and less than eight decision variables. They observe that when the dimensionality increases to ten decision variables, PSP does not offer any superiority over the others. Handling this weakness is mentioned as a future research direction in Khokhar et al. (2010).

To summarize, in this subsection, we have surveyed methods in type 1 of the adaptive framework. In the following section, methods in type 2 of this framework are considered. After surveying all methods in the adaptive framework, we summarize characteristics of them in Table 2 of Section 6.2.

Table 2 Characteristics of methods in the adaptive framework (k, m, n are the number of objective functions, inequality constraint functions and decision variables, respectively)

6 Adaptive framework: type 2

6.1 General flowchart

The flowchart in Fig. 6 outlines the main steps of methods belonging to type 2 of the adaptive framework. As mentioned earlier, the initial approximated Pareto frontier may not represent the exact Pareto frontier of the original problem. Thus, by solving and updating the surrogate problem iteratively, the approximated Pareto frontier is supposed to coincide with the Pareto frontier of the original problem. To do this, sampling new points is required iteratively. In type 1, sample points selected before assessing a stopping criterion are utilized to update the surrogate problem (Step 4 highlighted in Fig. 4). In type 2, not only the sample points generated before assessing the stopping criterion are considered (Step 4 highlighted in Fig. 6), but also new points are sampled after assessing the stopping criterion in other regions of the decision and/or objective space to update the surrogate problem (Step 6 highlighted in Fig. 6).

Fig. 6

Flowchart of the adaptive framework: type 2

As can be seen in the flowchart in Fig. 6, a set of initial points is sampled in Step 1, and then evaluated with the computationally expensive functions in Step 2. After this, the function values of the sample points are available. In Step 3, an initial surrogate problem is built. In Step 4, a set of new sample points is generated relying on the surrogate problem. Similar to type 1, these points can be generated and selected e.g., by solving the surrogate problem with a DM if available. In Step 5, a stopping criterion is checked, which may require to evaluate the selected sample points with the computationally expensive functions. If the criterion is not met, based on a method-dependent criterion, a subset of non-dominated solutions generated in Step 4, which may have been evaluated with the computationally expensive functions, is selected. Then, in Step 6, a set of new points in other regions of the decision and/or objective space is sampled. These points along with the sample points selected in Step 5 are considered, and Steps 2-5 are then repeated. Otherwise, the set of non-dominated (or Pareto optimal) solutions or the most preferred solution of the last surrogate problem, which may have been evaluated with the computationally expensive functions, is considered as either the approximated Pareto frontier of the original problem or the most preferred solution for a DM, respectively. These solutions can also be visualized by an appropriate visualization technique. In Section 6.2, we summarize the methods in type 2 of the adaptive framework. These methods are then compared with other methods in type 1 of the adaptive framework in Section 8.

6.2 Summary of methods in the adaptive framework: type 2

In Liu et al. (2008), an optimization-based method is introduced using a quadratic polynomial function. The authors claim that this method is highly efficient and is less dependent on the accuracy of the surrogate problem. From this point of view, they claim that the framework of their method is a new framework which covers surrogate-based methods, and consider it as a novel multiobjective optimization method based on an approximation model management technique. Type 2 of the adaptive framework has been inspired by this paper. In Chen et al. (2012) also an optimization-based method similar to the idea in Liu et al. (2008) is introduced. Without loss of generality, we summarize these methods together. In both methods, the sample points are selected within a trust region in the decision space. To do this, an initial trust region is considered in the decision space by initializing its parameters, i.e., trust region center, radius and bounds, threshold and control constants to update the trust region. The authors also define a set of equations to update the trust region in each iteration of the methods.

After initializing the trust region, in Liu et al. (2008) and Chen et al. (2012) initial points are sampled using OLHS and LHS, respectively, within the trust region in Step 1, and evaluated with the computationally expensive functions in Step 2. Each computationally expensive function is approximated in Step 3 with a quadratic polynomial function and a Gaussian RBF in Liu et al. (2008) and Chen et al. (2012), respectively, and the initial surrogate problem is constructed. In Step 4, non-dominated solutions of these surrogate problems are obtained by solving them using μ-MOGA (Liu and Han 2006). Then, in both methods, the set P _a consisting of a subset of evenly distributed non-dominated solutions in the decision space from the obtained non-dominated solutions is considered. In Step 5, the points in P _a are evaluated with the computationally expensive functions. The non-dominated solutions of the evaluated points are stored in an archive P _e . In order to check a stopping criterion, the set P _t =P _a ∩P _e is considered. Then, a ratio between the number of points in P _t and P _a is calculated. Based on this ratio, the predefined equations and the constants, the trust region is updated by adjusting its parameters.

In Liu et al. (2008), if the radius of the updated trust region is less than a given threshold, or the number of iterations of solving and updating the surrogate problem is more than a given threshold, the method stops. In (Chen et al. 2012), other criteria based on the calculated ratio or the accuracy of the surrogate problem are also checked. If either of the stopping criteria is met, in both methods, the set P _e is considered as the approximated Pareto frontier of the original problem in Step 7. Otherwise, in both methods, a set of new points is sampled with LHS in Step 6. These points and those points from P _e that fall into the updated trust region are considered. In Liu et al. (2008), Steps 2–5 are then repeated. In Chen et al. (2012), a subset of those points from P _e that are in the updated trust region is first removed with respect to a distance coefficient. This action avoids singularity in the matrix of updating the RBF. The remaining points along with the new sample points are selected, and Steps 2–5 are repeated.

These methods can capture nonconvex and disconnected Pareto frontiers. The authors in Liu et al. (2008) discuss that capturing such Pareto frontiers depends on the initial trust region radius. The efficiency of the method in Liu et al. (2008) was evaluated on a black-box biobjective optimization problem of variable binder force in a car sheet metal forming with three decision variables. LS-DYNA was employed as a simulator. As far as the method in Chen et al. (2012) is concerned, the distribution of the non-dominated solutions relies on the quality of μ-MOGA. The distance coefficient affects the performance of this method. Based on the obtained results using the benchmark problems, the authors suggest the best value for the distance coefficient. The performance of this method was evaluated on a structure optimization problem of a vehicle door with two black-box objective functions, two black-box constraint functions and five decision variables involving the FE method. In Liu et al. (2008), closeness of the Pareto frontiers of the surrogate and benchmark problems was considered to assess the quality. In Chen et al. (2012), the quality was assessed based on the spread of non-dominated solutions obtained by the surrogate problem and closeness of them to the Pareto frontier of the benchmark problems.

All the methods described in Sections 5 and 6 are compared in Section 8. Table 2 summarizes the characteristics of the methods belonging to both types 1 and 2 in the adaptive framework with respect to sampling techniques, metamodeling techniques, number of objective and constraint functions as well as decision variables in the considered benchmark and application problems, and whether the methods are optimization- or sampling-based. In this table, for every method, the most challenging MOP that was considered as a benchmark or an application problem is mentioned. Since the number of equality constraints in all problems are zero (p = 0), it is not mentioned in the table. As can be seen, most of the problems consist of two or three objective functions except (Zhou and Turng 2007; Gobbi et al. 2013) with five objective functions.

7 A hybrid method

In Messac and Mullur (2008), a two-stage optimization-based method called Pseudo Response Surface (PRS) which hybridizes both the sequential framework and type 1 of the adaptive framework is introduced. Since discussion on the frameworks utilized in Sections 4 and 5 are necessary to describe this method, we discuss it in this section. This method is compared with other methods in Section 8. PRS consists of two stages where handling computationally expensive constraint functions is not addressed. In the first stage, a surrogate problem is built and updated iteratively in the same way in type 1 of the adaptive framework to generate a set of as evenly distributed feasible solutions as possible near the Pareto frontier of the original problem. This set is utilized to build another surrogate problem in stage two with the sequential framework. The second surrogate problem is accurate near the Pareto frontier of the original problem and intentionally inaccurate in other regions of the objective space. By formulating and solving the second surrogate problem, an approximation of the Pareto frontier is represented.

In stage one of PRS, extreme solutions are calculated. The extreme solutions, the utopia hyperplane and normal constraint method (Messac et al. 2003; Messac and Mattson 2004) are employed to generate feasible solutions near the Pareto frontier of the original problem. In Step 1 of type 1 of the adaptive framework utilized in this stage, a set of evenly distributed points including the extreme solutions is generated on the utopia hyperplane. Near every point on the hyperplane, a set of new points is sampled with FFS or LHS. These points are evaluated with the computationally expensive functions in Step 2. The individual computationally expensive functions are then approximated with a multiquadric RBF in Step 3, and an initial surrogate problem is built. In Step 4, the surrogate problem is scalarized using the normal constraint method introduced in Messac et al. (2003) and Messac and Mattson (2004). A feasible solution near the Pareto frontier is generated by solving this scalarized problem. In Step 5, this point is evaluated with the computationally expensive functions, and replaced with the oldest sample point in the sample points set. The surrogate problem is then updated. Steps 4 and 5 are repeated until all points on the hyperplane are used. As a result, in the first stage, a set of evenly distributed feasible solutions near the Pareto frontier is obtained in Step 6. These points are considered as the evaluated initial sample points for Steps 1 and 2 of the sequential framework used in stage two.

As mentioned earlier, the second stage of PRS concentrates on building an accurate surrogate problem near the Pareto frontier and is intentionally inaccurate in other regions of the objective space. To do this, based on the dimensionality of the decision space, a number of new sample points is selected far from the sample points set obtained from stage one. Instead of evaluating the selected points with the computationally expensive functions, every objective function value of these points is set such that each point has a higher objective value in comparison with the objective function value of the nearest point among the sample points evaluated with the computationally expensive functions. Then, each computationally expensive function is approximated with an extension of RBF called E-RBF (Mullur and Messac 2005) in Step 3 of the sequential framework, and an initial surrogate problem is built. In Step 4, the accuracy of the surrogate problem is evaluated near the Pareto frontier of the original problem by RMSE. In Step 5, if the accuracy is not sufficient, new points near the Pareto frontier are obtained using the first stage, and the surrogate problem is updated in Step 3.

Having the accurate enough surrogate problem, the set of non-dominated solutions is obtained in Step 6 by solving the surrogate problem of the stage two. This set is considered as the approximated Pareto frontier of the original problem in Step 8. These solutions are not evaluated with the computationally expensive functions in Step 7. The performance of PRS was evaluated on benchmark problems with nonconvex Pareto frontiers. The PRS method was also applied to a complex structural optimization problem requiring the FE method and analysis of rigidified inflatable structures. It had two black-box objective functions, three black-box constraints and three decision variables. The authors claim that the computational cost in simulation-based MOPs can be reduced considerably since the surrogate problem obtained with PRS is accurate near the Pareto frontier. While, the authors state that the approximated Pareto frontier is the Pareto frontier of the original problem, mathematical proof of this statement was mentioned as a future research direction. This method assumes that the ranges of the objective function values are available to compute the extreme solutions. This assumption can be a challenge. Although the authors expect that PRS can capture a disconnected Pareto frontier, they mention handling multimodalities and disconnected Pareto frontiers as a future research direction.

8 Comparison of surrogate-based multiobjective optimization methods

After giving an overview of surrogate-based methods proposed in the literature, we compare them in this section. As mentioned in Section 1, in this comparison, we concentrate on the attributes of the methods in four aspects: 1) Can the methods handle general black-box functions where information regarding mathematical properties of the functions such as convexity and continuity is not available? 2) Can the methods capture different types of Pareto frontiers? 3) How many objective and constraint functions as well as decision variables can be handled by the methods? 4) What is the role of a DM during the solution process? For this comparison, we consider the results given by the authors of individual papers on the benchmark and application problems that they have used to evaluate the performance of their methods. Throughout this comparison, we also discuss future research directions.

As far as black-box functions are concerned, all the described methods except (Monz et al. 2008) can handle such functions. In Monz et al. (2008), the convexity of the objective functions is assumed which cannot be guaranteed when considering black-box functions. We observe that only in Jakobsson et al. (2010) dealing with noisy black-box functions is discussed. However, the authors evaluated the efficiency of their method on benchmark problems without noise. Based on these observations, more research to figure out how metamodeling techniques can be applied to handle noisy black-box functions is required.

As far as handling nonconvex and disconnected Pareto frontiers is concerned, we observe that capturing a potential region to select sample points for updating the surrogate problem has a vital and a critical role. In Shan and Wang (2004), Kitayama et al. (2013), Yun et al. (2009), Jakobsson et al. (2010) and Khokhar et al. (2010), metamodeling techniques not only are employed to build the surrogate problem, but also to introduce functions for sampling. In Shan and Wang (2004) and Khokhar et al. (2010) these functions choose sample points towards the extreme solutions and the Pareto frontier. In Jakobsson et al. (2010), the sampling function selects sample points from or close to the extended Pareto frontier of the surrogate problem. In Kitayama et al. (2013), the aim of employing the sampling function is to generate evenly distributed sample points. The authors argue that sampling evenly distributed points to build and update the surrogate problem may help to capture disconnected parts of the Pareto frontier.

In Zhou and Turng (2007), the sample points are selected based on the variances of the objective function values of the sample points predicted by the Kriging model. In addition, expected improvement is another criterion related to Kriging model used in nature-inspired methods (Wagner et al. 2010) to select a new point for updating a surrogate problem. Such a criterion can also be considered in non-nature inspired methods. In Yun et al. (2009), Lagrangian multiplier values given by the metamodeling technique play a role to select new sample points. In Liu et al. (2008) and Chen et al. (2012), the trust region strategy is employed to select sample points from the explored and unexplored regions in the decision and/or objective space. In both methods, the sample points are selected to update the surrogate problem before and after assessing a stopping criterion. In Wilson et al. (2001), a considerable number of sample points is selected to capture nonconvexity and discontinuity, which highly relies on the accuracy of the surrogate problem. In Goel et al. (2007), convex hulls are discussed to capture a nonconvex Pareto frontier. In this paper, a metamodeling technique is utilized to approximate a function which visualizes the approximated Pareto frontier. This function represents an objective as a function of other objectives.

The authors in Eskelinen et al. (2010) claim that a simple nonconvex Pareto frontier can be captured by their method, because a convex hull is applied. In the PAINT method (Hartikainen et al. 2012), which can capture a nonconvex Pareto frontier, an interpolation between sample points is built. In Messac and Mullur (2008) and Gobbi et al. (2013), the idea of the normal constraint method (Messac et al. 2003; Messac and Mattson 2004) is employed to generate sample points near the Pareto frontier of the original problem. In Messac and Mullur (2008), the surrogate problem is constructed by type 1 of the adaptive framework to generate initial sample points. These points are used to form a surrogate problem of a computationally expensive MOP by the sequential framework. However, handling a disconnected Pareto frontier in Messac and Mullur (2008), Goel et al. (2007), Hartikainen et al. (2012) and Zhou and Turng (2007) is not considered. Based on the above observations, developing a method to handle the issues of nonconvexity and discontinuity in the Pareto frontier deserves research efforts.

One can see that in Messac and Mullur (2008), Shan and Wang (2004), Kitayama et al. (2013), Jakobsson et al. (2010) and Khokhar et al. (2010), RBFs have been employed to handle computationally expensive MOPs. The benchmark or application problems in Messac and Mullur (2008) have nonconvex Pareto frontiers, while in Shan and Wang (2004), Kitayama et al. (2013), Jakobsson et al. (2010) and Khokhar et al. (2010), they have nonconvex and disconnected Pareto frontiers. Now, a question arises whether the type of a metamodel technique has any impact on capturing a nonconvex and disconnected Pareto frontier. In addition, we observe that many methods developed in the adaptive framework can capture a nonconvex and disconnected Pareto frontier. Based on this observation, we recommend employing the adaptive framework to handle the issue of nonconvexity and discontinuity in the Pareto frontier.

The methods of Hartikainen et al. (2012), Monz et al. (2008) and Eskelinen et al. (2010) introduce surrogate problems to approximate directly the Pareto frontier. Both methods in Hartikainen et al. (2012) and Eskelinen et al. (2010) lose the connection to the decision space when solving the surrogate problems. Nevertheless, the corresponding decision vector value is available after projecting the approximated preferred solution obtained by the surrogate problems to the Pareto frontier of the original problem (although, this can be time consuming). In contrast, the Pareto navigation method (Monz et al. 2008) keeps the connection to the decision space during the navigation in the objective space. Apart from an approximation of the Pareto frontier in the objective space, there is a possibility to approximate the set of Pareto optimal solutions in the decision space. In Bhardwaj et al. (2013), a method is proposed to approximate this set in the decision space rather than in the objective space. In this method, however, handling a computationally expensive MOP is not concerned. Moreover, this method requires differentiability of the objective and constraint functions, and, thus, we do not discuss it further. However, one can consider the idea of approximating the set of Pareto optimal solutions in the decision space as an approach to handle computationally expensive MOPs. In addition, developing a method to approximate the Pareto frontier directly rather than each computationally expensive function in which the connection to the decision space is kept, can be considered for further research.

As far as the number of objective and constraint functions as well as decision variables is concerned, except in Lotov et al. (2001), Su et al. (2011), Zhou and Turng (2007), Gobbi et al. (2013), the authors in other considered papers employed benchmark and/or application problems limited to at most three objective functions, four constraint functions and seven decision variables. The highest number of objective functions (k = 5) was considered in Lotov et al. (2001), Zhou and Turng (2007), Gobbi et al. (2013) and Monz et al. (2008). In Lotov et al. (2001), a surrogate problem is formed based on a sampling strategy, in Gobbi et al. (2013), based on a neural network, in Zhou and Turng (2007), based on a Kriging model and in Monz et al. (2008), based on the convex hulls. The sampling strategy, however, can be unstable to handle an MOP with a high number of decision variables. In addition, training a neural network is time consuming. In Lotov et al. (2001), Su et al. (2011), Zhou and Turng (2007) and Gobbi et al. (2013), it remains unclear how to capture a disconnected Pareto frontier. In (Monz et al. 2008), the convexity of the objective functions is required. An MOP with the highest number of constraint functions (m = 13) and decision variables (n = 31) was considered in Su et al. (2011) based on the sequential framework. In (Shan and Wang 2004; Khokhar et al. 2010), the authors note that their methods can be employed to solve a computationally expensive MOP with two or three objective functions and less than seven decision variables. Moreover, applying the method in Jakobsson et al. (2010) to handle an MOP with more than three objective functions and six decision variables is unsuitable. In other methods, the authors do not discuss upper bounds on the number of objective and constraint functions as well as decision variables. See Shan and Wang (2010) for a review on handling a high-dimensional design problem. The ideas may be extended to deal with an MOP with a high number of objective and constraint functions and decision variables.

Considering the role of a DM as defined in Section 2.1 in solving an MOP has been discussed in Kitayama et al. (2013), Lotov et al. (2001), Hartikainen et al. (2012), Yun et al. (2009), Monz et al. (2008) and Eskelinen et al. (2010). A DM provides his/her preferences in the form of weights in Kitayama et al. (2013) and Yun et al. (2009), while in Lotov et al. (2001), (s)he compares the generated solutions. In Monz et al. (2008), a DM provides his/her preferences as a goal for one of the objective functions and upper bounds for the other ones. In Eskelinen et al. (2010), (s)he can express the preferences by means of a classification or a reference point consisting of aspiration levels for all objectives. In this aspect, PAINT has a distinguished feature, because a mixed integer linear multiobjective surrogate problem of the original problem is created without involving preferences. Therefore, it can be employed with any interactive method. The aim in methods of Kitayama et al. (2013), Lotov et al. (2001), Hartikainen et al. (2012), Monz et al. (2008) and Eskelinen et al. (2010) is to provide the most preferred solution for a DM rather than to approximate the entire Pareto frontier. Involving a DM when solving an MOP has not been considered in many papers and, thus, can be considered as another future research direction.

As mentioned earlier, the quality of the approximated Pareto frontier can be assessed based on Wu and Azarm (2000), Okabe et al. (2003) and Zitzler et al. (2003, 2008), the number of solutions in the approximated Pareto frontier, the distribution and spread of these solutions and closeness of the approximated Pareto frontier to the Pareto frontier of the original problem. Evaluating the performance of the surveyed methods based on these aspects with respect to a limited number of computationally expensive function evaluations requires implementing and testing them on a common set of benchmark problems. Nevertheless, the benchmark problems considered in the surveyed papers were not computationally expensive. Thus, to assess the performance of surrogate-based methods to handle computationally expensive problems, developing computationally expensive benchmark problems is a future research topic.

9 Conclusions

Many real-world (engineering) problems involve multiple conflicting objectives (and possibly constraints) that are computationally expensive to evaluate. In order to deal with the high computational cost, various surrogate-based methods which are independent of the type of the optimization algorithms used in them, have been proposed in the literature. So far, however, no survey has been available summarizing their characteristics, similarities and differences. This survey provided an overview of the methods available and with it, one can find out whether there exist a method applicable for one’s own problems.

Based on when the surrogate problem is built and updated, we classified these methods into the sequential and the adaptive frameworks. A special case of the sequential framework termed as one-stage sampling was also considered. In this case, points were sampled only once to build the surrogate problem. In accordance with when sample points are selected to update the surrogate problem, we divided the adaptive framework into types 1 and 2. The considered papers were then summarized and compared. Based on this comparison, we can identify the following challenges as future research directions:

• handling noisy black-box functions,

• capturing a nonconvex and disconnected Pareto frontier,

• handling a high number of objective and constraint functions as well as decision variables,

• providing the most preferred solution for a DM when solving computationally expensive MOPs,

• developing computationally expensive benchmark problems.

In order to capture a nonconvex and disconnected Pareto frontier, we recommend developing a method in the adaptive framework. We hope that this survey opens new horizons for the researchers interested in this topic.