1 Introduction

With rising dependence on groundwater to meet domestic, irrigation and industrial demands, trend analysis and simulation of water table behaviour have become important fields of study (Noori and Singh 2021). Researchers worldwide have developed and applied a number of different models to forecast groundwater levels, particularly for areas where recharge is low and extraction is high. Although models available for forecasting are abundant, selecting a suitable model that accurately simulates groundwater behaviour is complex (Takafuji et al. 2019). Several factors have to be taken into account for model choice and performance–objective of the study and data availability being primary (Salvadore et al. 2015; Barzegar et al. 2017).

Numerical modeling techniques have gained immense popularity in recent years, mainly due to their ability to forecast the likely impacts of water management solutions (Singh 2014; Sarma and Singh 2021a). Although largely popular, numerical models may be limited by large data requirements and complex computations (Aguilera et al. 2019). Univariate forecasting can be beneficial for data-scarce study areas. Zhang et al. (2018) present a comprehensive review of commonly used data-driven models for hydrological processes. They classified data-driven models as conventional, AI-based and hybrid models for streamflow prediction.

Conventional time series models such as Autoregressive Integrated Moving Average (ARIMA) and Seasonal Autoregressive Integrated Moving Average (SARIMA) are easy to use and widely popular (Mirzavand and Ghazavi 2015; Choubin and Malekian 2017; Rahaman et al. 2019;). The ARIMA model assumes that data at time t will directly correlate with previous data at t-1, t-2, …. and associated errors (Narayanan et al. 2013). Many studies around the world have compared the performance of ARIMA or SARIMA with other models such as Holt-Winters’ Exponential Smoothing (HWES), Integrated Time Series model (ITS) and Artificial Neural Networks (ANN) (Shirmohammadi et al. 2013; Aguilera et al. 2019; Sakizadeh et al. 2019). The HWES model forecasting is based on Holt and Winters’ basic structures (Holt 1957; Winters 1960) and can be applied on data with non-constant trends and seasonal variations (Yang et al. 2017). In the study by Yang et al. (2017) for a coastal aquifer in South China, HWES outperformed ITS and SARIMA.

In recent years, ANNs have seen widespread applications in forecasting hydrological parameters (Chen et al. 2020; Mozaffari et al. 2022). ANN replicates biological neuron processing and consists of an input layer, one or more hidden layers and an output layer. Lallahem et al. (2005) evaluated the feasibility of using ANNs for groundwater level predictions and concluded that ANNs, particularly MLPs with minimal lags and hidden nodes, gave the best simulation results. Yang et al. (2009) reported that Back-Propagation Artificial Neural Network outperformed ITS in simulating groundwater levels in China. Aguilera et al. (2019) compared the performance of the Prophet model with other forecasting techniques–seasonal naïve, linear model, exponential smoothing, ARIMA and neural network autoregression (NNAR) for groundwater level data in Spain. Recent years have seen the growing use of a novel method called Extreme Learning Machine (ELM) in hydrology (Kalteh 2019; Parisouj et al. 2020). In a study by Natarajan and Sudheer (2020), ELM had the best performance compared to ANN, GP and SVM for groundwater level prediction at six locations in Andhra Pradesh, India. Poursaeid et al. (2022) compared the performance of some mathematical and Artificial Intelligence (AI) models and concluded that the ELM method showed the best performance for groundwater level simulation.

In this study, two conventional models – Holt-Winters’ Exponential Smoothing (HWES), Seasonal ARIMA and three AI-based models – Multi-Layer Perceptron (MLP), Extreme Learning Machine (ELM) and Neural Network Autoregression (NNAR) were applied on historical groundwater records of three monitoring wells in National Capital Territory of Delhi, India. The models were trained and tested as per standard procedure. The forecasting performance of each model was compared using accuracy measures–coefficient of determination (R2), Root Mean Squared Error (RMSE) and Mean Absolute Error (MAE). Finally, the best model was used to predict groundwater depth in 2025. To the best of our knowledge, this comparative analysis has been done for the first time in the study area.

2 Materials and Methods

2.1 Data Driven Models

2.1.1 Holt-winters’ Exponential Smoothing

The simple smoothing methodology given by Brown (1959) was limited by its inability to support a time series with trend components (Sakizadeh et al. 2019). Holt (1957) proposed the exponential smoothing method which incorporated a trend component given by the following equations:

Level

$${l}_{t}= \alpha {y}_{t }+(1-\alpha )({l}_{t-1}+ {b}_{t-1})$$
(1)

Trend

$${b}_{t}= {\beta }^{*}\left({l}_{t}- {l}_{t-1}\right)+(1- {\beta }^{*}){b}_{t-1}$$
(2)

Forecast

$${y}_{t+h|t}= {l}_{t }+ {b}_{t}h$$
(3)

where, \({l}_{t}\): level of time series at t time step, \({b}_{t}\):slope of the series, \({y}_{t+h|t}\): forecast for next h time steps, \(\alpha\), \({\beta }^{*}\): smoothing parameters (between 0 and 1). For a time series with variable seasonal fluctuations, simulations are made using the multiplicative form:

Level

$${l}_{t}= \alpha \frac{{y}_{t}}{{S}_{t-m}}+(1-\alpha )({l}_{t-1}+ {b}_{t-1})$$
(4)

Trend

$${b}_{t}= {\beta }^{*}\left({l}_{t}- {l}_{t-1}\right)+(1- {\beta }^{*}){b}_{t-1}$$
(5)

Seasonal

$${s}_{t}= \frac{\gamma {y}_{t}}{\left({l}_{t-1}+ {b}_{t-1}\right) }+\left(1- \gamma \right){s}_{t-m}$$
(6)

Forecast

$${y}_{t+h|t}=({l}_{t }+ {b}_{t}h){s}_{t-m+{h}_{m}^{+}}$$
(7)

where, m: length of time series, \({h}_{m}^{+}\): (h-1)mod \(m\) + 1, St: seasonal component at time t, \(\gamma\): a smoothing coefficient (between 0 and 1).

2.1.2 Seasonal ARIMA Model

An ARIMA model contains autoregressive (AR), integrated (I) and moving average (MA) parts which are expressed as ARIMA (p, d, q); where p is autoregressive part, d is integrated part and q is moving average part (Box and Jenkins 1976). AR describes the relationship between present and previous variables in the time series. If p = 1, then each variable is a function of only one last variable, i.e.

$${Y}_{t}=c+ {\varnothing }_{1}{Y}_{t-1}+ {e}_{t}$$
(8)

where, Yt: observed value at time t, Yt-1: previous observed value at time t-1, et: random error, c and φ1: constants. For p > 1, other observed values of the series can be included as:.

$${Y}_{t}=c+ {\varnothing }_{1}{Y}_{t-1}+ {\varnothing }_{2}{Y}_{t-2}+\dots +{\varnothing }_{p}{Y}_{t-p}+ {e}_{t}$$
(9)

The I part of the model denotes the stationarity of the series. For a non-stationary series, differencing has to be done. For linear trend in the time series, first-order differencing is done (d = 1), for a quadratic trend, d = 2 and so on. The MA part of the model identifies the relationship between the variable and previous q errors. If q = 1, each observation is a function of only one previous error i.e.

$${Y}_{t}=c+ {\theta }_{1}{e}_{t-1}+ {e}_{t}$$
(10)

where, c: constant, et: random error at time t, et-1: previous random error at time t–1. For q > 1, other errors can be included as:

$${Y}_{t}=c+ {\theta }_{1}{e}_{t-1}+ {\theta }_{2}{e}_{t-2}+\dots + {\theta }_{q}{e}_{t-q}+ {e}_{t}$$
(11)

The combined equation for non-seasonal ARIMA model of order (p, d, q) for a standard normal variable (Yt) is:

$$\varnothing \left(B\right){\left(1-B\right)}^{d}{Y}_{t}= \theta (B){e}_{t}$$
(12)

where, B: backshift operator. To account for seasonality, the ARIMA model is represented by ARIMA (p,d,q) × (P,D,Q)s with P, D and Q denoting the seasonal autoregression, integration (differencing), and moving average, respectively.

$${\varnothing }_{p}\left(B\right){\Phi }_{P}\left({B}^{s}\right){\nabla }^{d}{\nabla }_{s}^{D}{Y}_{t}= {\theta }_{q}(B){\Theta }_{Q}({B}^{s}){e}_{t}$$
(13)

where, Yt: original time series, et: normal independently distributed white noise residual series with mean zero and variance σ2, Φ and Θ: ARIMA structures between the seasonal observations, φ and θ: non-seasonal ARIMA structure, ϕp(B) and ΦP(Bs): non-seasonal and seasonal autoregressive operators of order p and P, respectively, θq(B) and ΘQ(Bs): non-seasonal and seasonal moving average operators of order q and Q, respectively, ∇d and ∇sD: non-seasonal and seasonal differencing operators of orders d and D. The Seasonal ARIMA procedure involves three major steps –

  1. (a)

    Model identification: the time series is first analysed for stationarity and normality and accordingly differenced and/or log-transformed. Autocorrelation (ACF) and partial autocorrelation (PACF) functions of the original and differenced series are examined. The best model is identified based on least Akaike Information Criterion (AIC) and Bayesian Information Criterion (BIC). The AIC or BIC is written in the form [-2logL + kp], where L: likelihood function, p: number of parameters in the model, and k: 2 for AIC and log(n) for BIC (Akaike 1974; Schwarz 2007).

  2. (b)

    Parameter estimation and diagnostic checking: autoregressive and moving average parameters of the identified model are estimated. Diagnostic checking is carried out from the residuals and accuracy measures to examine the suitability and assumptions of the model.

  3. (c)

    Forecasting: the selected model is used to forecast the variables for future time periods.

2.1.3 Multi-layer Perceptron

Several AI-based deep learning frameworks are available that can simulate time series data. Of these, MLP is a simple feed-forward layered technique that works on the principle of the backpropagation algorithm (Hecht-Nielsen 1989; Aslam et al. 2020). The data are processed in the forward direction by feeding into input nodes. These are then multiplied by a given weight and passed onto one or more hidden layer nodes. The hidden layer nodes add the weighted inputs, calculate loss or bias and then pass it on through a transfer function to give the result. The output nodes perform the same operations. During the training phase, the weights and biases are adjusted to minimise the errors via the backpropagation algorithm and a comparison is made between target outputs at each output node and output network (Lallahem et al. 2005). The backpropagation algorithm keeps repeating this iteration till the maximum improvement is achieved. Fig. S1 demonstrates a three-layer feed-forward MLP structure. The equation for MLP is given by:

$${y}_{k}= {S}_{1}({\sum }_{j=1}^{J}{w}_{j}{S}_{2} ({\sum }_{i=1}^{I}{w}_{i}{x}_{i} + {W}_{j}) + {W}_{k})$$
(14)

where, \({y}_{k}\) are outputs from the network, \({x}_{i}\) are inputs, \({w}_{i}\) are weights connecting input and hidden layer nodes, \({w}_{j}\) are weights connecting hidden and output layer nodes, \(I\) are input nodes, \(J\) are hidden nodes, \(K\) are output nodes, \({W}_{j}\) is bias for jth hidden neuron and \({W}_{k}\) is bias for kth output neuron. S1 and S2 are activation functions. Commonly, the logistic sigmoid function is used for activation:

$$S\left(x\right)= \frac{1}{1+ {e}^{-x}} S:R \to ]-1, 1 [$$
(15)

2.1.4 Extreme Learning Machine

ELM was developed to overcome traditional neural networks’ high computational cost and time (Huang et al. 2006). In the three-layered structure (single hidden layer feed-forward network) of ELM, weights between inputs and hidden nodes and bias values in the hidden layer are generated at random which are frozen during model training. The weights between hidden nodes and outputs are calculated using Moore–Penrose generalized inverse of the hidden-output matrix. This process makes ELM much faster than traditional ANNs because there is no iteration in learning. For a training set, ELM is expressed as:

$${\sum}_{i=1}^{\widehat{N}}{\beta }_{i}g\left({w}_{i}{x}_{j}+ {b}_{i}\right)= {o}_{j},j=1,\dots ,N$$
(16)

where, xi: input, \(\widehat{N}\): hidden nodes, wi: weight vector from input to ith hidden node, bi: bias of ith hidden node, βi: weight vector from ith hidden node to output, oj: output and g(x): non-linear activation function in hidden layer (Parisouj et al. 2020).

2.1.5 Neural Network Auto-regression

In an NNAR model, lagged values are used as inputs to a neural network. NNAR(p,k) indicates that there are p lagged inputs and k nodes in hidden layer. For seasonal data, last observed values from same season are used as inputs. It is denoted by NNAR(p, P, k)m which has (yt-1, yt-2, …, yt-p, yt-m, yt-2 m, …, yt-Pm) as inputs and k neurons in hidden layer. Unlike SARIMA, NNAR does not require stationarity of time series. Mathematically NNAR is:

$${y}_{t}=f\left({y}_{t-1}\right)+ {\varepsilon }_{t}$$
(17)

where, f: neural network, \({y}_{t-1}\): vector containing lagged values of series and \({\varepsilon }_{t}\): error series (assumed to be homoscedastic) (Hyndman and Athanasopoulos 2018).

2.2 Study Area and Data Used

The five forecasting models were applied on groundwater records of monitoring wells in the National Capital Territory (NCT) of Delhi. The NCT of Delhi in North India lies between 28° 24′ 15″ N to 28° 53′ 00″ N and 76° 50′24″ E to 77° 20′ 30″ E. It covers an area of 1483 km2, 75% of which is urbanized (Central Ground Water Board 2016). It is divided into 11 districts. Much of Delhi’s rain occurs during the monsoon months – July to September, bringing high humidity levels. Delhi’s geological formations vary from Quartzite to Older and Younger Alluvium making the aquifer geology complex (CGWB 2021a).

The Central Ground Water Board (CGWB) has over a 100 monitoring stations spread over Delhi’s alluvial and quartzitic area. Historical records of groundwater levels for monitoring stations in NCT of Delhi were obtained from CGWB for winter (January), pre-monsoon (May), monsoon (August) and post-monsoon (November) seasons. Mann–Kendall test on pre-monsoon and post-monsoon groundwater levels (in mbgl) for Delhi at the district level showed an increasing trend indicating that there has been a decline in the groundwater depth in the last two decades (Sarma and Singh 2021b).

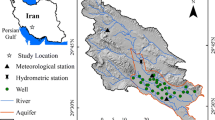
2.3 Data Pre-processing and Methodology of Study

To demonstrate the comparison between the time series models, data from three wells were chosen because of their declining groundwater level – Haiderpur (GW1), Bhatti (GW2) and Kitchner Road (GW3). Locations of these wells are presented in Fig. 1. The time period for study was selected depending on data availability – GW1 (1999–2019), GW2 (1996–2019) and GW3 (1983–2017). The datasets were analysed for completeness and a small number of missing values were imputed using the Multivariate Imputation by Chained Equations (MICE) package in R software (van Buuren and Groothuis-Oudshoorn 2011). Multiple imputation has an advantage over single imputation methods in that correlations error obtained from the imputations are not overestimated due to the inclusion of uncertainty because of missing data (Lee and Carlin 2010; Gao et al. 2018). The dataset was divided into two subsets for applying the time series models–80% for training and 20% for testing. To avoid larger values from overriding smaller ones and prevent saturation of hidden nodes, the dataset was normalized between 0 and 1 for MLP and ELM (Eq. (18)).

$${x}_{n}= \frac{({x}_{i}- {x}_{min})}{({x}_{max}- {x}_{min})}$$
(18)

where, xn: normalized data, xi: actual value, xmin: minimum value and xmax: maximum value in each dataset (Shirmohammadi et al. 2013). The HWES, NNAR, SARIMA, MLP and ELM algorithms were run on the training data using their respective packages in R software – forecast (Hyndman et al. 2008, 2019; Hyndman and Athanasopoulos 2018), astsa (Shumway and Stoffer 2016) and nnfor (Crone and Kourentzes 2010; Kourentzes et al. 2014). The complete methodology of the study is depicted in Fig. 2.

Fig. 1
figure 1

Locations of selected monitoring wells for the study – Haiderpur (GW1), Bhatti (GW2) and Kitchner Road (GW3)

Full size image
Fig. 2
figure 2

Methodology of study

Full size image

2.4 Evaluation of Model Performance

After fitting the training data, each model was used to forecast the groundwater level for the testing period. To assess model performance, accuracy measures–root mean square error (RMSE), mean absolute error (MAE) and coefficient of determination (R2) were compared. The model with the least RMSE and MAE and maximum R2 during the training and testing phases was determined as the best model for forecasting groundwater levels in the study area.

$$RMSE= \sqrt{\frac{1}{n} {\sum }_{i=1}^{n}{({O}_{i}- {P}_{i})}^{2}}$$
(19)
$$MAE= \frac{1}{n} {\sum }_{i=1}^{n}|\left({O}_{i}- {P}_{i}\right)|$$
(20)
$${R}^{2}= {[\frac{{\sum }_{i=1}^{n}\left({O}_{i}-\underline{O}\right)\left({P}_{i}- \underline{P}\right) }{\sqrt{{\sum }_{i=1}^{n}{\left({O}_{i}- \underline{O}\right)}^{2}{\sum }_{i=1}^{n}{\left({P}_{i}- \underline{P}\right)}^{2}}}]}{}^{2}$$
(21)

where, n: number of data points, \({O}_{i}\): observed variables with mean \(\underline{O}\) and \({P}_{i}\): predicted variables with mean \(\underline{P}\) (Choubin and Malekian 2017; Yan and Ma 2016).

3 Results and Discussion

3.1 Time Series Decomposition

The time series of the three wells were first decomposed into its trend, seasonal and residual components in R software (Fig. 3). Since the data are in metres below ground level (mbgl), all 3 wells showed increasing trend, implying continuous groundwater depletion during the time period of study. The trend ranged over 7 mbgl for GW1, 30 mbgl for GW2 and 15 mbgl for GW3. The seasonal component has an oscillatory amplitude of 0.3 mbgl for GW1, 3 mbgl for GW2 and 2 mbgl for GW3. The seasonal component has a peak in November and trough in May, according to the rainfall patterns in Delhi. Much of the rainfall is received during the monsoon season (July – September) which recharges the groundwater during the post-monsoon months (October – November). During January to June, scanty rainfall is unable to compensate for the groundwater abstraction, thus leading to a lower recharge in May. The residual component fluctuates between ± 1 mbgl for GW1, ± 5 mbgl for GW2 and ± 3 mbgl for GW3. This decomposition showed that for all 3 study wells, the trend has the largest component, followed by the residual and seasonal parts.

Fig. 3
figure 3

Seasonal decomposition of groundwater level time series of GW1, GW2 and GW3 into trend, seasonal and random components

Full size image

3.2 Holt-winters’ Exponential Smoothing

The Holt-Winters’ model predicts a future value by combining the influences from the level, trend and seasonality. Each component has an associated smoothing parameter that provides information about its influence on the model’s predictions (Table 1). The value of α is close to 1 for GW1 and GW2, indicating that prediction of a current observation is mostly based on the immediate past observations. For GW3, lower value of α implies that older observations are weighted more than the most recent ones. All three study wells had β* close to or equal to 0 indicating that the trend does not change much over time and remains fairly constant during each prediction. GW1 and GW3 have γ values close to 0 indicating that like trend, seasonality also does not change. However, for GW2, a larger γ value implies a strong seasonal component. Thus, for GW2, seasonal component of the current observation is based on the seasonality of the most recent observations.

Table 1 Smoothing parameters from HWES with trend and additive seasonal component
Full size table

3.3 Seasonal ARIMA

The autocorrelation (ACF) and partial autocorrelation (PACF) plots for the time series of GW1, GW2 and GW3 were inspected to check the stationarity. The plots did not tail off to zero indicating that the series were not stationary and required appropriate differencing. First order non-seasonal differencing was applied on GW1 and GW3 while GW2 required first order seasonal. This corroborated the results from HWES as GW2 showed a strong seasonal component while GW1 and GW3 did not have much influence from seasonality. The Augmented Dickey-Fuller (ADF) test was applied before and after differencing and the p-value was compared. The p-value before differencing was computed as 0.4451, 0.1118 and 0.0419 for GW1, GW2 and GW3 respectively. After the appropriate differencing, the p-value as determined from the ADF test was 0.01, rejecting the null hypothesis that the series has a unit root and is thus stationary.

With the appropriate differencing, the value of d or D of the SARIMA model was determined. Different combinations of p, P, q and Q were tested on trial-and-error method. The ACF and PACF plots of each of these models were inspected and model selection criteria AIC and BIC were compared (Table S1). The best model was selected based on the minimum AIC and BIC values. The final models selected were (1,1,1)(1,0,0)4, (1,0,0)(0,1,1)4 and (1,1,1)(1,0,1)4 for GW1, GW2 and GW3 respectively.

3.4 MLP, ELM and NNAR

The MLP networks were trained in R using a validation argument and specified number of lags to prevent overfitting the training data (Fig. 4). The grey inputs represent autoregressive lags and pink inputs represent seasonality. The mean square error (MSE) for the trained MLP networks were 0.0022, 0.0036 and 0.0127 for GW1, GW2 and GW3 respectively. The ELM networks were trained in R using the lasso regression method. The time taken for training was significantly lesser than the MLP networks. The mean square error (MSE) for the trained ELM networks were 0.0072, 0.0062 and 0.0156 for GW1, GW2 and GW3 respectively. The NNAR models were applied on the training data with Box-Cox transformation (lambda = 0). This transformation ensured that the residuals were homoscedastic. The descriptions of the resultant ELM and NNAR networks are presented in Table 2.

Fig. 4
figure 4

MLP network for a GW1 (5 inputs, 1 hidden layer, 4 nodes) b GW2 (7 inputs, 1 hidden layer, 2 nodes) and c GW3 (6 inputs, 1 hidden layer, 1 node)

Full size image
Table 2 ELM and NNAR model descriptions for the study wells
Full size table

3.5 Comparison of Model Performance

The accuracy measures were compared for the models for each study well (Table 3). For GW1 and GW2, MLP performed the best for both the training and testing phases with highest R2 and lowest RMSE and MAE. MLP best fitted the observed values with the predicted values during training and testing (Fig. 5). For GW3, HWES had the highest RMSE and MAE among all models. NNAR performed very well during training but gave unrealistic forecasts during testing. There may have been overfitting of data, indicated by the large parameters in the network, i.e. 9–5-1 network with 56 weights. The MLP network yielded low R2 values for both training and testing. MLP network for GW3 had only 1 hidden node (Fig. 4) and compared to GW1 and GW2, MSE for GW3 was higher. ELM presented very high RMSE and MAE for both training and testing. SARIMA had slightly better R2 but MLP had the lowest errors. Thus, MLP was considered the best performing model for GW3 as well.

Table 3 Comparison of accuracy measures for selected models
Full size table
Fig. 5
figure 5

Fitting the observed and simulated values for a training and b testing

Full size image

The best model MLP was used to forecast the groundwater level for the year 2025. MLP forecasts for May 2025 showed that groundwater level will fall by 2 mbgl and 21 mbgl below the 2019 level for GW1 and GW2 respectively and 3 mbgl below the 2017 level for GW3.

3.6 Discussion

The results from applying the five models suggest that with validation in the training set, MLP can train the model with R2 as high as 0.914. For GW1 and GW2, SARIMA and HWES also gave high R2 values during training. For the testing period, the R2 tends to decrease slightly for MLP and HWES and dramatically for SARIMA. Thus, fitting precision of a model may not necessarily imply accurate forecasting which makes evaluating the model forecasts against a testing subset a crucial step in the modeling process. ELM gave the lowest R2 for GW1 and GW2 during training. NNAR had overall low efficiency which was also observed in the study by Aguilera et al. (2019). These models may perform better by selecting the appropriate activation functions, lagged variables as inputs or numerical procedure (Faraway and Chatfield 1998). MLP, ELM, HWES and SARIMA did not perform well on the GW3 dataset. Even though the dataset for GW3 was large with 139 observations over 1983–2017, there was overall low performance of the models. Groundwater levels are influenced by factors like rainfall, soil properties, surface water and abstraction (Lee et al. 2019) and during interpretation of model results, it may be pertinent to analyse these influencing factors as well.

MLP forecast for 2025 presents an alarming result for GW2, a monitoring well located in the southern part of the study area (Fig. 1). Declining trends in the South district of Delhi have been reported by the CGWB, particularly due to over-exploitation (CGWB 2016, 2021b). Results of aquifer response modeling for Delhi using MODFLOW also showed a similar decline for GW2 (Bhatti) (CGWB 2016), necessitating an urgent and effective groundwater management plan in that region.

4 Conclusion

This study used univariate time series forecasting methods HWES, Seasonal ARIMA, MLP, ELM and NNAR for prediction of groundwater levels in Delhi, India. Decomposition of the time series of three monitoring wells showed increasing trend, indicating that the groundwater level has continuously declined over the study period. The parameters of HWES and SARIMA were calculated and MLP, ELM and NNAR models were trained and validated. The accuracy of the models was assessed based on the R2, RMSE and MAE. MLP had the least values of RMSE and MAE and highest R2 for two wells during training and testing, indicating that the MLP approach was most accurate in forecasting the groundwater levels. For the third well, MLP had a slightly lower R2 but least RMSE and MAE and was also concluded to be better than HWES, SARIMA, ELM and NNAR for making predictions.

Such univariate forecasting studies are particularly suitable for regions where large hydro-climatological data are unavailable. MLP was used to make further predictions for May 2025 for all three wells. Results indicate that groundwater level in the three wells will decline by 2–21 mbgl. This study has helped identify the areas that require urgent groundwater management decisions. Further research may be done on adding more arguments in the model algorithm to give the lowest errors. It is recommended that more comparison studies should be made for other regions in India so that the most accurate models help in identifying the areas where groundwater is declining rapidly.