1 Introduction

The Piano Key (PK) weir is a long crested weir that improves the capacity of discharge through the constant upstream head by increasing the length of the crest. Due to the resulting high discharge capacity of these types of weir, reservoir capacity is increased and dams are stabilised against flooding. The PK weir has been developed by Lempérière, HydroCoop, France and Blanc, Hydraulic and Environmental Laboratory, University of Biskra, Algeria (Lempérière and Ouamane 2003). The first PK weir was built in 2006 on the Goulours dam in France, with the second being installed in 2008 on Saint-Marc dam in France (Laugier 2007; Laugier et al. 2009).

Lempérière (2011) suggested the head – discharge relation for the PK weirs. Kabiri-Samani and Javaheri (2012) presented the experimental relations of discharge coefficients for these types of weirs in two free and submerged forms. Anderson and Tullis (2012) compared the hydraulic performances of labyrinth weirs and rectangular PK weirs. They indicated that the reduced loss of inlet keys, led to better performance from the PK weirs. Anderson and Tullis (2012) showed that for the value of \( \frac{W_i}{W_O} \)=1.25–1.5, the PK weir had the highest efficiency. Machiels et al. (2013) studied the effect of parapet walls on the hydraulic performance of this type of weir and pointed out its positive effect due to the increased height of the weir. In addition to structural and hydraulic studies, the application of artificial intelligence techniques for estimating the weirs’ discharge coefficients can be noted. Emiroglu et al. (2011) estimated the discharge coefficient of the triangular labyrinth side-weir on a straight channel using the Artificial Neural Network (ANN) model. Results of this model were more successful than the multiple non-linear regression model. By using the ANN model, Bilhan et al. (2011) estimated the discharge coefficient of triangular labyrinth side-weirs in curved channels. They suggested that the ANN model was more capable of estimating the discharge coefficient compared to the multiple non-linear regression model. Dursun et al. (2012) estimated the discharge coefficient of semi-elliptical side weirs by making use of Adaptive Neuro-Fuzzy Inference System (ANFIS). Their results indicated the success of this technique over Multiple Linear Regression (MLR) and Nonlinear Regression (NLR). Salmasi et al. (2012) estimated the discharge coefficient of compound broad-crested weirs by applying the Genetic Programming (GP) techniques and ANN. Results showed that the genetic programming technique is more capable than the ANN in terms of estimating the weir’s discharge coefficient. Ebtehaj et al. (2015) estimated the discharge coefficient of triangular labyrinth side-weirs using the gene expression programming. By using the Support Vector Regression (SVR), Zaji et al. (2016) predicted the modified discharge coefficient of diagonal side weirs (in triangular form). Results obtained from their investigation showed that SVR-RBF outperforms the SVR-poly. Shamshirband et al. (2016) estimated the optimum discharge coefficient of side weirs using the ANFIS model. Results showed the ANFIS model with five inputs was more accurate than the ANFIS model with a single input. Parsaie (2016) investigated the discharge coefficient of side weirs using the experimental formulas, Multi-Layer Perceptron (MLP) and Radial Basis Function (RBF). The MLP model yielded the best result. Haghiabi et al. (2018) estimated the discharge coefficient of triangular labyrinth side-weirs using the ANFIS. Results of this model were compared to MLP neural network’s results. Results achieved from comparing the MLP to ANFIS indicated that both models function very appropriately, but the ANFIS structure is more accurate.

There have been many applications of the Gaussian Process Regression (GPR) method in water engineering sciences. For example, Pasolli et al. (2010) estimated the concentration of chlorophyll in subsurface waters by the GPR method using remote sensing data. Grbić et al. (2013) predicted the stream water temperature based on the GPR method. Their technique can be used as a basis for prediction tools for water resource managers. Once an online Bayes filtering was made on the global surface temperature data, Wang and Chaib-draa (2017) analysed the temperature using the GPR method. They suggested this technique was better than various types of Gaussian Process (GP) and was seen as an accurate and efficient system for analysis of global temperatures. Karbasi (2017) investigated the 10-year statistical data (2000–2009) from Zanjan Synoptic Station, Iran, and predicted the multi-step ahead daily reference evapotranspiration by the method of Wavelet-GPR and GPR models. Results showed that the hybrid method of Wavelet-GPR was more capable and accurate over the GPR model in predicting the daily evapotranspiration.

A review of pertinent literature shows that previous studies regarding PK weirs have not investigated the effect of an additional gate on each of the inlet keys. This study is the first to examine such an effect. It also investigates other parameters of PK weirs, using the Gaussian Process Regression (GPR) method to predict coefficient of discharge (Cd) and compare this result with Support Vector Machines (SVM), Multi-Layer Perceptron (MLP), Generalized Regression Neural Networks (GRNN), multiple linear and nonlinear regression methods and with suggesting the relation for Cd. Thus, this study is distinguished from other studies in this area. In addition, the GPR method has not been used to investigate the discharge coefficient of weirs. The present study introduces this method for predicting discharge coefficient of weir.

2 Materials and Methods

2.1 Dimensional Analysis

Dimensional analysis aims at diagnosing the effective parameters in the studied phenomenon and determining the dimensionless ratios. Due to the geometrical complexity of Gated Piano Key weirs (GPK weirs), the discharge passing over them is subject to parameters of Eq. 1.

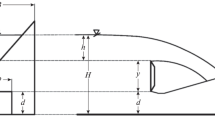
$$ Q=f\left(H,{H}_{up},{H}_{down},b,d,{H}_{gate},L,W,P,{W}_i,{W}_o,{B}_i,{B}_o,N,{S}_i,S{}_o,{T}_s,g,\mu, \sigma, \rho \right) $$
(1)

where Q is the discharge overflow from GPK weir, H is head on GPK weir, Hup is the upstream head, Hdown is the downstream head, b is the length of rectangular gate, d is the width of rectangular gate, Hgate is the water head from the rectangular gate center to the crest of weir, L is the crest length [L = N(Wi + Wo + 2B)], W is the total weir width or flume width, P is the total weir height, Wi is the inlet key width, Wo is the outlet key width, Bi is the downstream or inlet key overhang length, Bo is the upstream or outlet key overhang length, N is the weir cycle number, Si is the inlet key slope, So is the outlet key slope, Ts is the weir wall thickness, g is the gravitational acceleration, μis dynamic viscosity,ρis density and σ is surface tension. Figure 1 shows Gated Piano key weir geometric and hydraulic parameters.

Fig. 1
figure 1

(A) GPK weir hydraulic parameters, (B) The geometric parameters of gate in GPK weirs, (C) PK weir geometric parameters

Full size image

Since Hup and Hdown are function of the H, they can be excluded. The number of cycles, slope of inlet and outlet keys can be seen as a proportion of other parameters, hence, they can be excluded, too. Using the dimensional analysis and considering the dimensionless numbers of Reynolds (Re), Weber (We) and dimensionless ratios, Eq. 1 is reduced to Eq. 2.

$$ \frac{Q}{g^{\frac{1}{2}}{BH}^{\frac{3}{2}}}=f\left({R}_e,{W}_e,\frac{H}{P},\frac{L}{B},\frac{W_i}{W_o},\frac{B_i}{L},\frac{B_o}{L},\frac{b}{p},\frac{d}{p},\frac{H_{gate}}{P}\right) $$
(2)

In accordance with Eq. (2), it can said that Cd is subject to the geometrical parameters of GPK weirs and dimensionless numbers of Reynolds and Weber. The Reynolds number in channels is sufficiently large, hence the viscosity can be ignored (Henderson 1966) Therefore, the Reynolds and Weber numbers are deleted from Eq. 2. To investigate the geometrical parameters of GPK weir, Eq. 3 can be proposed.

$$ {C}_d=f\left(\frac{H}{P},\frac{L}{B},\frac{W_i}{W_o},\frac{B_i}{L},\frac{B_o}{L},\frac{b}{p},\frac{d}{p},\frac{H_{gate}}{P}\right) $$
(3)

2.2 Experimental Set up

These experiments were performed in the hydraulic laboratory, Department of Water Engineering, University of Tabriz, Iran. The experiments were conducted on a 10 m long and 0.933 m wide horizontal rectangular flume. The height of the first 3 m of the flume was 1 m with the rest of its length being 0.5 m in height. The floor of the flume was constructed from galvanized iron and the side walls from 10 mm thick glass. The GPK weir was installed on a 1 cm high ramp. The water circulation system included an underground tank equipped with a 100 hp. pump which provided a steady supply of water into a head tank. The upstream tank (head tank) provided water flow into the flume. The weir returned extra water from the head tank into the underground tank, thereby ensuring the discharge in the rotation system would be a fixed amount. The water flowed downstream through the flume, was collected in the collection tank, and then flowed into the underground tank to be pumped again into the head tank (Fig. 2).

Fig. 2
figure 2

The Schematic of laboratory flume and water circulation system

Full size image

The discharge rate was measured using an ultrasonic flow meter with 1% precision. Discharge measuring sensors were installed on a 10-in. pipe which supplied water to the flume. The discharge ranges were between 10 and 130 litters per second.

In order to reduce the turbulence of the input water flow from the pipe into the laboratory flume, the water travelled across a porous medium space created by sequential lattice plates placed along the first three meters of the laboratory flume. By placing the Styrofoam on the water surface oscillations were prevented and in this way the height of water was stabilized in the upstream of the GPK weir. The water depth was measured by a point gauge moveable along the flume, with a precision of 0.1 mm. Due to the limitations imposed by surface tension forces the limitation of input discharge, the measured range of H is varied from 1.5–8 cm depending on the model type.

In this study, a four-cycle GPK weir was used. Figure 3 provides the tested physical models in this study. The variables in this study are: gate dimensions (b and d), the different gate height (Hgate), different ratios of the inlet key width to the outlet key width (Wi/Wo), and the head over the GPK weir crest (H). It can be noted that in addition of GPK weirs, un-gated PK weirs also were tested in this study.

Fig. 3
figure 3

Physical models of PK and GPK weirs with different geometric specifications

Full size image

Tables 1 and 2 shows the PK and GPK weir geometric parameters in physical models. In Tables 1 and 2Pm is the weir wall height at the center of weir, B is the weir sidewall length and n is crest length to weir width ratio (n = L/W). The other parameters were defined previously.

Table 1 The PK weir geometric parameters in physical models
Full size table
Table 2 Different geometric parameters of the GPK weir in physical model
Full size table

All physical models were built from polyethylene plates with 12 mm thickness. Gates frames were built from PVC with 1 mm thickness.

2.3 Experimental Data

As can be seen in Table 2, from 188 experiments for both PK and GPK weirs, 156 data set was relevant to the GPK weir. From this data, 70% and 30% were used as the training data and model testing data, respectively.

The statistical parameters of training and test data are given in Table 3. Training and test data were used for training process of models and evaluation of models accuracy, respectively.

Table 3 Statistic parameters of training phase and test dataset
Full size table

2.4 Gaussian Process Regression (GPR)

The Gaussian Process is a suitable method to define the preferred distribution for the flexible models of regression and classification in which regression or class probability functions are not limited to the simple parametric forms.

One advantage of the Gaussian Process is the wide diversity of its covariance functions, which leads to functions with different degrees of smoothness, or various types of continuous structures, thereby allowing the scholar to choose appropriately from among them. These models can specify the distributions among the functions with one or more input variable. When this function defines the mean response in a regression model with Gaussian errors, the matrix calculations can be used for inference; this is feasible for those data sets with a sample of greater than one thousand. Gaussian processes are very important in statistical modeling, because they have normal characteristics (Neal 1997).

One can assume n observations in a desired dataset of Y = {y1,…,yn} as a single point sampled from the multiple Gaussian (It has n variables) distribution. Hence, data sets can be corresponded to a Gaussian process. The Gaussian process, therefore, is as simple as much as it is comprehensive. It is mostly assumed that the mean of correspondent the Gaussian process is zero everywhere. What connects one observation to another in such states is the covariance function, \( k\left(x,\overset{\acute{\mkern6mu}}{x}\right) \). Each observation y can be connected to a main function through the Gaussian noise model.

$$ y=f(x)+N\left(0,{\sigma}_f^2\right) $$
(4)

Where, \( N\left(0,{\sigma}_f^2\right) \) is the noise of normal distribution function with mean 0 and variance\( {\sigma}_f^2 \). Regression, in fact, means looking for f(x). To simplify the next step, a new way for noise combination in \( k\left(x,\overset{\acute{\mkern6mu}}{x}\right) \) is used by writing the following term:

$$ k\left(x,\overset{\acute{\mkern6mu}}{x}\right)={\sigma}_f^2\mathit{\exp}\left[\frac{-\Big(x-{\overset{\acute{\mkern6mu}}{x\Big)}}^2}{2{\tau}^2}\right]+{\sigma}_n^2\delta \left(x,\overset{\acute{\mkern6mu}}{x}\right) $$
(5)

where, \( \delta \left(x,\overset{\acute{\mkern6mu}}{x}\right) \) is the Kronecker delta function. Therefore, n observations of y is taken into account; the goal is to predict y*.

The predicted values of observations are the same in accordance with Eq. 4, but variances vary upon due to the observational noise process. To prepare the GPR for covariance function, Eq. 5 is calculated among all possible combinations of these points and findings are summarized in three matrices:

$$ k=\left[\begin{array}{ccc}k\left({x}_1,{x}_1\right)& k\left({x}_1,{x}_2\right)& \dots \kern0.5em k\left({x}_1,{x}_n\right)\\ {}k\left({x}_2,{x}_1\right)& k\left({x}_2,{x}_2\right)& \dots \kern0.5em k\left({x}_2,{x}_n\right)\\ {}\begin{array}{c}\vdots \\ {}k\left({x}_n,{x}_1\right)\end{array}& \begin{array}{c}\vdots \\ {}k\left({x}_n,{x}_2\right)\end{array}& \begin{array}{cc}\begin{array}{c}\ddots \\ {}\dots \end{array}& \begin{array}{c}\vdots \\ {}k\left({x}_n,{x}_n\right)\end{array}\end{array}\end{array}\right] $$
(6)
$$ {K}_{\ast }=\left[k\left({X}_{\ast },{X}_1\right)k\left({X}_{\ast },{X}_2\right)\dots k\left({X}_{\ast },{X}_n\right)\right],{k}_{ij}=k\left({x}_i,{x}_j\right) $$
(7)

It should also be noted that the diagonal elements, K, are in the form of \( {\sigma}_f^2 \)+\( {\sigma}_n^2 \) . When the x receives a large domain, the non-diagonal elements approaches zero (Ebden 2015).

2.5 Multilayer Perceptron Model

The Multilayer Perceptron Neural networks (MLP-NN) are the feed-forward networks including one or more hidden layers. One way to train the widely used MLP-NN is the back propagation training rule, which is based on the error correction learning rule (moving in the negative direction of momentary slope subject to the performance (error) function which reduces the model error)(Dibike and Solomatine 2001; Negnevitsky 2005).

The back propagation rule is composed of two main paths. On the first path, the inlet vector is applied to the multilayer network, the effects of which are propagated through the middle layers to the output layers. The outlet vector formed on the output layer makes the real response of MLP-NN. On the second path, known as the backward path, the parameters of MLP-NN are modified and regulated. Such regulation is done in accordance with the error correction rule. Similarly, the weights of neurons in the middle layers change in such a way that the error value between the output of neural network and real output is minimized (Demuth et al. 2014; Goh 1995; Rafiq et al. 2001). Once the artificial neural network is developed, data is usually divided into two training and test periods. There is no exact rule for determining the minimum size of training and test sets. As per such suggestions, approximately 70% of total data is sufficient for network training and the remaining 30% is used for network testing (Baum and Haussler 1989; Zare et al. 2012). In this study, structure and architecture of ANN was optimum as 1 × 11 × 1 on the basis of trial and error conducted on the number of neurons in the middle layer. This is a three-layer network where 1, 11 and 1 indicate the number of neurons in input, hidden and output layers, respectively. The activation functions of this network are hyperbolic tangent sigmoid (tansig) and linear (purelin) functions, respectively, for hidden and output layers. The learning algorithm is the error back-propagation algorithm on the basis of Levenberg–Marquardt optimization method.

2.6 Support Vector Machines (SVM) Regression Model

Support Vector Machines (SVM) include two categories: 1. Support vector classifier; 2. Support vector regression. The SVM is a supervised learning technique which was introduced by Vapnik (1995) and is based on statistical learning theory (SLT)(Vapnik 2013). In some cases, complicated and nonlinear structures are needed for data separation. In this case, the main data is mapped and rearranged in a new space by the SVM through applying a set of mathematical functions, known as kernel. A SVM algorithm looks for a hyperplane with maximum margin. From the geometrical perspective, margin is calculated by the distance between the hyperplane and the closest training samples. The shortest distance from a hyperplane to sample with label +1 is equal to the shortest distance from that hyperplane to the samples with label −1. In fact, the margin is calculated by doubling this distance. A separating hyperplane can be defined as below:

$$ W.X+b=0 $$
(8)

where, W = {w1,…, wn} is a vector in which the number of existing elements is equal to the attributes and is a constant. In 2D space where the data sets are defined with two attributes and one class label, Eq. 8 is rewritten as Eq. 9, assuming the w0 = b:

$$ {w}_0+{w}_1{x}_1+{w}_2{x}_2=0 $$
(9)

Accordingly, the samples (points) located on the space above this hyperplane complete the inequality (10) and the ones below this hyperplane complete the inequality (11).

$$ {w}_0+{w}_1{x}_1+{w}_2{x}_2>0 $$
(10)
$$ {w}_0+{w}_1{x}_1+{w}_2{x}_2<0 $$
(11)

Adjusting the W and b, we have:

$$ {\mathrm{w}}_0+{\mathrm{w}}_1{\mathrm{x}}_1+{\mathrm{w}}_2{\mathrm{x}}_2\ge 1\ \mathrm{if}\ {\mathrm{y}}_{\mathrm{i}}=+1 $$
(12)
$$ {\mathrm{w}}_0+{\mathrm{w}}_1{\mathrm{x}}_1+{\mathrm{w}}_2{\mathrm{x}}_2\le 1\ \mathrm{if}\ {\mathrm{y}}_{\mathrm{i}}=-1 $$
(13)

This means that each sample located over or on the hyperplane H1 belongs to the class +1 and the one below and on the hyperplane H2 belongs to the class −1. Those samples which are exactly on the hyperplane H1 and H2, are called “support vectors”(Burges 1998).

2.6.1 Kernel Functions

A common way to solve the nonlinear problems is to use the kernel functions; these functions are defined based on the inner product of given data. Designing the GPR techniques includes application of kernel function concept. In fact, with a nonlinear transformation from inner space to the attribute space with more dimensions (even infinite), problems can be separated linearly. By transforming the samples from the input space into the attribute space, the nonlinear separator will become linear.

$$ {w}^T\varnothing \left({x}_j\right)+b=0 $$
(14)

Primary and dual problems create the attribute space problem. With this difference: that instead of\( \left({x}_i^T.{x}_j\right) \) the value of xj = ∅T(xi) ∅ (xj) and k(xi) is used, where, k(xi, xj) is the kernel function for linearization of nonlinear problems. Among the most important kernels, linear, polynomial, normalized polynomial, Radial Basis Function (RBF) kernel and Pearson kernel function can be mentioned.

Simple polynomial kernel function:

$$ k\left({x}_i,{x}_j\right)={\left({x}_i^T{x}_j+1\right)}^p $$
(15)

Normalized polynomial kernel function:

$$ k\left({x}_i,{x}_j\right)=\frac{{\left({x}_i^T{x}_j+1\right)}^p}{\sqrt{\left({x}_i^T{x}_i\right)+\left({x}_j^T{x}_j\right)}} $$
(16)

Radial basis function:

$$ k\left({x}_i,{x}_j\right)=\mathit{\exp}\left(-Y{\left|{x}_i-{x}_j\right|}^2\right) $$
(17)

Pearson kernel function:

$$ k\left({x}_i,{x}_j\right)=\frac{1}{{\left[1+{\left(2\sqrt{x_i,{x}_j^2}\sqrt{2^{\frac{1}{w}}-\frac{1}{\varnothing }}\right)}^2\right]}^w} $$
(18)

These kernel functions have individual parameters in their structures, known as the hyper-parameters 1. The radial basis function, for instance, has Gamma hyper-parameter and Pearson function has the Sigma and Omega parameters. In addition, to select the optimum kernel function in applying the kernel function based methods, it is very important to determine the optimum hyper-parameter related to each function. The kernel based modeling techniques needs to create the appropriate parameters defined by the user, since the accuracy of this regression model is highly dependent on selection of these parameters. In addition to selecting the specific kernel parameters, GPR needs to specify the optimums of Gaussian noise level. To select the parameters chosen by the user (i.e. C, γ, σ, ω, ε and Gaussian noise), numerous techniques have been proposed; manual method (trial and error), network search method, Genetic Algorithm (GA) and particle swarm optimization. In the present study, the trial and error is used for selecting the parameters chosen by the user. The optimums of various parameters defined by the user are selected in such a way that they minimize the root-mean-square error (RMSE) and maximize the correlation coefficient (Pal and Deswal 2010).

2.7 Generalized Regression Neural Networks Model

The Generalized Regression Neural Networks (GRNN) are a set of Radial basis function networks together with a linear layer (Chen et al. 1991). GRNN model is based on a statistically standard technique, known as kernel regression (Cigizoglu and Alp 2006; Li et al. 2013). These networks, include 4 layers: input layer, pattern layer, summation layer and output layer (Cigizoglu and Alp 2006). The input layer receives the information. The number of neurons is equal to the input vector dimension. Then, the inlet neuron from the input layer transfers the data to the pattern layer which has nonlinear transformation from the input space to the pattern space. Neurons in the pattern layer (which are also called the “pattern neurons”) can keep the relationship between the input neuron and the proper response from the pattern layer and also the number of neurons equal to the input variables. The summation layer includes a simple summation and a weighted summation. The former calculates the output arithmetic sum from the pattern layer and the connection weight is 1. The latter calculates the output weighting sum from the pattern layer. Once the summated neurons are transferred to the output layer, output of the GRNN model can be measured. In these networks, the number of neurons in the output layer is equal to the output vector dimension (Li et al. 2013). Unlike the back propagation training algorithm, GRNNs do not need frequent training processes (Chen et al. 1991; Cigizoglu and Alp 2006). These networks take a radius into account around each observational data where each input data within that radius makes that data involved in its estimation for a new input value. The effect of the radius of GRNN used in this study was measured based on trial and error.

2.8 Statistical Criteria

To investigate the accuracy of models suggested in this study, the following statistical measures have been used:

$$ RMSE=\sqrt{\frac{\sum_{i=1}^N{\left({O}_i-{P}_i\right)}^2}{N}} $$
(19)
$$ NRMSE=\frac{RMSE}{\overline{O_i}}\times 100 $$
(20)
$$ MAPE=\frac{1}{N}{\sum}_{i=1}^N\left|\frac{O_i-{P}_i}{O_i}\right|\times 100 $$
(21)
$$ {R}^2=\frac{\Big({\sum}_{i=1}^N\left({O}_i-\bar {O_i}\right){\left({P}_i-\bar {P_i\Big)}\right)}^2}{\sum_{i=1}^N{\left({O}_i-\bar {O_i}\right)}^2{\sum}_{i=1}^N{\left({P}_i-\bar {P_i}\right)}^2} $$
(22)

In these equations, Qi is the mean of observations, Pi is the mean of predictions and N is the total number of data. Root Mean Square Error (RMSE) is the difference between the predicted and observed data. Mean Absolute Percentage Error (MAPE) shows the accuracy of model prediction. R2 describes the connection between the predicted and observed data.

Normalized Root Mean Square Error (NRMSE) is used for comparing the models with various measures. Model performance with regard to NRMSE is defined as below (Mihoub et al. 2016):

  • Excellent if: NRMSE <10%.

  • Good if: 10% < NRMSE <20%.

  • Fair if: 20% < NRMSE <30%.

  • Poor if: NRMSE >30%.

3 Results and Discussion

In this study, the results of artificial intelligence models, MLP, GPR, GRNN, SVM, together with two linear and nonlinear regression models, were investigated and assessed in terms of estimating the GPK weir discharge coefficient. The results of the various models are given below.

3.1 Multi-Layer Perceptron (MLP) Neural Network

A three-layer artificial neural network model (with a hidden layer) was used in this study. The input and output activation functions were selected as sigmoid and linear. Due to higher accuracy and speed, the Levenberg-Marquardt algorithm was used for network training (Lourakis and Argyros 2004; Ngia and Sjoberg 2000). The most important part in modeling using the MLP neural network was to determine the number of optimal neurons in the hidden layer. For this purpose, a trial and error method was applied. The number of neurons in the hidden layer was changed from 1 to 10 and the best number of neurons was chosen using the RMSE for the test data of model. Table 4 shows the modeling results by making use of the MLP neural network. From these results it can be determined that the MLP neural network with two neurons in the hidden layer has yielded the best outcome with RMSE = 0.024 and R2 = 0.961. Based on Table 4, it can be seen that as the number of neurons increases, the model accuracy decreases.

Table 4 Results of MLP model with different number of neuron at hidden layer
Full size table

3.2 Gaussian Process Regression (GPR) Model

Table 5 shows the results of the GPR model in estimating the GPK weir discharge coefficient. To investigate the effect of different kernels on the model accuracy, five types of kernels, i.e., Squared Exponential, Exponential, Matern 3/2, Matern 5/2 and Rational quadratic, were evaluated. The GPR model with the Squared Exponential kernel has yielded the best results concerning RMSE = 0.011, R2 = 0.992 and MAPE = 1.167%. Comparing different kinds of kernels (Squared Exponential, Exponential and etc.) indicated that application of different kernels had minor impact on model performance and varied from RMSE = 0.018 for the Rational quadratic kernel to RMSE = 0.015 for the Exponential kernel. Results revealed that the GPR model was not sensitive to the kernel changes. Figure 4 shows the Scatter plots of observed and predicted values of Cd for GPR model with different kernels. Closeness of the data to line 1:1 shows the appropriate accuracy of models in estimating the GPK weir discharge coefficient.

Table 5 Results of GPR model with different kernel types
Full size table
Fig. 4
figure 4

Scatter plots of observed and predicted Cd for GPR model with different kernels

Full size image

3.3 Support Vector Machine (SVM) Model

Table 6 shows the modeling results obtained from the SVM model. In this study, RBF, Linear and polynomial kernels were used for modeling. To find the optimum kernel parameters (ε and γ), the Bayesian optimization algorithm in MATLAB was used. The SVM model with the RBF kernel gave the best result with RMSE = 0.015, R2 = 0.982 and MAPE = 1.961%. Our results were consistent with ones obtained by Zaji et al. (2016) . Comparing two linear and polynomial kernels indicates the superiority of the SVM model with the linear kernel (RMSE = 0.042) over the polynomial model (RMSE = 0.057). Figure 5 shows Scatter plots of observed and predicted values of Cd for SVM model with different kernels.

Table 6 Results of SVM models with different kernels and optimized parameters
Full size table
Fig. 5
figure 5

Scatter plots of observed and predicted Cd for SVM model with different kernels

Full size image

3.4 Generalized Regression Neural Networks (GRNN) Model

Table 7 shows the modeling results of GRNN in estimating the GPK weir discharge coefficient. The optimal model was obtained by changing the Spread parameter in GRNN. In view of Table 7, the Spread parameter equal 0.001 yielded the best results for with RMSE = 0.073, R2 = 0.651 with further reduction of this parameter having no significant impact on results.

Table 7 Results of GRNN model with different spread parameter values
Full size table

3.5 Multiple Linear Regression

Analysis of multiple linear regression was conducted on the experimental data. The Dimensionless eq. (22) was obtained for estimating the discharge coefficient of the GPK weir. Analyses were made in MATLAB.

$$ {C}_d=0.672-1.618\left(\frac{H}{P}\right)+0.23\left(\frac{b}{P}\right)+0.056\left(\frac{d}{P}\right)+0.534\left(\frac{H_{gate}}{P}\right)+0.125\left(\frac{w_i}{w_0}\right) $$
(23)

3.6 Multiple Nonlinear Regression

To evaluate the nonlinear regression in estimation of the discharge coefficient of the GPK weir, an equation within the general form (23) was evaluated:

$$ {C}_d=\overset{\acute{\mkern6mu}}{a}{\left(\frac{H}{P}\right)}^{\overset{\acute{\mkern6mu}}{b}}{\left(\frac{b}{P}\right)}^{\overset{\acute{\mkern6mu}}{c}}{\left(\frac{d}{P}\right)}^{\overset{\acute{\mkern6mu}}{d}}{\left(\frac{H_{gate}}{P}\right)}^{\overset{\acute{\mkern6mu}}{e}}{\left(\frac{w_i}{w_0}\right)}^{\overset{\acute{\mkern6mu}}{f}} $$
(24)

Coefficients of \( \overset{\acute{\mkern6mu}}{a},\overset{\acute{\mkern6mu}}{b},\overset{\acute{\mkern6mu}}{c},\overset{\acute{\mkern6mu}}{d},\overset{\acute{\mkern6mu}}{e},\overset{\acute{\mkern6mu}}{f} \) were determined using MATLAB:

$$ {C}_d=0.375{\left(\frac{H}{P}\right)}^{-0.53}{\left(\frac{b}{P}\right)}^{0.096}{\left(\frac{d}{P}\right)}^{0.012}{\left(\frac{H_{gate}}{P}\right)}^{0.148}{\left(\frac{w_i}{w_0}\right)}^{0.276} $$
(25)

3.7 Comparing the Techniques of Artificial Intelligence and Regression Analysis

Table 8 compares the best model built in each method by artificial intelligence with linear and nonlinear regression analyses. In Table 8, the statistical parameters of RMSE, R2, MAPE and NRMSE were used for training and testing datasets. As seen in Table 8, three artificial intelligence models, GPR, SVM and MLP, outperformed the regression models and only the GRNN model did not give acceptable results. Comparison between the GPR, SVM and MLP models indicated that the GRP model yielded the best results with RMSE = 0.011, R2 = 0.992 and MAPE = 1.167%, followed by the SVM model with RBF kernel with RMSE = 0.015, R2 = 0.982 and MAPE = 1.961%. The MLP model with two neurons in the hidden layer is ranked as the third with RMSE = 0.024, R2 = 0.961 and MAPE = 3.441%. The GRNN model with RMSE = 0.073 was ranked sixth and yielded weaker results than the linear regression. Comparison between the two regression models indicated the superiority of nonlinear regression model over the linear one. With RMSE = 0.035, R2 = 0.961 and MAPE = 4.562%, nonlinear regression gave acceptable results for estimating the discharge coefficient of GPK weir. In the linear regression model, values of RMSE = 0.061, R2 = 0.865 and MAPE = 9.491% were obtained. Figure 6 shows the Scatter plots of observed and predicted values of Cd for all of the six models compared in Table 8. As can be seen in Fig. 6, the data for GPR model is closer to line 1:1.

Table 8 Comparison of best models
Full size table
Fig. 6
figure 6

Scatter plots of observed and predicted values of Cd for the six methods

Full size image

Figure 7 shows the points related to the observational and estimated data together with a confidence interval (CI) 95% for the GPR model. With regard to this figure, most of the observed data points are within the CI 95%.

Fig. 7
figure 7

Point and interval predictions of Cd by GPR model

Full size image

3.8 Sensitivity Analysis

In order to evaluate the impact of input parameters on estimated discharge coefficient of the GPK weir, the sensitivity analysis was conducted using the GRP model (given its less error). In this analysis, each time a parameter was omitted from the model inputs, the model was implemented and accuracy was evaluated. The deleted parameter with the highest effect on decreased model accuracy and increased model error was evaluated as the most important parameter. In view of the analysis results, seen in Table 9, deleting the parameter H/P had the highest effect on accuracy and caused the RMSE to increase to 0.128. The error percentage achieved MAPE = 16.621%. Parameter wo/wi was the second most effective parameter on the discharge coefficient of the GPK weir. With its deletion RMSE increased to 0.079.

Table 9 Sensitivity analysis of input variables
Full size table

Comparison of the parameters related with gate \( \left(\frac{H_{gate}}{P},\frac{b}{P},\frac{d}{P}\right) \) showed that \( \frac{H_{gate}}{P} \) (RMSE = 0.032) affected more than two parameters of \( \frac{b}{P} \) (RMSE = 0.029) and \( \frac{d}{P} \) (RMSE = 0.027). Given the statistical measures, two parameters of \( \frac{b}{P} \) and \( \frac{d}{P} \) had the same effect on model accuracy.

4 Conclusion

Designing weirs with high discharge capacity is important in order to control flood flows entering the rivers and reservoirs of dams and maintaining safe levels. The GPK weir was proposed as a new idea in order to increase the capacity of weir discharge and improve its performance. In this study, effective parameters on the GPK weir discharge were investigated using soft computing methods MLP, GPR, SVM, GRNN, linear and non-linear regressions.

For this purpose, data from 156 laboratory tests was collected and processed in MATLAB software 2018. The results of this study showed that H, Wi/Wo, Hgate, b and d, (defined in fig. 1), had the greatest effect on the GPK weir discharge coefficient, respectively. Three artificial intelligence models, GPR, SVM and MLP, outperformed the regression models and only the GRNN model did not give acceptable results. Comparison between the GPR, SVM and MLP models indicated that the GRP model yielded the best results, followed by the SVM model with RBF kernel. The MLP model with two neurons in the hidden layer was ranked third. The GRNN model was ranked sixth and yielded weaker results than the linear regression. Comparison between the two regression models indicated the superiority of the nonlinear regression model over the linear one. According to the results of artificial intelligence techniques in this study, the GPR method was found to be a new and accurate method for predicting the discharge coefficient of weirs.