Inventory Theory-Based Stochastic Optimization for Reservoir Water Allocation

Abstract

This study aims to develop an effective model for reservoir water allocation under conditions of uncertainty. To identify a practical method that increases the benefits by optimizing the water allocation policies while reducing the costs by optimizing the water transfer scheme, several stochastic programming models (EOQ-TSP models) were developed by integrating economic order quantity (EOQ) models into a two-stage stochastic programming (TSP) framework. The EOQ-TSP models are advantageous for analyzing the effects of the water inventory scheme on the reservoir water allocation benefits and better at optimizing water allocation policies while also considering uncertainties regarding different flow levels and different water inventory conditions in a water supply-inventory-demand system. Finally, the feasibility of the developed EOQ-TSP models was demonstrated by applying the models to a real-world case study. The results show that the benefits of the optimal water allocation policy will be further increased by optimizing the water transfer scheme, and these proposed models will be helpful for systematizing reservoir water management and identifying optimal reservoir water allocation plans in uncertain environments.

1 Introduction

Modeling analysis is a particularly important way to research water resource management problems in uncertain environments; thus, the modeling approach has been increasingly used by scholars, especially when conflicts related to water allocation among users occur (Jakeman et al. 2006; Loukas et al. 2007; Zhang et al. 2016).

Water resource management problems are complicated due to uncertainties, such as the random characteristics and the uncertainty of natural factors, financial factors, technical factors, social factors and even political factors (Li et al. 2009, Li et al. 2019). Uncertainties could comprehensively affect the water resources management of a system and make the management of the system more complex. Previously, a number of studies researched the above questions by using stochastic programming models (Mobasheri and Harboe 1970; Trezos and Yeh 1986; Kelman et al. 1990; Huang 1998; Li et al. 2006; Li et al. 2019, 2019; Fu et al. 2018;). The two-stage stochastic programming model (TSP), which is an effective method for analyzing problems under uncertain conditions, has received extensive attention over the past decade and has been used to research various water resource management problems in uncertain environments by many scholars (Schultz et al. 1996; Huang and Loucks 2000; Kovacs et al. 2007; Li et al. 2010a; Zhang et al. 2014).

Although TSP models are an effective method for analyzing problems related to the management of water resources under conditions of uncertainty, these models cannot adequately address the water inventory problem that widely exists in reservoir water resource management systems (Li et al. 2011). For example, water is transferred from areas with relatively abundant water to reservoirs that need to be replenished for allocation purposes during water shortages. The water inventory risk and transferring costs are increased if too much water is transferred; in contrast, it is possible to add an insufficient amount of water to the water-user sectors, which would also cause large economic losses if the amount of transferred water is too low. Therefore, it is necessary to develop effective optimization models to comprehensively solve the questions related to the transfer of water from abundant areas to reservoirs that must be replenished due to water shortages and to optimize the reservoir water allocation policy under conditions of uncertainty. Many stochastic inventory models have been established by researchers (Schmitta and Shen 2010; El Saadany and Jaber 2010; Duan et al. 2012; Zhou et al. 2017; Zhang et al. 2014). For example, inventory theory was integrated with stochastic programming methods to analyze the water resources management of a reservoir (Suo et al. 2011). The model was based on inventory theory, and inexact chance-constrained multistage stochastic optimization was used to research water management systems under conditions of multiple uncertainties (Suo et al. 2011). However, few studies that address the problem have conducted contrastive analysis of the water allocation polices based on different water transfer schemes. For example, the problem related to the water transfer policy with planned shortages could increase the benefits of reservoir water allocation or not. Thus, the traditional inventory-based stochastic programming models need to be further improved to solve more complex supply-inventory-demand problems in reservoir water resource management systems.

Thus, this study aims to develop a series of new models by integrating EOQ models into the TSP framework. The developed models are capable of (1) quantitatively reflecting the relationship between the reservoir water resource allocation scheme and the reservoir inventory strategy by coordination optimization of the two parts; and (2) gaining insight into the variation trends of reservoir water resource allocation benefits under different reservoir storage strategies based on the comparison of different EOQ-TSP models. Furthermore, these new models will also be applied in a real-world case study of the H.Q. reservoir, which is located in Qinghai Province, China, to demonstrate how EOQ-TSP models can optimize reservoir water transfer policies and water allocation policies and help managers identify more reasonable and optimal reservoir water resource allocation plans under different flow levels and different water transfer scenarios under uncertain conditions.

2 Methodology

Transferring water from areas with abundant water is an effective way to replenish reservoir water shortages that require more water for allocation; this scenario can be described as a supply-inventory-demand problem. The reservoir water transfer scheme will influence the optimal reservoir water allocation policy. Thus, analyzing the water allocation problem under the above conditions should include effectively researching the reservoir water inventory policy.

2.1 EOQ Models

Optimizing the inventory policy to minimize costs is one of the most important aims of inventory studies, and the EOQ model is one effective method that can be used to address this optimization problem (Hillier 2001). The EOQ model can be divided into four submodels with different assumptions: the basic EOQ model (B-EOQ), the EOQ model with planned shortages (EOQ-S), the EOQ model with a production parameter (EOQ-P) and the EOQ model with both planned shortages and a production parameter (EOQ-SP).

2.1.1 Basic EOQ Model (B-EOQ)

Assumptions of the B-EOQ Model

The B-EOQ model can be depicted as shown in Fig. 1, and the detail assumptions of the B-EOQ model can be described as follows (Hillier 2001).

• 1) The demand rate per unit time is fixed constant;

• 2) Every ordered batch used to replenish inventory arrives simultaneously when the inventory level drops to zero;

• 3) Planned shortages are not allowed.

Fig. 1

Diagram of inventory level as a function of time for the B-EOQ model. Note: X is the demand rate per unit time; D is the ordered batch size; T is the ordering period

Optimal Inventory Policy of the B-EOQ Model

The optimal inventory policy based on the B-EOQ model contains three main components:

• 1) The optimal ordering period (T^*) is given by Formula (1a), which is the optimal cycle length.

$$ {T}^{\ast }=\sqrt{\frac{2 Cs}{Ch\cdot X}} $$

(1a)

• 2) The optimal ordering batch is given by D^*, which is the economic order quantity during a cycle.

$$ {D}^{\ast }=\sqrt{\frac{2 Cs\cdot X}{Ch}} $$

(1b)

• 3) The optimal total cost per unit time is given by f^∗:

$$ {f}^{\ast }=\sqrt{2 Ch\cdot Cs\cdot X}+ Cp\cdot X $$

(1c)

where Ch is holding cost per unit per unit of time held in inventory; Cs is the setup cost for ordering one batch; Cp is the unit cost for producing each unit; X is the demand rate per unit time.

2.1.2 EOQ Model with Production Parameter (EOQ-P)

The EOQ-P model is suitable for solving the inventory problem, which assumes the condition of supplying with limited speed or with limited supply.

Assumptions of the EOQ-P Model

The EOQ-P model can be depicted as shown in Fig. 2; the only different assumption of the EOQ-P model to the B-EOQ model is that there is a supplying rate (namely, g, and g > X) to replenish the inventory when the inventory level drops to zero (i.e., the second assumption of the B-EOQ model).

Fig. 2

Diagram of inventory level as a function of time for the EOQ-P model. Note: X is the demand rate per unit time; D is the ordered batch size; T is the ordering period; g is supplying rate (g > X) to replenish the inventory and T_j is the inventory replenishing time; S is the maximized inventory quantity during each ordering period

Optimal Inventory Policy of the EOQ-P Model

The optimal inventory policy of the EOQ-P model contains four main components:

• 1) The optimal ordering period based on the EOQ-P model is given by T^*:

$$ {T}^{\ast }=\sqrt{\frac{2 Cs\cdot g}{Ch\cdot X\cdot \left(\mathrm{g}-\mathrm{X}\right)}} $$

(2a)

• 2) The optimal ordering batch is given by D^*:

$$ {D}^{\ast }=X\cdot {T}^{\ast }=\sqrt{\frac{2 Cs\cdot X\cdot g}{Ch\cdot \left(\mathrm{g}-\mathrm{X}\right)}} $$

(2b)

• 3) The optimal total cost per unit time is given by f^∗:

$$ {f}^{\ast }=\sqrt{2 Ch\cdot Cs\cdot X\cdot \frac{g-X}{g}}+ Cp\cdot X $$

(2c)

• 4) The optimal replenishing time is given by Tj^∗, which is the optimal inventory replenishing time span during T^*:

$$ {T_j}^{\ast }={D}^{\ast }/g $$

(2d)

where g is the inventory replenishing rate per unit time.

2.1.3 EOQ Model with Planned Shortages (EOQ-S)

The EOQ-S model is suitable for solving the inventory problem, which includes the condition that allows inventory shortages.

Assumptions of the EOQ-S Model

The EOQ-S model can be depicted as shown in Fig. 3; the only different assumption of the EOQ-S model to the B-EOQ model is that planned shortages are allowed (i.e., the third assumption of the B-EOQ model).

Fig. 3

Diagram of inventory level as a function of time for the EOQ-S model. Note: X is the demand rate per unit time; D is the ordered batch size; T is the ordering period; T_q is the shortage period; B is the maximum shortage quantity; S is the maximized inventory quantity during each ordering period

Optimal Inventory Policy of the EOQ-S Model

Because the planned shortages are allowed, the optimal inventory policy of the EOQ-S model contains five main components:

• 1) The optimal ordering period based on the EOQ-S model is given by T^*:

$$ {T}^{\ast }=\sqrt{\frac{2 Cs\left( Ch+ Cq\right)}{Ch\cdot Cq\cdot X}} $$

(3a)

• 2) The optimal ordering batch is given by D^*:

$$ {D}^{\ast }={T}^{\ast}\cdot X=\sqrt{\frac{2 Cs\cdot X\left( Ch+ Cq\right)}{Ch\cdot Cq}} $$

(3b)

• 3) The optimal total cost per unit time, i.e., f^∗, is:

$$ {f}^{\ast }=\sqrt{\frac{2 Ch\cdot Cq\cdot Cs\cdot X}{Ch+ Cq}}+ Cp\cdot X $$

(3c)

• 4) The maximum shortage quantity, i.e., B^*, is:

$$ {B}^{\ast }=\sqrt{\frac{2 Ch\cdot Cs\cdot X}{Cq\cdot \left( Ch+ Cq\right)}} $$

(3d)

• 5) The shortage period is given by Tq^*, which is the time span of inventory shortage that exists during T^*:

$$ {Tq}^{\ast }=\frac{B\ast }{X}=\sqrt{\frac{2 Ch\cdot Cs}{Cq\cdot \left( Ch+ Cq\right)\cdot X}} $$

(3e)

2.1.4 EOQ Model with Planned Shortages and Production Parameter (EOQ-SP)

The EOQ-SP model is suitable for solving the inventory problem, which includes the condition that allows supplying with limited speeds and inventory shortages.

Assumptions of the EOQ-SP Model

The EOQ-SP model can be depicted as shown in Fig. 4. The EOQ-SP model is different than the B-EOQ model in that the ordering batch used to replenish the inventory has a replenishing rate (namely, g) when the inventory level drops to zero (i.e., the second assumption of the B-EOQ model). Furthermore, planned shortages are allowed (i.e., the third assumption of the B-EOQ model).

Fig. 4

Diagram of inventory level as a function of time for the EOQ-SP model. Note: X is the demand rate per unit time; D is the ordered batch size; T is the ordering period; B is the maximum shortage quantity; S is the maximized inventory quantity during each ordering period; g is the supplying rate (g > X) to replenish the inventory; T_j is the inventory replenishing time

Optimal inventory policy of the EOQ-SP model

The optimal inventory policy of the EOQ-SP model contains six components:

• 1) The optimal ordering period based on the EOQ-SP model is given by T^*:

$$ {T}^{\ast }=\sqrt{\frac{2 Cs}{Ch\cdot X}}\cdot \sqrt{\frac{\left( Ch+ Cq\right)}{Cq}}\cdot \sqrt{\frac{g}{g-X}} $$

(4a)

• 2) The shortage period, i.e., Tq^*, is:

$$ {Tq}^{\ast }={T_2}^{\ast }=\frac{Ch}{\left( Ch+ Cq\right)}\cdot {T}^{\ast }=\sqrt{\frac{2 Cs\cdot Ch}{Cq\left( Ch+ Cq\right)X}}\cdot \sqrt{\frac{g}{g-X}} $$

(4b)

• 3) The optimal ordering batch, i.e., D^*, is:

$$ {D}^{\ast }={T}^{\ast}\cdot X=\sqrt{\frac{2 Cs\cdot X}{Ch}}\cdot \sqrt{\frac{\left( Ch+ Cq\right)}{Cq}}\cdot \sqrt{\frac{g}{g-X}} $$

(4c)

• 4) The maximum shortage quantity, i.e., B^*, is:

$$ {B}^{\ast }=\sqrt{\frac{2 Cs\cdot Ch\cdot X}{Cq\left( Ch+ Cq\right)}}\cdot \sqrt{\frac{g-X}{g}} $$

(4d)

• 5) The optimal total cost per unit time, i.e., f^∗, is:

$$ {f}^{\ast }=\sqrt{2 Ch\cdot Cs\cdot X}\cdot \sqrt{\frac{Cq}{\left( Ch+ Cq\right)}}\cdot \sqrt{\frac{g-X}{g}}+ Cp\cdot X $$

(4e)

• 6) The optimal replenishing time is given by Tj^∗:

$$ {T_j}^{\ast }={D}^{\ast }/g $$

(4f)

2.2 Two-Stage Stochastic Programming

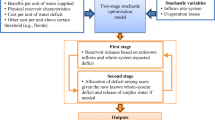
TSP is an effective method that can be used to solve problems with uncertain factors (Dantzig 1983, Ahmed et al. 2004). The TSP model can be expressed as follows (Birge and Louveaux 1997, Zhang and Li 2014, Li et al. 2010a, 2010b):

$$ \operatorname{Max}\ f=N\cdot w-\sum \limits_{i=1}^I{p}_i\cdot \mathrm{Q}\left({x}_{\mathrm{i}},{\delta}_i\right) $$

(5a)

$$ s.t.\left\{\begin{array}{l}\mathrm{A}\cdot w\le b\\ {}W\left({\delta}_{\mathrm{i}}\right)\cdot w+\mathrm{T}\left({\delta}_{\mathrm{i}}\right)\cdot {x}_{\mathrm{i}}=H\left({\delta}_{\mathrm{i}}\right)\\ {}w\ge 0{x}_{\mathrm{i}}\ge 0\end{array}\right.,\forall \mathrm{i}=1,2\dots, n $$

(5b)

where δ is the random variable (δ ∈ Ω), and w is the decision variable of the first stage when the random variable δ does not occur. x is the decision variable of the second stage, which depends on the realization of δ. N is the benefit parameter. Q(x_i, δ_i) is the second-stage cost function (penalty function) when δ_i occurs, and P_i is the probability level of δ_i realized ($\sum \limits_{i=1}^I{p}_i=1$). f reflects the final benefit of a certain policy that aims to maximize the value between the first stage and second stage as large as possible. A and b represent the matrix of the model parameters.{W(δ), H(δ), T(δ)| δ ∈ Ω} are the random model parameters, which are all the functions of the random variable δ.

2.3 TSP Model Based on the EOQ Models

Transferring water from water-abundant areas is an effective way to solve reservoir water shortages that affect the allocation of water to users; however, many questions must be solved by managers during this process, such as whether the total quantity of water that should be transferred from the relatively abundant areas should be transferred all at once or divided into several small batches. Furthermore, it is necessary to determine whether the total water shortage amount of the reservoir should be replenished fully or with planned shortages during this water transfer process. Moreover, it is necessary to determine whether the speed of the water replenishment affects the benefits related to water allocation. All of the above questions can be characterized as reservoir water supply-inventory-demand problems under conditions of uncertainty.

The traditional TSP model is an effective method to address the water allocation problem under uncertain conditions, but it cannot optimize the reservoir water transfer scheme to reduce the cost, which is the specialized output of the EOQ models. Therefore, in this section, the EOQ models will be integrated into the TSP framework to develop a series of new models (EOQ-TSP models) to optimize the water allocation policy that is integrated with the water transfer policy under uncertainties.

2.3.1 TSP Model Based on the B-EOQ Model

The B-EOQ model was integrated into the TSP framework to set up a new model, namely, the B-EOQ-T model. Based on models (1) and (5), the B-EOQ-T model can be depicted as follows.

Objective function:

$$ {\displaystyle \begin{array}{l}\operatorname{Max}\ Z=N\cdot \mathrm{w}-\sum \limits_{i=1}^I{p}_i\cdot f\left({x}_i\right)\\ {}=N\cdot \mathrm{w}-\sum \limits_{i=1}^I{p}_i\cdot \left(\frac{1}{2} Ch\cdot X\cdot T+ Cp\cdot X+\frac{Cs}{T}\right)\end{array}} $$

(6a)

Subject to:

$$ s.t.\left\{\begin{array}{l}\mathrm{A}\cdot w\le b\\ {}W\left({\delta}_{\mathrm{i}}\right)\cdot w+\mathrm{T}\left({\delta}_{\mathrm{i}}\right)\cdot {x}_{\mathrm{i}}=H\left({\delta}_{\mathrm{i}}\right)\\ {}w\ge 0\;{x}_{\mathrm{i}}\ge 0\end{array}\right.,\forall \mathrm{i}=1,2\dots, n $$

(6b)

where Z is the final benefit of reservoir water allocation; w is the promised water allocation target of the reservoir, which is the decision variable of the first stage; x_i is the water quantity of the allocation target that cannot meet user I when the random variable occurs, which is the decision variable of the second stage; P_i is the probability level of x_i realized ($\sum \limits_{i=1}^I{p}_i=1$); f(x_i) is the penalty function of cost when the promised water allocation target runs short, and f(x_i) is dependent on the reservoir water transfer scheme. Z reflects that the final benefits of reservoir water allocation are equal to the value difference between the benefits of the target water allocation and the cost of water transfer. A and b represent the matrix of the model parameters.{W(δ), H(δ), T(δ)| δ ∈ Ω} are the random model parameters.

The B-EOQ-T model aims not only to maximize the economic benefits of reservoir water allocation by optimizing the reservoir water allocation policy but also to minimize the cost of replenishing insufficient reservoir water by optimizing the reservoir water transfer scheme under uncertainties accordingly. Based on model (1), the f^∗(x_i) is the optimal value of f(x_i), and model (6) can be transformed into model (7), which is the final form of the B-EOQ-T model.

Objective function:

$$ {\displaystyle \begin{array}{l}\operatorname{Max}\ Z=N\cdot \mathrm{w}-\sum \limits_{i=1}^I{p}_i\cdot {f}^{\ast}\left({x}_i\right)\\ {}=N\cdot \mathrm{w}-\sum \limits_{i=1}^I{p}_i\cdot \left(\sqrt{2 Ch\cdot Cs\cdot {X}_i}+ Cp\cdot {X}_i\right)\end{array}} $$

(7a)

where Z represents the final benefits of reservoir water allocation under the condition of the B-EOQ inventory scheme. The objective function is subject to the same conditions as those for Formula (6b).

2.3.2 TSP Model Based on the EOQ-P Model

Similarly, the EOQ-P-T model can be depicted as model (8).

Objective function:

$$ {\displaystyle \begin{array}{l}\operatorname{Max}Z=N\cdot \mathrm{w}-\sum \limits_{i=1}^I{p}_i\cdot {f}^{\ast}\left({x}_i\right)\\ {}=N\cdot \mathrm{w}-\sum \limits_{i=1}^I{p}_i\cdot \left(\sqrt{2 Ch\cdot Cs\cdot {X}_i\cdot \frac{g-{X}_i}{g}}+ Cp\cdot {X}_i\right)\end{array}} $$

(8a)

where Z represents the final benefits of reservoir water allocation under the condition of the EOQ-P inventory scheme. f^∗(x_i) is the penalty function when the inventory replenishing speed is g. The objective function is subject to the same conditions as those for Formula (6b). This model is suitable for solving the problem of optimizing reservoir water allocation under the condition of transferring water from relatively abundant areas at a limited speed under uncertainties.

2.3.3 The EOQ-S Based on Two-Stage Stochastic Programming

Similarly, the EOQ-S-T model can be depicted as model (9).

Objective function:

$$ {\displaystyle \begin{array}{l}\operatorname{Max}\ Z=N\cdot \mathrm{w}-\sum \limits_{i=1}^I{p}_i\cdot {f}^{\ast}\left({x}_i\right)\\ {}=N\cdot \mathrm{w}-\sum \limits_{i=1}^I{p}_i\cdot \left(\sqrt{\frac{2 Ch\cdot Cq\cdot Cs\cdot {X}_i}{Ch+ Cq}}+ Cp\cdot {X}_i\right)\end{array}} $$

(9a)

where Z represents the final benefits of reservoir water allocation under the condition of EOQ-S inventory scheme. f^∗(x_i) is the penalty function for allowing the inventory plan shortage. The objective function is subject to the same conditions as those for Formula (6b). The EOQ-S-T model is developed to analyze the problem of optimizing reservoir water allocation under the condition of a replenished reservoir with insufficient water with planned shortages.

2.3.4 The EOQ-SP Based on Two-Stage Stochastic Programming

Similarly, the EOQ-SP-T model can be depicted as model (10).

Objective function:

$$ \operatorname{Max}\ Z=N\cdot \mathrm{w}-\sum \limits_{i=1}^I{p}_i\cdot \left(\sqrt{2 Ch\cdot Cs\cdot {X}_i}\cdot \sqrt{\frac{Cq}{\left( Ch+ Cq\right)}}\cdot \sqrt{\frac{g-{X}_i}{g}}+ Cp\cdot {X}_i\right) $$

(10a)

where Z represents the final benefits of reservoir water allocation under the condition of the EOQ-SP inventory scheme. f^∗(x_i) is the penalty function for allowing an inventory plan shortage where the inventory replenishing speed is g. The objective function is subject to the same conditions as those for Formula (6b). The EOQ-SP-T model is used to solve the problem of optimizing reservoir water allocation under the condition of a replenished reservoir with insufficient water that has planned shortages and is replenished at a limited speed.

Figure 5 shows a schematic of the developed EOQ-TSP models.

Fig. 5

Schematic of the EOQ-based TSP models

3 Case Study

3.1 Study Area

The research area is located in the northeast part of Qinghai Province, which consists of the Datong basin and Huang basin. The S.X. hydrostation and H.Q. reservoir are located along the Datong River and the Huang River, respectively, and the connection between them is shown in Fig. 6. One of the key tasks of the H.Q. reservoir is to allocate water to the agricultural, industrial and municipal water users in the downstream areas. Water is transferred from the Datong River each year to replenish the shortage of water in the H.Q. reservoir.

Fig. 6

The hydraulic connection between the S.X. hydrostation and H.Q. reservoir

This study spans a 15-year planning horizon, which contains three 5-year periods. During these periods, the stream flow distributions of the Datong River and the Huang River are shown in Table 1, and the water allocation targets from the H.Q. reservoir to the water users in downstream areas are shown in Table 2.

Table 1 The distribution of stream flows

Table 2 Water allocation targets of H.Q. reservoir

As shown in Tables 1 and 2, during these periods, the stream flows of the Huang River at the highest level are less than 1.9 × 10⁹ m³; however, the total water allocation target of the H.Q. reservoir to water users in the downstream area is more than 4.8 × 10⁹ m³. Therefore, a water transfer from the S.X. hydrostation (water supply area) to the H.Q. reservoir (water shortage area) is necessary to solve this water allocation shortage problem. During the water transfer process, a large batch size will increase the storage backlogs and cost of water management. However, if the amount of transferred water is too low, the transfer period and the allocated shortage risk will increase. Therefore, determining the optimal water transfer and allocation policies that maximize the benefits of water allocation in an uncertain environment is a key problem that the managers of the H.Q. reservoir must focus on. Based on the above analyses, the problems that must be solved in relation to the management of water transfer and allocation of the H.Q. reservoir can be summarized as follows.

• (1) How can an optimal water transfer plan for reservoirs, which contains an optimal transfer batch and period, minimize the management costs?

• (2) Do planning shortages in the process of replenishing reservoir water increase the total benefits of reservoir water allocation?

• (3) Does replenishing reservoir water with a limited speed increase the total benefits of reservoir water allocation?

• (4) How should the limited available water be allocated to the water-user sectors (e.g., agricultural, industrial and municipal) to obtain the maximum benefits under different water transfer policies and different flow levels of the Huang River?

The most suitable plan can be identified using the EOQ-TSP models to solve the questions outlined above. The economic data on the process of water transfer for the H.Q. reservoir are shown in Table 3.

Table 3 Economic data

3.2 EOQ-TSP Models for Reservoir Water Allocation

• (1) Application of the B-EOQ-T Model. The B-EOQ-T model is suitable for analysis of the H.Q. reservoir water allocation plan when the insufficient water is fully replenished by transferring water from Datong River. Based on model (7), the B-EOQ-T model, in this case, can be depicted as follows.

Objective function:

$$ {\displaystyle \begin{array}{l}\operatorname{Max}\ Z={\mathrm{Z}}_{\mathrm{f}}\left({\mathrm{w}}_{it}\right)\hbox{-} {\mathrm{Z}}_{\mathrm{s}}\left({x}_{\mathrm{itl}}\right)\\ {}\kern2.75em =\sum \limits_{i=1}^I\sum \limits_{t=1}^T{N}_{it}\cdot {\mathrm{w}}_{it}-\sum \limits_{i=1}^I\sum \limits_{t=1}^T\sum \limits_{l=1}^L{p}_{tl}\cdot {f}^{\ast}\left({x}_{\mathrm{itl}},{\delta}_{tl}\right)\\ {}\kern2.75em =\sum \limits_{i=1}^I\sum \limits_{t=1}^T{N}_{it}\cdot {\mathrm{w}}_{it}-\sum \limits_{i=1}^I\sum \limits_{t=1}^T\sum \limits_{l=1}^L{p}_{tl}\cdot \left(\sqrt{2{Ch}_t\cdot {Cs}_t\cdot {X}_{it l}}+{Cp}_t\cdot {X}_{it l}\right)\end{array}} $$

(11a)

where i represents water users (agricultural, industrial and municipal, i = 1, 2, 3); l is stream flow level (high, medium and low, l = 1, 2, 3); t is the time period of research (t = 1, 2, 3); P_tl is the probability of stream flow level l in period t; N_it is the benefit to user i per unit of allocated water during period t (Yuan/ m³); w_it is water allocation target for water user i during period t (m³); x_itl is quantity of the water allocation target that is not met to water user i when the flow of Huang River is q_tl; Ch_t is the holding cost per unit water per unit time during period t (contains the maintenance costs, operation management cost and engineering depreciation of the reservoir and abstraction works from the supply area to the shortage area, Yuan/ m³); Cs_t is the setup cost for water transferred in one batch during period t (contains communication expenses and administrative costs, Yuan per order); Cp_t is the unit cost for producing each unit of water during period t (Yuan/ m³); Z_f represents the benefits function of the target water allocation (first stage), which is used to determine the first-stage variables (w_it) by meeting the promised water allocation target; Z_s is the cost function of water replenishing (second stage), which is used to minimize the penalty function of the water replenishing cost by optimizing the water transfer cost (f^∗(x_itl, δ_tl)) when the reservoir water allocation target could not be met; Z represents the final benefits of the water allocation of the H.Q. reservoir under uncertainties, which is equal to the difference in values between Z_f and Z_s.

Subject to:

• 1) Constraint of available water quantity (Formulas (11b)), which indicates that the total available water quantity in period t should be no less than the quantity of the water allocation target ($\sum \limits_{i=1}^I{w}_{it}$) and no more than the quantity of the maximum allowable water allocation ($\sum \limits_{i=1}^I{w}_{it\max }$).

$$ \sum \limits_{i=1}^I{w}_{it}\le {q}_{tl}+\sum \limits_{i=1}^I{x}_{it l}+{Q}_{\left(\mathrm{t}-1\right)\mathrm{l}}\le \sum \limits_{i=1}^I{w}_{it\begin{array}{c}\end{array}\max },{\displaystyle \begin{array}{c}\end{array}}\forall t;{\displaystyle \begin{array}{c}\end{array}}l=1,2\dots l $$

(11b)

where w_it is the water allocation target for water user i during period t (m³); q_tl is available water from the Huang River in the stream flow level l during period t (m³); Q_(t-1)l is the surplus available water during period t-1 when the flow level of the Huang River is l (m³); w_{it max} is the maximum allowable water allocation quantity for water user i during period t (m³).

• 2) The constraint of reservoir capacity (Formula (11c)) indicates that the quantity of surplus water in period t should be less than the storage volume of the H.Q. reservoir.

$$ {q}_{tl}+\sum \limits_{i=1}^I{x}_{it l}+{Q}_{\left(\mathrm{t}-1\right)\mathrm{l}}\hbox{-} \sum \limits_{i=1}^I{w}_{it}\le CR,{\displaystyle \begin{array}{c}\end{array}}\forall t;{\displaystyle \begin{array}{c}\end{array}}l=1,2\dots l $$

(11c)

where CR is utilizable capacity of the H.Q. reservoir (m³).

• 3) The constraint of surplus water quantity (Formula (11d)) indicates that the quantity of surplus water in period t (Q_tl) should be equal to the total available water quantity minus the quantity of water allocation in this period.

$$ {Q}_{\mathrm{tl}}={q}_{tl}+\sum \limits_{i=1}^I{x}_{it l}+{Q}_{\left(\mathrm{t}-1\right)\mathrm{l}}\hbox{-} \sum \limits_{i=1}^I{w}_{it},{Q}_{0l}=0;{\displaystyle \begin{array}{c}\end{array}}\forall t;{\displaystyle \begin{array}{c}\end{array}}l=1,2\dots l $$

(11d)

where Q_tl is the surplus available water during period t when the flow of the Huang River is q_tl (m³).

• 4) The constraint of the optimal water transfer period (Formula (11e)) is the optimum time span of one ordering cycle to replenish the reservoir water shortage, which is based on Formula (1a).

$$ {T_{tl}}^{\ast }=\sqrt{\frac{2{Cs}_t}{Ch_t\cdot \sum \limits_{i=1}^I{X}_{itl}}},{\displaystyle \begin{array}{c}\end{array}}\forall t;{\displaystyle \begin{array}{c}\end{array}}l=1,2\dots l $$

(11e)

where T_tl is the water transfer period when the flow of the Huang River is q_tl (5-year period).

• 5) The constraint of optimal water transfer batch (Formula (11f)) is the economic ordering quantity during a cycle to replenish the reservoir water shortage, which is based on Formula (1b).

$$ {D_{tl}}^{\ast }=\sqrt{\frac{2{Cs}_t\cdot \sum \limits_{i=1}^I{X}_{itl}}{Ch_t}},{\displaystyle \begin{array}{c}\end{array}}\forall t;{\displaystyle \begin{array}{c}\end{array}}l=1,2\dots l $$

(11f)

where D_tl is water transfer batch when the flow of the Huang River is q_tl (m³).

• 6) The nonnegativity constraint is shown as Formula (11g).

$$ {X}_{itl}\ge 0,{\displaystyle \begin{array}{c}\end{array}}\forall t;{\displaystyle \begin{array}{c}\end{array}}l=1,2\dots l $$

(11g)

• (2) Application of other EOQ-TSP models. The application of other EOQ-TSP models is shown in the Appendix 1 to 3.

4 Results Analysis

4.1 B-EOQ-T and EOQ-S-T Models

The main difference between these two models is that the planned water shortage for replenishing is allowed or not when transferring water from the abundant area. The results based on these two models are shown in Figs. 7 and 8.

• (1) The total amount of water transferred based on these two models (namely, Y_tl). The Y_tl based on these two models will vary as a result of different flow levels of the Huang River. The results indicated that more water would be transferred from the Datong River to replenish a shortage under low-flow conditions of the Huang River; conversely, less water would be transferred from the Datong River when the Huang River has high flow.

Fig. 7

Results based on the B-EOQ-T model. Note: Y_tl is the total amount of water transferred; D_tl and T_tl are the water transfer batches and periods, respectively

Fig. 8

Results based on the EOQ-S-T model. Note: Y_tl is the total amount of water transferred; D_tl and T_tl are the water transfer batches and periods, respectively; B_tl is the maximum water shortage quantity; Tq_tl is the water shortage period

• (2) As shown in Figs. 7 and 8, the values of water transfer batches (D_tl) based on these two models are negatively correlated with the flow level of the Huang River. However, the solutions of water transfer periods (T_tl) based on these two models are all positively correlated with the flow level of the Huang River.

• (3) Maximum water shortage quantity (B_tl) and water shortage period (Tq_tl). Compared with the B-EOQ-T model, the main difference in the optimal water allocation policy based on the EOQ-S-T model is that the planned water shortage is allowed. Therefore, two main factors were added (B_tl and Tq_tl) in the EOQ-S-T model. As shown in Fig. 8, B_tl increases as the flow level of the Huang River decreases; however, Tq_tl becomes shorter as the flow level of the Huang River declines.

4.2 EOQ-P-T and EOQ-SP-T Models

The EOQ-P-T and EOQ-SP-T models were used to analyze the H.Q. reservoir water allocation problem when the insufficient water in the H.Q. reservoir was replenished at a limited speed from the Datong River. The main difference between these two models is also that the planned water shortage for replenishing is allowed or not in the water transfer plan. The results based on these two models are shown in Figs. 9 and 10.

Fig. 9

Results based on the EOQ-P-T model. Note: Y_tl is the total amount of water transferred; D_tl and T_tl are the water transfer batches and periods, respectively; Tj_tl is the water replenishment period

Fig. 10

Results based on the EOQ-SP-T model. Note: Y_tl is the total amount of water transferred; D_tl and T_tl are the water transfer batches and periods, respectively; B_tl is the maximum water shortage quantity; Tq_tl is the water shortage period; Tj_tl is the water replenishment period

• (1) Total amount of water transferred (Y_tl). The results indicated that more water would be transferred from the Datong River when the Huang River was under low-flow conditions, and vice versa.

• (2) As shown in Figs. 9 and 10, the solutions of water transfer batches (D_tl), water transfer periods (T_tl) and the water replenishment period (Tj_tl) based on these two models were all negatively correlated with the flow level of the Huang River.

• (3) Maximum water shortage quantity (B_tl) and water shortage period (Tq_tl). The planned water shortage for the H.Q. reservoir water replenishing is allowed in the optimal water allocation policy based on the EOQ-SP-T models. Therefore, two main factors were added (B_tl and Tq_tl) in the EOQ-SP-T model. Figure 10 shows the solutions of B_tl and Tq_tl. As shown, the B_tl is minimized when the flow of the Huang River is low during periods 1 and 2. The solutions of B_tl are negatively correlated with the flow level of the Huang River during period 3. The Tq_tl is always negatively correlated with the flow level of the Huang River.

5 Discussion

5.1 Comparison Between the B-EOQ-T Model and the EOQ-S-T Model

A comparison of the water allocation policies between the B-EOQ-T and EOQ-S-T models was used to analyze whether the planned shortage in the water replenishment process could reduce the total cost of it when the effect of the water transfer speed on the benefits of water allocation of the H.Q. reservoir was not considered.

The final benefit of the water allocation in the application based on the B-EOQ-T model was approximately 525,391 × 10⁷Yuan, which was less than the benefit based on the EOQ-S-T model, which was approximately 524,982 × 10⁷Yuan. Therefore, the water allocation policy based on the EOQ-S-T model is better than that based on the B-EOQ-T model. The reasons are as follows.

• (1) Figure 11 shows the values of the total amount of water transferred (Y_tl) based on the B-EOQ-T model minus the value based on the EOQ-S-T model, and the results were all greater than or equal to zero during each period; thus, the total amount of water transferred based on the EOQ-S-T model was no more than the amount based on the B-EOQ-T model. As such, the total water inventory cost and water transfer cost based on the EOQ-S-T model will be less than the associated costs based on the B-EOQ-T model.

Fig. 11

D-value analysis based on B-EOQ-T and EOQ-S-T models. Note: Y_tl is the total amount of water transferred; D_tl and T_tl are the water transfer batches and periods, respectively

• (2) Figure 11 also shows that the values of D_tl and T_tl that were calculated based on EOQ-S-T minus the values of D_tl and T_tl that were calculated based on B-EOQ-T are all greater than zero, i.e., compared with the B-EOQ-T model, the water transfer amount of each batch based on the EOQ-S-T model increased in this application. At the same time, the water transfer frequency based on the EOQ-S-T model reduced during period t (t = 1, 2, 3), which would lead to decreased management costs and simplified water management tasks during the water transfer process.

From the analysis above, it can be seen that planning shortages in the water replenishment process could reduce the total cost of this process and increase the final water allocation benefits when the effect of the water transfer speed on the water resource allocation benefit is not considered.

5.2 Comparison between the EOQ-P-T Model and the EOQ-SP-T Model

A comparison of the water allocation policies between the EOQ-P-T and EOQ-SP-T models was used to analyze whether the planned shortage in the water replenishment process could bring better economic benefits when the effect of the water transfer speed on the benefit of the reservoir water allocation was considered.

The objective benefit of the water allocation in the application based on the EOQ-P-T model was approximately 524,985 × 10⁷Yuan, which was less than the policy objective benefit based on the EOQ-SP-T model, which was approximately 525,392 × 10⁷Yuan. Therefore, the water allocation policy based on the EOQ-SP-T model was better than that based on the EOQ-P-T model. The reasons for this difference are as follows.

• (1) Figure 12 shows the values of the total amount of water transferred (Y_tl) based on the EOQ-P-T model minus that based on the EOQ-SP-T model, and the results were approximately no less than zero during each period, i.e., in general, the total amount of water transferred based on the EOQ-SP-T model was less than that based on the EOQ-P-T model, which could reduce the cost of water inventory and transferring. Thus, the benefits of water allocation based on the EOQ-SP-T model were generally better than that based on the EOQ-P-T model.

Fig. 12

D-value analysis based on EOQ-P-T and EOQ-SP-T models. Note: Y_tl is the total amount of water transferred; T_tl is the water transfer period; Tj_tl is the water replenishment period

• (2) Figure 12 also shows the values of T_tl and Tj_tl based on the EOQ-SP-T model minus the values of T_tl and Tj_tl based on the EOQ-P-T model. The differences in the T_tl values between the EOQ-SP-T model and the EOQ-P-T model are all very small, i.e., the frequency of water transfer based on these two models was approximately the same. However, the values of the water replenishment periods (Tj_tl) based on the EOQ-SP-T model were much smaller than those based on the EOQ-P-T model; namely, the time span of water replenishment based on the EOQ-SP-T model was much shorter than that based on the EOQ-P-T model. This result indicated that compared with the EOQ-P-T model, the time span of water replenishment based on the EOQ-SP-T model was much lower when the water transfer frequency of these two models was at a similar level. Therefore, the water allocation policy based on the EOQ-SP-T model would decrease the costs of reservoir water resource management and simplify reservoir water management tasks.

From the analysis above, it can be seen that the planned shortage in the water allocation process could also reduce the total cost of this process and increase the final water allocation benefits when the effect of the water transfer speed on the reservoir water allocation benefit is considered.

5.3 Comparison Between the EOQ-S-T Model and the EOQ-SP-T Model

A comparison of the water allocation policies between the EOQ-S-T and EOQ-SP-T models was used to analyze the effect of the water transfer speed on the benefit of reservoir water allocation, when the planned shortage in the water replenishment process was allowed.

Comparing the objective benefits based on these two models reveals that the benefit based on the EOQ-S-T (524,982 × 10⁷Yuan) model is less than that based on the EOQ-SP-T model (525,392 × 10⁷Yuan). This result means that the water allocation benefits of the reservoir increased as the water transfer speed changed from infinitely great to finite. Therefore, transferring water from relatively abundant areas with a reasonable limited speed to replenish the water allocation shortage of reservoirs would obtain better economic benefits.

5.4 Comparison between EOQ-TSP Models and TSP Model

The problem of transferring water from the Datong River to replenish the water allocation shortage of the H.Q. reservoir under conditions of uncertainty can also be analyzed using the traditional TSP model, which optimizes the reservoir water allocation policy without considering the effect of the water transfer scheme.

Based on Fig. 13, the objective benefit (15 years) based on the TSP model in this application is approximately 522,339 × 10⁷Yuan, which is far less than that derived from the policies based on the EOQ-TSP models. This result reflected that the benefits of the optimal reservoir water allocation policy will be further increased by optimizing the water transfer scheme; additionally, the EOQ-TSP models can more adequately address the complexity of the reservoir water resources management system.

Fig. 13

Comparison of objective benefits among models. Note: Yuan is the unit of Chinese currency

Furthermore, as shown in Fig. 13, the policy of reservoir water allocation based on EOQ-SP-T model is the optimal plan for the H.Q. reservoir when the planned water shortage is allowed,; the optimal policy of allocating water to the three water-user sectors based on the EOQ-SP-T model is shown in Table 4, and the optimal policy for water transfer schemes is shown in Fig. 10. Otherwise, the policy of reservoir water allocation based on the EOQ-P-T model is the optimal plan for the H.Q. reservoir when the planned water shortage is not allowed; the optimal policy of allocating water to the three water-user sectors based on the EOQ-P-T model is shown in Table 5, and the optimal policy for water transfer schemes is shown in Fig. 9.

Table 4 Optimal water allocation policy when the planned water shortage is allowed

Table 5 Optimal water allocation policy when the planned water shortage is not allowed

6 Conclusions

In this research, the EOQ models were integrated into the TSP framework to establish a series of new EOQ-TSP models, and a case study was provided to assess the feasibility of the EOQ-TSP models. Based on this study, the following conclusions were obtained.

• (1) Compared with the TSP model, the EOQ-TSP models were better for analyzing the reservoir water supply-inventory-demand problem, and the EOQ-TSP models could more adequately respond to the complexity of the reservoir water resources management system.

• (2) The benefits of the optimal reservoir water allocation will be further increased by optimizing the water transfer scheme.

• (3) Reservoir water allocation and transfer policies with planned shortages could increase the final water allocation benefits, regardless of whether the effect of water transfer speed on the water resource allocation benefits is considered.

• (4) Transferring water from a relatively water-abundant area using a reasonably limited speed to replenish the shortage obtains better economic benefits.

These new EOQ-TSP models are not only suitable for analyzing the reservoir water management problem but can also be used to research other resource management scenarios with imbalances between the quantities of the resource demand and supply under uncertainties, such as the problems of supplying materials for plants or supplying food for the market, where the materials or food play the same role as that of water, and the purchases and supplies of different areas can be described as the supply-inventory-demand phenomenon.

Further research is needed on how to incorporate the EOQ-TSP models with interval linear programming and dynamic programming to establish more practical stochastic inventory models.

Appendices

Appendix 1

The applications of the EOQ-P-T model are described as follows. The EOQ-P-T model is suitable for analyzing the water allocation and transfer problems of a reservoir when the reservoir’s insufficient water is fully replenished by transferring water from the Datong River, and when assuming the replenishment has a limited speed (runoff of the Datong River). Based on model (8), the EOQ-P-T model can be depicted as follows.

$$ \operatorname{Max}\ Z=\sum \limits_{i=1}^I\sum \limits_{t=1}^T{N}_{it}\cdot {\mathrm{w}}_{it}-\sum \limits_{i=1}^I\sum \limits_{t=1}^T\sum \limits_{l=1}^L{p}_{tl}\cdot \left(\sqrt{2{Ch}_t\cdot {Cs}_t\cdot {X}_{it l}\cdot \frac{g_{tl}-{X}_{it l}}{g_{tl}}}+{Cp}_t\cdot {X}_{it l}\right) $$

(12a)

$$ s.t.\left\{\begin{array}{l}\sum \limits_{i=1}^I{w}_{it}\le {q}_{tl}+\sum \limits_{i=1}^I{x}_{it l}+{Q}_{\left(\mathrm{t}-1\right)\mathrm{l}},\forall t;l=1,2\dots l\\ {}\sum \limits_{i=1}^I{w}_{it\begin{array}{c}\end{array}\max}\ge {q}_{tl}+\sum \limits_{i=1}^I{x}_{it l}+{Q}_{\left(\mathrm{t}-1\right)\mathrm{l}}\begin{array}{c},\end{array}\forall t;l=1,2\dots l\\ {}{q}_{tl}+\sum \limits_{i=1}^I{x}_{it l}+{Q}_{\left(\mathrm{t}-1\right)\mathrm{l}}\hbox{-} \sum \limits_{i=1}^I{w}_{it}\le CR\begin{array}{c},\end{array}\forall t;l=1,2\dots l\\ {}{Q}_{\mathrm{t}\mathrm{l}}={q}_{tl}+\sum \limits_{i=1}^I{x}_{it l}+{Q}_{\left(\mathrm{t}-1\right)\mathrm{l}}\hbox{-} \sum \limits_{i=1}^I{w}_{it}\begin{array}{c},\end{array}\forall t;l=1,2\dots {l}_{\mathrm{t}};{Q}_{0l}=0\\ {}{T_{tl}}^{\ast }=\sqrt{\frac{2{Cs}_t\cdot {g}_{tl}}{Ch_t\cdot \sum \limits_{i=1}^I{X}_{it l}\cdot \left({\mathrm{g}}_{tl}-\sum \limits_{i=1}^I{X}_{it l}\right)}}\begin{array}{c},\end{array}\forall t;l=1,2\dots l\\ {}{D_{tl}}^{\ast }=\sqrt{\frac{2{Cs}_t\cdot \sum \limits_{i=1}^I{X}_{it l}\cdot {g}_{tl}}{Ch_t\cdot \left({\mathrm{g}}_{tl}-\sum \limits_{i=1}^I{X}_{it l}\right)}}\begin{array}{c},\end{array}\forall t;l=1,2\dots l\\ {}{T^{\ast}}_{jtl}={D}^{\ast }/g\\ {}{X}_{it l}\ge 0\begin{array}{c},\end{array}\forall t;l=1,2\dots l\end{array}\right.\kern0.75em $$

(12b)

where g_tl is the stream flow of the Datong River when the flow level is l during period t (m³); Tj_tl is the water replenishing period when the flow of the Huang River is q_tl (5-year period);

Appendix 2

The applications of the EOQ-S-T model are described as follows. The EOQ-S-T model is suitable for analyzing the water allocation and transfer problems of the H.Q. reservoir when the insufficient water in the H.Q. reservoir is replenished using planned shortages. Based on model (9), the EOQ-S-T model can be depicted as follows.

$$ \operatorname{Max}\ Z=\sum \limits_{i=1}^I\sum \limits_{t=1}^T{N}_{it}\cdot {\mathrm{w}}_{it}-\sum \limits_{i=1}^I\sum \limits_{t=1}^T\sum \limits_{l=1}^L{p}_{tl}\cdot \left(\sqrt{\frac{2{Ch}_t\cdot {Cq}_t\cdot {Cs}_t\cdot {X}_{it l}}{Ch_t+{Cq}_t}}+{Cp}_t\cdot {X}_{it l}\right) $$

(13a)

$$ s.t.\left\{\begin{array}{l}\sum \limits_{i=1}^I{w}_{it}\le {q}_{tl}+\sum \limits_{i=1}^I{x}_{it l}+{Q}_{\left(\mathrm{t}-1\right)\mathrm{l}},\forall t;l=1,2\dots l\\ {}\sum \limits_{i=1}^I{w}_{it\begin{array}{c}\end{array}\max}\ge {q}_{tl}+\sum \limits_{i=1}^I{x}_{it l}+{Q}_{\left(\mathrm{t}-1\right)\mathrm{l}}\begin{array}{c},\end{array}\forall t;l=1,2\dots l\\ {}{q}_{tl}+\sum \limits_{i=1}^I{x}_{it l}+{Q}_{\left(\mathrm{t}-1\right)\mathrm{l}}\hbox{-} \sum \limits_{i=1}^I{w}_{it}\le CR\begin{array}{c},\end{array}\forall t;l=1,2\dots l\\ {}{Q}_{\mathrm{t}\mathrm{l}}={q}_{tl}+\sum \limits_{i=1}^I{x}_{it l}+{Q}_{\left(\mathrm{t}-1\right)\mathrm{l}}\hbox{-} \sum \limits_{i=1}^I{w}_{it}\begin{array}{c},\end{array}\forall t;l=1,2\dots {l}_{\mathrm{t}};{Q}_{0l}=0\\ {}{T_{tl}}^{\ast }=\sqrt{\frac{2{Cs}_t\left({Ch}_t+{Cq}_t\right)}{Ch_t\cdot {Cq}_t\cdot \sum \limits_{i=1}^I{X}_{it l}}}\begin{array}{c},\end{array}\forall t;l=1,2\dots l\\ {}{D_{tl}}^{\ast }=\sqrt{\frac{2{Cs}_t\cdot \sum \limits_{i=1}^I{X}_{it l}\left({Ch}_t+{Cq}_t\right)}{Ch_t\cdot {Cq}_t}}\begin{array}{c},\end{array}\forall t;l=1,2\dots l\\ {}{B_{tl}}^{\ast }=\sqrt{\frac{2{Ch}_t\cdot {Cs}_t\cdot \sum \limits_{i=1}^I{X}_{it l}}{Cq_t\cdot \left({Ch}_t+{Cq}_t\right)}}\begin{array}{c},\end{array}\forall t;l=1,2\dots l\\ {}{{Tq_{\begin{array}{c}\end{array}}}_{tl}}^{\ast }=\sqrt{\frac{2{Ch}_t\cdot {Cs}_t}{Cq_t\cdot \left({Ch}_t+{Cq}_t\right)\cdot \sum \limits_{i=1}^I{X}_{it l}}}\begin{array}{c},\end{array}\forall t;l=1,2\dots l\\ {}{X}_{it l}\ge 0\begin{array}{c},\end{array}\forall t;l=1,2\dots l\end{array}\right. $$

(13b)

where Cq_t is the shortage cost (penalty) per unit water per unit time during period t (Yuan/ m³); B_tl is the maximum water shortage quantity when the flow of the Huang River is q_tl (m³); B_itl is the water shortage quantity to water user i when the flow of the Huang River is q_tl; Tq_tl is the water shortage period when the flow of the Huang River is q_tl (5-year period).

Appendix 3

The applications of the EOQ-SP-T model are described as follows. The EOQ-SP-T model is suitable for analyzing the water allocation and transfer problems of a reservoir when the insufficient water is replenished using planned shortages and assuming the replenishment is limited by the speed of runoff in the Datong River. Based on model (10), the EOQ-SP-T model can be depicted as follows.

$$ {\displaystyle \begin{array}{l}\mathrm{M}\ \mathrm{a}\ \mathrm{x}\kern0.5em Z\\ {}=\sum \limits_{i=1}^I\sum \limits_{t=1}^T{N}_{it}\cdot {\mathrm{w}}_{it}-\sum \limits_{i=1}^I\sum \limits_{t=1}^T\sum \limits_{l=1}^L{p}_{tl}\cdot \left(\sqrt{2{Ch}_t\cdot {Cs}_t\cdot {X}_{it l}}\cdot \sqrt{\frac{Cq_t}{\left({Ch}_t+{Cq}_t\right)}}\cdot \sqrt{\frac{g_{tl}-{X}_{it l}}{g_{tl}}}+{Cp}_t\cdot {X}_{it l}\right)\end{array}} $$

(14a)

$$ s.t.\left\{\begin{array}{l}\sum \limits_{i=1}^I{w}_{it}\le {q}_{tl}+\sum \limits_{i=1}^I{x}_{it l}+{Q}_{\left(\mathrm{t}-1\right)\mathrm{l}},\forall t;l=1,2\dots l\\ {}\sum \limits_{i=1}^I{w}_{it\begin{array}{c}\end{array}\max}\ge {q}_{tl}+\sum \limits_{i=1}^I{x}_{it l}+{Q}_{\left(\mathrm{t}-1\right)\mathrm{l}}\begin{array}{c},\end{array}\forall t;l=1,2\dots l\\ {}{q}_{tl}+\sum \limits_{i=1}^I{x}_{it l}+{Q}_{\left(\mathrm{t}-1\right)\mathrm{l}}\hbox{-} \sum \limits_{i=1}^I{w}_{it}\le CR\begin{array}{c},\end{array}\forall t;l=1,2\dots l\\ {}{Q}_{\mathrm{t}\mathrm{l}}={q}_{tl}+\sum \limits_{i=1}^I{x}_{it l}+{Q}_{\left(\mathrm{t}-1\right)\mathrm{l}}\hbox{-} \sum \limits_{i=1}^I{w}_{it}\begin{array}{c},\end{array}\forall t;l=1,2\dots {l}_{\mathrm{t}};{Q}_{0l}=0\\ {}{T_{tl}}^{\ast }=\sqrt{\frac{2{Cs}_t}{Ch_t\cdot \sum \limits_{i=1}^I{X}_{it l}}}\cdot \sqrt{\frac{\left({Ch}_t+{Cq}_t\right)}{Cq_t}}\cdot \sqrt{\frac{g_{tl}}{g_{tl}-\sum \limits_{i=1}^I{X}_{it l}}}\begin{array}{c},\end{array}\forall t;l=1,2\dots l\\ {}{D_{tl}}^{\ast }=\sqrt{\frac{2{Cs}_t\cdot \sum \limits_{i=1}^I{X}_{it l}}{Ch_t}}\cdot \sqrt{\frac{\left({Ch}_t+{Cq}_t\right)}{Cq_t}}\cdot \sqrt{\frac{g_{tl}}{g_{tl}-\sum \limits_{i=1}^I{X}_{it l}}}\begin{array}{c},\end{array}\forall t;l=1,2\dots l\\ {}{B_{tl}}^{\ast }=\sqrt{\frac{2{Cs}_t\cdot {Ch}_t\cdot \sum \limits_{i=1}^I{X}_{it l}}{Cq_t\cdot \left({Ch}_t+{Cq}_t\right)}}\cdot \sqrt{\frac{g_{tl}-\sum \limits_{i=1}^I{X}_{it l}}{g_{tl}}}\begin{array}{c},\end{array}\forall t;l=1,2\dots l\\ {}{Tq_{tl}}^{\ast }=\sqrt{\frac{2{Cs}_t\cdot {Ch}_t}{Cq_t\left({Ch}_t+{Cq}_t\right)\sum \limits_{i=1}^I{X}_{it l}}}\cdot \sqrt{\frac{g_{tl}}{g_{tl}-\sum \limits_{i=1}^I{X}_{it l}}}\begin{array}{c},\end{array}\forall t;l=1,2\dots l\\ {}{T^{\ast}}_{jtl}={D}^{\ast }/g\\ {}{X}_{it l}\ge 0\begin{array}{c},\end{array}\forall t;l=1,2\dots l\end{array}\right. $$

(14b)