1 Introduction

Among all problems which water researchers and hydraulic engineers have been faced, water conveyance is considered to be one of not only the inevitable but also the expensive ones. In fact, water conveyance is a mean to meet sort of human society needs such as irrigation, municipal and flood control ones. Lined channels have been widely used for this purpose since they can be constructed on different topographies and soil conditions and also prevent water from wasting. Although any cross section shapes can theoretically be used in lined channels design, common shapes such as triangular, rectangular, trapezoidal and circular are practically in used. Design of such cross sections was and still is an active area of research area in favor of finding optimal section variables, i.e. side slope, bottom width, flow depth and radius.

Based on water conveyance project purposes, channel cross section optimization problems may have different scenarios. In other words, these optimization problems can have either different objective function or different constraints. The former can be defined as minimization of flow area or cost of construction for a specified flow rate while the latter may be confining the average flow velocity or one of the section variable parameters. This variety of scenarios accompanied by the importance of the issue is probably the reason why the literature is filled with a majority of researches in this area.

Chow (1959, 1973) and French (1994) have published the most hydraulically efficient section relations. Their objective function was minimization of the flow area while the Manning’s equation was the constraint. Swamee and Bhatia (1972) developed optimal design curves for trapezoidal, rounded bottom and rounded corner sections. Guo and Hughes (1984) presented optimum section variables comprising freeboard for trapezoidal sections. Loganathan (1991) studied optimality conditions for a parabolic channel section. (Monadjemi 1994) showed that the same optimal section variables can be achieved by minimization of either flow rate or wetted perimeter. Froehlich (1994) recommended simple relations for optimum section variables of trapezoidal sections in terms of discharge. Moreover, he presented design graphs for optimal section variables. Swamee (1995) and Swamee et al. (2000) proposed explicit equations for optimum section variables for minimization of flow rate and channel construction cost, respectively. In the latter study, the channel cost is a function of not only the cost of earthwork and lining materials but also an additional cost. The additional cost originates from different cost of earthwork in different depths. Aksoy and Altan-Sakarya (2006) suggested two models for computing optimal section variables following similar procedure. Although more similar researches were conducted utilizing new optimization techniques (Jain et al. 2004; Bhattacharjya and Satish 2007; Turan and Yurdusev 2011; Kaveh et al. 2012), the proposed models were not sufficiently precise in comparison with the benchmark solutions as it will be prescribed latter. Therefore, it seems that the cross section optimization requires to be revisited with some emerging powerful meta-heuristic optimization techniques not only in favor of achieving more accurate design results but also in light of simpler explicit relations.

In this paper, a powerful meta-heuristic optimization technique invariably called Modified Honey Bee Mating Optimization (MHBMO) algorithm was utilized to find the optimal channel cross sections. The objective function considered is the construction cost which it is a function of three different parameters in its ideal condition as it was mentioned. The Manning’s equation was selected as the problem constraint. The optimal section variables of common section shapes in practice, i.e. triangular, rectangular, trapezoidal and circular, were calculated using the MHBMO algorithm and finally, a new simple explicit model for calculating cross section parameters was proposed. The results of four sample problems demonstrate that the proposed model was more accurate in comparison with the existing models in literature.

2 Optimization Problem Definition

The aim of constructing of the channels is to properly convey desirable amount of water from one to another location. As a contractor is asked to build one, his/her preferable option is to accomplish the project in its least possible expenditure form. Hence, the channel construction is somehow a kind of optimization problem in real-life projects. The minimization of total cost spending for construction is playing the role of the sole objective function while the hydraulic requirements of conveying a specific discharge simultaneously have to be satisfied as problem constraint.

The actual cost of channel construction can be affected by lots of known and sometimes unpredictable factors in practical situation such as the geographical condition of channel route, the accessibility of ground surface, the contractors equipment properties, possible need for constructing sustainable structures, haul distance, etc. If the unpredictable factors were put aside, others probably may differ from one to another project. In order to comprise an extensive range of such projects, the most reality-based cost function in literature was considered (Swamee et al. 2000). According to that cost function, the total cost per unit length of channel structures consists of earthwork and lining cost. The former originates from two major sources: (1) the earthwork cost per unit area (β E ) and (2) the earthwork cost per unit area per unit depth below the ground surface (β A ), so called the additional earthwork cost. Since the ground surface was assumed as the top level of the channel section in literature, the earthwork is solely the excavation cost (Jain et al. 2004; Bhattacharjya and Satish 2007; Turan and Yurdusev 2011; Kaveh et al. 2012). The additional earthwork cost was considered to account for the overburden pressures on deeper soil strata and the supporting costs of deep excavations (Aksoy and Altan-Sakarya 2006) which surely result different cost of earthwork at different depths. Therefore, the total channel construction cost per unit length of a lined channel section (C) can be defined as

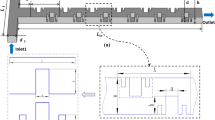
$$ C = \beta_{L}P+\beta_{E}A+\beta_{A}{\int}_{\!\!\!0}^{y_{n}} \mathrm{a}\,\mathrm{d}\eta $$
(1)

In which β L is the unit cost of lining per unit length of lining, P is the wetted perimeter, A is the excavated cross section area, y n is the water normal depth, a is the flow area at height η and d η is the unit length of earthwork at height η where η represents the vertical axis of channel geometry (Fig. 1).

Fig. 1
figure 1

A typical channel cross section

Full size image

As the total cost of channel construction was clearly identified, the channel cross section optimization problem can be defined as the minimization of the total cost (Eq. 1) subjected to the Mannings relation that can be formulized for uniform flow as following:

$$ Q-\frac{1}{n}AR^{\frac{2}{3}}\sqrt{S}=0 $$
(2)

Where Q is the volumetric discharge, n is the Mannings roughness coefficient, R is the hydraulic radius and S is the channel bottom slope.

In order to generalize the defined problem for any possible values of involved parameter, the nondimensional variables were considered. This conversion also makes the investigation of different variable affection on the problem much simpler. By defining a new term invariably called a length scale, λ, all variables of the problem can be converted to nondimensional terms. The length scale is introduced in Eq. 3.

$$ \lambda = \left(\frac{Qn}{\sqrt{S}}\right)^{\frac{3}{8}} $$
(3)

Using the length scale, the new dimensionless variables, which is subscripted by an asterisk sign, can be presented as below:

$$ C_{\ast} = \frac{C}{\beta_{E}\lambda^{2}} $$
(4)
$$ \beta_{L\ast} = \frac{\beta_{L}}{\beta_{E}\lambda} $$
(5)
$$ \beta_{A\ast} = \frac{\beta_{A}\lambda}{\beta_{E}} $$
(6)
$$ A_{\ast} = \frac{A}{\lambda^{2}} $$
(7)
$$ P_{\ast} = \frac{P}{\lambda} $$
(8)
$$ b_{\ast} = \frac{b}{\lambda} $$
(9)
$$ y_{n\ast} = \frac{y_{n}}{\lambda} $$
(10)
$$ r_{\ast} = \frac{r}{\lambda} $$
(11)

Where the asterisk sign as a subscript for a parameter shows its nondimensional form. For instance, C ∗ is the nondimensional forms of total cost.

Using the new variables, the optimization problem can be redefined as below:

$$ \textit{minimize} \, C_{\ast} = \beta_{L\ast}P_{\ast}+A_{\ast}+\frac{\beta_{A\ast}{\int}_{0}^{y_{n}} \mathrm{a}\,\mathrm{d}\eta}{\lambda^{3}} $$
(12)
$$ \textit{subjected} \, \textit{to} \,1-A_{\ast}^{5/3}P_{\ast}^{-2/3}=0 $$
(13)

Like some other real-life case studies in water resources engineering, the optimum channel design can be handled by utilizing contemporary optimization techniques (Cheng et al. 2005; Muttil and Chau 2006; Wu et al. 2009). The defined optimization problem (Eq. 12 and 13) was solved for common cross section shapes utilizing a novel meta-heuristic optimization technique, i.e. the MHBMO algorithm, which it was shortly described in next section.

3 HBMO Algorithm

Honey bees, one of the social groups of insects, produce their own community and live as a colony. Their community consists of three categories: the queen, the drones and the workers. In the single objective HBMO algorithm, a drone mates with the queen probabilistically using the following equation:

$$ \textit{prob}(Q,D)=e^{\frac{-\varDelta (f)}{S(t)}} $$
(14)

Where prob(Q,D) is the probability of a successful mating or in other words, the probability of adding the sperm of Drone (D) to the spermatheca of Queen (Q), Δ (f) is the absolute difference between the fitness of D (i.e., f(D)) and the fitness of Q (i.e., f(Q)); and S(t) is the speed of the queen at time t. It is apparent that this function acts as an annealing function, where the probability of mating is high when the queen is still at the beginning of her mating flight. Therefore, her speed is high when the fitness of the drone is as good as the queens (Marinakis et al. 2011). After each transition in space, the queens speed and energy, E(t), decays according to the following equations:

$$ S(t+1)=\alpha \times S(t) $$
(15)
$$ E(t+1)=\alpha \times E(t) $$
(16)

Where α is a decreasing factor varying from 0 to 1.0. In this study, the queen’s speed reduction factor was considered equal to 0.981. At the start of a mating flight, drones are generated randomly and the queen selects a drone in the basis of a probabilistic rule which is defined in Eq. 14. If the mating procedure is successful (i.e. the drone passes the probabilistic decision rule), the drone’s sperm will be stored in the queen’s spermatheca. Using the sperm of the drone’s and the queen’s genotypes, a new brood (trial solution) will be generated. Then, this new brood will be improved by employing some workers (Niknam et al. 2011).

4 Modified HBMO Algorithm (MHBMO)

In order to avoid local optima in the original HBMO, a modification was proposed to improve the brood generation (Niknam et al. 2011). In the proposed modification, three sperm (S P k1, S P k2, S P k3) are randomly chosen from the queens spermatheca so that k 1≠k 2≠k 3. The two improved new drones will be calculated in the next step utilizing the following equations (Esmi Jahromi and Afzali 2013; Niazkar and Afzali 2014).

$$ \ X_{improved1} = SP_{k1} + rand \times (SP_{k2} - SP_{k3}) \; $$
(17)
$$ \ X_{improved1} = [x_{im1}^{1} \quad x_{im1}^{2} \quad {\ldots} \quad x_{im1}^{n}] \; $$
(18)
$$ \ X_{Brood1} = [x_{Br1}^{1} \quad x_{Br1}^{2} \quad {\ldots} \quad x_{Br1}^{n}] \; $$
(19)
$$ x_{Br1}^{j} = \left\{\begin{array}{cc} x_{im1}^{j} & if~ \gamma_{1} \leq \gamma_{2} \\ x_{SP_{k1}}^{j} & otherwise \end{array}\right. \quad j= 1, {\ldots} ,n $$
(20)
$$ \ X_{improved2} = X_{Queen} + rand \times (SP_{k2} - SP_{k3}) \; $$
(21)
$$ \ X_{improved2} = [x_{im2}^{1} \quad x_{im2}^{2} \quad {\ldots} \quad x_{im2}^{n}] \; $$
(22)
$$ \ X_{Brood2} = [x_{Br2}^{1} \quad x_{Br2}^{2} \quad {\ldots} \quad x_{Br2}^{n}] \; $$
(23)
$$ x_{Br2}^{j} = \left\{\begin{array}{cc} x_{im2}^{j} & if ~\gamma_{3} \leq \gamma_{2} \\ x_{best}^{j} & otherwise \end{array}\right.\ \quad j= 1, {\ldots} ,n $$
(24)

In the above equations, X i m p r o v e d1 and X i m p r o v e d2 are first and second improved new drones; \(x_{Br1}^{j}\) and \(x_{Br2}^{j}\) are first and second generated brood; γ 1, γ 2 and γ 3 are random numbers in the range of 0 to 1. The best individual between X B r o o d1, X B r o o d2 and that concluded in the original HBMO is considered as a new brood (Esmi Jahromi and Afzali 2013; Niazkar and Afzali 2014).

The MHBMO algorithm parameters were set as: Number of initial population, N i p o p =1000; number of broods, N B r o o d =1500; number of drones, N D r o n e =1500; spermatheca size, N S p e r m =1500 and number of worker, N W o r k e r =10. These values were calculated by trial and error method and they are in the range of values which have been used by previous researches. Additionally, the sensitivity analysis, which was conducted in previous studies, was shown that these values guarantee both good accuracy and rate of convergence in this optimization algorithm (Niazkar and Afzali 2014).

5 Application and Results

5.1 The \(\beta _{A}^{\ast }=0\) condition

The defined cross section optimization problem was solved for common cross section shapes utilizing the MHBMO algorithm. According to Eq. 1, the \(\beta _{A}^{\ast }=0\) condition is to assume equal earthwork cost for excavation at different depths which is a simplified assumption for real channel constructions. The optimal section variables for \(\beta _{A}^{\ast }=0\) condition was computed for all common channel cross section shapes (Table 1). The optimum section variables for \(\beta _{A}^{\ast }=0\) condition were also computed by Langrange Multipliers (LM) (Aksoy and Altan-Sakarya 2006) and Differential Evolution Algorithm (DEA) (Turan and Yurdusev 2011) in previous studies which those values were compared with the MHBMO algorithm results in Table 1. As it is shown in Table 1, the obtained optimum values using the MHBMO algorithm were similar to those which were reported by previous researches in literature. Therefore, all these optimization techniques reached to a unique solution for optimal channel design under the circumstance of no additional earthwork cost.

Table 1 Optimum nondimensional section variables for β A =0 for different common channel section shapes
Full size table

In order to trace the effect of \(\beta _{A}^{\ast }\) and \(\beta _{L}^{\ast }\) values on the optimal channel section design, the variation of the optimum values of section variables for different values of \(\beta _{A}^{\ast }\) and \(\beta _{L}^{\ast }\) were investigated. The nondimensional side slope and normal water depth values of triangular section were calculated for two scenarios; in the first scenario, the \(\beta _{L}^{\ast }\) parameter was freeze equal to 1.0 and the optimal values of m ∗, y ∗ and the corresponding total cost were computed for different values of \(\beta _{A}^{\ast }\) (Fig. 2). The second scenario was exactly vice versa except that the \(\beta _{A}^{\ast }\) was fixed equal to 0.5. The results of second scenario were depicted in Fig. 3. The obtained values for the first and second scenarios were compared to those reported in previous studies (Fig. 2 and Fig. 3). According to Fig. 2c, the optimal section variable values calculated by the MHBMO algorithm results to lower construction costs for the first scenario whereas quite similar cost values were obtained for the second scenario for all of the applied techniques (Fig. 3c). In the second scenario, different combinations of slope and depth lead to the same optimal solution. In fact, the MHBMO algorithm obtains the optimal combination with larger slopes and lower depth than the LM and DEA algorithms in that scenario while all combinations lead to nearly similar construction cost. The obtained results demonstrates that the obtained section variable values were better to those which are present in literature especially for the first scenario. This clearly shows that the MHBMO algorithm can be utilized as an effective tool for channel cross section optimization problems.

Fig. 2
figure 2

Variation of optimum triangular nondimensional variables: (a) side slope, (b) normal depth and (c) total construction cost with β A (β L =0)

Full size image
Fig. 3
figure 3

Variation of optimum triangular nondimensional variables: (a) side slope, (b) normal depth and (c) total construction cost with β L (β A =0.5)

Full size image

For considering more general conditions, a new design model for section variables will be proposed in the next section. The proposed model along with the MHBMO algorithm was compared with other present models in literature using four design problems.

5.2 Proposed Model

Due to effectiveness of the MHBMO algorithm in the lined channel design, which was proved in previous section, simple explicit equations were proposed to easily compute nondimensional section variables for channel section designs. The advantage of these relations is that the optimum values of section variables can be explicitly calculated for any values of nondimensional cost terms, i.e. \(\beta _{A}^{\ast }\) and \(\beta _{L}^{\ast }\). The new proposed relations were shown in Eq. 25 to Eq. 28.

$$ m^{\ast} = Z_{m0}+\alpha_{1}(\beta_{A}^{\ast})^{\alpha_{2}}(\beta_{L}^{\ast})^{\alpha_{3}} $$
(25)
$$ b^{\ast} = Z_{b0}+\alpha_{1}(\beta_{A}^{\ast})^{\alpha_{2}}(\beta_{L}^{\ast})^{\alpha_{3}} $$
(26)
$$ y_{n}^{\ast} = Z_{y0}[\alpha_{1}+\alpha_{2}(\beta_{A}^{\ast})^{\alpha_{3}}(\beta_{L}^{\ast})^{\alpha_{4}}]^{\alpha_{5}} $$
(27)
$$ r^{\ast} = Z_{r0}+\alpha_{1}(\beta_{A}^{\ast})^{\alpha_{2}}(\beta_{L}^{\ast})^{\alpha_{3}} $$
(28)

The first terms, i.e. Z m0, Z b0, Z y0 and Z r0, are the optimum section variables for \(\beta _{A}^{\ast }=0\) condition which for all common cross section shapes were given in Table 1. The α i (for i=1,2,3,4,5) coefficients were evaluated for numerous set of computational problems for all common cross section shapes which were optimized using the MHBMO algorithm. The upper and lower bounds for \(\beta _{A}^{\ast }/\beta _{L}^{\ast }\) for these problems were considered equal to 2 and 0, respectively, similar to a previous study (Aksoy and Altan-Sakarya 2006). The α i coefficient values for common cross section shapes (i.e. triangular, rectangular, trapezoidal and circular sections) were calculated using the MHBMO algorithm and presented in Table 2. Therefore, these explicit equations can be utilized for channel cross section design problems only if the value of \(\beta _{A}^{\ast }/\beta _{L}^{\ast }\) is located between 0 and 2.

Table 2 The coefficients of proposed model for optimal nondimensional section variables for common channel section shapes
Full size table

5.3 Design Examples

In order to compare the proposed model with other models in literature, a typical problem (Swamee et al. 2000) was solved using all models. This design example was presented and solved solely for trapezoidal cross section in the literature (Swamee et al. 2000; Aksoy and Altan-Sakarya 2006). In order to provide a comprehensive comparison between all proposed models for all common channel shapes, the given data of this example was utilized not only for trapezoidal section but also for constructing triangular, rectangular, and circular cross sections. Hence, four design examples were solved to better compare the recommended models. The given data of this example includes: Q=125m 3/s, n=0.0015, S=0.0002, β E /β A =7.0m and β L /β E =12m. The procedure of problem solving of this example was presented in the following steps:

  1. 1.

    Computing the length scale (λ) using Eq. 3.

  2. 2.

    Calculating the nondimensional unit cost of additional earthwork (\(\beta _{A}^{\ast }\)) using Eq. 6.

  3. 3.

    Calculating the nondimensional unit cost of lining (\(\beta _{L}^{\ast }\)) using Eq. 5.

  4. 4.

    Checking that the value of the \(\beta _{A}^{\ast }/\beta _{L}^{\ast }\) is located between 0 and 2.

  5. 5.

    Calculating the optimum section variables using the related explicit equations (Eq. 25, 26, 27 and 28).

This procedure of problem solving were conducted for this example using all proposed models. The optimum section values can be obtained according to the specification of the project. In the previous studies, the LM and DEA algorithms were utilized to find explicit relation in order to find non-dimensional section variable directly only from the cost units. Although these kind of explicit formula simplify the design process in the first place, their accuracy are in major of interest since they are supposed to be used in practical projects. Keeping that in mind, those equations should be modified not only to improve their result accuracy but also to save the concept of simplicity of this method. In the present study, a new powerful optimization algorithm, so called MHBMO, was utilized to proposed new simple relations in favor of improving both accuracy and simplicity of channel design with explicit equations. The obtained results for all common channel shapes were compared with the numerical computation which was the problem benchmark (Tables 3, 4, 5 and 6). According to all these tables, the model which was proposed in this study is much more close to the benchmark solution than all other models for all common channel section shapes. Therefore, the proposed model can be confidently altered the present models in literature and subsequently utilized in optimal lined open channel design problems.

Table 3 The triangular optimum results of different models for the design example
Full size table
Table 4 The rectangular optimum results of different models for the design example
Full size table
Table 5 The trapezoidal optimum results of different models for the design example
Full size table
Table 6 The circular optimum results of different models for the design example
Full size table

6 Conclusion

The design of the channel cross sections, as a mean of water conveyance, have been arisen a need to investigate on computing the best hydraulically efficient sections. By emerging new powerful optimization techniques, the optimal channel design was revisited using the Modified Honey Bee Mating Optimization (MHBMO) algorithm. Since the total construction cost of channels play an essential role in the related designs, it was selected as the objective function of this paper. The Manning’s equation was chosen as the problem constraint. The total cost consists of lining, earthwork cost and additional earthwork cost which originates from different excavation cost at different depths. At first, the optimal section variables of common channel shapes, i.e. triangular, rectangular, trapezoidal and circular, were computed under the circumstances of no additional earthwork cost. The obtained results for this condition were similar to the previous studies in literature. In order to consider the additional earthwork cost in the channel design, a new explicit model was proposed to directly compute the optimum section variables of common channel shapes. The new model was compared to the present explicit models in literature using four design examples. The computational results indicate that the proposed model achieve the closest values to the benchmark solution. Moreover, it can be concluded that the recommended model along with the obtained coefficients, which were computed using the MHBMO algorithm, can be confidently utilized in channel design problems. According to the simplicity and accuracy of the proposed model, the lined channel design using explicit relation probably can be of interest not only practical projects but also for future studies while more realistic cost function, more channel sections and alternative algorithms may be considered.