1 Introduction

Design of water conveyance structures such as channels and canals has been an essential part of hydraulic engineers concerns. Since water conveyance projects usually carry water to relatively far distances, these projects require considerable amounts of budget. In this regard, the optimum design of such structures not only can decrease the total required budget to a minimum possible value, but also enhance functionality of these structures in securely conveying water.

Water shortage problem in many parts of the world and consideration of water as an economic good provide the necessity for more rigorous investigation on optimum design of water conveyance structures. The optimum design of channels, as a typical water conveyance structure, can be treated as an optimization problem. In this optimization problem, the aim of the conveyance system dictates what the objective function is. In practical projects, where budget plays a key role, the objective function is commonly minimizing the cost of channel construction. Likewise, the construction cost has been extensively considered as the objective function in many researches in this area (Aksoy and Altan-Sakarya 2006; Swamee et al. 2000; Niazkar and Afzali 2015a). The construction cost, in its most general definition, comprises three items: (1) excavation cost, (2) lining cost, and (3) additional cost associated with different costs of earthwork in different depths. Furthermore, a resistance equation such as Manning’s equation is usually designated as the constraint for the optimization problem to control flow field in the channel. Finally, based on the cross section selected for the channel, optimum values may be obtained for section parameters through an optimization process.

In early attempts to optimally design channel sections, Chow (1959, 1973) and French (1994) presented efficient relations for the best hydraulic section. Their objective function was minimization of flow area subjected to Manning’s equation as the sole constraint. Swamee and Bhatia (1972) published design curves for trapezoidal, rounded bottom, and rounded corner cross sections. Guo and Hughes (1984) studied optimum design of a trapezoidal section with freeboard. Loganathan (1991) investigated the optimal conditions for a parabolic channel section. Monadjemi (1994) proved that the optimum cross section achieved by minimizing the flow rate yields the same results as when minimizing the wetted perimeter. French (1994) proposed both simple discharge-related equations and design graphs for design of optimum trapezoidal sections. Swamee (1995) suggested explicit correlations for optimum section variables obtained by minimizing the flow rate. Swamee et al. (2000) introduced the general form for construction cost and proposed new equations for optimum design of channel sections. Aksoy and Altan-Sakarya (2006) recommended two models for computing the optimal section variables using the general form for constructional cost. More recently, Niazkar and Afzali (2015a) applied a powerful optimization algorithm, invariably called the MHBMO algorithm, to minimize the generalized form of construction cost. They presented new accuracy-improved models for optimum design of lined channel for common cross sections in practice. Similar researches were also conducted utilizing some other optimization techniques for optimum design of channels (Jain et al. 2004; Bhattacharjya and Satish 2007; Nourani et al. 2009; Turan and Yurdusev 2011; Kaveh et al. 2012). Previous experiments show that, in partially filled circular channels, Manning’s coefficient is a function of the angle associated with water surface. In other words, the Manning roughness coefficient varies with flow depth in a circular channel. Field measurements show that, for a typical circular channel, this coefficient has a greater value when the channel is partially full compared to when it is completely full (Yarnell and Woodward 1920; Wilcox 1924; Zaghloul 1992). Variation of Manning coefficient with relative water depth, i.e., the ratio of water depth to section diameter, is depicted in Fig. 1. This figure illustrates two things: (1) Manning roughness coefficient for a partially filled circular channel is larger than that for a completely filled pipe, and (2) maximum and minimum Manning coefficients pertain to relative depths of 0.25 and close to zero, respectively. In spite of many efforts conducted in optimum design of circular channels, variation of roughness coefficient with water depth was not taken into account. Since this variation may affect values of the optimum section variables, it should be considered in an optimal design of circular channels.

Fig. 1
figure 1

Variation of relative roughness with the relative depth

Full size image

In this study, variation of Manning roughness coefficient with water depth was implemented in optimization of a circular channel design. In other words, this paper intends to investigate its effects, and implement it in new explicit design equations. In this regard, the generalized form of construction cost and Manning’s equation were considered as objective function and hydraulic constraint, in the optimization process, respectively. A new hybrid method, which combines two optimization algorithms, the Modified Honey Bee Mating Optimization (MHBMO) and Generalized Reduced Gradient (GRG) algorithms, were utilized to solve the defined optimization problem. The results show that considering variation of roughness coefficient with water depth noticeably affects the optimum section variables. In order to simplify design procedure of lined circular channels, new explicit equations were proposed in which Manning’s roughness variability was taken into account. These non-dimensional equations facilitate the optimum design of cross section parameters for a wide range of flow rates. A typical problem of channel design was solved using the new proposed equations. Results demonstrate that the new equations accurately design the circular channel compared to the benchmark solution.

2 The Problem of Optimum Design of Circular Channels

Channels, as one of the common water conveying structures, mainly aim to properly transfer a certain flow of water along short or long distances. One of the major concerns in channels construction is to accomplish the project in its least possible expenditure form. Therefore, the channel construction project can be treated as an optimization problem most of the time. This optimization problem comprises minimization of total construction cost subjected to a hydraulic resistance equation.

In the design procedure of channels, the selection of suitable function for construction cost significantly affects the final result. The total cost is affected by many factors. These factors include: (1) the accessibility of ground surface, (2) the geographical condition of the channel route, (3) the applicability of contractor’s equipment, (4) the need for constructing sustainable structures and (5) Haul distance. (Niazkar and Afzali 2015a). However, all factors may not be considered in practice, since some of them are not predictable. Since each project possesses its exclusive specifications, determining vital factors are required to address an adequate solution for a certain channel construction project.

In this study, the most generalized form of the cost function in the literature (Swamee et al. 2000) was adopted. In this cost function, it is assumed that the ground surface is the top level of the channel section (Niazkar and Afzali 2015a). This assumption dictates that the earthwork cost is solely the excavation cost. Based on this cost function, the total construction cost per unit length of channel consists of two major costs: (1) the earthwork cost and (2) the lining cost. The former comprises two items: (1) the earthwork cost per unit area (β E) and (2) the additional earthwork cost (β A). The additional earthwork cost, which is the earthwork cost per unit area per unit depth below the ground surface, is considered to account for the overburden pressures on deeper soil strata and the supporting costs in deep excavations (Aksoy and Altan-Sakarya 2006). This cost causes different cost of earthwork at different depth levels. Finally, the total channel can be formulated as:

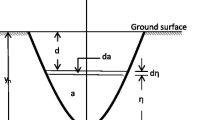
$$C = \beta_{\text{L}} P + \beta_{\text{E}} A + \beta_{\text{A}} \int\limits_{0}^{{y_{\text{n}} }} {a{\text{d}}\eta }$$
(1)

where C is total construction cost per unit length of a lined channel section, L is unit cost of lining per unit length, P is wetted perimeter, A is channel cross section area, y n is water normal depth, a is flow area at height η and dη is unit length of earthwork at height η where η represents the vertical axis of channel geometry (Fig. 2).

Fig. 2
figure 2

A typical channel cross section (Niazkar and Afzali 2015a)

Full size image

In order to relate channel geometry to hydraulic-related parameters, a resistance equation such as Manning may be utilized. This resistance equation, which has been extensively applied for open-channel flows, reassures applicability of optimization final results from a hydraulic perspective. Manning equation may be written in SI units as:

$$Q - \frac{1}{n}AR^{2/3} \sqrt S = 0$$
(2)

In Eq. 2, Q is the channel flow rate, n is the Manning’s roughness coefficient, R is the hydraulic radius and S is the channel bottom slope.

In order to extend applicability of the solution to a wide range of possible values for involved parameters, dimensionless variables were utilized. The conversion of dimensional to dimensionless parameters was conducted using a new parameter, the so-called a length scale (λ), introduced in Eq. 3:

$$\lambda = \left( {\frac{Qn}{\sqrt S }} \right)^{3/8}$$
(3)

Using λ, all hydraulic variables with dimensions may be converted to dimensionless ones. For a circular cross section, involving parameters include: (1) the total cost (C), (2) the earthwork cost per unit area (β E), (3) the additional earthwork cost (β A), (4) the lining cost per unit length (β L), (5) the excavated channel area, i.e., \(A = 0.5r^{2} (\theta - \sin \theta )\) where \(\theta\) is water depth angle, (6) the wetted perimeter (\(P = \theta r\)), (7) the normal water depth (y n) and (8) the channel radius (r). These parameters can be converted to their dimensionless forms using λ and β E. The new dimensionless variables, subscripted by an asterisk sign, are presented in Eqs. 4 to 10.

$$C_{*} = \frac{C}{{\beta_{\text{E}} \lambda^{2} }}$$
(4)
$$\beta_{{{\text{A}}*}} = \frac{{\beta_{\text{A}} \lambda }}{{\beta_{\text{E}} }}$$
(5)
$$\beta_{{{\text{L}}*}} = \frac{{\beta_{\text{L}} }}{{\beta_{\text{E}} \lambda }}$$
(6)
$$A_{*} = \frac{A}{{\lambda^{2} }}$$
(7)
$$P_{*} = \frac{P}{\lambda }$$
(8)
$$y_{{{\text{n}}*}} = \frac{{y_{\text{n}} }}{\lambda }$$
(9)
$$r_{*} = \frac{r}{\lambda }$$
(10)

The objective function and the constraint of this optimization problem may be rewritten as Eqs. 11 and 12, respectively.

$${\text{minimize}}\quad C_{ *} = \beta_{{{\text{L}}*}} P_{*} + A_{*} + \frac{{\beta_{{{\text{A}}*}} \int_{0}^{{y_{\text{n}} }} {a{\text{d}}\eta } }}{{\lambda^{3} }}$$
(11)
$$s{\text{ubjected}}\quad {\text{to}}\quad 1 - {\text{A}}_{ *}^{ 5 / 3} P_{*}^{ - 2/3} = 0$$
(12)

In the optimization problem defined as Eqs. 11 and 12, variation of Manning’s coefficient with relative water depth is not considered. In order to implement this variation, roughness coefficient in Manning’s equation (Eq. 2), i.e., n, should be modified. In other words, the Manning’s coefficient varying with relative water depth in a circular cross section, which is given in Eq. 13, should substitute n.

$$n = n_{f} \times \left[ {0.9987 + 3.4616\left( {\frac{{y_{n} }}{D}} \right) - 14.7108\left( {\frac{{y_{n} }}{D}} \right)^{2} + 27.2574\left( {\frac{{y_{n} }}{D}} \right)^{3} - 23.4963\left( {\frac{{y_{n} }}{D}} \right)^{4} + 7.4909\left( {\frac{{y_{n} }}{D}} \right)^{5} } \right]$$
(13)

where D is the circular channel diameter, and n and n f are the Manning’s roughness coefficients associated with a partially and completely full cross section, respectively. Equation 13 is an appropriate equation, obtained by fitting high order polynomials (reported in Zaghloul 1992) to the curve shown in Fig. 1. Although this equation indicates the relation between Manning’s roughness coefficients for partially and completely full cross sections, this relation can be presented as a function of water depth angle, i.e., \(\theta\), instead of relative water depth. Hence, Eq. 13 with the aid of the geometry relation between the water depth angle and the relative water depth, i.e., \(\frac{{y_{\text{n}} }}{D} = 0.5[1 - \cos (\frac{\theta }{2})]\), may be rewritten as a function of water depth angle (Akgiray 2004). Equation 13 may be rewritten such that direct calculation of Manning’s coefficient is possible using water depth angle:

$$n = n_{f} \times (1 + 0.18(2\pi - \theta )[0.1 + \exp ( - \,0.3\theta )\sin^{2} (0.38\theta )]$$
(14)

Implementing Eq. 14 in Eq. 2, optimum design of a lined circular channel may be reformulated incorporating a variable roughness coefficient. Objective function and constraint of the reformulated optimization problem are shown in Eqs. 15 and 16, respectively. In order to better demonstrate the problem, the terms \(A_{*}\), \(P_{*}\), and \(\int\nolimits_{0}^{{y_{\text{n}} }} {a{\text{d}}\eta }\) are given as a function of \(r_{*}\), \(y_{{{\text{n}}*}}\), and \(\theta\) in these equations.

$${\text{minimize}}\quad {\text{C}}_{ *} = \beta_{{{\text{L}}*}} \theta r_{*} + 0.5r_{*} (\theta - \sin \theta ) + 0.5\beta_{A*} r_{*} \left[ {(y_{n*} - r_{*} )\theta + \frac{{4r_{*}^{2} + 2(y_{{{\text{n}}*}} - r_{*} )^{2} }}{{3r_{*}^{2} }}\sqrt {r_{*}^{2} - (y_{{{\text{n}}*}} - r_{*} )^{2} } } \right]$$
(15)
$${\text{subjected}}\;{\text{to}}\;n_{f} \times (1 + 0.18(2\pi - \theta )[0.1 + \exp ( - \,0.3\theta )\sin^{2} (0.38\theta )] - [0.5r_{*} (\theta - \sin \theta )]^{5/3} (\theta r_{*} )^{ - 2/3} = 0$$
(16)

The only conceptual difference between the design problem defined by Eqs. 11 and 12 with the one described by Eqs. 15 and 16 is consideration of a Manning roughness coefficient which varies with water depth. In other words, the former considers a constant Manning’s coefficient for both completely and partially full cross section, while the results obtained from the latter take into account a Manning’s coefficient which is a function of water depth.

3 The New Hybrid Method

A new hybrid method is developed which is a combination of search-based and deterministic optimization algorithms (Niazkar and Afzali 2016a, b, 2017a). The former is the MHBMO algorithm, which has already been utilized for solving many problems in water resources engineering (Niazkar and Afzali 2014, 2015a, 2017b; Afzali et al. 2016; Afzali 2016) while the latter is the GRG algorithm. MHBMO algorithm was proved to be applicable in one of the previous studies in which Manning’s coefficient was assumed to be invariant with water depth. GRG algorithm is embedded in any Excel spreadsheet, has been utilized for solving many engineering problems, and may be conveniently used by researchers and engineers (Niazkar and Afzali 2015b, 2016c, 2017c, d).

Any research-based optimization algorithm may fall into local optima, while deterministic ones may reach different solutions based on the utilized initial guess. Therefore, problems of trapping in a local optimal value and initial guess requirement are known shortcomings of MHBMO and GRG algorithms, respectively. The initial guess requirement restricts users in their selection of a proper value for decision variables at the beginning of the latter algorithm. Since the optimum values of these variables are the objective of optimization process and are definitely unknown at the beginning, finding appropriate initial guesses for GRG algorithm is a challenging task. This shortcoming may be somehow addressed by using a powerful search-based approach to find appropriate initial values as initial guesses for this algorithm. Consequently, the new MHBMO–GRG hybrid method not only provides the suitable initial guesses for the decision variables for its deterministic algorithm but also enhances the chance of reaching global optima.

A flowchart for the new hybrid method is depicted in Fig. 3. According to this figure, the method utilizes the algorithms in two successive steps. In the first step, the MHBMO algorithm simulates mating process of honey bees. The main five stages of the MHBMO algorithm are (Niazkar and Afzali 2015a):

Fig. 3
figure 3

Flowchart of the hybrid MHBMO–GRG algorithm used in this study (Niazkar and Afzali 2017a)

Full size image

  • At the beginning, the queen as the best solution, commences the mating flight and probabilistically selects drones to form the spermatheca. One drone is randomly selected for creation of the broods,

  • Producing new broods, i.e., trial solutions,

  • Performing a local search on new broods by workers,

  • Adjusting workers fitness based on achieved improvements on the broods, and

  • Comparing the queen with the best brood and replacing the weaker queen(s) by fitter brood(s).

A comprehensive detail of this algorithm may be seen in Esmi Jahromi and Afzali (2014) and Niazkar and Afzali (2014, 2015a). Numerical values utilized for algorithm parameters were the ones used by Niazkar and Afzali (2015a).

In the second step, GRG algorithm completes the optimization process using final solutions achieved by MHBMO algorithm as its initial guesses. Although this algorithm, like other deterministic ones, has a mathematical background, it requires initial values for the decision variables. In order to use this algorithm, the problem should be implemented in an Excel spreadsheet first. Afterward, the objective function accompanied with the problem constraint should be introduced in corresponding part of the Excel spreadsheet.

4 Application and Results

The hybrid MHMO–GRG algorithm was utilized to solve two different approaches for optimum design of a circular channel. The obtained results for two approaches were compared with each other to investigate the effects of considering variable roughness Manning’s coefficient. Afterward, the optimum values for section parameters were computed to present explicit design equations. Finally, a typical design problem from literature was solved using proposed explicit equations.

4.1 Constant Versus Variable Roughness

In this section, two approaches for optimum design of a circular channel are presented. The first approach considers constant roughness coefficient for flow in a circular section either completely or partially full, whereas the second one takes into account variation of Manning’s coefficient with water depth angle. Here, solutions for the former and latter are referred to as constant and variable roughness coefficient solutions, respectively. The former is introduced in Eqs. 11 and 12, while the latter is defined in Eqs. 15 and 16.

First variations of \(r_{*}\), \(y_{{{\text{n}}*}}\), and \(\theta_{*}\) (the water depth angle associated with \(r_{*}\) and \(y_{*}\)) and \(C_{*}\) for different values of \(\beta_{{{\text{L}}*}}\) and \(\beta_{{{\text{A}}*}}\) were computed using the proposed hybrid MHBMO–GRG algorithm. In other words, the two approaches defined in Eqs. 11, 12 and Eqs. 15, 16 were separately solved using the algorithm. Results for both approaches are shown in Figs. 4 and 5. Utilized ranges for dimensionless lining and additional costs are the same as the ones used in previous studies (Aksoy and Altan-Sakarya 2006; Niazkar and Afzali 2015a). Figure 4(a) depicts results for zero-additional cost, but variable \(\beta_{{{\text{L}}*}}\) when manning coefficient may be constant or variable. As shown, constant optimum values (for radius and depth) were obtained for \(r_{*}\) and \(y_{{{\text{n}}*}}\) in the constant roughness approach, whereas these parameters varied with \(\beta_{{{\text{L}}*}}\) in the variable roughness approach. The difference between optimum dimensionless radius of the circular channel for constant and variable roughness is significant for \(\beta_{{{\text{A}}*}} = 0\) and \(\beta_{{{\text{A}}*}} = 0.2\) (Fig. 4a, b). This difference becomes somewhat inconsiderable for \(\beta_{{{\text{A}}*}} = 0.4\),\(\beta_{{{\text{A}}*}} = 0.6\), \(\beta_{{{\text{A}}*}} = 0.8\) and \(\beta_{{{\text{A}}*}} = 1.0\) (Figs. 4c, 5), especially for larger values of \(\beta_{{{\text{L}}*}}\). On the other hand, the difference between optimum \(y_{{{\text{n}}*}}\) values for constant and variable approaches is considerably large for almost all \(\beta_{A*}\) and \(\beta_{{{\text{L}}*}}\) values (Figs. 4, 5). The existing discrepancy for optimum values of circular channel parameters, especially \(y_{{{\text{n}}*}}\), is obviously considerable. One may conclude that it is necessary to consider variation of roughness coefficient with water depth angle in optimum design of lined circular channels.

Fig. 4
figure 4

Variation of dimensionless radius and water depth with \(\beta_{{{\text{L}}*}}\) for: a \(\beta_{{{\text{A}}*}}\) = 0, b \(\beta_{{{\text{A}}*}}\) = 0.2, and c \(\beta_{{{\text{A}}*}}\) = 0.4

Full size image
Fig. 5
figure 5

Variation of dimensionless radius and water depth with \(\beta_{{{\text{L}}*}}\) for: a \(\beta_{{{\text{A}}*}}\) = 0.6, b \(\beta_{{{\text{A}}*}}\) = 0.8, and c \(\beta_{{{\text{A}}*}}\) = 1

Full size image

4.2 Optimum Values for Circular Channel Parameters

The design problem for variable roughness coefficient introduced in Eqs. 15 and 16 was solved utilizing MHBMO–GRG algorithm by specifying lining and additional costs. The utilized range for the costs was the same as the one utilized in the literature for these parameters (Aksoy and Altan-Sakarya 2006; Niazkar and Afzali 2015a). Results for \(r_{*}\),\(y_{{{\text{n}}*}}\),\(\theta_{*}\) and \(C_{*}\) variations for different values of \(\beta_{{{\text{L}}*}}\) and \(\beta_{{{\text{A}}*}}\) are shown in Figs. 6, 7, 8 and 9, respectively. According to Fig. 6, larger optimum dimensionless radii were obtained for larger \(\beta_{{{\text{A}}*}}\) values, especially in the lower ranges of \(\beta_{{{\text{L}}*}}\). An opposite trend is seen in Fig. 7 for the optimum dimensionless water depth values. Based on Fig. 7, smaller dimensionless water depths were obtained for larger \(\beta_{{{\text{L}}*}}\) values, especially in the lower ranges of \(\beta_{{{\text{A}}*}}\). Water angle has a similar trend as the dimensionless water depth with respect to \(\beta_{{{\text{L}}*}}\) (Fig. 8). Figure 9 depicts the monotonic increase in dimensionless total cost with \(\beta_{{{\text{L}}*}}\) increase for different values of \(\beta_{{{\text{A}}*}}\). The database produced in this section is later utilized to develop simple explicit design equations and optimize r and y with respect to the cost.

Fig. 6
figure 6

Variation of dimensionless radius with \(\beta_{{{\text{L}}*}}\) for different values of \(\beta_{{{\text{A}}*}}\)

Full size image
Fig. 7
figure 7

Variation of dimensionless water depth with \(\beta_{{{\text{L}}*}}\) for different values of \(\beta_{{{\text{A}}*}}\)

Full size image
Fig. 8
figure 8

Variation of water angle with \(\beta_{{{\text{L}}*}}\) for different values of \(\beta_{{{\text{A}}*}}\)

Full size image
Fig. 9
figure 9

Variation of dimensionless total construction cost with \(\beta_{{{\text{L}}*}}\) for different values of \(\beta_{{{\text{A}}*}}\)

Full size image

4.3 Explicit Design Equations

Simple explicit equations are proposed to determine optimum values for \(r_{*}\) and \(y_{*}\) using MHBMO–GRG algorithm. As mentioned, variation of Manning’s roughness coefficient with water depth angle has been taken into account and these equations may be utilized to conveniently design an optimum lined circular channel incorporating a variable roughness. These equations for \(r_{*}\) and \(y_{*}\) are shown in Eqs. 17 and 18, respectively.

$$r_{*} = 0.9493\beta_{{{\text{L}}*}}^{0.0202} + 0.3542\beta_{{{\text{A}}*}}^{1.0351} \beta_{{{\text{L}}*}}^{ - 0.702}$$
(17)
$$y_{*} = 1.1663\beta_{{{\text{L}}*}}^{ - 0.01} - 0.1557\beta_{{{\text{A}}*}}^{0.9322} \beta_{{{\text{L}}*}}^{ - 0.5489}$$
(18)

In order to evaluate performance of these two equations against classical approaches, similar relations are obtained using Genetic Algorithm (GA) shown in Eqs. 19 and 20.

$$r_{*} = 0.9539\beta_{{{\text{L}}*}}^{0.0175} + 0.3501\beta_{{{\text{A}}*}}^{1.0352} \beta_{{{\text{L}}*}}^{ - 0.705}$$
(19)
$$y_{*} = 1.1598\beta_{{{\text{L}}*}}^{ - 0.0114} - 0.1618\beta_{{{\text{A}}*}}^{1.0695} \beta_{{{\text{L}}*}}^{ - 0.5676}$$
(20)

Performance of these relations may be evaluated by two error indices: (1) root-mean-square error (RMSE) and (2) coefficient of determination (R2). These indices for \(y_{*}\) are defined as:

$${\text{RMSE}} = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^{N} {(y_{\text{database}} - y_{\text{explicit}} )^{2} } }$$
(21)
$$R^{2} = \left( {\frac{{\sum\limits_{i = 1}^{N} {\left[ {\left( {y_{\text{database}} - \frac{{\sum\nolimits_{i = 1}^{N} {y_{\text{database}} } }}{N}} \right)\left( {y_{\text{explicit}} - \frac{{\sum\nolimits_{i = 1}^{N} {y_{\text{explicit}} } }}{N}} \right)} \right]} }}{{\sqrt {\sum\limits_{i = 1}^{N} {\left[ {\left( {y_{\text{database}} - \frac{{\sum\nolimits_{i = 1}^{N} {y_{\text{database}} } }}{N}} \right)^{2} \left( {y_{\text{explicit}} - \frac{{\sum\nolimits_{i = 1}^{N} {y_{\text{explicit}} } }}{N}} \right)^{2} } \right]} } }}} \right)^{2}$$
(22)

In these relations, \(y_{\text{database}}\) and \(y_{\text{explicit}}\) are the \(y_{*}\) values from the prepared database and computed \(y_{*}\) values using the proposed explicit equations, respectively. Similar equations may be written for \(r_{*}\).

Performance of the equations for optimum design of a lined circular channel is compared in Table 1. As shown, all error indices are very low, demonstrating that the equations are all acceptably accurate. Although accuracy of the equations is quite close, equations obtained using the MHBMO–GRG algorithm perform relatively better than the ones achieved by GA based on RMSE criterion. Comparison of \(R^{2}\) values shown in Table 1 also indicates that these equations perform acceptably well.

Table 1 Performance of the proposed explicit equations
Full size table

Similar to previous studies, the proposed explicit equations are applicable for the range of \(0 \le \frac{{\beta_{{{\text{A}}*}} }}{{\beta_{{{\text{L}}*}} }} \le 2\) (Aksoy and Altan-Sakarya 2006; Niazkar and Afzali 2015a). These equations facilitate the optimum design of a lined circular channel without any tedious trial-and-error procedure; a procedure that is conventionally practiced. Moreover, unlike the available explicit relations in the literature for optimum design of lined circular channel, these equations consider a variable Manning’s roughness with water depth angle. Applicability of the recommended equations was investigated for a typical problem.

4.4 A Typical Design Problem

A typical design problem was solved for optimum circular cross section using both constant (Swamee et al. 2000) and variable (present work) Manning roughness coefficient. Given information in this problem includes: (1) the flow rate (Q = 125 m3/s), (2) the Manning’s roughness coefficient associated with completely full section (n f  = 0.015), (3) the bottom slope (S = 0.0002), (4) the ratio of the unit excavation cost to the unit additional cost (\(\frac{{\beta_{{{\text{E}}*}} }}{{\beta_{{{\text{A}}*}} }} = 7.0\,{\text{m}}\)) and (5) the ratio of the unit lining cost to the unit excavation cost (\(\frac{{\beta_{{{\text{L}}*}} }}{{\beta_{{{\text{E}}*}} }} = 12.0\,{\text{m}}\)).

A five-step procedure was followed to solve this problem using suggested equations:

  1. 1.

    Compute the length scale (λ) using Eq. 3.

  2. 2.

    Calculate dimensionless unit cost of additional earthwork (\(\beta_{{{\text{A}}*}}\)) using Eq. 5.

  3. 3.

    Calculate dimensionless unit cost of lining (\(\beta_{{{\text{L}}*}}\)) using Eq. 6.

  4. 4.

    Verify that \(\frac{{\beta_{{{\text{A}}*}} }}{{\beta_{{{\text{L}}*}} }}\) falls between 0 and 2.

  5. 5.

    Calculate optimum circular variables using equations proposed in Eqs. 17 and 18.

Results of applying different models are compared against numerical computation results as the benchmark solution for both constant and variable roughness approaches (Table 2). Comparing constant to variable roughness results (parts A and B) of the table, one notices that totally different results are obtained for the two approaches (up to 22% difference). It reiterates the importance of considering roughness variation in an optimum design of lined circular channels. On the other hand, when variable roughness approach is undertaken, it is shown that results of the proposed relations are in a very good agreement with the corresponding benchmark solution, with a maximum difference of 0.03%. In order to evaluate the proposed equations by the MHBMO–GRG algorithm (Eqs. 17 and 18), the problem is also solved using relations achieved by GA (Eqs. 19 and 20). The obtained results using these equations shown in Table 2 demonstrate the superiority of the hybrid MHBMO–GRG algorithm. It may be concluded that the proposed equations using MHBMO–GRG algorithm are capable of appropriately designing an optimum circular channel. Further investigations are required to implement such roughness variations in optimum design of other channel sections. Finally, it may be concluded that the proposed equations would be utilized for optimum design of lined circular channels in practice.

Table 2 The optimum results achieved by different models for the circular design problem
Full size table

5 Conclusions

According to the shortage of water in some parts of the world and the relatively high amount of required budget for constructing channels, the optimum design of channels becomes one of the active areas of investigations in water resources engineering. In this paper, the optimum design of lined circular channels incorporating a variable roughness is presented. According to the conducted literature review, in almost all of the studies on the optimum design of circular sections, variation of Manning’s coefficient with water depth angle was not taken into account. Hence, this variation, which was previously approved based on experimental studies on the circular channels, was implemented in the optimal design of lined circular channels. Moreover, a new hybrid optimization algorithm, the so-called the MHBMO–GRG algorithm, was utilized to solve the defined optimization design problem. The considerable discrepancy between the optimum results obtained in constant and variable roughness approaches obviously shows the necessity of considering the variation in the design procedure of circular channels. Based on the results of the variable roughness approach, a database for various values of dimensionless unit costs was prepared. New explicit equations for optimum design of lined circular channels were proposed using this data base. The proposed equations perform with acceptable accuracy based on the prepared database. Furthermore, the performance of the recommended design equations was investigated in solving a typical problem in the literature. The results demonstrate the accuracy and applicability of the new explicit equations comparing with the ones available in the literature. It can be concluded that not only is considering variation of Manning’s roughness in optimum design of circular channels necessary, but also the proposed explicit design equations in this study can be used by water resources engineers and researchers for optimum design of lined circular channels.