Directional Multiscale Analysis and Optimization for Surface Textures

Abstract

Surface texturing has a potential to become a cost effective and easy way to improve the tribological performance of lubricated interfacing surfaces. Effects of surface textures on the performance of machine elements as frictional pairs have been investigated over the past two decades. However, despite this research only a limited number of analytical solutions have been proposed as the majority of studies have been experimental and results obtained have not been optimal. This is because the commonly used surface characterization methods are not able to quantify surface textures over a range of scales at different directions and the optimization methods used work only for relatively simple textures and specific constraints imposed on pressure, film thickness, sliding velocity and lubricant rheology. Previous studies have addressed these issues, to some degree, by developing directional fractal signature methods and unified computational approach for texture optimization. In this article, recent advancements in the development of fractal methods and optimization of surface textures are presented.

1 Introduction

Surface textures are used as a means of reducing friction, increasing load capacity and reducing wear, obtaining good electrical contact, formability, paintability, specific optical properties, and others [1, 2]. The beneficial effects of surface textures have been long known. However, characterization and optimization of surface textures that are essential to achieve the improvements still remain unresolved problems. This is because surface textures have complex spatial arrangements of topographical features ranging from hundreds of micrometers to sub-nanometers. They can be grouped as follows:

• structured: geometric shapes/objects (e.g., dimple, groove, chevron, pillar, finger, pyramids) are located on the surface according to rules which are explicitly defined to obtain particular patterns [1, 3],

• self-structured: features are arranged on the surface through multiple interactions among components (molecules) according to certain self-organization rules which are not explicitly tied to any particular pattern [4, 5],

• stochastic: spatial relationships of features is governed mainly by probability laws (e.g., Gaussian distribution of heights) [6, 7],

• irregular: distribution of features is erratic. In other words, it does not follow any known pattern, there are no periodic sequences of “valleys’ and “peaks” and texture has cloud-like appearance (e.g., after peening or shot blasting) [6, 7].

1.1 Characterization

Because of the variety and multiscale nature of texture patterns, there is no a uniform standard, universal, or optimal method for the numerical characterization of geometry of surface textures. Each method was developed for a particular purpose and has its own advantages and disadvantages [2]. Existing methods for characterization of texture images can be generally grouped as non-fractal and fractal. Non-fractal methods characterize local changes in texture and spatial interrelationships between them using statistical and/or structural properties of the surface image. They are roughness parameters such as average roughness, S _a, peak-to-peak height, S _max, average roughness asperity spacing, S _m (to name a few), that are routinely used in surface quality control. Studies showed that these methods can accurately characterize many surface textures [6, 8]. However, when surface textures do not have periodic/quasi-periodic structure, for example, exhibit “strange” shapes such as lotus-leaf like [9], flora-like crystal [10], fiber mat [11], self-organized nanolayers [4, 5] and mutually grafted nanolayers [12], or have roughness and directionality that vary with scales these methods do not work well. The reasons are scale-dependency, i.e., values of texture descriptors these methods produce depend on the measurement scale, and lack of measurement of texture anisotropy at different scales. Fractals are a promising alternative approach [7]. Fractal methods are scale-independent, i.e., they do not need periodicity in texture and quantify texture roughness and directionality at different scales. Recent developments are the calculation of fractal dimensions (FDs) in different directions and at individual scales and the construction and use of fractal models of an entire surface texture.

1.2 Optimization

Current approach to the optimization of surface textures in lubricated contacts with aims of minimizing friction or maximizing load capacity is, in most cases, by ‘trial and error’, i.e., changes are introduced and their effects are studied. The optimization problem has been solved to some extent using numerical optimization methods such as conjugate sequential, sequential quadratic programming (SQP) [13, 14], and genetic [15, 16] techniques for relatively simple surface textures and specific constraints imposed on pressure, film thickness, sliding velocity, and lubricant rheology. These studies have also showed that different methods handle the same constraints differently. This leads to difficulties when the texture shape optimization is subject to new, complex, and/or more realistic constraints. So far this problem has only been partially addressed by modifying the existing methods or developing a new one. Consequently, a proliferation of various ways of solving the optimization problem has been observed and there are great difficulties associated with the selection of an appropriate method. A much needed solution is the development of a general and systematic optimization approach that works within a wide range of constraints for arbitrary surface textures.

In this article, recent developments and methods used in fractal analyses and optimization of surface textures are represented. Directional fractal signatures (DFS) and unified optimization approach are focal points.

2 Characterization of Surface Textures by Fractal Methods

The use of fractal methods in the numerical characterization is justified by the fact that topographical features of surface textures exhibit to, some extent, similarities at different length scales (self-similarity, multi-scale nature). When the methods are applied into the surface image (for example, a range image containing three-dimensional (3D) information about surface topography), a single value of FD for the entire texture is calculated. However, the single FD provides limited information, i.e., the anisotropic nature of texture (changes in statistical characteristic with direction) is not quantified. Therefore, DFS methods were developed to rectify the problem by calculating FD at individual scales and directions. Also, a partition iterated function system (PIFS) was developed to encapsulate the entire texture image data in a fractal model of the surface. These two approaches will be discussed.

2.1 Surface Data Presentation

Surface texture data is represented by a digital image of N _x  × N _y pixels, where N _x and N _y are the number of pixels in the horizontal and vertical directions, respectively. Assuming that $L_{x} = \{ 1,2, \ldots ,N_{x} \}$ and $L_{x} = \{ 1,2, \ldots ,N_{x} \}$ are spatial domains X and Y, respectively, and $L_{z} = \{ 1,2, \ldots ,N_{z} \}$ is the gray-scale level domain Z, the image is an elevation function $z = I(x,y)$ defined on a horizontal plane $(x,y) \in L_{x} \times L_{y}$. $z \in L_{z}$ is the gray-scale value, x and y are integer numbers representing coordinates of pixels in X and Y spatial domains, respectively, and N _z is the number of gray-scale level values.

2.2 DFS Methods

DFS methods have unique ability to characterize accurately surface roughness and anisotropy in all possible directions at individual scales. This is achieved by calculating a fractal signature (FS) (i.e., a set of FDs at individual scales) in different directions. The methods are divided into two groups, i.e.,

• fractional Brownian motion (fBm) methods, and

• area measurement methods

on the basis of whether the surface texture image is fractal Brownian.

The texture image is Brownian fractal if its gray-scale values change with scale, i.e.,

$$ {\text{Var}}\left({\left|{\Updelta I_{d}}\right|} \right)\left\|d\right\|^{-2H} = {\text{Var}}\left({\left| {\Updelta I_{d = 1}} \right|}\right), $$

where ${\text{Var}}({|{\Updelta I_{d}}|})$ is the variance value of the change over distance d and H is a real number in (0,1), called the Hurst coefficient [17]. The fractalness is confirmed if two criteria are satisfied, i.e., (i) texture image data exhibit a normal distribution and (ii) data points of a log–log plot of variances against pixel distances can be fitted with a line. To check the normality of data distribution, first, quantile–quantile (Q–Q) plots of expected normal values against gray-scale level differences for all possible directions and pixel distances are constructed. If the plots are approximately linear it can be assumed that the image data exhibit a normal distribution. Variances of gray-scale level differences are then calculated, and plotted against pixel distances on a log–log scale for all possible directions. If for each plot data points fall onto a line this implies that the texture image is Brownian fractal. Non-Brownian and Brownian fractal texture images together with two examples of their Q–Q and log–log plots are shown in Figs. 1 and 2. Directions used were ranging from 0° to 180° in step of 5°. Thirteen distances used were from 4 to 16 pixels.

Fig. 1

a Atomic force microscope image of self-structured surface texture formed on a molecular azo glass film (taken from Wang et al. [4]). b, c Quantile–quantile plots obtained in the vertical and horizontal directions at scale 10 and 13 pixel distances. d, e Log–log plots of variances of gray-scale level values versus pixel distances. The surface texture is not Brownian fractal as data points of the plots (solid line) deviate from the lines (dashed line)

Fig. 2

a Scanning electron microscope image of abrasive wear particle surface texture (taken from Wolski et al. [18]). b, c Quantile–quantile plots obtained in the vertical and horizontal directions at scale 9 and 12 pixel distances, d, e Log–log plots of variances of gray-scale level values versus pixel distances. The surface texture is assumed to be Brownian fractal as data points of the plots fall closely onto a straight line

2.2.1 fBm Methods

fBm methods were developed, assuming that surface texture images are a close approximation of 2D fractal Brownian motion functions over a range of scales [17]. If the assumption is satisfied FD can be calculated as FD = 3 − H, where H is the Hurst coefficient obtained from a slope of log–log plots.

DFS methods that belong to the fBm group [19] are

• FS Hurst orientation transform (FSHOT), and

• variance orientation transform (VOT).

FSHOT Method The method calculates differences in gray-scale values of all pairs of pixels within a ring region. The inner and outer radii of the region are chosen by the user according to image sizes and scales of interest. Typical values for 256 × 256 pixel images are 4 and 16 pixels, respectively (Fig. 3a). As the region moves across the entire image, one pixel at a time, all the gray-scale differences, the corresponding directions and distances between paired pixels are stored. The direction α is defined as an angle between a line running through the pair of pixels and the image horizontal axis (Fig. 3a).

Fig. 3

Schematic illustration of FSHOT and VOT methods (adapted from Wolski et al. [18])

FSHOT method uses the greatest absolute difference between gray-scale values of all pairs of pixels in each direction. The absolute differences are plotted against between-pixel distances in log–log coordinates (Fig. 3b). The log–log data points are divided into overlapping five-data point subsets with a line fitted to each subset (Fig. 3c). For a given direction, there are subsets/lines in each log–log plot, and for each line the slope and the between-pixel distance corresponding to the central log–log data point are recorded. The between-pixel distance represents the individual subset scale, and the slope of the line being H. The FD is determined as FD = 3 − H.

The Hurst coefficients are plotted using polar coordinates as a function of direction at each scale (image size) and an ellipse is fitted to each plot (Fig. 3d). From the fitted ellipses, the following FSs and texture aspect ratio signature (StrS) are calculated

• ${\text{FS}}_{{{\text{S}}_{\text{ta}} }}$ is defined as the set of FDs calculated at individual surface texture image sizes in a direction along the roughest part of the texture (i.e., the direction with the highest value FD). This direction is the angle between a line parallel to the horizontal axis of the image and the minor axis of the fitted ellipse, with ${\text{FS}}_{{{\text{S}}_{\text{ta}} }}$ defined as 3 − S _ta, where S _ta is half the minor axis length of the ellipse.

• FS_H and FS_V are defined as the sets of FDs calculated at individual surface texture image sizes in the horizontal or vertical directions, respectively.

• StrS is defined as the set of ratios of the minor axes to the major axes of the fitted ellipses. This measures the degree of surface texture anisotropy at different texture image sizes. StrS values range from 0 to 1, with lower values representing higher surface texture anisotropy.

VOT Method In VOT method, variances of the difference between gray-scale values of all pairs of pixels in each direction are calculated instead of the absolute differences. The FD is calculated as FD = 3 − H, where H is equal to a half of the slope of line fitted to log–log plots.

The FSHOT and VOT methods have been applied to images of artificial images of fractal surfaces and also to trabecular bone textures obtained from healthy and osteoarthritic knee radiographs [19, 20]. The VOT method showed lesser sensitivity to measurement conditions such as image noise, blur, magnification and projection angle and higher accuracy in measuring surface roughness and anisotropy than those obtained for the other methods. Because of this, the VOT method was used in subsequent studies [18].

The VOT method has been applied to 3D real engineering surfaces, i.e., sandblasted and grounded surfaces. These surfaces cannot be reliably characterized by commonly used roughness parameters. This is because values of an average roughness parameter, R _a, 3D average roughness parameter (S _a) and fastest decay auto-correlation rate (S _al) obtained for the surfaces are approximately equal [18]. Using the VOT method, statistical significant differences in roughness were found between the surfaces at small and medium scales. It was also found that sandblasted surfaces have significantly lower anisotropy than grounded surfaces at all scales. The VOT method has also been applied to surface textures of adhesive wear particles. Three sets of the wear particles were generated using a pin-on-disk apparatus. The first set contained particles generated by wear occurring for “running in” (a period of high friction coefficient) conditions under low load. The next set had the particles, but generated at high load. The third set contained particles generated by wear occurring under “steady-state” conditions (a period of low friction coefficient), and under low load. Surface characterization methods used so far were not able to detect minute changes occurring in the particle textures. This includes highly capable methods such as a combination of Discrete Wavelet Transform and statistical co-occurrence, which had a classification error rate of 33 % [21]. The VOT method, however, was able to differentiate between surface textures of wear particles generated under different operating conditions. Differences were detected at small scales and it was found that changes in load had the greatest effect on particle textures [18].

2.2.2 Area Measurement Methods

These methods do not require that surface textures are Brownian fractals. The reason is that they are based on surface areas instead of the statistical properties of the image data such as variances and greatest distances. These methods use blankets (i.e., dilation and erosion of an image) with either rotating grid or shearing-image.

Blanket with Rotating-Grid (BRG) Method The method is a generalization of the FS analysis (FSA) method [22] into all possible directions [19]. For directions other than vertical and horizontal, first, a grid of N _g × N _g pixels is generated and superimposed on the image in such a way that they are concentric and their borders are parallel. The grid is then rotated by a given angle. The size N _g equals to ${\text{floor}}( {{{\hbox{min} \{ {N_{x} ,N_{y} }\}}/{\sqrt 2 }}})$. This size ensures that the whole grid remains within the image area during rotation. All image pixels covered by the grid constitute a new image of N _g × N _g pixels. The new image data are dilated and eroded using rod-shape structural elements (SE) of different lengths. The lengths of SEs are chosen by the user according to image sizes and scales of interest. For example, for 256 × 256 pixel images, SE lengths ranging from 6 to 14 pixels in step of 1 were chosen [23]. For each length, the volume enclosed between the dilated and the eroded images is calculated. Surface area is then obtained as a difference divided by two between the volumes calculated for two consecutive SE lengths. A log–log plots of surface areas are plotted against SE lengths. The plot data are divided into overlapping sets (five data points) shifted by one data point. A line is fitted to each set and the “Hurst coefficient” is calculated as a slope (B) of the line fitted minus one, i.e., H = 1 − B. The length of SE associated with the middle point of each set represents an individual scale. As a result, Hurst coefficients are obtained at different scales in the first direction. Next, the grid is rotated around its center by predefined angles. For each grid rotated the above procedure of the calculation of Hurst coefficients is repeated. For vertical and horizontal directions, the difference is that the image dilation and erosion are performed on the original image data using horizontal and vertical SEs, respectively. Finally, Hurst coefficients calculated at individual scales in different directions are obtained.

Augmented BRG (ABRG) Method The method is an augmented version of the BRG method in which sizes of the rotating grid, i.e., N _g × N _h are dynamically adjusted for each direction [23]. This adjustment is achieved using the following formulas:

$$ N_{\text{g}} = {\text{abs}}\left( {{\text{floor}}\left( {N_{x} \cos \left( \alpha \right) + N_{y} \sin \left( \alpha \right)} \right)} \right), $$

$$ N_{\text{h}} = {\text{abs}}\left( {{\text{floor}}\left( {N_{x} \sin \left( \alpha \right) + N_{y} \cos \left( \alpha \right)} \right)} \right), $$

where the angle α lies within the intervals 0° ≤ α < 90° and 180° ≤ α < 270°. For other directions, negative values of the angle (i.e., −α) are used. Pixels covered by the adjustable grid are dilated and eroded by the horizontal SE in all possible directions. Because of this, the whole texture image is used in calculations. The original BRG method misses data located at corners as the rotating grid is too small to cover the entire image.

Blanket with Shearing-Image (BSI) Method The method is same as the BRG method, except that the new image data are generated using an image shearing instead of the rotating grid [23]. A skewed version of the original image is obtained by shearing the image over calculated distance using a cubic interpolation algorithm. Previous study showed that dilation and erosion operations with horizontal SEs on skewed images as compared to those using interpolated SEs on the original image are a good compromise between accuracy and computational efficiency [24].

The area measurement methods have been evaluated for the accuracy in measuring surface roughness and directionality and the capacity for quantifying multi-patterned textures. This evaluation was performed using images of self-structured surfaces that are (i) isotropic with decreasing roughness (i.e., R _a = 0.025, 0.018, 0.011 μm; a cut-off value of 0.8 μm), (ii) anisotropic with 20° and 110° dominating directions, and (iii) multi-patterned with isotropic and anisotropic texture components. The surface images were produced by a specially developed motif texture generator (MTG). The generator uses a half-ellipsoid motif (i.e., a recurring surface element) that is described by

$$ m_{\text{h}} (x_{l} , y_{l} ) = r_{3} \sqrt {1 - \frac{{\left( {x_{\text{l}} \cos \alpha - y_{l} \sin \alpha } \right)^{2} }}{{r_{1}^{2} }}{ - }\frac{{\left( {x_{\text{l}} \sin \alpha + y_{\text{l}} \cos \alpha } \right)^{2} }}{{r_{2}^{2} }}} , $$

where m is the motif surface height, r ₁, r ₂, and r ₃ are the ellipsoid radii, x ₁ and y ₁ are local coordinates with their origin located at the center of the ellipsoid ($x_{1} , \, y_{1}$), and α is the orientation measured with respect to the image horizontal axis (Fig. 4).

Fig. 4

A half-ellipsoid motif used to generate self-structured surface textures (taken from Wolski et al. [23])

The motif is repeatedly placed over an empty image (i.e., image with zero gray-scale levels) according to pre-defined rules. For overlapping motifs, the maximum values of heights in the common image area are taken. Examples of isotropic, anisotropic, and multi-patterned surface images generated with the motif and their rose plots of slopes are shown in Fig. 5.

Fig. 5

Examples of computer images of self-structured surfaces. a Isotropic, b anisotropic with 20° and 110° dominating directions, c partially isotropic multi-pattern and AFM images of g circularly and h linearly polarized self-structured surfaces. Their corresponding rose plots of slopes at 8 pixel scale obtained using the BRG , ABRG , and BSI methods are shown in (d–f) and (i, j) (taken from Wolski et al. [23])

Results showed that the ABRG method is accurate and performs better than the two other methods. The fractal methods were also evaluated in the detection of differences in texture between AFM images of self-structured surfaces produced by circularly and linearly polarized laser beams. It was found that the BRG and ABRG methods were the most sensitive.

Future study will focus on the evaluation of effects of AFM acquisition conditions (i.e., image resolution, tip size, and noise) on values of Hurst coefficients.

2.3 Partitioned Iterated Function System (PIFS)

Another way of surface texture characterization is through the use of fractal model which encapsulates an entire image data [25, 26]. The fundamental basis of the model is the self-transformability of surface texture, meaning that one part of the texture image can be transformed into another part of the image reproducing itself almost exactly. This allows for an encapsulation of the image data into a set of mathematical transformations, i.e., into a fractal model. The set contains N contractive affine transformations, i.e., ${\text{PIFS}} = \bigcup\nolimits_{j = 1}^{N} {f_{j} ({\text{DOM}}_{j} )} .$ Each transformation converts a larger part of the surface texture image (called domain) DOM _j into a smaller part (called range) RAN_j located elsewhere on the same image, i.e., $f_{j} ({\text{DOM}}_{j} ) = {\text{RAN}}_{j} ,\;j = 1,2, \ldots ,N .$ An example of the transformation is shown in Fig. 6. The fractal model constructed is called a PIFS. If such a model is obtained for a surface texture image it will contain detailed information including dimple shape, dimple spacing, depth, size and orientation [26].

Fig. 6

Surface texture with marked self-transformable parts. A larger part of the image converts to a smaller part of the image using mathematical transformations containing information about location, scale, translation, rotation, contrast and brightness. A set of these transformations gives the fractal model (PIFS) of the texture image

When an arbitrary image is applied iteratively to the PIFS, a sequence of decoded images (called intermediate images or transition frames) converging to the attractor is obtained (Fig. 7).

Fig. 7

Example of surface texture and its images obtained after decoding the PIFS. At each iteration, an intermediate image or a transition frame is generated (taken from Stachowiak and Podsiadlo [26])

A focus of our recent work is on use of PIFS models as a surface characterization method for 3D analyses of textured surfaces in hydrodynamic bearings [27]. Decoded image obtained from PIFS model is not an exact copy of the original surface texture, resulting in loss of some texture details, i.e., the details that are not encapsulated in the transformations. Subsequently, when the surface texture encoded in PIFS model is used in the analyses of hydrodynamic bearings, errors occur in calculations of load capacity and friction force. To minimize the errors, the PIFS model needs to be optimized. In the recent study [27], optimal models were found through an exhaustive search for all possible combinations of parameters such as tolerance, recursive depth, scaling and offset. The models were evaluated using a hydrodynamic parallel pad bearing textured with four different configurations of 64 elliptical dimples (denoted by S1, S2, S3, and S4) having increasing complexity (Fig. 8). Surface texture S1 exhibits dimples aligned along the x-axis direction (Fig. 8a). All dimples on S1 are identical. S2 differs from S1 in that one half of the dimples is deeper than the second half (Fig. 8b). S3 is the same as S1, except that half of the dimples is aligned along the y-axis direction (Fig. 8c). S4 exhibits random dimples of different shapes, depths and orientations (Fig. 8d). For each surface texture, a range-image was encoded into the optimal PIFS model and then the model was decoded. This resulted in eight decoded range images of surface textures. Each surface was separately used in the parallel square slider bearing and pressure distributions were calculated. Differences in pressure distribution between the original image and the corresponding decoded image were calculated and they are shown as 256 gray-scale level images in Fig. 9. The black color represents the value of 0 (no difference) and the white color stands for the maximum absolute difference equals to 0.2. Pressure values ranged from 0 to 6.

Fig. 8

Range images of textured surfaces. a S1, b S2, c S3, and d S4 (adapted from Wolski et al. [27])

Fig. 9

Difference in pressure distributions between the original images and the image obtained after decoding PIFS. a S1, b S2, c S3 and d S4. Darker color represents smaller differences

Using the pressure generated in bearings, both load capacity and friction force were calculated and percentage differences between the original and the decoded images were recorded. Results showed that the optimal PIFS models produced the load and friction that were slightly different (i.e., <2 % and <0.04 %, respectively) from those calculated for the original surface images [27]. This indicates that PIFS is accurate and it would be useful for the characterization of textured surfaces. Further studies, however, are needed to confirm the performance of PIFS in bearings textured with other patterns and working under other lubrication regimes (e.g., elastohydrodynamic).

3 Optimization of Surface Textures

Geometry of surface textures in bearings and seals has been optimized with aims of lowering friction, minimizing wear and high load capacity. Finding the optimal textures is complex and highly nonlinear problem. Dynamic behaviors of bearings and seal-like structures are nonlinear and Reynolds or Navier–Stokes equations are required for the analysis. In addition, the effects of temperature, cavitation, turbulent flow, and lubricant properties need to be accounted for and geometry of surface textures can be of any possible shape. Because of these, there is no guarantee that the solution would be a global optimum.

In general, the optimization of surface textures can be stated as a constrained optimization problem, i.e., find the surface texture $h\left( {x,z} \right)$ that minimizes (or maximizes)

$$ g\left( h \right) $$

subject to the following constraints: the governing nonlinear partial differential equation (PDE), i.e., the Navier–Stokes equations ${\text{NSE}}\left( {{\mathbf{q}};h} \right) = 0$, boundary conditions that pressure vanishes at bearing edges and initial conditions of lubricant velocities, where

• g is the objective functional, e.g., objectives commonly used in the bearing design such as a coefficient of friction $\mu = {{\iint\limits_{\Upomega } {\tau {\text{d}}x{\text{d}}z}} \mathord{\left/ {\vphantom {{\iint\limits_{\Upomega } {\tau {\text{d}}x{\text{d}}z}} {\iint\limits_{\Upomega } {p{\text{d}}x{\text{d}}z}}}} \right. \kern-0pt} {\iint\limits_{\Upomega } {p{\text{d}}x{\text{d}}z}}}$, a friction force $F = \iint\limits_{\Upomega } {\tau {\text{d}}x{\text{d}}z}$ or a load $W = \iint\limits_{\Upomega } {p{\text{d}}x{\text{d}}z},$

• ${\mathbf{q}} = [u\;\;v\;\;w\;\;p]^{T}$ is the state vector that contains the lubricant velocity field and the pressure field, respectively,

• $x,\;z$ are the planar coordinates,

• $h\left( {x,z} \right)$ is the texture shape, also called the film thickness,

• τ is the shear stress field, and

• Ω is a planar region that represents the bearing surface.

The y direction is defined through the film thickness ($y = h\left( {x,z} \right)$).

Currently, common approaches are based on “trial and error” methods, intuition and observations from nature and they provide solutions using results obtained from experiments, design charts [3, 28], numerical simulations of system dynamics conducted for various sets of parameters and conditions [29–31] and heuristic optimization algorithms [15, 16]. Although these approaches can produce improved results there is no theoretical guarantee that these solutions are optimal or even feasible. Also, the approaches require long computational time as the governing equations are solved at each step of optimization.

Another approach is through the analytical solutions. Necessary and sufficient conditions for the optimality are calculated using the calculus of variation to find optimal surface textures. However, due to the fact that the dynamic equations are complex the approach produced optimal textures for only simple cases such as step bearings and specific constraints imposed on pressure, film thickness, sliding velocity and lubricant rheology [32, 33].

In light of the above difficulties computational mathematical approaches appear as the method of choice for texture optimization. Recent studies have been based on a SQP method. In the method, a quasi-Newton algorithm is employed to solve the first-order necessary conditions (a gradient of the Lagrangian function vanishes to zero). Optimal solution is found by solving a sequence of subproblems. Each subproblem is defined as the minimization of a quadratic approximation of the Lagrangian function subject to a linear approximation of the constraints. The SQP method was used to optimize the groove geometry of thrust air bearings for various objective functions such as bearing flying height, surface friction torque, dynamic stiffness, a product of the height and stiffness, and a ratio of the torque and stiffness [34]. The groove was described by a third degree of spline function and the film pressure was obtained from Reynolds equation. In other study, a 2D slider bearing the film thickness was represented by a polynomial [35]. Parameters (called design variables) of the polynomial were optimized with the aim of minimizing the coefficient of friction (at given minimum film thickness) subject to pressure, shape, load and center of pressure constraints. Dynamics of the bearing was governed by Reynolds equation coupled with a stress field. For SQP, the user is required to supply values of the objective function and constraints, as well as their gradients. In all previous studies, the gradients were not provided explicitly to the SQP solver, instead finite-difference estimates were used. However, a choice of the perturbation vector that gives accurate estimates is highly non-trivial [36]. And also, if several and more optimal parameters of surface textures need to be found, the optimization task becomes increasingly time-consuming and error-prone. One exception could be the study conducted by Ostayen [14], who calculated analytically the gradients. However, it was not shown/discussed whether the gradients were used in actual optimization.

In the above studies, different methods handle the boundary and initial constraints differently. This leads to difficulties when the surface texture optimization is subject to new, complex and/or more realistic constraints. So far this problem has only been partially addressed by modifying the existing methods or developing new ones. This approach results in a proliferation of various ways of solving the optimization problem and the great difficulties associated with the selection of an appropriate method. Therefore, a much needed solution is the development of a general and systematic optimization approach that works within a wide range of constraints for arbitrary surface textures.

A first step in this development is a unified computational approach based on optimal control [37]. The underlying idea is to reformulate the surface texture optimization problem as a combined optimal control and optimal parameter selection problem. For 1D cases, the combined problem is

Maximize (or minimize) an objective functional

$$ G_{0} (u,{\mathbf{z}}) = \varphi_{0} ({\mathbf{x}}(t_{f} ),{\mathbf{z}}) + \int\limits_{{t_{s} }}^{{t_{f} }} {g_{0} \left( {t,{\mathbf{x}}\left( t \right),u\left( t \right),{\mathbf{z}}} \right)} \,{\text{d}}t $$

with respect to the control function $u\left( t \right) \in R$ and the system parameters ${\mathbf{z}} = \left[ {z_{1} , \ldots ,z_{{n_{z} }} } \right]^{\text{T}} \in R^{{n_{z} }}$, subject to

• the system dynamics

  $$ {\dot{\mathbf{x}}}\left( t \right) = {\mathbf{f}}\left( {t,{\mathbf{x}}\left( t \right),u\left( t \right),{\mathbf{z}}} \right) $$

• the initial conditions

  $$ {\mathbf{x}}\left( {t_{s} } \right) = {\mathbf{x}}^{0} \left( {\mathbf{z}} \right), $$

• all-time control constraints

  $$ \alpha_{k} u\left( t \right) + \beta_{k} \ge 0,\quad k = 1,2, \ldots ,n_{gl} , $$

• the canonical form constraints

  $$ G_{k} (u,{\mathbf{z}}) = \varphi_{k} \left( {{\mathbf{x}}\left( {\tau_{k} } \right),{\mathbf{z}}} \right) + \int\limits_{{t_{s} }}^{{\tau_{k} }} {g_{k} \left( {t,{\mathbf{x}}\left( t \right),u\left( t \right),{\mathbf{z}}} \right)} \,{\text{d}}t \ge 0,\quad k = 1,2, \ldots ,n_{gc}, \ {\text{and}}$$

• the system parameter only constraints

  $$ G_{k} \left( {\mathbf{z}} \right) \ge 0,\quad k = 1,2, \ldots ,n_{gz} , $$

where $\left[ {t_{s} ,t_{f} } \right]$ is the time interval, ${\mathbf{x}}\left( t \right) = \left[ {x_{1} \left( t \right), \ldots ,x_{{n_{s} }} \left( t \right)} \right]^{\text{T}} \in R^{{n_{s} }}$ is the state function vector, ${\mathbf{f}} = \left[ {f_{1} ,f_{1} , \ldots ,f_{{n_{s} }} } \right]^{\text{T}}$ is a vector of functions, $\tau_{k} \in \left( {0,t_{f} } \right]$ is the characteristic time associated with the constraint G _k , α _k , and β_k are scalar parameters, g ₀, g _k , ϕ₀, and ϕ_k are scalar functions, n _z , n _s , n _gc , n _gl , and n _gz are number of system parameters, state variables, canonical constraints, all-time control constraints, and system parameter only constraints, respectively.

In the new unified approach proposed the correspondences between the shape optimization and the combined problem are employed by replacing

• spacial variable with time ($x = t$),

• film thickness with control signal ($h\left( x \right) = u\left( t \right)$),

• integration constants and film shape parameters with system parameters,

• load or friction with objective functional,

• Reynolds equation with system dynamics, and

• pressure boundary conditions with all-time control and canonical form constraints.

Let the control function be parametrized by a weighted sum of basis functions with parameters $\left\{ {\sigma_{j} ,j = 1,2, \ldots ,k} \right\}$

$$ u\left( t \right) = \sum\limits_{j = 1}^{k} {\sigma_{j} B_{j} } \left( t \right) $$

where $B_{j} \left( t \right) = \left\{ {\begin{array}{*{20}c} {1,\quad \quad t_{j - 1} \le t \le t_{j} } \\ {0,\quad \;\quad \,{\text{otherwise}}} \\ \end{array} } \right.$ is a piecewise constant function defined over a set of knots $\left\{ {t_{s} = t_{0} ,t_{1} , \ldots ,t_{k} = t_{f} } \right\}$. Once the control signal is parametrized (called control parametrization) the objective functional and all the constraint functionals become functions of the parameter vector $\Uptheta = \left[ {\sigma_{1} , \ldots ,\sigma_{k} ,z_{1} , \ldots ,z_{{n_{z} }} } \right]^{\text{T}} \in R^{{n_{p} }}$ and the combined problem becomes a nonlinear mathematical programming problem (NLMP), i.e.

$$ \mathop {\text{minimize}}\limits_{\Uptheta } \quad \tilde{G}_{0} \left( \Uptheta \right) $$

subject to the constraints

$$ \tilde{G}_{i} \left( \Uptheta \right) = 0,\quad i = 1,2, \ldots ,n_{e} $$

$$ \tilde{G}_{i} \left( \Uptheta \right) \ge 0,\quad i = n_{e} + 1, \ldots ,n_{gc} $$

$$ u_{j}^{L} < \sigma_{j} < u_{j}^{U} ,\quad j = 1, \ldots ,k $$

$$ z_{k}^{L} < z_{k} < z_{k}^{L} ,\quad k = 1, \ldots ,n_{z} , $$

where $u_{ij}^{L}$, $z_{k}^{L}$ and $u_{ij}^{U}$, $z_{k}^{L}$ are the lower and upper limits of the control signal and the system parameters, respectively. The NLMP can be efficiently solved using existing software packages.

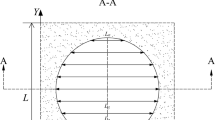
Our initial study showed that the above approach/method works for 1D cases for which the Reynolds equation can be transformed into a set of ordinary differential equations (ODEs) [37]. In this study, a partially textured infinitely long parallel bearing was optimized for the maximum load capacity. As an example, the optimal solution of a partially textured parallel bearing is shown in Fig. 10. The film thickness of the bearing is given by

$$ h\left( {x,\xi ,\varepsilon } \right) = \left\{ {\begin{array}{*{20}c} \xi & {l_{0} < x < l_{1} \quad {\text{and}}\quad \bmod \left( {x - l_{0} ,\varepsilon {D \mathord{\left/ {\vphantom {D {\left( {\left( {1 + \varepsilon } \right)m - 1} \right)}}} \right. \kern-0pt} {\left( {\left( {1 + \varepsilon } \right)m - 1} \right)}}} \right)} \\ {1.0} & {\text{otherwise}} \\ \end{array} } \right., $$

where $\xi = {h \mathord{\left/ {\vphantom {h {h_{m} }}} \right. \kern-0pt} {h_{m} }}$ is the dimple height ratio, $\varepsilon = {{l_{\text{D}} } \mathord{\left/ {\vphantom {{l_{\text{D}} } l}} \right. \kern-0pt} l}$ is the dimple length ratio, m is number of dimples and D is the length of textured portion.

Fig. 10

Example of the geometry of the partially textured parallel bearing optimized for the maximum load carrying capacity. The optimal ratios of $\varepsilon_{\text{opt}} = 1.52$ and $\xi_{\text{opt}} = 0.15$ were calculated for the bearing textured with two dimples $m = 2$ and the untextured portions $l_{0} = 0.5$ and $l_{1} = 0.125$. These results agree with data published in [32]

An extension of this approach into 2D cases governed by Reynolds equations will be a focus of future study. Also, further developments will focus on the optimization of bearings governed by Navier–Stokes equations for any geometry of texture shapes and any lubricant rheology. This would include the construction of efficient and accurate solvers of PDEs with exponential convergence capacity. Current solvers are relatively slow (algebraic convergence) and require a large memory for storing the fine grids that capture all necessary details of surface textures (except for h–p finite element method [38]). For the optimization calculations of analytical gradients of discretized objective functions and various effects including cavitation would need to be addressed [39, 40].

4 Conclusions

The following conclusions can be drawn from this study:

• 1. Surface texture image needs to be checked for Brownian fractalness before directional multiscale analysis:

  • If the surface texture is fractal Brownian then the VOT is the method of choice. It has higher accuracy and lesser sensitivity to measurement conditions than other methods.

  • For surface textures exhibiting the fractal Brownian motion (e.g., self-structured surfaces) the ABRG method is recommended. For self-structured surfaces the method has the high accuracy in measuring surface roughness and directionality and the capacity for quantifying multi-patterned textures.

• 2. A PIFS can model and describe the entire surface texture image. There are small differences between the friction and the load results (i.e., <2 % and <0.04 %, respectively) obtained from PIFS models and these calculated for the original surfaces.

• 3. A unified computational approach based on optimal control can be used to find the maximum load capacity or the minimum friction coefficient for all bearings governed by 1D Reynolds equations.

• 4. Future study would focus on the optimization of bearings governed by 2D Reynolds or Navier–Stokes equations, especially on development of a solver with exponential convergence capacity and calculations of analytical gradients of discretized objective functions.