Micro-texture design and optimization in hydrodynamic lubrication via two-scale analysis

Abstract

A novel computational surface engineering framework is developed to design micro-textures which can optimize the macroscopic response of hydrodynamically lubricated interfaces. All macroscopic objectives are formulated and analyzed within a homogenization-based two-scale setting and the micro-texture design is achieved through topology optimization schemes. Two non-standard aspects of this multiscale optimization problem, namely the temporal and spatial variations in the homogenized response of the micro-texture, are individually addressed. Extensive numerical investigations demonstrate the ability of the framework to deliver optimal micro-texture designs as well as the influence of major problem parameters.

1 Introduction

Computational frameworks for the design of microstructures has been of significant interest in all fields of engineering as a means for influencing and tuning the response of macrostructures. There are two major ingredients in such multiscale design problems. First, an ability to precisely and efficiently characterize the microstructural influence is required. Here, homogenization theory has emerged as a theoretically reliable and numerically robust tool (Sanchez-Palencia 1980; Torquato 2002). Second, the design goals must be formulated in the context of a nonlinear constrained optimization problem that is capable of probing a sufficiently flexible design space in order to achieve optimal designs. Here, topology optimization offers methodologies with which the microstructure description can be arbitrarily refined and the large number of design variables which emanate from such a description can be efficiently handled through dedicated algorithms (Bendsøe and Sigmund 2004; Christensen and Klarbring 2010). These powerful tools together offer a general framework for addressing a broad range of multiscale design problems and constitute the focus of this work.

For present purposes, multiscale design problems will be categorized into two classes, depending on the scale at which the optimization objective is focused. In micro-objective optimization (MicOO), emphasis is on the macroscopic constitutive response of the microstructure without a direct consideration of a macrostructural problem. An ability to construct a material, which is described by a unit-cell that is periodically repeated throughout the space, with a desired macroscopic stiffness tensor (Sigmund 1994; Neves et al. 2000; Chen et al. 2001) or one that displays a desired inelastic behavior (Zhang and Sun 2006; Huang et al. 2015) is an example to such design problems. Further examples involve the design of microstructures which macroscopically display non-conventional Poisson’s ratios or thermal expansion coefficients (Sigmund and Torquato 1996; Sigmund 2000; Chen et al. 2001) — see Bendsøe and Sigmund (2004) for an overview. An ability to address MicOO allows one to shift emphasis to macro-objective optimization (MacOO) where the microstructure design is driven directly by the response of the macrostructure, for instance to maximize its stiffness to deflection under prescribed boundary conditions (Fujii et al. 2001; Nakshatrala et al. 2013; Kato et al. 2014), possibly with a concurrent optimization of the macrostructural geometry (Rodrigues et al. 2002; Niu et al. 2009; Yan et al. 2014; Sivapuram et al. 2016), where the microstructure may additionally vary throughout the macrostructure (Zhou and Li 2008; Coelho et al. 2008; Xia and Breitkopf 2014, 2015). Contrary to design problems which focus only on a macrostructure and aim to optimize its geometry based on a prescribed material behavior, the macroscopic geometry can be fixed in MacOO and the only variable in optimization is then the pointwise constitutive response on the macroscale, which is determined by the microstructure and reflected onto the macroscale via two-scale analysis.

The foregoing examples were in the context of material design. As a particular class of interface problems, the macroscopic tribological response may also be tuned by optimizing the surface texture. Within tribology, the present study concentrates on hydrodynamic lubrication problems (Hamrock et al. 2004; Szeri 2011). Under suitable conditions on the geometrical features of the heterogeneous interface, the multiscale mechanics of hydrodynamic lubrication is governed by a thin-film formulation at all scales, which corresponds to the classical Reynolds formulation at the scale of the texture features. Based on the assumption of an incompressible Newtonian flow at the interface in the absence of unilateral constraints such as contact or cavitation, the thin-film formulation is free of all physical nonlinearities and constitutes a convenient starting point for the construction of a multiscale optimization framework. This formulation delivers information on both dissipative and non-dissipative behavior at the interface. The non-dissipative behavior is the pressure that is generated in the fluid, which is the solution of the thin-film equation, leading to a net load bearing capacity of the interface. The dissipative behavior is associated with the shearing of the interface fluid, leading to macroscopic friction. In the context of MacOO, therefore, classical macroscopic objectives typically attempt to maximize the load capacity and minimize frictional dissipation. In this context, the target of a limited number of relevant design studies was to determine optimal mesoscopic texture patterns with prescribed geometrical features such as circular or square holes and pillars (Buscaglia et al. 2006; Dobrica et al. 2010; Guzek et al. 2013; Scaraggi 2014). Due to the lack of a scale separation in such design studies, a reliable application of homogenization theory is not possible so that the interface problem is instead solved directly at the fine scale, which would lead to a high computational cost for fine patterns. Moreover, in view of predetermined geometrical features, the topological description of the surface is already well-defined so that optimization concentrates solely on the determination of the size and position distribution of these features. On the one hand, such a setup is realistic in view of various surface texturing techniques which operate within limitations with respect to scale resolution and geometrical flexibility (Costa and Hutchings 2015). On the other hand, advanced manufacturing techniques that have been developed over the recent years allow endowing materials and surfaces with complex microstructural features which are periodically repeated over large scales with high precision at small scales (Lee et al. 2012; Park et al. 2016). Consequently, it is of interest to extend MacOO design problems in hydrodynamic lubrication to a setting where homogenization theory is used to reflect the influence of intricate micro-texture patterns onto the macroscopic interface response and topology optimization is employed to optimize the pattern itself. The goal of this study is to realize this extension.

As in material design, the construction of a suitable MicOO framework is a first step towards the stated goal in order to characterize and evaluate the sensitivity of the micro-texture description to design variables. Although relevant MicOO studies have assigned the micro-texture some degree of flexibility in shape (Fesanghary and Khonsari 2011; Shen and Khonsari 2015; Zhang et al. 2017), a homogenization-based topology optimization framework has been realized only recently in Waseem et al. (2016). Based on the capabilities developed therein, the MacOO framework to be developed presently will address two key features of multiscale hydrodynamic lubrication problems that are non-standard, in the sense that two-scale material optimization problems typically do not display them. These are the temporal and spatial variations in the constitutive tensors which characterize the homogenized response of the micro-texture, the variations naturally arising due to the operating conditions of tribological interfaces in order to generate a load capacity. The prototypical problems which involve these variations are introduced in Section 2 where the two-scale formulation, micro-texture design variables, sensitivities of macroscopic objective functions and major numerical parameters of the multiscale problem are additionally discussed. Subsequently, Sections 3 and 4 individually address temporal and spatial variations, respectively, and demonstrate MacOO results as well as the optimality of the micro-texture designs. In order to rapidly explore the design space, an approximation of the homogenized response based on Taylor expansion is also demonstrated. The study is concluded with a discussion of possible extensions of the developed MacOO framework towards a comprehensive two-scale interface engineering framework.

Fig. 1

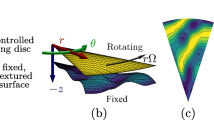
The prototypical squeeze-film and wedge problems of hydrodynamic lubrication are depicted, the former involving temporal variations in h ₀ and the latter involving spatial variations. By default, both macroscopic problems are subject to homogeneous Dirichlet boundary conditions on the pressure p ₀ over the whole interface boundary. The upper surface is smooth and moving while the lower one is micro-textured and stationary. For the squeeze-film problem the surfaces are parallel and for the wedge problem they may be inclined along both directions. The vertical dimension is exaggerated for a clear depiction of the interface geometry

2 Two-scale optimization framework

2.1 Macroscopic problems

In order to address micro-texture design in the context of MacOO and to develop a versatile numerical framework, two representative macroscopic problems that commonly occur in hydrodynamic lubrication, namely squeeze-film and wedge problems, will be analyzed (Fig. 1). In both of these problems, the mean film thickness h ₀ varies between a maximum value $h_{0}^{\max }$ and a minimum value $h_{0}^{\min }$. In the squeeze-film problem where the two surfaces are parallel, this variation is temporal, due to the purely vertical motion of the upper surface with a prescribed $\frac {\partial h_{0}}{\partial t}$. In the wedge problem, the upper surface moves again but only with a purely tangential velocity $\overline {\boldsymbol {U}}$ so that the variation of h ₀ is spatial, due to the inclination between the two surfaces. Hence, these two prototypical problems individually address the two types of variations in film thickness that are primarily responsible for the generation of pressure within the fluid at the interface and hence for its load bearing capacity. Micro-texture design in the context of macroscopic problems which involve combinations of these fundamental variations can easily be pursued based on the optimization framework to be demonstrated in this work.

In both problems, the moving upper surface is assumed to be microscopically smooth while the lower one is stationary and assigned a periodic texture across the whole macroscopic interface. It is noted, in particular for the wedge problem, that the optimization framework applies in a straightforward manner to cases where both surfaces are moving so long as only one surface –either upper or lower– is micro-textured (Waseem et al. 2016). The micro-texture height variation with zero mean is described by $\overline {h}$, the variation being periodic over a microscopic unit-cell $\mathcal {Y}$ and the same over all unit-cells at the interface. The latter assumption essentially assigns a single texture to the interface, as opposed to a case where different texture geometries may be assigned around different macroscopic points. The local film thickness over a unit-cell governs the microscopic response and may now be expressed as

$$ h(\boldsymbol{x},\boldsymbol{y},t) = h_{0}(\boldsymbol{x},t) - \overline{h}(\boldsymbol{y}) $$

(2.1)

where x indicates the macroscopic position across the interface, which is essentially two-dimensional, and y refers to a particular point within the microscopic unit-cell. Note that a varying microstructure across the interface would imply a position dependence of the form $\overline {h}(\boldsymbol {x},\boldsymbol {y})$. In (2.1), for the squeeze-film problem x-dependence is dropped and for the wedge problem t-dependence is dropped. It is assumed that the oscillations in h are sufficiently fast as the interface is traversed laterally such that a scale separation assumption may be invoked which allows applying classical homogenization analysis based on an asymptotic expansion in order to reflect the influence of the micro-texture onto the macroscopic response. For hydrodynamic lubrication, the microscopic physics of which can be described accurately by the Reynolds equation, this analysis was rigorously carried out by Bayada et al. (2006) in a general setting where both surfaces can be rough and moving. For brevity, only the final outcome of such an analysis will be stated here in a form that is suitable for the class of problems that are addressed presently. Specifically, if Q indicates the macroscopic fluid flux per unit area of the interface then one may write

$$ \boldsymbol{Q} = - \boldsymbol{A} \nabla p_{0} + \boldsymbol{C} \overline{\boldsymbol{U}} $$

(2.2)

where p ₀, the interface pressure that is generated in the fluid, is the solution of the macroscopic problem that is described by

$$ - \nabla \cdot \boldsymbol{Q} = \frac{\partial h_{0}}{\partial t} \quad\text{in}\quad {\Omega} $$

(2.3)

with Ω as the two-dimensional macroscopic interface. By default, this problem will be subject to homogeneous Dirichlet boundary conditions on ∂Ω in all examples such that the solution may be interpreted as being relative to the ambient pressure — exceptions will be noted. The macroscopic constitutive tensors {A,C} represent the homogenized response of the texture and inherit the dependence of h on x and t depending on whether the squeeze-film or the wedge problem is being considered. For either case, these tensors do not remain constant, which significantly increases the computational cost of MacOO. Specifically, a single A value applies to the whole squeeze-film problem interface, C being irrelevant since $\overline {\boldsymbol {U}} = \boldsymbol {0}$, but because h ₀ changes with time this tensor must be recomputed at each macroscopic temporal integration point through the solution of a microscopic cell problem. Throughout the wedge problem interface where h ₀ varies, the values of {A,C} are pointwise constant since $\frac {\partial h_{0}}{\partial t} = 0$ yet a separate set of two cell problems, one for each tensor, must be recomputed at each macroscopic spatial integration point during the evaluation of the weak form associated with the finite element formulation. To summarize these problems, let μ indicate the viscosity of the fluid, which is set to 0.14 Pa ⋅ s in all examples. Upon defining the coefficients

$$ a = \frac{h^{3}}{12\mu} \quad,\quad b = \frac{h}{2} $$

(2.4)

and introducing the gradients

$$ {\lambda_{i}^{j}} = \frac{\partial \omega_{j}}{\partial y_{i}} \quad,\quad {{\Lambda}_{i}^{j}} = \frac{\partial {\Omega}_{j}}{\partial y_{i}} $$

(2.5)

of two vectorial unknowns ω and Ω, the cell problems which need to be solved in the unit-cell $\mathcal {Y}$ subject to periodic boundary conditions are

$$ \frac{\partial }{\partial y_{i}} \left( a \delta_{ij} + a {\lambda_{i}^{j}} \right) = 0 \quad,\quad \frac{\partial }{\partial y_{i}} \left( b \delta_{ij} + a {{\Lambda}_{i}^{j}} \right) = 0 $$

(2.6)

where δ _{i j} are the components of the identity tensor I. Denoting the average of a quantity over the unit-cell by $\left \langle {\cdot } \right \rangle$, the constitutive tensors may then be computed via

$$ A_{ij} = \left\langle {a \delta_{ij} + a {\lambda_{i}^{j}}} \right\rangle \quad,\quad C_{ij} = \left\langle {b \delta_{ij} + a {{\Lambda}_{i}^{j}}} \right\rangle \quad. $$

(2.7)

Alternative forms that are equivalent to these expressions are

$$\begin{array}{@{}rcl@{}} A_{ij} &=& \left\langle {a (\delta_{ik} + {\lambda^{i}_{k}})(\delta_{jk} + {\lambda^{j}_{k}})} \right\rangle ,\\ C_{ij} &=& \left\langle {b (\delta_{ij} + {\lambda^{i}_{j}}) + a ({{\Lambda}_{i}^{j}} + {\lambda_{k}^{i}} {{\Lambda}_{k}^{j}})} \right\rangle \quad, \end{array} $$

(2.8)

which are advantageous in terms of establishing a clear link to the sensitivity analysis that will be required for micro-texture design in the next section. Clearly, A is a symmetric positive-definite tensor while C is non-symmetric in general. For a homogeneous interface ($\overline {h} = 0$), the macroscopic constitutive tensors have the explicit Reynolds form

$$ \boldsymbol{A}_{{\hom}} = \frac{{h_{0}^{3}}}{12 \mu} \boldsymbol{I} \quad,\quad \boldsymbol{C}_{{\hom}} = \frac{h_{0}}{2} \boldsymbol{I} \quad. $$

(2.9)

The solutions of the two problems from Fig. 1 in this homogeneous case are summarized in Fig. 2 for future reference.

Fig. 2

For the squeeze-film and wedge problems of Fig. 1 based on the parameters described in Section 2.1, solutions with a homogeneous interface ($\overline {h} = 0$) are provided as 2D and 3D plots. For the squeeze-film problem $\frac {\partial h_{0}}{\partial t} = -1~\mu \text {m/s}$ has been employed at the instance of h ₀ = 1 μ m while for the wedge problem $\overline {\boldsymbol {U}} = 1\,\text {m/s}$ with 𝜃 = 0 and $\{h_{0}^{\min },h_{0}^{\max }\} = \{0.2,1\}$ (in μ m) with β = 0. In all 2D plots, x ₁ is the rightward and x ₂ is the upward direction. One or both of the 2D and 3D views will be chosen in order to display aspects of the solution. $L_{{\hom }}$ indicates the load capacity as defined in (2.15) ₁. Pressure distributions will always be depicted with this color scheme

At this point, it is useful to reconsider the assumptions which govern the validity of the Reynolds equation on the microscale and their implications on the two-scale formulation summarized above. To begin with, it is assumed in all cases that the Reynolds equation accurately describes the physics of the homogeneous interface, which requires a vanishingly small film thickness h ₀ in comparison to a representative macroscopic dimension ℓ _M . Among other standard assumptions which lead from the three-dimensional Navier-Stokes equations to the Reynolds equation (Hamrock et al. 2004; Szeri 2011), pressure variations across the film thickness as well as nonlinear effects such as micro-inertia are omitted and a slowly varying film thickness is assumed. The last assumption is particularly volatile to the presence of a micro-texture and has been rigorously analyzed in Bayada and Chambat (1988). Assuming that the period λ of the micro-texture is sufficiently small with respect to ℓ _M for a two-scale formulation to make sense, they have shown that the major non-dimensional parameter which governs the validity of the Reynolds equation on the microscale is γ = h ₀/λ. Indeed, earlier studies (see Mitsuya and Fukui 1986 for an example) have shown that the physics of the interface is well-represented by the Reynolds equation as long as γ < 0.1 roughly holds, i.e. the period should be small but not too small. When violated, the quality of the predictions based on the Reynolds equation can deteriorate mildly or significantly, depending on the remaining geometrical parameters of the interface, such as the ratio of the micro-texture amplitude to h ₀. In order to assess the degree of deterioration, one must revert to the next accurate model in the hierarchy of two-scale models for this problem, which is achieved by only omitting micro-inertia in the three-dimensional Navier-Stokes equations and therefore solving Stokes equations on the microscale. In such a setting, the Reynolds-type formulation (2.3) still accurately describes the macroscopic physics but the cell problems (2.6) as well as the definitions for A and C must be reformulated based on Stokes equations — see Fabricius et al. (2017) and Yıldıran et al. (2017) for the numerical demonstration of the theory developed in Bayada and Chambat (1988). Therefore, in the context of this study, it is assumed that the micro-texture designs to be obtained are applied to a macroscopic interface so as to satisfy the requirement γ < 0.1. Note that, as long as this assumption is satisfied, sharp features in the micro-texture do not adversely influence the validity of the Reynolds equation on the microscale in the context of the two-scale formulation of Bayada and Chambat (1988).

2.2 Micro-texture design variables

The description of a micro-texture design over a unit-cell, the cell problems which deliver {A,C} over such a design based on the h-distribution as well as the computation of their sensitivities with respect to the design variables have been discussed extensively in Waseem et al. (2016). Presently, only relevant details will be briefly mentioned.

In view of the film thickness description (2.1), design of a single texture which is periodically repeated throughout the macroscopic interface may be realized by a common description of the texture height $\overline {h}$ for all the unit-cells associated with the macroscopic points. For this purpose, first a design variable s ∈ [0,1] is introduced over the unit-cell and discretized over its mesh. In particular, s might be assigned degrees of freedom s ^I over the nodes of this mesh or over each element. The former choice can lead to qualitatively better textures but the latter is computationally more efficient and hence will be adopted in this work. Subsequently, the discretization of s is filtered within a prescribed radius R around each degree of freedom in order to assign a length scale to the texture, leading to a morphology variable ρ ∈ [0,1] with element-wise constant degrees of freedom ρ ^I. Following standard topology optimization approaches (Bendsøe 1989; Rozvany et al. 1992), the texture height $\overline {h} \in [\overline {h}_{\min },\overline {h}_{\max }]$ is then described by

$$ \overline{h} = \overline{h}_{\min} + (\overline{h}_{\max} - \overline{h}_{\min}) \rho^{\eta} $$

(2.10)

subject to the restriction that its average over the unit-cell vanishes:

$$ \left\langle {\overline{h}} \right\rangle = 0 . $$

(2.11)

As particular choices to be employed, a value of η = 1 delivers smooth variations in ρ from 0 to 1 and hence a smooth micro-texture that will be referred to as a 0-to-1 design, while η = 3 delivers sharp variations in ρ between 0 and 1 and hence a surface with sharp variations in height that will be referred to as a 0-or-1 design. Morphology filters $\mathcal {F}$, delivering $\rho = \mathcal {F}(s)$, which are commensurate with these designs are the linear filter for 0-to-1 and the exponential erode filter for 0-or-1 (Svanberg and Svärd 2013). In both cases, the radius of the filter will be assigned in terms of the number of elements. A summary of these filters as well as the default value of the filter radius are provided in Appendix A. On any given s-distribution, therefore, one may first obtain $\rho = \mathcal {F}(s)$ and then construct $\overline {h}$ and hence $h = h_{0} - \overline {h}$ so that the cell problems can be solved and subsequently the macroscopic tensors {A,C} may be evaluated together with their sensitivities $\{\frac {\partial \boldsymbol {A}}{\partial s^{I}},\frac {\partial \boldsymbol {C}}{\partial s^{I}}\}$. Through a variational analysis of the cell problems (2.6), one may show that these sensitivities can also be calculated through cell averaging without the need for the solution of additional sensitivity problems, thereby contributing to two-scale computational efficiency. The resulting forms are closely related to (2.8):

$$\begin{array}{@{}rcl@{}} \frac{\partial A_{ij}}{\partial s^{I}} &=& \left\langle {\frac{\partial a}{\partial s^{I}} (\delta_{ik} + {\lambda^{i}_{k}})(\delta_{jk} + {\lambda^{j}_{k}})} \right\rangle \quad,\\ \frac{\partial C_{ij}}{\partial s^{I}} &=& \left\langle\frac{\partial b}{\partial s^{I}} (\delta_{ij} + {\lambda^{i}_{j}}) + \frac{\partial a}{\partial s^{I}} ({{\Lambda}_{i}^{j}} + {\lambda_{k}^{i}} {{\Lambda}_{k}^{j}})\right\rangle \quad. \end{array} $$

(2.12)

The local sensitivities $\frac {\partial a}{\partial s^{I}}$ and $\frac {\partial b}{\partial s^{I}}$ that are needed here may be obtained in a straightforward fashion based on (2.4) and (2.10), by implicitly making use of the particular filter formulation.

2.3 Numerical discretization

In order to comment on the computational cost of MacOO as the framework is developed, fundamental numerical discretization parameters are introduced next. In both macroscopic problems, the interface Ω is an ℓ _M × ℓ _M square domain with an edge length of ℓ _M = 200 μ m. The solution of the macroscopic problem on this interface will be realized by a N _M × N _M finite element mesh. Only bilinear quadrilateral elements will be employed, on which N _G × N _G Gauss-Legendre integration will be carried out with N _G = 2. Hence, in the case of the wedge problem, microscopic analysis must be carried out at (N _M N _G )² points. The total number of nodal degrees of freedom of this mesh will be indicated by its order of magnitude ${N_{M}^{2}}$ in upcoming discussions. Since the variation of p ₀ over the interface will be smooth in both macroscopic problems, a value of N _M = 20 was found to provide a sufficiently accurate solution while limiting the cost associated with two-scale analysis. For the solution of microscopic problems in order to compute {A,C}, the unit-cell is discretized by a N _m × N _m mesh with bilinear elements, using N _m = 40. The absolute edge length ℓ _m of the unit-cell $\mathcal {Y}$ does not influence the homogenized response and can be chosen arbitrarily. Note that this is due to the assumption that Reynolds equation is valid on the microscale. When the underlying assumptions do not hold, a first step in generalizing the present framework would be to employ three-dimensional Stokes equations on the microscale — see Section 2.1. In such a setting, ℓ _m can significantly influence the macroscopic solution and therefore must be chosen carefully.

The velocities $\frac {\partial h_{0}}{\partial t}$ and $\overline {\boldsymbol {U}}$ for the two problem settings will be specified later. Here, it is only noted that a periodic reciprocating motion will be assigned to the upper surface in the squeeze-film problem such that it is necessary to carry out computations over only half a cycle, which will be resolved with N _T = 10 time steps. When necessary, time integration will be carried out with an explicit Euler scheme so that any time-dependent quantity must also be evaluated N _T times.

2.4 Sensitivity analysis

All macroscopic objectives in this work will be formulated in terms of the solution p ₀ to the macroscopic problem (2.3) and hence require the evaluation of the sensitivity $\frac {\partial p_{0}}{\partial s^{I}}$ for the ${N_{M}^{2}}$ degrees of freedom s ^I associated with the micro-texture description. For this purpose, upon solving (2.3) to obtain p ₀ with a given s-distribution, one may differentiate it with respect to s ^I to obtain the relevant sensitivity problem

$$ - \nabla \cdot \left( - \frac{\partial \boldsymbol{A}}{\partial s^{I}} \nabla p_{0} - \boldsymbol{A} \nabla \pi_{I} + \frac{\partial \boldsymbol{C}}{\partial s^{I}} \overline{\boldsymbol{U}} \right) = 0 $$

(2.13)

where, in view of (2.12), the only unknown is

$$ \pi_{I} = \frac{\partial p_{0}}{\partial s^{I}} \quad, $$

(2.14)

subject to homogeneous Dirichlet or Neumann boundary conditions on portions of ∂Ω, according to the corresponding boundary conditions for (2.3).

Once π _I are determined, the sensitivity of a macroscopic objective which is formulated in terms of p ₀ may readily be evaluated. The cost associated with this type of a sensitivity computation may be slightly reduced through the adjoint method (Bendsøe and Sigmund 2004), which is briefly commented upon in the context of the wedge problem where there is no time-dependence. A particular macroscopic quantity of interest is the load bearing capacity L ₀ of the interface:

$$ L_{0} = {\int}_{\Omega} p_{0}\ \ \mathrm{d}{\Omega} \quad\longrightarrow\quad \frac{\partial L_{0}}{\partial s^{I}} = {\int}_{\Omega} \pi_{I} \ \ \mathrm{d}{\Omega} \quad. $$

(2.15)

Let the finite element formulation of (2.3) be indicated by

$$ \boldsymbol{K} \boldsymbol{p}_{0} = \boldsymbol{f} $$

(2.16)

where the array p ₀ incorporates all the degrees of freedom of p ₀, K is the matrix associated with the A∇p ₀ term and all known quantities associated with the $\boldsymbol {C} \overline {\boldsymbol {U}}$ term contribute to the array f. Simultaneously, one may write L ₀ = w ⋅p ₀ where w is the array associated with the numerical integration of the finite element discretization of p ₀. Indicating the array of degrees of freedom for π _I with π _I , the discrete form of (2.13) may be symbolically denoted by

$$ \frac{\partial \boldsymbol{K}}{\partial s^{I}}\boldsymbol{p}_{0} + \boldsymbol{K} \boldsymbol{\pi}_{I} = \frac{\partial \boldsymbol{f}}{\partial s^{I}} $$

(2.17)

so that (2.15) ₂ may be expressed as

$$ \frac{\partial L_{0}}{\partial s^{I}} = \boldsymbol{w} \cdot \boldsymbol{\pi}_{I} = \boldsymbol{w} \cdot \boldsymbol{K}^{\text{--}1} \left( \frac{\partial \boldsymbol{f}}{\partial s^{I}} - \frac{\partial \boldsymbol{K}}{\partial s^{I}}\boldsymbol{p}_{0}\right) \quad. $$

(2.18)

Now, taking one step further by making use of the symmetry of K and defining λ as the solution of the adjoint problem

$$ \boldsymbol{K} \boldsymbol{\lambda} = \boldsymbol{w} \quad, $$

(2.19)

one obtains the alternative macroscopic sensitivity expression

$$ \frac{\partial L_{0}}{\partial s^{I}} = \boldsymbol{\lambda} \cdot \left( \frac{\partial \boldsymbol{f}}{\partial s^{I}} - \frac{\partial \boldsymbol{K}}{\partial s^{I}}\boldsymbol{p}_{0} \right) \quad. $$

(2.20)

Here, a cost reduction immediately arises from the fact that only a single linear system must be solved, namely for the adjoint variable λ. On the other hand, the direction evaluation of (2.15) ₂, in other words (2.18), requires the explicit solution of (2.13) ${N_{M}^{2}}$ times. Despite the seemingly large difference, the computational savings offered by this adjoint sensitivity approach are marginal due to the two-scale setting of the present optimization problem. For instance, in the context of the wedge problem, each of the (N _M N _G )² microscopic cell problems is individually processed on an N _m × N _m micro-texture mesh to assemble $\frac {\partial \boldsymbol {K}}{\partial s^{I}}$ and $\frac {\partial \boldsymbol {f}}{\partial s^{I}}$. Independent of whether the direct or the adjoint sensitivity approach is employed, this process must be repeated ${N_{M}^{2}}$ times for the determination of all π _I which, therefore, dominates the overall computational cost. Presently, the direct solution of (2.13) for π _I will be preferred since this will allow evaluating the sensitivities of arbitrary macroscopic objectives in a straightforward manner without the need for the construction of objective-specific adjoint problems. Further details on the sensitivity analysis and its verification are provided in Appendix B.

2.5 Optimization problems

The four classes of optimization problems of interest are depicted in Fig. 3. In all cases, the objective φ is a function of the distribution of the design variable s over the unit-cell and the aim is to minimize the objective, while ensuring that the constraint $\chi (s) = \left \langle {\overline {h}(s)} \right \rangle = 0$ is satisfied. Hence, the standard problem statement is:

$$ \textit{minimize }\varphi(s), \textit{subject to }\chi(s) = 0\textit{ and }s\in [0,1] . $$

(2.21)

The value of the objective function φ and its sensitivities $\frac {\partial \varphi }{\partial s^{I}}$ are employed within the MMA (method of moving asymptotes (Svanberg 1987)) algorithm to iteratively update an initial s-distribution. In all examples, the iterations are continued until the objective remains virtually constant. This is achieved in less than 1000 iterations in most examples.

Fig. 3

The optimization problems considered are depicted together with the relevant objectives. MicOO path ①→④ goes directly from ① to ④. MacOO path ①$\curvearrowright$④ goes from ① to ④ indirectly, through ② and ③

Among the four optimization problem paths in Fig. 3, ①→④ describes MicOO, as extensively investigated in Waseem et al. (2016). Here, the aim is to generate a micro-texture which delivers a desired combination of target {A ^∗,C ^∗} values as closely as possible. A suitable objective is

$$ \varphi(s) = \frac{1}{2} \left( \frac{\left\| \boldsymbol{A}(s) - \boldsymbol{A}^{\ast} \right\|}{\left\| \boldsymbol{A}^{\ast} \right\|} + \frac{\left\| \boldsymbol{C}(s) - \boldsymbol{C}^{\ast} \right\|}{\left\| \boldsymbol{C}^{\ast} \right\|} \right) $$

(2.22)

If the target values are determined based on the homogenization of a known micro-texture, i.e. the target values are physically realizable, then MicOO is essentially equivalent to microstructure reconstruction. If the values are assigned independently from a micro-texture, for example to get as close as possible to a significantly non-symmetric C ^∗, then MicOO represents a tool for designing surfaces with non-conventional macroscopic properties.

The remaining three problems in Fig. 3 describe different MacOO settings, which are the subject of the present study. These are constructed in the order of increasing complexity, primarily with respect to computational cost. Each problem uniquely addresses a particular aspect of the framework and hence will be discussed in a separate section together with relevant numerical investigations. The numerical cost associated with each problem per optimization iteration step is summarized in Table 1.

Table 1 The computational cost of MACOO problems of Fig. 3 is summarized using the notation of Section 2.3

3 Squeeze-film problem

3.1 Optimization path ①$\curvearrowright$④

This first MacOO problem (Fig. 3, path ①$\curvearrowright$④) is based on the squeeze-film setup (Fig. 1) at a given time instant where h ₀ = 1 μ m with $\frac {\partial h_{0}}{\partial t} = -1\,\mu \text {m}/s$. For micro-texture description, $\{\overline {h}_{\min },\overline {h}_{\max }\} = \{-0.5,0.5\}$ (μ m) will be employed. The solution of this setup with a homogeneous interface was provided in Fig. 2a where the maximum homogeneous pressure is $p_{{\hom }}^{\max } = 6,804\,\text {Pa}$. The aim will now be to design a micro-texture which can deliver a desired macroscopic pressure distribution $p_{0}^{\ast }(\boldsymbol {x})$ in Ω. The ability to match complex pressure distributions requires assigning a varying microstructure $\overline {h}(\boldsymbol {x},\boldsymbol {y})$ across the interface which, however, is outside the scope of the present study. Instead, in order to generate a physically realizable input, a target 0-or-1 micro-texture is first assigned to the interface as shown in Fig. 4a-1 and subsequently the corresponding macroscopic pressure distribution $p_{0}^{\ast }(\boldsymbol {x})$ is calculated (Fig. 4a-2). The significant difference between $p_{0}^{\ast ,\max }$ and $p_{{\hom }}^{\max }$ is an indication of the considerable influence that micro-texturing can have on the load capacity of the interface. Subsequently, the objective function

$$ \varphi(s) = \frac{{\int}_{\Omega} (p_{0}(s) - p_{0}^{\ast}){~}^{2} \ \ \mathrm{d}{\Omega}}{{\int}_{\Omega} p_{0}^{\ast}{~}^{2} \ \ \mathrm{d}{\Omega}} $$

(3.1)

is driven to zero in order to obtain a micro-texture design which delivers the same pressure distribution as the target micro-texture. This MacOO problem setting will also allow for a visual assessment of MacOO performance in a two-scale analysis setting in terms of its capability of reconstructing a given micro-texture.

Fig. 4

For optimization path ①$\curvearrowright$④ of Section 3.1, the input pressure distribution $p_{0}^{\ast }$ delivered by the target 0-or-1 micro-texture is shown together with the micro-texture design and the corresponding output pressure distribution p ₀. Note that the (weak) anisotropy of the micro-texture delivers a macroscopic pressure distribution that is qualitatively different from the homogeneous one (cf. Fig. 2a). 0-or-1 micro-texture designs will always be depicted with this color scheme. Here and in all subsequent three-dimensional depictions of a micro-texture, the numbers on the vertical axis indicate $\{\overline {h}_{\min },\overline {h}_{\max }\}$. Additionally, although optimization employs a single unit-cell, a 3 × 3 tiling of the unit-cell is preferred in the graphical depiction of the optimization results for a more clear visual representation of the micro-texture geometry

The output micro-texture design and its macroscopic pressure distribution are shown in Fig. 4a-1 and a-2, respectively. Note that the maximum pressure $p_{0}^{\max }$ is very close to $p_{0}^{\ast ,\max }$ and the micro-texture design has feature size and directionality that closely resembles the target micro-texture. Nevertheless, a perfect match between the two is not attained due to well-known non-uniqueness in microstructure design. This non-uniqueness can be observed more clearly in a 0-to-1 setting, as summarized in Fig. 5. 0-to-1 micro-texturing provides a larger degree of freedom for the surface topology, which is seen to reflect more strongly in the difference between the target and the design micro-textures although $p_{0}^{\ast ,\max }$ and $p_{0}^{\max }$ match perfectly. The influence of 0-to-1 micro-textures, e.g. the difference between $p_{{\hom }}^{\max }$ and $p_{0}^{\max }$, is less than for 0-or-1 due to smoother variations in the surface topology. Consequently, one may anticipate that if the objective is to maximize the load capacity of the interface then the optimal choice is 0-or-1 for a given set of design limitations, presently described by $\{\overline {h}_{\min },\overline {h}_{\max }\}$ together with the constraint $\left \langle {\overline {h}} \right \rangle = 0$. This aspect will be investigated further next.

Fig. 5

For optimization path ①$\curvearrowright$④ of Section 3.1, the input pressure distribution $p_{0}^{\ast }$ delivered by the target 0-to-1 micro-texture is shown together with the micro-texture design and the corresponding output pressure distribution p ₀. 0-to-1 micro-texture designs will always be depicted with this color scheme

3.2 Optimization path ②$\curvearrowright$④

Another way of addressing the difficulty in generating realizable target pressure distributions $p_{0}^{\ast }$ for optimization purposes is to represent a target distribution indirectly. In this MacOO problem (Fig. 3, path ②$\curvearrowright$④), the same time instant as in Section 3.1 is considered. However, instead of matching a local quantity of interest such as the pressure, the goal will be to match a global quantity of interest, namely the corresponding load bearing capacity (2.15) ₁. The target load capacity $L_{0}^{\ast }$ will be prescribed as a factor f _l of the load capacity of the homogeneous interface ($L_{{\hom }} = 94\,\mu \text {N}$)

$$ L_{0}^{\ast} = f_{l} \, L_{{\hom}} $$

(3.2)

and the relevant objective function to be driven to zero is

$$ \varphi(s) = \frac{(L_{0}(s) - L_{0}^{\ast{}})^{2}}{{L_{0}^{\ast}}^{2}} \quad. $$

(3.3)

Results for this optimization problem are summarized in Fig. 6, again employing $\{\overline {h}_{\min },\overline {h}_{\max }\} = \{-0.5,0.5\}$ (μ m). Despite the fact that the 0-or-1 type design is constructed to deliver sharp transitions between maximum and minimum limits of $\overline {h}$, one observes smooth features at low values of f _l = 1.1. This is due to the fact that the constraint $\left \langle {\overline {h}} \right \rangle = 0$ must additionally be satisfied such that sharp features necessarily lead to larger values of f _l . Indeed, as f _l is increased to twice the load capacity of the homogeneous interface, the transitions sharpen. Simultaneously, while the 0-to-1 type design is constructed to deliver smooth textures, large load capacities can only be attained with sharp transitions, as anticipated in the previous section. Consequently, the surface topologies for both types of micro-texture design demonstrate similar features with increasing f _l where the isolated wells deepen and their walls thicken. These variations in the micro-textures are further visualized in Fig. 7 where the sample profiles along the lines depicted in Fig. 6 are compared for each design type.

Fig. 6

For optimization path ②$\curvearrowright$④ of Section 3.2, 0-or-1 (top row) and 0-to-1 (bottom row) micro-texture designs for different load factors f _l are shown. The sample texture profiles along the black lines are compared in Fig. 7

Fig. 7

The sample profiles of the textures from Fig. 6 are compared

The ability to determine a micro-texture which can deliver a prescribed load capacity is a practical engineering design problem. On the other hand, in various problems it is simply desirable to maximize the load capacity. Moreover, the macroscopic problem parameters are often time-dependent. These two aspects are addressed together next.

3.3 Optimization path ③$\curvearrowright$④ with temporal variations

In order to address load capacity maximization with temporal variations in the macroscopic problem parameters (Fig. 3, path ③$\curvearrowright$④), two types of reciprocating motion will be assigned to the motion $\frac {\partial h_{0}}{\partial t}$ of the top surface:

• 1. square-wave velocity profile with a constant speed of $\left | \frac {\partial h_{0}}{\partial t} \right | = 1\,\mu \text {m/s}$ and an instantaneous direction switch at $h_{0}^{\min }$ and $h_{0}^{\max }$,

• 2. sinusoidal velocity profile with $\frac {\partial h_{0}}{\partial t} = -sin(2\pi t / T)$ and a period of T = 1.5 s.

In both cases, the motion starts at $h_{0}^{\max }$ and is between $\{h_{0}^{\min },h_{0}^{\max }\} = \{1,2.5\}$ (in μ m). For comparison purposes, $\{\overline {h}_{\min },\overline {h}_{\max }\} = \{-0.5,0.5\}$ (μ m) is employed as in earlier sections. As noted earlier in Section 2.3, computations are carried out only over a half-cycle (compression).

Time-dependence is addressed by maximizing the load capacity over the cycle in an integral manner

$$ \varphi(s) = - \frac{{\int}_{T} {\int}_{\Omega} p_{0}(s)^{2} \ \ \mathrm{d}{\Omega} \ \ \mathrm{d}{t}}{{\int}_{T} {\int}_{\Omega} p^{2}_{\text{ref}} \ \ \mathrm{d}{\Omega} \ \ \mathrm{d}{t}} $$

(3.4)

where the square of the pressure is employed since the solution is relative to the ambient pressure, and hence negative over a half-cycle (suction), while the negative sign is employed to turn the optimization problem into a minimization statement in order to apply MMA. Scaling is often beneficial to faster convergence and for this purpose $p_{\text {ref}} = p_{{\hom }}$ is employed. Note that the constraint $\chi (s) = \left \langle {\overline {h}} \right \rangle = 0$ is common not only to all Ω but also to the whole time cycle. Consequently, both φ and χ are functions of the time-independent design variable distribution alone. Hence, based on the explicit Euler scheme for integration in time (Section 2.3), the optimization algorithm consists of the solution of a macroscopic problem together with a sensitivity analysis at N _T time steps for a given s-distribution, i.e. at each macroscopic optimization iteration. Consequently, the cost of this MacOO problem directly scales with N _T in comparison to the previous two MacOO problems (Table 1).

Results of optimization are summarized in Fig. 8. It is interesting to observe that, despite the significantly different velocity profiles, the micro-texture designs are almost identical, indicating that the optimal micro-texture is probably not very sensitive to macroscopic loading conditions for this problem. This is supported by the cross-check results in Fig. 9 where the micro-texture obtained with one velocity profile setting delivers almost identical curves in the other setting. As discussed in the previous section, even the 0-to-1 design setting delivers significantly sharp features that are essential for load maximization. With these micro-textures, the variation of the load over the half-cycle is computed via two-scale analysis. The variations in Fig. 9 show the significantly higher load capacity of micro-textured interfaces. It should be remarked that although 0-to-1 designs have sharp features, the use of a linear filter (Section 2.2) limits the degree of sharpness such that the corresponding load capacity at any instance is less than that corresponding to a 0-or-1 design. Finally, the optimality of these designs with respect to the micro-textures of Fig. 6 may be assessed, by calculating their load factors for the setup of Section 3.2. These load factors are also provided in Fig. 8 for each micro-texture design, which therefore indicate the physically realizable limits to the target values $L_{0}^{\ast }$ that could be used within the optimization problem of Section 3.2.

Fig. 8

For the time-dependent MacOO problem of Section 3.3, 0-or-1 and 0-to-1 micro-texture designs are shown for a square-wave and b sinusoidal velocity profiles. The load factors f _l are calculated by evaluating these micro-textures in the setting of Section 3.2

Fig. 9

Variation of the load bearing capacity of over the whole squeeze-film cycle based on the micro-texture designs of Fig. 8 for the two velocity profiles. 100 time steps were employed in generating the curves for a better resolution of the load variations. Note that the maximum load for the sinusoidal profile occurs before T/2 because the speed decreases together with the gap, whereas the speed is constant for the square-wave profile. For both cases, the dotted lines represent a cross-check: for the square-wave (sinusoidal) profile, sin (swv) indicates that the microstructures obtained under the sinusoidal (square-wave) profile have been used for calculating the load variation

Increasing the number of time steps N _T used in optimization from the default value of 10 will lead to higher computational costs. However, this default number was found to already deliver accurate optimization results. This is demonstrated in Fig. 10, where only 0-or-1 type design is employed for compactness. Clearly, even N _T = 5 is sufficiently accurate. This may be explained by the fact that optimization for a given time instant, essentially corresponding to N _T = 1, was also found to deliver micro-textures which are similar to the ones summarized in Fig. 8. Retaining the time integral in the objective function using a moderate value for N _T is nevertheless desirable because it eliminates the arbitrariness in the particular choice of a time instant as well as its possibly large influence. Consequently, recalling that the micro-textures do not appear to be sensitive to the particular velocity profile, one might expect that the default choice N _T = 10 would apply to alternative velocity profiles just as well, leading to a clear estimate of the computational cost of MacOO problems for such time-dependent problems. On the other hand, even for the moderate macroscopic spatial resolution employed, the cost of MacOO problems in the context of the wedge geometry is already more than two orders of magnitude higher (Table 1). Hence, although the temporal and spatial variations in the homogenized response can be handled in algorithmically similar frameworks, the latter setting is numerically more challenging and will be addressed next. Moreover, so far the parameters which control the geometrical features of the micro-texture have not been probed. This aspect of MacOO will also be addressed in the following investigations.

Fig. 10

For the setup of Fig. 8, the influence of changing the number of time steps used in optimization from its default value N _T = 10 is demonstrated via 0-or-1 type design. As in Fig. 9, 100 time steps were employed in generating the curves for a better resolution of the load variations

4 Wedge problem

4.1 Optimization path ③$\curvearrowright$④ with spatial variations

MacOO problems based on the wedge geometry (Fig. 1) will follow path ③$\curvearrowright$④ of Fig. 3 wherein the spatial variations in h ₀, and hence in {A,C}, must be addressed. The homogeneous solution for the wedge setup in the default setting (homogeneous boundary conditions, $\overline {\boldsymbol {U}} = 1\,\text {m/s}$ with 𝜃 = 0 and $\{h_{0}^{\min },h_{0}^{\max }\} = \{0.2,1\}$ (in μ m) with β = 0) was provided in Fig. 2b where the maximum homogeneous pressure is $p_{{\hom }}^{\max } = 104\,\text {MPa}$ and the corresponding load capacity is $L_{{\hom }} = 1.4\,\text {N}$. Similar to Section 3.2, the influence of micro-texturing may be monitored by its performance metrics through a pressure (f _p ) and a load (f _l ) factor:

$$ f_{p} = \frac{p_{0}^{\max}}{p_{{\hom}}^{\max}} \quad,\quad f_{l} = \frac{L_{0}}{L_{{\hom}}} \quad. $$

(4.1)

The default micro-texture geometry parameters are chosen as $\{\overline {h}_{\min },\overline {h}_{\max }\} = \{-0.2,0.1\}$ (μ m). In all subsequent optimization studies, load maximization will be targeted via the objective

$$ \varphi(s) = - \frac{{\int}_{\Omega} p_{0}(s) \ \ \mathrm{d}{\Omega}}{{\int}_{\Omega} p_{\text{ref}} \ \ \mathrm{d}{\Omega}} $$

(4.2)

where p _ref corresponds to the pressure distribution that is obtained with $h = h_{0} - \overline {h}_{\min }$ (cf. (2.1) and (2.10)) delivering p _ref > p ₀. The filter radius will be chosen as R = 8 for 0-or-1, whereas it will be kept at the default value R = 4 for 0-to-1.

Only varying the velocity angle 𝜃 of $\overline {\boldsymbol {U}}$ in this default setting, the load capacity maximization results are summarized in Fig. 11 for 0-or-1 and 0-to-1 micro-texture designs where the pressure and load factors for each micro-texture design are indicated together with the homogeneous interface values. Note that maximum load capacity is achieved, as in earlier cases, by holes on the surface rather than pillars since the former have a stronger influence on the macroscopic response under identical constraints. For the 0-or-1 type design of this example alone, a continuation approach was employed such that the value of η in (2.10) was gradually increased from 1 to 3 in order to eliminate regions with intermediate values of the design variable s ∈ [0,1] that were observed otherwise. In the 0-to-1 result, a slight but continuous change in the directionality of the micro-texture is observed with increasing 𝜃 in order to ensure a maximum load capacity. The pressure distribution itself remains qualitatively similar to the homogeneous one because these micro-textures are not very strongly anisotropic and for a perfectly isotropic macroscopic response $\overline {U}_{2}$ has no pressure generating effect when β = 0 (Fig. 1). Because $\overline {U}_{1}$ decreases in proportion to $\cos (\theta )$, the maximum pressure and the load capacity do change yet the load and pressure factors show little sensitivity to these changes. This may be justified as follows. If $\overline {U}_{2}$ was set artificially to zero to isolate the stronger influence of $\overline {U}_{1}$, the remaining optimization problem setup is identical to preserving 𝜃 = 0 and only decreasing the magnitude of $\overline {\boldsymbol {U}}$. But in view of (2.3), magnitude scaling would only serve to scale p ₀ at each point in Ω and would not influence the micro-texture design outcome in any way. Presently, $\overline {U}_{2}$ is non-zero yet the relatively weak anisotropy of the micro-textures causes the influence of $\overline {U}_{1}$ variation to dominate. It is also noted that the 0-or-1 filter radius R = 8 deviates from the default value R = 4 in order to safely eliminate fine features that were sometimes observed with the default value. These fine features do not necessarily provide additional flexibility in attaining more optimal designs, e.g. when R = 1 with 𝜃 = 0 one obtains the 0-or-1 performance metrics f _l = 1.54 and f p = 1.79, which are in fact slightly smaller than those obtained with R = 8. Rather than monitoring the performance metrics, however, the motivation in eliminating them was merely practical rather than a necessity — very fine features may limit the ability to efficiently apply micro-texture designs during manufacturing.

Fig. 11

Optimal micro-textures corresponding to the wedge problem of Section 4.1: a 0-or-1 design (with continuation), b 0-to-1 design. The influence of the micro-texture is noted above it by its pressure and load factors (4.1) with respect to the homogeneous interface response $p_{{\hom }}^{\max }$ and $L_{{\hom }}$

In order to demonstrate the negligible degree of anisotropy of the micro-texture designs from Fig. 11 and additionally assess their optimality, the micro-textured interface is rotated through an angle α, which results in modified constitutive tensors A ^α = Q A Q ^T and C ^α = Q C Q ^T, with Q(α) as the rotation tensor in two dimensions. The load capacity $L_{0}^{\alpha }$ of the modified interface is then recomputed through two-scale analysis. If the micro-texture designs are optimal within this test space of micro-textures, one would expect $L_{0}^{\alpha } \le L_{0}$ for all α. The results in Fig. 12 for selected micro-textures from Fig. 11 further show that the anisotropy in both cases is very weak. Nevertheless, in both cases, the designs are clearly optimal with respect to all rotations, which is an indication of the effectiveness of the MacOO optimization framework. A further cross-check may be carried out for the 0-to-1 results, which display comparatively stronger anisotropy, by employing the micro-texture design for 𝜃 = π/8 in the setting of 𝜃 = 3π/8. One obtains the performance metrics f _p = 1.74 and f _l = 1.49, which are close to the optimal values but slightly smaller, as expected.

Fig. 12

The load capacity $L_{0}^{\alpha }$ is computed via two-scale analysis with selected 0-or-1 and 0-to-1 micro-texture designs from Fig. 11 after rotating the micro-textured interface through an angle α : 0→ 360^∘. The circular line for the homogeneous response $L_{{\hom }}$ is provided as a reference and the circular line at the load capacity L ₀ that is delivered by the original micro-texture is provided as a guide, deviations from which indicate anisotropy

4.2 Taylor expansion approximation

The costs of MacOO for temporal and spatial variations in h ₀, and hence in the macroscopic interface variables, were compared in Section 3.3. Due to the large number of microscopic problems and sensitivity computations which are necessary in the case of spatial variations, assessment of the relation between different problem parameters and the optimal micro-structure cannot be rapidly carried out. In order to circumvent this difficulty, the Taylor expansion approach that was originally proposed in Buscaglia and Jai (2000) will be employed. For this purpose, note that if the micro-texture is fixed then $\overline {h}$ in (2.1) is fixed so that the only remaining parameter that controls the pointwise macroscopic response {A,C} at the interface is h ₀. This parameter may vary temporally or spatially through complex global patterns, i.e. over the whole period or interface. However, the global patterns are irrelevant since the determination of {A,C} for the given micro-texture requires only the local value of h ₀, i.e. at a given time or point. Consequently, while a Taylor expansion of a generic macroscopic function g with respect to time or space would be challenging and highly problem dependent, expansion with respect to h ₀ about a reference value $h_{0}^{\text {ref}}$ is straightforward and in principle applicable across multiple problem settings. An order n Taylor expansion would be

$$ g(h_{0}) = g (h_{0}^{\text{ref}}) + \sum\limits_{i=1}^{n} \frac{1}{i!}(h_{0} -h_{0}^{\text{ref}})^{i} \left.\frac{\partial^{i} g}{\partial {h_{0}^{i}}}\right|_{h_{0}^{\text{ref}}} \quad. $$

(4.3)

Moreover, defining $\gamma _{I} = \frac {\partial g}{\partial s^{I}}$ for compactness, the sensitivity of this expansion simply corresponds to the expansion of the sensitivity:

$$ \gamma_{I}(h_{0}) = \gamma_{I} (h_{0}^{\text{ref}}) + \sum\limits_{i=1}^{n} \frac{1}{i!}(h_{0} -h_{0}^{\text{ref}})^{i} \left.\frac{\partial^{i} \gamma_{I}}{\partial {h_{0}^{i}}}\right|_{h_{0}^{\text{ref}}} \quad. $$

(4.4)

Based on numerical experiments, it was found that n = 4 is an accurate choice. Note that at least n = 3 is required for the expansion to deliver exact results for a homogeneous interface (cf. (2.9)). Derivatives of order i > 1 appearing in the Taylor expansion are not easily expressible analytically so that a 4th-order accurate finite difference scheme will be employed in order to approximate them. Such a scheme will require a total of D = 7 evaluations of {A,C} and $\{\frac {\partial \boldsymbol {A}}{\partial s^{I}},\frac {\partial \boldsymbol {C}}{\partial s^{I}}\}$: at $h_{0}^{\text {ref}}$ as well as at points that are {±δ h ₀,±2δ h ₀,±3δ h ₀} away from $h_{0}^{\text {ref}}$, with δ h ₀ = 0.01 μ m. The corresponding reduction in MacOO cost is summarized in Table 1. The reduction in the microscopic problems and microscopic sensitivity analysis is by a factor of N _T /D in the case of temporal variations. Note that the macroscopic sensitivity cost remains unaltered for both temporal and spatial variations. However, for the latter, the microscopic cost reduction factor is (N _M G)²/D, which leads to significant savings. Overall, for the set of problem variables employed, this reflects as more than one order of magnitude reduction for MacOO cost in the context of the wedge problem (from several days down to several hours; on a standard computer using OpenMP parallelization) and thereby enables exploring the parameter space more efficiently.

In order to choose an expansion point, the present wedge problem setup is revisited by assigning the 0-or-1 micro-texture of Fig. 11a-1 as a representative case where {A,C} change considerably across the interface. Subsequently, the predictions based on the Taylor expansion approximation of these tensors are compared with the exact homogenized response. The results in Fig. 13 indicate that for this problem setup it is favorable to choose $h_{0}^{\text {ref}}$, as one might expect, far from either extreme to obtain a p ₀-distribution that is as close as possible to the exact homogenized one. In all subsequent studies, the midpoint ($h_{0}^{\text {ref}} = 0.6\,\mu \text {m}$) will be employed. Further analysis (not shown) employing different micro-texture parameters, also in the context of the squeeze-film problem, have indicated that this is a good choice in most cases. The series of micro-texture design problems from Fig. 11 based on exact homogenization are now repeated with the Taylor expansion approximation and the results are summarized in Fig. 14. 0-to-1 design results are almost identical to those obtained earlier while the 0-or-1 surface topologies are now closer to the 0-to-1 ones. The good qualitative and quantitative agreement between the results in Figs. 11 and 14 indicates that this approximation method is a viable tool to rapidly explore the design space. For a more accurate design assessment, selected cases of interest may then be subjected to an error-free treatment based on exact homogenization. In the remaining sections, the Taylor expansion approximation will be employed to assess the influence of various problem parameters that have so far been kept constant. Only 0-to-1 micro-texture designs will be demonstrated for brevity. In each case, the objective is the maximization of the load capacity of the interface.

Fig. 13

Predictions of p ₀ based on Taylor expansion approximations (Section 4.2) with different expansion points $h_{0}^{\text {ref}} \in [h_{0}^{\min },h_{0}^{{\max }}] = [0.2\,\mu \text {m},1\,\mu \text {m}]$ are compared with the exact homogenized and homogeneous interface responses along the midline of the pressure distribution. The micro-texture is borrowed from the 0-or-1 result of Fig. 11 at 𝜃 = 0. A 200 × 200 macroscopic mesh has been employed in this example for a smoother depiction of the pressure variation

Fig. 14

The series of micro-texture design problems in Fig. 11 are repeated with the Taylor expansion approximation of Section 4.2

4.3 Macroscopic gap distribution

The macroscopic interface geometry is defined by Ω and the distribution of the gap h ₀ on this domain. Since h ₀ is the major variable macroscopic variable which influences p ₀ for any choice of Ω, its distribution will be parametrized on the fixed square domain Ω. Specifically, the surfaces will be tilted with respect to one another through an angle β as shown in Fig. 1. Note that $\{h_{0}^{\min },h_{0}^{\max }\} = \{0.2,1\}$ (in μ m) will be preserved. Recalling that the edge length of Ω is 200 μ m, if the gap varies by 0.1 μ m along x ₂ then this will induce a very small tilt angle β ≈ 0.029^∘. Nevertheless, tilt angles of this magnitude are sufficient to induce considerably different macroscopic pressure distributions, which are summarized in the load capacity maximization results of Fig. 15. Here, the tilt has been imposed on the case with a velocity angle of 𝜃 = π/4 since this case was shown to deliver a visible micro-texture orientation in Fig. 14 and therefore might enable detecting tilt angle influences more easily through orientation changes. It is observed that the micro-texture design does not depend very strongly on the angle of tilt, indicating that the optimality of a micro-texture is independent from the particular h ₀-distribution to a large extent. Indeed, studies with different h ₀ distributions (not shown), such as an exponential distribution, have indicated that a surface with near-circular holes is an optimal micro-texture in a broad range of scenarios. This observation is advantageous from a computational efficiency point of view because, instead of using topology optimization in such cases, one may consider schemes where a smaller number of degrees of freedom can parametrize the microstructure — see Balzani et al. (2014) and Noël and Duysinx (2016) for recent examples in the context of materials.

Fig. 15

Based on the Taylor expansion approximation, load capacity optimization is carried out at a velocity angle of 𝜃 = π/4 but with different tilt angles β in Fig. 1. For each tilt angle, the corresponding optimal 0-to-1 micro-texture design, its macroscopic pressure distribution and the performance metrics are shown. β = 0^∘ case corresponds to the 0-to-1 design for 𝜃 = π/4 in Fig. 14 and is included for comparison

4.4 Variations in the optimal micro-texture

While most of the macroscopic problem parameters have so far been shown not to have a very strong influence on the optimal micro-texture design, different boundary conditions employed in the solution of (2.3) lead to significantly different results that are exemplified in Fig. 16. The default boundary conditions employed in all previous applications enforced a vanishing pressure on the boundary of the domain. Instead of such homogeneous Dirichlet boundary conditions, if the normal component of the interface fluid flux (2.2) is forced to vanish on the top edge of the boundary, the micro-texture displays elongated features. When such homogeneous Neumann boundary conditions are imposed on both top and bottom edges, the optimal micro-texture corresponds to grooves which run perpendicular to these edges, which is an intuitive result in view of the intrinsic one-dimensionality of the setup in this case. In Fig. 17, the optimality of these designs which display moderate to strong anisotropy are again verified with respect to the test space of rotated interfaces that was introduced in Section 4.1.

Fig. 16

The wedge problem with the default parameter choices is revisited using the Taylor expansion approximation in order to study the influence of boundary conditions on the optimal micro-structure (Section 4.4): a default case, with homogeneous boundary conditions on p ₀ on ∂Ω, b the boundary condition at top edge of Ω is modified to enforce vanishing normal component of the flux Q in (2.2), c vanishing flux is enforced both at the top and bottom edges. Left and right edges are subject to p ₀ = 0 in all cases

Fig. 17

Similar to the analysis of Fig. 12, the load capacity $L_{0}^{\alpha }$ is computed via two-scale analysis for micro-texture designs (b) and (c) from Fig. 16 after rotating the micro-textured interface through an angle α : 0→ 360^∘

As a final investigation, the influence of the micro-texture profile parameter set $\{\overline {h}_{\min },\overline {h}_{\max }\}$ is demonstrated in Fig. 18 where the values of the minimum and maximum height values are simultaneously increased. Since all designs are subject to the constraint $\left \langle {h} \right \rangle = 0$, this shift forces the wells to spread. The accompanying rise in the pressure and load factors further highlight the significant influence that optimal micro-textures can have on the macroscopic response of lubrication interfaces.

Fig. 18

Micro-texture profile parameters $\{\overline {h}_{\min },\overline {h}_{\max }\}$ (in μ m) are simultaneously increased to observe their influence on the optimal design. In all cases, the performance metrics are with respect to $p_{{\hom }} = 104\,\text {MPa}$ and $L_{{\hom }} = 1.4\,\text {N}$

5 Conclusion

The macroscopic response of tribological interfaces where hydrodynamic lubrication conditions prevail may be considerably altered by texturing the interface. From a surface engineering perspective, therefore, it is of interest to maximize quantities of interest such as the load bearing capacity of the interface by determining the optimal texture topology. Earlier studies in the literature towards such goals have concentrated on mesoscopic texture patterns which required a full resolution of the interface pressure across the textured macroscopic interface, which becomes increasingly inefficient from a numerical perspective as the length scale of the pattern becomes increasingly smaller. Moreover, these textures were based on a prescribed surface topology that restricted the geometrical features mostly to simple constructions such as circular or square holes and pillars. In the present study, a novel computational surface engineering framework was presented where macroscopic objectives were formulated and analyzed within a homogenization-based two-scale setting and the micro-texture design was achieved through topology optimization schemes. Homogenization-based analysis allows an efficient assessment of the local influence of micro-textures while topology optimization allows attaining arbitrary surface topologies in order to ensure a macroscopically optimal performance. The demonstration of this novel framework was carried out through two key problems which individually address fundamental features of macroscopic lubrication interfaces. The first problem addressed temporal variations of the micro-texture influence in the context of the squeeze-film problem and the second one addressed spatial variations of its influence in the context of the wedge problem. A Taylor expansion approximation was additionally employed in order to enable a rapid and accurate exploration of the design space. Although the optimization algorithm employed does not guarantee attaining the global optimum, extensive numerical investigations have demonstrated the ability of the framework to deliver micro-texture designs with optimal performances that were verified through various cross-check studies as well as the influence of major problem parameters on these optimal designs.

The presented micro-texture design framework constitutes a novel direction in computational surface engineering which delivers both numerical efficiency and topological flexibility. However, further investigations are necessary in order to further assess and broaden its capabilities. First, the present study considered only interface pressure distributions and load capacities as macroscopic objectives. In various problems, engineering the dissipative characteristics of the interfaces, specifically frictional losses, is additionally of interest. In the context of hydrodynamic lubrication, this requires formulating the frictional traction in a two-scale setting and analyzing its sensitivity with respect to the design variables. Second, a single texture was assigned to the entire interface which, despite the variations in its influence in time and space, enabled an efficient treatment of the macro-objective optimization. In general, within design limitations, optimal surface engineering may require assigning different micro-textures to different regions of the interface or even a continuously evolving micro-texture as the interface is traversed. A major challenge towards this possibility lies in the fact that a larger number of microscopic design variables would be needed, which directly impacts the numerical cost of the optimization problem. Third, the macroscopic domain and the gap distribution between the two interacting surfaces over this domain were both prescribed a priori. It would be advantageous to benefit from existing approaches which have proposed the optimization of both of these macroscopic topology ingredients. In combination with the previous two items, an ability to design an optimal micro-texture distribution simultaneously with an optimal macro-topology would lead to a comprehensive two-scale interface engineering framework which can help explore new possibilities in computational multiscale tribology.

Appendices

Appendix: A: Filter formulations

Topology optimization based on an element-wise constant design variable distribution is prone to checkerboard patterns (Diaz and Sigmund 1995; Sigmund and Petersson 1998). This instability may be avoided by employing filters. The morphology filter $\mathcal {F}$ of Section 2.2 operates on the design variable distribution s ∈ [0, 1] within a neighborhood $\mathcal {D}^{K}$ in order to deliver the morphology variable degree of freedom $\rho ^{K} = \mathcal {F}(\mathcal {D}^{K},s)$. Different filter formulations and their performances have recently been discussed in Svanberg and Svärd (2013) — see also Bourdin (2001) and Sigmund (2007). For their formulation, conic weights w ^KI ∈ [0, 1] with the property ${\sum }_{I} w^{KI} = 1$ are defined in order to ensure that ρ ^K remain within [0, 1]:

$$ w^{KI} = \left\{ \begin{array}{cc} \frac{R - d(K,I)}{{\sum}_{J\in \mathcal{D}^{J}} R - d(K,J)} & I \in \mathcal{D}^{K}\\ 0 & I \ne \mathcal{D}^{K} \end{array} \right. \quad. $$

(A.1)

The neighborhood $\mathcal {D}^{K}$ is defined as the set of elements I whose distance d(K,I) to element K are less than or equal to a radius R. The distance of element K to I is measured by $d(K,I) = \sqrt {(X_{K} - X_{I})^{2}+(Y_{K} - Y_{I})^{2}}$ where (X,Y ) denote the element index coordinates, each coordinate lying in the interval [1,N _m ] where N _m = 40 is the number of elements per edge (Section 2.3). With respect to this measure of distance, the default value of the radius is chosen as R = 4 in all numerical investigations, unless otherwise noted. It is remarked that checkerboard patterns do not appear if the design and morphology variables are interpolated (Matsui and Terada 2004; Guest et al. 2004). Even in this case, a filter is useful for assigning a length scale to the micro-texture pattern — see Waseem et al. (2016) for a study of filter radius influence on the micro-texture. In this work, a linear (LN) filter will be employed for 0-to-1 type micro-texture design and an exponential erode (EE) filter for 0-or-1. For a given s-distribution, they deliver ρ ^K which respectively satisfy the following formulations:

$$ \rho^{K}_{LN} = \sum\limits_{I} w^{KI} s^{I} \quad,\quad e^{\alpha(1 - \rho^{K}_{EE})} = \sum\limits_{I} w^{KI} e^{\alpha \left( 1 - s^{I} \right)} \quad. $$

(A.2)

For the exponential erode formulation, α = 100 is employed.

Appendix: B: Sensitivity expressions

In Section 2.4, the sensitivity analysis of the governing macroscopic equation (2.3) had been outlined. Note that the right-hand side of (2.3) applies only to the time-dependent problem but its sensitivity vanishes in that case as well, because the mean film h ₀ is independent of the micro-texture by construction. Moreover, the rate of the primary solution field p ₀ does not enter the governing macroscopic equation, thus rendering the present analysis different with respect to other transient optimization problems (Michelaris et al. 1994). Hence, the expression (2.13) is a generic form that applies to both temporal and spatial variations of h ₀, with the term involving C further vanishing in the former case due to the special structure of the squeeze-film problem. In that case, in order to eliminate the influence of a particular choice of the time instant for optimization (see also the discussion in Section 3.3), the macroscopic objective function (3.4) was formulated in terms of a time integral. Upon solving for $\pi _{I} = \frac {\partial p_{0}}{\partial s^{I}}$ from (2.13) at each discrete time, its sensitivity may be evaluated as

$$ \frac{\partial \varphi}{\partial s^{I}} = - \frac{{\int}_{T} {\int}_{\Omega} 2 \pi_{I} p_{0}(s) \ \ \mathrm{d}{\Omega} \ \ \mathrm{d}{t}}{{\int}_{T} {\int}_{\Omega} p^{2}_{\text{ref}} \ \ \mathrm{d}{\Omega} \ \ \mathrm{d}{t}} \quad. $$

(B.1)

For the wedge problem, the relevant expression is simplified due to the absence of a time-integral in (4.2). However, because the sensitivity of both A and C must be evaluated in order to determine π _I from (2.13) and because these terms are spatially varying, the overall cost is significantly higher.

The microscopic analysis dominates the overall computation time, both in obtaining the solution p ₀ as well as in the sensitivity analysis (Table 1). Consequently, as noted in Section 2.4, gains due to an adjoint sensitivity approach for the macroscopic sensitivity analysis are negligible and the more straightforward direct approach has been preferred instead for calculating π _I . However, it should be highlighted that the gains due to an efficient microscopic sensitivity analysis are significant and an appropriate formulation for determining $\{\frac {\partial \boldsymbol {A}}{\partial s^{I}},\frac {\partial \boldsymbol {C}}{\partial s^{I}}\}$ is crucial to an effective optimization algorithm construction. In this context, it is noted that the variational approach presented in Waseem et al. (2016) for this purpose does not follow a standard adjoint sensitivity approach but the results are consistent with known adjoint sensitivity results that apply to one part of the analysis, namely $\frac {\partial \boldsymbol {A}}{\partial s^{I}}$, in view of its similarity to sensitivity analysis for heat conduction problems (Bendsøe and Sigmund 2004). The term $\frac {\partial \boldsymbol {C}}{\partial s^{I}}$ has no direct counterpart in material design problems.

The sensitivity expressions (2.12) for $\{\frac {\partial \boldsymbol {A}}{\partial s^{I}},\frac {\partial \boldsymbol {C}}{\partial s^{I}}\}$ have been verified in Waseem et al. (2016) by comparing the analytical (A) expressions with numerical (N) differentiation results. Here, a similar study is carried out for verifying the analytical sensitivity expressions for $\frac {\partial \varphi }{\partial s^{I}}$ which were discussed above. For this purpose, representative 0-or-1 and 0-to-1 type designs are selected from both types of macroscopic problems. For numerical differentiation, following the earlier study for $\{\frac {\partial \boldsymbol {A}}{\partial s^{I}},\frac {\partial \boldsymbol {C}}{\partial s^{I}}\}$, second-order finite difference is employed where each s ^I is sequentially perturbed by 10⁻⁴. The aim is to observe, at each point of the micro-texture, a factor of less than 10⁻³ between $\left | (\partial {\varphi }/\partial {s^{I}})_{A}-(\partial {\varphi }/\partial {s^{I}})_{N} \right |$ and the maximum value of $\left | (\partial {\varphi }/\partial {s^{I}})_{A} \right |$ throughout the micro-texture. The results summarized in Fig. 19 demonstrate this, thereby verifying the derived sensitivity expressions. Employing a perturbation value smaller than 10⁻⁴ is generally not desirable due to possible numerical ill-conditioning errors but a fourth-order scheme would clearly further decrease the relative difference. However, the evaluation of the second-order scheme is already significantly more costly than the analytical expressions, which also highlights the efficiency gains due to use of the latter.

Fig. 19

The analytical (A) sensitivity distributions (∂ φ/∂ s ^I) _A are provided and compared with the numerical (N) sensitivities (∂ φ/∂ s ^I) _N through the difference $\left | (\partial {\varphi }/\partial {s^{I}})_{A}-(\partial {\varphi }/\partial {s^{I}})_{N} \right |$ on converged 0-or-1 and 0-to-1 type textures: for (a)–(b) from Fig. 8 of the squeeze-film problem (S) for the sinusoidal velocity profile, and for (c)-(d) from Fig. 11 of the wedge problem (W) for 𝜃 = 0. Note that the ratio between the difference and the analytical sensitivity is less than 10⁻³ for all cases

Figure 20 depicts the change of the objective function value with the number of iterations in attaining the micro-textures employed in the analysis of Fig. 19. For completeness, the results for the square-wave velocity profile have also been included. Note that the initial guess employed does not necessarily satisfy the optimization constraint, which can lead to initial rapid changes in the objective. Once the micro-texture starts to develop, the objective function decreases almost monotonically to convergence. The rate of convergence can be strongly influenced by the MMA parameters. In view of the large number of test cases considered, no attempt was made to tune these parameters for faster or smoother convergence on a case-by-case basis and, instead, the default choices which were previously outlined in Waseem et al. (2016) were preserved.

Fig. 20

The variation of the objective function with the number of iterations is summarized for the squeeze-film problem results of Fig. 8 and for the wedge problem results of Fig. 11 (for 𝜃 = 0)