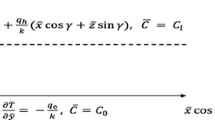Robin Boundary Effects in the Darcy–Rayleigh Problem with Local Thermal Non-equilibrium Model

Abstract

The contribution of Robin boundaries on the onset of convection in a horizontal saturated porous layer covered by a free surface on the top is investigated here. The saturated solid matrix is assumed in a regime where the temperature profile of the solid phase differs from a fluid one. Two energy equations are adopted as a consequence of the local thermal non-equilibrium model (LTNE), and four Biot numbers are arising out of the third kind of boundaries imposed on both surfaces. The dimensionless parameters H and $\gamma$ which rule the transition from local thermal equilibrium (LTE) to non-equilibrium one or vice versa are taken into account. The cases of equal and different Biot numbers have been considered beside the asymptotic limits of LTE and LTNE one. A linear stability analysis of the basic motionless state has been performed. The perturbation terms of the main steady flows are evaluated in the form of plane waves. The eigenvalue problem is solved either analytically or numerically depending on the temperature gradient of the fluid phase. The analytical solution is handled through a dispersion relation, while the numerical one is computed by the Runge–Kutta solver combined with the shooting method. The variation in Darcy–Rayleigh number and wave number is obtained with respect to Biot numbers for all resulting cases.

1 Introduction

The convection heat transfer in porous media is one of the widespread phenomena in the thermal engineering applications, and it is usually investigated in the condition where both phases are in local thermal equilibrium (LTE). The hypothesis of LTE implies that the solid and fluid phases have an equal temperature profile so that a single energy equation is used to model the common temperature field (Tyvand 2002; Barletta 2011). However, there exist some situations where LTE is required to be relaxed. For instance, when hot fluid with higher thermal conductance flows into cold insulating solid matrix significant difference will arise in the temperature distribution of the saturated medium which in turn will cause the local thermal non-equilibrium model (LTNE) (Nield 2012; Kaviany 2012; Rees and Pop 2005; Kuznetsov 1998). In this example, the temperature of the solid matrix will be equal to the fluid one only after the passage of a certain specific time. This feature does not admit that the LTNE occurs only in unsteady flows as it can also happen in steady regimes. Two models of energy equation are employed to account for the difference in the temperature fields between the solid matrix and the saturating fluid. The term of h combines the separate temperatures in both energy equations and rules the heat lost or gained from one phase to another. Small and vanishing values of h correspond to a weak transfer of heat between solid and fluid phases, while conversely, such values as a large to an infinite give rise to strong equilibrium effects. This behavior cannot be assured without supplement conditions imposed on thermal conductivities $k_s$ and $k_f$. Banu and Rees (2002) came up with two dimensionless numbers H and $\gamma$ which are modeled by a heat transfer coefficient h, as well as volumetric thermal conductivities, to account for the LTNE effects on the onset of convection in Darcy–Bénard configuration. The critical value of Darcy–Bénard problem using LTNE may arrive at $4\pi ^2$ if the limit of $H\rightarrow \infty$ with $\gamma \approx O(1)$ or $\gamma \rightarrow \infty$ with $H \approx O(1)$ is taken into consideration (Banu and Rees 2002; Lapwood 1948; Horton and Rogers 1945; Rees 2000). Barletta et al. (2015) adopted the setup of a Darcy–Bénard problem with a free surface on the top and rigid isothermal wall at the bottom. The upper layer was subjected to Robin boundary condition whose effect beside LTNE brings about two different Biot numbers. Instead of having a perfect thermal conducting wall at the bottom, Celli et al. (2017) assumed the case where the lower surface is heated by uniform heat flux (Model A). Celli et al. (2017) pointed out that the case of $H\rightarrow 0$ has the most stable configuration when a free surface behaves as an isoflux layer. On the other hand, using rough boundary conditions can hinder the convective instability in Rayleigh–Bénard problem (Siddheshwa 1995). Celli and Kuznetsov (2018) noticed that the increase in roughness effects at the boundaries enhances the stability behavior of the fluid medium.

In the present paper, we extend the previous problems by modeling both thermal layers as a Robin boundary conditions with two different external ambient temperatures. The thermal boundaries will give rise to four different Biot numbers, and more than one limiting cases will be studied. The eigenvalue problem obtained from the normal modes method is handled either numerically by using a Runge–Kutta procedure in combination with a shooting method or analytically by defining an implicit dispersion relation.

Fig. 1

A horizontal porous channel

2 Problem Statement and Formulation

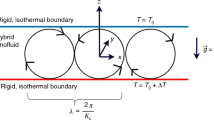
Let us consider the archetype of Darcy–Bénard configuration with one free surface on the top and one rigid wall at the bottom; see Fig. 1. Both surfaces are subjected to Robin boundaries with two different external temperatures $T_{1} > T_{2}$. The direction of gravity force contrasts with the unit vector $\mathbf {e_z}$ in the form of $\mathbf {g}=-g \mathbf {e_z}$. The hypothesis of Oberbeck–Boussinesq approximation and Darcy’s law are taken into account. The temperature distribution of fluid phase differs to solid one as a consequence of local thermal non-equilibrium model. More than two different Biot numbers are considered due to Robin boundaries. The Newton’s law of cooling is used to model the layers exposed to external fluid in thermal boundary conditions. The governing energy equations and Darcy’s law are thus written as

$$\begin{aligned}&\displaystyle {{\nabla }^{\star }}\cdot \mathbf {{u}}^{\star }=0, \end{aligned}$$

(1a)

$$\begin{aligned}&\displaystyle \dfrac{\mu }{K}~ {\nabla }^{\star }\times \mathbf {{u}}^{\star }-{\rho _f}{\beta }{g}{\nabla }^{\star }\times [({T}^{\star }_{f}-T_{1}) \mathbf {ez}]=0, \end{aligned}$$

(1b)

$$\begin{aligned}&\displaystyle (1-{\phi }) \dfrac{\partial {{T}^{\star }_{s}}}{\partial {t^{\star }}}=(1-{\phi }){\alpha _s}~{{\nabla }^{\star }}^2 {T}^{\star }_{s}+\dfrac{h}{{(\rho C)}_{s}}({T}^{\star }_{f}-{T}^{\star }_{s}), \end{aligned}$$

(1c)

$$\begin{aligned}&\displaystyle {\phi }\dfrac{\partial {{T}^{\star }_{f}}}{\partial {t^{\star }}}+\mathbf {{u}}^{\star }\cdot {{\nabla }^{\star }}{T}^{\star }_{f}=\phi {\alpha _f}~{{\nabla }^{\star }}^2 {T}^{\star }_{f}-\dfrac{h}{{(\rho C)}_{f}}({T}^{\star }_{f}-{T}^{\star }_{s}). \end{aligned}$$

(1d)

The pressure gradient is neglected from Darcy’s law in Eq. (1b) by the curl operator. The subscripts f and s denote the properties of the saturating fluid and of the solid matrix, respectively. The star notation indicates dimensional variables and operators, where $\mathbf {u}$ is velocity field (u, v, w), $\alpha$ is thermal diffusivity [m$^2$/s], $\beta$ is thermal expansion coefficient [K$^{-1}$], C is heat capacity [J/(Kg K)], $\phi$ is porosity, h is inter-phase heat transfer coefficient [W/m$^3$ K], $\mu$ is dynamic viscosity [Pa s], $\rho$ is density, t is time, d is the layer thickness [m] and K is the permeability of the medium [m$^2$].

As the roughness of the boundaries is not taken into account, the relevant boundary conditions are

$$\begin{aligned} {{z}^{\star }}= & {} d:\quad \dfrac{\partial {{w}^{\star }}}{\partial {z^{\star }}}=0, \quad -k_{s}\dfrac{\partial {{T}^{\star }_{s}}}{\partial {z^{\star }}}= h_{s2}({T}^{\star }_{s}-T_{2}),\quad -k_{f}\dfrac{\partial {{T}^{\star }_{f}}}{\partial {z^{\star }}}= h_{f2}({T}^{\star }_{f}-T_{2}). \end{aligned}$$

(2a)

$$\begin{aligned} {{z}^{\star }}= & {} 0:\quad {{w}^{\star }}=0,\quad k_{s}\dfrac{\partial {{T}^{\star }_{s}}}{\partial {z^{\star }}}= h_{s1}({T}^{\star }_{s}-T_{1}),\quad k_{f}\dfrac{\partial {{T}^{\star }_{f}}}{\partial {z^{\star }}}= h_{f1}({T}^{\star }_{f}-T_{1}). \end{aligned}$$

(2b)

The velocity boundary condition has just one equation on each surface which is the impermeability and the free surface. This feature is due to low derivative order of Darcy’s model in the local momentum balance equation. k is the thermal conductivity [W/(mK)], while the subscript “1” denotes the external environment below a rigid wall and the subscript “2” denotes the external environment above a free surface.

3 Nondimensionlization

The dimensionless quantities are used to rescale the physical variables of this problem in the form of

$$\begin{aligned} {\nabla }^{\star }\rightarrow {\nabla } \dfrac{1}{d}, \quad {t}^{\star } \rightarrow t \dfrac{{d}^2}{\alpha _f}, \quad \mathbf {u}^{\star } \rightarrow \mathbf {u} \frac{{\phi }{\alpha _f}}{d},\quad {T}^{\star }_{s,f} \rightarrow T_{2}+ {T_{s,f}}{(T_{1}-T_{2})}. \end{aligned}$$

(3)

The non-dimensional parameters are evaluated as :

$$\begin{aligned} H= & {} \dfrac{{h}{{d}^2}}{{\phi }{k_f}},\quad {\gamma }=\dfrac{{\phi }{k_f}}{(1-{\phi }){k_s}},\quad R=\dfrac{{\beta }{\varDelta {T}}{g}{K}{d}}{{\nu }{\alpha _m}},\quad \varDelta {T}=T_{1}-T_{2},\nonumber \\ B_{s1}= & {} \dfrac{h_{s1} d}{k_{s}},\quad B_{f1}=\dfrac{h_{f1} d}{k_{f}}, \quad B_{s2}=\dfrac{h_{s2} d}{k_{s}},\quad B_{f2}=\frac{h_{f2} d}{k_{f}}, \nonumber \\ {\lambda }= & {} \dfrac{\alpha _f}{\alpha _s},\quad k_m=(1-{\phi })k_s+{\phi }k_f,\quad {\alpha _f}=\dfrac{k_f}{({\rho }C)_f}, \quad {\alpha _m}=\dfrac{k_m}{({\rho }C)_f}. \end{aligned}$$

(4)

The parameters H and $\gamma$ are the dimensionless inter-phase heat transfer coefficient and thermal conductivity ratio, respectively. The symbol B defines the Biot number and the symbol R indicates the Darcy–Rayleigh number.

The dimensionless quantities defined in Eqs. (3) and (4) are substituted into the governing equations as well as into the boundary conditions. The dimensionless forms of the governing equations and boundary conditions are given with respect to the stream functions $\varPsi$ in the form of

$$\begin{aligned}&\nabla ^2 \varPsi +\dfrac{1+\gamma }{\gamma } R \dfrac{\partial {{T_f}}}{\partial {x}}=0, \end{aligned}$$

(5a)

$$\begin{aligned}&{\lambda }\dfrac{\partial {T_s}}{\partial {t}}=\nabla ^2 {T_s}+{\gamma }H({{T_f}}-{{T_s}}), \end{aligned}$$

(5b)

$$\begin{aligned}&\dfrac{\partial {{T_f}}}{\partial {t}}+\dfrac{\partial {\varPsi }}{\partial {z}}\dfrac{\partial {T_f}}{\partial {x}}-\dfrac{\partial {\varPsi }}{\partial {x}}\dfrac{\partial {T_f}}{\partial {z}}=\nabla ^2{T_f}+H({{T_s}}-{{T_f}}), \end{aligned}$$

(5c)

$$\begin{aligned}&z=1: \quad \dfrac{\partial {\varPsi }}{\partial {z}}=0,\quad -\dfrac{\partial {T_s}}{\partial {z}}=B_{s2} T_{s},\quad -\dfrac{\partial {T_f}}{\partial {z}}=B_{f2} T_{f}, \end{aligned}$$

(5d)

$$\begin{aligned}&z=0:\quad \varPsi =0,\quad \dfrac{\partial {T_s}}{\partial {z}}=B_{s1}(T_{s}-1),\quad \dfrac{\partial {T_f}}{\partial {z}}=B_{f1} (T_{f}-1), \end{aligned}$$

(5e)

where the stream functions used in Eq. (5) are

$$\begin{aligned} u=-\dfrac{\partial {\varPsi }}{\partial {x}}, \quad w=\dfrac{\partial {\varPsi }}{\partial {z}}. \end{aligned}$$

(6)

4 Basic Flow

In the rest state, there is no motion of the Newtonian fluid through the solid skeleton which means

$$\begin{aligned} {\varPsi }_\mathrm{b}=0. \end{aligned}$$

(7)

The subscript b refers to the basic state. The current expressions of $T_{s, b}$ and $T_{f,b}$ possess a huge number of governing parameters which lead both temperature fields to show a large mathematical form in comparison with other limiting cases. Consequently, the two basic temperature profiles are summed up in the following form:

$$\begin{aligned} T_{f, b}=\dfrac{ N_{f, b}}{ D_{sf, b}} \quad \text {and}\quad T_{s, b}=\dfrac{ N_{s, b}}{ D_{sf, b}}. \end{aligned}$$

(8)

The term $N_{f, b}$ is the numerator function of the basic solution obtained for the fluid phase. Thus, the expression of $N_{f, b}$ can be evaluated as

$$\begin{aligned} N_{f,b}= & {} F_0+(F_3 +F_4 -F_5)\varOmega \cosh \varOmega +(F_8 -\varOmega F_1 ) \cosh (\varOmega z )\nonumber \\&-(F_9+F_2) \sinh ( \varOmega z)-(F_6+F_7)\sinh \varOmega . \end{aligned}$$

(9)

In the meantime, the numerator function of the solid phase $N_{s, b}$ is written as

$$\begin{aligned} N_{s,b}= & {} F_0+ (F_3+F_4-F_5)\varOmega \cosh \varOmega +\gamma \cosh ( \varOmega z )(\varOmega F_1-F_8)\nonumber \\&+\gamma \sinh ( \varOmega z )(F_2+F_9)-(F_6+F_7)\sinh \varOmega . \end{aligned}$$

(10)

The coefficients $F_0$, $F_1$,..., $F_9$ are defined as variable functions for $N_{s, b}$ as well as $N_{f, b}$, namely

$$\begin{aligned} \underset{}{}{\left\{ \begin{array}{ll} F_0 =\gamma \varOmega (B_{s1}-B_{f1}) (B_{f2}-B_{s2}),\\ F_1= (B_{f2}-B_{s2}) (B_{s1}+\gamma B_{f1}), \\ F_2= B_{f1} B_{s1} (B_{f2}-B_{s2}) (1+\gamma ),\\ F_3=B_{s1} (\gamma B_{s2} +B_{f2} (1-B_{s2} (z-1) (1+\gamma ))),\\ F_4= B_{f1}(\gamma B_{f2}+\gamma B_{s2} (\gamma -B_{f2} (z-1) (1+\gamma ))), \\ F_5= B_{f1}B_{s1} (1+\gamma ) (B_{s2} (z-1)-1+\gamma (B_{f2} (z-1)-1)) ,\\ F_6= B_{f1} B_{s1} (1+\gamma )(- \gamma B_{s2}+B_{f2} (B_{s2} (z-1) (1+\gamma )-1)),\\ F_7= \varOmega ^2 (B_{s1}+\gamma B_{f1}) (-1+B_{s2} (z-1)+(B_{f2} (z-1)-1) \gamma ),\\ F_8= (B_{f1}-B_{s1}) ((B_{s2}+\gamma B_{f2}) \varOmega \cosh \varOmega +B_{f2} B_{s2} (1+\gamma ) \sinh \varOmega ),\\ F_9= (B_{f1}-B_{s1})(B_{f2} B_{s2} (1+\gamma ) \cosh \varOmega +(B_{s2}+\gamma B_{f2} ) \varOmega \sinh \varOmega ). \end{array}\right. } \end{aligned}$$

(11)

Otherwise, there is only one denominator function $D_{sf,b}$ employed here as both basic temperature solutions have the same bottom part in a fraction. Thus, denominator function $D_{sf,b}$ is defined as

$$\begin{aligned} D_{sf,b}= & {} \{-2 \gamma \varOmega (B_{f1}-B_{s1}) (B_{f2}-B_{s2}) + \varOmega \cosh \varOmega ((B_{f1}+B_{f2}) (B_{s1}+B_{s2}+B_{s1} B_{s2})\nonumber \\&+\,\gamma (2 B_{f1} B_{f2}+B_{f1} (2+B_{f2}) B_{s1}+((2+B_{f1}) B_{s1}+B_{f2} (2+B_{f1}+B_{s1})) B_{s2}) \nonumber \\&+\,(B_{f1}+B_{f2}+B_{f1} B_{f2}) (B_{s1}+B_{s2}) \gamma ^2) +((1+\gamma ) (B_{f1} B_{f2} (B_{s1}+B_{s2}+B_{s1} B_{s2})\nonumber \\&+\,\gamma B_{s1} B_{s2} (B_{f1}+B_{f2}+B_{f1} B_{f2}))+(B_{s1}+B_{s2}+B_{s1} B_{s2}+(B_{f1}+B_{f2}+B_{s1}\nonumber \\&+\,B_{f2} B_{s1}+B_{s2}+B_{f1} B_{s2}) \gamma +(B_{f1}+B_{f2}+B_{f1} B_{f2}) \gamma ^2) \varOmega ^2) \sinh \varOmega \}. \end{aligned}$$

(12)

Therefore, the difference in temperature profiles between the solid and fluid phases for the general case endows that

$$\begin{aligned} T_{f, b}-T_{s, b}= (1+\gamma ) \times \{ \varOmega \dfrac{-F_1 \cosh ( \varOmega z )+ \cosh \varOmega (1 -z )(B_{f1}-B_{s1}) (B_{s2}+ \gamma B_{f2} )}{D_{sf,b}}\nonumber \\ -\dfrac{(1+\gamma )(B_{f1} B_{s1} (B_{f2}-B_{s2}) \sinh ( \varOmega z )+B_{f2} (B_{s1}-B_{f1}) B_{s2} \sinh \varOmega (1 -z)))}{ D_{sf,b}}\}. \nonumber \\ \end{aligned}$$

(13)

The dimensionless number of ${\varOmega }$ is developed as

$$\begin{aligned} {\varOmega }=\sqrt{H (1+\gamma )}. \end{aligned}$$

(14)

4.1 Limiting Case $B_{f1}= B_{s1}$ and $B_{f2}= B_{s2}$

The two phases can simultaneously have the same basic solution as the condition of $\dfrac{ B_{f1}}{ B_{s1}}=\dfrac{ B_{f2}}{ B_{s2}}=1$ is taken into account. We find that the local thermal equilibrium is present for whatever value of H and $\gamma$. Therefore, the basic solution of the two phases can be written as

$$\begin{aligned} T_{s,b}=T_{f,b}=\dfrac{{B_{f1}} (1+{B_{f2}}(1-{z}))}{{B_{f1}}+{B_{f2}}+{B_{f1}} {B_{f2}}}. \end{aligned}$$

(15)

4.2 Local Thermal Equilibrium (LTE)

There are just two different limits whose basic solution behaves as in the local thermal equilibrium regime regardless of the Biot number effects :

• Limit $H\rightarrow \infty$ with $\gamma \approx O(1)$ (1st case of LTE):

  The limiting case of $h\rightarrow \infty$ with $k_f \approx O(1)$ describes a necessary condition for getting the occurrence of LTE between both phases. Under this condition, the basic temperature profiles of the solid and fluid phases display again an identical form defined as

  $$\begin{aligned} T_{s, b}=T_{f, b}=\dfrac{{B_{m1}} (1+{B_{m2}}-{B_{m2}} {z})}{{B_{m1}}+{B_{m2}}+{B_{m1}} {B_{m2}}}. \end{aligned}$$

  (16)

  The Robin boundary conditions define two effective Biot numbers, one for the lower rigid wall $B_{m1}$ and one for the upper free surface $B_{m2}$. Thus, these two parameters can be given as:

  $$\begin{aligned} B_{m1}=\dfrac{B_{s1}+{\gamma } B_{f1}}{1+{\gamma }}\quad \text {and} \quad B_{m2}=\dfrac{B_{s2}+{\gamma } B_{f2}}{1+{\gamma }}. \end{aligned}$$

  (17)

  The difference in the asymptotes between the temperature gradients of the solid and fluid phases in limit $H\rightarrow \infty$, with the condition of $\dfrac{ B_{f1}}{ B_{s1}}\ne \dfrac{ B_{f2}}{ B_{s2}} \ne 1$, is an expected result as both layers are exposed to third kind of boundary conditions. Therefore, the limits of the temperature gradients for all possible values of z in the range of [0, 1] are obtained as

  $$\begin{aligned} \underset{H\rightarrow \infty }{T'_{f, b}}={\left\{ \begin{array}{ll} -\dfrac{B_{f1} B_{m2}}{B_{m1}+B_{m2}+B_{m1} B_{m2}}, &{}\text {if} \quad {z}=0 \\ -\dfrac{B_{m1} B_{m2}}{B_{m1}+B_{m2}+B_{m1} B_{m2}}, &{}\text {if} \quad 0<{z}<1 \\ -\dfrac{B_{f2} B_{m1}}{B_{m1}+B_{m2}+B_{m1} B_{m2}}, &{}\text {if} \quad {z}=1 \end{array}\right. }, \end{aligned}$$

  (18)

  while

  $$\begin{aligned} \underset{H\rightarrow \infty }{T'_{s, b}}={\left\{ \begin{array}{ll} -\dfrac{B_{s1} B_{m2}}{B_{m1}+B_{m2}+B_{m1} B_{m2}}, &{}\text {if} \quad {z}=0 \\ -\dfrac{B_{m1} B_{m2}}{B_{m1}+B_{m2}+B_{m1} B_{m2}}, &{}\text {if} \quad 0<{z}<1 \\ -\dfrac{B_{s2} B_{m1}}{B_{m1}+B_{m2}+B_{m1} B_{m2}}, &{}\text {if} \quad {z}=1 \end{array}\right. }. \end{aligned}$$

  (19)

  Owing to Robin boundaries Eq. (5), the temperature profiles and their gradient limits behave strangely at vicinity regions of $z=0$ as well as $z=1$ despite the large value of H as vividly exhibited in Fig. 2.

• Limit $\gamma \rightarrow \infty$ with $H\approx O(1)$ (2nd case of LTE):

  The special case describes the situations where the fluid phase has a higher capability to conduct heat than a solid one. The feature breaks down the local thermal non-equilibrium regime and gives rise to equilibrium one only if the condition of nonvanishing value in the volumetric heat transfer coefficient is taken into account. As the limiting case is fulfilled, both temperature phases have a congruence form in the basic solution which is expressed as

  $$\begin{aligned} T_{f, b}=T_{s, b}=\dfrac{{B_{f1}} (1+{B_{f2}}-{B_{f2}} {z})}{{B_{f1}}+{B_{f2}}+{B_{f1}} {B_{f2}}}. \end{aligned}$$

  (20)

Fig. 2

Plots of $T_{s, b}$ and $T_{f, b}$ for $\gamma =100$, $B_{f1}=1$ and $B_{f2}=1$ with $H=10^3$

4.3 Limiting Case $H \rightarrow 0$

The convection mode does not occur between both phases when the limit of $h\rightarrow 0$ is considered. The special case of $H\rightarrow 0$ is valid if the conduction process exists with the condition of $\gamma \approx O(1)$. In this case, both phases display unequal and decoupled temperature profiles. However, we can notice a strong mathematical resemblance between the temperature profile of solid and fluid phases. The basic solution of the two phases is

$$\begin{aligned} T_{s, b}=\frac{{B_{s1}} (1+{B_{s2}}-{B_{s2}} {z})}{{B_{s1}}+{B_{s2}}+{B_{s1}} {B_{s2}}}, \quad T_{f, b}=\frac{{B_{f1}} (1+{B_{f2}}-{B_{f2}} {z})}{{B_{f1}}+{B_{f2}}+{B_{f1}} {B_{f2}}}. \end{aligned}$$

(21)

4.4 Limiting Case ${\gamma } \rightarrow 0$

The assumption $k_s\gg k_f$ with $H\approx O(1)$ is stemmed from the higher ability of the solid matrix in conducting heat. This effect sustains the inverse behavior of LTE which drives to different temperature fields. However, the two phases are slightly coupled to each other in the basic temperature profile by means of Biot numbers. Consequently, the basic solutions of the special case are written as

$$\begin{aligned} T_{s, b}= & {} \dfrac{B_{s1} (1+B_{s2}-B_{s2} z)}{B_{s1}+B_{s2}+B_{s1} B_{s2}}, \end{aligned}$$

(22)

$$\begin{aligned} T_{f, b}= & {} \dfrac{B_{s1} (B_{s2}-B_{f2}) {\sqrt{H}} \cosh ({\sqrt{H}} z)+B_{f1} B_{f2} B_{s1} \sinh {\sqrt{H}}}{(B_{s1}+B_{s2}+B_{s1} B_{s2}) ((B_{f1}+B_{f2}) {\sqrt{H}} \cosh {\sqrt{H}}+(B_{f1} B_{f2}+H) \sinh {\sqrt{H}})}\nonumber \\&+\,\dfrac{B_{f1} B_{f2} B_{s1} B_{s2} \sinh {\sqrt{H}}+(B_{f1}+B_{f2}) B_{s1} {\sqrt{H}} (1-B_{s2} (z-1)) \cosh {\sqrt{H}}}{(B_{s1}+B_{s2}+B_{s1} B_{s2}) ((B_{f1}+B_{f2}) {\sqrt{H}} \cosh {\sqrt{H}}+(B_{f1} B_{f2}+H) \sinh {\sqrt{H}})}\nonumber \\&+\,\dfrac{B_{s1} H \sinh {\sqrt{H}}+B_{s1} B_{s2} H \sinh {\sqrt{H}}+(B_{f1}-B_{s1}) B_{s2} {\sqrt{H}} \cosh ({\sqrt{H}} (z-1))}{(B_{s1}+B_{s2}+B_{s1} B_{s2}) ((B_{f1}+B_{f2}) {\sqrt{H}} \cosh {\sqrt{H}}+(B_{f1} B_{f2}+H) \sinh {\sqrt{H}})}\nonumber \\&-\,\dfrac{B_{f1} B_{f2} B_{s2} \sinh ({\sqrt{H}} (z-1))-B_{f1} B_{f2} B_{s1} B_{s2} z \sinh {\sqrt{H}}-B_{s1} B_{s2} H z \sinh {\sqrt{H}}}{(B_{s1}+B_{s2}+B_{s1} B_{s2}) ((B_{f1}+B_{f2}) {\sqrt{H}} \cosh {\sqrt{H}}+(B_{f1} B_{f2}+H) \sinh {\sqrt{H}})}\nonumber \\&-\,\dfrac{B_{f2} B_{s1} B_{s2} \sinh ({\sqrt{H}} (z-1))+B_{f1} B_{s1} (B_{s2}-B_{f2}) \sinh ({\sqrt{H}}z)}{(B_{s1}+B_{s2}+B_{s1} B_{s2}) ((B_{f1}+B_{f2}) {\sqrt{H}} \cosh {\sqrt{H}}+(B_{f1} B_{f2}+H) \sinh {\sqrt{H}})}. \nonumber \\ \end{aligned}$$

(23)

5 Stability Analysis

As the momentum and the energy equations are nonlinear, the perturbation method is applied. Thus, the dependent variables are written as

$$\begin{aligned} \begin{aligned} \underset{}{}{\left\{ \begin{array}{ll} T_{fs}={T_{fs, b}}+ {\epsilon } {\tilde{T}}_{fs}(x, z, t), \\ {\varPsi }={{\varPsi }_b}+{\epsilon } {\tilde{\varPsi }}(x, z, t). \end{array}\right. } \end{aligned} \end{aligned}$$

(24)

The coefficient $\epsilon$ is a small amplitude fluctuation assumed as $\epsilon<<1$, while the rescaled streamfunction amplitude is noted as ${\tilde{\varPsi }}$. Both ${\tilde{T}}_{f}$ and ${\tilde{T}}_{s}$ are, on the other hand, the perturbation temperature profile of the solid and the fluid phases, respectively. By substituting Eq. (24) into Eq. (5), the linear form of the governing equations is obtained as

$$\begin{aligned}&\nabla ^2 {{\tilde{\varPsi }}}=-R \dfrac{1+\gamma }{\gamma }\dfrac{\partial {\tilde{T_s}}}{\partial {x}}, \end{aligned}$$

(25a)

$$\begin{aligned}&{\chi }\dfrac{\partial \tilde{T_s}}{\partial {t}}=\nabla ^2 {{\tilde{T}}}_s +{\gamma }H({\tilde{T_f}}-{\tilde{T_s}}), \end{aligned}$$

(25b)

$$\begin{aligned}&\dfrac{\partial {\tilde{T_f}}}{\partial {t}}-\dfrac{\partial {{{\tilde{\varPsi }}}}}{\partial {x}} T'_{fb}=\nabla ^2 \tilde{T_f} +H({\tilde{T_s}}-{\tilde{T_f}}). \end{aligned}$$

(25c)

The perturbation functions can be evaluated by means of normal modes method as standing waves, which are expressed as

$$\begin{aligned} \Big \{ {\tilde{\varPsi }}(x,z,t), \tilde{T_s}(x,z,t), \tilde{T_f}(x,z,t) \Big \}=\Big \{ i{\psi }(z), {\varphi }(z),{\theta }(z) \Big \} e^{i(ax-{\omega }t)}. \end{aligned}$$

(26)

The functions ${\psi }(z), {\varphi }(z)$ and ${\theta }(z)$ are the dimensionless amplitudes of the normal modes. The perturbation forms of Eq. (26) are substituted into Eq. (25) which give rise to a set of ordinary differential equations with a dimensionless complex frequency $\omega =\omega _R+i\omega _I$ and a wavenumber a. The imaginary part $\omega _I$ is the temporal growth rate of fluctuation, while the real part $\omega _R$ is the angular frequency of the wave. Consequently, the ordinary differential equations are written as

$$\begin{aligned}&{\psi }_{,zz}-a^2 {\psi }+a R \dfrac{1+\gamma }{\gamma }{\theta } =0, \end{aligned}$$

(27a)

$$\begin{aligned}&{\varphi }_{,zz}-a^2 {\varphi }+{\gamma }H({\theta }-{\varphi })+i {\omega }{\chi }{\varphi }=0, \end{aligned}$$

(27b)

$$\begin{aligned}&{\theta }_{,zz}-a^2 {\theta }+H({\varphi }-{\theta })-a {\psi } T_{fb,z}+i {\omega }{\theta }=0. \end{aligned}$$

(27c)

The subscript zz refers to the second derivative with respect to z-axis. The principle of exchange of instabilities has to be valid for whole cases before looking forward to the analytical or numerical procedures used for investigating the stability behavior of the basic flows. The condition under which the eigenvalues problem satisfies the principle of exchange of instabilities is when no traveling modes arising out of the perturbed basic solution. A formal proof is carried out in Appendix A for a limiting case $H\rightarrow 0$. The procedure that is used to valid the principle of exchange of instabilities in Appendix A can also be applied to other cases. The variable coefficients of $T'_{fb}$ in the general case and $\gamma \rightarrow 0$ hinder the condition of $\omega _R=0$ to be analytically demonstrated. However, the numerical results exhibit the absence of the oscillatory modes in these two cases. Otherwise, as the linear stability analysis is looking for neutral modes, the condition of $\omega _I=0$ must be taken into consideration. Therefore, the eigenvalues problem can be simplified as

$$\begin{aligned}&{\psi }_{,zz}-a^2 {\psi }+a R \dfrac{1+\gamma }{\gamma }{\theta } =0, \end{aligned}$$

(28a)

$$\begin{aligned}&{\varphi }_{,zz}-a^2 {\varphi }+{\gamma }H({\theta }-{\varphi })=0, \end{aligned}$$

(28b)

$$\begin{aligned}&{\theta }_{,zz}-a^2 {\theta }+H({\varphi }-{\theta })-a {\psi } T_{fb,z}=0, \end{aligned}$$

(28c)

while the boundary conditions are

$$\begin{aligned} {\psi }(0)=0, \quad {\varphi }_{,z}(0)- {\varphi }(0) B_{f1}=0,\quad {\theta }_{,z}(0)-{\theta }(0) B_{f1}=0, \end{aligned}$$

(29a)

$$\begin{aligned} {\psi }_{,z}(1)=0, \quad {\varphi }_{,z}(1)+ {\varphi }(1) B_{f2}=0,\quad {\theta }_{,z}(1)+{\theta }(1) B_{f2}=0. \end{aligned}$$

(29b)

6 Analytical Solutions

The analytical solution for each case is restricted with such common condition related to the nature coefficients of $T_{fb,z}$. On the whole, the dispersion relation can be determined analytically from those limiting cases whose basic solution displays the expression $T_{fb,z}$ as an independent function of the variable z.

6.1 Limiting Case $B_{f1}=B_{s1}$ and $B_{f2}=B_{s2}$

The eigenvalue problem for this special case is defined as

$$\begin{aligned}&{\psi }_{,zz}-a^2 {\psi }+ a R\frac{{\gamma }+1}{\gamma }{\theta }=0, \end{aligned}$$

(30a)

$$\begin{aligned}&{\varphi }_{,zz}-a^2 {\varphi }+ H{\gamma }({\theta }-{\varphi })=0, \end{aligned}$$

(30b)

$$\begin{aligned}&{\theta }_{,zz}-a^2 {\theta }-H({\theta }-{\varphi })+a {\tilde{B}}_{f12}{\psi }=0. \end{aligned}$$

(30c)

$$\begin{aligned}&z=0: \quad {\psi }=0, \quad {\varphi }_{,z}- {\varphi } B_{f1}=0,\quad {\theta }_{,z}-{\theta } B_{f1}=0, \end{aligned}$$

(30d)

$$\begin{aligned}&z=1: \quad {\psi }_{,z}=0, \quad {\varphi }_{,z}+ {\varphi } B_{f2}=0,\quad {\theta }_{,z}+{\theta } B_{f2}=0. \end{aligned}$$

(30e)

The solution of Eq. (30) is obtained by expressing the functions ${\psi }(z)$, ${\varphi }(z)$ and ${\theta }(z)$ as sequence of exponential forms written as

$$\begin{aligned} {\psi }(z)= & {} \displaystyle \sum _{n=1}^{6} C_{n} e^{{{\chi }_n}z}, \end{aligned}$$

(31a)

$$\begin{aligned} {\varphi }(z)= & {} \displaystyle \sum _{n=1}^{6}\frac{a {\tilde{B}}_{f12} (a^2+H \gamma -{\chi _{n}}^2)}{ (a^2-{\chi _{n}}^2) (a^2+H+H \gamma -{\chi _{n}} ^2)} C_{n} e^{{{\chi }_n}z}, \end{aligned}$$

(31b)

$$\begin{aligned} {\theta }(z)= & {} \displaystyle \sum _{n=1}^{6} \frac{a H \gamma {\tilde{B}}_{f12} }{(a^2-{\chi _{n}}^2) (a^2+H+H \gamma -{\chi _{n}}^2)}C_{n} e^{{{\chi }_n}z}. \end{aligned}$$

(31c)

The coefficients ${{\chi }_n}$ are defined as

$$\begin{aligned} {\chi _{1,2}}= \pm (\sigma _{1})^{1/2}, \quad {\chi _{3,4}}= \pm (\sigma _{2})^{1/2}, \quad {\chi _{5,6}}= \pm (\sigma _{3})^{1/2}. \end{aligned}$$

(32)

The root parameters ${\sigma _{1}}$, ${\sigma _{2}}$ and ${\sigma _{3}}$ can be obtained from the following equation:

$$\begin{aligned} a^2\frac{ R {\tilde{B}}_{f12} (1+\gamma )}{\gamma } (a^2+H \gamma -\sigma )- (a^2-\sigma )^2 (a^2+H+H \gamma -\sigma )=0, \end{aligned}$$

(33)

The dimensionless number ${\tilde{B}}_{f12}$ is given as

$$\begin{aligned} {\tilde{B}}_{f12}= \frac{ B_{f1} B_{f2}}{(B_{f1}+B_{f2}+B_{f1} B_{f2})}. \end{aligned}$$

(34)

Now, we substitute Eq. (31) into the boundary conditions Eq. (30) to obtain a linear homogeneous system composed of six algebraic equations. These resulting equations yield a square matrix $\mathbf {M}$ multiplied by a column vector $\mathbf{c}=\{C_1, \ldots ,C_6\}$ written as

$$\begin{aligned} \mathbf {M} \cdot \mathbf{c}=0. \end{aligned}$$

(35)

The determinant of the matrix $\mathbf {M}$ is strictly null if the constraint $\{C_1, \ldots ,C_6\}\ne 0$ is satisfied. The validity of this condition can be admitted through the boundary conditions defined in Eq. (30). The resulting function which is obtained from the determinant of the matrix $\mathbf {M}$ is the dispersion relation of the marginal stability curves R(a) drawn for every fixed value of $(H,\gamma , B_s)$. The dispersion relation is defined as a combination of the parameters $a, R, H, B_{f1}, B_{f2}$, and for the sake of brevity it is not reported here.

6.2 Limiting Case $H\rightarrow \infty$ (LTE)

The analytical solution of LTE case is investigated by rescaling the parameters $\theta _{m}$ and ${\hat{\psi }}$ as :

$$\begin{aligned} \theta _{m}=\frac{\gamma \theta +\varphi }{1+\gamma }, \quad {\hat{\psi }}=\frac{\gamma }{1+\gamma } \psi . \end{aligned}$$

(36)

The temperature fields became equal when LTE case is hold which means $\theta =\varphi$. On account of Eq. (36), we can infer that $\theta =\varphi =\theta _m$. Consequently, Eqs. (28) and (29) are simplified to

$$\begin{aligned}&\hat{\psi }_{,zz}-a^{2} \hat{\psi }+a R {\theta }_{m}=0, \end{aligned}$$

(37a)

$$\begin{aligned}&{\theta }_{m,zz}-a^{2} {\theta }_{m}+a\frac{{B_{fm1}} {B_{fm2}}}{{B_{fm1}}+{B_{fm2}}+{B_{fm1}} {B_{fm2}}} \hat{\psi }=0. \end{aligned}$$

(37b)

$$\begin{aligned}&z=0: \quad \hat{\psi }(0)=0,\quad {\theta }_{m,z}(0)- {\theta }_{m}(0) B_{m2}=0, \end{aligned}$$

(37c)

$$\begin{aligned}&z=1: \quad \hat{\psi }_{,z}(1)=0, \quad {\theta }_{m,z}(1)+{\theta }_{m}(1)B_{m1}=0. \end{aligned}$$

(37d)

The analytical solution of ${\hat{\psi }}(z)$ and $\theta _{m}(z)$ is evaluated in the following form:

$$\begin{aligned} {\hat{\psi }}(z)= & {} C_1 e^{\eta _{1} z} + C_2 e^{-{\eta _1} z}+ C_3 e^{{\eta _2} z} + C_4 e^{-{\eta _2} z} \end{aligned}$$

(38a)

$$\begin{aligned} \theta _{m}(z)= & {} \sqrt{\frac{B_{m1} B_{m2}}{(B_{m1}+B_{m2}+B_{m1} B_{m2}) R}}( C_4 e^{-{\eta _2} z} + C_3 e^{{\eta _2} z}-C_2^{-{\eta _1} z} - C_1 e^{{\eta _1} z} ), \end{aligned}$$

(38b)

while the coefficients of $\sigma _1$ and $\sigma _2$ are determined as

$$\begin{aligned} \sigma _{1,2}=\sqrt{a (a\pm \sqrt{\frac{B_{m1} B_{m2} R}{B_{m1}+B_{m2}+B_{m1} B_{m2}}})}. \end{aligned}$$

(39)

The dispersion relation for a LTE case is computed by the same procedure employed for a special one $B_{f1}=B_{s1}$ and $B_{f2}=B_{s2}$. The case of LTE contrasts with the previous one in the number of vectors $C_n$. The linear algebraic equations resulted by substituting Eqs. (38) into (37) give rise to a just five coefficients in the column vector of $\mathbf {c}$ and $4 \times 4$ matrix. The determinant of the square matrix $\mathbf {M}$ defines a dispersion relation in a function of a, R, H, $\gamma$, $B_{m1}$ and $B_{m2}$.

6.3 Limiting Case $H\rightarrow 0$

The complete thermal decoupling case highlighted by limit $H\rightarrow 0$ with $\gamma \approx O(1)$ yields the following eigenvalues problem:

$$\begin{aligned}&{\psi }_{,zz}-{a}^{2} {\psi }+a \dfrac{1+{\gamma }}{{\gamma }} R {\theta }=0, \end{aligned}$$

(40a)

$$\begin{aligned}&{\theta }_{,zz}-a^{2} {\theta }+a {\tilde{B}}_{f12} {\psi }=0. \end{aligned}$$

(40b)

$$\begin{aligned}&z=0: \quad {\psi }(0)=0,\quad {\theta }_{,z}(0)-{\theta }(0) B_{f1}=0, \end{aligned}$$

(40c)

$$\begin{aligned}&z=1: \quad {\psi }_{,z}(1)=0,\quad {\theta }_{,z}(1)+{\theta }(1) B_{f2}=0. \end{aligned}$$

(40d)

We mention that the eigenvalues problem considered in the case of LTE is nearly the same as the one obtained when $H\rightarrow 0$. The two opposite behaviors of $H\rightarrow \infty$ and $H\rightarrow 0$ differ in the Darcy–Rayleigh number just by an overall scaling factor $\dfrac{\gamma }{\gamma +1}$, namely

$$\begin{aligned} \dfrac{1+{\gamma }}{{\gamma }} R \rightarrow R. \end{aligned}$$

(41)

Therefore, the modified dispersion relation can be analytically inferred from that of $H\rightarrow \infty$ by applying

$$\begin{aligned} B_{m1} \rightarrow B_{f1}, \quad B_{m2} \rightarrow B_{f2}. \end{aligned}$$

(42)

7 Numerical Solutions

The numerical procedure adopted in looking for the neutral stability curves is applicable for all basic state in contrast to the analytical method which is not available for a full case and $\gamma \rightarrow 0$. Consequently, the two cases are solved only numerically by employing the sixth-order Runge–Kutta solver with the shooting method. The same numerical procedure can be followed by other limiting cases to assess the compatibility between the analytical and numerical results. The use of a sixth-order Runge–Kutta technique required from the boundary conditions to be supported by such additional initial conditions at target $z=0$:

• The supplement conditions for general case,

  $$\begin{aligned} \psi '(0)=1,\quad \theta (0)=s_{1},\quad \varphi (0)=s_{2}. \end{aligned}$$

  (43)

• The supplement conditions for limiting case $\gamma \rightarrow 0$,

  $$\begin{aligned} \psi '(0)=1,\quad \theta (0)=s_{1}. \end{aligned}$$

  (44)

  As the governing equations are homogeneous, the normalization condition of $\psi '(0) = 1$ is fixed in both cases. The parameters $s_{1}$ and $s_{2}$ are denoted as unknown values for $\varphi (0)$ and $\theta (0)$, respectively. On the other hand, the eigenvalue R is, in fact, computed alongside the parameters $s_1$ and $s_2$ by means of a shooting method to fulfill the constraints imposed by the boundary conditions at $z=1$.

  • For the general case,

    $$\begin{aligned} \psi '(1)=0,\quad \theta '(1)+B_{f2}\theta (1)= 0,\quad \varphi '(1)+B_{s2}\varphi (1)= 0. \end{aligned}$$

    (45)

  • For the limiting case $\gamma \rightarrow 0$,

    $$\begin{aligned} \psi '(1)=0,\quad \theta '(1)+B_{f2}\theta (1)= 0. \end{aligned}$$

    (46)

  The Runge–Kutta solver and the shooting method are together implemented in the Mathematica 8 (© Wolfram Research) environment, through the built-in functions $\textit{NDSolve}$ and $\textit{FindRoot}$, respectively. The former function is employed in the numerical procedure as to deal with the initial value problem defined in Eqs. (28) and (29), while the latter one is used to valid the constraints of Eqs. (45) and (46). Moreover, the input data ($H, \gamma$, a, $B_{f1}, B_{s1}, B_{f2}, B_{s2}$) are required to be assigned in the overall numerical procedure to obtain the absolute minimum of the neutral stability curve R(a), which in turn describes the threshold values $(a_\mathrm{cr}, R_\mathrm{cr})$ for the initiate of the convective instability.

Table 1 Critical wave number and Darcy–Rayleigh number for different values of $B_{f1}$ and $B_{f2}$ in the limiting case $H \rightarrow 0$

Table 1 elucidates a comparison in the general case, of the numerical and analytical results tackled by using a shooting method and a dispersion relation for $H=0$ with $\gamma =10$. The congruence between the numerical and analytical values of the critical wavenumber and the critical Rayleigh–Darcy number is very clear, in particular with first eight figures.

8 Discussion of the Results

In a general case, the authors try to explore an explicit relationship between the Biot numbers by adjusting the request porosity of the medium as 1 / 2 and the heat transfer coefficients as the following form: ${h_{s1}}/{h_{f1}}={h_{s2}}/{h_{f2}}=1$.

8.1 General Case $B_{f1}=\gamma B_{s1}$ and $B_{f2}=\gamma B_{s2}$

The relative behavior of the general case Eq. (28) is highlighted in Figs. 3 and 4. The results plotted in these figures are, briefly, obtained by means of the numerical technique defined in Sect. 7. We would remind that stable flows always lay below each marginal stability curves which means less destabilization effects are concentrated in the thermoconvective region. The marginal stability curves in Fig. 3 show the familiar shape of stability problems related to Horton–Rogers–Lapwood configuration. Figure 3 exhibits the neutral curves of R against a for a different range of values of Biot numbers, with fixed $H=1$ and $\gamma =10$. If we compare the curves of the upper frames with those of the lower one, we notice a minor difference between the lowest branch of the marginal stability curves of $B_{s1}=1$ and $B_{s2}=1$, and also between those of $B_{f1}=1$ and $B_{f2}=1$. Comparison of $B_{s1}=1$ or $B_{s2}=1$ with $B_{f1}=1$ or $B_{f2}=1$ exhibits that the variation in R(a) is more sensitive to the Biot numbers of the solid phase than the fluid one as the marginal curves show the largest threshold values when solid boundary layers have a poor ability to absorb or lose heat to the external medium.

Fig. 3

General case $B_{s1}=\gamma B_{f1}$ and $B_{s2}=\gamma B_{f2}$: neutral stability curves relative to $H=1$ and $\gamma =10$ with various values of Biot numbers

Otherwise, to uphold the remarks deduced from the neutral curves, Fig. 4 displays the main trend of $R_c$ and $a_c$ for various values of $\gamma$ with $H=1$. The curves of R in the left frames show a clear non-monotonic increasing behavior with the Biot numbers of the solid phase and $\gamma$, whereas in the right frames, the trend of $a_c$ is an increasing function of $B_{s1}$ and $B_{s2}$, on the other hand, a decreasing function of $\gamma$. In other words, the basic solution always is stable when both layers behave as an insulating surface, but as one layer approaches Dirichlet boundary conditions, the destabilization effects grow in a porous medium and a basic solution becomes less stable with maximum critical values $R_c=974.213$ and $R_c=581.367$ attained for $\gamma \rightarrow \infty$. Otherwise, the increasing behavior of $R_c$ with respect to $\gamma$ resembles the one defined for a more general case in Barletta et al. (2015) and Celli et al. (2017). The peculiar shape of the curves defined in Fig. 4 refers to the implicit role of the factor $\gamma$ in the assumption assigned by the authors for a general case and in a transition effect of the Biot numbers from an adiabatic state to an isothermal one. Shortly, the basic flow exhibits the most stable state in the configurations of $B_{s1} \rightarrow 0$, $B_{s2} \rightarrow 0$, $B_{s1} \approx \gamma \rightarrow \infty$ and $B_{s2}\approx \gamma \rightarrow \infty$.

Fig. 4

General case $B_{s1}=\gamma B_{f1}$ and $B_{s2}=\gamma B_{f2}$: the trend of $R_c$ and $a_c$ with $H=1$ for different values of $\gamma$. The upper frames display curves for $B_{s1}=1$, while the lower frames display curves for $B_{s2}=1$

8.2 Limiting Case $B_{f1}=B_{s1}$ and $B_{f2}=B_{s2}$

The analytical results defined for this limiting case are illustrated in Fig. 5. Figure 5 displays the change in $R_c$ and $a_c$ versus Biot numbers for different values of $\gamma$ and fixed value of $H=1$. The trend of $R_c$ in Fig. 5 is monotonically increasing function as $B_{s1}$ or $B_{s2}$ decreases. In this case, the basic solution experiences the stability behavior only when surface layers have a poor ability to exchange heat with external fluid. The figure also exhibits that an infinite value of $R_c$ appears in the case where a perfect conducting fluid phase is present. This would imply that for an insulating solid boundary layer and with an infinite thermal conductivity ratio the basic flow always is stable. Otherwise, increasing $B_{s1}$ or $B_{s2}$ means a monotonic decreasing behavior of $R_{c}$ with a maximum critical values $R_c =26.070$ and $R_c=40.640$ obtained when a fluid phase has the highest thermal conductivity. This implies that the destabilization effects increase as the solid boundary layers become nearer to isothermal state. We remind that Barletta et al. (2015) have attained $R_c= 26.749$ in the conditions where $H=10$ and $\gamma =10$ for a configuration of isothermal Robin boundary conditions. On the other hand, the variation in $a_c$ versus $B_{s1}$ and $B_{s2}$ displays a monotonic increasing behavior as $B_{s1}$ or $B_{s2}$ increases. The asymptotic dashed line in the curves of the critical wavenumber refer to cases defined by $B_{s1} \approx \gamma \rightarrow \infty$ and $B_{s2}\approx \gamma \rightarrow \infty$ where $a_c=1.787$ and $a_c=1.959$, respectively. Broadly speaking, despite the infinite value of $\gamma$ in this limiting case the porous layer is considered less stable in the configuration of $B_{s1} \rightarrow \infty$ and $B_{s2} \rightarrow \infty$ than the general one, whereas in the configuration of $B_{s1}\rightarrow 0$ or $B_{s2} \rightarrow 0$ both cases show the same stabilization effects.

Fig. 5

Limiting case $B_{s1}= B_{f1}$ and $B_{s2}=B_{f2}$: the trend of $R_c$ and $a_c$ with $H=1$ for different values of $\gamma$

8.3 Special Case of LTE

The analytical results plotted for LTE case are based on the dispersion relation defined in Sect. 6.2. Figure 6 summarizes both variation in $R_c$ and $a_c$ versus $B_{m1}$ for a case of $B_{m2} \rightarrow \infty$. The trend of $a_{c}$ in Fig. 6 has a monotonically increasing behavior as $B_{m1}$ increases, while the curves of $R_c$ decreases as $B_{m1}$ increases. We remark that $R_c$ is bounded by an infinite value when $B_{m1} \rightarrow 0$ and by $R_c=27.0976$ when $B_{m1} \rightarrow \infty$. The threshold values $R_c=27.0976$ and $a_c=2.3262$ are attained for a configuration where both layers have a perfect conducting effective temperature surface. We recall that $R_c=27.0976$ and $a_c=2.3262$ are the standard critical values obtained for Darcy– Bénard problem with one free surface and Dirichlet temperature conditions. The limits of $B_{m1} \rightarrow \infty$ and $B_{m2}\rightarrow \infty$ can adopt several configurations at the same time. For example, it can correspond to $B_{f1}\approx B_{f2}\rightarrow \infty$ with $\gamma =B_{s1}=B_{s2}\approx O(1)$ or $B_{s1}=B_{f1}\rightarrow \infty$ and $B_{s2}=B_{f2}\rightarrow \infty$ with $\gamma \approx O(1)$. On the whole, the more the values of $B_{m1}$ approach isothermal case, the more the porous medium produces destabilization effects.

Fig. 6

Local thermal equilibrium: the trend of $R_c$ and $a_c$ versus $B_{m1}$ in the limiting case $H \rightarrow \infty$

8.4 Limiting Case $H \rightarrow 0$

The suitable analytical results of the limiting case $H\rightarrow 0$ are concluded from the dispersion relation defined in the LTE case. We would remind that the two cases of LTE and $H\rightarrow 0$ are formally similar in the eigenvalues problem as $B_{m1}\rightarrow B_{f1}$ and $B_{m2}\rightarrow B_{f2}$. We prescribe the ordinate axes of the frames with $R_c$ instead of $({1+{\gamma }}/{\gamma }) R_c$ to facilitate the interpretation of the plots displayed in Fig. 7. This latter describes how the trend of $R_c$ can vary with respect to $B_{f1}$ and $B_{f2}$ for different values of $\gamma$. The curves of $R_c$ exhibit a non-monotonic decrease as one of the Biot numbers and $\gamma$ increase. We notice that the threshold values of $R_c=40.640$ and $R_c=26.070$ in the configuration of $B_{f2}=\gamma \rightarrow \infty$ and $B_{f1}=\gamma \rightarrow \infty$ are exactly the same to those highlighted in the special case of $B_{f1}=B_{s1}$ and $B_{f2}=B_{s2}$ with one perfect conducting fluid boundary. Figure 7 also displays that the basic flow always has a stable configuration when one of the fluid boundaries behaves as a perfect insulating medium. Otherwise, the stability behavior has a more significant effect in the case of $B_{f2}\rightarrow \infty$ than the case of $B_{f1}\rightarrow \infty$.

Fig. 7

Limiting case $H \rightarrow 0$: plots of $R_{c}$ versus $B_{f1}=1$ (right frame) and $B_{f2}=1$ (left frame) for different values of ${\gamma }$

8.5 Limiting Case $\gamma \rightarrow 0$

The numerical results in this limiting case are usually reported by the rescaled term of the Darcy–Rayleigh number ${\hat{R}}$ which is defined as

$$\begin{aligned} {{\hat{R}}}=\dfrac{1+\gamma }{\gamma } R \approx O(1). \end{aligned}$$

(47)

The scaling procedure is performed to improve the understanding of this limiting case as $R\rightarrow 0$. Furthermore, the numerical procedure is computed with the presence of $B_{f1}=B_{s1}$ and $B_{f2}=B_{f2}$ in order to optimize the large number of the input parameters. Figure 8 exhibits the variation plots of $\hat{R_c}$ and $a_c$ for various values of H ranging from 0 to $10^{2}$. The upper frames display that increasing $B_{s2}$ and H, consequently, leads to a monotonic increase in both $\hat{R_c}$ and $a_c$. On the other hand, the lower frames elucidate the monotonic decrease in ${\hat{R}}_c$ when $B_{s1}$ and H increase. The plots of $a_c$ change as function of H and $B_{s2}$, and they become strictly horizontal as $B_{s1}$ and H increase. This would mean that the basic flow attains the most stable configurations when one of the situations defined with $B_{s1}\rightarrow 0$ and $B_{s2}\rightarrow \infty$ or $B_{s2}\approx B_{s1} \rightarrow 0$ is satisfied: $\hat{R_c}=635.205$, $a_c=6.033$ and $\hat{R_c}=208.817$, $a_c=4.168$, respectively.

Fig. 8

Limiting case $\gamma \rightarrow 0$: plots of ${\hat{R}}_c$ versus $B_{s1}=1$ (right frame) and $B_{s2}=1$ (left frame) for the sample case of $B_{f1}=B_{s1}$ and $B_{f2}=B_{s2}$ with different values of H

9 Conclusion

The stability of the basic stationary flow in the modified version of the Darcy–Bérnad problem has been investigated. A horizontal porous layer with infinite extent is saturated by a Newtonian fluid, confined between a free surface on the top and rigid wall at the bottom. Both surface layers are modeled as Robin boundary conditions in which different heat exchange coefficients are considered. The number of the characteristic dimensionless parameters stemmed from Robin boundaries has increased into four Biot numbers besides H and $\gamma$ whose effects are taken into account due to LTNE. The difference in Biot numbers between the free surface on the top and rigid wall in the bottom provided more limiting cases and variables. On the other hand, the response to a small linear fluctuation is adopted by means of normal modes method. The resulting eigenvalue problem is solved either analytically or numerically. The main results obtained for different choices of the governing parameters ($H, \gamma , B_{f1}, B_{s1}, B_{f2}, B_{s2}$) in every special case are summarized as:

• The Biot numbers in limits of perfect insulating layers for the more general case have the more stabilization effect on medium than isothermal boundaries.

• When the LTE behavior is taken into account, the basic solution defined for a more general case in the configurations of $B_{s1}\rightarrow \infty$ with $B_{s2}\approx O(1)$ or $B_{s2}\rightarrow \infty$ with $B_{s1}\approx O(1)$ is much more stable than the special one of $B_{f1}=B_{s1}$ and $B_{f2}=B_{s2}$.

• The prevailing effect of buoyancy forces in a solid matrix with a poor thermal resistance than the saturating fluid is less efficient in the case where a solid phase has a higher heat transfer coefficient at the upper free surface. The basic solution also shows the more stable configurations when both layers have a weak ability to exchange heat with the surrounding medium.

• The case characterized by no thermal energy transferred from one phase to another behaves exactly as we have simultaneously the case of the LTE model with the condition of $B_{f1}=B_{s1}$ and $B_{f2}=B_{s2}$.

Appendix A : The Principle of Exchange of Instabilities for Limiting Case \(H\rightarrow 0\)

The eigenvalue problem obtained for the case characterized by no transfer of the heat is carried out between the two phases is

$$\begin{aligned}&{\psi }{''}-a^2 {\psi }+a \dfrac{1+\gamma }{\gamma } R{\theta } =0, \end{aligned}$$

(48a)

$$\begin{aligned}&{\theta }''-a^{2} {\theta }+a {\tilde{B}}_{f12}{\psi } +i {\omega _R} \dfrac{\chi +\gamma }{1+\gamma }\theta =0. \end{aligned}$$

(48b)

$$\begin{aligned}&z=0: \quad {\psi }(0)=0,\quad {\theta }'(0)+B_{f1} {\theta }(0)=0, \end{aligned}$$

(48c)

$$\begin{aligned}&z=1: \quad {\psi }'(1)=0, \quad {\theta }'(1)+B_{f2} {\theta }(1)=0. \end{aligned}$$

(48d)

Multiplying Eqs. (48a), (48b) by the complex conjugate quantities $\bar{\psi }$ and $\bar{\theta }$, respectively, gives rise to two complex resulting equations. These equations are integrated by part with the use of boundary conditions, namely

$$\begin{aligned}&-\int _0^1 | \psi ' |^2\ \hbox {d}z - a^2 \int _0^1 | \psi |^2\ \hbox {d}z + a \, \, R \, \dfrac{1+\gamma }{\gamma } \int _0^1 \theta \, {\overline{\psi }} \ \hbox {d}z=0, \end{aligned}$$

(49a)

$$\begin{aligned}&\quad B_{f1}|\theta (0)|^2 -B_{f2}|\theta (1)|^2 - \int _0^1 |\theta '|^2 \ \hbox {d}z - a^2 \int _0^1 |\theta |^2 \ \hbox {d}z \nonumber \\&\quad +a {\tilde{B}}_{f12} \int _0^1 \psi \, {\overline{\theta }} \ \hbox {d}z + i{\omega _R} \dfrac{\chi +\gamma }{1+\gamma } \int _0^1 |\theta |^2 \ \hbox {d}z= 0. \end{aligned}$$

(49b)

After multiplying Eq. (49a) by the parameter $\dfrac{-\gamma {{\tilde{B}}}_{f12}}{R(1+\gamma )}$, we can now add it to Eq. (49b) to obtain

$$\begin{aligned}&\dfrac{\gamma {{\tilde{B}}}_{f12}}{R(1+\gamma )} \left( \int _0^1 | \psi ' |^2\ \hbox {d}z + a^2 \int _0^1 | \psi |^2\ \hbox {d}z \right) \nonumber \\&\quad + B_{f1}|\theta (0)|^2 -B_{f2}|\theta (1)|^2 - \int _0^1 |\theta '|^2 \ \hbox {d}z - a^2 \int _0^1 |\theta |^2 \ \hbox {d}z + i{\omega _R} \dfrac{\chi +\gamma }{1+\gamma } \int _0^1 |\theta |^2 \ \hbox {d}z= 0 .\nonumber \\ \end{aligned}$$

(50)

The two parts of real and imaginary in Eq. (50) have to be independently equal to zero to satisfy the condition of

$$\begin{aligned} \omega _R \int _0^1 |\theta |^2 \ \hbox {d}z= 0 . \end{aligned}$$

(51)

Equation (51) defines two different assumptions. The first one is $\theta =0$ which means no secondary flow exists in the basic state. This condition cannot be acceptable because it would imply a contradiction with what we are looking for. Thus, this result supports the validity of the second assumption which is $\omega _R=0$. Consequently, we can assure that the eigenvalue problem of this limiting cases holds the principle of exchange of instabilities.