1 Introduction

The first notable works were done by Horton and Rogers (1945) and Lapwood (1948). They studied a problem similar to the Rayleigh–Bénard problem over a porous medium. They have considered a horizontal porous layer where the boundaries are at constant temperature (the lower boundary being hotter than the upper one) and found that the critical Rayleigh number for the onset of convection is \(4\pi ^2\). Weber (1974) discussed the combined effect of horizontal and vertical temperature gradient in a horizontal porous medium bounded by perfectly conducting boundaries. A basic flow is induced by the horizontal temperature gradient. It is shown that the critical Rayleigh number increases in the presence of small horizontal temperature gradient. Nield (1991) extended the analysis of Weber (1974) by including horizontal gradient of large magnitudes. A detailed discussion on the thermal convection can be found in Nield and Bejan (2013).

Recently instead of only thermal convection researchers are showing interest on thermosolutal convection. The stability of the convection induced by vertical thermal and solutal gradients in a porous medium is studied by Nield (1968). His analysis is extended by Taunton et al. (1972) to study the onset of salt finger formation in a horizontal porous layer in the presence of both thermal and solutal gradients. Nield et al. (1993) studied the thermosolutal convection induced by inclined thermal and solutal gradients. Later Manole et al. (1994) analyzed the thermosolutal convection due to inclined temperature gradient in a horizontal porous layer in the presence of horizontal mass flow.

In the above-mentioned works, the cross-coupling between thermal and solutal gradients is neglected. However, the cross-diffusion effects can be significant in case of binary or multicomponent liquids. In a binary fluid, two components diffuse at different rates and eventually the fluid at rest can become unstable. The concentration flux due to the thermal gradient is called the Soret effect, and the thermal flux due to the concentration gradient is called the Dufour effect. In liquid mixtures, the Dufour effect can be considered as negligible.

Hurle and Jakeman (1971) studied the Soret-driven double-diffusive convection to analyze the effect of Soret number on Rayleigh–Jeffreys problem. Both numerical and experimental results are given. It is reported that over-stability may occur depending on the magnitudes of the Soret number. Patil and Rudriah (1980) have investigated the Soret effect on the convective instability in a horizontal fluid layer bounded by two rigid surface. A stability can be found even if the layer is heated from below and salted from above. Brand and Steinberg (1983) studied the instability in a cell filled with binary fluid mixture considering both the case of heating from above or below. The Soret effect in the medium is considered. They found that an oscillatory instability can also occur when the medium is heated from above. Charrier-Mojtabi et al. (2007) have performed an analytical study of the Soret-driven convection in a horizontal porous medium cell filled with a binary fluid. Both analytical and numerical techniques are incorporated to study the monocellular flow at the onset of convection. The Soret effect on double-diffusive convection induced by inclined thermal and solutal gradients in a horizontal porous layer is analyzed by Narayana et al. (2008). Galerkin method is used to investigate both stationary and oscillatory instability. Gaikwad et al. (2009) have performed linear and nonlinear stability analysis to study the effect of Soret coefficient in an anisotropic porous layer which is heated and salted from below. For small values of \(Ra_\mathrm{S}\), negative Soret coefficient shows a destabilizing effect and positive Soret coefficient shows a stabilizing effect. This trend reverses for large \(Ra_\mathrm{S}\). Recently Deepika (2018) analyzed the effect of Soret parameter on the double-diffusive convection using both linear and nonlinear stability theories. In these studies of nonlinear stabilities also, the effect of viscous dissipation is neglected.

During recent years it is noted that viscous dissipation can have a significant effect on vigorous natural convection, e.g., if the viscosity of the medium is very high but the conductivity is small. These type of fluids is very common in petroleum engineering etc. Gebhart (1962) investigated the effect of viscous dissipation on natural convection considering a vertical surface. He introduced a number to represent the effect of viscous dissipation to the medium. Gebhart and Mollendorf (1969) studied the effect of viscous dissipation on external natural convection. The effect of viscous dissipation on Bénard convection is enquired by Turcotte et al. (1974). A review paper on modeling of viscous dissipation term in a porous medium is published by Nield (2007). Recently, the linear stability analysis of the convection induced by viscous dissipation in a horizontal porous layer is done by Barletta et al. (2009). A base flow in the horizontal plane is assumed. The lower boundary is considered as adiabatic and upper boundary as isothermal. Viscous dissipation shows a destabilizing effect. Barletta et al. (2010) extended this analysis by considering a horizontal temperature gradient along the upper boundary. The effect of viscous dissipation on the Hadley–Prats flow is presented by Barletta and Nield (2010). It is found that for sufficiently large horizontal temperature gradient, instability can occur even in the absence of a vertical temperature difference. The double-diffusive convection induced by viscous dissipation is also studied by Barletta and Nield (2011) by including a horizontal throughflow. The preferred mode of instability (longitudinal or transverse) depends on the value of the dissipation parameter. Recently Roy and Murthy (2015) studied the effect of the Soret parameter on the double-diffusive convection caused solely due to the viscous dissipation. They have also considered a basic horizontal flow. The critical Rayleigh number might increase or decrease in the presence of Soret parameter depending on the values of the viscous dissipation parameter.

Many articles on the stability in a horizontal porous layer bounded above and below by two walls can be found in the literature. However, in many practical situations the upper boundary can be open, e.g., the Earth’s surface. The Earth’s mantle consists of different types of fluids. Therefore, the double-diffusive convection plays a major role in these areas. Moreover, a mass flux may be produced by the geothermal heating, solar heating, etc. To study the fertilizer distribution in soil, waste management, oil separation, etc., it is important to study the double-diffusive convection in a porous medium with an open boundary and significant Soret effect. Furthermore, for high viscous fluids like oil, the viscous dissipation can have significant effect. Nield (1968) explored the rise of instability in a binary solution in a horizontal porous layer happening due to vertical thermal and solutal gradient. He reported that if the upper boundary is open, the critical Rayleigh number for the onset of convection is \(\pi ^2\) which is less than the critical Rayleigh number (\(4\pi ^2\)) of Horton–Rogers–Lapwood (HRL) convection. Lu et al. (1999) found that if the porous medium is filled with ideal gas and the top boundary is open, the critical Rayleigh number is less than \(\pi ^2\). The effect of viscous dissipation on the stability of the flow in a horizontal porous layer with an upper open boundary is studied by Barletta and Storesletten (2010). The viscous dissipation has a destabilizing effect, and horizontal temperature gradient is stabilizing.

Although several studies exist to analyze the linear stability of the convective flow considering significant Soret effect, no work is done to discuss the effect of Soret parameter when the top boundary is open. In this work the Soret effect on double-diffusive convection in the presence of significant viscous dissipation is studied considering the upper surface to be open. The lower boundary is impermeable and subjected to a heat flux and a constant concentration \(C_0\). There is a horizontal temperature gradient along the upper boundary. A constant concentration \(C_l\) is maintained throughout the upper boundary. A linear stability analysis is done by adopting normal modes. The numerical solution that is obtained is analyzed by varying the governing parameters.

2 Mathematical Formulation

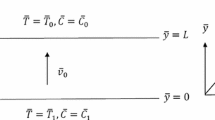
A horizontal plane porous layer of thickness l is considered (Fig. 1). The porous medium is saturated by a binary fluid mixture. The boundary at \(\bar{y}=l\) is open, whereas the boundary at \(\bar{y}=0\) is taken as impermeable. The boundaries have uniform concentrations, and the concentration is denoted by \(\bar{C}\). The lower boundary is heated with a uniform flux \(q_0\). The temperature is varying linearly along the upper boundary in horizontal direction. Here ‘bar’ denotes dimensional quantities. \(\bar{y}\) is taken as the vertical axis so that the gravitational acceleration is \(\mathbf {g}=-g\mathbf {e}_y\). The effect of viscous dissipation in the medium is included. The mass flux generated due to the thermal diffusion (Soret effect) is taken into account. The assumptions made are (i) Darcy model holds and (ii) Oberbeck–Boussinesq approximation can be applied.

Fig. 1
figure 1

Physical configuration of the system

Full size image

2.1 Governing Equations

Under these assumptions the governing equations for the problem is given by

$$\begin{aligned}&\bar{\nabla }\cdot \bar{\mathbf {u}}=0, \end{aligned}$$
(1)
$$\begin{aligned}&\frac{\mu }{K}\bar{\mathbf {u}}=-\bar{\nabla }\bar{p}+\rho _0 g\left[ \beta _T(\bar{T}-T_{0})+\beta _C(\bar{C}-C_{0})\right] \mathbf {e}_y, \end{aligned}$$
(2)
$$\begin{aligned}&\sigma \frac{\partial \bar{T}}{\partial \bar{t}}+\bar{\mathbf {u}}\cdot \bar{\nabla }\bar{T}=\alpha \bar{\nabla }^{2}\bar{T}+ \frac{\nu }{Kc}\bar{\mathbf {u}}\cdot \bar{\mathbf {u}}, \end{aligned}$$
(3)
$$\begin{aligned}&\phi \frac{\partial \bar{C}}{\partial \bar{t}}+\bar{\mathbf {u}}\cdot \bar{\nabla }\bar{C}=D\bar{\nabla }^{2}\bar{C}+D_{CT} \bar{\nabla }^{2}\bar{T}, \end{aligned}$$
(4)

where \(\bar{\mathbf {u}}=(\bar{u},\bar{v},\bar{w})\) is the velocity, \(\mu \) and \(\nu \) are the dynamic viscosity and kinematic viscosity, respectively, K is the permeability, \(\bar{p}\) is the pressure, \(\rho _0,\, T_0,\,C_0\) are the reference density, temperature and concentrations, respectively. \(\beta _T\) and \(\beta _C\) are thermal and concentration expansion coefficients, respectively, \(\phi \) is the porosity of the layer, \(\sigma \) is the ratio between the average volumetric heat capacity of the fluid saturated porous medium and the volumetric heat capacity of the fluid (\(\rho _0c\)). c is the heat capacity per unit mass of the fluid, \(D_{CT}\) is the Soret coefficient (Nield and Bejan 2013), \(\alpha \) is the thermal diffusivity, D is the mass diffusivity. The boundary conditions are

$$\begin{aligned} \bar{y}&=0:\,\bar{v}=0,\,\frac{\partial \bar{T}}{\partial \bar{y}}=-\frac{q_0}{k},\,\bar{C}=C_{0}, \end{aligned}$$
(5)
$$\begin{aligned} \bar{y}&=l:\,\bar{p}=p_0,\,\bar{T}=\bar{T_{0}}+\frac{q_h}{k}(\bar{x}\cos \gamma +\bar{z}\sin \gamma )T,\nonumber \\ \bar{C}&=C_{l}. \end{aligned}$$
(6)

Since the upper boundary is open, it is assumed that a constant pressure (\(p_0\)) is maintained at the top boundary. k is the thermal conductivity, \(q_0\) is the heat flux at the bottom boundary and \(q_h\) is the applied horizontal heat flux along the top boundary, \(\gamma \) is the angle between the x-axis and the imposed temperature gradient.

2.2 Non-dimensionalization

The governing Eqs. (1)–(6) are non-dimensionalized using the following non-dimensional variables

$$\begin{aligned}&(\bar{x},\bar{y},\bar{z})=(x,y,z)L,\, \bar{t}=t\frac{\sigma L^{2}}{\alpha },\, (\bar{u},\bar{v},\bar{w})=(u,v,w)\frac{\alpha }{L},\nonumber \\&\bar{T}=\bar{T_{0}}+T\frac{\nu \alpha }{g\beta _{T}lK} ,\,\bar{C}=C_l+C(C_0-C_l),\,\bar{p}=\bar{p_{0}}+p\frac{\mu \alpha }{K}. \end{aligned}$$
(7)

The non-dimensional governing equations and boundary conditions are given by

$$\begin{aligned}&\nabla \cdot \mathbf {u}=0, \end{aligned}$$
(8)
$$\begin{aligned}&\mathbf {u}=-\nabla p+\left( T+\frac{Ra_\mathrm{S}}{Le}C\right) \mathbf {e}_y, \end{aligned}$$
(9)
$$\begin{aligned}&\frac{\partial T}{\partial t}+\mathbf {u}\cdot \nabla T=\nabla ^{2}T+Ge\,\mathbf {u}\cdot \mathbf {u}, \end{aligned}$$
(10)
$$\begin{aligned}&\varLambda \frac{\partial C}{\partial t}+\mathbf {u}\cdot \nabla C=\frac{1}{Le}\nabla ^{2}C+Sr\nabla ^{2}T, \end{aligned}$$
(11)
$$\begin{aligned}&y=0:\quad v=0,\quad \frac{\partial T}{\partial y}=-Ra,\quad C=1, \end{aligned}$$
(12)
$$\begin{aligned}&y=1: \quad p=0, \quad T=Ra_{H}(x\cos \gamma +z\sin \gamma ),\,C=0. \end{aligned}$$
(13)

Using the governing equations, the boundary condition \(p=0\) at \(y=1\) can be substituted by \(u=0\) and \(w=0\). The non-dimensional parameters are defined as

$$\begin{aligned} Ge&=\frac{\beta _T gl}{c},\quad Ra=\frac{\beta _T g q_0Kl^2}{\nu \alpha k},\quad Ra_\mathrm{H}=\frac{\beta _T g q_hKl^2}{\nu \alpha k},\quad Ra_\mathrm{S}=\frac{\beta _C(C_0-C_l) g Kl}{\nu },\nonumber \\ Le&=\frac{\alpha }{D},\quad \varLambda =\frac{\phi }{\sigma },\quad Sr=\frac{D_{CT}\nu }{\beta _T g Kl(C_0-C_l)}. \end{aligned}$$
(14)

where Ge is the Gebhart number, Ra is the thermal Rayleigh number corresponding to the heat flux at the bottom boundary, \(Ra_\mathrm{H}\) is horizontal thermal Rayleigh number, \(Ra_\mathrm{S}\) is the solutal Rayleigh number, Le is the Lewis number, and Sr is the Soret parameter.

2.3 Basic Solution

The imposed horizontal gradient induces a basic horizontal flow. A basic solution of Eqs. (8)–(13) is assumed to be

$$\begin{aligned} u_{B}&=u_B(y),\quad v_{B}=0,\quad w_{B}=w_B(y),\nonumber \\ T_{B}&= T_{B} (x,y,z),\quad C_{B}=C_{B}(y), \quad p_{_B}= p_{_B} (x,y,z). \end{aligned}$$
(15)

Solving Eqs. (8)–(13) for \(u_B, w_B, T_B, p_B, C_B\), the following expressions are obtained,

$$\begin{aligned} u_B(y)&=Ra_H(1-y)\cos \gamma ,\quad v_B(y)=0,\quad w_B(y)=Ra_H(1-y)\sin \gamma , \end{aligned}$$
(16)
$$\begin{aligned} T_B(y)&=Ra_H(x\cos \gamma +z\sin \gamma )+Ra(1-y)-\frac{Ra_H^2}{12}[Gey^4-2(2Ge-1)y^3 \nonumber \\&\quad +6(Ge-1)y^23Ge+4], \end{aligned}$$
(17)
$$\begin{aligned} C_B(y)&=1-y+LeRa_H^2Sr \left[ \left( \frac{y}{3}-\frac{y^2}{2}+\frac{y^3}{6}\right) \right] -Ge\left( \frac{y}{4}-\frac{y^2}{2}+\frac{y^3}{3}-\frac{y^4}{12}\right) ,\qquad \end{aligned}$$
(18)
$$\begin{aligned} p_{_B}(y)=&-Ra_H(x\cos \gamma +z\sin \gamma )(1-y)-\frac{1}{2Le} (Le\,Ra+Ra_\mathrm{S})(1-y)^2\nonumber \\&\quad +\frac{Ra_H^2}{120}(1-y)^2(Ra_\mathrm{S}\,Sr-1)y [2Ge\,y^2-(6Ge-5)y+6Ge-10]. \end{aligned}$$
(19)

The thermal convection with this physical configuration is considered by Barletta and Storesletten (2010). It is seen that the Soret effect does not change the basic velocity and temperature profiles. However, there is a significant change in the pressure distribution. Since Soret effect in the medium is considered, a basic concentration profile with Soret parameter is obtained.

2.4 Linear Stability Analysis

The aim of this study is to find the stability of the basic flow to infinitesimal disturbances. Therefore, a small perturbation \(\varepsilon \) is introduced to the basic solution.

$$\begin{aligned} \mathbf {u}=\mathbf {u}_{B}+\varepsilon \mathbf {U},\quad T=T_{B}+\varepsilon \theta ,\quad C=C_{B}+\varepsilon \chi . \end{aligned}$$
(20)

\(\mathbf {U}\) is given by (U, V, W). Equation (20) is substituted into Eqs. (8)–(13) and then linearized with respect to \(\varepsilon \) by discarding second and higher-order terms of \(\varepsilon \). The final set of linearized governing equations and boundary conditions are

$$\begin{aligned}&\nabla \cdot \mathbf {U}=0, \end{aligned}$$
(21)
$$\begin{aligned}&\nabla \times \mathbf {U}=\nabla \times \left[ \left( \theta +\frac{Ra_\mathrm{S}}{Le}\chi \right) \mathbf {e}_y\right] , \end{aligned}$$
(22)
$$\begin{aligned}&\frac{\partial \theta }{\partial t}+\mathbf {u}_B\cdot \nabla \theta +\mathbf {u}\cdot \nabla T_B=\nabla ^{2}\theta +2Ge\,\mathbf {u}_B\cdot \mathbf {u}, \end{aligned}$$
(23)
$$\begin{aligned}&\varLambda \frac{\partial \chi }{\partial t}+\mathbf {u}_B\cdot \nabla \chi +\mathbf {u}\cdot \nabla \chi _{_B}=\frac{1}{Le}\nabla ^{2}\chi +Sr\nabla ^{2}\theta , \end{aligned}$$
(24)
$$\begin{aligned}&y=0:\quad V=0,\quad \frac{\partial \theta }{\partial y}=0,\quad \chi =0, \end{aligned}$$
(25)
$$\begin{aligned}&y=1:\quad U=0,\quad W=0,\quad \theta =0,\quad \chi =0. \end{aligned}$$
(26)

Any disturbance can be assumed to have a two-dimensional form. Therefore, the solutions are made independent of z-axis and the velocity components are written in terms of stream function \(\psi \).

$$\begin{aligned} U=\frac{\partial \psi }{\partial y},\quad V=-\frac{\partial \psi }{\partial x}. \end{aligned}$$
(27)

The stream function temperature formulation of the problem (21)–(26) is given by

$$\begin{aligned}&\frac{\partial ^2\psi }{\partial x^2}+\frac{\partial ^2\psi }{\partial y^2}=-\left( \frac{\partial \theta }{\partial x}+\frac{Ra_\mathrm{S}}{Le}\frac{\partial \chi }{\partial x}\right) , \end{aligned}$$
(28)
$$\begin{aligned}&\frac{\partial \theta }{\partial t}+u_B\frac{\partial \theta }{\partial x}+\frac{\partial \psi }{\partial y}\frac{\partial T_B}{\partial x}-\frac{\partial \psi }{\partial x}\frac{\partial T_B}{\partial y}=\nabla ^2\theta +2Ge\,u_B\frac{\partial \psi }{\partial y}, \end{aligned}$$
(29)
$$\begin{aligned}&\varLambda \frac{\partial \chi }{\partial t}+u_B\frac{\partial \chi }{\partial x}-\frac{\partial \chi }{\partial x}\frac{\partial C_B}{\partial y}=\frac{1}{Le}\nabla ^2\chi +Sr\nabla ^2\theta , \end{aligned}$$
(30)
$$\begin{aligned}&y=0:\quad \frac{\partial \psi }{\partial x}=0,\quad \frac{\partial \theta }{\partial y}=0,\quad \chi =0, \end{aligned}$$
(31)
$$\begin{aligned}&y=1:\quad \frac{\partial \psi }{\partial y}=0,\quad \theta =0,\quad \chi =0. \end{aligned}$$
(32)

Usually the disturbance propagates in wave-like form. Hence, the plane wave solution of Eqs. (28)–(32) is expressed as

$$\begin{aligned} \psi =\mathfrak {R}\{if(y)e^{i[ax-\lambda t]}\}, \quad \theta =\mathfrak {R}\{h(y)e^{i[ax-\lambda t]}\},\quad \chi =Le\mathfrak {R}\{q(y)e^{i[ax-\lambda t]}\}. \end{aligned}$$
(33)

where \(\mathfrak {R}\) implies real part, a is the wave number, \(\lambda =\xi +i\omega \) is a complex parameter. f, h and q are complex functions. Let us substitute Eq. (33) into Eqs. (28)–(32) to obtain,

$$\begin{aligned}&f''-a^2f+a(h+Ra_\mathrm{S}\,q)=0, \end{aligned}$$
(34)
$$\begin{aligned}&h''-(a^2-i\xi )h+iRa_\mathrm{H}\,\cos \gamma [\{2Ge(1-y)-1\}f'-(1-y)ah]-aT_b'[y]f=0,\qquad \end{aligned}$$
(35)
$$\begin{aligned}&q''-(a^2-iLe\varLambda \xi +iRa_\mathrm{H}a(1-y)\cos \gamma )q-af\frac{dC_B}{dy}+Sr(h''-a^2h)=0, \end{aligned}$$
(36)
$$\begin{aligned}&y=0:\quad f=h'=q=0, \end{aligned}$$
(37)
$$\begin{aligned}&y=1:\quad f'=h=q=0. \end{aligned}$$
(38)

The final set of Eqs. (34)–(38) define an eigenvalue problem where Ra is the eigenvalue. By varying the value of \(\gamma \), different types of rolls can be obtained. \(\gamma =\frac{\pi }{2}\) will produce longitudinal rolls, whereas the oblique rolls are represented by \(0\le \gamma <\frac{\pi }{2}\). The transverse rolls are represented by \(\gamma =0\). The aim of this study is to analyze the marginal stability of the basic flow for which \(\xi \) can be set to 0. Also in case of longitudinal rolls (\(\gamma =\frac{\pi }{2}\)), setting \(\omega =0\) reduces the system of Eqs. (34)–(38) to a real-valued eigenvalue problem.

2.5 Numerical Solution

Equations (34)–(38) is solved using sixth-order Runge–Kutta method coupled with the shooting method. For a set of given parameters \((a,\,Le,\,Ge,\,Sr,\,Ra_\mathrm{S},\,Ra_\mathrm{H},\,\varLambda )\), the eigenvalues Ra and \(\omega \) can be evaluated. Then, the critical Rayleigh number \(Ra_\mathrm{cr}\) is calculated by finding the minimum of the function Ra(a). The solutions are obtained using the Mathematica 9.0 software.

2.5.1 Validation of the Results

To validate the present solution a comparison has been made between the results given by Barletta and Storesletten (2010) and tabulated in Table 1. The critical Rayleigh numbers for longitudinal rolls are obtained. The parameters \(Ra_\mathrm{S}\) and Sr are taken to be zero. The thermal and solutal diffusivity are considered as equal.

Table 1 Comparison between the results obtained by Barletta and Storesletten (2010) and present results with \(Ra_\mathrm{S}=0,\,Sr=0,\,Le=1,\,Ge=0.5\) for longitudinal rolls
Full size table

It is found that the present results are correct up to three decimal places. Nield (1968) studied the double-diffusive convection in a porous layer under a set of different boundary conditions. A Fourier series method is used to calculate the thermal and solutal Rayleigh numbers. He mentioned that if the upper boundary is open and at constant pressure and constant temperature, the lower rigid boundary is subjected to a constant heat flux, then critical Rayleigh number and wavenumber in the case of thermal convection will be \(Ra_\mathrm{cr}=17.65\) and \(a_\mathrm{cr}=1.75\), respectively. This results are verified by Barletta and Storesletten (2010). They have considered a special case with \(Ra_\mathrm{H}\rightarrow 0,\,Ge=0\) and found \(Ra_\mathrm{cr}=17.65365\) and \(a_\mathrm{cr}=1.749861\). In the above considered problem taking \(Ra_\mathrm{S}\rightarrow 0, Sr=0\) and \(Le=1\) along with \(Ra_\mathrm{H}\rightarrow 0,\,Ge=0\), it is obtained that \(Ra_\mathrm{cr}=17.65365\) and \(a_\mathrm{cr}=1.749359\).

3 Discussion of the Results

The governing parameters, horizontal Rayleigh number (\(Ra_\mathrm{H}\)), solutal Rayleigh number (\(Ra_\mathrm{S}\)), Lewis number (Le), Gebhart number (Ge) and Soret parameter (Sr), are varied to show the effect of different internal and external circumstances. The value of the parameter \(\varLambda \) is taken as 0.5 throughout the calculation.

3.1 Effect of Lewis Number

The effect of Lewis number on the system both in the presence and absence of the Soret parameter is seen through Figs. 2, 3 and 4 with \(Ra_\mathrm{S}=1,\,Ra_\mathrm{H}=1\). Le is taken from 0.1 to 10. It is verified that the effect of Lewis number does not change with further increase in its value when \(Ra_\mathrm{S}\) and \(Ra_\mathrm{H}\) are unchanged. Figure 2 corresponds to the case when \(Sr=0\), i.e., the case of thermosolutal convection with negligible Soret effect. It is seen that the critical Rayleigh number increases with Le. Moreover, the longitudinal rolls remain unaffected by the change in Lewis number. Since for longitudinal rolls \(\gamma =\frac{\pi }{2}\), the governing Eqs. (34)–(38) become independent of Le when \(Sr=0\). The longitudinal rolls are more unstable than the oblique rolls. As Le increases, thermal diffusion becomes dominant than solutal diffusion and the effect of Le on \(Ra_\mathrm{cr}\) becomes more prominent for oblique rolls. The effect of Lewis number remains unchanged in the presence of viscous dissipation as seen in Fig. 2b.

Fig. 2
figure 2

Effect of Lewis number on \(Ra_\mathrm{cr}\) when \(Sr=0, Ra_\mathrm{S}=1, Ra_\mathrm{H}=1\). (a) Ge = 0, (b) Ge = 0.5

Full size image
Fig. 3
figure 3

Effect of Lewis number on \(Ra_\mathrm{cr}\) when \(Sr=-\,0.1, Ra_\mathrm{S}=1, Ra_\mathrm{H}=1\). (a) Ge = 0, (b) Ge = 0.5

Full size image

The effect of negative Soret parameter is shown in Fig. 3 by taking \(Sr=-\,0.1\). A similar trend as in \(Sr=0\) is seen for \(Sr=-\,0.1\), i.e., \(Ra_\mathrm{cr}\) increases with Le. The critical Rayleigh number of longitudinal rolls also changes with Le unlike the case of \(Sr=0\). The longitudinal rolls are the preferred mode of instability for all values of Lewis number. Viscous dissipation shows a destabilizing effect. A similar effect of the Lewis number is seen for \(Sr=0,\,-\,0.1\) in the work by Narayana et al. (2008) where the Soret-driven convection induced by inclined thermal and solutal gradients is dealt.

Fig. 4
figure 4

Effect of Lewis number on \(Ra_\mathrm{cr}\) when \(Sr=0.1, Ra_\mathrm{S}=1, Ra_\mathrm{H}=1\). (a) Ge = 0, (b) Ge = 0.5

Full size image

To show the effect of positive Soret parameter Sr is chosen as 0.1 and presented in Fig. 4. Unlike the case of non-positive Soret parameter, \(Ra_\mathrm{cr}\) decreases with Le. The longitudinal rolls are more unstable when \(Le\le 1\). But if Lewis number is greater than 1, i.e., \(\alpha >D\), the preferred mode for the onset of instability changes. In this scenario the transverse rolls are more unstable compared to the longitudinal rolls. The destabilization nature of viscous dissipation prevails even for positive Soret parameter.

As the longitudinal rolls are the preferred mode of instability in most cases, in the next sections the effects of horizontal Rayleigh number, solutal Rayleigh number and Soret parameter are investigated on longitudinal rolls.

3.2 Effect of Horizontal Rayleigh Number (\(Ra_\mathrm{H}\))

In the next section, the change in the critical wavenumber (\(a_\mathrm{cr}\)) and critical Rayleigh number (\(Ra_\mathrm{cr}\)) of longitudinal rolls for different values of \(Ra_\mathrm{H}\) is presented in Figs. 5 and 6, respectively, by taking \(Ra_\mathrm{S}=1\) and changing the Lewis number and Soret parameter. Since the critical Rayleigh number is unaffected by the Lewis number when \(Sr=0\), only results corresponding to \(Le=1\) is presented for \(Sr=0\). Both \(a_\mathrm{cr}\) and \(Ra_\mathrm{cr}\) increase with \(Ra_\mathrm{H}\) irrespective of the Soret parameter.

Fig. 5
figure 5

Effect of horizontal Rayleigh number on \(a_\mathrm{cr}\) for different values of the Soret parameter and Lewis number, \(Ra_{_\mathrm{S}}=1\). (a) Ge = 0, (b) Ge = 0.5

Full size image
Fig. 6
figure 6

Effect of horizontal Rayleigh number on \(Ra_\mathrm{cr}\) for different values of the Soret parameter and Lewis number, \(Ra_{_\mathrm{S}}=1\). (a) Ge = 0, (b) Ge = 0.5

Full size image

The effect of Lewis number on the flow changes when \(Ra_\mathrm{H}\) takes larger magnitudes. From Fig. 4, it is seen that \(Ra_\mathrm{cr}\) decreases with the increase in Le when Soret parameter is positive (\(Sr=0.1\)). A same trend is seen here for \(Ra_\mathrm{H}<20\), i.e., Lewis number shows a destabilizing effect. But as the horizontal Rayleigh number increases further, the critical Rayleigh number increases with an increase in Le even for \(Sr=0.1\). When \(Ra_\mathrm{H}\) is very high and also \(Le>1\), the maximum to minimum solute concentration difference between the boundaries increases. This leads to a stabilizing concentration gradient. As a result thermal critical Rayleigh number increases.

An opposite effect is seen in case of negative Soret parameter. For smaller values of \(Ra_\mathrm{H}\), the flow gets stabilized with the increase in Le. However, when \(Ra_\mathrm{H}>20\), a decrease in \(Ra_\mathrm{cr}\) and an increase in \(a_\mathrm{cr}\) is seen with a rise in Le. The horizontal Rayleigh number shows a stabilizing effect for \(Sr=-\,0.1,\,0,\,0.1\). This stabilizing nature of \(Ra_\mathrm{H}\) is also seen in case of pure thermal convection with an upper open boundary (Barletta and Storesletten 2010). Since the presence of Soret parameter does not alter the basic temperature and velocity profiles, the basic velocity is always in the direction of the applied temperature gradient. The fluid moves in such a way that there is a heating along the upper boundary. This results in a stabilizing effect of the horizontal temperature gradient.

Fig. 7
figure 7

a Streamlines, b isotherms, c isosolutes for \(Ra_{_\mathrm{S}}=1, Ra_\mathrm{H}=50, Le=5\)

Full size image

3.3 Convective Rolls

There is a possibility of different flow patterns due to the involvement of a large number of parameters in the governing equation. The effects of horizontal Rayleigh number (\(Ra_\mathrm{H}\)), solutal Rayleigh number (\(Ra_\mathrm{S}\)) and Lewis number (Le) on the convective rolls, i.e., streamlines, isotherms and isosolutes of longitudinal rolls, are presented through Figs. 7, 8, 9, 10, 11 and 12.

Fig. 8
figure 8

a Streamlines, b isotherms, c isosolutes for \(Ra_{_\mathrm{S}}=1, Ra_\mathrm{H}=15, Le=0.1\)

Full size image

In Fig. 7 the effect of higher value of \(Ra_\mathrm{H}\) is seen on convective rolls with smaller Sr, viz. \(Sr=-\,0.1,0,0.1\), respectively. When \(Ra_\mathrm{H}\) is very large (\(Ra_\mathrm{H}=50\)), the streamlines and isosolutes both are pushed downward for small values of Soret parameter. When horizontal Rayleigh number is very high, the flow experiences a streamwise heating. As a result the convective rolls get pushed to the lower boundary irrespective of the Soret parameter. However, when Sr is large and \(Le\ge 1\), the effect of Sr on convective rolls may change. This is described in the following figures by taking larger values of Sr and varying Le.

Fig. 9
figure 9

Convective rolls for \(Ra_{_\mathrm{S}}=1, Ra_\mathrm{H}=15, Le=1\). a Sr = \(-0.5\), b Sr = 0.5

Full size image

Lewis number has no effect on the convective rolls in case of \(Sr=0\). The positive and negative Soret effects are represented by choosing \(Sr=0.5\) and \(Sr=-0.5\), respectively. The shapes of the streamlines in Fig. 8a are because of the open boundary. From Figs. 8, 9, 10 it is seen that the convective rolls are affected most by the Soret parameter for \(Le\ge 1\) because whenever \(Le<1\), the solutal diffusivity is greater than thermal diffusivity and the solutal diffusion dominated the thermal diffusion showing a lesser intense Soret effect. With the increase in thermal diffusion, the concentration gradients are modified due to the Soret parameter. As a result the isosolutes are becoming two-cellular when thermal diffusivity and solutal diffusivity are equal (\(Le=1\)). As Le increases further, the thermal diffusion becomes dominant. Since \(Sr=0.5\) is also large, the plumes will rise due to the positive Soret effect, and eventually the streamlines and isosolutes are seen more to the top layer. The presence of the negative Soret parameter pushes the streamlines closer to the lower boundary when \(Le>1\).

Fig. 10
figure 10

Convective rolls for \(Ra_{_\mathrm{S}}=1, Ra_\mathrm{H}=15, Le=5\). a Sr = \(-0.5\), b Sr = 0.5

Full size image

The change in isotherms for both \(Sr=0.5\) and \(Sr=-0.5\) is not much significant when \(Le\le 1\) since in that case thermal diffusivity is less than the solutal diffusivity.

Fig. 11
figure 11

a Streamlines, b isotherms, c isosolutes for \(Ra_{_\mathrm{S}}=-5, Ra_\mathrm{H}=1, Le=0.1\)

Full size image

Figures 11 and 12 show the effect of Soret parameter on the convective rolls in the presence of positive and negative solutal Rayleigh number, respectively. In the previous cases the convective rolls exhibit a significant change for thermal diffusion when \(Le\ge 1\). The streamlines, isotherms and isosolutes vary due to Soret parameter in the presence of solutal Rayleigh number also. This change becomes prominent when \(Le<1\).

Fig. 12
figure 12

a Streamlines, b isotherms, c isosolutes for \(Ra_{_\mathrm{S}}=5, Ra_\mathrm{H}=1, Le=0.1\)

Full size image

From Fig. 11 it is seen that when \(Ra_\mathrm{S}=-5\), only the streamlines and isosolutes for \(Sr=-0.5\) are pushed downward. However, the change in isosolutes is much smaller compared to the streamlines. The isosolutes in case of \(Sr=0.5\) are pushed upward. A complete opposite effect is seen in case of the positive solutal Rayleigh number in Fig. 12. Here the streamlines corresponding to positive Soret parameter are seen more near the lower boundary. Consequently, the isosolutes for \(Sr=0.5\) are pushed downward and for \(Sr=-0.5\), they are pushed upward.

3.4 Effect of Soret Parameter on Longitudinal Rolls

The effect of Soret parameter on longitudinal rolls in the presence of both horizontal and solutal Rayleigh number is reported in Table 2 with \(Ra_\mathrm{S}=1,\,Ra_\mathrm{H}=5\) and in Table 3 with \(Ra_\mathrm{S}=-1,\,Ra_\mathrm{H}=5\). By the definition of the parameters \(Ra_\mathrm{S}\) and Sr, it is evident that they are interconnected. When \(Ra_\mathrm{S}>0\) and \(Ra_\mathrm{H}\) is small, the solutal gradient generated due to negative (positive) Soret coefficient is aiding (delaying) the destabilization process. As a result the critical Rayleigh number decreases or increases with negative or positive Soret parameter, respectively. The critical wave number (\(a_\mathrm{cr}\)) is a decreasing function of Sr.

In Table 3, the solutal Rayleigh number is considered as negative. From Table 2 and Table 3 it is clear that the effect of Soret parameter reverses with the change in sign of the \(Ra_\mathrm{S}\). The presence of open boundary makes the system more prone to instability in case of both thermal and double-diffusive convection with significant Soret effect.

3.5 Effect of Solutal Rayleigh Number

The effect of the solutal Rayleigh number on the onset of instability is presented in this section taking \(Ra_\mathrm{H}=5\). When \(Sr=0\), the calculations are made taking \(Le=1\) and presented in Table 4. \(Ra_\mathrm{cr}\) decreases as \(Ra_\mathrm{S}\) takes positive values from negative ones. Viscous dissipation is showing a destabilizing effect in case of \(Sr=0\).

Table 2 Effect of Soret parameter on longitudinal rolls, \(Ra_\mathrm{S}=1, Ra_\mathrm{H}=5, Ge=0\)
Full size table
Table 3 Effect of Soret parameter on longitudinal rolls, \(Ra_\mathrm{S}=-1, Ra_\mathrm{H}=5, Ge=0\)
Full size table
Table 4 Effect of solutal Rayleigh number when \(Sr=0, Le=1, Ra_\mathrm{H}=5\)
Full size table

When \(Sr=0.1\), an increase in \(Ra_\mathrm{S}\) raises \(Ra_\mathrm{cr}\) (Fig. 13). The effect of solutal Rayleigh number is more prominent when \(Le<1\), i.e., \(\alpha <D\), and this effect lessens significantly with an increase in Le. This follows naturally as the solutal Rayleigh number is associated with the vertical concentration gradient. The effect of Lewis number changes as \(Ra_\mathrm{S}\) changes from negative to positive. For \(Ra_\mathrm{S}<0\), the critical Rayleigh number increases with Le. However, \(Ra_\mathrm{cr}\) decreases markedly with Le as \(Ra_\mathrm{S}\) becomes positive. The viscous dissipation takes a significant role when Sr is positive and \(Ra_\mathrm{S}\) has high magnitudes. Viscous dissipation at first shows a destabilizing effect. But when \(Le>5\) and \(Ra_\mathrm{S}>10\), viscous dissipation starts to exhibit a stabilizing nature.

Fig. 13
figure 13

Effect of solutal Rayleigh number when \(Sr=0.1, Ra_\mathrm{H}=5\). a Ge = 0, b Ge = 0.5

Full size image
Fig. 14
figure 14

Effect of solutal Rayleigh number when \(Sr=-\,0.1, Ra_\mathrm{H}=5\). a Ge = 0, b Ge = 0.5

Full size image

A complete opposite effect of \(Ra_\mathrm{S}\) is seen in case of negative Soret parameter (Fig. 14). The critical Rayleigh number decreases with \(Ra_\mathrm{S}\). The role of Le is also different for \(Sr=-\,0.1\). An increase in Lewis number destabilizes the flow when \(Ra_\mathrm{S}<0\), but stabilizes the flow for positive \(Ra_\mathrm{S}\). The viscous dissipation displays a destabilizing role for all values of \(Ra_\mathrm{S}\) when \(Sr<0\).

4 Conclusions

The effect of positive and negative Soret parameter on the thermosolutal convection in the presence of significant viscous dissipation is investigated with the help of linear stability analysis. The upper boundary is considered as open and assumed to be at constant pressure. The lower boundary is subjected to a heat flux, and there is a horizontal temperature gradient along the upper boundary. Constant concentrations are maintained at two horizontal boundaries. The basic flow induced by horizontal temperature gradient is subjected to infinitesimal disturbance to study the stability of the system. The Lewis number has no effect on the stability of the flow when \(Sr=0\). Viscous dissipation shows a destabilizing effect except when Sr is positive and solutal Rayleigh number also takes positive values of higher magnitudes. The effect of Lewis number on longitudinal rolls depends on the values of other governing parameters. The longitudinal rolls are the preferred mode of instability for non-positive values of the Soret parameter. In case of positive Soret parameter the preferred mode of instability depends on the value of the Lewis number. It is seen that for \(Sr=0.1\), when \(Le\le 1\), the disturbances grow as longitudinal rolls. But if \(Le>1\), the transverse rolls are the preferred mode for the onset of convective instability. The effect of the Soret parameter on the convective rolls also depends on the intensity of horizontal thermal gradient, Lewis number and the solute concentrations at the boundaries. When \(Ra_\mathrm{S}>0\), positive Soret parameter shows a stabilizing effect, whereas negative Soret parameter destabilizes the flow. An opposite effect of the Soret parameters are seen when \(Ra_\mathrm{S}<0\).